Ansoft有限长螺线管空间磁场仿真分析
2023-02-14乌兰察布供电公司王亚杰
◇乌兰察布供电公司 李 阳 王亚杰
为进一步研究螺线管空间磁场分布,通过前者对多种磁场分析软件的研究探讨,选择求解度更高的有限元Ansoft软件对螺线管磁场进行仿真研究。通过二维和三维螺线管模型静态磁场仿真,对比和讨论不同长度和螺距螺线管仿真结果。根据电磁感应定律和螺线管磁场的特点,验证了结果的准确性,证明利用Ansoft软件对电磁场仿真分析更直观、便利,具有先进性和实用性,为分析、设计和研究电磁设备提供一定的参考。
1 引言
随着电气产品结构复杂化和对产品性能要求的提高,传统的方法难以满足实际需要。近年来利用有限元软件对磁场仿真的应用研究成为工程人员和研究人员的一大研究热点,有限元法成为研究磁场问题的主要手段。以往对磁场的研究基于麦克斯韦方程进行解析计算,采用模拟试验法得到近似结果,与实际存在一定差距,且这些传统方法对现代设备难以满足[1-2]。直流螺线管产生的磁场常常得到广泛应用,它具有磁场强度和场形分布易于调节、杂散场小、在大工作空间内可获得高场强等优点[3-4]。由此可见,螺线管磁场的计算特别重要。本文据毕奥-萨伐尔定律和安培环路定理对螺线管电磁场进行仿真分析,采用有限元Ansoft软件对螺线管仿真分析,对螺线管建立不同参数的静态磁场仿真模型,对比分析磁场特性,结果更具有先进性。
2 螺线管计算模型
将密绕带电螺线管线圈等效为n个电流环,电流环置于直角坐标系xy平面,图1表示一个圆环,圆心与坐标原点重合,面法线与z轴重合,环的半径为a,环内电流为I,由于电流仅有切向分量,向量磁位也仅有切向分量Aθ,Aθ与θ无关,电流环在空间P点产生的磁感应强度B可表示成如下形式[5-9]。
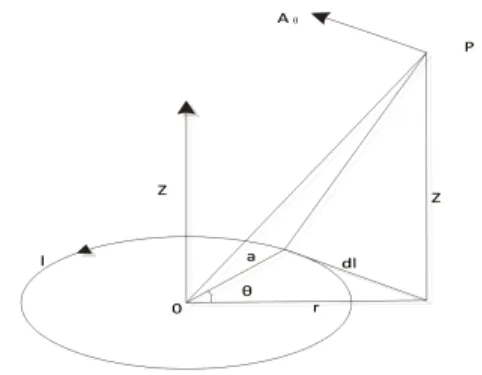
图1 圆环电流向量磁位


式中,K和E分别为第一类和第二类完全椭圆积分;
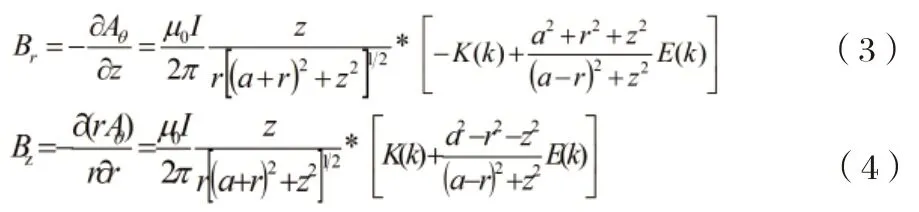
进一步分析可得圆环电流平面内部的磁感应强度。
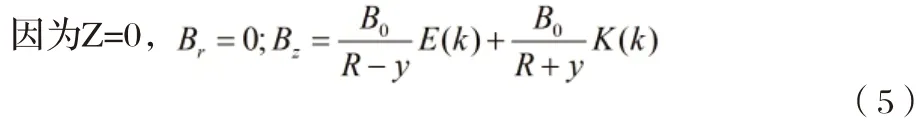
圆环中心处的磁感应强度:

3 螺线管Ansoft有限元仿真模型
Ansoft有限元软件主要用来设计分析电机、变压器等电气设备在不同工作环境下的工作特性,可建立二维模型、三维模型并对其在静态磁场、瞬态磁场、涡流场、交直流电场仿真分析[10]。本文在Ansoft软件中对螺线管模型进行二维平面和三维实体静态磁场仿真分析。二维平面建模更容易、占内存小、计算速度快,但对问题的描述有一定的局限性;三维实体分析法建模比较复杂、占内存大、计算速度比较慢,但能够模拟所有工程实例,应用更加广泛。因此,本文对螺线管分别建立二维和三维模型,在三维模型下直观得到空间磁场分布,并在二维模型下讨论不同螺线管的磁场特性[11]。
3.1 三维模型的建立
静态磁场下建立10匝螺线管模型,端面施加电流激励,得到螺线管磁通分布及磁力线空间分布图如下所示。与以往二维抽象的磁场分布不同,三维模型可以更加形象的表现出螺线管在三维空间的磁场分布。

图2 三维模型磁通密度
从图3磁力线分布中可以看到,磁力线在螺线管中心区域最密集,成闭合回路且互不相交。磁力线空间分布特性与教材一致,在求解域边界处仍然存在微弱的磁力线。以上分析也说明Ansoft有限元软件对电磁场仿真的准确性和可靠性。

图3 三维模型磁力线
3.2 二维模型
所有物体都是三维的,由于螺线管关于中心轴对称且在二维和三维下结果相近,因此选用二维模型进行分析求解,所研究的螺线管三维轴对称模型简化成理想二维平面模型。
建立二维模型,螺线管截面为单个独立圆,螺线管内径R=5cm,螺距a=1mm,匝数N=13匝,螺线管长度L=5cm。每匝圆面设为串联连接,螺线管材料为copper,每匝施加相同电流激励I,求解域的边界和外边界施加气球边界条件,并进行自适应网格剖分,通过在matrix中设置可求得螺线管自感值,最后求解得出螺线管磁场分布,计算结果如下所示。
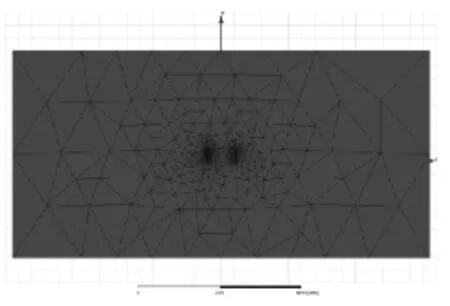
图4 二维模型自适应剖分

图5 二维模型电场线分布
通过matrix设置求得13匝线圈的电感系数为144.11uH,电感值等于电感系数乘以匝数的平方,即得螺线管电感值。为更好地研究螺线管磁场与L/R的关系,本文建立四种螺线管模型L/R分别为0.4、3、9,仿真结果如图6所示。
图6可得有限长螺线管磁场的磁力线不相交,且成闭合曲线,螺线管内磁力线的方向几乎平行螺线管轴线,且随着螺线管长度L的增加,螺线管内磁力线愈发平行轴线。随着螺线管长度的增加磁力线在数值上在不断变大,当螺线管趋于无限长的极限情况时,整个管内空间的磁力线方向就平行于螺线管轴线,螺线管外侧的磁力线由近及远逐渐减小,边缘效应也越小。从图6(c)看出,多条磁力线从螺线管侧壁穿出,是由于有限长螺线管在某处产生磁场的矢量和不等于零。随着螺线管长度的增加,以上的分析不仅说明螺线管内外的磁场分别是匀强磁场,还说明管内外的磁场都必须是有限磁场,通过对螺线管磁场的仿真中发现,只有在至少7倍的求解域中螺线管磁场才能被完全正确表示。
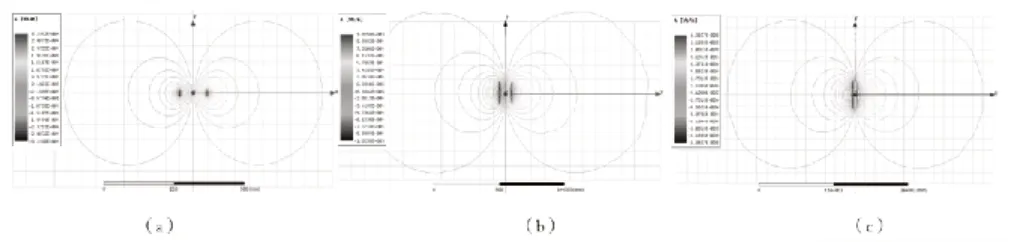
图6 二维模型磁力线线分布
本文对比螺线管长度L与半径R比值,观察讨论螺线管内部和周围磁场分布,仿真结果如下所示。
螺线管空间磁场关于xy呈二维正态分布,螺线管中心磁场强度最大,远离中心磁场强度逐渐减弱,图7中圆形线圈在其中心点的磁场达到最大值Bm,在中心点附近很小的范围内轴向磁场变化较小,且从L/R比值可以看出,随着有限长螺线管长度的增加,中心区域场强愈发平整,且Bm值越大。随着y轴上的点不断地远离中心点,其轴向磁场急剧下降,在无穷远处,磁场强度迅速减弱至趋近为0。
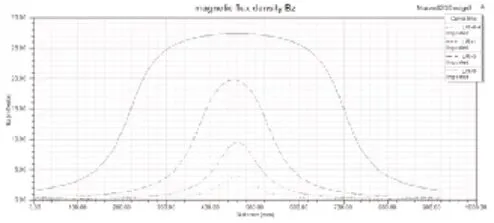
图7 轴向磁通
从图8中得到在靠近螺线管壁时,磁场沿径向分量已超过沿轴线分量,磁场先增加然后迅速下降最终达到螺线管中心磁场最大值Bm。对比四种模型可以看出,L/R越大螺线管中部匀强磁场区域越大,接近管口Bx与Bm差值逐渐减小,且减小幅度较大(曲线较陡)。当L/R=9,中心磁场变化很小,理想情况下L/R为无穷大时此种现象可完全消失,且磁场在轴线方向的最小值和图7的最大值Bm一样。在端点位置,磁场发生很大的变化是因为螺线管电流对磁力线的“约束”导致磁力线在螺线管边缘的剧变,反映磁力线密度变大,磁感应强度变大,也就是螺线管在端部磁力线反常,即边缘效应。

图8 径向磁通
从图9可以看出,在螺线管中点位置是不存在磁场的,且磁场关于坐标原点对称,大小随着中点位置向两端不断增大,到螺线管边界达到最大值,随后到达无从远处衰减为0。
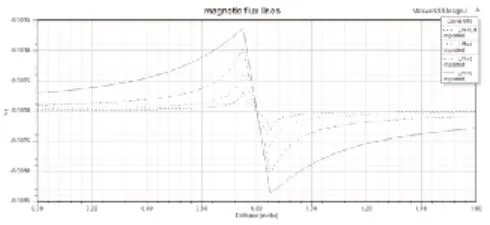
图9 径向磁力线
以上分析可得出对密绕型螺线管L/R值至少等于9,边缘效应可忽略不计。当螺线管为无限长时,螺线管内靠近两端的磁场不均匀区域相对于整个螺线管内的区域越来越小,两端内有明显侧边缘效应的区域趋于零,此时整个螺线管内都为匀强磁场。
3.3 不同螺距
选取上文所用第二组模型L/R=1,a=1建立螺线管不同螺距a=7模型进行仿真对比分析,仿真图如下所示。
从图10可见:当螺距较大时,在轴线附近的中心区域内磁感应强度B的分布也不是均匀的,与密绕圆柱形螺线管B的分布有着明显的区别。当螺距较大时,螺线管端部的边缘效应更加明显,且漏磁严重导致磁场最大值Bm明显变小,除中间匀强磁场段轴线上相同位置的磁场越大。
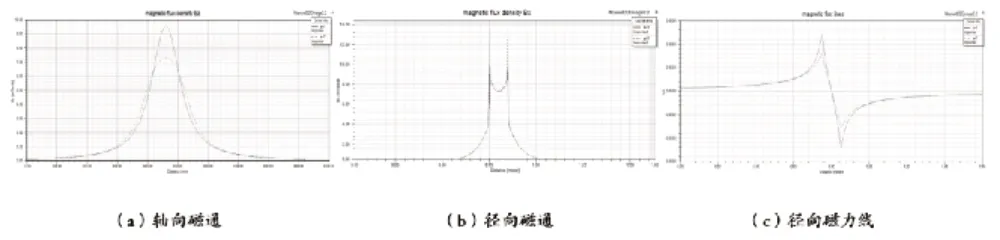
图10 不同螺距仿真对比
4 结束语
本文采用有限元Ansoft软件对有限长螺线管空间磁场再探索,并利用毕奥一萨伐尔定律推导出空间磁感应强度的数学表达式。运用有限元的方法建立了螺线管二维磁场仿真模型,绘制不同螺线管长度和半径比时的磁力线分布和磁感应强度分布,及螺线管边缘效应的磁场分布。通过螺线管磁场测定进行了计算机实验仿真,并对仿真数据分析,仿真结果分析完全符合螺线管磁场理论特性,验证了有限元法对螺线管磁场仿真模型的有效性,为螺线管磁场相关研究奠定了一定的软件分析基础,对螺线管模型和空间磁场的深入理解有一定价值。
