基于人工神经网络的仪器地震烈度预测模型研究

李水龙, 陈以伦, 于伟恒, 周施文

(1. 福建省地震局, 福建 福州 350001; 2. 上海逸舟信息科技有限公司, 上海 200065)

0 引言

作为一种新兴的减小震害的方式,地震预警得到了广泛的关注,其有效时间为首次P波触发开始到破坏性S波到达城市或重点工程之间。在这段宝贵的时间之中,若能快速获得有用的地震信息,就能尽早提供预警服务,留出较长的反应时间。因此,充分利用已触发台站有限的波形信息就显得非常重要。仪器烈度参数是烈度快速评估的重要参数可直接影响到灾害评估的准确性以及救援物资的分配。基于对宏观烈度与地震动参数之间的定量关系研究成果[1],仪器烈度预测是地震预警中的一部分,它是在地震发生后通过有限的波形数据对最终的仪器烈度进行预测,从而做到在破坏性地震波到来之前,快速预测出震中附近区域受地震影响的程度,对人员的逃生以及灾后的应急救援有着重要的意义。

根据工作方式的不同,地震预警可以分为现地预警和异地预警。在现地预警中,一般无法获得准确的震源参数,仪器地震烈度的预测仅仅靠P波触发后几秒的地震动信息来完成。国内外很多学者利用P波触发后3 s内的数据与完整波形的PGA、PGV、仪器烈度等参数进行相关性分析[2]。这种方法比较简单实用,并利用了所有触发台站的信息。但考虑到地震事件的复杂性,每个台站的场地条件和震中距离都不相同,单纯的线性模型很难完整预测所有台站的峰值参数。另外,也有部分研究人员通过分析烈度的变化规律,通过特征函数的形式描述烈度的变化情况[3-4]。这种方法打破传统预测方法,结合了地震预警参数,考虑了震源距离对预测结果的影响。这种预测方法有着更好的精度,但需要提前计算震源距才能实现,其对近震台站的预测时效性不佳。

异地预警能够通过地震定位和震级测算方法计算出地震三要素[5-8],然后通过地震动参数的衰减关系预测地震波未到达区域的烈度[9-10],这种方法充分考虑了震源参数,并通过统计得到的衰减关系预测烈度,不需利用所有台站的波形信息就能预测出整个烈度场的烈度分布。但这种方法的时效性不如现地预警,有较大的预警盲区,且预测出的烈度分布一般是按一定规律分布,等烈度线一般为圆形,而实际的烈度分布往往是不均匀的,更有一些烈度异常区域的存在。因此,通过衰减关系的预测也有一定的局限性。

本文希望能够结合现地预警和异地预警的优势,在既能保证预测的时效性,又能充分将地震动参数和震源参数相结合的前提下,能够对地震仪器烈度进行实时预测。在此之前,人工神经网络算法已经被广泛应用到了地震研究中[11]。首先,在地震预报中,国内外学者发现BP神经网络可以很好的反映震前出现异常的种类和异常时间与未来地震参数之间的较强非线性关系[12-13];在震害预测方面,相关研究结果表明,神经网络是一种有效提高预测精度的方法[14-15];在震相识别和震相划分方面,有学者认为人工神经网络用于确定地震震相和到时是十分有效的,特别是对于信噪比较高的地震记录效果更好。可以看出,BP算法在地震预报方面有着较多的研究成果[14],在地震预警方面的研究却相对比较少。

本文将BP神经网络算法引入地震预警当中,希望通过P波触发后20 s内的7个参数对仪器烈度进行实时预测,并在获得震源距和震级之后将其应用到烈度预测中,以获得更好的预测效果。

1 数据选取

1.1 数据来源

人工神经元网络算法的训练结果很大程度取决于训练样本的好坏,因此在数据选择的时候需尽量考虑所有的情况,既要有足够的数据量,又要保证数据分布的均匀性[15-16]。本文首先选用了日本KiK-net强震台网记录的1999—2016年发生的629次地震事件进行研究,震级分布从MS3.7到MS9.0。其中7级以下地震事件较多,并且分布均匀,7级以上的地震事件相对较少。对此,本文重点分析了8级以上的两个地震,分别是2003年9月26日的8.0级地震和2011年3月11日的9.0级地震,它们均发生在日本海域,最近触发的台站分别为103 km和145 km。在分析测试中,发现这两次地震无法准确预测陆地上发生的大震的烈度情况,如汶川地震,尤其在预测近台仪器烈度的时候会出现误差较大的状况。因此,决定在样本中加入2008年5月12日汶川地震、1999年9月21日集集地震、2014年8月3日鲁甸地震的强震数据。所有用于测试的地震事件共有632次。

1.2 数据选择

如果数据选择过多,类型各异,会增加网络训练的难度,同时提高预测的难度;如果数据选择过少,又无法提供足够的样本类型,使训练样本没有说服力。在台站的选择上,尽可能选择有较大预测价值的台站,排除没有意义和异常台站的影响。应当考虑以下几点:

(1) 日本KiK-net强震观测台网的每个台站分为地表台和井下基岩台,本次使用的全部为井下基岩台的三分向数据,后加入的三次地震因为数据来源有限,是地表台的数据;

(2) 按照《中国地震烈度表(GB/T 17742—2020)》的说明[17],剔除实际计算当中烈度小于1的台站;

(3) 震源深度较深的地震传播路径复杂且影响没有浅源地震大,本文将预测的重点目标放在浅源地震上,剔除震源深度大于50 km的地震触发台站;

(4) 小震和震源距较大的大震不是预警研究的对象,在记录筛选中,按照地震的影响范围找到了震级和震源距的关系,如下式:

lgR≤0.86+0.17M

(1)

式中：R为震源距,M为震级;在数据选择的过程中也要剔除出现丢头、数据异常等情况的台站。按照这样的规则,本文一共选择了2 231个台站。这些台站的震源距和震级以及烈度的关系分布如图1和图2所示。本文选取的台站分布尽可能均匀,并且能代表绝大多数地震台站的触发情况。

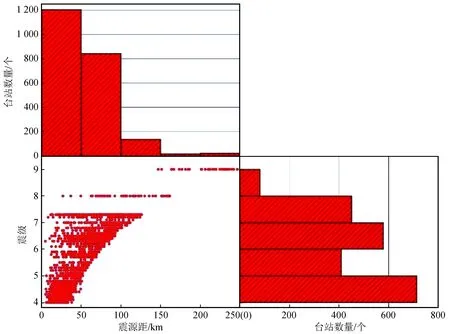
图1 本文选用地震事件台站震源距和震级的关系Fig.1 Relationship between hypocentral distance of stations and magnitude of seismic events selected in this study

1.3 数据处理

按照《中国地震烈度表(GB/T 17742—2020)》中提供的仪器烈度计算方法,对上述所选原始数据进行基线校正,使用0.1～10 Hz的带通滤波器进行滤波处理,计算三分向合成的加速度记录和速度记录,计算三分向合成的地震动参数PGA和PGV,并通过STA/LTA和AIC方法对P波震相进行自动捡拾。计算烈度公式如下:

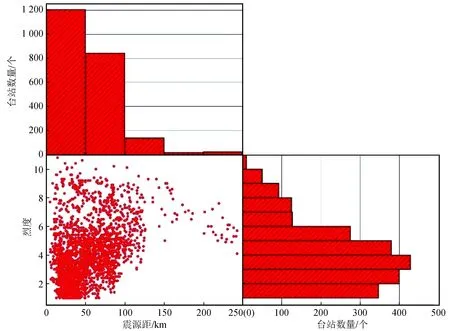
图2 本文选用地震事件台站震源距和烈度的关系Fig.2 Relationship between hypocentral distance of stations and intensity of seismic events selected in this study

IA=3.17lg10(PGA)+6.59

(2)

IV=3.00lg10(PGV)+9.77

(3)

(4)

其中:IA为使用PGA计算的烈度值,IV为使用PGV计算的烈度值,II为综合计算得到的烈度值。

烈度的范围1～12,并保留一位小数。本文也统计了按照此公式计算后台站的震源距和烈度的关系分布(图3)。可以看出,在震源距150 km以内的台站数据当中,烈度分布从1～11较为均匀,对于震源距大于150 km 的台站数据按照式(1)只会有较大地震的台站分布。

2 三种地震仪器烈度预测模型

人工神经元网络(Artificial Neural Networks，下文简称ANN)是在现代神经科学的基础上提出和发展起来的,可以描述多个参数之间复杂的非线性关系。地震的成因复杂,传统烈度预测模型大部分是线性模型,很难准确的描述地震参数和烈度之间的关系[18-21]。我们希望利用ANN方法找到相关参数和烈度之间合适的非线性关系来提高预测精度,并最终选择了向后传播算法(Back-Propagation),其可通过最速下降法不断修正输入参数的权值和阈值,以得到最优的结果。

2.1 BP神经网络参数选择

地震动参数的类型很多,其含义也不尽相同[22-23],其中包含与周期、幅值、强度相关的参数。作为神经网络的输入参数,需要与地震的破坏程度有着紧密的关系,并且能够进行实时计算。最终,选择如下7个参数:

(1)Pa:垂直向波形实时测定的加速度峰值,与幅值相关,与烈度计算直接相关。

(2)Pv:垂直向波形实时测定的速度峰值,与幅值相关,与烈度计算直接相关。

(3)Pd:垂直向波形实时测定的位移峰值,与幅值相关,与PGV有着良好的线性关系,也可以用来预测震级[24]。

(4)A0.5:三分向合成有效峰值加速度,与幅值相关,比峰值PGA更为可靠,能更好的反映地震动强度[25]。

(5)CAV:累计绝对速度[26],用三项加速度计算,与强度相关,可作为判断地震是否具有破坏性的关键指标,计算公式如下:

(5)

式中:a(t)为加速度时程;tmax是加速度时程记录的时间长度。

(6)IA:阿尔亚斯烈度,用三分向加速度记录计算,与强度有关,一定程度上能反映震害程度,计算公式如下:

(6)

式中:a(t)为地震动加速度时程;T0为加速度时程的持续时间;g为重力加速度。

(7)afft:垂直向波形实时测定的卓越频率,与周期相关,能反映地震波包含的频率信息。

除地震动参数之外,也可以利用地震预警中已经计算出的震源参数。试验表明,加入震源参数可以将计算精度进一步提高。选择震源距d和震级M作为附加参数,能够更好的预测结果。

2.2 三种模型建立

本文建立的模型均采用包含输入层、隐含层、输出层的三层模型。三种模型的输入参数如下:

(1) 从首台P波触发开始,即可从实时波形数据中计算出上述7个地震动参数,它们随着地震的发生不断更新,为保证预测的时效性,将这7个参数作为模型一的输入参数。

(2) 在地震预警当中,随着更多台站的触发,可以得到地震三要素的结果,其中地震定位结果先于震级结果产出,模型二的输入参数定为上述7个地震动参数加上实际震源距d,共8个参数。

(3) 当预警定位结果和震级结果都有产出之后,模型三的输入参数定为7个地震动参数加上实际震源距d和震级M,共9个参数。

隐藏层节点数和输入层节点数关系紧密,理想的节点数应当既有良好的拟合效果,又不会出现过度拟合现象,最终三个模型的隐含层节点数依次定为5、5和6。三个模型的输出层均为一个节点,即最终需要预测的仪器烈度值。两个传递函数均选择对数S型传递函数logsig,其具体形式为:

(7)

三个模型的示意图如图3所示。

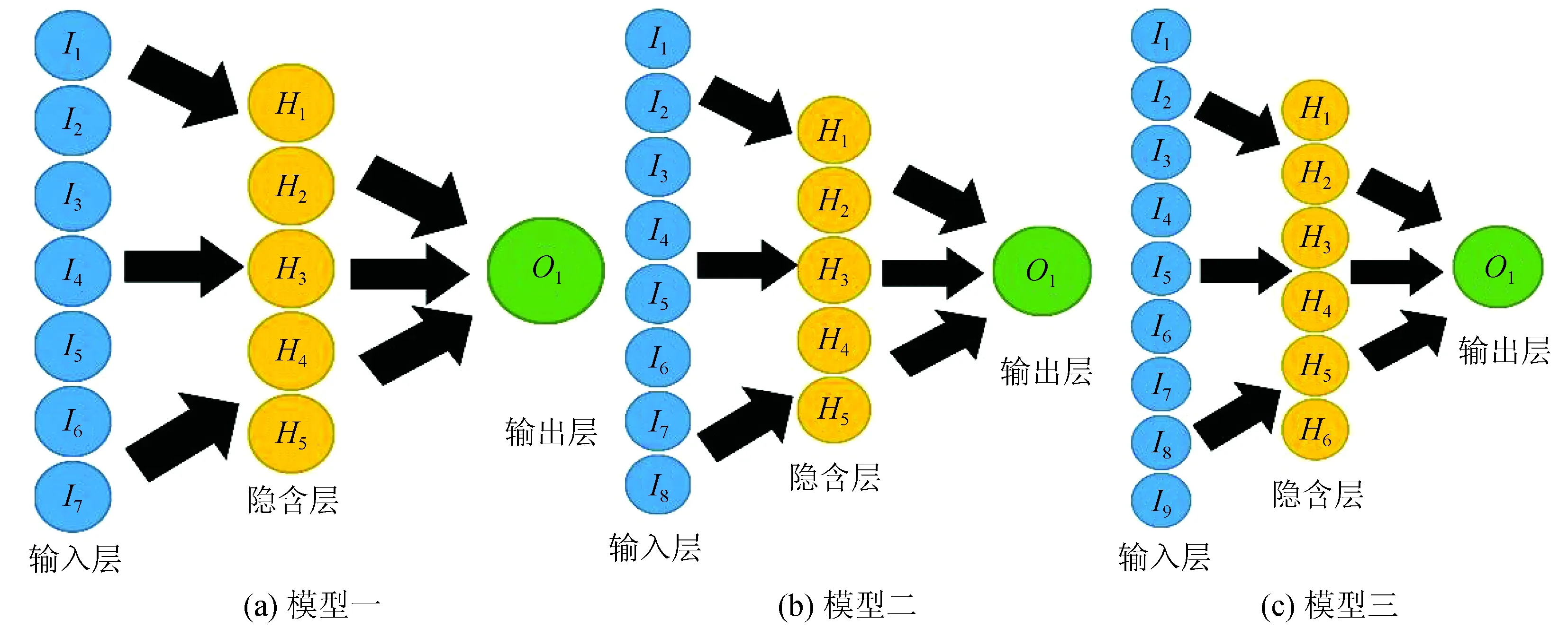
图 3 三个模型的示意图Fig.3 Schematic diagram of the three models

在这三个模型中,模型一从首台P波触发开始即可使用,有着最好的时效性,尤其对于近震台站的预测有着一定的优势,可以作为台站实时阈值报警的参考依据;模型二中加入震源距作为输入参数,预测结果更好,但时效性不如模型一,需事先知道比较可靠的震源距结果才能使用,可以利用此种模型计算出的烈度和震级的关系,预测烈度震级,作为预测震级的参考;模型三中加入了震级的因素,预测时有着最好的结果,但其时效性不如前两种,对于近震台触发的前几秒未获得地震三要素之前不可用,在获取比较可靠的震源距和震级信息之后方能使用,可以用作前两种模型的信息更新和地震影响区域的烈度分布场的预测。

2.3 三种模型的计算和结果分析

首先,将第二节中所选的2 231个台站数据进行分类,按照6∶2∶2将所有数据随机分为训练样本、确认样本和试验样本。其中,训练样本有1 339个,用于对网络的训练;确认样本有446个,用于对训练过程中误差的监视,一般随着隐含层节点数的增加,训练样本的拟合精度会越来越高,确认样本的拟合精度则会在节点数为某个值时达到最大,当节点数进一步增加时,它的精度会下降,隐含层节点数的确定就是通过不断尝试,找到使训练样本和确认样本的拟合精度都比较高的值;试验样本有446个,可以用来比较不同网络模型的好坏。分类时需保证不论按照震源距、烈度或震级,三个样本中台站数量的分布都大致均匀,这样才能使训练样本有代表性。

经过测试和分析,用于预警的黄金时间是台站触发后的20 s之内,在这段时间内,烈度的预测值有明显的提高。因此,计算所有台站触发后1～20 s内每秒的7个地震动参数值,并提取实际震源距、震级和仪器烈度信息。在训练之前,找出9个参数的取值范围,对它们进行归一化处理,烈度值也需归一化到0～1之间。随后,即可利用训练样本对网络进行训练,由系统随机的赋予权值和阈值,并用L-M优化算法对其进行调整,以达到最优结果。为了尽量避免局部最小值和全局最小值有过大的差异,对每个网络的计算都从多个随机选定的初值点出发,进行多次计算。对于每种模型,都由1～20 s的参数分别进行拟合,因此共有60个网络模型。本文对算出的每种模型进行结果统计,用每个网络来预测训练样本和确认样本中每个台站烈度差值绝对值,并以其平均值作为判别标准,具体结果如图4所示。

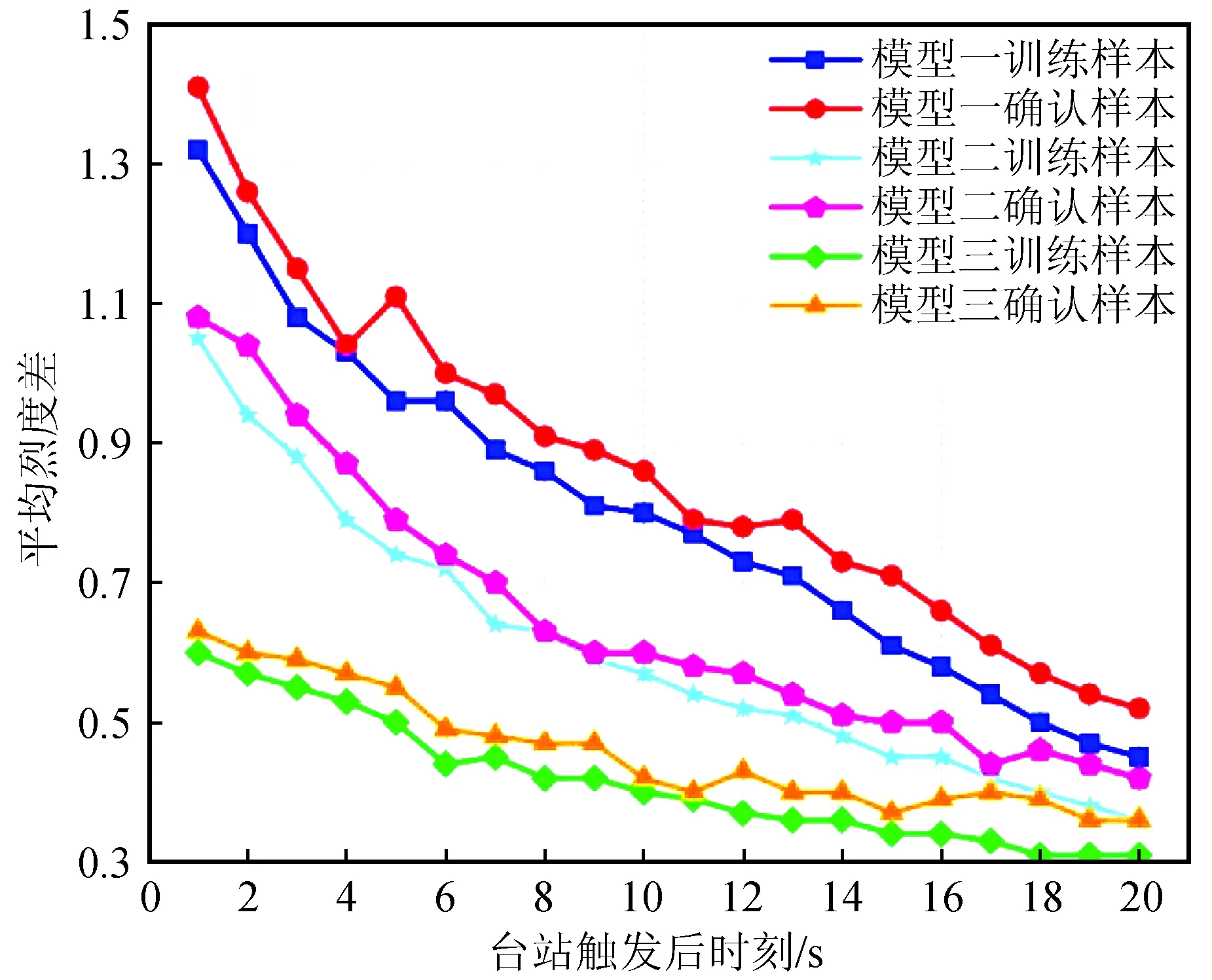
图4 三个模型 1～20 s的预测平均烈度差绝对值的变化Fig.4 Change of the absolute value of average intensity error from 1 to 20 seconds predicted by three models

从图4中可以得出如下结论:

(1) 预测结果随时间增加而变好,前15 s效果增长的较快。

(2) 模型三预测结果优于模型二,模型二优于模型一,模型三从第一秒开始就有着较好的预测结果,说明准确的震源距和震级对烈度的预测有着很大的提升作用。

(3) 训练样本的预测结果略优于确认样本,说明模型对于没有用于训练的同类型数据也能进行较好的预测。

(4) 三个模型的预测结果到20 s时均小于0.6,在实际应用中对结果取整后大部分烈度差都为0或1。

在实际预测中,若烈度差绝对值能在1以内,对其取整的值也在1以内,是地震预警中能接受的较好结果。图4中,分析的是烈度差平均值的变化,与此同时也对烈度差的分布情况进行了分析。首先,利用三种模型对训练样本有代表性的第1 s和第20 s的平均烈度差比进行详细分析(图5),其他中间时刻的情况没有一一列举,它们是一个逐渐变化的过程。从图5中可以看出,第1 s的时候,通过模型三预测烈度差小于1的比例要明显高于其他两个模型,模型一的预测效果不佳,7.92%的预测烈度差大于 3;到第20 s时,三个模型的预测效果比较好,预测烈度差小于1的比例均高于90%,有着较为准确的结果。其次,本文分析了 1～20 s三个模型对训练样本的预测烈度差小于1的比例(图 6),可以一定程度上反应图5中未列举的中间时刻的情况。从图6中可以看出,烈度差小于1的比例呈逐渐上升的趋势,前10秒上升的速度较快,其中模型一上升的速度最明显。这意味着三种模型的预测情况随着时间的推移都将有一个大的提升,并在20 s时都达到90%以上,预测结果良好。

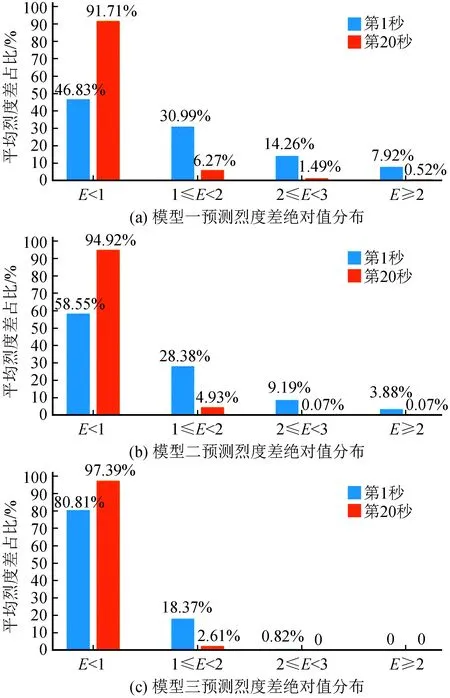
图5 三个模型第1 s和第20 s预测烈度差绝对值的分布 Fig.5 Distribution of the absolute value of intensity error in 1 and 20 seconds predicted by three models

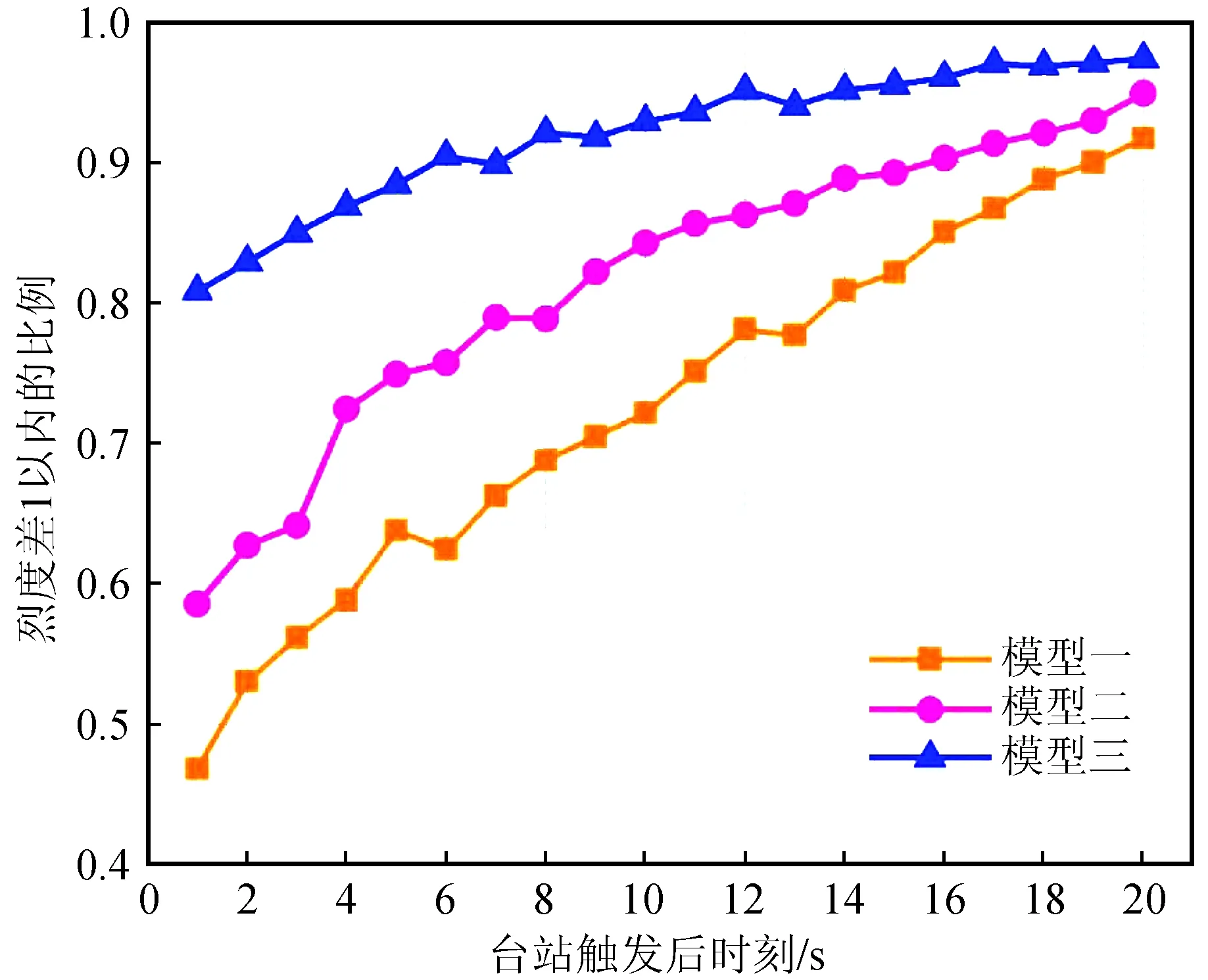
图6 三个模型预测烈度差在1以内的比例变化Fig.6 The proportion change of intensity error within 1 predicted by three models

3 模型的应用

为了检验模型的预测效果,本文利用福建测震台网信息记录到的两次震级较大的地震对模型进行检验,它们分别是 2013年9月4日发生于福建仙游的5.0级地震和2016年2月6日发生于台湾高雄的6.7级地震。福建仙游地震震中位于福建省内,并且震中附近的测震台站密度较高,近震台站均在福建省内。台湾高雄地震震中位于台湾岛上,震中附近台站均为台湾台站,分布较为稀疏。值得注意的是,这两次的地震数据都是速度记录,不同于统计时使用的加速度记录。这也能够检验利用强震记录计算出的网络模型在预测测震记录的时候能否使用。另外,也对其他测震和强震的地震数据进行了测试,这两次地震的结果是有代表性的。

3.1 仙游 5.0 级地震预测效果

按照上述台站筛选规律,此次地震触发台站在范围之内的有 XYXY、PTLC、YTGY、YTGL 四个台站。应用上述三个模型对它们进行烈度预测,结果如表1所列。

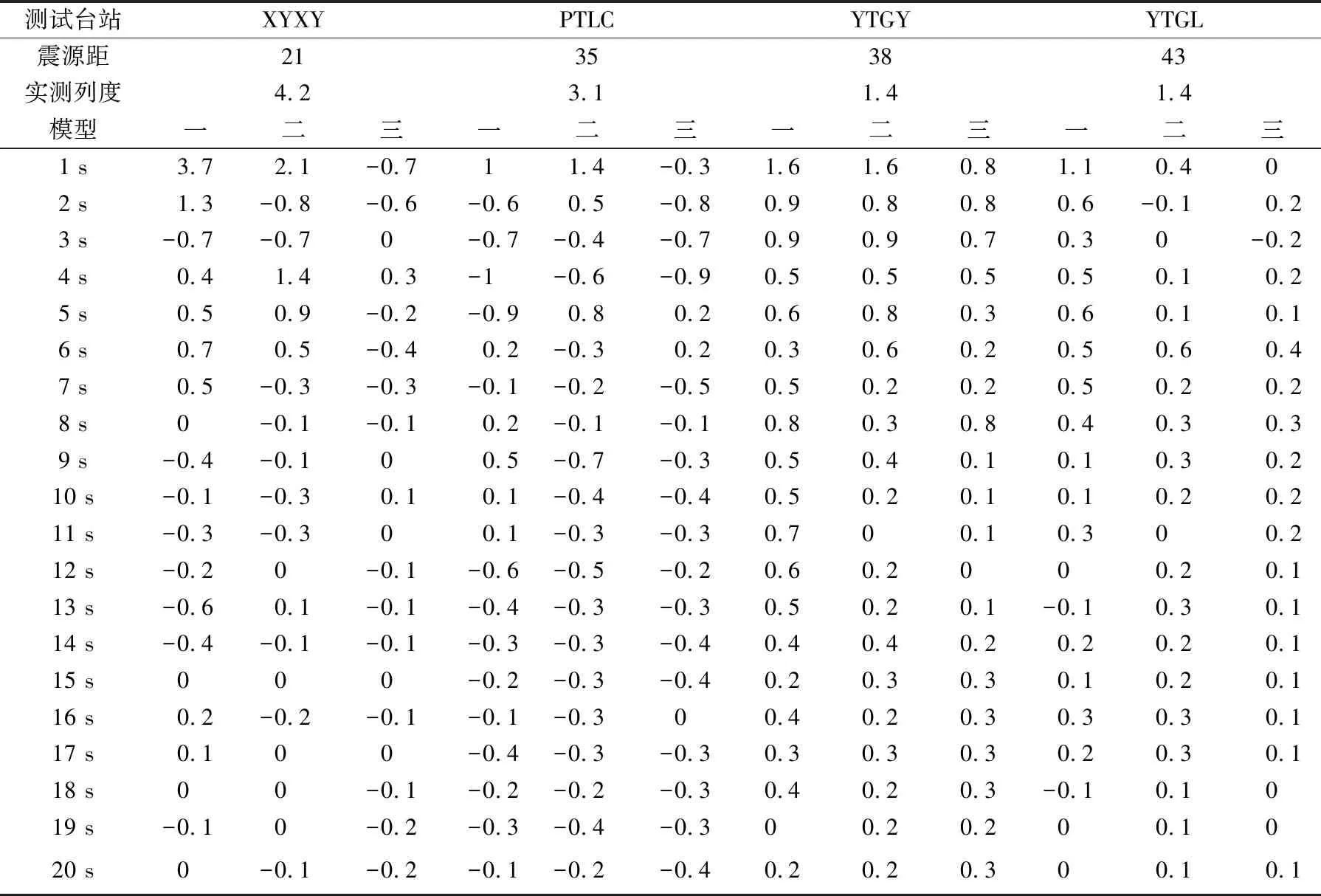
表1 对仙游地震四个触发台站的烈度预测偏差

从表1中的结果看,上述模型对此次地震的预测有着较为理想的效果。实际计算时,烈度值取整数,以此为标准,上述4个台站的预测结果中46.25%和真实值相同,49.58%和真实值偏差为1,剩余 4.17%和真实值偏差大于1。此次预测中,模型一和模型二在1 s时的预测偏差较大,但随着时间推移,这一问题基本得到解决;模型三的预测效果一直较好,预测偏差一直在1以内。这次地震的预测结果符合之前对三种模型预测情况的分析,说明这次地震的情况在训练样本之内。

3.2 高雄 6.7 级地震预测效果

按照上述台站筛选规律,此次地震触发台站在范围之内的有 MASB、TPUB、TWGB、YULB 四个台站。应用上述三个模型对它们进行烈度预测,结果如表2所列。

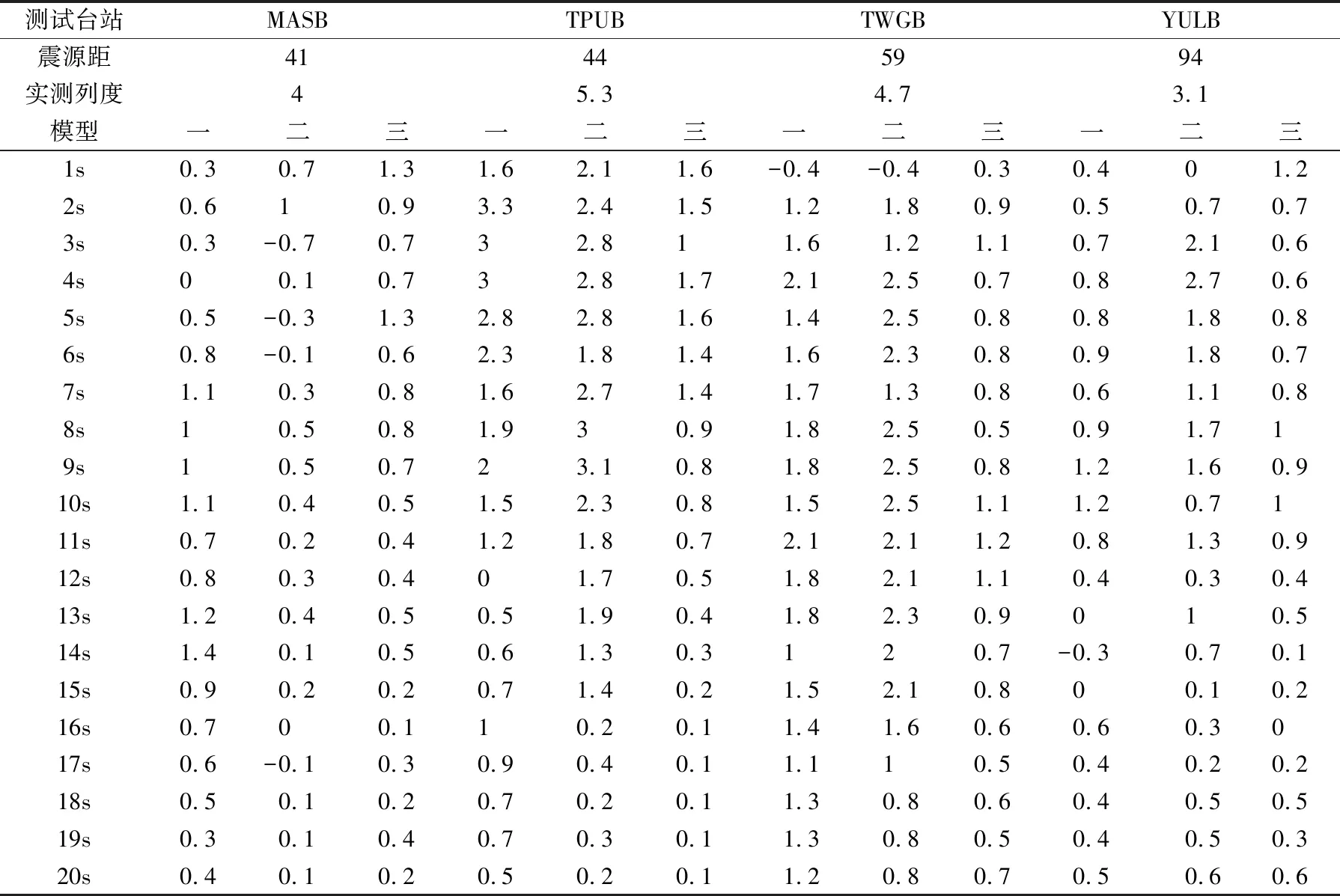
表2 对高雄地震四个触发台站的烈度预测偏差

从表2中的结果看,上述模型对MASB和YULB两个台站的预测有着较为理想的效果。若烈度值取整数,上述4个台站的预测结果中23.33%和真实值相同,53.33%和真实值偏差为1,剩余23.33%和真实值偏差大于1。从数值上看,其预测结果不如仙游地震,主要在对TPUB和TWGB两个台站的预测情况不佳。对这种情况进行分析后,发现虽然此次地震也在台网内,但台站的分布较为稀疏,且利用到的台站存在着限幅和漂移的问题。这也说明,台站的质量一定程度上影响着预测的准确性。

4 讨论与结论

本文将BP神经网络算法引入到地震预警的烈度预测中,通过对大量震例样本的分析得到了可靠的网络模型,并以此模型为例,对两次地震的台站进行烈度预测,得到如下结论:

(1) 将BP神经网络算法引入到烈度预测之中,能够自首台触发开始对台站烈度进行实时预测并更新,有着很好的时效性和准确性。本文计算了触发后20 s的数据,预测的平均误差结果也逐渐减小,可以应用到实际工作中。

(2) 本文提出的三种预测模型虽都用来预测烈度,但各有特点。模型一的时效性最好,可用作阈值报警;模型二利用震源距的信息,时效性和准确性居中,可用作烈度震级的预测;模型三利用震源距和震级的信息,精度最高,若对整个地震影响区域进行插值计算,即可获得较为精确的烈度场分布情况。

(3) 由于大震资料有限,本文将KiK-net台网中的基岩台数据中加入了汶川、集集、鲁甸三次地震的强震数据,但这些数据并不都是基岩台所记录,有可能会对训练的结果造成影响,这一点还需更多地震记录来做检验。

(4) 本文所用台站使用了一定的范围限制,这样做的目的是尽量选择震中附近有较大利用价值的台站数据,排除其他干扰,使训练结果更加理想。

此外需要注意的是,BP算法也有不确定性的问题。首先,这种方法所寻找的是局部最优点,这与初值所选的位置有关,虽然本文通过使用多个初值值点运算取最优的方式一定程度上解决了这个问题,但并不能保证结果一定是全局最优。其次,本方法的学习能力和样本的选择有很大关系,使用不同的样本将会训练出完全不同的结果,本文尽量做到选择各种震级分布、各种震源距分布、各种烈度分布的台站数据,以保证样本的完整性,但仍不能包括全部的可能性。在之前的测试中,并未加入汶川地震、集集地震、鲁甸地震的强震数据,然而训练出的网络模型并不能够对汶川地震进行准确的预测,偏差较大,究其原因是因为汶川地震作为陆地上的8级的地震,并不在训练样本之中得到体现,这也说明了样本选择的重要性。如果在后续的研究当中发现了新类型的地震数据,可以将其加入训练样本中重新训练,以得到更好的网络模型。最后,考虑到地震预警的时效性,在模型二和模型三中用到的震源距和震级信息是预警中产出的结果,在保证其准确性的前提下方能使用,不然可能影响预测的结果。对于这些问题,还需要更多震例的测试和更深入的研究才能确定。