交通荷载作用红层填料道路沉降细观模拟

2023-02-13余云燕刘武通付艳艳罗崇亮朱明哲

地震工程学报 2023年1期

余云燕, 刘武通, 付艳艳, 罗崇亮, 朱明哲

(兰州交通大学土木工程学院, 甘肃兰州 730070)

0 引言

红层泥岩土作为G6京藏高速兰州—海石湾段路基的主要填料,具有易风化、稳定性差、遇水软化等特点,在工程完工后常出现路基变形和不均匀沉降等严重病害。运用数值模拟方法研究其作为路基填料在荷载作用下的沉降,对探究其病害形成机理及后期病害处治有重要意义。

对公路软弱路基沉降变形的相关仿真研究,主要基于ADINA[1]、COMSOL[2-3]、FLAC3D[4-5]及ABAQUS[6-10]等有限元及有限差分法软件。许多学者[1-9]对级配不良等特殊路基在冻融、交通荷载等因素影响下的沉降和应力变化规律展开了研究,严战友等学者[10-13]则在交通荷载作用下公路路面的应力、位移响应的研究领域颇有成果。对交通荷载作用下路基的累积变形及响应等问题的理论研究[14-18],大量学者基于弹性理论解积分、半解析有限元法、以Timoshenko梁理论为基础的两阶段分析法等方法陆续展开。

因土体具有碎散性、多相性和自然变异性等特点,传统的基于连续介质力学理论的有限元软件无法准确体现土体作为散体材料在荷载作用下位移不连续等现象,而基于颗粒离散元理论的PFC在研究土体的碎散特性及细观表现方面具有明显的优势,能高效求解计算105数量级颗粒间的位移-速度的传递方程,能较为直观地观察模型内部力的传递情况及颗粒的动态变化,能更真实地模拟土体的力学行为。

基于离散元软件PFC的相关研究,着眼于渗流模拟[19-21]、边坡[22-25]和管桩沉桩过程[26-29]等方面的研究成果颇丰。在道路路基方面,不少学者运用PFC对道路结构层展开相关研究。贺莹[11]基于PFC离散元软件,建立二维沥青路面结构数值模型,模拟在冲击荷载及振动荷载作用下沥青路面结构力学性能。王朝辉[12]利用PFC构建了多层沥青路面结构模型,分别研究了冲击荷载、简谐激励下的沥青路面力学响应。严战友[30]运用PFC研究了车辆荷载和不同温度作用下的沥青路面结构层细观力学响应及颗粒变化规律。赵宏伟[31]基于PFC建立沪宁高速地基土模型,进行不同荷载工况的路基路面数值模拟,得出地基土侧向位移规律。

综上所述,基于细观力学理论的离散元法,交通荷载作用下分析路基路面的细观力学行为研究文献较少,而且在红层泥岩土作为路基填料的离散元模拟存在空白。因此,本文基于颗粒流软件PFC(Particle Flow Code)进行二次开发,对G6京藏高速兰州—海石湾段道路的沉降问题展开研究,建立二维路基路面模型并采用冲击荷载与半正弦荷载模拟车辆荷载对路基的作用,通过高阶迭代计算演变,得到各层颗粒的位移和应力时程曲线,揭示其内部应力变化、层间位移变化趋势,较为真实模拟实际工况下道路在交通荷载作用下的力学行为,对该路段常年发生沉降的原因、机理及后期路基病害整治有积极作用。

1 路基路面模型及加载

1.1 路基路面模型

建立二维路基路面模型,由面层(上面层、下面层)、基层(上基层、下基层和基底层)和红层填料组成,共分为六层,如图1所示。由于模型计算过程中每个计算步都需考虑力与位移的平衡,颗粒数目过大,计算时间长,为了减少颗粒间计算量,在保证计算精度的前提下,根据以往研究,路床深度80 cm下车辆载荷影响较小,故本模型高度设为115 cm。设定红层填料的接触模型为接触黏结模型,基层和面层的接触模型均为平行黏结模型。颗粒的粘结性能不同,则土体颗粒的破坏模式不同,接触黏结模型和平行黏结模型在黏结破坏后退化为线性接触模型,前者适用于黏结材料,后者适用于刚性材料。

图1 路基路面结构图Fig.1 Subgrade and pavement structure diagram

1.2 加载模型的建立

《公路沥青路面设计规范》[32]规定,路面设计使用双轮组单轴载荷100 kN作为标准载荷,以BZZ-100表示。本文将轮胎载荷视为当量圆形均布载荷,轮胎压力均匀分布在接触面上。沥青颗粒及土颗粒单元由ball单元模拟,轮胎由clump单元模拟,每个clump由9个pebble集结而成;运用ball distribute命令分层生成符合半径、压实度等要求的颗粒,利用property命令赋予其已标定好的细观参数,并压实、削平至符合模型要求的尺寸;各层颗粒完全生成好后,利用contact model命令赋予各层颗粒间的接触模式及接触属性;利用clump replicate及clump.force.apply命令生成“车轮”并对模型施加荷载;利用history命令记录力学响应。clump与ball之间接触模型为线性接触模型;考虑到不同结构层层间的接触对象不同,除路基层以外其余各层层间接触皆为平行黏结模型,底基层与红层路基层层间接触的对象性质差异较大,因此采用线性接触模型;由于离散元软件在处理多种属性颗粒与同一墙体间接触的局限性,在不影响主要分析对象结果的准确性的情况下,土颗粒与墙体间的接触简化为线性接触模型。模型颗粒间接触模型如图2所示,红色线条为线性接触,绿色线条为平行黏结,蓝色线条为接触黏结。图3为设置重力场且平衡后模型的接触力链分布图,受拉力链为绿色,受压为蓝色,线条越粗则接触力越大。由图3可知,由于沥青的胶结作用,模型上部成块状,两侧均为受拉区,沥青层与碎石砂砾层的接触部分,以及碎石砂砾层的两侧,都存在少量受拉区;从整体看,整个路基成拱形,接触力从上至下递增。

图2 接触模式示意图Fig.2 Schematic diagram of contact mode

图3 接触力链分布图Fig.3 Distribution diagram of contact force chain

2 模型细观参数标定

路基路面的宏观参数不能直接在离散元软件中使用,须相应调整各模型对应的细观参数,使其细观参数与试验结果一致。基层的细观参数直接选用王朝辉[12]的标定结果,面层的细观参数由王朝辉[12]的AK-13沥青混合料40 mm×80 mm试样单轴压缩试验结果模拟得到,如图4所示。对红层填料,取自G6京藏高速公路兰州至海石湾方向K1615+100下行线方向维修工程的红层泥岩路基填料,其最优含水率为17.4%,最大干密度为1.769 g/cm3,取最优含水率下压实度为96%的红层填料制备高度为120 mm,直径为61.8 mm的圆柱体试样,采用意大利产WF非饱和土三轴仪,控制50 kPa、150 kPa和200 kPa三种围压,进行三轴UU试验。由于离散元软件无法直接输入土体的宏观参数,因此,基于试验所得的应力-应变曲线,建立三轴UU试验模型,通过不断调整PFC内置细观参数,得到相同工况下的模拟应力-应变曲线,使试验结果与模拟曲线的形态、应力峰值趋近一致,得到的土颗粒细观参数用以建立模型,试验结果及模拟曲线如图5所示。

图5 围压为50 kPa、150 kPa、200 kPa下红层填料UU试验与模拟曲线对比Fig.5 Comparison between UU test and simulation curves of red beds filling under confining pressures of 50 kPa,150 kPa,and 200 kPa

由图4可知,模拟曲线趋势与试验曲线基本一致,峰值应力相近,说明调试的细观参数可较好地模拟沥青混合料的力学性能。由图5可知,围岩为50 kPa的红层填料三轴应力-应变曲线为稳定型,围压为150 kPa、200 kPa的三轴应力-应变曲线呈硬化型,模拟曲线的变化趋势与试验结果一致,峰值应力也相近,可认为标定的红层填料细观参数合理。路面结构层颗粒的半径,参照文献[12]选取。对红层填料颗粒的半径,基于室内颗粒筛分试验得到的结果,并综合考虑颗粒半径对模型运算效率的影响,选取质量占比60%以上颗粒半径分布范围,即6～8 mm。各层颗粒半径分布服从正态分布。对各层颗粒间的阻尼系数,设置其细观参数damp,参数damp在标定过程中影响试样的破坏模式及形态,对路基红层填料颗粒,设置damp为0.7,对路面结构层颗粒,设置damp为0.4。经过一系列迭代运算,路面各结构层的基本参数如表1所列,红层路基填料的基本参数如表2所列。

表1 路面各结构层基本参数

表2 红层填料基本参数

3 冲击荷载及半正弦荷载作用下路基路面结构动态响应

3.1 加载过程模拟

路基路面结构的动态响应考虑两种荷载作用,分别为冲击荷载和半正弦荷载。

当汽车位于定点位置正上方时,为最不利工况,为研究该种情形下路基路面结构的力学响应,参照以往的研究[11],可考虑冲击系数1.2,设置作用时间为0.03 s,对模型施加如图6(a)所示30 kN的冲击荷载,并考虑重力荷载作用。

图6 冲击荷载及半正弦荷载与时间关系曲线Fig.6 Curves of impact load and half-sine load versus time

当汽车以60 km/h的速度行驶时,对路基路面定点位置的影响作用时间约为0.05 s。因此,使用y.app.force命令设置clump车轮的荷载作用峰值为25 kN,频率为10 Hz,对模型施加如图6(b)所示的半正弦荷载,并考虑重力荷载作用。荷载施加完成后增加0.01 s记录颗粒加载后力学行为。

测量圆是用于测定一定范围应力水平的工具,尺寸过大则影响模型初始化平衡的效率,过小则影响试验过程中数据采集的真实性,参照以往的研究[11],设定其半径为2 cm。如图7所示,共布置5个测量圆,其坐标如表3所列。

图7 测量圆示意图Fig.7 Schematic diagram of measuring circle

表3 测量圆坐标表

3.2 冲击荷载作用下路基路面力学响应

从细观角度,研究冲击荷载作用下路基路面的应力和位移随时间的变化规律。

3.2.1 竖向、水平应力时程曲线

采集ID为121～125测量圆的竖向、水平应力在加载过程的时程曲线,如图8～9所示。由图8可知,加载初期,竖向应力时程曲线波动剧烈,这是由于土颗粒发生错动并逐渐压实,随着时间的增长,竖向应力保持恒定,模型整体保持相对稳定状态;随着深度的增加,竖向应力逐渐减小。面层的最大压应力为0.139 MPa,加载后期,路基层压应力已衰减至面层的30%。由图9可知,面层的水平应力最大,拉、压应力都存在,处于复杂的应力状态,基层和红层填料中的水平应力都较小,基层中的水平应力为拉应力,红层填料中的水平应力为压应力,基层的水平拉应力达到水泥稳定砂砾层的极限抗拉强度后会出现裂缝,随着车载的持续进行,裂缝逐渐扩展并延伸至地表。

3.2.2 位移时程曲线

路基路面整体竖向位移即为沉降量,《公路沥青路面设计规范(JTG D50—2017)》[32]规定,在标准轴载作用下,单轴双轮组单侧两轮中间位置的竖向位移可作为路面的弯沉量。

图8 冲击荷载作用下路基路面竖向应力时程曲线图Fig.8 Time-history curve of vertical stress of subgrade and pavement under impact load

图9 冲击荷载作用下路基路面水平应力时程曲线图Fig.9 Time-history curve of horizontal stress of subgrade and pavement under impact load

图10为荷载作用0.03 s后路基路面竖向位移云图,最大沉降发生在两轮胎作用中心点处,为0.063 mm,在深度1.0 m处,红层填料的竖向位移趋近于零。由于周围土体的挤密作用,模型上部两侧颗粒有上移趋势,路基路面整体竖向位移沿荷载作用点向路面以下的土体半空间呈弧形衰减。因基层与红层填料的材料不同,采用的接触模型也不同,因此在位移云图上可以看到基层与红层填料交界面处有明显的界限,在该交界面处竖向位移不连续,基层对红层填料的挤压作用非常明显。

图10 冲击荷载作用0.03 s后路基路面竖向位移云图Fig.10 Vertical displacement cloud diagram of subgrade and pavement after 0.03 seconds of impact load

图11为荷载作用0.03 s后路基路面水平位移云图,由图可知,基层与红层填料交界面处水平位移不连续,出现位移分层现象,最大水平位移位于基层与红层填料的交界面上,该位置受横向约束作用弱于结构层,受上部车轮荷载的挤压作用,土颗粒向两侧滑移作用明显。由于路面的弯沉作用,使得车轮两侧的土颗粒向车载作用位置靠拢,且靠拢趋势沿路面两侧递减。红层填料颗粒的水平位移变化趋势与结构层相同,因为附加应力的衰减,其数值较小。

追踪图12所示10个位置的竖向位移和竖向速度,其坐标位置如表4所列,并绘制了相应位置的时程曲线图。

图11 冲击荷载作用0.03 s后路基路面水平位移云图Fig.11 Cloud diagram of horizontal displacement of subgrade and pavement after 0.03 seconds of impact load

图12 追踪测量颗粒位置图Fig.12 Position of tracking g and measuring particles

表4 追踪测量颗粒坐标表

图13为编号1～5号追踪颗粒的竖向位移时程曲线。由图可知,与室内三轴试验变形规律相似,土体颗粒经历弹塑性变形,前期位移剧增,随着时间的增长,逐渐趋于稳定值,土颗粒发生不可恢复的塑性变形;随着深度的增加,竖向位移逐渐减小,路基层位移约衰减至面层的30%。图13进一步揭示了加载过程中土体颗粒间能量的传递规律,沥青结构层耗能远远大于红层填料路基层。

图13 冲击荷载作用编号1～5号追踪颗粒的竖向位移时程曲线图Fig.13 Vertical displacement time-history curves of No.1-5 tracking particles under impact load

3.3 半正弦荷载作用下路基路面力学响应

3.3.1 竖向、水平应力时程曲线

采集ID为121～125测量圆的竖向、水平应力在加载过程的时程曲线,如图14～15所示。

图14为半正弦荷载作用下路基路面的竖向应力时程曲线图,由图可知,竖向应力随时间的变化趋势总体上符合半正弦荷载形式,加载初期,存在应力集中现象,离地表越近,曲线振荡就越剧烈,这是由于颗粒的挤密作用和应力重分布,因路基层中的测量圆125号离地表最远,其竖向应力最小,且时程曲线的振荡幅度很小,基本保持半正弦荷载形式。

图14 半正弦荷载作用路基路面竖向应力时程曲线图Fig.14 Time history curve of vertical stress of subgrade and pavement under half-sine load

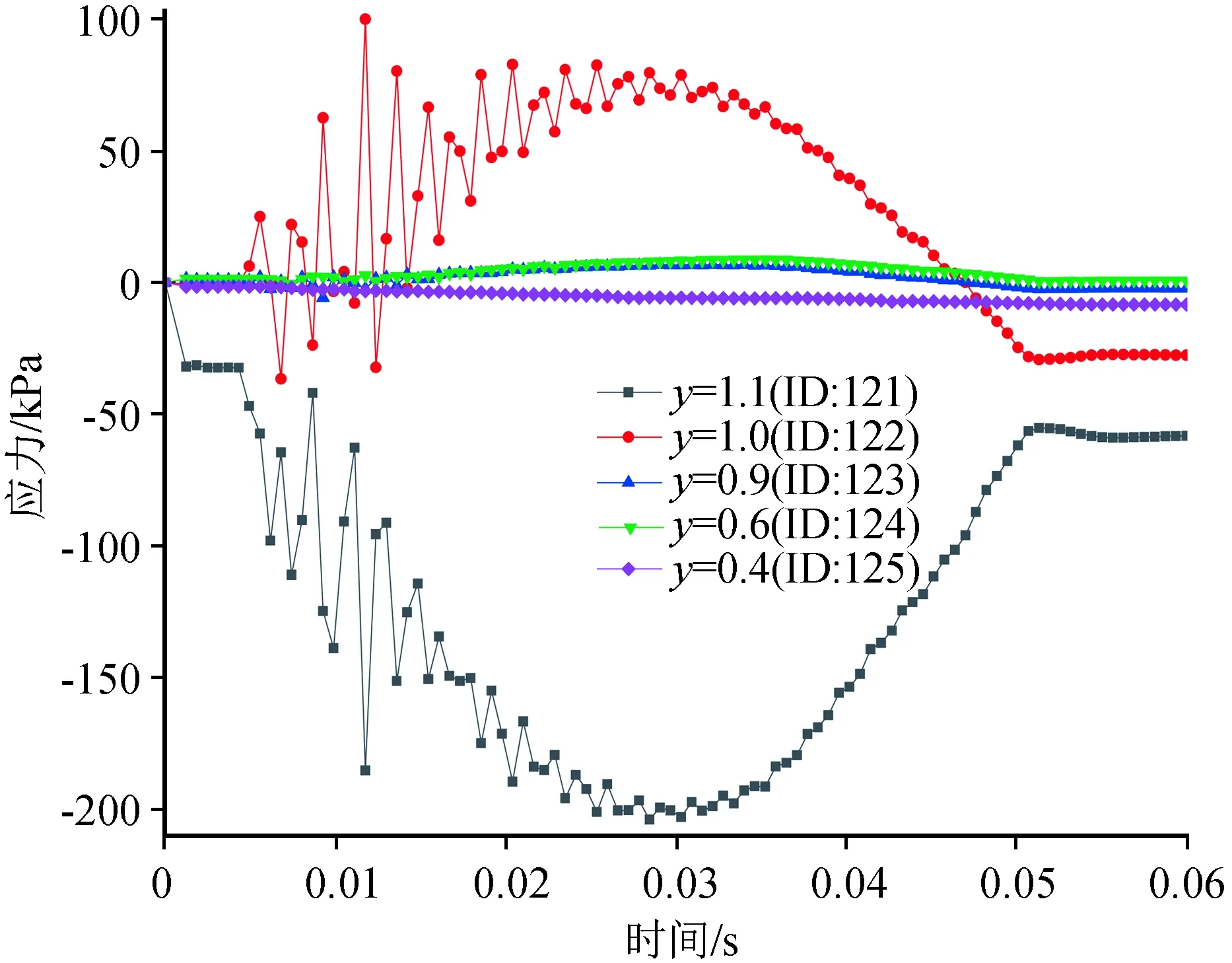
图15 半正弦荷载作用路基路面水平应力时程曲线图Fig.15 Time history curve of horizontal stress of subgrade and pavement under half-sine load

图15为半正弦荷载作用下路基路面的水平应力时程曲线图,可见,面层存在拉、压应力,处于复杂应力状态,且应力数值很大,加载初期,存在应力集中现象,时程曲线振荡;基层主要为拉应力,最大值约0.21 MPa,红层填料层为压应力。基层的拉应力达到水泥稳定碎石层的极限抗拉强度后会出现裂缝,随着车载的持续作用,裂缝会逐渐延伸至地表,这与冲击荷载作用情况相同。因此,在公路运营过程中应定期重点监测该区域裂缝的发生,防止进一步加剧道路的塌陷沉降。

3.3.2 位移时程曲线

图16为半正弦荷载作用0.06 s后路基路面结构竖向位移云图。由图可知,最大沉降发生在车载中心位置,为6×10-3mm,基层与红层填料交界面上竖向位移不连续,结构层中车载中心线附近区域的位移云图呈柱状分布,两侧呈对称状态,路面两端的土颗粒有上移趋势;红层填料层在车载作用区域沉降最大,向两侧逐渐减小,呈盆状分布;基层与红层填料交界面两端的上方,土颗粒有上移趋势,图中呈蓝色。

图17为半正弦荷载作用0.06 s后路基路面结构水平位移云图,由于基底层刚度比红层填料的刚度大,且基底层底部与红层填料层顶部接触面的侧向约束明显比其他部位弱,基层与红层填料交界面处的水平位移不连续,出现水平位移分层现象,在车载作用位置正下方,红层填料底层的土颗粒水平位移最大,并向两侧逐渐递减;基层底面处,离车载作用中心线稍远位置,发生最大水平位移,且向地表逐渐衰减;路基部分使用的模型为接触黏结模型,故当荷载作用在中间位置时,红层填料有向两侧移动的趋势,由于红层填料颗粒间的拉应力强度较低,基层刚度远大于红层填料的刚度,红层填料层更容易发生水平位移,因此,红层填料中的最大水平位移大于基层中的最大水平位移,但从整体上看,二者数值上的差异较小,均属于较低水平。

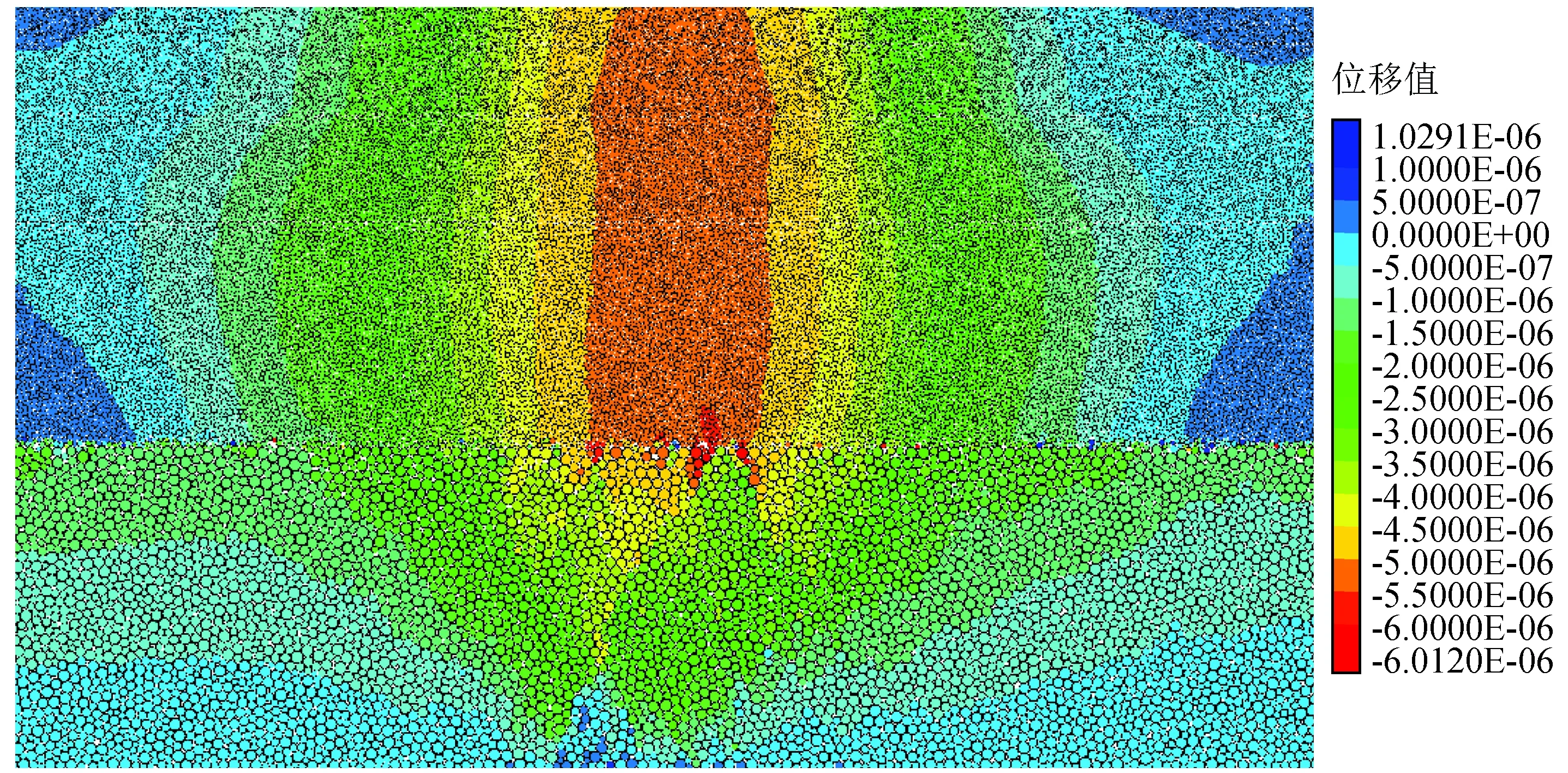
图16 半正弦荷载作用0.06 s后路基路面结构层颗粒竖向位移云图Fig.16 Vertical displacement cloud diagram of particles of subgrade and pavement structure layer after 0.06 seconds of half-sine load

图17 半正弦荷载作用0.06 s后路基路面结构层颗粒水平位移云图Fig.17 Vertical displacement cloud diagram of particles of subgrade and pavement structure layer after 0.06 seconds of half-sine load

图18为半正弦荷载作用编号1～5号追踪颗粒的竖向位移时程曲线图。竖向位移时程曲线的变化趋势与半正弦荷载形式基本相同,加载初期,曲线振荡,随着深度的增加,曲线振荡的时间就越短,位移峰值点出现的时间滞后于半正弦荷载峰值出现的时间约0.005 s,可见车辆行驶后颗粒的弹性恢复变形具有滞后性。因此,在行车过程中保持安全车距对防止道路沉降变形过大有积极作用;面层的最大竖向位移值为0.048 mm,基层的最大竖向位移衰减为面层的37%;时间经历0.05 s后,编号1～5号颗粒发生不同程度的残余变形,与图16路面附近位移变化趋势相同,这较好地符合图16车载作用中心线附近区域颗粒的位移云图变化规律。