Navier-Stokes方程的二阶解耦BDF格式的稳定性和收敛性分析
2023-02-13牟小凤夏泽宇李茂军
牟小凤,夏泽宇,李茂军
(电子科技大学 数学科学学院,成都 611731)
不可压粘性Navier-Stokes方程是流体运动模拟的基本问题之一,其数学理论以及数值解是非常重要的研究领域。本文考虑下列定常不可压Navier-Stokes方程:
ut-μΔu+u·∇u+∇p=0,x∈Ω,t∈(0,T],
(1)
∇·u=0,x∈Ω,t∈(0,T],
(2)
u=0,x∈∂Ω,t∈(0,T],
(3)
u(·,0)=u0,x∈Ω,
(4)
在过去的几十年里,已经有许多工作致力于不可压Navier-Stokes方程的理论研究和数值分析。从Girault和Raviart的专著[1]中可以看到关于Navier-Stokes方程的数学理论和数值算法。对于Navier-Stokes方程数值方法的稳定性和收敛性的研究,Codina和Blasco[2-3]设计了稳态Stokes方程的稳定数值格式,并将其推广到了非线性Navier-Stokes方程;Nochetto和Pyo[4]提出了一个关于Navier-Stokes问题的数值格式,并分析了该格式无条件稳定性;He[5]对Navier-Stokes方程提出了一种完全离散的惩罚有限元方法,并给出了最优误差估计。另外还有许多其他关于Navier-Stokes方程数值格式的稳定性和误差分析的工作,如文献[6-7]及其参考文献。这些离散格式大多是非对称格式,而有些学者则通过解耦的技巧使方程对称化。Shen[8]对非定常不可压Navier-Stokes方程解耦格式进行了严格的误差分析。Shen和Yang[9]提出了两相不可压流相场模型的解耦格式,并证明了该格式的无条件能量稳定性。Mu和Zhu[10]提出了Stokes/Darcy流问题的解耦有限元格式,此结果被推广到不同域的不同时间步长[11]。基于Crank-Nicolson(CN)方法和FEM,一种能量稳定且唯一可解的求解磁流体方程的解耦格式在文献[12]中被提出,该文首次使用引入中间映射来证明不可压磁流体的最优收敛速率。针对不可压Navier-Stokes方程解耦格式的研究还有很多,如文献[13]。二阶BDF法作为常微分方程的时间离散方法得到了广泛的应用[14]。二阶BDF格式具有稳定性强、精度高等优点,成为目前常用的多步方法之一。
本文采用常规的半隐半显技巧对非线性移流项u·∇u进行了线性化处理,进而得到了线性的离散系统。尽管已经有许多工作致力于不可压Navier-Stokes方程的稳定性分析,但是通过添加时间步长平方阶的修正项,首次对二阶BDF解耦格式求解Navier-Stokes方程进行了严格的无条件能量稳定性的证明。能量稳定性结合线性确保了离散系统对应的齐次方程组只有零解,进而得到了方程的唯一可解性。在最优误差分析中,通过利用文献[12]中证明不可压磁流体方程的技巧,即引入中间映射并给出相应估计,也是首次使用该方法完成了对二阶BDF解耦格式解Navier-Stokes方程的最优收敛速率的证明。本文得到了速度场在L∞([0,T],L2)范数下的最优收敛阶(τ2+hr+1),其中r表示多项式函数空间的次数,h和τ分别表示空间网格尺寸和时间步长。最后提供算例验证本文所证明的格式的性质。
1 变分形式
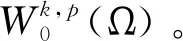
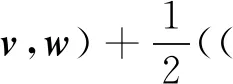
(5)
b(u,v,w)=-b(u,v,w),b(u,v,v)=0。
(6)
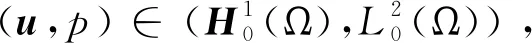
(ut,v)+μ(∇u,∇v)+b(u,u,v)-(p,∇·v)=0,
(7)
(∇·u,q)=0。
(8)
2 全离散格式和稳定性
2.1 数值离散
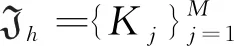
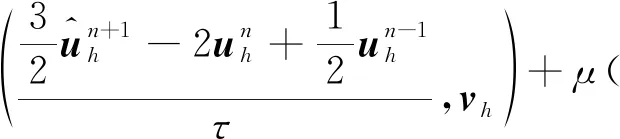
(9)
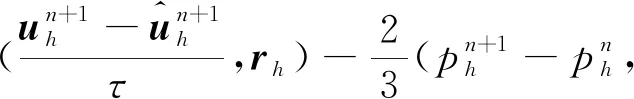
(10)

(11)

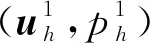
2.2 能量稳定性
本节主要证明全离散格式(9)—(11)的无条件能量稳定性。需要定义如下离散梯度算子∇h∶Mh→Xh:
(vh,∇hqh)=-(∇·vh,qh),∀(vh,qh)∈(Xh,Mh)。
(12)

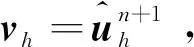
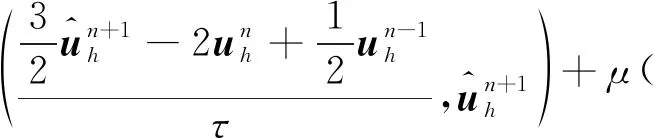
(13)
根据
(14)
以及三线性形式的性质(6),消去非负项后可以将式(13)化为
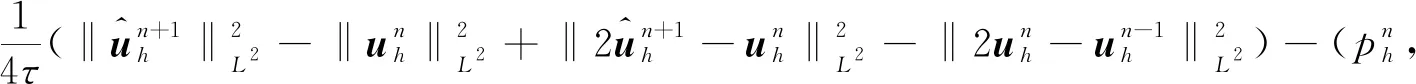
(15)
(16)
(17)
(18)

(19)
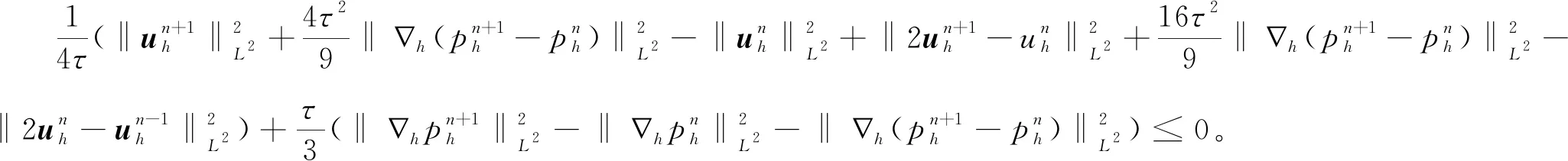
综上所述,定理1得证。
3 最优误差估计
本节主要分析全离散格式(9)—(11)的最优收敛速率。先进行正则性假设:
‖uttt‖L∞(0,T;L2)+‖utt‖L∞(0,T;H1)+‖ut‖L∞(0,T;Hr+1)+‖u‖L∞(0,T;Hr+2)+‖ptt‖L∞(0,T;L2)+‖pt‖L∞(0,T;Hr+1)≤M。
(20)
3.1 预备知识
为了估计二阶解耦BDF-FEM所得近似解的误差,本节将引入一些重要的投影算子和已有的结论。
定义L2投影算子Ph:L2(Ω)→Mh(或L2(Ω)→Xh)为:
(Phv,qh)=(v,qh), ∀(v,qh)∈(L2(Ω),Mh)(或(v,qh)∈(L2(Ω),Xh))。
(21)

(22)
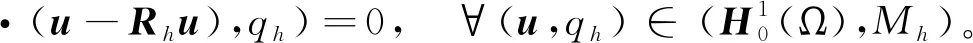
(23)
由参考文献[15-16]可知,L2投影算子和Stokes投影算子有如下性质。
引理1针对(21)中定义的L2投影算子和(22)—(23)中定义的Stokes投影算子,其满足如下估计:
对于n=0,1,0≤l≤r,1≤q≤∞有
‖Phv‖Wn,q≤C‖v‖Wn,q,
(24)
‖v-Phv‖L2≤Chl+1‖v‖Hl+1。
(25)
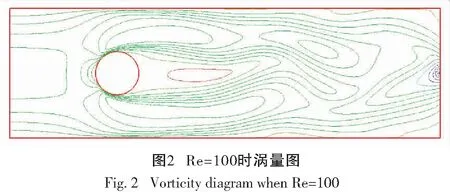
对于0≤l≤r,1 ‖u-Rhu‖Lq+h‖u-Rhu‖Wl,q≤Chl+1(‖u‖Wl+1,q+‖p‖Wl,q), (26) ‖u-Rhu‖Lq+h‖u-Rhu‖Wl,q≤Chl+1(‖u‖Wl+1,q+‖p‖Wl,q), (27) ‖p-Rhp‖Lq≤Chl(‖u‖Wl+1,q+‖p‖Wl,q), (28) ‖∂t(u-Rhu)‖Lq+‖∂t(p-Rhp)‖Lq≤Chl+1(‖∂tu‖Wl+1,q+‖∂tp‖Wl,q)。 (29) 其中所有的C都是不依赖于h的正常数。 此外,引入文献[17]中的如下逆不等式。 引理2存在不依赖于h的正常数C,使得对于所有的uh∈Mh,Xh满足下面的估计 (30) 其中d表示空间的维数。 根据离散梯度算子∇h在(12)中的定义与文献[12],给出如下引理3和引理4。 引理3对于所有qh∈Mh,有 ‖∇hqh‖L2≤Ch-1‖qh‖L2, (31) 其中C是不依赖于h的正常数。 引理4如果正则性假设(20)成立,则满足 ‖∇hPh∂tp-Ph∇∂tp‖L2≤Ch, (32) 其中C是不依赖于h和τ的正常数。 引理5如果正则性假设(20)成立,则满足 ‖∇h(Rhpn+1-Rhpn)‖L2≤Cτ, (33) 其中C是不依赖于h和τ的正常数。 证明利用正则性假设可知 ‖∇h(Rhpn+1-Rhpn)‖L2=Cτ‖∇hRh∂tpn+1‖L2(利用泰勒展开)≤Cτ(‖∇hRh∂tpn+1-∇hPh∂tpn+1‖L2+‖∇hPh∂tpn+1-Ph∇∂tpn+1‖L2+‖Ph∇∂tpn+1‖L2)≤Cτ(Ch-1‖Rh∂tpn+1-∂tpn+1‖L2+Ch-1‖∂tpn+1-Ph∂tpn+1‖L2+Ch+C)(利用(24)和(32))≤Cτ(Ch-1Ch2+Ch-1Ch2+Ch+C) (利用(25)和(28))≤Cτ。 综上所述,此引理得证。 (34) 上式可以等价的写为下面的形式:对于所有rh∈Xh,有 (35) 因此,结合上面定义的变量和函数,以及利用3.1节中定义的投影算子,变分形式(7)—(8)可以转化为:对于所有(vh,qh)∈(Xh,Mh)和n=1,2,…,N-1,有 (36) (∇·Rhun+1,qh)=0, (37) 对于所有(vh,rh,qh)∈(Xh,Xh,Mh)和n=1,2,…,N-1,误差函数满足 (38) (39) (40) 基于3.2节中的讨论,针对所提出的二阶解耦算法,有如下的最优误差估计。 (41) 其中C0是一个不依赖于τ和h的正常数。 (42) (43) (44) (45) ≤C(T2+hr+1)2+ (46) 估计式(46)中第一行右端的第一项‖∇(∇hRhpn+1-∇hRhpn)‖L2可以被以下不等式控制 ‖∇(∇hRhpn+1-∇hRhpn)‖L2 =Cτ‖∇(∇hRh∂tpn+1)‖L2(利用泰勒展开) ≤Cτ(‖∇(∇hRh∂tpn+1-∇hPh∂tpn+1)‖L2+‖∇(∇hPh∂tpn+1-Ph∇∂tpn+1)‖L2)+Cτ‖∇(Ph∇∂tpn+1)‖L2 ≤Cτ(Ch-2‖Rh∂tpn+1-Ph∂tpn+1‖L2+Ch-1‖∇hPh∂tpn+1-Ph∇∂tpn+1‖L2)+Cτ‖∇∂tpn+1‖H1(利用(24)和(31)) ≤Cτ(Ch-2‖Rh∂tpn+1-∂tpn+1‖L2+Ch-2‖∂tpn+1-Ph∂tpn+1‖L2+Ch-1Ch1)+Cτ(利用(32)) ≤Cτ(Ch-2Ch2+Ch-2Ch2)+Cτ(利用(25)和(28))≤Cτ, 其中正则性假设(20)被多次使用。注意到(34),因此有 (47) (48) (49) 利用等式(39)和(40),还可以得到 (50) (51) 然后将以上估计(45)—(51)代入不等式(44)的两端,整理可得 (52) 时也成立。最后,利用三角不等式,投影误差估计(27)和估计(52)即得结论(41),完成了定理2的证明。 本小节中,以有限元软件FreeFem++为平台进行编程,通过数值算例来检验二阶解耦BDF-FEM数值格式的精度。为了方便起见,本文考虑在区域Ω×[0,T]=[0,1]×[0,1]×[0,1]上满足Dirichlet边界条件(3)和初始条件(4)的不可压Navier-Stokes方程: ut-μΔu+u·∇u+∇p=f,x∈Ω,t∈(0,T], (53) ∇·u=0,x∈Ω,t∈(0,T], (54) 其中μ=0.1,以及源项f对应于如下真解: 采用全离散解耦格式(9)—(11)求解Navier-Stokes方程(53)—(54)。在实验中,有限元离散使用二次元逼近u以及线性元逼近p。为了验证时间误差收敛阶(τ2),选择足够小的空间网格尺寸h=1/100使得空间离散误差可以忽略不计,并取时间步长τ=1/10,1/20,1/40,1/80,在T=1处的时间误差和收敛阶见表1:速度u在L2范数下的误差随时间步长τ的逐渐减小而降低,说明在时间上数值方法是收敛的。数值结果也验证了时间误差分析得到的二阶收敛速度,这与定理2中的理论分析保持一致。类似地,为了验证空间精度的收敛阶,固定τ=1/10000,并且选择逐渐减半的的空间网格尺寸h=1/10,1/20,1/40,1/80,得到在T=1处相应的数值结果如表1所示:误差随着空间网格尺寸h的减小而降低,并且空间收敛速度与定理2中理论预测一致,保持三阶的收敛阶。 表1 二阶解耦BDF-FEM的误差和收敛阶 为了验证所提算法的有效性,采用有限元方法求解二维Navier-Stokes方程,对雷诺数Re=100的二维圆柱绕流进行数值模拟。针对不可压缩粘性流体,其运动规律可以用Navier-Stokes方程来描述,我们考虑在区域Ω×[0,T]=[-1,1]×[-0.3,0.3]×[0,10]上的控制方程: 一个直径D=0.2 m且无穷长的圆柱体,放置在无穷远来流速度为1.0 m·s-1,不受干扰的均匀横流中。计算区域大小为上游边界距圆柱圆心为2.5D,下游边界距圆柱圆心7.5D,顶部和底部边界均距圆柱圆心1.5D。选取固定空间网格尺寸h=1/80和时间步长τ=1/100。雷诺数Re由圆柱体直径D和自由来流速度U确定:Re=ρUD/μ,其中ρ表示流体密度,μ表示动力粘度。经过上述的网格划分和参数设置,模拟雷诺数为100时的绕流流动,得到的涡量图如图2所示。从图中可以观察出,圆柱上下游的流线逐渐不具有对称性。 本文针对不可压Navier-Stokes问题,基于时间离散的二阶BDF和Taylor-Hood有限元空间离散,提出了相对应的解耦算法,并对解耦算法进行了理论分析与数值模拟,证明了数值格式的无条件能量稳定性和唯一可解性,并进一步严格地给出了最优收敛阶。最后,通过数值实验验证了该方法求解Navier-Stokes问题的精度、无条件能量稳定性以及算法的有效性。本文首次对二阶解耦BDF格式求解Navier-Stokes方程进行了严格的稳定性证明。在最优误差估计证明中,引入中间映射算子的技巧可以被推广到其他有中间变量的格式中用于理论分析。在将来的工作中会将解耦格式及其理论分析应用于更复杂的模型。
3.2 误差方程
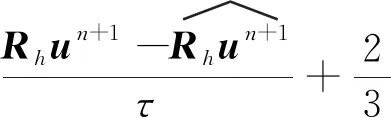
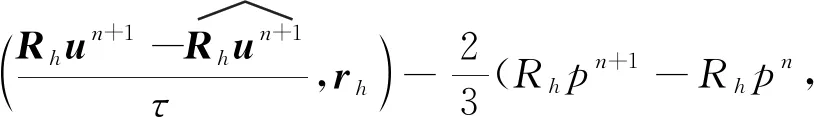
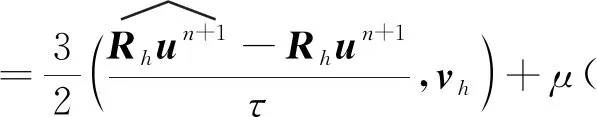

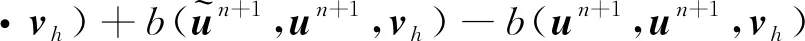
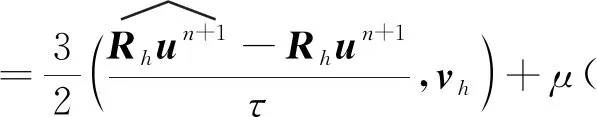
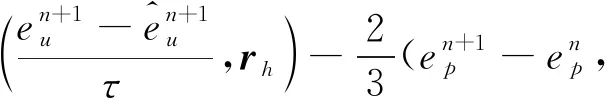

3.3 最优误差估计

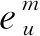
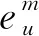
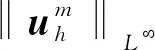
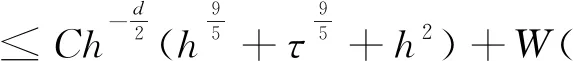

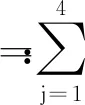





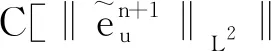
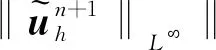
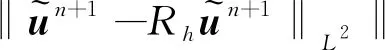
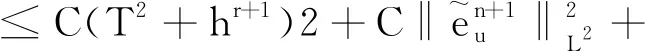
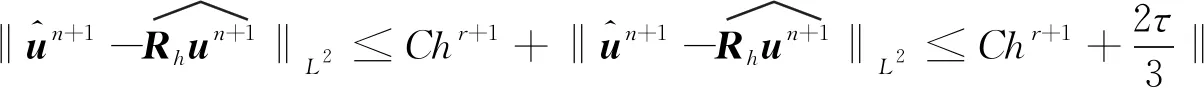
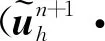
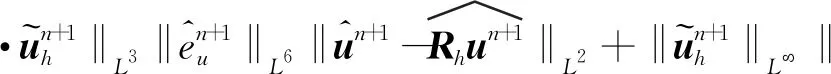
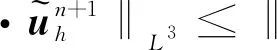
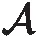
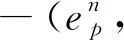

4 数值算例
4.1 算例1
4.2 算例2
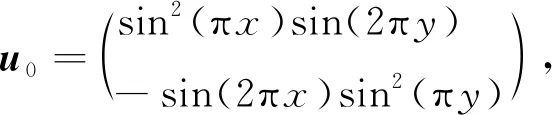

4.3 算例3
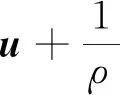
5 结论与展望
