低碳合金钢18CrNiMo7-6齿轮弯曲疲劳试验研究与误差分析

陈地发，刘怀举，朱加赞，徐永强，魏沛堂，何海风

(1.重庆大学 机械传动国家重点实验室，重庆 400044；2.中国航发四川燃气涡轮研究院，成都 610599)

齿轮作为机械传动系统中应用最广泛的重要部件之一，其疲劳性能已成为影响机械设备工作性能的重要因素[1]。齿轮在工作过程中，轮齿近似悬臂梁，其齿根部位受到较大的弯曲应力，在循环载荷下产生疲劳裂纹，最终引起轮齿弯曲疲劳失效。随着工程技术不断发展，弯曲疲劳强度成为齿轮功率密度和可靠性提升的重要限制因素，且弯曲疲劳失效比齿面失效更具危险性[2]。国内外已开展了大量齿轮弯曲疲劳性能研究。Hong等[3]为研究全释放和全反转两种载荷条件下齿轮的高周弯曲疲劳性能，基于传统接触疲劳试验机自主研发了可施加全释放和全反转两种载荷的试验机，并开发了试验终止的自适应诊断方法，通过疲劳试验验证了该方法的有效性。Lisle等[4]将ISO 6336:2006和AGMA 2101-D04标准计算及有限元仿真的直齿轮齿根弯曲应力与应变片测试结果进行了比较，仅比较齿根弯曲应力最大值，ISO标准的计算结果较实测值高5.2%，而AGMA较实测结果低6.4%。王明旭等[5]采用成组法和爬山试验相结合的方法对某大型升船机用大模数齿条新材料A35CrNiMo的感应淬火齿轮弯曲疲劳特性开展研究。徐科飞等[6]探讨了18CrNiMo7-6渗碳淬火齿轮齿根弯曲应力计算中的若干问题，发现在计算喷丸齿轮的相对齿根表面状况系数时，可不考虑测量方向带来的测量误差，直接沿齿宽方向测量齿根表面粗糙度即可，同时发现使用实测抗拉强度1 224 MPa与标准参考抗拉强度1 080 MPa分别计算出的齿根弯曲应力相差仅为0.28%，因此在不需精确计算齿根弯曲应力时，可不开展拉伸试验。刘子强等[7]就单齿脉动加载试验中的若干问题进行了讨论，认为跨齿数和加载点的确定应与计算方法相一致，齿形系数和应力集中系数计算的准确性对最终结果影响很大，推荐采用几何法得到真实的齿根几何参数来计算齿形系数和应力集中系数。

现有文献中鲜有讨论齿轮几何精度、装夹误差以及设备加载精度等试验过程误差对齿轮弯曲疲劳试验结果的影响。本研究的目的是探究试验过程误差对试验结果的影响。基于GB/T 14230—1993《齿轮弯曲疲劳强度试验方法》[8]制定齿轮弯曲疲劳试验方案，根据滚刀参数以及留磨量利用Romax DESIGNER软件生成精确齿形，确定加载点位置和相关参数，获得加载力与齿根弯曲应力关系式，并根据循环特性系数进行转换；采用ABAQUS进行齿根弯曲应力仿真和电阻应变片测试以验证试验方案的正确性；开展18CrNiMo7-6喷丸齿轮弯曲疲劳试验以获取其弯曲疲劳极限；并分析试验过程误差对弯曲疲劳极限的影响，为齿轮弯曲强度准确评估提供参考。

1 试验方案

依据GB/T 14230—1993《齿轮弯曲疲劳强度试验方法》中的B试验法，在Zwick Vibrophore 1 000 kN弯曲疲劳试验机上以单齿加载方式进行齿轮弯曲疲劳试验。B试验法加载频率高，可大大缩短试验时间，齿轮弯曲疲劳试验多采用此方法[9-11]。Zwick Vibrophore 1 000 kN弯曲疲劳试验机如图1所示，基本参数见表1。该试验机可适用于模数2.5～50.0 mm，齿顶圆直径49～1 000 mm齿轮的疲劳寿命测试。根据滚刀参数以及留磨量，利用Romax DESIGNER软件构建试验齿轮精确齿形。根据安装位置确定计算齿根弯曲应力的相关参数，获取加载力与齿根弯曲应力关系式。同时依据循环特性系数，转换齿根弯曲应力。

图1 Zwick Vibrophore 1000 kN弯曲疲劳试验机

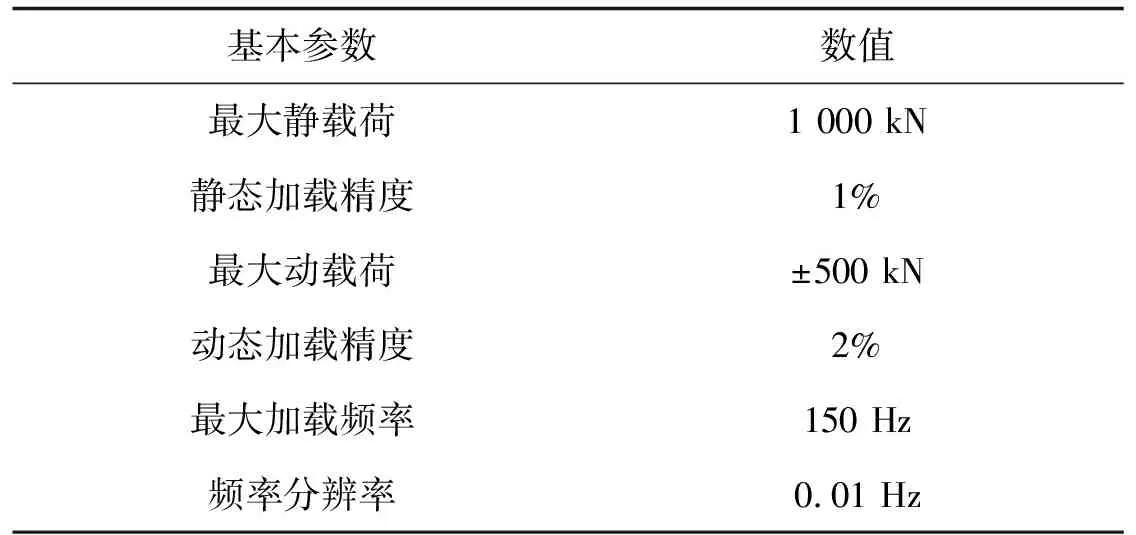
表1 Zwick Vibrophore 1000 kN高频试验机基本参数

1.1 试验齿轮精确齿形

试验所用齿轮图纸及实物如图2所示，其基本几何参数见表2。齿轮材料为18CrNiMo7-6，所有齿轮表面经渗碳淬火处理，表面硬度为58～62 HRC，渗碳硬化层深度为1.0～1.3 mm，芯部硬度为35 HRC。齿根表面粗糙度Ra为3.2 μm。试验齿轮经喷丸强化处理，喷丸强度为0.45A，覆盖率为200%。

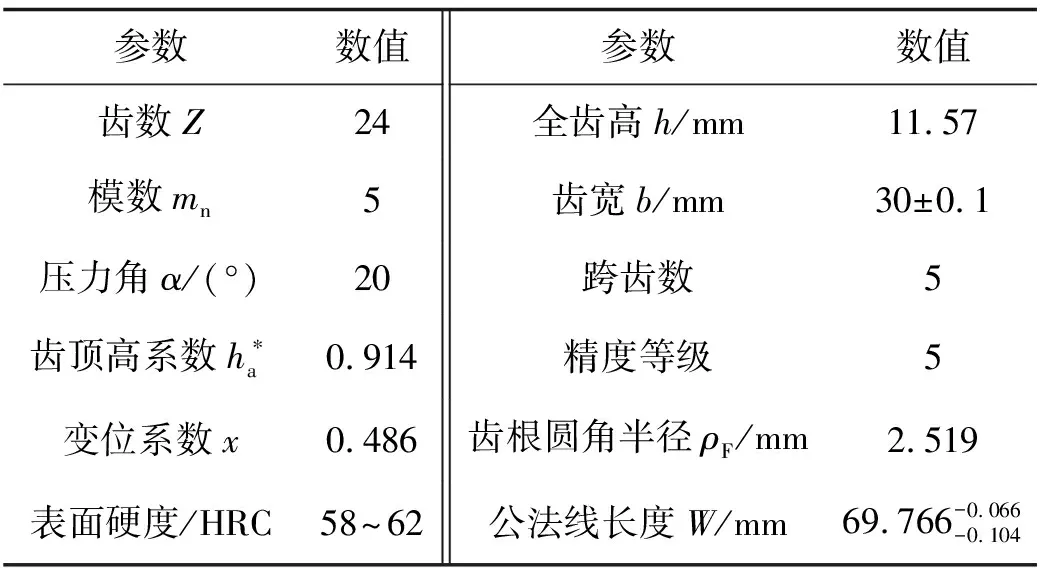
表2 齿轮基本几何参数

试验齿轮的加工工序为：滚齿→热处理→喷丸→磨齿。为保证齿根强度，采用留磨滚刀[12]加工，滚刀参数如图3(a)所示。依据滚刀参数以及留磨量，使用Romax DESIGNER软件构建试验齿轮精确齿形如图3(b)所示。由Romax DESIGNER提供的结果报告获得轮齿危险截面齿厚SFn=11.026 mm，以及危险截面所在位置圆直径DS=112.816 mm。

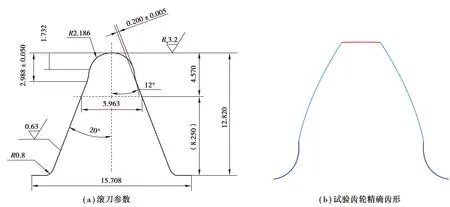
图3 滚刀参数及试验齿轮齿形

1.2 加载点确定和齿根弯曲应力计算

GB/T 3480—1997《渐开线圆柱齿轮承载能力计算方法》[13]中以载荷作用于单对齿啮合区外界点为基础计算齿根弯曲应力，本次试验采用单齿加载方式，无配对齿轮，因此以压头只受竖直方向作用力为原则确定加载点[14]，确保加载力的作用线与齿轮基圆相切。试验齿轮的基圆半径为rb=56.382 mm。采用对称跨五齿加载，则加载点e到齿轮中心的半径为re=66.3 mm。加载点e确定后，也确定了加载点e处的压力角αen。在CAXA软件中根据压头与试验齿轮的几何尺寸确定试验齿轮的安装尺寸，如图4所示。根据试验齿轮的安装尺寸以及加载力作用线与齿轮基圆相切，对试验齿轮做受力分析如图5所示。图中Fn为试验载荷。

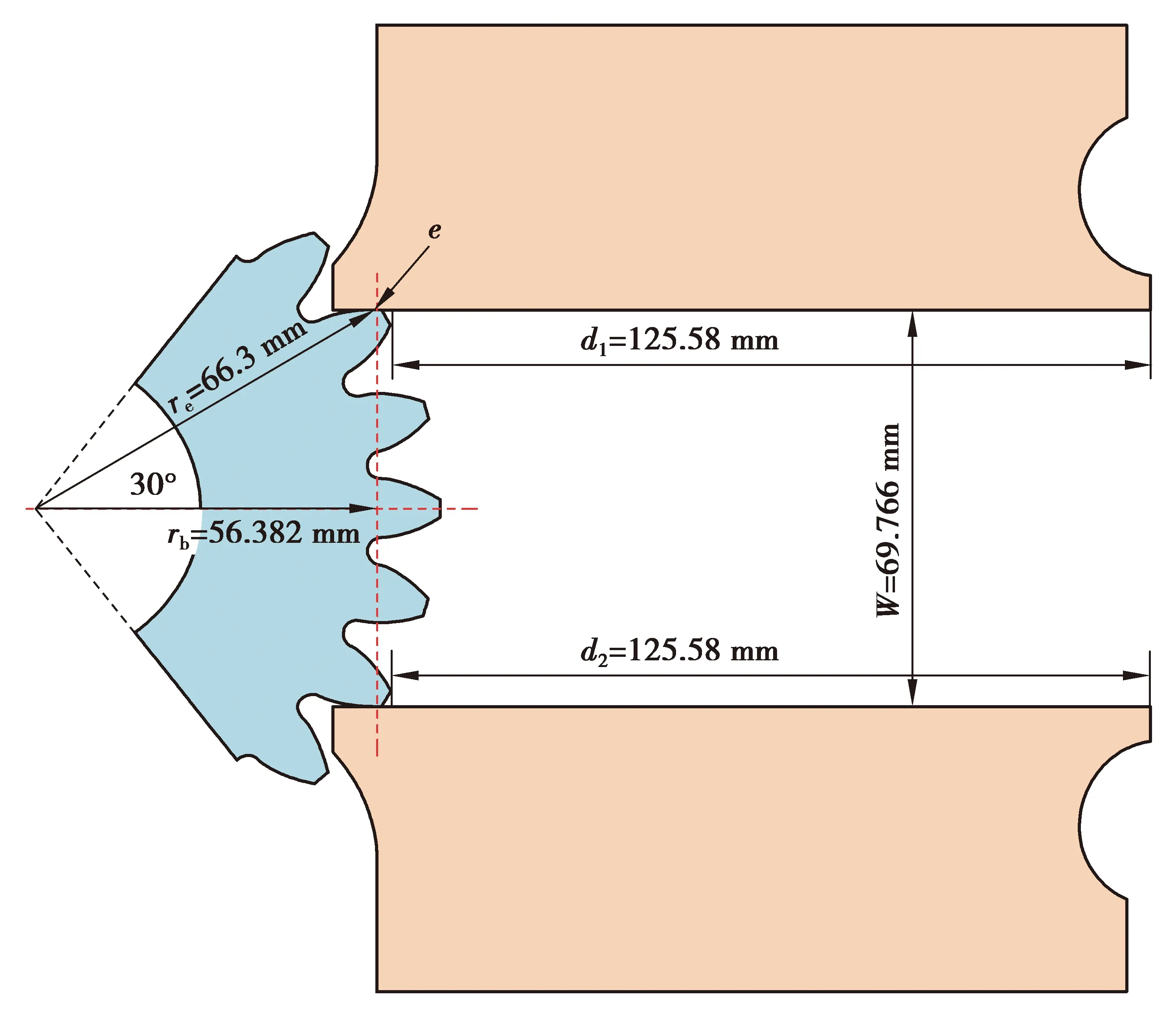
图4 试验齿轮安装尺寸

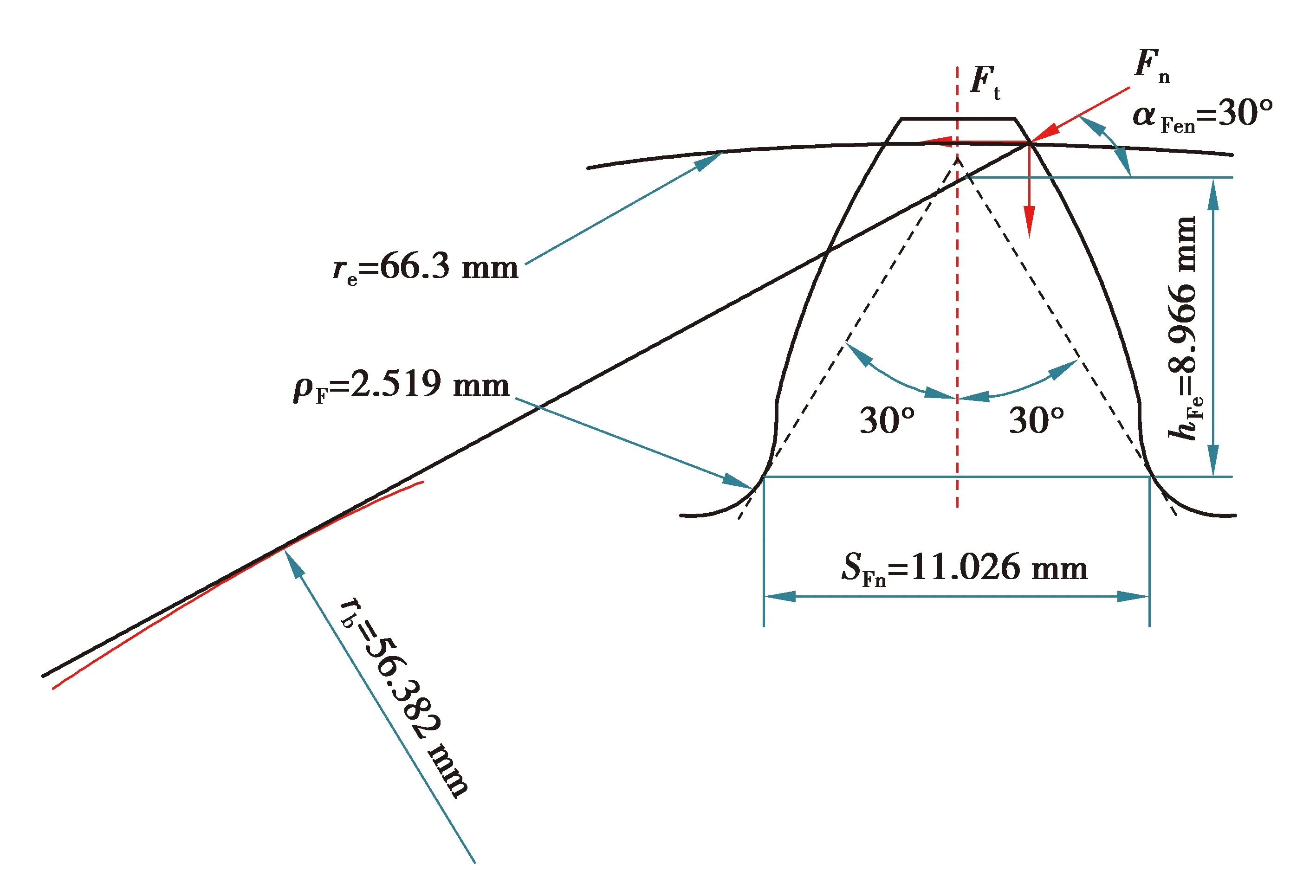
图5 受力分析

参考国标GB/T 3480—1997确定齿根弯曲应力计算参数，图5中载荷作用角αFen按式(1)计算。

αFen=αen-γe，

(1)

式中：αen为加载点处压力角，γe为加载点处齿厚半角，按式(2)和式(3)计算。

(2)

(3)

式中：Zn为当量齿数；αn为齿轮压力角20°。

参考国标GB/T 3480—1997，齿根弯曲应力基本值按式(4)计算：

(4)

式中：Ft为名义切向力，N；YF为作用点齿形系数；YS为作用点应力修正系数；Yβ为螺旋角系数，取1。

参考国标GB/T 14230—1993中的B试验法，齿根弯曲应力按式(5)计算：

(5)

式中：YST为应力修正系数，取2.0；YX为尺寸系数，取1；YFe为加载点e齿形系数，YSe为加载点e应力修正系数，YδrelT为相对齿根圆角敏感系数，YRrelT为相对齿根表面状况系数，计算公式如下。

(6)

(7)

(8)

YRrelT=1.674-0.529(RZ+1)0.1。

(9)

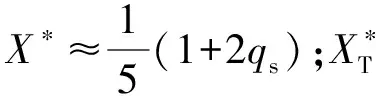
则齿根弯曲应力计算参数结果如表3所示。

表3 齿根弯曲应力计算参数结果

由此可得加载力与齿根弯曲应力基本值的关系式为

σF0=0.023 8FncosαFen。

(10)

加载力与齿根弯曲应力关系式为

σ′F=0.012 4FncosαFen。

(11)

受试验机限制，在进行弯曲疲劳试验时，必须保证最小加载力，即取循环特性系数γF=0.05，以防止试验齿轮掉落。因此需要将齿根弯曲极限应力转换为γF=0的对应值，其转换公式为

(12)

式中σb为18CrNiMo7-6的抗拉强度1 080 MPa。

2 齿根弯曲应力验证

为校验试验方案中齿根弯曲应力计算的准确性，采用有限元仿真和电阻应变片测试进行验证。

2.1 有限元仿真

采用ABAQUS对齿根弯曲应力进行有限元仿真。仿真模型如图6所示，试验中采用跨五齿对称加载。为了简化模型，根据第一节生成的精确齿形，建立七齿模型。根据真实几何尺寸以及力的作用关系对上、下压头建模。试验齿轮与上、下压头根据图4中的安装尺寸装配。试验齿轮所用材料为18CrNiMo7-6，其弹性模量[15]E=210 GPa，泊松比ν=0.3。为增加模型的计算精度，对轮齿与上、下压头的接触区域进行网格加密，其网格尺寸为0.05 mm，其他区域采用渐疏网格。齿根弯曲应力仿真可视为平面应变问题[16]，因此有限元模型中网格类型选用平面应变网格CPE4R。对试验齿轮分别施加10～80 kN的载荷，间隔为10 kN，分别提取不同载荷下的最大主应力作为齿根弯曲应力[17]，部分载荷作用下的齿根弯曲应力云图如图7所示。

图6 齿轮弯曲疲劳试验有限元仿真模型

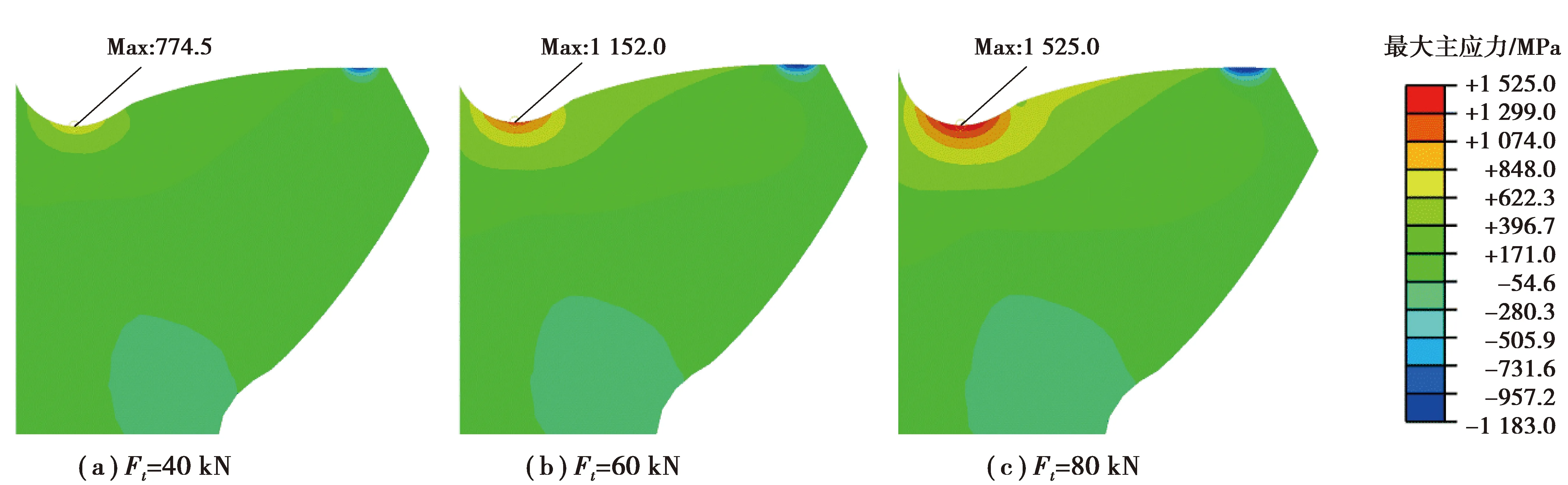
图7 齿根弯曲应力云图

2.2 电阻应变片测试

在试验齿轮危险截面处粘贴电阻应变片，并将其接入测试电路，将测得的应变结果转换后即可得到齿根弯曲应力。因此必须准确确定危险截面位置[18]，根据齿轮精确齿形以及危险截面位置，利用CAXA软件确定应变片粘贴位置。试验齿轮为5模数，齿根位置狭窄，为方便粘贴应变片，对部分轮齿进行线切割处理。同时采用型号为BFH 120-2 AA的微型电阻应变片，其基底长宽尺寸为：4.5 mm ×2.4 mm，丝栅长宽尺寸为：2.0 mm ×1.0 mm，电阻值为：(120±0.1)Ω，灵敏系数：2.0±1%。测试采用DRA-30 A多通道动静应变仪，其能进行多通道同步采样[19]。采用四分之一桥路方式进行接线，测试原理以及测试现场如图8所示。以间隔10 kN，载荷从10 kN逐级增加至80 kN，将应变结果转换成对应的齿根弯曲应力值。

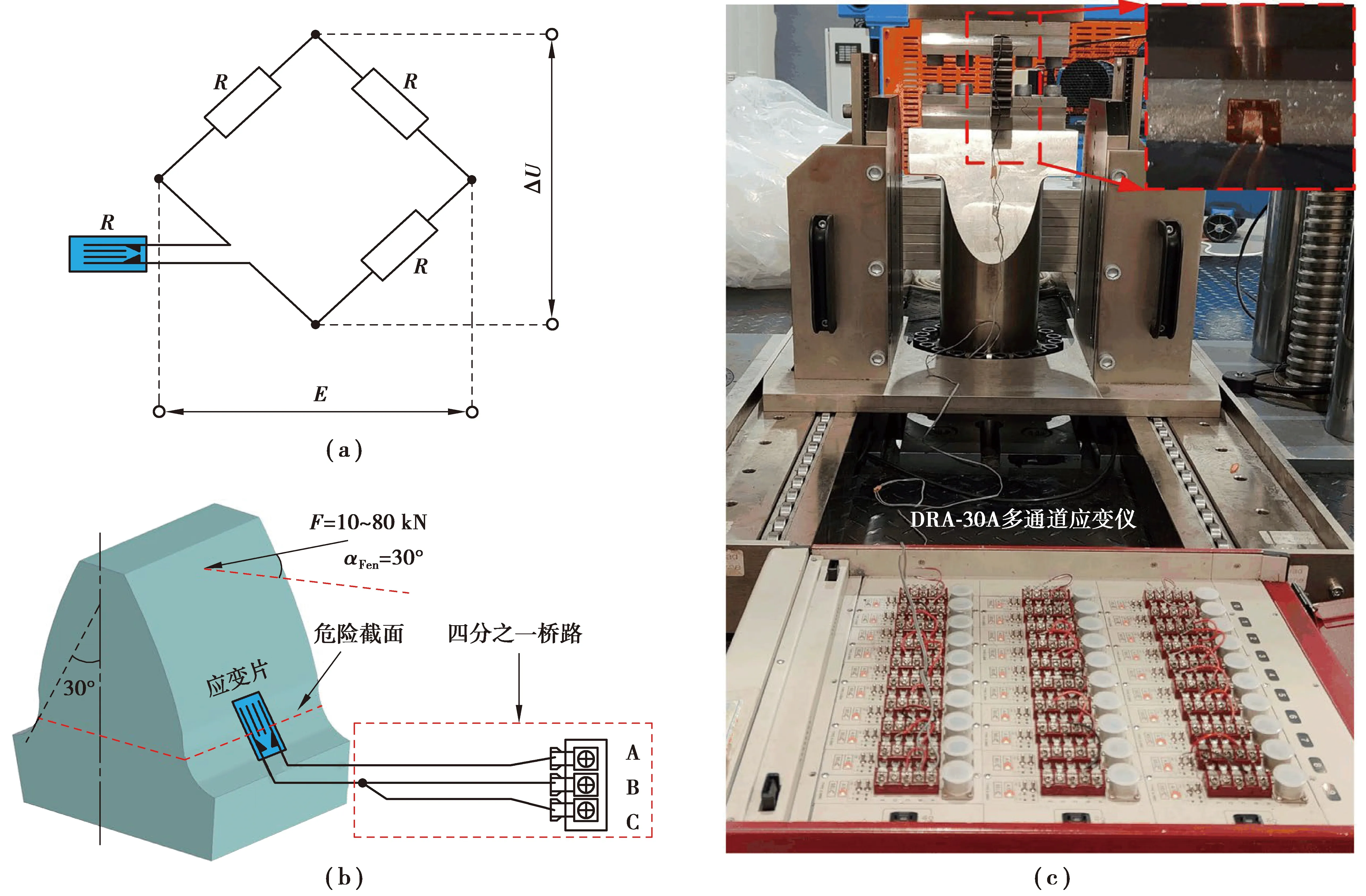
图8 齿根弯曲应力检测原理及测试现场

2.3 齿根弯曲应力对比验证

通过有限元仿真、电阻应变片测试以及试验方案数值计算3种方式得到的齿根弯曲应力基本值如表4所示。由表4可知，根据试验方案得到的齿根弯曲应力与有限元仿真以及电阻应变测试的结果的最大误差为8.7%，满足工程需求。通过对齿根弯曲应力基本值的校验从而验证了弯曲疲劳试验方案的正确性。

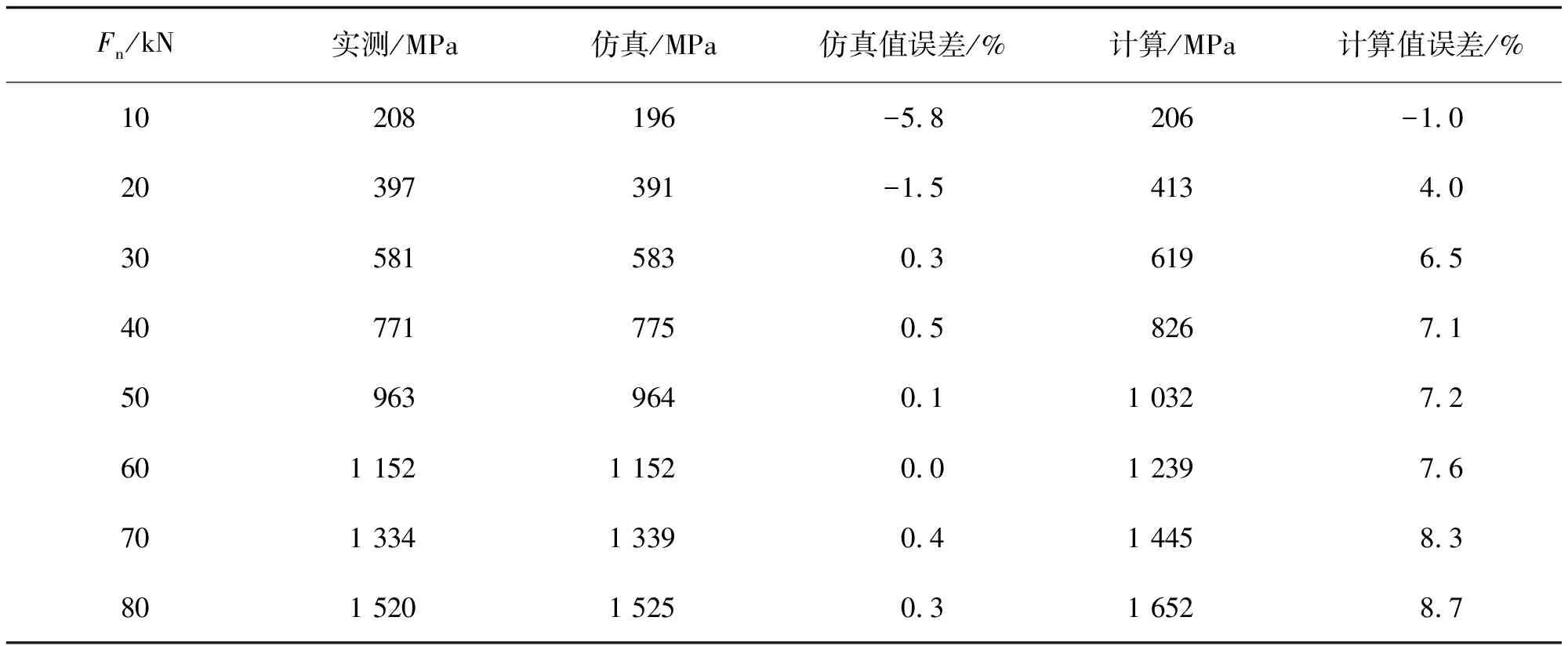
表4 三种方式齿根弯曲应力对比表

3 试验案例

在正式进行齿轮弯曲疲劳试验之前，对试验齿轮的弯曲疲劳承载能力进行摸底测试，根据摸底测试结果确定采用试验载荷范围为Fn=72～80 kN，载荷间隔为2 kN，共5个应力级，采用升降法测定试验齿轮的弯曲疲劳强度极限。结合式(11)、式(12)得到不同试验载荷对应的齿根弯曲应力，如表5所示。为确保试验满足可靠性要求[20]，共获得有效试验点20个，弯曲疲劳试验数据如表6所示，升降法试验结果如图9所示。

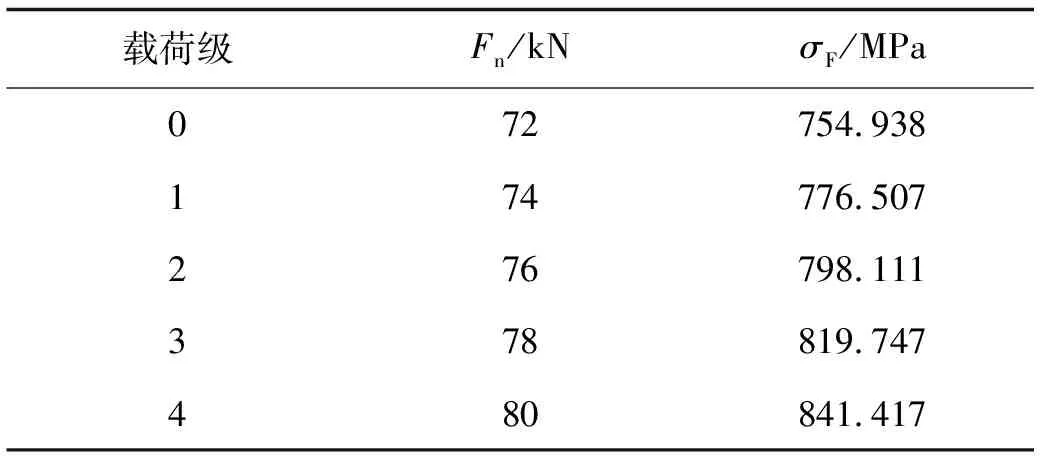
表5 不同载荷级下齿根弯曲应力

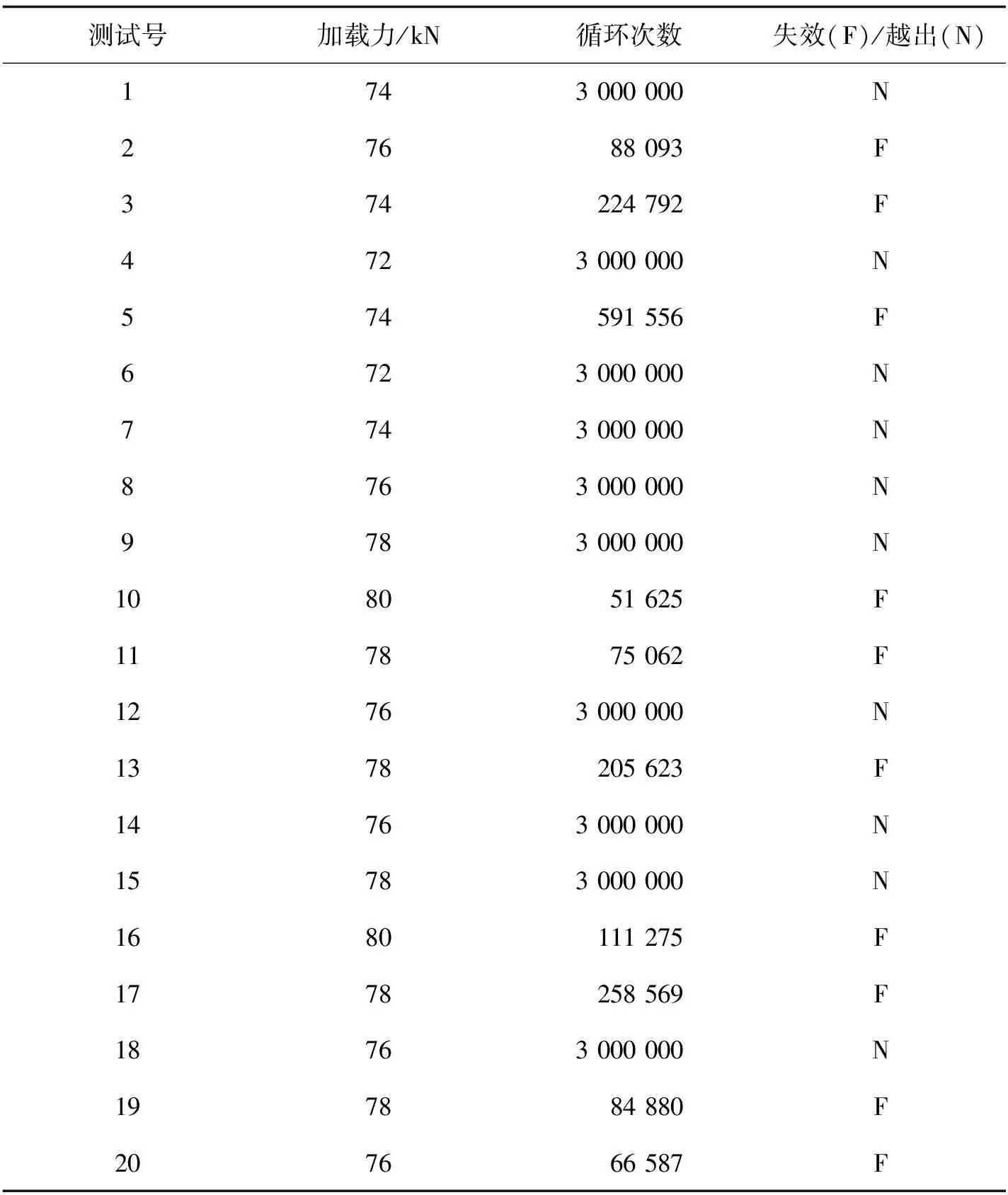
表6 弯曲疲劳试验数据

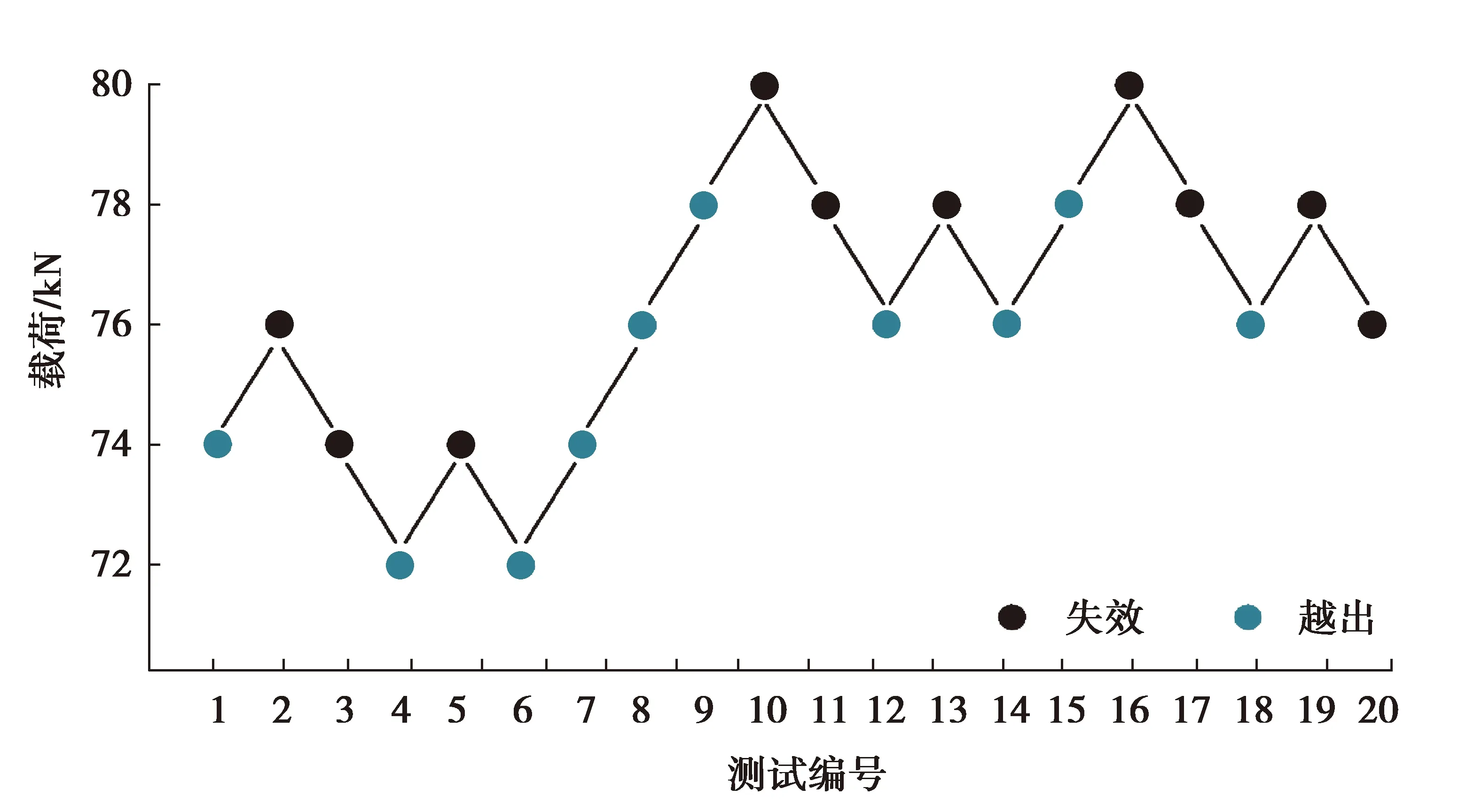
图9 升降法试验结果

根据国标GB/T 24176—2009《金属材料疲劳试验数据统计方案与分析方法》[21]对升降法试验结果进行数据处理，将失效点按加载水平升序排序，结果如表7所示。

表7 升降法试验结果分析

则预估的50%可靠度下的中值载荷为

(13)

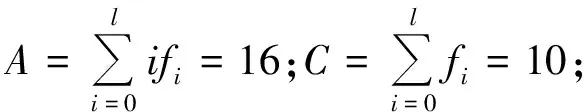
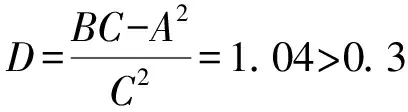
(14)

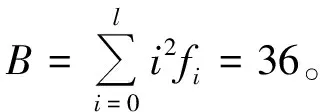
取不同可靠度R=99.9%,99%,95%,90%，则对应的标准正态分布分位数Φ-1(1-R)=-3.090,-2.326,-1.645,-1.282。本试验采用B试验法即采用脉动型加载方式开展，其试验结果与A试验法即运转型试验结果存在转换系数，该转换系数[22]为fp=0.9，则不同可靠度的载荷计算见公式(15)。联合公式(11)(12)(15)，可得试验齿轮在不同可靠度下的弯曲疲劳极限，如表8所示。

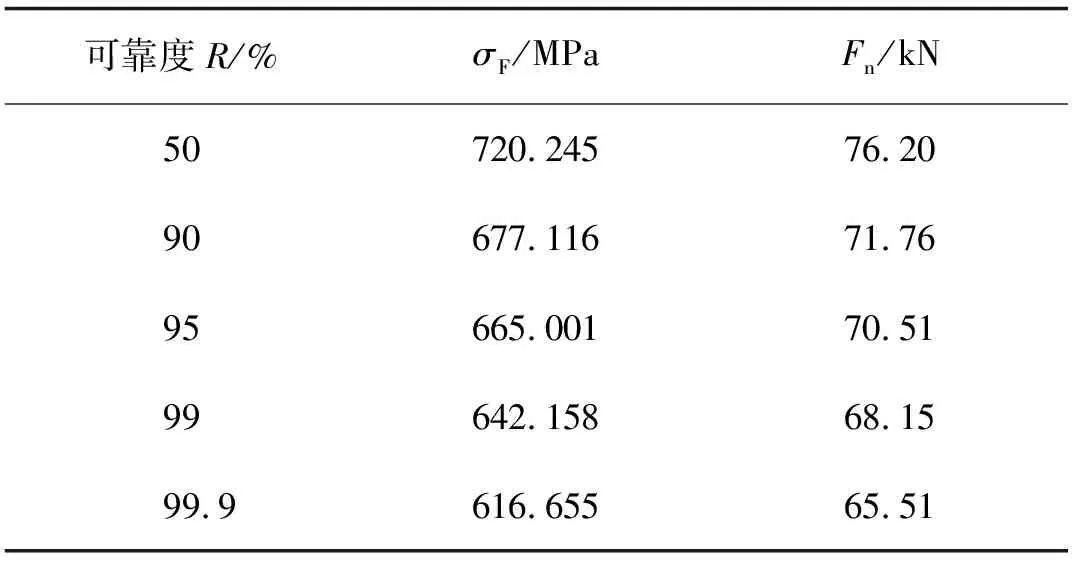
表8 不同可靠度下弯曲疲劳极限

F=fp(μF+Φ-1(1-R)σ)。

(15)

4 弯曲疲劳极限误差分析

根据齿轮名义尺寸确定加载点和计算齿根弯曲应力。试验齿轮的精度等级为5级，齿轮几何尺寸在满足5级精度的公差范围内波动，则实际加载点会随齿轮尺寸变化而发生改变；加载点的位置是依靠装夹来保证的，在试验齿轮装夹过程中也存在装夹误差；且试验设备的加载力也存在加载精度。因此有必要开展上述误差对齿轮弯曲疲劳试验结果的影响分析。

4.1 几何精度对弯曲疲劳极限的影响

试验齿轮的跨五齿名义公法线长度为W=69.766 mm，5级精度下，公法线长度在W=69.662～69.700 mm范围内波动。公法线长度的改变将导致加载位置的改变，从而引起弯曲力臂hFe与载荷作用角αFen发生变化进而引起齿根弯曲应力的改变。不同公法线长度下加载位置如图10所示，相关应力计算参数结果见表9。结合公式(11)(12)以及表8、9得到考虑不同公法线长度下的不同可靠度齿轮弯曲疲劳极限，如表10所示。

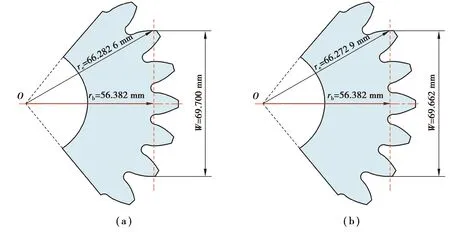
图10 不同公法线长度加载位置

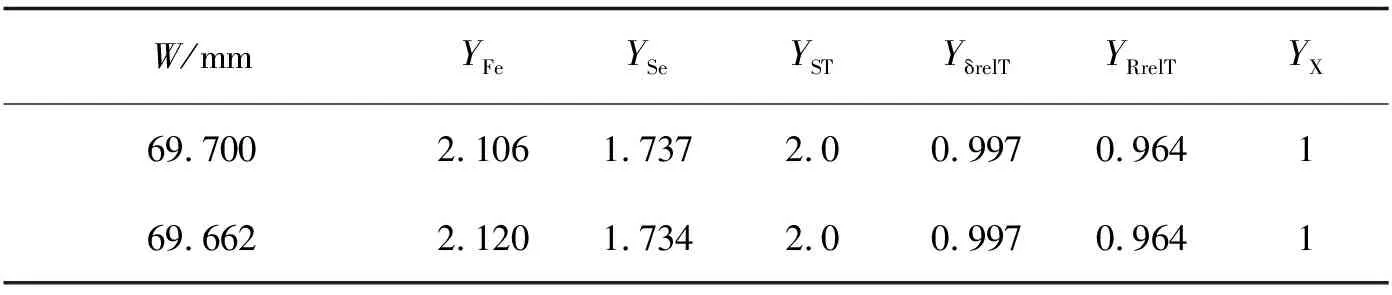
表9 不同公法线长度下齿根应力参数结果

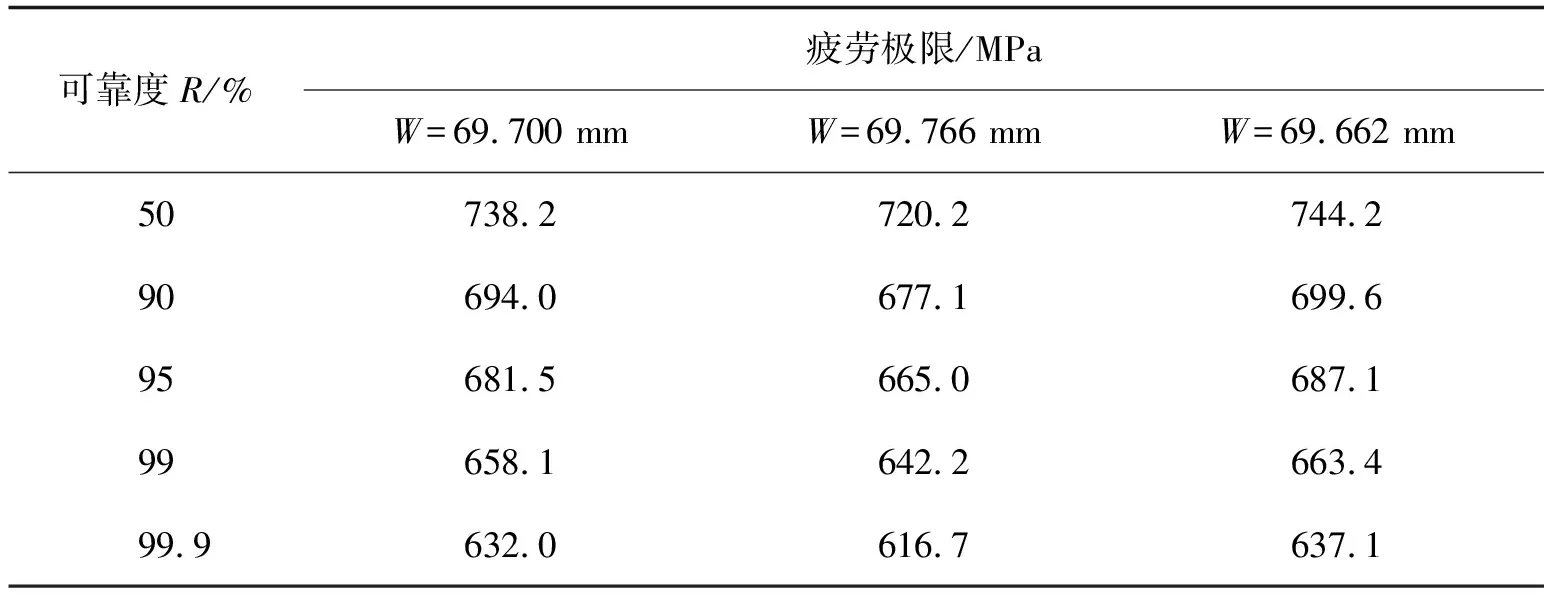
表10 不同公法线长度下不同可靠度的弯曲疲劳极限

由表10可知，在不同公法线长度下，不同可靠度的弯曲疲劳极限都大于名义公法线长度的对应值。与名义公法线长度情况相比，公法线长度为W=69.700 mm时的弯曲疲劳极限最大误差值为+2.50%，公法线长度为W=69.662 mm时的弯曲疲劳极限最大误差值为+3.33%，故不同公法线长度情况下弯曲疲劳极限的误差在+2.50%～+3.33%之间波动。

由式(5)可知，齿宽同样是影响齿根弯曲应力的重要参数，且齿宽和齿根应力成反比关系。试验齿轮的名义齿宽为b=30 mm。但实际齿宽在b=(30.0±0.1)mm范围内波动。结合公式(5)和(12)以及表3和8可得考虑不同齿宽下的不同可靠度的齿轮弯曲疲劳极限，如表11所示。

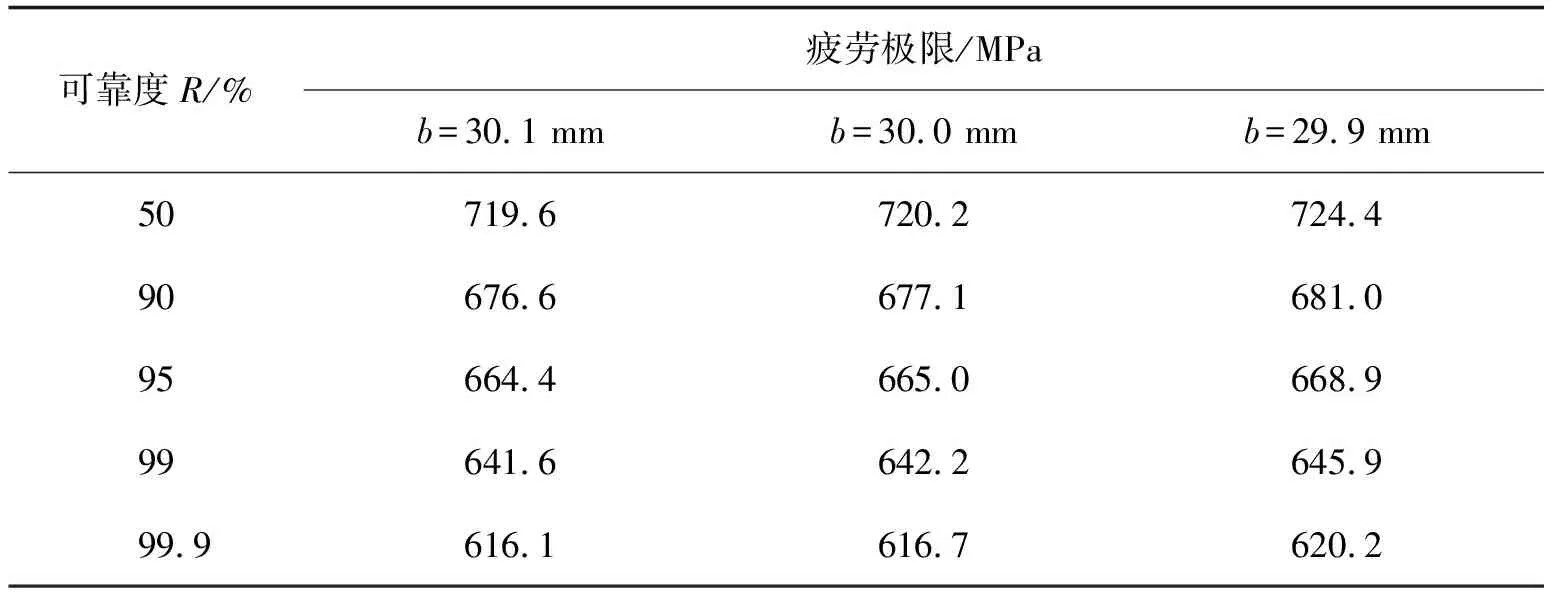
表11 不同齿宽下不同可靠度的弯曲疲劳极限

由表11可知，与名义齿宽情况相比，齿宽为b=30.1 mm时的弯曲疲劳极限最大误差值为-0.1%，齿宽为b=29.9 mm时的弯曲疲劳极限最大误差值为+0.59%，故不同齿宽情况下弯曲疲劳极限的误差在-0.10%～+0.59%之间波动。

4.2 装夹误差对弯曲疲劳极限的影响

试验齿轮装夹过程中存在装夹误差，在不考虑装夹时齿轮左右偏斜，则装夹误差体现在加载点位置变化上。加载点到齿轮中心的名义半径为re=66.3 mm。认为试验的装夹误差为±0.1 mm，即加载点到齿轮中心的半径在re=66.2～66.4 mm范围内波动。装夹误差如图11所示。考虑装夹误差的齿根应力参数结果见表12。结合公式(11)(12)及表8、12得到考虑装夹误差的不同可靠度的齿轮弯曲疲劳极限，见表13。

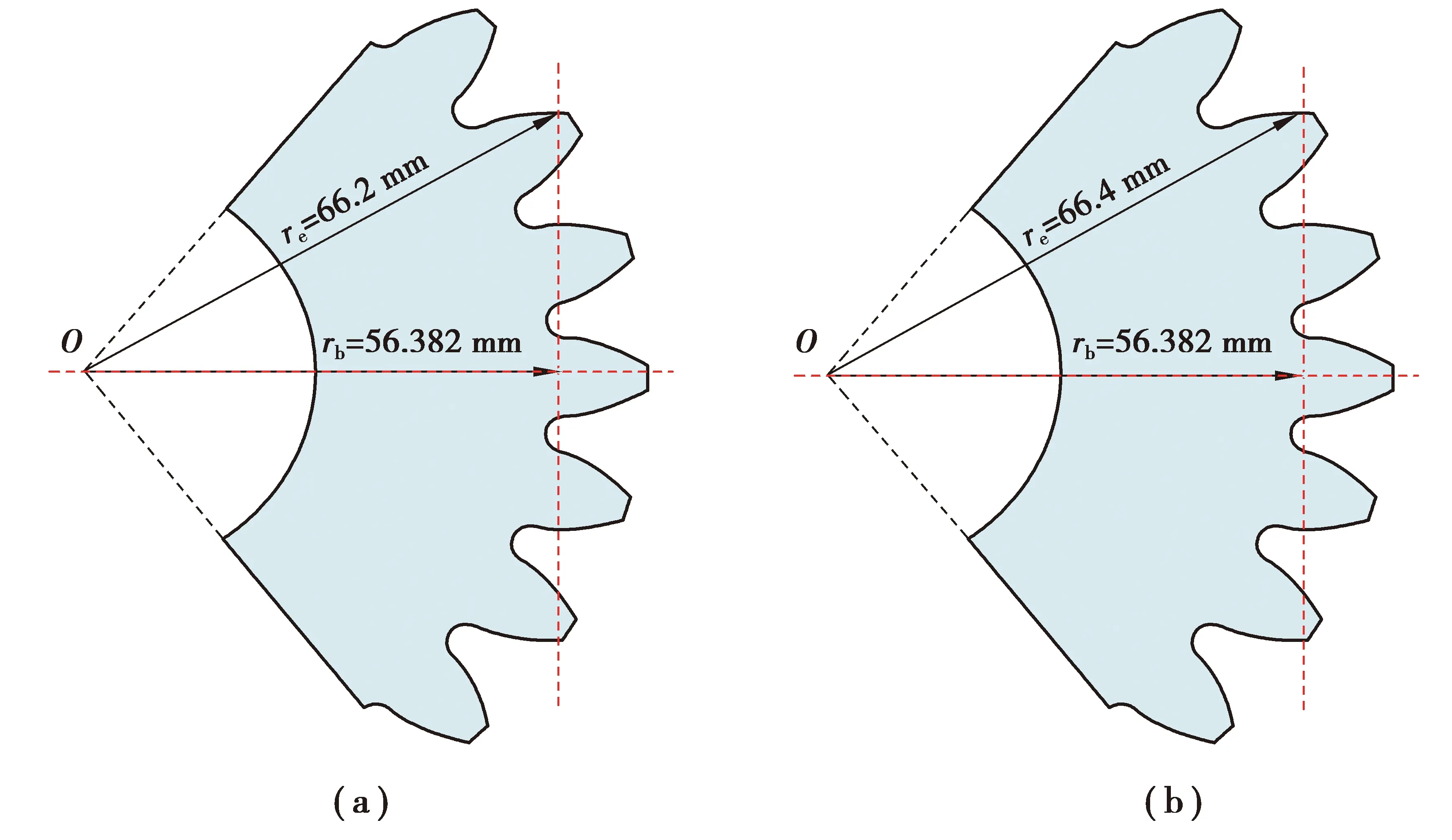
图11 装夹误差

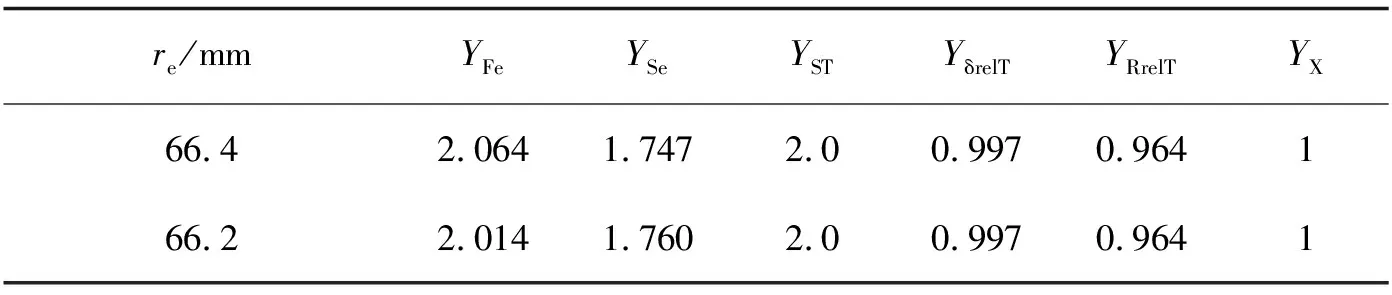
表12 不同装夹误差下齿根应力参数结果

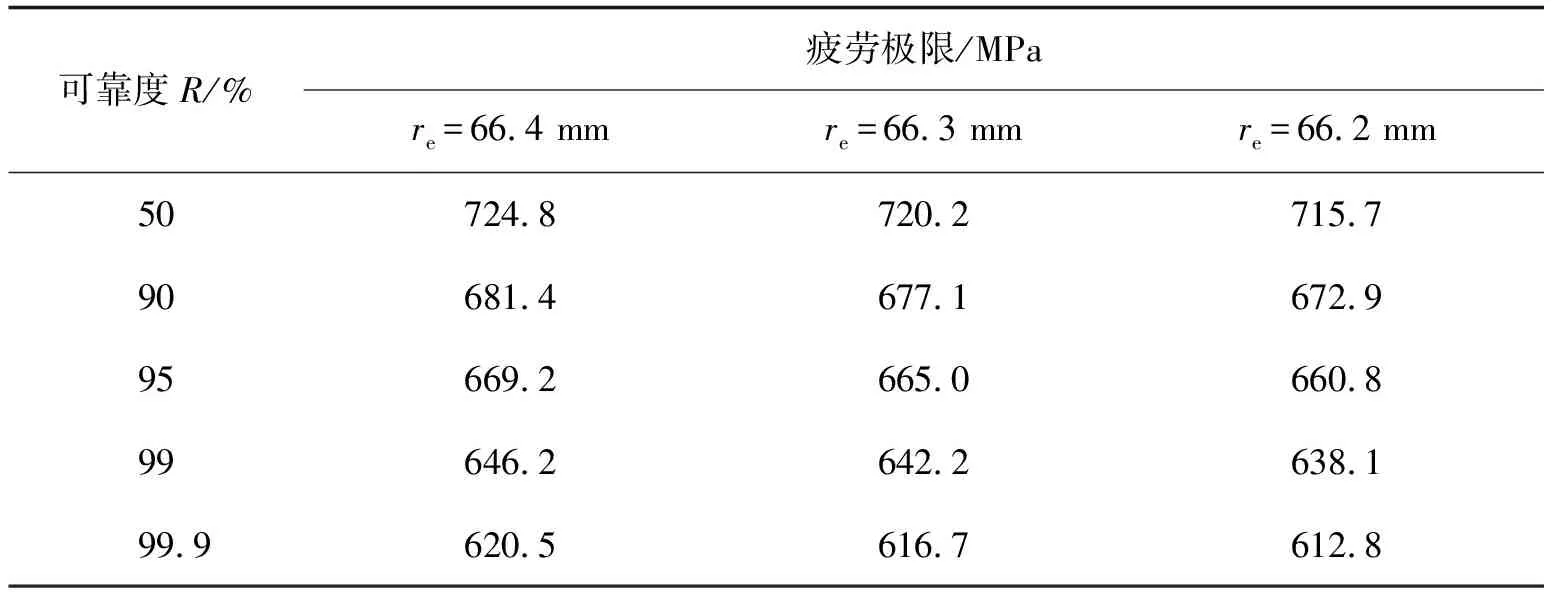
表13 不同装夹误差下不同可靠度的弯曲疲劳极限

由表13可知，与名义装夹位置相比，re=66.4 mm时的弯曲疲劳极限最大误差值为+0.64%，re=66.2 mm时的弯曲疲劳极限最大误差值为-0.64%，故不同装夹误差情况下弯曲疲劳极限的误差在-0.64%～+0.64%范围内波动。

4.3 设备加载精度对弯曲疲劳极限的影响

本弯曲疲劳试验采用的设备为Zwick Vibrophore 1000 kN试验机，由表1可知其动态加载精度为2%，结合公式(11)和(12)及表8，得到考虑设备精度影响下不同可靠度下齿轮的弯曲疲劳极限(见表14)。

表14 考虑设备精度的不同可靠度下的弯曲疲劳极限

由表14可知，与名义加载力相比，+2%加载力时的弯曲疲劳极限最大误差值为+2.07%，-2%加载力时的弯曲疲劳极限最大误差值为-2.06%，故由试验设备本身加载精度引起的齿轮弯曲疲劳极限误差在-2.06%～+2.07%范围内波动。

综上可知由齿轮几何误差以及设备加载精度引起的试验误差占比较大，因此在进行弯曲疲劳试验时，必须保证试验齿轮的几何精度以及试验设备的加载精度。上述4项误差同时出现极限值的概率极低，对误差值进行加权平均，得到综合考虑试验过程误差对弯曲疲劳强度极限的影响为2.43%。

5 结论

开展了齿轮弯曲疲劳试验方法研究，针对齿轮弯曲疲劳试验过程中的误差进行影响规律分析，得到如下结论：

1)根据标准制定弯曲疲劳试验方案，并开展齿根弯曲应力有限元仿真以及电阻应变片测试，试验方案计算弯曲应力与实测弯曲应力最大误差为8.7%，满足工程应用需求。

2)获得99%可靠度下18CrNiMo7-6喷丸齿轮弯曲疲劳强度极限为642 MPa，相比国标GB/T 3480—1997《渐开线圆柱齿轮承载能力计算方法》中MQ级的500 MPa，提高了28%，标准设计偏保守，为工程应用提供参考。

3)开展了弯曲疲劳试验过程中的相关误差对弯曲疲劳极限的影响分析，发现公法线长度偏差、齿宽误差、装夹误差和设备加工精度引起的误差分别为：+2.5%～+3.33%、-0.10%～+0.59%、-0.64%～+0.64%和-2.06%～+2.07%。弯曲疲劳试验时，应尽量保证试验设备的加载精度以及试验齿轮的制造精度。上述4项误差同时出现极限值的概率极低，对误差值进行加权平均，得到综合考虑试验过程误差对弯曲疲劳强度极限的影响为2.43%。