基于灰色数据预处理的WD-LSTM模型对乳制品质量安全风险的预测预警分析

陈晨，尹佳，董曼，穆书敏，陈锂，郭鹏程，文红*，桂预风*

（1.武汉理工大学理学院，湖北武汉 430070）（2.湖北省食品质量安全监督检验研究院，湖北省食品质量安全检测工程技术研究中心，国家市场监管重点实验室（动物源性食品中重点化学危害物检测技术），湖北武汉 430075）

乳制品富含营养物质，可促进机体营养均衡、调节人体免疫机能。在疫情爆发初期，国家卫健委发布的《新型冠状病毒感染的肺炎防治营养膳食指导》[1]指出，科学的营养膳食和每日合理的乳制品摄入是提高机体抵抗力、预防与救治新冠肺炎的有效途径。我国人均乳制品消费呈上升趋势，在行业迅速发展的同时，还存在部分企业重产量而忽视质量管控的现象，如何加强对乳制品质量安全风险的识别，提高生产企业对质量安全的控制能力，已成为保障我国乳制品行业健康发展迫切需要解决的问题。因此，对问题产品或可能存在的风险发出及时预警，实现乳制品综合性、动态性的监管和控制，提供靶向性监管技术支持是非常有必要的[2]。

当前，专家学者们针对乳制品质量安全风险预警从不同方向开展了有关研究。如Tian等[3]基于主成分分析对生乳质量安全指标体系风险进行了评估；Zhang等[4]构建了乳制品质量安全追溯系统，使供应环节可追溯；部分学者通过乳品供应链环节构建了乳制品质量风险预警指标体系[5,6]；陈嘉惠等[7]从三个层面分别对乳制品中的危害因素进行风险评估。此外，也有学者重点研究预警方法，将机器学习引入到食品风险的预测中，结合深度径向基函数[8]、集成极限学习机[9]、层次分析法[10]、BP神经网络[11]、LSTM 模型[12]等新型预警方法，对乳制品进行深度层次预警建模，在一定程度上实现了对乳制品安全风险预警的预测和防控。

上述研究成果为我国乳制品质量安全预警的实践提供了良好的理论基础和方法依据。但目前针对海量抽检数据的风险预警研究还鲜有涉及，主要利用传统的数理统计、典型病例通报等手段，对历史抽检数据进行食品安全状况的评价和风险警示，该方法是对食品安全状况的事后分析，缺少深度的分析与应用[13-15]。我国已积累海量的乳制品检测数据，乳制品按照分类不同和每年食品安全状况的调整，检测项目存在差异，且并非每天都进行抽样检测，同时数据中存在缺失检测结果的大量空值。现有的乳制品检测数据中包含众多灰色数据[16,17]，这种情况下，对数据进行预处理，从风险因素中挖掘分析，提炼出有价值的信息尤为重要。

因此本文利用我国乳制品历史抽检信息为数据源，依据国家标准对检测结果中的灰色数据进行去量纲化处理，采用softmax、数据分箱等方法进行数据预处理，通过小波对数据进行分解，对分解后不同细节的分量采用LSTM模型进行预测，并通过symmetric模式重构，输出最终的预测风险等级。通过测试集对本文构建的WD-LSTM组合模型预测准确度进行验证，该模型与同类模型相比有明显提高，可以为我国乳制品食品质量安全风险预警提供有力支持和参考。

1 材料与方法

1.1 实验材料

1.1.1 数据类型

本文选取2015-2020年对外公开以及检测机构内部自行检测获得的543 336条乳制品检测信息作为数据源，对原始数据进行分析可得，不同产品类别的检测信息存在差异，不同年份的检测信息也存在差异，为了更加全面的得到乳制品存在的风险预警，将所有项目都考虑在内，建立了乳制品风险预警的检验项目指标体系。指标体系共包括12个项目类别，76个检验项目，见表1。

表1 乳制品风险预警的检验项目指标体系Table 1 Index system of inspection items for risk warning of dairy products

由于获取的乳制品类别、年份以及检测项目的结果单位不同，存在数据属性类别多且格式杂乱，检验结果中信息不完全、不充分以及数据的多样化问题[18]，使其无法按照统一的规则转换为风险等级。此类灰色数据的高复杂度特点也提高了风险分析的难度，若直接将原始数据划分训练集和测试集，带入模型训练，所得到的结果可能存在较大的误差，因此需要对检测数据进行分类、去量纲化、数据分级等预处理。部分乳制品检测信息如表2所示。

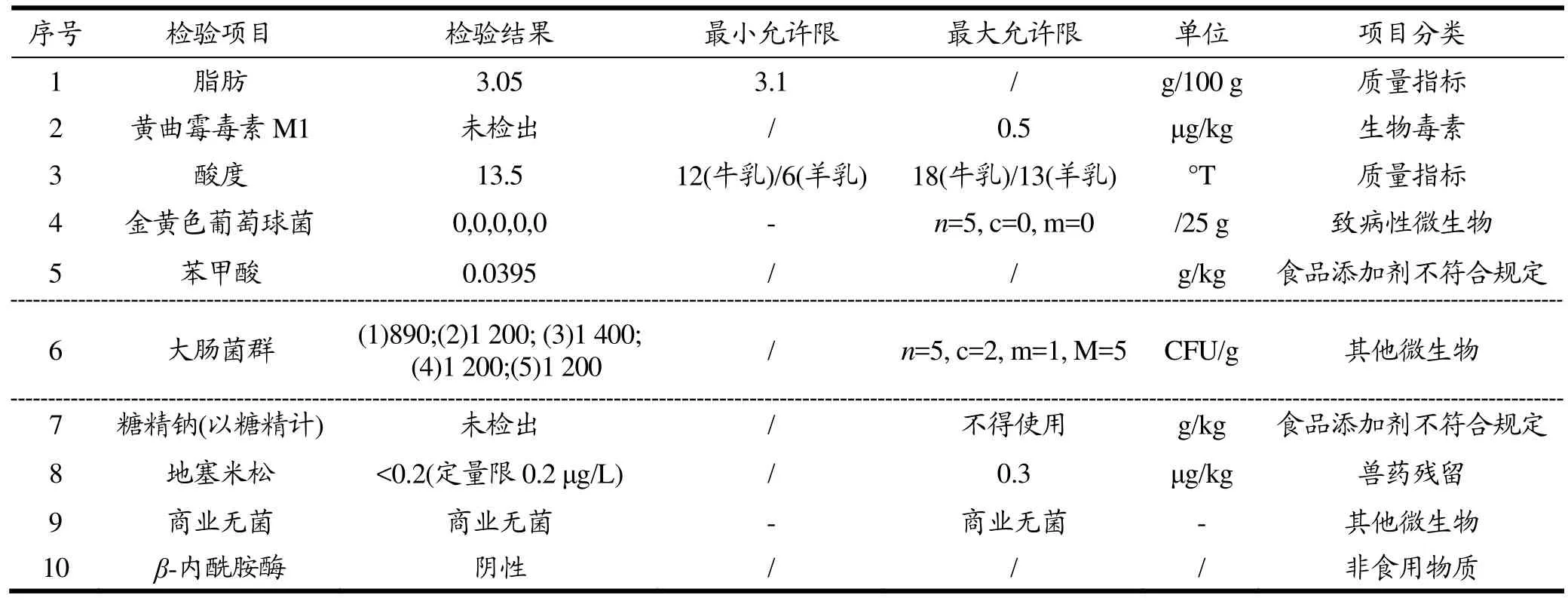
表2 部分乳制品检测信息Table 2 Partial detection information of dairy products

1.1.2 灰色数据预处理

对于上述缺省数据多且容易受到多种噪声污染的灰色数据，通常需要进行数据清洗、集成、变换等预处理。数据清洗主要是按照一定的规则和标准对存在缺失、奇异值和离群点等问题的数据剔除；数据集成则是将混杂的数据按照一定的特征相互匹配，以提高数据的统一性；数据变换是将原始数据转换为满足一定的条件数据，主要包括运用分箱、聚类等进行数据光滑、将数据集中汇总进行数据聚集、使用高级概念代替低级概念的数据概化、将原始数据按特征缩放规范、构造新的特征并汇合到原本特征集中[19]。

1.1.2.1 数据去量纲化处理

根据检测结果结合国家标准进行去量纲化处理。对于有最大允许限的项目Xi和有最小允许限的项目Yi，分别使用公式1、2对其进行标准化和去量纲化。

式中：

Xi和Yi——预处理后的检验数值；

xstandard和ystandard——标准允许限的值；

xi和yi——标准化数值。

1.1.2.2 数据分级处理

将去量纲化后的数据，根据检验项目类别的不同，将检验项目划分为四部分，分别是有最大允许限的项目Xi，有最小允许限的项目Yi，有限定范围允许限的项目Ri和检验结果为5个数值的项目Zi。该风险等级划分难以采用技术方法进行定量分析，故采用专家打分法进行风险等级的划分，邀请十位专家通过无记名投票的方法，得到专家确定的等级，使用加权评价法得到最终的评价结果，进行评判。结合检验项目风险等级划分标准和专家打分法将乳制品检验项目划分为5个风险等级，1级为安全无风险，2级为轻微风险，3级为轻度风险，4级为中度风险，5级为不合格产品。其中1~4级风险是符合国家标准的，但风险系数不同，而5级为不符合国家标准。具体划分标准见表3。

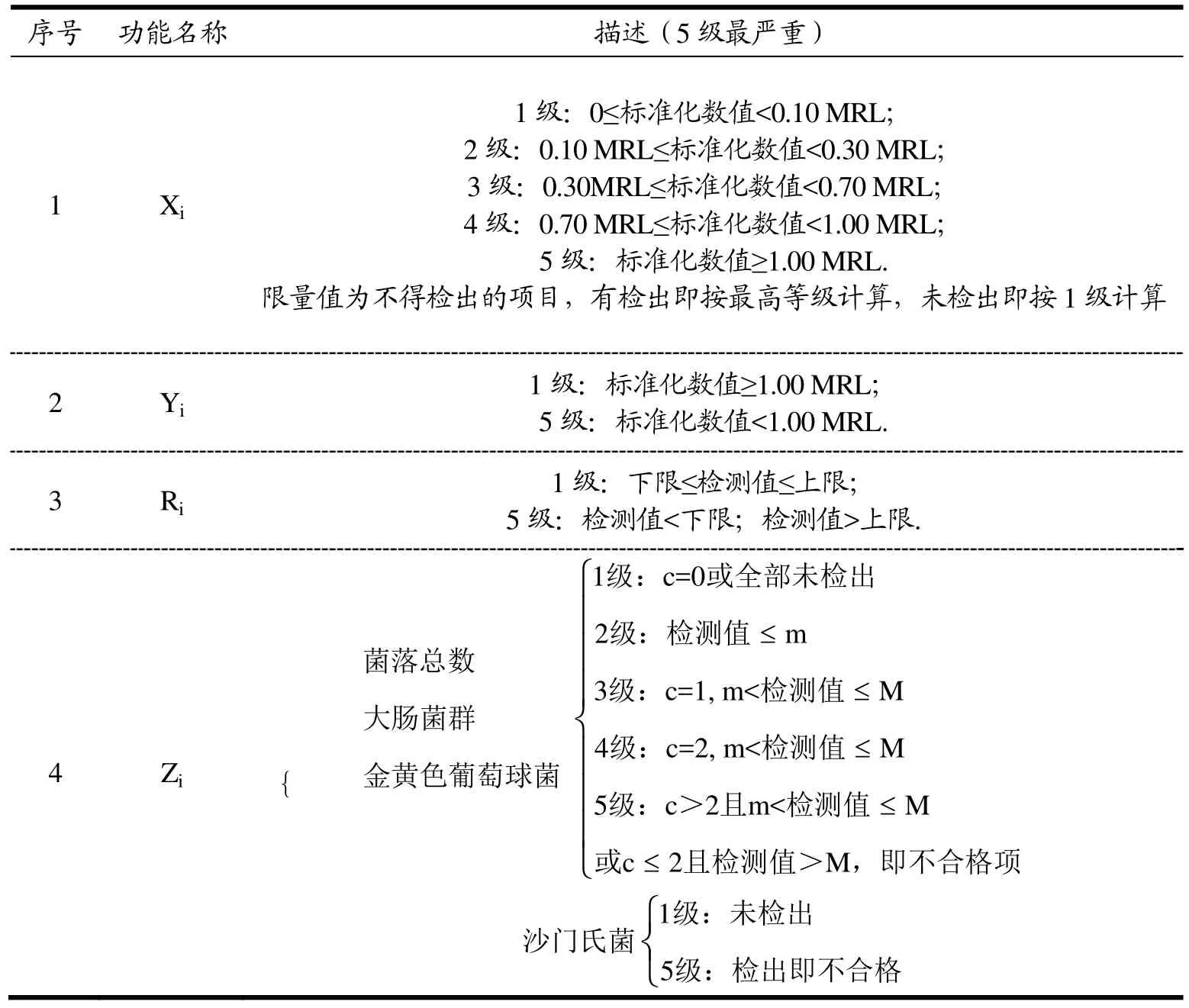
表3 检验项目的风险等级划分标准Table 3 Risk classification standard of inspection items

经过初步的数据预处理，去掉因条件缺失无法判别的数据后，共518 640条乳制品项目风险等级数据，其中1级499 371条，2级14 054条，3级3 993条，4级1 008条，5级214条。分析2015~2020年抽检数据，前5年数据的检测项目基本一致，2020年根据以往的检测结果，对风险较大和较少发现问题的项目进行了增减，致使2020年食品数据检测项目与前5年不一致，同时乳制品又分亚类、次亚类、细类，即使细类也包括了不同产品标准，其要求的项目也不同，最终造成即使同一细类产品中也存在项目不同的问题，使得用于分析的数据存在同类产品中项目缺失、同一标准产品中不同年度项目缺失问题。

针对此类处理后的灰色异构数据（区间灰数、离散灰数等），不同产品因所属食品类别不同而导致检验项目存在差异，故仅对有检测结果的项目风险赋予权重，对缺失项目予以忽略。由于低风险等级的数据占绝大多数，若直接采用简单的加权平均来获得最终的产品风险等级，会导致整体风险等级偏低，不能反应真实的风险。在食品安全风险等级预警中，风险等级高的数据对最终的风险等级影响更大，故应该有更大的权重，风险等级低的数据权重应该较低，且如果在某一产品中存在一个不合格项目，则该产品综合风险等级应直接划分为5级。为体现权重的变化，采用改进的 softmax函数来计算产品的综合风险等级（公式3），通过softmax函数中指数权重的变化来调节风险等级的权重。

式中：

Level——该产品的综合风险等级；

I——该检测项目的风险等级；

ωi——该风险等级在该产品中的占比。

1.1.2.3 数据分箱

乳制品检测数据的样品生产日期存在不连续，同一天生产日期样品数量也不相同，因此从时序序列考虑，数据存在不均匀分布，存在缺失和稠密性差异，需要对经过预处理的检测数据进行分箱处理后再带入模型进行预测研究。数据分箱即是将一定时间段的数据划分为一个数据集，并对分箱数据选择合适的方法处理，得到各分箱数据集的综合等级。本文采用每个自然日作为一个分箱，忽略缺失日期数据后进行时间压缩，并通过风险权重等比例映射的方法计算各分箱数据的综合等级。

1.2 风险预测方法与模型

1.2.1 小波分解（Wavelet Decomposition，WD）

小波分解是一种信号时频分析方法。它将一个波形分解成N个低频部分和M个高频部分的和，只针对信号的低频部分，即信号的趋势部分做进一步分解，而对于高频部分，也就是信号的噪声部分，不再继续分解，低频部分能够反映原始数据在平稳条件下本身的变化规律，高频部分包含原始数据的波动性和非线性等细节，所以小波变换可以对以低频信息为主要成分的信号做很好的表征[20]。图1为小波分解的示意图。

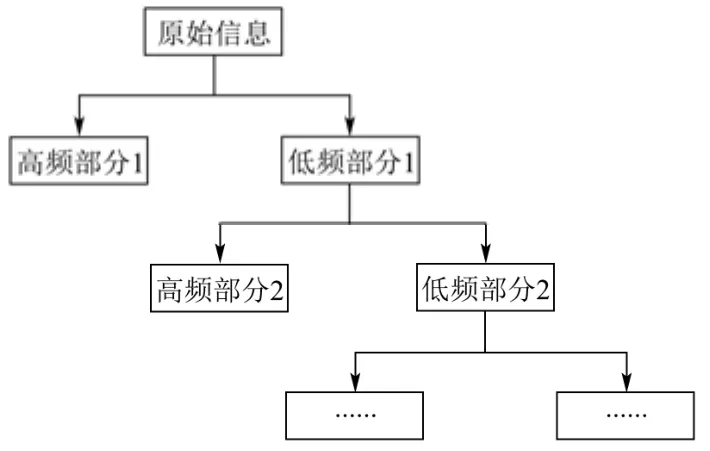
图1 小波分解示意图Fig.1 Wavelet decomposition diagram

由于食品类检测数据的随机性和不确定性，所得到的乳制品风险等级是一个非平稳的离散时间序列，若直接使用LSTM模型对该数据进行预测，其噪声会导致学习曲线复杂，且预测精度受到影响。经典的傅里叶变换（公式 4）尽管能对信号的整体内涵进行反映，但噪声会使其频谱复杂化；短时傅里叶变换可以部分定位时间，但由于窗口的大小是固定的，故仅对频率波动小的平稳信号适用。小波变换既保留了局部变换的思想，又将无限长的三角函数基换成了有限长的会衰减的小波基（公式5），能从不同尺度上对信号进行分解，按照频率自动调整窗口大小，提取非平稳信号的局部特征，是一种可以进行多分辨率分析的自适应时频分析方法[21]。

傅里叶变换公式：

小波变换公式：

式中：

t——时刻；

w——频率；

α——尺度因子，控制小波函数的伸缩；

τ——平移因子，控制小波函数的平移。

小波变换是对原始信号和小波基函数以及尺度函数做内积运算，因此一个小波基和一个尺度函数就能够确定一个小波变换。小波分解中使用到的小波函数具有多样性，同一个小波基函数可以通过平移和缩放生成不同的小波基，故对同样的问题，不同的小波基会产生不一样的结果。

根据本文所用数据波动性大，在时间上具有连续性的特征，选择小波分解中的一维多阶次离散小波分解，即 WaveDec算法，该算法是采用离散小波变换（Discrete Wavelet Transformation，DWT）得到原始信号的低频部分和高频部分，再将经过DWT变换后的低频成分再进行DWT变换，循环次数由分解层数决定。常用的小波族有很多种，每个小波族又有多种系数可供选择，其中Daubechies小波函数由法国著名的小波分析学者Inrid·Daubechies提出，简称为dbN，其中N代表小波的阶数[22]。dbN是非线性相位，没有固定的核函数，通常情况下，Daubechies族中消失矩的阶数越大，小波越光滑。结合数据特征选择了光滑性比较好的db8作为小波函数[23]，按照输入序列的复杂情况分解为频率不同的子序列，各个子序列包含原序列中不同频率的信息，且其长度不发生改变，提取小波分解系数对其进行分析，各子序列带入模型得到预测结果后再通过symmetric模式进行重构。

1.2.2 长短期记忆神经网络模型（Long Short-Term Memory，LSTM）

LSTM是基于传统循环神经网络RNN的一种改进，不仅能学习时间规律，还可以适应非线性的复杂数据。LSTM在RNN的基础上新增了一个间隔多个时间步长来传递信息的被称为“门”的内部机制，可以调节信息流，循环结构之间保持一个持久的单元状态不断传递下去[24]。“门”结构中包括激活函数sigmoid，与tanh函数将值压缩到-1~1之间不同，sigmoid函数会把值压缩至0~1，更加有利于“门”对信息的保存或遗忘。

1.2.3 WD-LSTM组合模型

本研究在预测乳制品风险等级时，使用的是WD-LSTM组合模型，具体流程见图2。该模型在单个LSTM模型的基础上，增设能够适应非平稳信号的小波分解，非线性、非平稳且波动性强的原始序列通过小波分解得到各分量，再将各分量分别代入LSTM模型，模型根据输入序列计算其对后面的综合风险等级的影响，同时考虑到后面的综合风险等级对该序列的影响，前后影响值的大小决定了保留或遗忘多大程度，并且通过单元状态实时更新到下一步的预测。各分量预测结果经过symmetric模式重构，得到最终的预测结果。

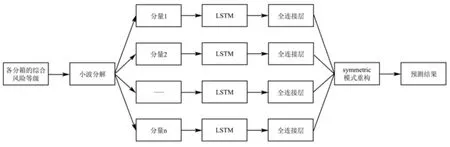
图2 WD-LSTM组合模型流程图Fig.2 Flow chart of WD-LSTM combined model

1.2.4 模型参数的搭建和设置

为实现LSTM神经网络的双向构造，方便模型训练，需预先确定网络结构。本文构建的是一个4层神经网络，将待预测的前20个乳制品综合风险等级作为神经网络的输入，即输入层的神经元个数为20；待预测的乳制品综合风险等级作为网络的输出，即输出层的神经元个数为1；中间设置了一个LSTM层和一个全连接层作为两个隐藏层，其中全连接层在整个网络卷积神经网络中起到“特征提取器”的作用，结点数设定为16。依据本文所用的数据集和实际目标需求，确定相关参数的调整方向，采用能更好反映预测值误差的实际情况的平均绝对误差（Mean Absolute Error，MAE）作为损失函数，优化器使用能基于训练数据迭代地更新神经网络权重的Adam优化算子，数据集按照2:1的比例划分为训练集和测试集，一次训练所选取的样本数为64，训练轮次定为100。

1.2.5 经验模态分解（Empirical Mode Decomposition，EMD）

经验模态分解可以对非线性非平稳信号的进行分析处理，能依赖信号本身的特征做自适应分解，无需事先设定基函数，也克服了基函数存在的无自适应性问题；分解后得到的各层信号分量，即为一系列的固有模态函数（Intrinsic Mode Functions，IMF），任何信号都可以被分解成若干个IMF之和，各分量分别代表原始信号中各频率分量，按照由高到低的频率顺序依次排列，可以反映原始信号的局部特征[25]。

1.2.6 数据分析

本文使用编程语言Python 3.7.0，利用Tensorflow作为搭建平台。采用改进的softmax和数据映射方式对灰色数据进行预处理，将分箱数据集的综合等级时间序列输入到建立的WD-LSTM组合模型，进行风险预测预警分析，通过 matplotlib画图软件包绘制预测各级分量和风险预测示意图，预测准确率作为评估模型优劣的指标。

2 结果与讨论

2.1 灰色数据分箱及等级划分

2.1.1 分箱时间间隔的选择

分箱处理的时间间隔会直接影响数据集个数，从而影响预测结果的准确性，因此，选择合适的时间间隔至关重要。本文分别采用了1、4、7、15、30 d为一个数据集进行分箱处理，计算综合等级。经过对比，若采用7 d及7 d以内进行分箱，间隔较短会导致缺失值过多，需要插值的数据过多而影响真实性，且使学习曲线更加复杂；而采用太长的时间间隔，则会导致数据集过小，导致模型学习过程太短，预测误差变大。结合实际情况和模型的预测效果，最终选择采用每个自然日作为一个分箱，对缺失数据的日期予以跳过处理。

2.1.2 分箱数据综合等级划分

试验中分别采用5种不同的综合风险等级公式，对数据分箱计算风险等级。

式中：

i——风险等级；

ω(i)——风险等级i的占比。

Y4和Y5当数据集中只含有一种风险等级时，该风险等级即为该分箱的综合风险等级，数据集中的风险等级不唯一时，Y4通过公式9计算每个风险等级的权重，对权重最大的两个风险等级求平均值，若平均值为小数则采用向上取整；Y5通过公式10计算出该数据集的综合风险，根据产品原始的各风险等级占比，使用风险权重等比例映射的方法，按照相应的比例使用公式11对综合风险进行划分。部分数据集不同计算公式的风险等级对比见表4。

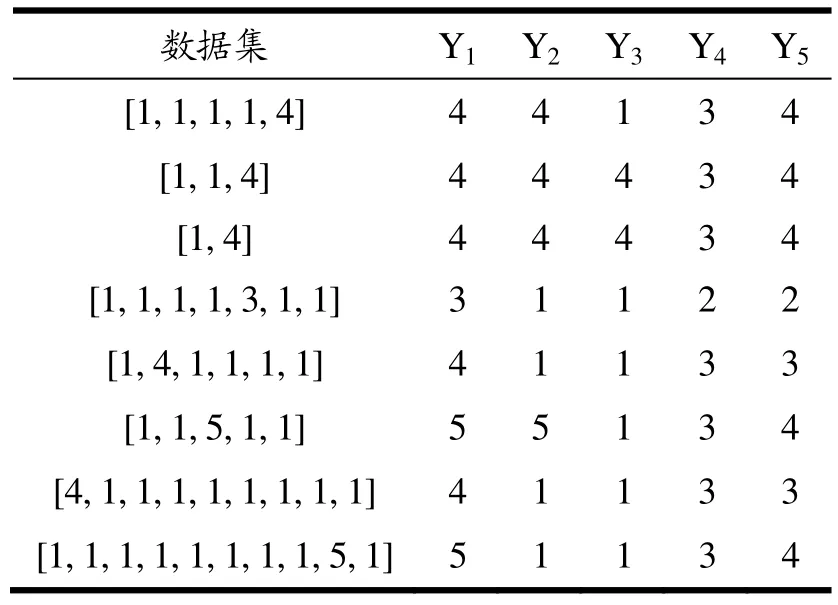
表4 部分数据集不同风险等级公式对比Table 4 Comparison of formulas for different risk levels of some dataset

经过对比，认为公式6会导致对风险等级高的产品赋予过大的权重；公式7和公式8对公式6的指数进行了调节，但导致高风险等级权重过小，难以确定合适的权重；Y4采用了平均法，无法体现对风险等级的侧重；通过得到的风险等级与原始数据的风险程度比较，公式10更符合实际风险的划分。因此，本文采用公式10结合公式11计算风险等级，共得到14 037条综合风险等级，其中1级13 171条，2级49条，3级151条，4级542条，5级124条。

2.2 结果分析

2.2.1 模型训练

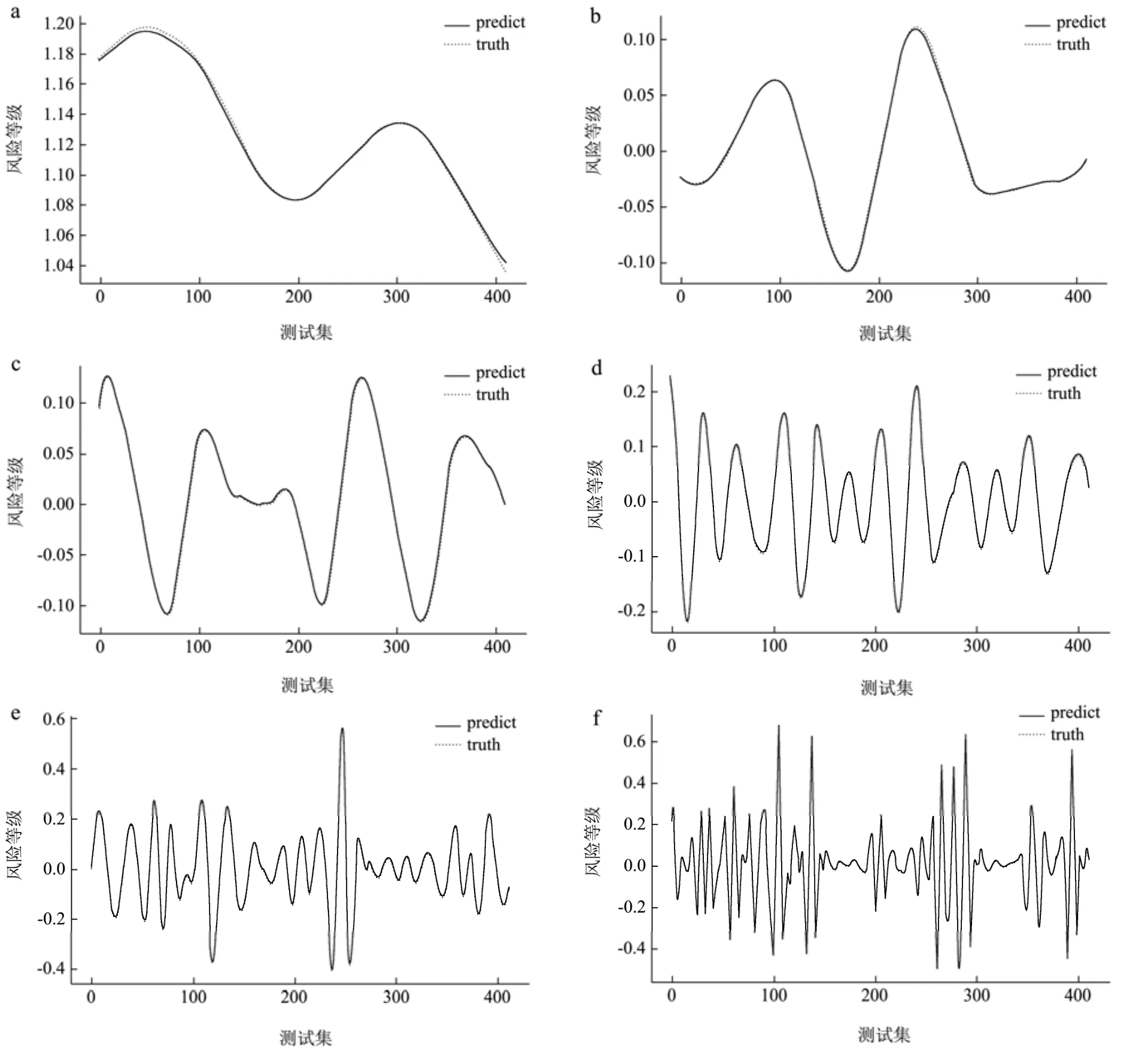
在本文中，将数据分箱后的综合风险等级输入到建立的组合模型，其中前2/3作为训练集，1/3作为测试集，对其进行小波分解，再通过长短期记忆神经网络对小波分解得到的各个分量进行预测，将各分量重构后输出最终的预测结果。其中测试集用来验证该模型的精确度。图3为N1地区的乳制品数据经小波分解后各级分量预测示意图。橙线为各分量的真实值，蓝线为各分量的预测值。

图3 N1地区乳制品数据WD各级分量预测示意图Fig.3 Schematic diagram of WD components of dairy products data in N1

2.2.2 有效性分析

由于本文构建的LSTM 模型初始权重的随机性，在每轮预测时可能会存在误差，为验证该模型的稳定性，连续将该模型运行5次，得到该模型的平均误差为0.03，波动较小，因此该模型的运行结果是可靠的。为了全面验证模型的有效性和适用性，将29个地区的风险等级序列经小波分解后带入LSTM模型进行预测，采用平均绝对值误差（Mean Absolute Error，MAE）和平均绝对百分比误差（Mean Absolute Percent Error，MAPE）衡量该模型的误差（公式 12、13），该值越大表明误差越大，当预测值与真实值完全吻合时等于0。该模型在29个地区中预测的最大MAE为0.07，最大MAPE为2.71%，整体MAE和MAPE的平均值为0.02和0.83%。通过公式14，可以计算出该模型预测的准确率，准确率最低为86.49%，其余均在92.45%以上，整体平均准确率为97.54%，标准偏差为0.03。该结果表明，本文建立的WD-LSTM模型可以对乳制品质量安全风险等级有较好的预测。29个地区的预测结果见表5。

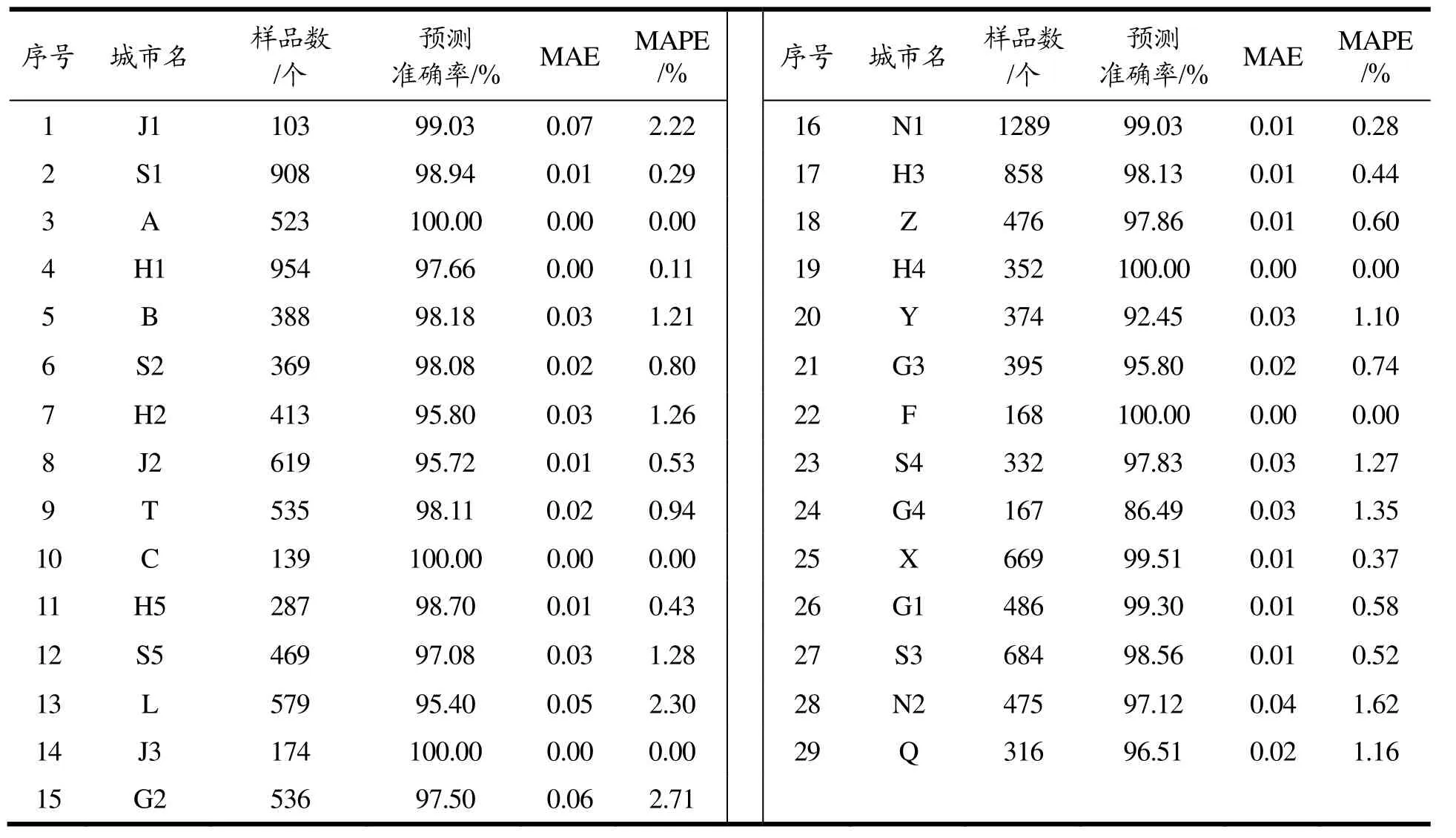
表5 29个地区乳制品风险等级预测结果Table 5 Prediction results of risk grade of dairy products in 29 regions

MAE的计算公式：

MAPE的计算公式：

式中：

A——预测准确率；

B——预测正确的样本数量；

C——测试集的样本数量。

以N1地区乳制品质量安全预测结果为例，图4中，橙线为分箱数据集的综合风险等级，蓝线为WD-LSTM模型得到的预测风险等级（图a为预测风险等级，图b为取整后的预测风险等级）。由图中两种颜色的线段重合度可以看出，二者吻合度较高，说明该模型预测的准确性较好。

图4 N1地区乳制品风险预测示意图Fig.4 Schematic diagram of risk prediction of dairy products in N1

2.2.3 模型比较与分析

本次研究中，还分别构建了EMD-LSTM模型和有选择性重构且间隔为2的WD-LSTM模型，通过对数据采用不同的分解方法和选取不同的间隔来验证本文所使用的WD-LSTM模型在乳制品灰色数据上的拟合效果，表6为不同模型的预测准确率对比。

模型1是EMD-LSTM组合模型。对29个地区的2015~2020年乳制品检测数据做同样的预处理后，模型1将分箱数据带入EMD模型进行分解，将得到的各分量IMFs输入LSTM模型，预测结果表明，准确率最低仅为29.73%，整体准确率仅为86.97%，标准偏差为0.14。总体上看，模型1的准确率与小波分解-LSTM模型相比明显降低，且预测结果差距较大，不够稳定。平均MAE和MAPE分别为0.27和12.95%，且最大MAE和MAPE为1.95和54.91%，均明显高于WD-LSTM模型。由于EMD的模态混叠现象严重，会导致特征提取、模型训练、模式识别变得困难，IMF的特征不再是单一尺度[26]。因此，经过 EMD-LSTM模型分解后得到的各个分量IMFs波动仍然较为强烈，预测误差变大，从而导致重构后的模型预测误差较大。而小波变换频带是固定的，在带入模型预测前采用了具有更好的光滑性的db8小波基，有效的减小了各分量变化趋势的复杂性，分解后得到更光滑的的各分量也使得LSTM模型预测的准确度更高[27]。

模型2与本文建立的WD-LSTM模型类似，也是一个小波分解后将各分量代入LSTM预测的组合模型，对各分量有选择性的进行重构，重构后的序列再通过LSTM模型进行预测。在本文中有选择性重构所选择的间隔为 2，以验证间隔大小对该模型产生的影响。该模型与对原始序列进行平滑处理类似，会对部分细节信息有所损失，预测精度也有所降低，J1地区的准确率仅为66.67%，整体准确率为92.42%，标准偏差为0.07，平均MAE和MAPE分别为0.09和4.83%。故对比表6，在整体预测精度和误差上，本文所用的WD-LSTM模型均优于模型1和2。

表6 不同预测模型的准确率对比Table 6 Comparison of accuracy of different prediction models

续表6

3 结论

针对目前备受关注的乳制品质量安全问题，本文对近六年具有“贫信息”且类型多样性的乳制品灰色数据进行了充分的预处理，按检测项目性质的不同划分为四部分，结合专家打分法得到各检测项目的风险等级后分别代入改进的softmax公式，并根据产品中风险等级的占比对数据分箱划分区间。将29个地区的检测数据转换为综合风险等级后带入构建的WD-LSTM模型，得到整体准确率为97.54%，标准偏差为0.03，MAE和MAPE的平均值为0.02和0.83%，而本文设置的对比模型 1、2的整体准确率分别为 86.97%和92.42%，标准差分别为0.14和0.07，平均MAE分别为0.27和0.09，平均MAPE分别为12.95%和4.83%。该预测结果意味着本文构建的WD-LSTM模型预测准确性较好，且在精度和稳定性方面均优于类似的相关模型，说明该模型对乳制品质量安全预测是准确且有效的，可以起到对乳制品质量安全中潜在的风险防控和监督的作用，并在日常检测的过程中提供技术支持。对于未来的工作，可以从以下两个方向进行改善：一是通过优化模型算法，调整参数，使模型在其他类别的产品得以推广使用；二是研究如何对长时间序列的内在关联性和数据严重不平衡使用更好的处理方法。