基于误差校正的高精度三维测量系统

李博宇

(中国航发北京航空材料研究院 信息中心,北京 100095)

基于结构光的三维重建技术是指通过某种投射装置将具有一定模式的结构光投射到场景中，再用相机捕获这些被场景中物体调制了的结构光图案，并从拍摄的图像中恢复出场景的三维信息。该技术已经被广泛应用于三维建模[1-3]、逆向工程[4-6]和生物医学[7-10]等领域。近年来，随着数字投影技术的发展，基于投影仪与相机的结构光测量系统得到了越来越多的研究与应用[11-14]。

使用投影仪结构光系统进行三维测量的首要问题是如何由拍摄的投影图像恢复出每个像素点对应的相位值。标准的四步相移算法是一种常用的相位恢复方法[15-16]，该方法能够有效地抑制系统的观测噪声，因此被广泛地使用。然而，由于投影仪和摄像机都存在一定的非线性特性，直接采用四步相移算法恢复的相位图像存在一定的误差，进而降低了三维测量的精度。现有的误差校正方法可以分为主动校正法和被动校正法。主动校正法指通过某种算法改变投影仪投射出的图像灰度值，进而抑制整个系统的测量误差[17-19]。被动校正法指不改变投影图像，直接对计算得到的相位误差进行补偿，例如通过建立查找表[20]、提取光带图像特征点[21]和分区域补偿[22]等。但这些方法存在计算量大、有累积误差或容易受环境光影响等问题。通过研究发现，投影仪结构光系统中存在的误差与被测物体无关，并且可以用二次多项式来表示。因此，笔者提出了一种基于二次型误差校正的高精度相位恢复算法，并用于三维测量。实验证明笔者提出的算法比现有算法精度更高。

1 系统构成

结构光探测系统的测量精度与探测距离有关，减小探测系统与被测物体之间的距离可以提高系统的测量精度，但同时也会减小探测系统的视场范围。为了对大尺寸物体进行精确的三维测量，往往需要在物体的一侧布置2个甚至多个结构光测量模块。而且为了实现物体的360°重建和测量，需要在物体的不同方向布置多个测量模块，并且应保证各模块的视场范围存在足够的重叠区。虽然利用探测系统与被测物体之间相对运动的方式也可以实现物体的全方位扫描，但这会降低系统的稳定性并增加系统的扫描时间。综合考虑上述因素，笔者采用了三维测量系统硬件构成，如图1所示。

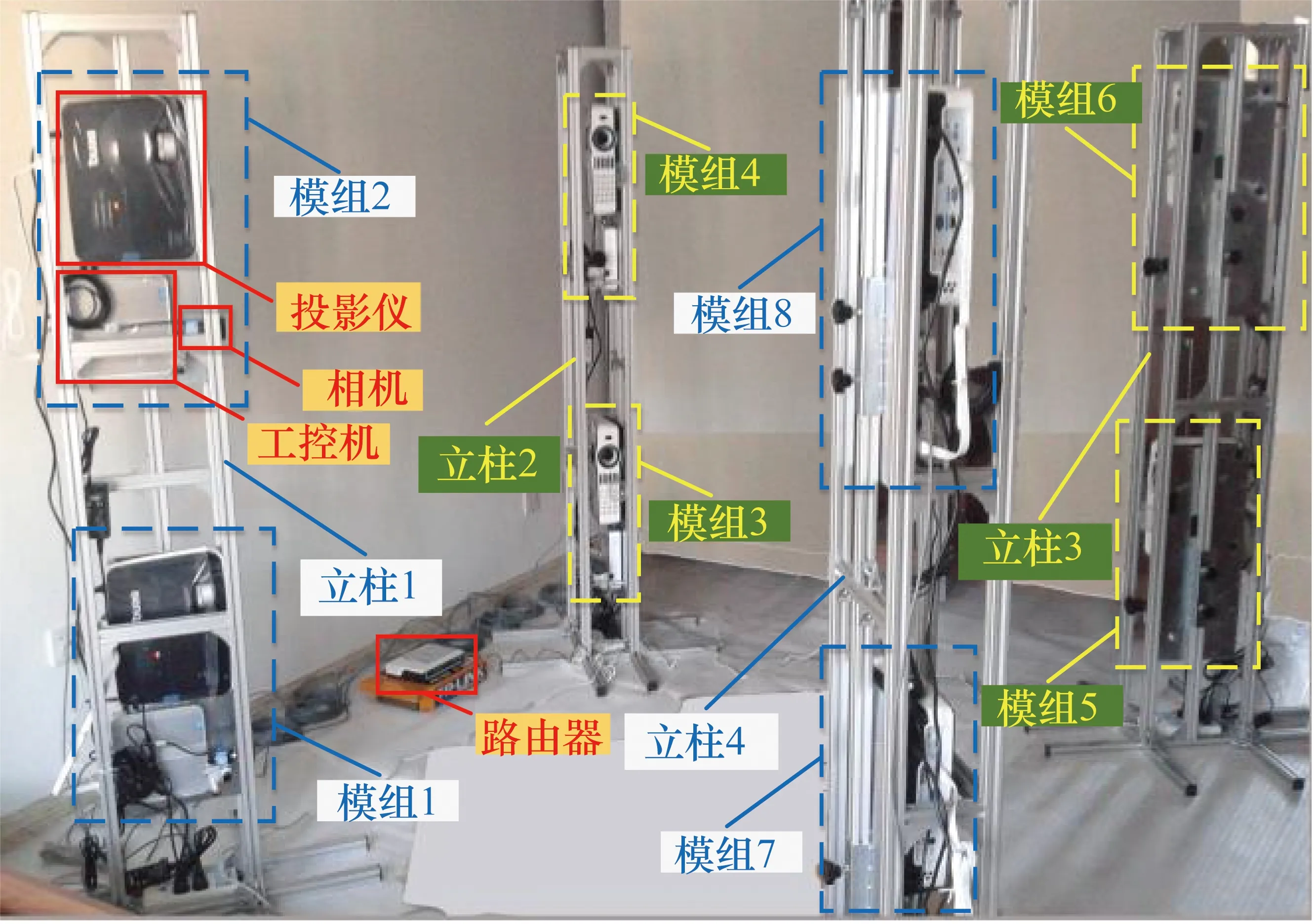
图1 系统硬件构成

系统由4根立柱构成，这些立柱被放置在一个边长为2 m的正方形的4个顶点处。每根立柱包含垂直安装的2个模组，即图1中虚线框标记的部分。每个模组由1个工控机、1个相机和1个投影仪构成。工控机控制投影仪向场景中投射一系列的结构光图案，并通过相机采集被场景调制后的结构光图像。用户计算机通过路由器与这8个模组相连，相位恢复和三维测量算法均在用户计算机上完成。为了避免相邻模组投射的图像相互影响，同时提高系统的采集速度，处在对角线上的两个模组同时工作，其工作顺序为模组1和模组6、模组2和模组5、模组3和模组8、模组4和模组7。

系统的标定包含2个方面：单个模组的标定和模组间的标定。由于本研究在融合不同视场数据进行三维重建时采用的是迭代最近点(Iterative Closest Point，ICP)算法，因此仅需要根据各个模组的安装位置和角度估计一个初始值，不需要进行模组间的精确标定。在标定单个模组时，采用红蓝棋盘格作为标定板，首先,用投影仪分别投射横、竖光栅条纹，并用相机进行图像采集；然后,在相机图像中提取出棋盘格角点坐标，并通过相位恢复算法找到投影图像中的对应角点；最后,采用张正友标定法完成单个模组的标定。详细方案可参考文献[23]，下面将对相位计算及误差校正方法进行详细论述。

2 初始相位恢复

2.1 基于四步相移的相位恢复

标准的四步相移算法是一种基于相位移原理的相位恢复算法，对测量系统的偶次谐波及观测噪声具有较好的抑制作用。该方法利用投影仪依次向场景中投射相差为π/2的4幅正弦光栅图像，并利用相机采集这些被物体表面调制了的光栅图像，假设相机采集的4幅图像为

(1)

式中：I′(u,v)为相机采集图像的平均灰度值;I″(u,v)为采集图像的灰度变化幅值;φ(u,v)为相机坐标系中像素点(u,v)处的相位值。由式(1)可以推导出计算相位值φ(u,v)的函数表达式，并将其取值转换到(0,2π]区间，可得式(2)。图2为四步相移算法求解的相位示意图。

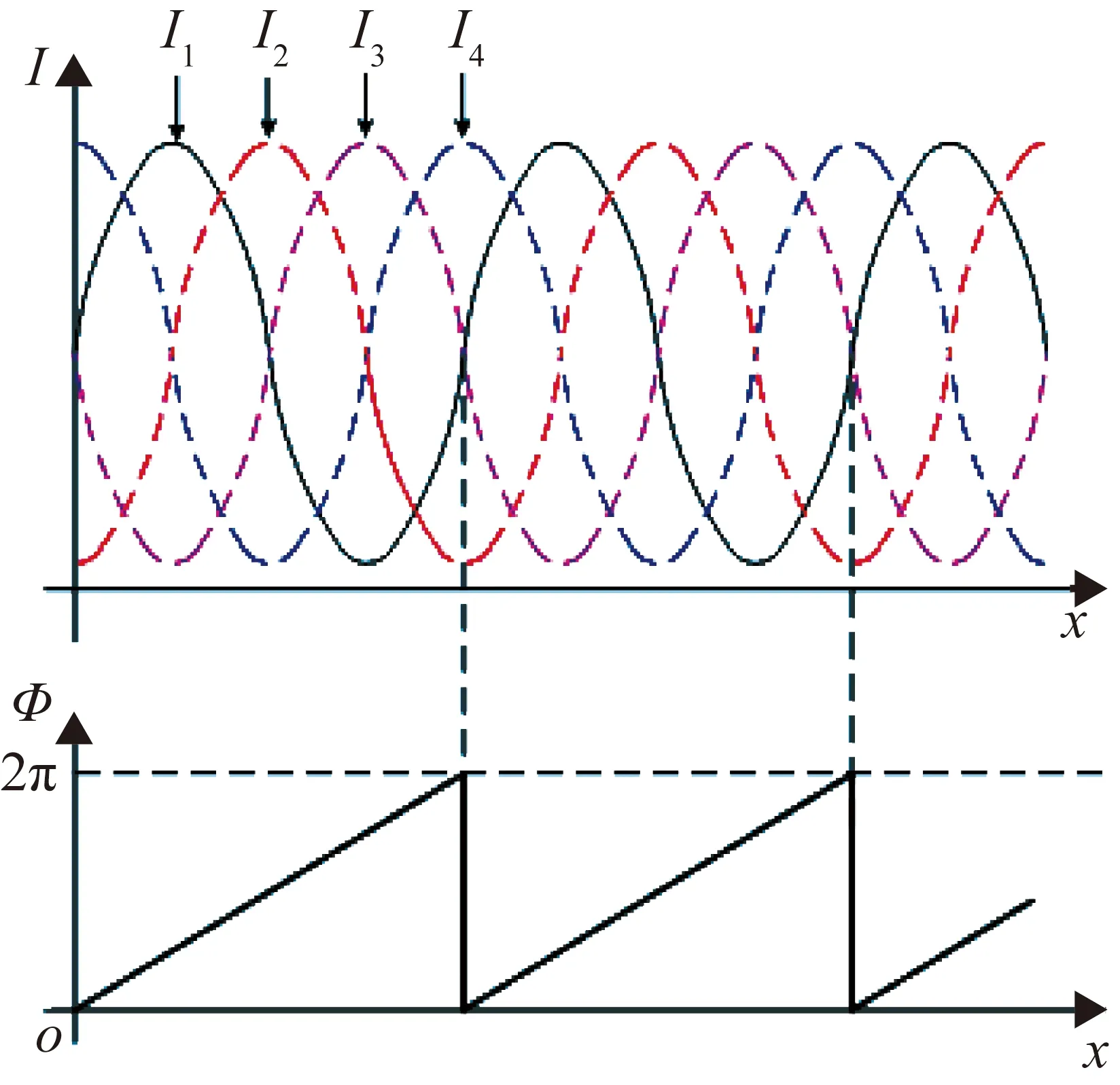
图2 四步相移算法求解相位示意图

φ(u,v)=atan2(I4-I2,I1-I3)+π

(2)

式中：Ii为Ii(u,v),i=1,2,3,4。

在实际的测量过程中，由于投影仪视场及相机视场不能完全重合，并且物体之间存在一定的遮挡，投影仪投射出的图像在场景中存在一定的盲区，这样会导致从另一个角度拍摄的图像中存在没有光栅条纹的区域。如果直接对整幅图像进行相位求解，会在上述盲区产生大量的噪声点，如图3(a)所示。为了消除这些噪声点，需要在图像中区分出有效数据区域和盲区。

首先，计算出4幅相移图像的灰度均值。

(3)

然后,判断每一个像素点处的灰度值是否满足式(4)、式(5)两个条件。

|I1(u,v)-I′(u,v)|>ε且|I3(u,v)-I′(u,v)|>ε

(4)

|I2(u,v)-I′(u,v)|>ε且|I4(u,v)-I′(u,v)|>ε

(5)

式中:ε为灰度阈值，该值可以通过实验确定。如果像素点(u,v)满足式(4)或者式(5)，则认为该点为有效像素点；否则，认为该点为盲区中的像素点。图3为相位求解结果，其中图3(b)是在有效数据区域进行的相位求解，可以看到所有的噪声点都被过滤掉了。

图3 相位求解结果

2.2 基于三频外差的相位解包裹

为了实现基于投影结构光的三维测量，需要计算出相机图像中每个像素点的相位值。由式(2)计算出的相位值取值范围为(0,2π]，因此需要对上述恢复出的相位图像进行解包裹处理。本研究采用三频外差[24-25]的方法实现相位解包裹。

外差原理是指将2幅较高频率的相位图像作差，可以得到一幅频率较低的相位图像。例如相位图像φa(u,v)包含的正弦条纹周期数为Ta=6，相位图像φb(u,v)包含的正弦条纹周期数为Tb=5，则2幅图像做差后得到的相位图像为

(6)

其中包含的正弦条纹周期数为Tc=Ta-Tb=1。图4给出了外差算法计算过程示意图，分别为相位图像φa(u,v)、φb(u,v)、φc(u,v)的第100行数据。由于得到的相位图像φc(u,v)只包含一个相位周期，所以每个像素点的相位值都可以区分开来。

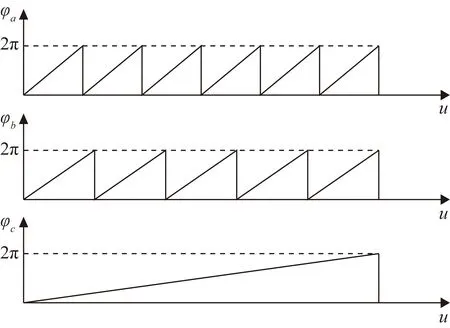
图4 外差算法计算过程示意图

在实际的相位解包裹过程中，仅使用2个频率的光栅图像会对投影仪和相机的精度提出非常苛刻的要求，因此使用三频外差方法进行相位展开。即先后向场景中投射周期数为70、64、59的四步相移图像，并恢复出3个频率的相位图；然后，由前2个频率的相位图像作差得到周期数为6的相位图，由后2个频率的相位图像作差得到周期数为5的相位图；最后，由这两个相位图像计算出只包含一个周期的相位图像。根据该相位图即可反解出3种频率光栅图像的绝对相位值[25]，本文仅对周期数为64的光栅图像进行绝对相位展开，即相位范围为(0,128π]。

3 误差校正

3.1 相位误差分析

按照2.2节给出的相位恢复方法，向一个标准平板投射3组四步相移正弦光栅图像，并根据相机采集的图像进行了相位恢复，标准平板的相位图像如图5所示。这里截取的是横坐标范围[1,900]像素、纵坐标范围[121,721]像素内的有效数据区域。

图5 标准平板的相位图像

由图5可以看出，相位恢复的结果是正确的。为了进一步以定量的方式分析相位恢复的精度，提取该相位图像的第200行，如图6(a)所示。标准平板上恢复出的相位值应该是完全线性的，即恢复出的相位图像的某一行应该是一条直线。因此，将图6(a)中的相位数据进行直线拟合，并将这些相位数据与拟合得到的数据作差，得到如图6(b)所示的误差曲线。所有误差中的最大值为3.2059 rad，最小值为-6.0890 rad，标准差为1.9430 rad。从该误差曲线可以看出，除了上下波动外，其整体分布也具有一定的规律，即呈现类似抛物线的形状。如果能够用一个二次多项式对相位值进行校正，那么将有效地减小相位误差，使其成线性分布。

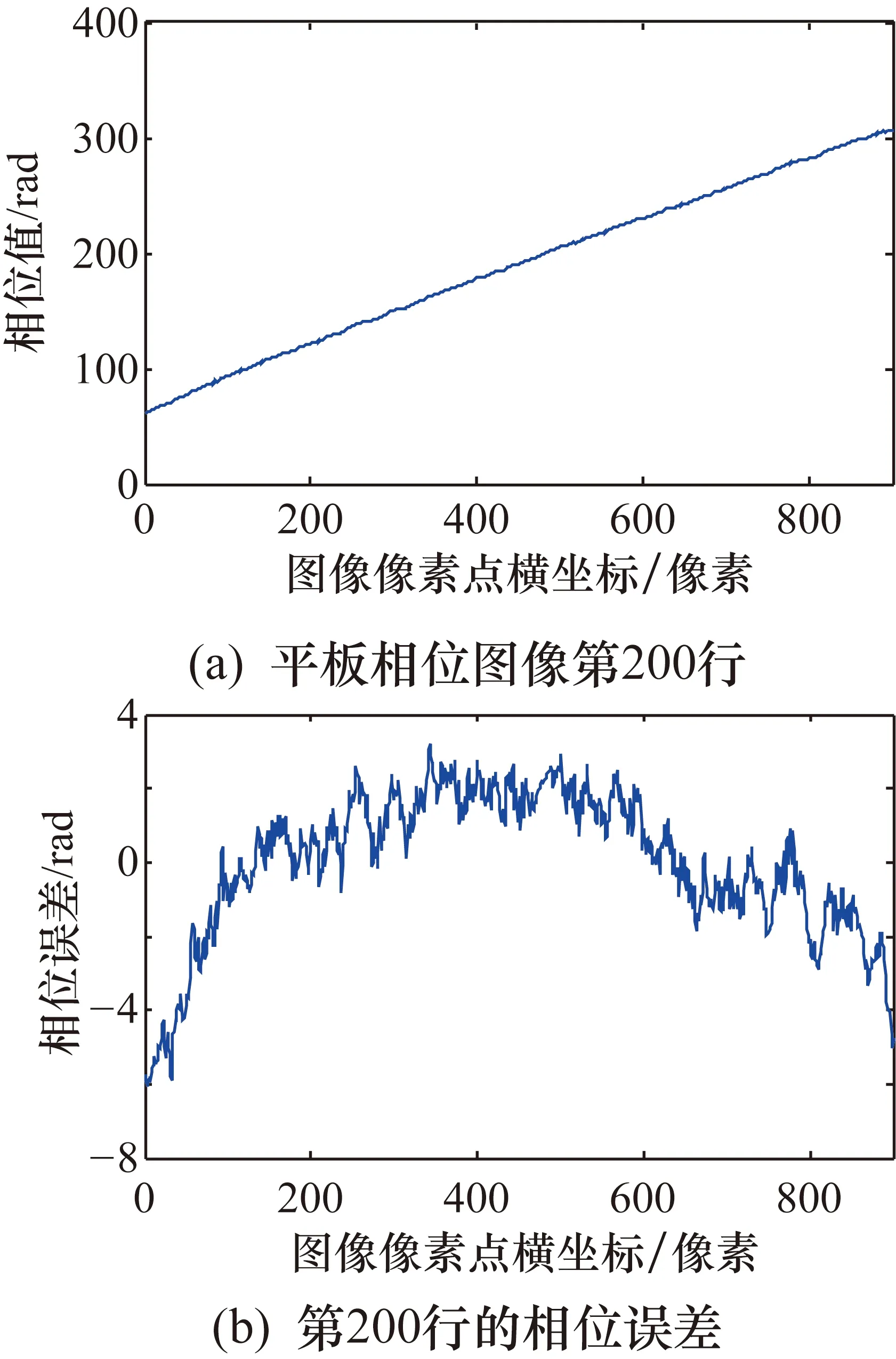
图6 标准平板相位误差分析

3.2 相位校正

为了找到投影结构光系统的相位误差分布规律，用二次多项式对平板的相位误差进行逼近。通过实验发现相位图像不同行的误差分布非常接近，因此，针对整幅图像共用一组多项式系数进行误差校正。为了进一步提高校正精度，可以从多个角度对平板进行相位恢复，并从每一幅相位图像中均匀地选择多行数据进行误差分析，拟合得到最终的多项式系数。假设误差分布近似为

e(x)=ax2+bx+c

(7)

首先，变换标准平板的位置，分别投射12幅正弦图像，并采用2.2节给出的方法进行相位恢复；然后，提取每一幅相位图像的第100、200、300、400、500、600行数据，求出这些相位值的误差；最后，将这些相位误差数据进行最小二乘拟合，采用MATLAB中的polyfit函数，得到的二次多项式系数为

a=-2.8551×10-5，b=0.0257，c=-3.8672

(8)

拟合得到的相位误差分布函数如图7所示。

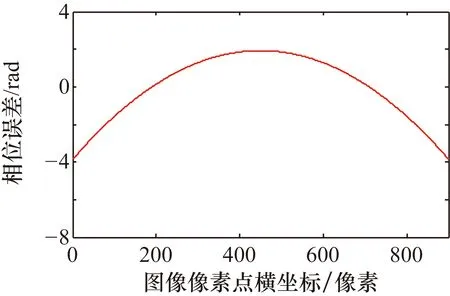
图7 二次多项式相位误差分布函数

下面将根据求出的误差分布规律对平板的相位图像进行校正。假设按照2.2节给出方法恢复出的相位图像为φ(u,v)，则任意一个像素点(u,v)处经过二次型校正后的相位值可由式(9)求出。

φ(u,v)=φ(u,v)-au2-bu-c

(9)

对图5中相位图像的第200行进行误差校正，得出校正结果如图8(a)所示。将这些校正后的相位数据重新进行直线拟合，并计算出如图8(b)所示的误差分布曲线。所有误差中的最大值为2.1425 rad，最小值为-2.8518 rad，标准差为0.8948 rad。从该误差曲线中可以看出，系统的非线性误差被有效地抑制了，最终的相位计算精度也有了较大幅度的提高。

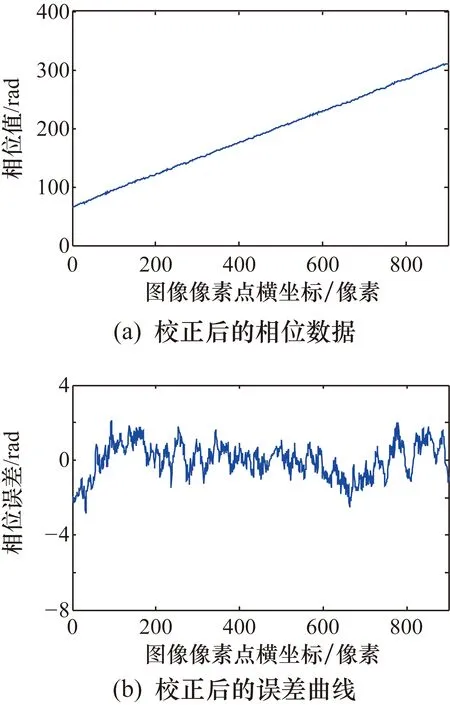
图8 二次多项式误差校正结果

除了二次多项式外，本研究采用更高阶多项式进行了类似的误差校正分析。图9和图10分别为采用三次多项式和四次多项式得到的误差分布函数及校正后的误差分布曲线。采用三次多项式校正后的最大误差为2.2260 rad，最小误差为-2.6199 rad；采用四次多项式校正后的最大误差为2.1448 rad，最小误差为-2.4668 rad。从误差曲线以及数值结果可以看出，采用高次多项式进行误差校正的结果与采用二次多项式非常接近，说明系统误差以二次为主，因此本研究最终采用二次多项式进行误差校正。

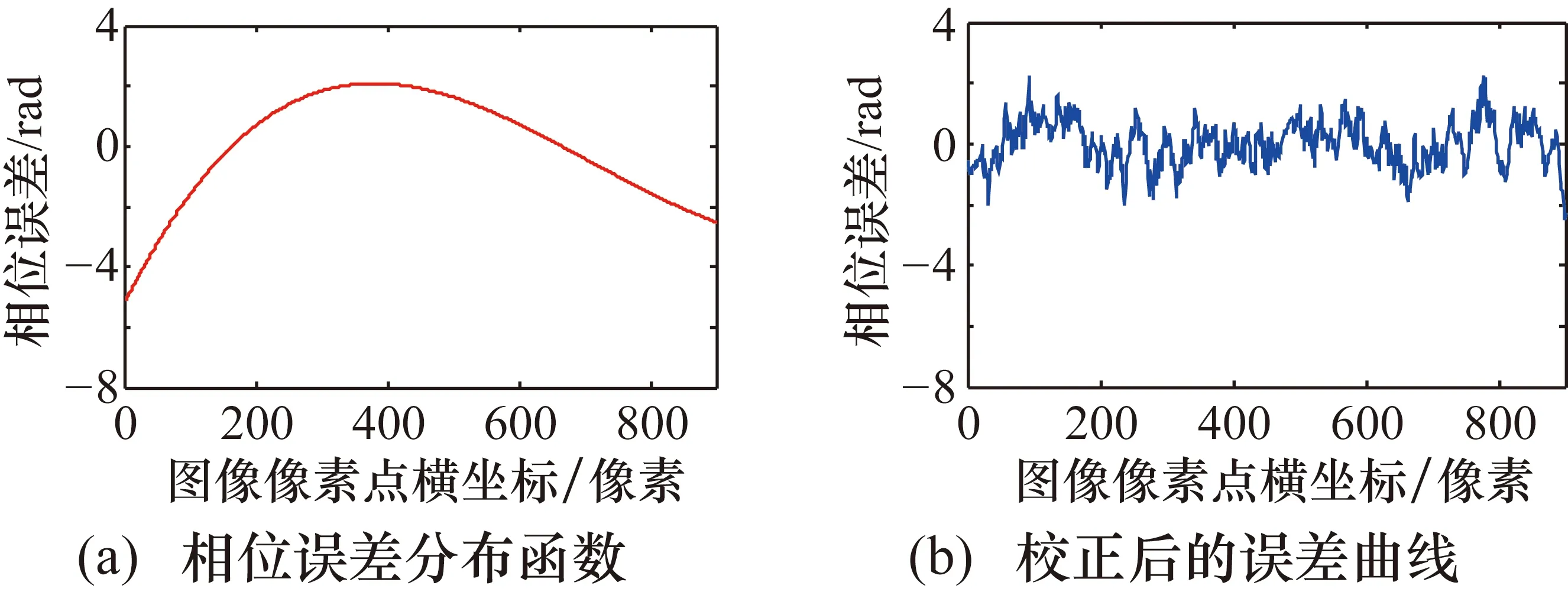
图9 三次多项式误差校正曲线及结果

4 实验分析

为了验证本文所提出的基于二次型误差校正的相位恢复算法及三维测量系统的精度，本节将给出相应的对比实验。在实验中，投影图像的分辨率为1920像素×1080像素，相机的分辨率为1292像素×964像素，水平视场角和垂直视场角分别为79.0°和59.4°，水平方向和垂直方向的焦距分别为3.63 mm和3.64 mm。

在验证相位恢复精度方面，本文与两种现有算法进行了对比。文献[23]采用四步相移+格雷码的相位恢复方案，即首先通过4幅相移图像计算相位主值，再用6幅格雷码图像实现相位的解包裹，本文记为算法1。文献[25]采用三频外差的方法实现相位恢复，并提出基于相邻像素点斜率和叠栅条纹的相位修正方法，本文记为算法2。为了验证算法的通用性，在实验过程中将标准平板变换不同的姿态，并取相位图像中的不同行进行分析。平板相位恢复误差的对比结果如图11所示。可以看出，现有的相位恢复方法存在较大的误差，而本文所提出的相位恢复方法可以有效地减小相位误差，并且该方法对平板不同的姿态都是适用的。更为量化的对比结果如表1所示。表1中的数据同样可以验证本文所提出的算法是有效的。

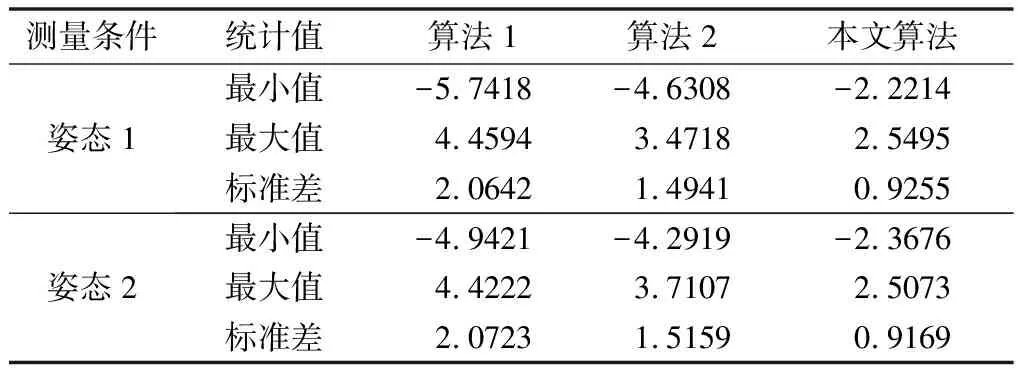
表1 平板相位恢复误差量化对比结果 单位：rad

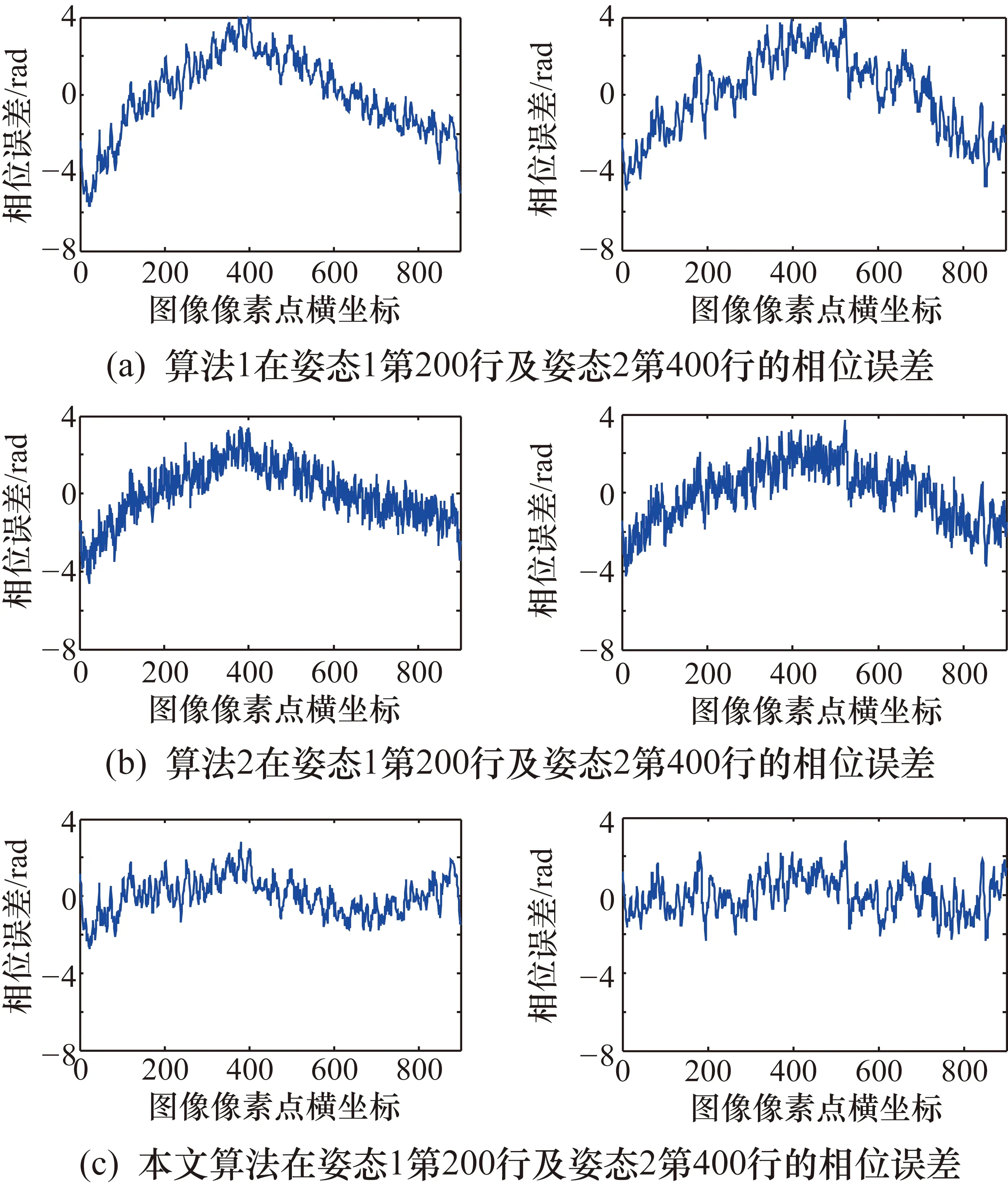
图11 平板相位恢复误差对比图

为了进一步验证本文所提出的相位恢复算法在实际三维测量系统中的效果，对标准如图12(a)所示的物体进行了三维重建，结果如图12(b)所示，可以看出重建结果较好地复原了被测物体。为了定量验证本文所提出系统的测量精度，分别采用本文提出的方法和现有算法[23]对如图13所示的标准尺寸进行了测量。

图12 三维重建结果

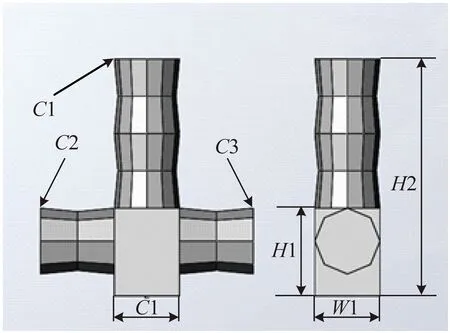
图13 被测物体的尺寸标注

两种算法均采用三角测量原理对单个结构光模块测得的数据进行三维重建，然后采用ICP方法对不同模块的重建结果进行融合。二者的区别主要体现在相位恢复部分，文献[23]采用的是四步相移+格雷码的相位恢复方法，其对比结果如表2所示，其中L、W、H为长度，C为截面周长。可以看出，本文所提出的三维测量系统具有更高的测量精度，同时也验证了本文所提出的误差校正模型也适用于一般类型的场景。

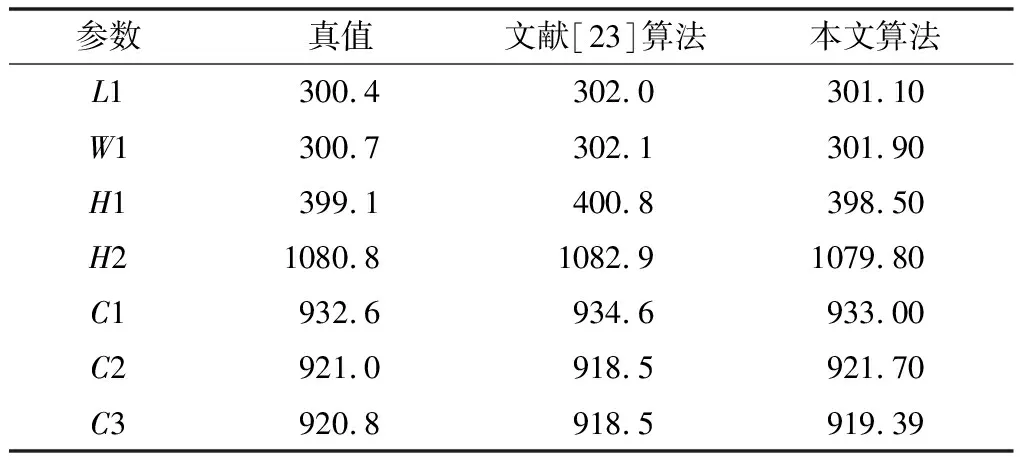
表2 三维测量对比结果 单位：mm

5 结束语

笔者提出了一种基于二次型误差校正的高精度三维测量系统。首先,采用标准的四步相移算法对投影仪结构光系统进行相位恢复，然后,采用三频外差的方法对初始相位进行解包裹。通过这2个步骤得到的相位值存在一定的误差，对该误差进行了分析，发现该误差呈抛物线分布且与被测物体无关。进而，用一个二次多项式模型对误差进行逼近，再利用该模型对相位进行修正以提高系统的测量精度。与传统算法的对比实验验证了本文所提出方案的有效性。