历史数据下优化GRU模型的测控设备相位预测

孙 岩, 雷 超，董 恒，史新虎，屈渊博

(中国人民解放军63726部队，宁夏 银川 750004)

当前形势下，航天发射任务密度越来越高，机动参试逐渐常态化。测控设备到达机动点位后，设备准备周期相对较短，相位标定校准经常受到环境、天气、周边架设标校信标机位置等条件的影响，本文通过设备历史记录数据进行相位值预测，解决人工经验值装填可用性、稳定性差等局限性问题。

传统无对塔标校环境下，采用理论计算、经验值推导实验等方法计算可用值。如王健等[1]通过分析微波自检校相值与信号频率之间的关系,归纳出相应的计算公式,提出了利用公式进行相位快速修正的方法。该方法解决了海上快速相位修正问题，但需较为烦琐的理论模型建立及统计方法推导，同时存在环境适应性差和可推广应用性等问题。随着硬件条件的改善，数据库和人工智能等技术的发展，目前基于数据驱动的序列预测方法已经普遍应用于各个行业，测控领域也逐渐应用算法辅助决策，数据驱动方法主要分为统计分析和机器学习2类，统计学方法利用统计模型或随机过程模型描述参数，通过统计参数变化规律进一步分析总结规律。而机器学习的方法自适应性能好，无须过多地关注建模过程，利用原始记录数据即可实现设备的关键参数长期分析预测。如杨罗兰等[2]针对测控系统关键指标预测的问题,探索基于历史数据的指标预测方法,具体分析了基于支持向量机(Support Vector Machine，SVR)的单步和多步指标预测方法,并使用实测数据进行了试验和分析；岳瑞华等[3]针对设备校准中的预测问题,提出了基于粒子群优化支持向量机的预测方法，取得了较好的效果。Sokullu等[4]研究了利用全连接深度神经网络实现信道估计的方法，讨论了不同导频尺寸下模型的性能。支持向量机和全连接神经网络在预测领域取得了一定的效果，但存在泛化能力弱和无效连接过多等问题，本文进一步选用循环神经网络开展预测，其作为机器学习中深度学习模型较为成功的方法之一，广泛应用于时间序列预测与回归过程中，在信息处理、参数序列建模、设备指标预测等领域起到了很好的效果。

循环神经网络(Recurrent Neural Network，RNN)的主体思想是通过数据的隐藏层循环，实现序列演进方向的递归且所有节点按链式传播。具体计算过程为

ht=f(U·Xt+W·ht-1)

(1)

Ot=g·(V·ht)

(2)

式中：ht为隐藏层输出；f、g为激活函数；U、W为权重值；Xt为原始输入值；Ot为模型输出值。从结构和计算公式可以看出，输出结果与输入和隐藏层状态有关，通过串联式的记忆单元，实现了时间序列的前后关联。

循环神经网络记忆单元如图1所示。本文选用循环神经网络改进型门控循环单元(Gated Recurrent Unit，GRU)模型，通过优化超参数选择机制，实现相位值准确的预测估计，为设备在无塔标校条件下，提供可用参考装填值。

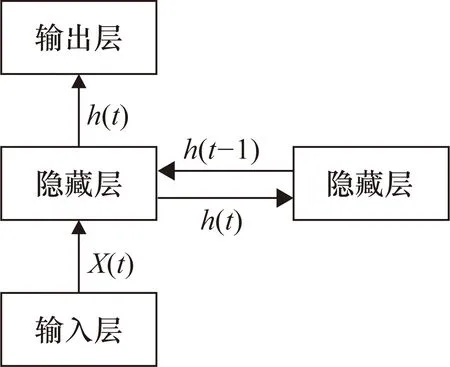
图1 循环神经网络记忆单元

1 基本算法

1.1 GRU网络

GRU网络是循环神经网络的一种，是传统循环神经网络和长短时记忆网络(Long-Short Term Memory RNN，LSTM)的改进模型[5]，相较于LSTM训练参数较少，利用更新门代替了LSTM的输入门和遗忘门，简化了LSTM结构，GRU模型单元如图2所示。

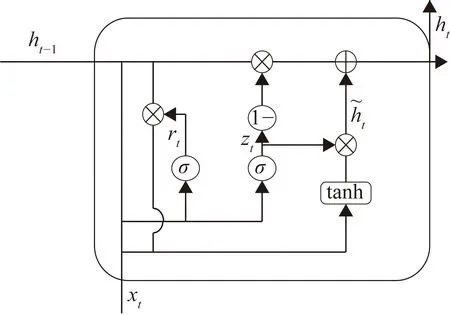
图2 GRU模型单元

单元的主要计算过程如下。

① 重置门计算，控制状态结果受上一状态的影响。

rt=σ(Wr·[ht-1,xt]

(3)

当前的状态为

(4)

② 更新门和当前值计算：

zt=σ(Wz·[ht-1,xt]

(5)

计算隐状态为

(6)

式中:σ为sigmoid型激活函数；tanh为双曲正切型激活函数；W为权值。

1.2 鲸鱼算法

近年来，多种仿生群智能算法被提出和应用于各个领域，大部分算法结合群体性生物特点，进行随机性和趋向性寻优迭代，具有速度快、准确性高的优势。仿生类鲸鱼算法(Whale Optimization Algorithm，WOA)是一种新颖的、受自然启发的元启发式优化算法，通过模拟座头鲸的狩猎行为，建立泡沫网搜索策略。在座头鲸围猎时，会通过对鱼虾群位置的判断，移动自己的位置吐出气泡，将鱼虾群不断围绕在随自身位置变化吐出的气泡中，最终将鱼虾群锁定。气泡网狩猎策略融合了座头鲸收缩包围猎物和螺旋狩猎方式的局部开发能力，以及随机搜索猎物的全局寻优特点，具有操作简单、搜索能力强、能够跳出局部最优且收敛速度更快等优点[6]。本文利用WOA算法对GRU网络模型参数进行优化，将每条鲸鱼个体看作每种优化策略，并将鲸鱼位置的维数对应GRU模型待优化参数的个数，可在鲸鱼不断更新自身位置的过程中获得网络的最优参数组合。与最终预测模型评估指标损失函数一致，同样选择适应度函数为均方根误差(Root Mean Square Error，RMSE),可得：

(7)

式中:m为组内样本个数;h(x)为预测值;y为实际校相值。算法主要计算过程分为以下3个步骤。

(1)包围猎物过程。

鲸鱼算法模拟自然界鲸鱼捕猎，发现猎物后迅速更新位置进行包围，计算公式为

D=|CX*(t)-X(t)|

(8)

X(t+1)=X*(t)-AD

(9)

式中:t为当前迭代次数；D为搜索个体与当前最优解的距离；A和C为系数；X*为当前最好的鲸鱼位置向量，X(t)为当前鲸鱼的位置向量。

A、C系数采用随机生成变换，实现群智能算法常见的随机搜索，可得：

A=2a·r-a

(10)

C=2r

(11)

a=2-2·t/M

(12)

式中：r和a分别为[0,1]、[0,2]的随机数；M为算法的设置迭代次数。

(2)狩猎过程。

鲸鱼狩猎过程最大的特点是采用螺旋式扫描的方式，不断缩小范围从而捕获目标，其变换过程数据模型公式为

D=|X*(t)-X(t)|

(13)

X(t+1)=D·ebl·cos(2π·l)+X*(t)

(14)

式中：b为螺旋形状控制参数；l为范围[-1,1]的随机 数。

游走变换后，位置同步模型过程中，以概率p完成收缩包围，在狩猎过程中，鲸鱼将以50%的概率包围猎物(完成迭代寻优过程)。

(15)

(3)随机重捕过程。

若|A|>1，那么鲸鱼将离开现在所包围的猎物去寻找新的猎物，即重复迭代过程。

鲸鱼优化算法是一种新型元启发式算法,通过鲸鱼的狩猎行为，抽象出螺旋搜索过程算法，较其他智能优化算法有更好的避免局部最优的能力，但仍可能存在局部最优的可能，本文算法用于GRU模型神经元个数和步长寻优，主要作用是规避人为难以定义的参数值，可能出现偏离程度大、无准确规则的问题。鲸鱼寻优算法陷入局部最优解时，提供的参数非最优情况，本文实验过程中对10次迭代寻优和10次的一次寻优(取最差值)模型结果进行了比对，一次寻优即使出现陷入局部最优解，仍达到网络模型参数优化设置要求，如表1所示。

表1 经验值、局部最优、多次寻优对比

1.3 WOA优化序列模型(GRU)

序列网络GRU的预测准确性受到超参数神经元个数和时间步长设置的影响。时间步长为循环单元结构的个数，表示了某一个时刻的信息最多可由该时刻之前的若干个时刻的信息综合得来。时间步长过小会失去不同时刻间信息的关联性，过大则会减弱神经网络的学习能力[7]。目前隐藏层神经元个数和时间步长获取只能根据经验，人工挑选一个大致可选的神经元个数范围。本文针对隐藏层神经元个数和时间步长两个超参数选择问题，利用鲸鱼算法WOA进行自适应参数寻优，避免人工设置影响预测准确性，通过寻优可得神经元个数为64，步长为5。WOA优化GRU模型过程如图3所示。

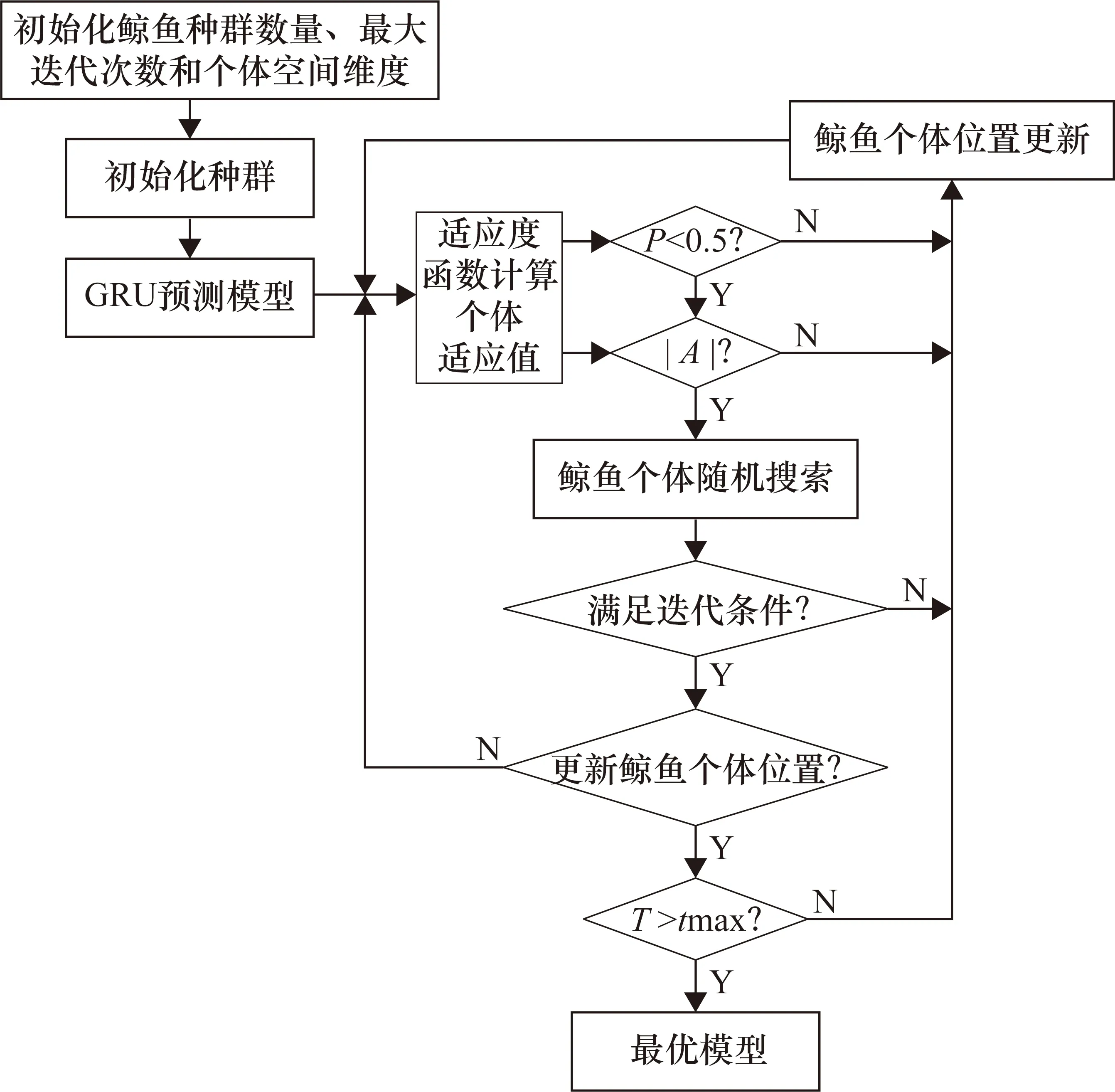
图3 WOA优化GRU模型过程

2 基于改进GRU模型的相位值预测

2.1 数据预处理

以某型号设备相位历史数据为例，采用软件自动记录每次校相结果的方式，区分组合号(信道中各设备区分组合)，不同组合号和频点状态下的数据分别进行分组，因信道影响较大，不能同时进行预测。将远场信标机和设备天线上偏馈校零一体机数据分别记录，本文预处理过程中若远场和偏馈校相时间在20 min内则认为是同一组数据，此时偏馈校相数据同样作为输入条件使用；若校相记录中同一组数据中无偏馈校相结果，则将组内值全部取0，屏蔽此处神经元作用[8]。校相记录数据示例如表2所示。

表2 校相记录数据示例

从表2中可以看出，温湿度、相位值样本间差异相对较大，需要进行参数值归一化运算，通过最大最小值比例归一化数据情况，温度范围为0～40 ℃，湿度范围为0～100%，相位值范围为0～360，利用范围值进行归一化处理，最终结果进行范围恢复，可得：

(16)

通过缺失值和异常值剔除、归一化等数据清洗[9]操作后，所得可用样本总数量2392，训练集和验证集按8:2比例随机划分，训练集样本数1913，验证集样本数479。

2.2 模型训练验证

WOA算法利用Python编写，GRU模型基于Pytorch开源深度学习框架进行设计，使用 Intel®CoreTMi5-6300HQ CPU(主频2.3 GHz)，WIN7 64 位操作系统。

WOA优化模型迭代损失值(每轮组平均均方误差最小值)变化情况如图4所示。

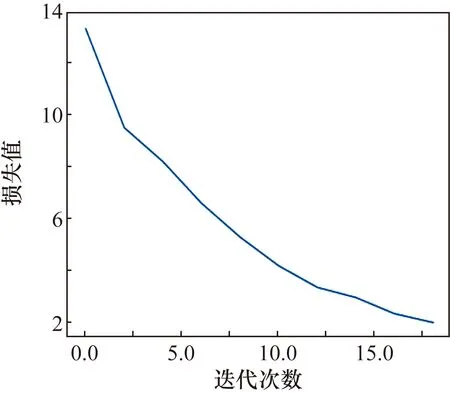
图4 WOA迭代损失值变化情况

利用迭代优化后选定的超参数，构建预测序列模型，为了更好地评估构建改进GRU模型的预测效果，选取 Adam 优化器对训练损失值(Loss)进行优化，Adam 是目前深度学习模型训练中比较流行的一种优化器，相较于其他优化器能够自适应参数学习，具有收敛速度快、对内存需求小、能较好地处理噪音样本等优点[10]，经过模型训练验证，得到模型结果，利用设备早、中、晚不同时间段(温湿度对相位值影响较大)多次校正相位值现场验证，得到方位、俯仰相位值真实值与预测值对比情况，统计结果中对应的方位、俯仰校相值与预测值差的均值及标准差[11]，如表3所示。

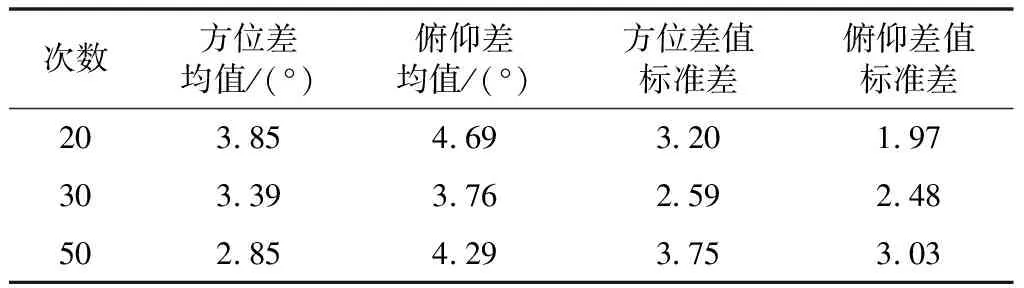
表3 校相记录数据示例

从表3中可以看出，均值和标准差值均在5以下，预测值完全满足设备使用标准，选取其中5次对比情况，如图5所示。

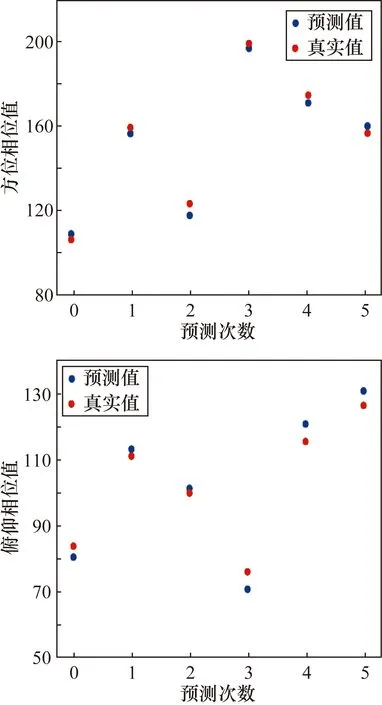
图5 相位预测值与真实值对比

2.3 算法对比

为进一步说明WOA优化GRU模型的优势，比较了传统循环神经网络、GRU模型(传统参数值)和本文方法，在不同样本划分比例下的损失值比较情况如表4所示。

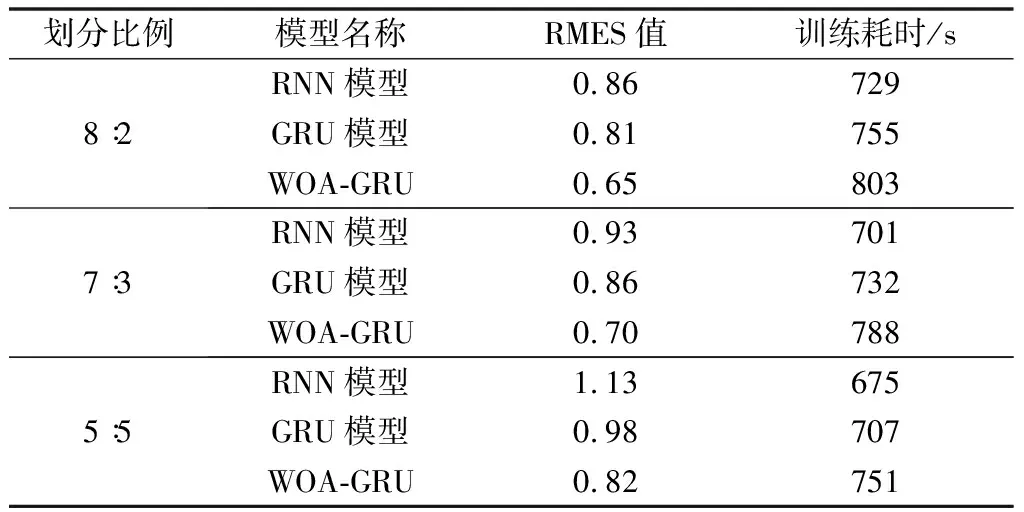
表4 不同划分比例下模型情况

可以看出，在不同样本划分比例下，不明显提高训练时间的情况下，损失值有明显的下降，经过计算后可得，在设备记录数据上，WOA-GRU 模型相比GRU和RNN模型，其RMSE指标分别提升了 19.7% 和 24.4% 左右,能够得到效果更好的模型预测结果。

3 结束语

针对测控设备使用中的相位值预测这一问题进行分析，提出一种利用仿生学鲸鱼算法WOA优化序列模型GRU的预测方法，试验后得出如下结论:WOA-GRU模型与普通GRU及RNN模型相比，在预测结果上更贴近实际相位值，拟合程度高，损失值更小，可以看出优化后的 GRU模型在预测相位值这类序列问题上具有较好的表现，证明了方法的可行性，能够为测控设备机动参试状态下的标校参数辅助选择提供一种新的思路和方法。