一种基于APGD方法的随钻核磁共振测井快速反演算法
2023-02-13李沐尧朱万里程晶晶葸春平
李沐尧,朱万里,滕 朔,程晶晶*,葸春平
(1.华中科技大学 人工智能与自动化学院,湖北 武汉 430074;2.中国石油集团测井有限公司 测井技术研究院,陕西 西安 710077)
随钻核磁测井技术是一种非放射性的孔隙度测量技术,可以检测泥浆滤液侵入前或者侵入很浅时的底层特征。与传统电缆核磁测井相比,其可以更真实地反映储层特征,评估精度更高[1]。受水平井或大斜度井限制,随钻测井系统无法采用电缆进行数据通信,仅能选取传输速率为4~10 bit/s的泥浆脉冲遥测技术[2]。在低传输速率下,无法直接上传大量的原始测量数据,因此需要在井下的嵌入式设备中完成T2谱反演算法,上传数据量较少的反演结果。
在反演算法方面,传统算法包括奇异值分解法[3]、正则化方法[4]、非负最小二乘法[5]等。近些年开始对传统算法进行改进。2009年,Prange等[6]提出了一种高效的Monte Carlo反演算法,并检查光谱解决方案的统计特性。2015年,Martakusumah等[7]分别使用LM方法和Occam方法进行反演算法设计,对结果进行比较。2018年,岳鑫等[8]提出奇异值分解法的改进算法。赵宏晨等[9]对于Tikhonov正则化方法进行研究,建立了不适定问题方程组。2019年,Song等[10]提出正则化和约束矩阵拟合的反演方法。目前实际应用较多的方法为奇异值分解法和非负最小二乘法。奇异值分解法涉及大量的矩阵运算,移植到井下嵌入式设备中增加硬件逻辑资源,降低算法执行效率,严重影响井下快速反演的评价效果。
根据实时性要求并结合原始回波串数据特点,设计一种基于加速投影梯度下降(Accelerated Projected Gradient Descend,APGD)方法的回波T2谱反演算法,并充分利用FPGA硬件资源,采用分布式算法,将APGD算法中的矩阵乘法转换为查找表和移位累加操作,并在FPGA中对算法进行化简,减少FPGA硬件电路规模,提高算法执行效率。
1 核磁共振测井反演算法
1.1 反演算法模型
随钻核磁测井仪采用CPMG序列测量得到的原始回波串信号是多种横向弛豫共同作用的结果,信号的波形呈多指数衰减[11]。T2谱信号的离散表达式为
(1)
式中:bi为i时刻的原始回波幅度;n为横向弛豫分量数目,也表示布点数;xj为对应于T2j分量零时刻信号幅度的贡献值,也就是反演所要得到的T2谱幅值,此参数必须满足非负约束条件;ti为i×TE,TE为回波间隔;T2j为第j中弛豫分量的横向弛豫时间;εi为实际测量产生的随机噪声信号;m为原始回波串的回波个数;e-ti/T2j用矩阵表示为
(2)
则式(1)可表示为
bm×1=Am×nxn×1
(3)
式中:A为系数矩阵,与回波设置的参数和布点数有关;b为原始回波串幅度,两项为已知矩阵,且m>n时此公式为超定方程,这种方程通常是严重病态的,其结果非常不稳定[12]。求解x这类不适定问题可以采用非负约束最小二乘(Non-Negative Least Square,NNLS)的思想进行求解[13]。NNLS模型为
(4)
设p=ATb,Q=ATA,则
▽f=Qx-P
(5)
xk=[xk-1-tk(Qxk-1-p)]+
(6)
式中:tk设为1/L,L为Lipschitz常数,L=‖Q‖2。将式(6)展开整理得:
xk+1=[θ1xk+θ2]+
(7)
(8)
式中:k为迭代次数;xk为每次迭代结果;当满足停止迭代条件时xk为反演结果。
1.2 APGD算法设计
APGD算法结合了Nesterov加速算法和投影梯度下降(Projected Gradient Descend, PGD)法,采用自适应重置参数使算法单调。
FPGA中实现的APGD算法流程如下面的算法1所示,APGD算法共分为两部分,主体部分执行APGD算法,当残差值增大时,切换到PGD算法对数据和参数进行更新和重置[14]。

算法 1:APGD for NNLS初始化:x0=y0=0,θ1=In-ATA‖ATA‖2,θ2=ATb‖ATA‖2,k=1,α0∈(0,1)while(不满足迭代停止条件) do xk=[θ1yk-1+θ2]+(投影梯度步骤) αk=12(α4k-1+4α2k-1-α2k-1),βk=αk-1(1-αk-1)α2k-1+αk yk=xk+βk(xk-xk-1)(外推) if(残差增加) do xk+1=[θ1xk+θ2]+(投影梯度步骤) yk+1=xk+1(重启) αk=α0(参数复位) endif k=k+1end
2 FPGA算法实现
引入分布式算法和查找表操作在FPGA中实现APGD算法,并且通过算法的并行处理方式和部分计算步骤的简化,使得FPGA硬件电路规模缩减,同时算法执行速度加快,实现反演算法在井下的快速处理。
FPGA总体程序设计结构如图1所示,共分为5个模块。SPI模块和Flash模块为外部通信驱动;APGD模块负责算法的主体逻辑流程,将矩阵变量组合成地址以备查表,并在算法完成后将反演结果送入主控系统;查找表模块存储了预先计算好的矩阵乘法部分积和加速参数结果β,部分积需要后续计算,加速参数结果则送入APGD模块;矩阵计算模块将部分积进行移位累加计算得到矩阵乘法结果,并将其返回至APGD模块参与算法计算。系统各模块之间由数据线和使能控制信号连接,严格保证算法的执行步骤和时序逻辑。
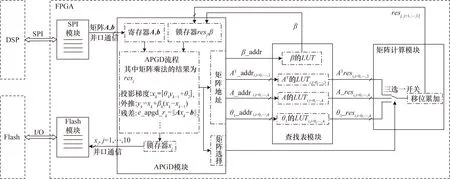
图1 FPGA程序设计结构图
2.1 基于分布式算法的累乘加快速计算
APGD算法中存在大量的矩阵与列向量相乘,采用分布式算法完成多组累乘加的快速计算以提高计算效率。分布式算法则通过查找表获得部分积结果,再对查找表结果进行累加和移位获得算法结果[15]。一个标准的乘加运算为
(9)
式中:y(n)为累乘加计算结果;Ak为常数;xk(n)为输入变量。xk(n)采用B位二进制补码表示为
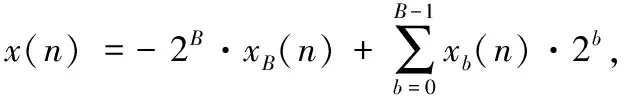
xB(n),xb(n)∈[0,1]
(10)
式中:xB(n)为x(n)的符号位;xb(n)为x(n)的第b位。将式(10)代入式(9),可得:
(11)
式(11)将标准的乘加转换为查找表操作和累加,输入变量的位作为地址进行查找表映射,在FPGA中将映射值通过移位实现对应的二次幂加权,得到输出结果。
2.2 多部分表并行计算结构
将完整表分割成多个部分表,部分表并行操作,可以进一步减小查找表规模[16],令N=L1+L2+…+Lk,则:

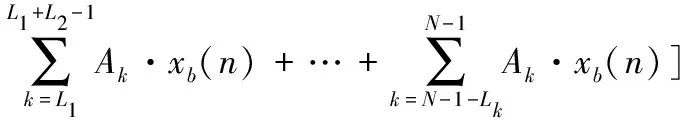
(12)
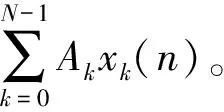

表1 乘加数据举例
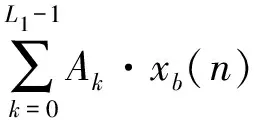
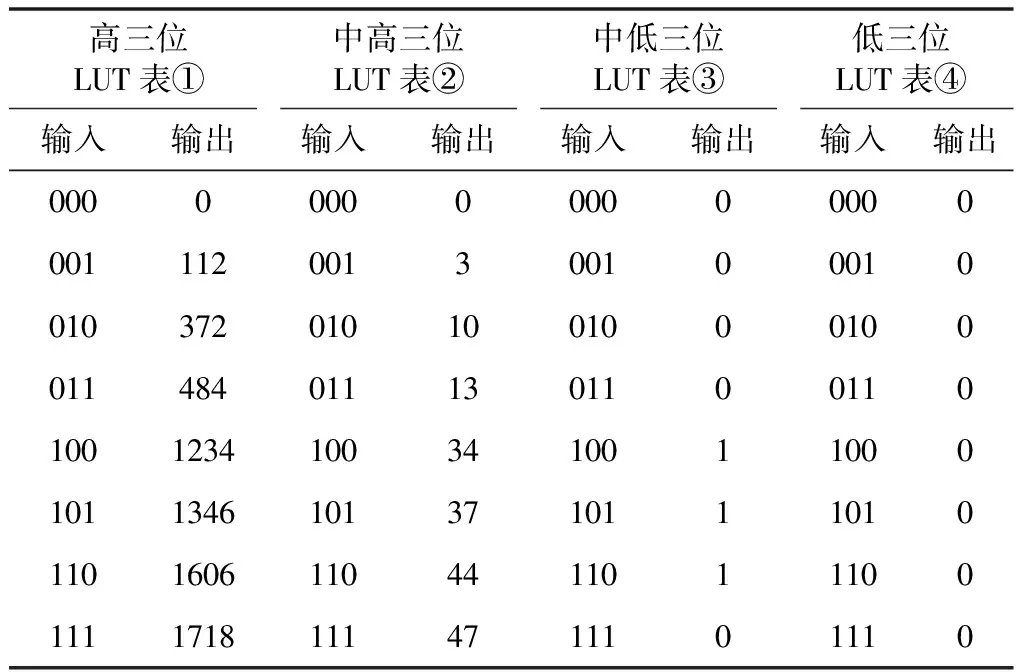
表2 查找表构造规则
图2为分割查找表的硬件结构框图,输入变量x通过拼接构成多组查找表地址,按序移入查找表中完成映射得到部分积,部分积在状态机的控制下经过累加器和移位寄存器输出最终结果。
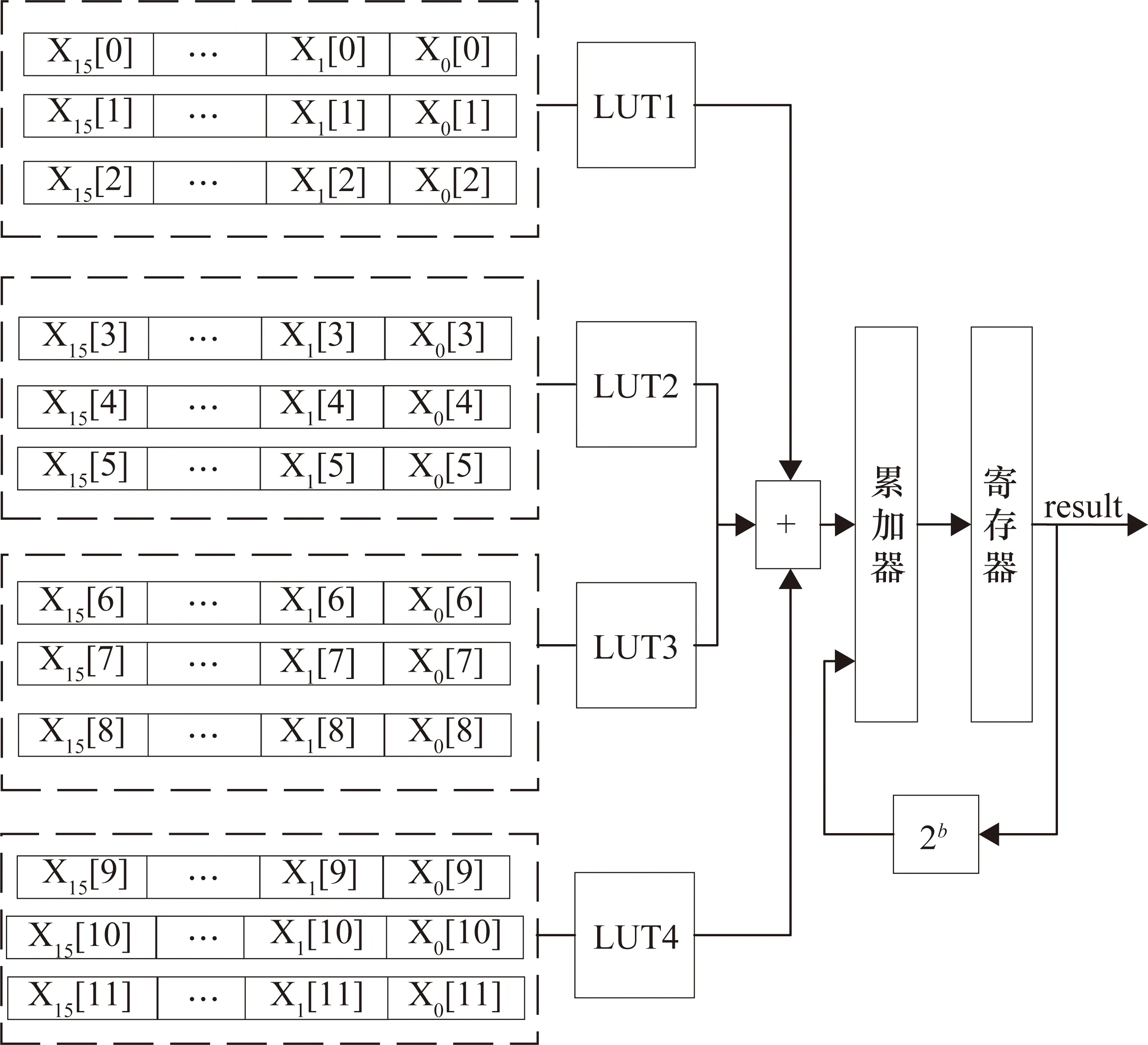
图2 分割查找表硬件结构图
在APGD算法中,有3个不同的常数矩阵需要做矩阵乘法,分别为A、AT、θ1,对应列向量累乘加数为N=12、10、10,所以具体构造3组分割查找表为4×23、5×22、5×22。加速参数α和β与迭代次数有关,以迭代次数作为地址构造查找表映射,当参数需要重置时地址重新赋值为零,参数查找表操作省略了开方、除法、方根等运算过程,减少了FPGA逻辑单元的使用,提高了算法处理速度。
在计算残差的过程中需要开根号计算,本设计FPGA选用ACTEL公司的A3P1000,其不具有对应功能的IP核可以应用。经分析残差在该算法中仅需要比较大小,不需输出具体结果,所以在FPGA中用较大空间来存储开根号前的数据,再进行数据比较。
2.3 仿真测试
采用ModelSim仿真软件对所设计的APGD算法进行仿真验证,系统时钟SYSCLK设置为30 MHz,迭代次数设置为100次,回波数据采用一组随机数[17],并与在MATLAB环境下APGD算法的运行结果作对比说明。
图3为FPGA下APGD算法的仿真结果,在迭代第60次时取出残差值c_a[0~11]和反演结果值x[0~9]。残差值基本保持不变,选取第60次的结果作为仿真测试的结果。
图4为MATLAB和FPGA的算法残差归一化收敛曲线对比,从图4中看出两种实现方式对应的残差衰减基本相同,以验证APGD算法的收敛性和FPGA实现此算法的可行性。
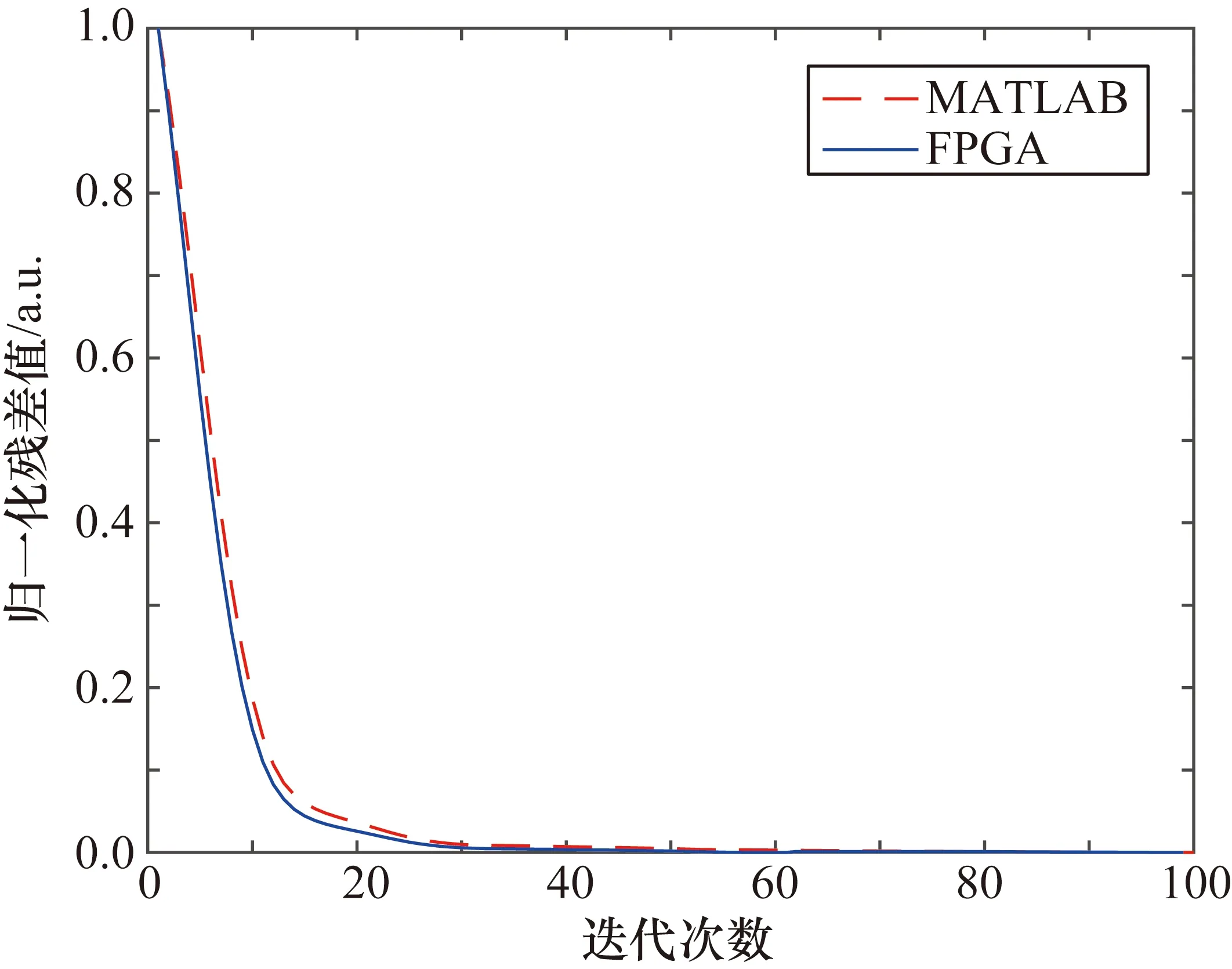
图4 PC端与FPGA残差迭代
3 实验结果与分析
3.1 实验环境与实验装置
正在研制的随钻核磁共振测井仪器处于实验室样机验证阶段,为验证回波反演算法的性能,在仪器的回波采集和数据处理电路中运行所设计的回波快速反演算法。回波串采集和数据处理电路如图5所示,电路采用DSP+FPGA的结构作为电路的核心,FPGA选用ProASIC3系列的A3P1000,实现回波串采集和基于APGD方法的回波反演计算功能。DSP采用TMS320F2812,通过RS485接口将数据发送至主控电路。
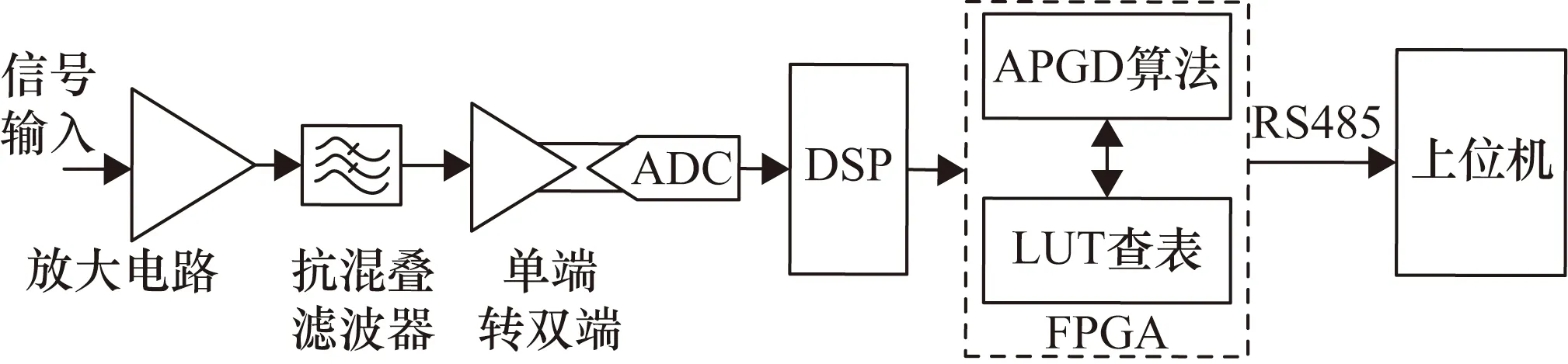
图5 回波串采集和数据处理电路功能框图
测试中配置一定浓度的CuSO4溶液加入刻度箱中,使用刻度箱环境模拟真实地层特性,设置100%孔隙度的地层信息作为原始模拟数据,用于算法结果的对比分析。
3.2 实验操作与过程
实验中采集电路通过探头向外界发射CPMG(Garr-Purcell-Meiboom-Gill)脉冲序列,设置回波间隔TE=0.6 ms。电路接收到原始回波串后,设置横向弛豫时间在区间0.5~5000 ms上均匀布点,布点数n=10。已知以上参数,可根据式(2)计算出Am×n。对原始回波串信号进行预处理校正和信号抽样,抽样个数m=12,回波幅度为bm×1。一组典型的抽样后的回波衰减曲线如图6所示。
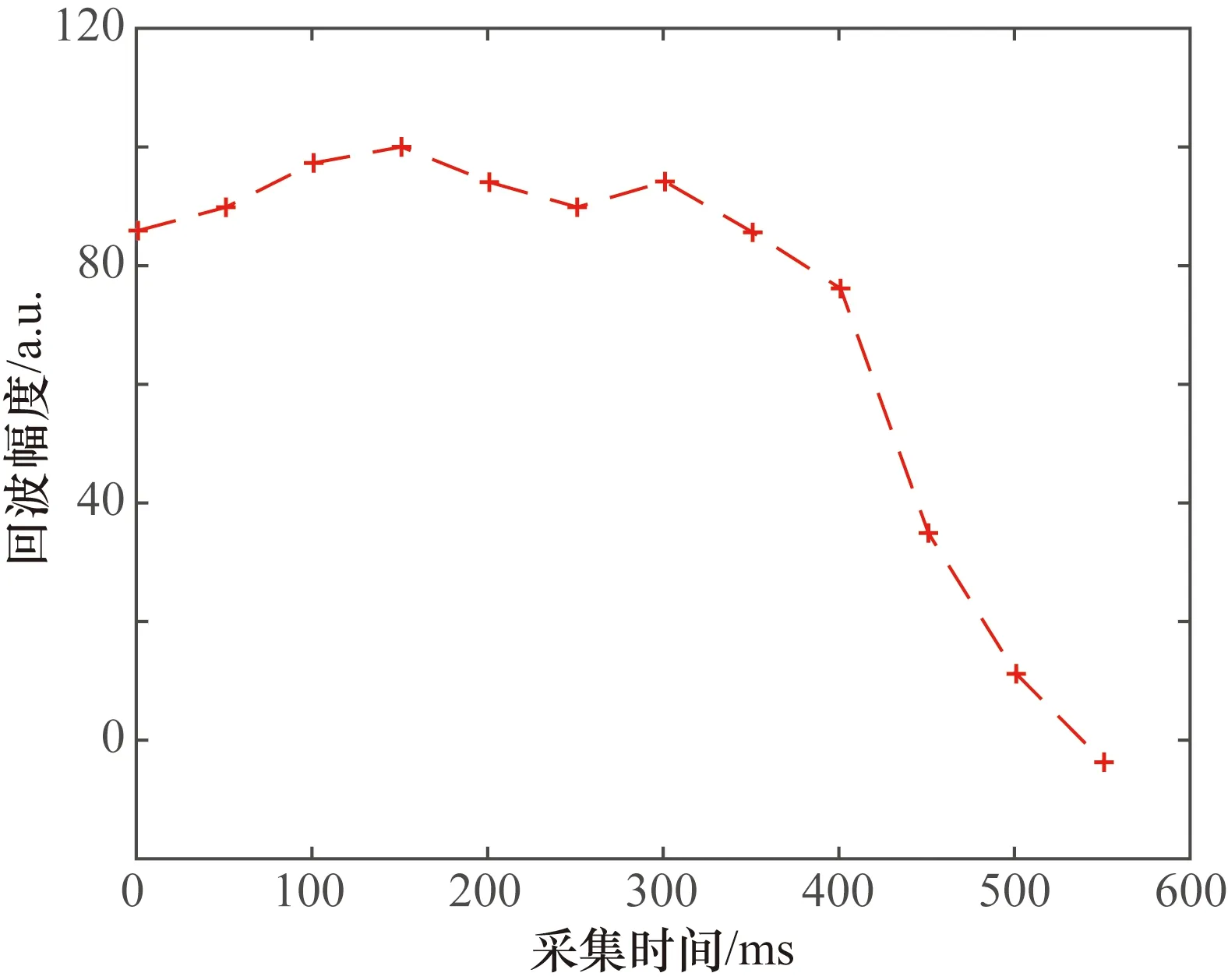
图6 原始回波串信号
3.3 实验数据分析
实验条件下刻度箱设为100%孔隙度的地层特性,地层孔隙度为T2谱幅值累加值。PC端与FPGA反演结果对比如图7所示,可以看出所得反演结果T2谱呈单峰性,MATLAB和FPGA反演结果的孔隙度分别为97.47%和96.81%。将预设的孔隙度数据Xmod与反演结果Xinv代入式(13)中,计算相对误差RX。
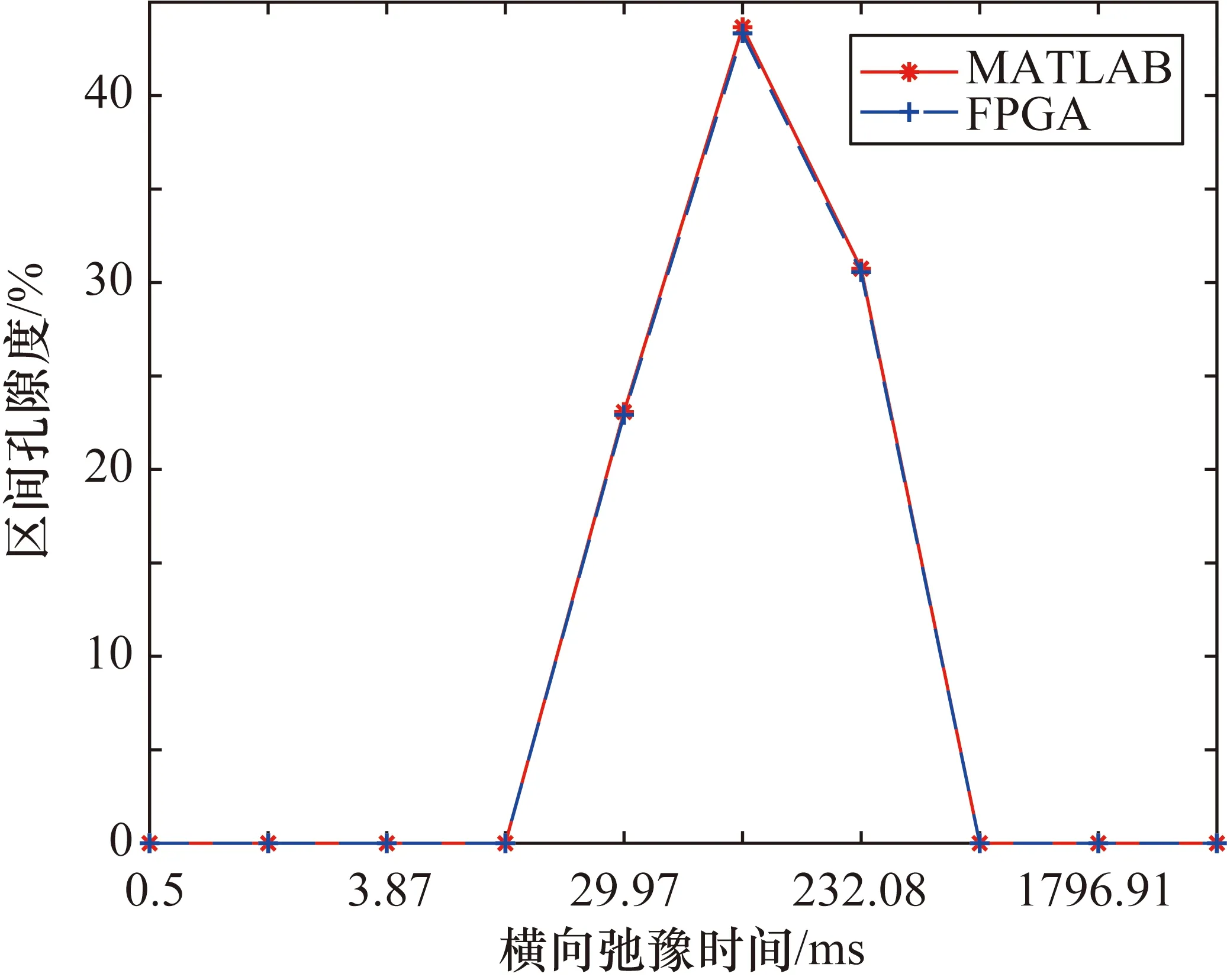
图7 PC端与FPGA反演结果对比
(13)
在MATLAB和FPGA中反演相对误差分别为2.53%和3.19%,可见使用实际回波串数据验证该算法其结果精度仍然较高,可以满足井下快速反演的需求。
3.4 方法设计评估
表3为A3P1000中的片上IP资源使用情况和所占总资源的比率。片上共有24567触发器资源和144 KB的RAM,通过分布式算法简化分割查找表,仅消耗15.97%的RAM资源。

表3 IP资源和内存消耗
分别在PC端、DSP、FPGA上测试此算法执行时间,对算法耗时进行对比。PC端算法实验在Win10系统下进行配有2.40 GHz的Intel Core i5-10200H处理器。DSP和FPGA均在30 MHz频率系统时钟下工作。分别对APGD算法的单次执行不更新参数、单次执行更新参数和完整迭代流程进行计时,算法耗时对比如表4所示,从耗时来看DSP>PC端>FPGA。
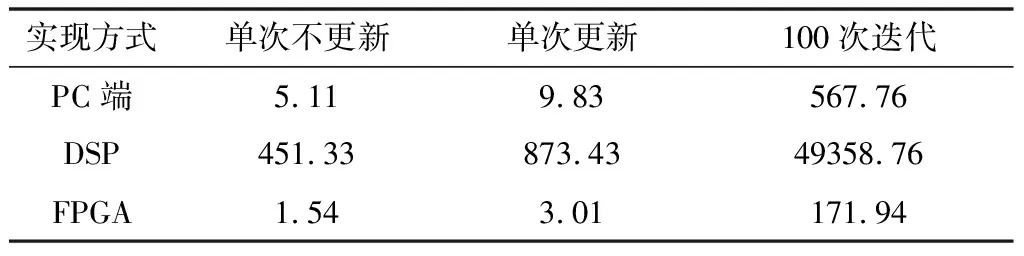
表4 FPGA和DSP算法耗时比较 单位:μs
通过以上实验算法效率和结果精度对比可以看出,FPGA作为反演算法在井下快速实现的嵌入式设备具有十分重要的意义和研究价值,对比其他现有工作,在FPGA上实现APGD算法在处理效率和性能上均具有较大优势。
4 结束语
针对随钻核磁共振测井仪器的井下快速反演问题,提出了一种基于FPGA的APGD算法实现方法。该方法应用了分布式算法,将矩阵乘法中复杂的累乘加运算转化为查找表操作,同时在FPGA中简化原算法,不仅提高了算法的执行效率,而且节约了硬件电路规模。通过自主研发的随钻核磁共振测井仪实验室刻度实验结果表明,该方法相对误差较低,算法执行效率较高,实时性和准确率满足随钻核磁测井仪器快速反演的需求,为核磁共振井下反演提供一种可行的快速实现方式。
