多元宇宙样分析：简介及应用*

黄顺森 陈豪杰 来枭雄 代欣然 王 耘

(北京师范大学认知神经科学与学习国家重点实验室,北京 100875)

1 背景

科学研究的可重复性主要有两层含义：一是对同一个数据集,由不同的研究者使用相似的方法对原研究结论进行验证(一般用reproducibility表示);二是不同研究者使用相似的方法,收集新的数据检验已有研究结果的可靠性(一般用replicability表示) (Artner et al.,2020;Nosek et al.,2022)。一直以来,心理科学研究备受可重复性危机的诟病,引发了国内外心理学研究者的广泛关注(Aarts et al.,2015;Nosek et al.,2022;Pashler &Wagenmakers,2012;Tackett et al.,2019;朱滢,2016;胡传鹏 等,2016;骆大森,2017)。开放科学联盟(Open science collaboration,OSC)在Science期刊发表了一篇探讨心理学研究可重复性的文章,发现大部分心理学研究结果不可重复,并提出最关键的原因是“可疑操作”,即选择性分析、选择性呈现研究结果,或者不充分呈现研究结果(Aarts et al.,2015)。换言之,对于任何数据集,研究者都有大量可操作的空间,可以自由、自主地选择只呈现某一种分析结果,这种单一结果的非代表性加剧了可重复性危机 (Aarts et al.,2015;Simonsohn et al.,2020;Steegen et al.,2016)。国内研究者通过分析OSC 的研究材料,进一步区分可重复危机产生的两大源头(传统统计学体系的局限和人为偏差)的差异,发现原研究的阳性结果中,真阳性结果不到三分之一,相当部分的结果,极有可能是人为偏差造成的(骆大森,2017),例如p值操纵(P-hacking)、研究者自由度(researcher degree of freedom)、“小径分叉的花园” (garden of forking paths) (Gelman &Loken,2014;Simmons et al.,2011;胡传鹏 等,2016)。这种人为偏差主要体现在研究者设计、分析、发表过程中对变量选择、分析策略的主观操作上。而过于追求阳性或显著性的结果是导致研究者选择分析变量、选择性报告结果的重要原因。因此,心理科学研究中常常出现两种现象——过度追求统计显著性或夸大化效应(inflated effects)、抵制或忽略小效应(Götz et al.,2020;Ioannidis,2008;胡传鹏 等,2016)。社会科学的研究更看好有利或者预期的大效应(Fanelli et al.,2017),这种偏向通常会暗示或鼓励研究者报告夸大化的效应;同时,研究者期待好的结果,认为小的效应是不正常的(Götz et al.,2020;王珺 等,2021)。但是,小效应或不显著的效应也有其存在的意义,不应该忽视和回避(例如基因研究中通常只有小的效应;Götz et al.,2022)。心理学的现象很复杂,并不只是由单个因素决定的,忽视小效应可能意味着忽视真效应,容易造成错误的认识,阻碍理论的发展(Götz et al.,2022;Prentice &Miller,1992)。

近年来,研究者在应对心理学可重复性危机中进行了许多探索,提出了许多的尝试性解决方式(Klein et al.,2018;Laraway et al.,2019;刘佳等,2018;胡传鹏 等,2016)。例如研究预注册、严格执行预注册计划、完整分析数据、专业期刊共同努力(如完善投稿要求、重视研究设计)等。由于研究者主观偏差对效应量有着重要影响(骆大森,2017),如何解决研究者在研究中选择性分析和选择性报告的问题,对提升心理学研究的可重复性具有重要意义(Simonsohn et al.,2020;Steegen et al.,2016)。所以针对选择性报告和选择性分析这一问题,研究者提出检验结果报告的稳健性,即使用不同的分析策略,对已有研究结果的效应进行可靠性检验。基于此,研究者提出了效应颤动分析(Vibration of effects,VoF) (Patel et al.,2015)、多模型分析(Multimodel analysis) (Young &Holsteen,2017)、多元宇宙分析(Multiverse analysis)(多元宇宙样分析的一种) (Steegen et al.,2016)、规范曲线分析(Specification curve analysis) (Simonsohn et al.,2015,2020)等分析方法。这些方法的核心共同点在于：不再选择性呈现分析结果,而是报告数据集中所有可能的分析结果,并进行稳健性检验,综合确定变量间关系和效应大小。图1 展示了这类方法的特征,对于某一数据集的变量,不同研究者可以选择不同分析策略组合,产生不同的分析结果。假设研究者想要探讨自变量与因变量的关系,在模型和数据集都一样的情况下,研究者A 可以选择报告一种分析策略的结果(图中线条被椭圆标记的组合),研究者B 则选择报告另一种分析策略的结果(图中线条被方形标记的组合),通常不同的组合结果不同,这样就使得研究结论可能存在不可重复性。而多元宇宙样分析则强调报告图中所有分析策略的结果,并进行效应稳健性检验。

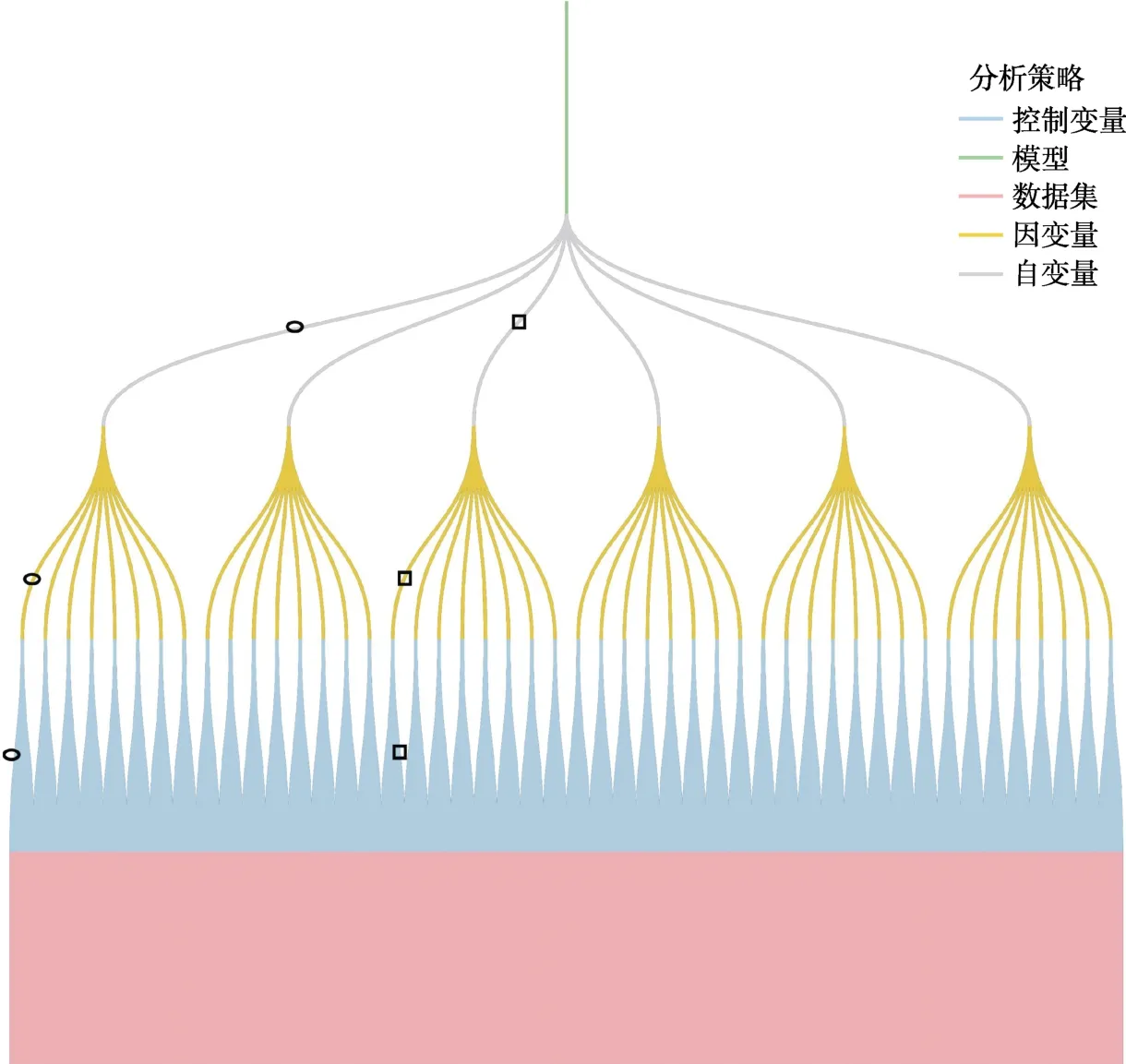
图1 多元宇宙样分析的分析策略组合树状图

本研究旨在结合实例介绍多元宇宙样分析及其在心理学研究中的应用,并对其优势和局限性进行讨论和总结。

2 多元宇宙样分析

如前文所述,多元宇宙样分析指代一组有着核心共同点的统计分析方法。Patel 等(2015)第一次提出相关的概念——效应颤动分析,即描述一个给定的效应估计在多种不同的模型分析下的变化程度。通过呈现不同分析策略的效应和显著性,来确定变量间的关系是否稳定(效应变化幅度越大越不稳定)。Steegen 等(2016)提出了多元宇宙分析,指对一个数据集中的变量进行操纵(例如,变量如何分类、变量如何组合、变量如何转变、数据排除的标准等等),每次操纵将获得多种选择,这些不同的选择放在一起就获得不同的组合——即多个世界或宇宙。Young 和Holsteen (2017)提出了多模型分析,指通过选择协变量、改变函数形式和回归模型等形成大量不同的分析策略,同时多模型分析呈现不同分析策略的结果以检验稳健性。Young 和Holsteen (2017)将不同的分析策略命名为规范(Specification)。Simonsohn 等(2020)在前人的基础上提出了规范曲线分析,指的是将所有可能的分析策略的效应结果分布在一个规范曲线中,并对该曲线进行统计推断,检验研究所关心效应的稳健性。

总之,这些相关分析方法都具有一个共同特征,主张报告多种分析策略的结果,并对这些所有可能的结果进行稳健性检验,避免选择性分析和报告,减少研究者主观偏差的影响,增加结果的可靠性和透明性,有利于解决有争议的话题。因而,近年来的一些研究者将以上这类方法统称为“多元宇宙样分析(Multiverse-style analysis)”(Del Giudice &Gangestad,2021;Rijnhart,Twisk et al.,2021)。本研究中也使用多元宇宙样分析这一术语。

3 基本步骤和实例分析

以往研究者指出,多元宇宙样分析主要分为三个步骤：(1)确定所有分析策略的全集;(2)对所有分析策略的效应进行估计和描述;(3)对所有分析策略进行整体上的统计推断(Patel et al.,2015;Simonsohn et al.,2015,2020;Steegen et al.,2016)。由于效应颤动分析、多模型分析等只完成了前两步,而Simonsohn 等(2020)提出的规范曲线分析囊括了所有步骤,因此,本文主要以规范曲线分析的步骤为例进行介绍。

(1)确定所有分析策略组合的全集。

列举所有的数据分析策略,并生成所有可能的分析策略组合,排除不可行或冗余的组合(Patel et al.,2015;Simonsohn et al.,2015,2020;Steegen et al.,2016)。通常可以对数据集选择、变量类型、变量测量方式、模型估计选择、控制变量等方面进行不同的操作,并将这些操作进行组合,形成一个有大量不同分析策略的集合(Lonsdorf et al.,2022;Patel et al.,2015;Simonsohn et al.,2020;Steegen et al.,2016)。

(2)对所有分析策略的效应进行估计和描述。呈现所有合理组合的估计结果的分布情况,并确定哪些分析策略是最重要的。

(3)统计推断。共同考虑所有这些合理的组合结果与零假设有多不一致。早期多元宇宙样分析的研究仅仅完成前两个步骤,根据显著性结果的占比来推论研究关心的效应(例如Steegen et al.,2016),或仅仅依靠所有估计值的中位数、均值等进行描述性说明(例如Young &Holsteen,2017),未进行统计推断。

不同于单个分析模型,多元宇宙样分析中不同的分析策略模型是相互独立的。要构建零假设分布,可以通过在空值下重新抽样实现,这需要修改观测数据以保证零假设为真,然后随机多次抽取(例如500 次)修改后的数据样本(Simonsohn et al.,2015,2020)。接着计算这些抽取的样本的感兴趣的检验统计量,得到的分布就是检验统计量在零假设下的估计分布(Simonsohn et al.,2015,2020)。最后用实际估计效应与零分布情况进行比较,检验零假设(在y=F(x,z)的函数中,x对y没有效应。其中y为因变量,x是自变量,z为混杂变量)是否为真(Simonsohn et al.,2015)。研究者认为实验数据和非实验数据来源于两种不同的情境,由于非实验数据中协变量与预测变量更可能存在相关,所以实验数据在零假设情况下的抽样比非实验数据更直观(Simonsohn et al.,2015,2020)。为此,研究者使用置换检验和bootstrap 方法分别对两种数据进行统计推断(Simonsohn et al.,2015,2020)。

对于实验性数据(如实验组和对照组),使用置换检验较为简单和直观(Simonsohn et al.,2015)。首先将随机分配的变量(例如为探讨飓风名字不同是否造成不同影响,飓风的名字被随机分配到男性化和女性化组(Simonsohn et al.,2015))进行重新打乱排序。打乱的数据集保留原始数据集的所有其他特征(如共线性、偏度等),此时打乱数据集里面的自变量和因变量没有关系(此时零假设为真)。然后对每一个打乱数据集的所有规范进行估计。重复这个步骤若干次(例如500 次),就能得到在零假设情况下规范曲线的分布(Simonsohn et al.,2020)。

对于非实验性数据,在回归模型中主要有两种修改数据的方式从而产生零假设分布。一种是强制为零然后打乱残差数据集,另一种是强制为零后对数据集进行随机抽样。研究者认为使用后者更为合理(具体论证见Simonsohn et al.,2015,2020)。具体来讲,对每一个组合的观测数据进行模型估计,即估计y=a+bx+cz+e的参数a,b和c。然后通过创建新的因变量y*的方式将数据集强制为零,这个y*此时减去了x对y估计效应(即是b 的取样估计值)。对于y*,现在可以获得零假设为真的模型——y*=a+b*x+cz+e,此时,b*=0 (即x与y*之间没有效应,零假设成立) (Flachaire,1999;Simonsohn et al.,2020)。为了生成理论/期待结果的分布(零假设情况下的取样分布),使用放回抽样对数据集的行进行抽取(以*y而不是y为因变量)。每个重新抽样的样本量与原样本相同。在所有重新抽样过程中获得的的分布用来评估在零假设情况为真时观察到的的极限性。具体步骤是(Simonsohn et al.,2020)：

①估计观测数据的所有K个分析策略组合,这会产生K个不同的估计值但如果因变量在不同的分析策略中一样,对于多个或所有分析策略组合来讲,可能相等。

②产生零假设情况下的K个不同分析策略组合的因变量,即使yk取不同值的数量小于K,也会存在K个不同的,因为在不同的策略组合下是不一样的。所以现在数据集中每一行有x 的值和K个不同的值。

③有放回地在矩阵(步骤②中形成的零假设数据集)中随机抽取N行(N为样本量) (这样会形成一个相同样本的新数据集),并且在所有K个规范上执行。

④依据步骤③抽取的数据计算这K个分析策略组合的估计值,形成一个(估计值由小到大的)曲线。

⑤重复步骤③和④多次(例如500 或1000 次)。

⑥每个抽取的样本都有K个估计值,一种分析策略组合对应一个。计算在多大程度上,重复抽样的分析策略组合形成的曲线的统计指标(如估计值中位数)在总体上与观测到的真实数据存在差异。

规范曲线分析提供了3 个统计推断指标：(1)估计值的中位数(Medianβ),即将估计值按从小到大排列,并选取中位数;(2)主要方向上的显著的结果(the number of significant results in the predominant direction,NSRPD),即多种分析策略组合的估计值中,统计上显著的估计值占主导地位(显著性结果的数量)的方向(正向或负向);(3)每个p值的Z分数转换的均分(Simonsohn et al.,2015,2020)。统计推断就是,检验估计值的中位数是否不同于所有分析组合估计值为零(零假设为真)的情况;主要方向上的显著结果是否多于或高于所有规范估计值为零假设的情况;不同于第二种检验指标,第三个指标将所有p值进行累加,然后平均每个分析组合的p值对应的Z分数,最后检验平均的Z分数是否不同于所有组合在零假设下的情况(Simonsohn et al.,2020)。

总的来说,多元宇宙样分析三步法已获得了许多研究者的认可。目前研究者可以使用多种软件进行多元宇宙样分析,例如Stata 软件、Python和R 软件。研究者开发了许多R 软件包,如specr(Masur &Scharkow,2020),multiverse(Sarma,2021),rdfanalysis(Gassen,2021),multifear(Lonsdorf et al.,2022)等。对于Python 软件,有specification_curve(Turrell,2021),Boba(Liu et al.,2021)等软件包。对于Stata 软件,有speccurve(Sievertsen &Kim,2020)以及分析网站(Young &Holsteen,2017)等。实例中依托的是R 软件包specr。

(4)实例分析

为进一步理解多元宇宙样分析,我们以探讨智能手机使用与智能手机压力之间的关系为实例(以下简称实例),阐释多元宇宙样分析的具体操作。本实例相关的代码和数据可从网址(https://osf.io/fc8he/)获取。需要说明的是,为了充分展示该方法的应用范围,实例囊括了尽可能多的变量操作和策略分析组合,有些变量操作(如将连续变量人为划分为分类变量)未必是单数据集多元宇宙样分析的合理操作,但在多数据集多元宇宙样分析中比较常见(例如对同一变量,有的数据集使用连续变量,有的则用分类变量)。因此,本文的实例仅作为演示方法的样例,不作为方法实际应用的规范。研究者应从实证研究中学习多元宇宙样分析在不同应用情境下的具体操作。

步骤一：在本实例中,数据集中有青少年智能手机使用时间、智能手机压力以及4 个人口学变量等变量(Huang et al.,in press)。表1 中展示了研究者在探讨智能手机使用与智能手机压力关系时可能的分析策略。本实例中,共产生了768 个分析策略组合(见表1)。

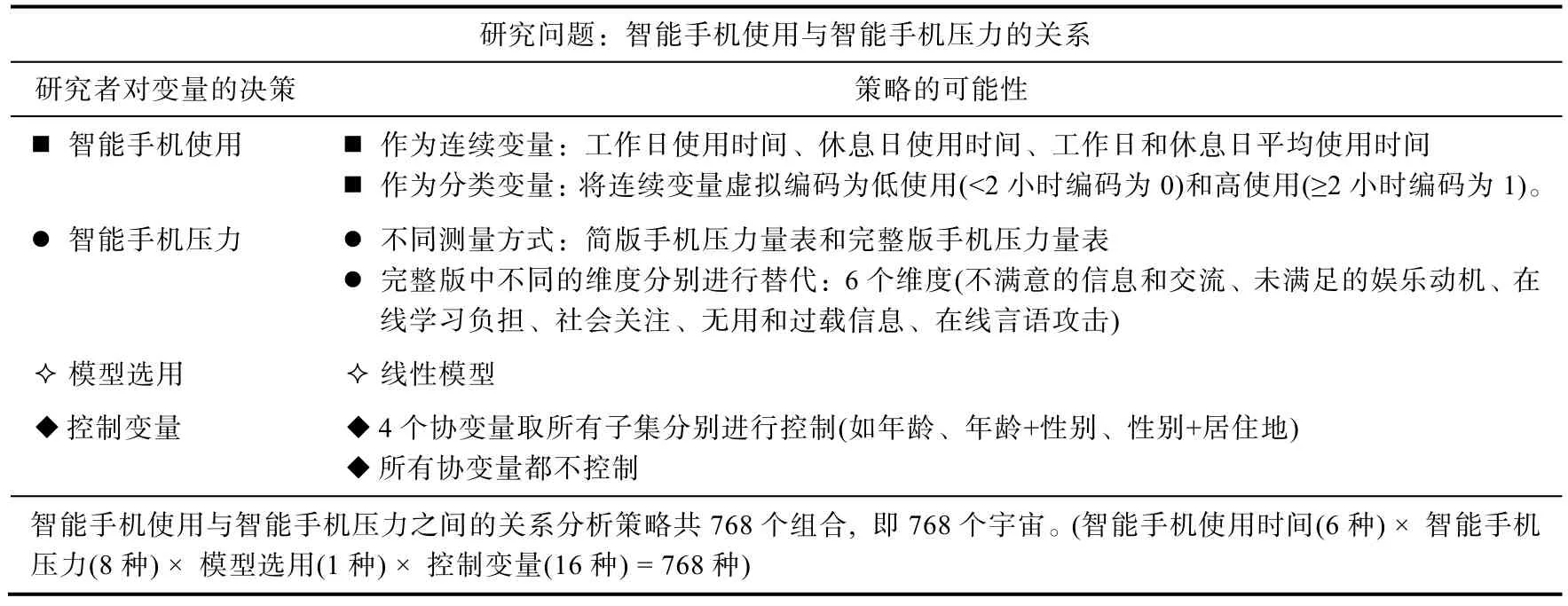
表1 探究智能手机使用与智能手机压力关系的分析策略

步骤二：图2 描述了不同分析策略下智能手机使用对智能手机压力的预测效应。768 个策略(从图2 左边到右边)的总体预测效应在0.026 到0.31 之间,735 个组合获得了显著的结果,33 个组合效应不显著,这说明了效应随分析策略不同而变化。例如,如果研究者报告第5 个分析策略的结果,则智能手机使用对手机压力没有显著预测作用(β=0.003,p>0.05);如果研究者报告第123个分析策略的结果,则智能手机使用对手机压力有显著预测作用,但是效应较小(β=0.11,p<0.05);如果研究者报告第719 个分析策略的结果,则智能手机使用对手机压力有显著且较大的预测效应(β=0.27,p<0.001)。此外,当智能手机使用的评估指标为休息日的使用时间时,预测效应更大,而指标为工作日使用时间时,预测效应更小。当只通过受到的言语攻击来衡量手机压力时,研究者会得到较小的预测效应。

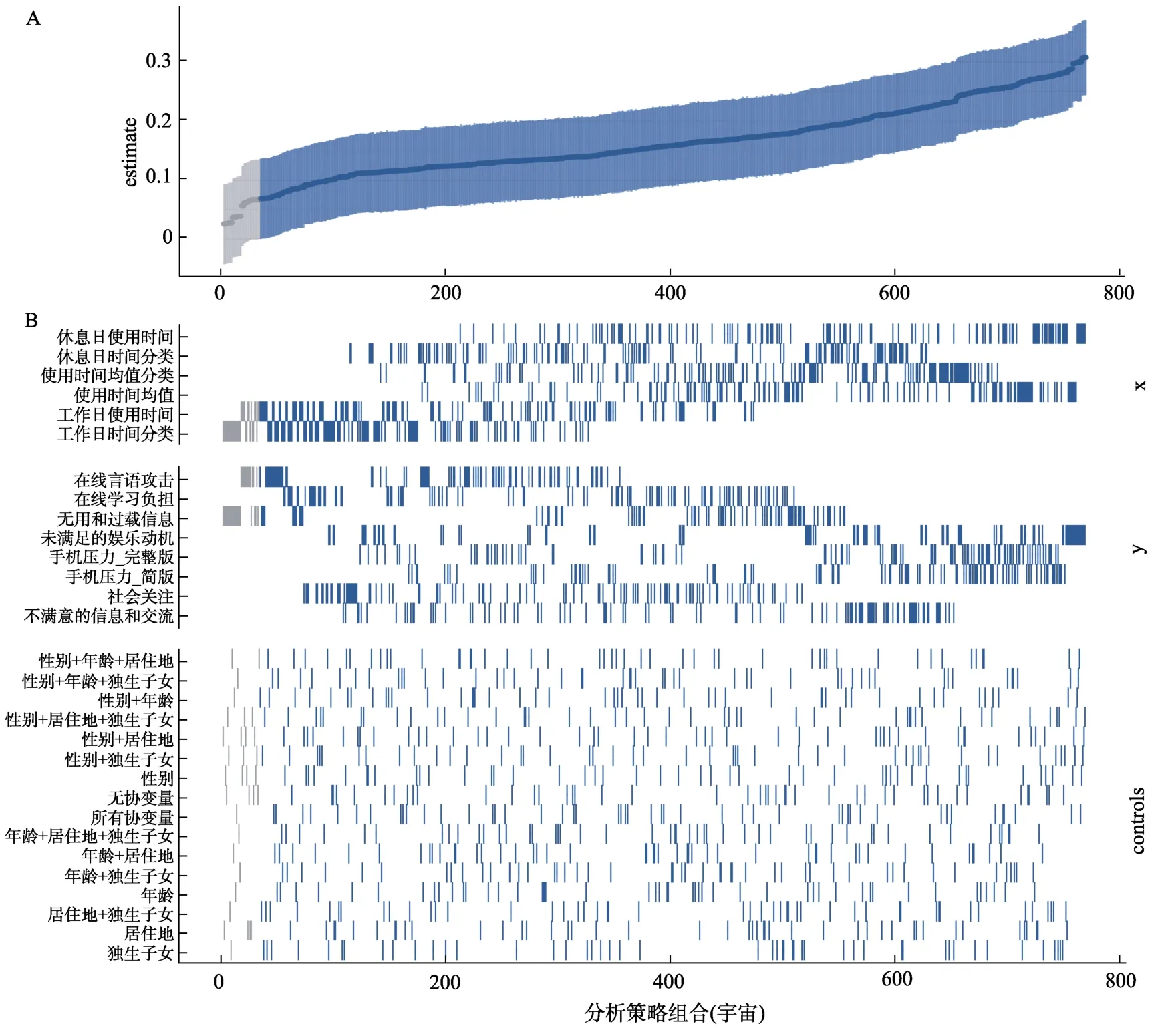
图2 多元宇宙样分析策略结果描述

步骤三：由于估计值中位数和主要方向上的显著结果(NSRPD)这两个统计推断指标简明易懂的特点(Simonsohn et al.,2020),在以往的研究中较为常用(如Orben &Przybylski,2019a,2019b),本实例也使用这两个指标。实例为非实验数据,使用bootstrap 进行统计推断,零假设为智能手机使用对手机压力没有影响。实例展示了不同智能手机使用与智能手机压力之间的关系的统计推断结果(表2),可见无论何种分析策略下,智能手机使用对手机压力的作用都是显著且稳健的(Medianβ=0.12 to 0.20,p<0.001;NSRPD=106/128 to 128/128,p<0.001)。

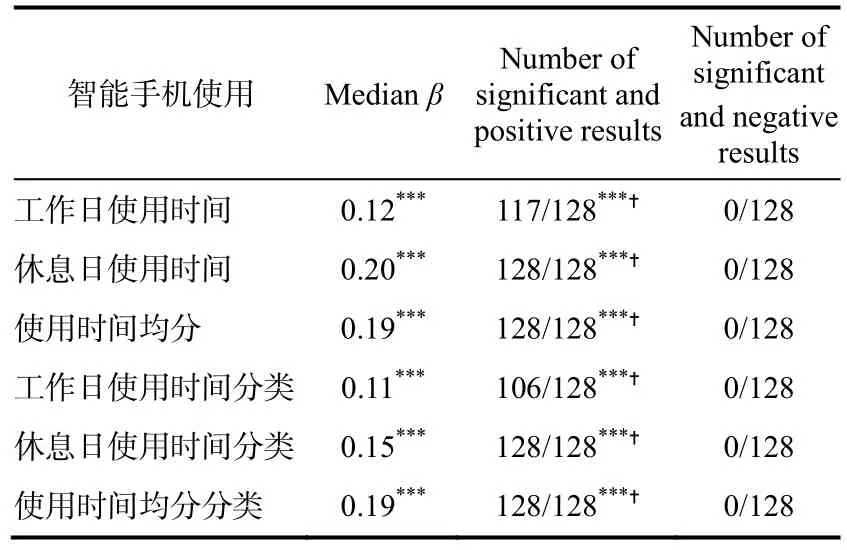
表2 多元宇宙样分析的统计推断结果

由于本实例仅仅对变量进行了不同操纵,未来研究还应该考虑恰当的参数估计方法(如极大似然或贝叶斯估计)、模型选择指标(如BIC或AIC)、抽样算法(如bootstrap 或马尔科夫-蒙特卡洛)等,从而更好地发挥多元宇宙样分析的优势。

4 多元宇宙样分析的应用

近年来,多元宇宙样分析越来越受到研究者的关注。从2015 年到2021 年,以多元宇宙样分析为主题的文章从9 篇上升到40 篇(如图3)。该方法近年来在许多领域内得到应用,Web of Science 的检索结果表明,以多元宇宙样分析为主题或应用该类方法的研究分布在行为科学领域、心理学领域、神经科学领域、精神病学领域等。

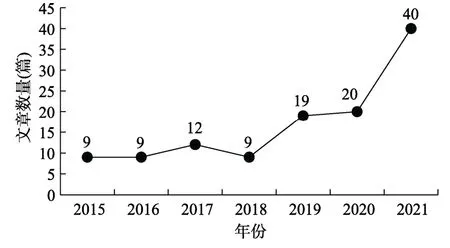
图3 多元宇宙样分析在Web of Science 数据库中的发文量(2015～2021)

4.1 应用于自我报告类数据

多元宇宙样分析广泛运用于横向自我报告数据中。在媒体心理学领域,媒体使用是否影响青少年心理健康一直是备受争议的话题。研究者为了探讨智能设备使用与心理健康和主观幸福感的关系,使用规范曲线分析进行了大量研究。Orben和Przybylski (2019a)使用3 个国家的大型数据集探索了屏幕时间(11 种操作：回溯性自我报告、时间日记测量、工作日和休息日使用等)与幸福感(3种操作：优势与困难问卷、自尊问卷、主观幸福感问卷)的关系,并对控制变量进行控制(2 种)。最后发现二者间并没有实质性联系,即使存在微弱的负向预测关系,这种关系也不稳健。所以他们认为以往关于屏幕时间不利于心理健康的说法是站不住脚的。此外,他们的另一项使用规范曲线分析的研究也发现类似的结果,即媒体设备的使用与心理健康之间没有实质性的联系(Orben &Przybylski,2019b)。Modecki 等(2020)使用多元宇宙分析探讨父母智能手机使用对父母教养方式的影响,发现父母使用智能手机对其教养方式的影响是非常小的,并且亲子间不受技术干扰影响时,更多智能手机使用与更高质量的教养方式有正向关系。

近年来,多元宇宙样分析也逐渐运用于追踪研究。为了探讨青年失业与未来心理健康关系的稳健性,Wright 等(2021)对2008 年经济危机后进入劳工市场的青年进行第一次测量,在其25 岁时进行第二次测量,同时对若干控制变量进行操纵。在12 万个分析策略中,他们发现青年失业经历会导致未来的不良心理健康状况,这种长时效应具有稳健性(79.42%的模型在统计上具有显著性,0.04%的模型发现相反的预测效应)。为了探讨口服避孕药对女性青少年未来抑郁的影响,Anderl 等(2022)使用规范曲线分析了女性青少年(16～19 岁)自我报告的口服避孕药使用情况和成年早期(20～25 岁)自我报告的抑郁情况,在818 个分析策略中,他们发现女性青少年的口服避孕药使用与成年早期的抑郁有着较小但稳健的关系。

4.2 应用于脑成像与混合类数据

一些脑科学和生物学相关的研究也正在使用多元宇宙样分析方法进行稳健性检验(Bloom et al.,2022;Cosme et al.,2020;Cosme &Lopez,2020;Voracek et al.,2019)。例如,额叶α 波不对称性(Frontal alpha asymmetry,FAA)是否是抑郁障碍病人脑电图(EEG)的一个指标仍然存在争议,为了回答这个问题并检验该指标的有效性,Kołodziej 等(2021)对5 个独立研究的脑电图数据集,使用多元宇宙分析对统计模型、信号空间、协变量控制等进行操作,对270 种可能的组合进行稳健性分析,发现仅有13 种组合呈现显著的结果,因此他们认为 FAA 与抑郁障碍之间没有联系。在功能性磁共振成像(fMRI)研究领域,为了探讨食物线索反应、调节和评估的神经机制是否与身体状况(如BMI 指数、身体肥胖比例)及实际饮食行为有关,研究者使用5 个fMRI 数据集,对脑区激活与饮食行为间的关系稳健性进行检验,规范曲线分析结果表明,食物反应线索的神经机制与饮食行为指标之间的关系是可靠的、稳健的(Cosme &Lopez,2020)。

最近也有研究者将多元宇宙样分析方法应用于混合类数据。例如Möschl 等(2021)结合问卷报告、生理指标和实验任务,使用规范曲线分析研究慢性压力(多种自我报告测量和头发皮质醇浓度)与执行功能(多种实验任务)的关系,发现二者的关系取决于不同的分析策略——大部分分析策略显示零效应,仅小部分策略发现二者间是正向或负向的关系。

4.3 与其他分析方法结合

随着多元宇宙样分析方法及原理的扩展,研究者开始将其与其他方法进行结合。较为突出的几个例子是将其应用于探讨中介效应或变量间作用机制的稳健性,结合网络分析方法探讨核心症状的稳定性,以及结合元分析进行组合性元分析。

中介效应分析在社会科学各个学科中得到广泛的应用(MacKinnon et al.,2007;温忠麟 等,2005;温忠麟,叶宝娟,2014),特别是在探讨因果关系的作用机制时,中介效应分析显得尤其重要(MacKinnon et al.,2007;Rijnhart,Lamp et al.,2021)。因此,在心理科学可重复性危机的情况下,中介效应的稳健性值得进一步探讨(Rijnhart,Twisk et al.,2021)。Rijnhart,Twisk 等(2021)将多元宇宙样分析方法扩展到中介效应分析中,他们认为研究者除了以往提到的可操作空间外,还可以对中介变量、中介变量分析方法、确定中介效应存在的标准进行操作。基于此,他们使用一项追踪数据探讨体重改变对骨矿物质的影响在多大程度上受到身体成分(体脂率和四肢肌肉质量)的中介作用。在108 种间接效应、108 种直接效应和36 种总体效应组合中,他们发现间接效应为正向中介机制,显著且具有稳健性;91.7%的直接效应不显著;66.7%的总体效应为积极预测效应,且55.6%的效应显著。因此,他们认为体脂率是稳健的中介机制。

近年来,随着精神疾病网络理论和网络分析方法的发展,寻找症状网络中的核心症状或核心变量有助于精神疾病的干预和治疗,但是该领域也同样出现了可重复性危机,网络指标中心性的不稳定性备受研究者争论(Bringmann et al.,2019;Dablander &Hinne,2019;Rodebaugh et al.,2018)。Black 等(2021)对青少年内化问题症状和幸福感症状的动态网络进行分析,并根据网络中心性指标确定网络的核心症状。同时,为了减少网络构建过程中症状的选择性操作,研究者(通过操作症状、使用不同估计方法)构建了32 个不同的网络,以确定不同网络下中心性指标的稳定性。结果发现,思维清晰、不高兴、应对压力和担忧的中介性具有跨不同分析策略的稳定性,表明这些指标在青少年心理健康发展过程中的重要作用。

元分析领域的研究有时也受到批评,例如纳入分析研究的标准,使用什么估计模型等等。为此,研究者提出采纳、修改多元宇宙样分析的方法,将其框架使用在元分析中——即组合性元分析(combinatorial meta-analysis) (Olsson-collentine et al.,2021;Voracek et al.,2019),用于解决有冲突的元分析结果、有争议的证据。Voracek 等(2019)使用了组合性元分析探讨了指长比与睾丸激素敏感性的关系。通过操作元分析的分析方法(效应量指标选择、元分析估计模型)和纳入的研究的特征(性别、年龄群体、群体状态、种族、指长比的测量方式、研究的发表状态),形成了1592 个不同元分析的策略组合。最后组合性元分析结果表明,指长比与睾丸激素在很大程度上不存在关联。

4.4 应用研究小结

总的来说,不同研究在策略组合选择上有不同偏向,例如有些研究较为侧重测量方式的选择,有些研究更加重视不同模型的选择。这意味着进行多元宇宙样分析时,应当特别考虑这种情况(如对测量方式争议的考虑、对估计模型争议的考虑等),这有助于研究者确定具体分析策略。但对不同测量方式争议的检验,这依赖于现有数据集是否支持(比如数据集的确使用了不同测量方式)。此外,在与其他方法进行融合的时候,也是聚焦原有方法不足之处(原有方法仍然产生争议性话题和不可重复性问题)。但是,通过与其他方法的结合,不仅促进原方法存在问题的解决,也将有利于心理科学领域中研究方法的创新和发展。

5 多元宇宙样分析的优势与不足

多元宇宙样分析方法可以减少研究者的选择性分析与报告,增加研究的透明度,揭示效应的稳健性,在一定程度上可以缓解由选择性分析、选择性报告带来的可重复性危机。此外,揭示所有的效应、包容小效应、寻求稳健的效应有利于修正现有理论,促进理论的发展,并进一步促进研究结果在临床中的应用(Lonsdorf et al.,2022;Prentice &Miller,1992;Voracek et al.,2019)。

多元宇宙样分析可以囊括多种数据集和多种测量方法。例如Kołodziej 等(2021)、Cosme 和Lopez (2020)囊括了多个数据集进行多元宇宙样分析,这种分析有利于解决因取样偏差或地区/文化差异导致的争议问题,并提高结果的可靠性。另外,心理学研究测量方式很大程度上依赖于自我报告,这种方式受到一些研究者的质疑,而多元宇宙样分析可以纳入多种测量方式并报告所有的结果,再检验结果的可靠性。例如Möschl 等(2021)使用多种自我报告问卷和头发皮质醇浓度指标反映个体的慢性压力水平,Orben 和Przybylski(2019a)使用自我报告和回溯法评估个体数字媒体设备的使用情况。总之,多元宇宙样分析能够考虑多样化的变异(如群体差异、测量差异、模型估计方法差异等),并给出稳健性的结果。

如上所述,结合多元宇宙样分析的应用研究可以发现,该方法有利于回答争议性的问题,即某两个变量之间的效应究竟怎样？在这一点上,多元宇宙样分析与元分析类似,能将多种结果放在一起检验效应的稳健性。虽然元分析也可以解决许多有争议性的问题,但是,多元宇宙样分析与元分析并非对立。不少研究者采用全世界研究者在不同时间地域采集的不同样本,进行多元宇宙样分析(如Orben &Przybylski,2019a),这样的分析策略兼有元分析样本多样性强和多元宇宙样分析主观偏差少的优势,这也启发研究者将该多元宇宙样分析的灵活性应用到元分析中(如Voracek et al.,2019)。另外,需要注意的是,多元宇宙样分析还可以被用于实证研究积累尚不充足、难以开展元分析的新兴研究领域,具备元分析所不具有的独特价值(例如,有研究者将规范曲线分析用于单个参与者的元分析(individual participant meta-analysis;Ballou &Zendle,2022)。

多元宇宙样分析也有其局限性。第一,这种分析方法非常耗时(Liu et al.,2020),特别是分析策略增加,样本量增大,且进行统计推断时。研究者认为提高分析过程的自动化程度可以减少分析策略,例如使用Young 和Holsteen (2017)提供的Stata 分析模块。此外,研究者还可以减少样本量(例如对大样本中随机抽取出的小样本进行分析)来减少运算时间(Rijnhart,Twisk et al.,2021)。第二,在进行不同策略组合的时候,默认所有分析策略都有同样的统计推断权重,且所有的策略组合在理论上都是合理的、统计上是有效且非冗余的。虽然理论上可以通过计算加权后的统计推断指标(如加权后的中位数),但是研究者仍难以确定哪种分析策略更优,应给予哪种策略更多的权重(Simonsohn et al.,2020)。第三,虽然多元宇宙样分析大幅扩展了分析策略的范围,对选择性分析与报告进行了限制,但该方法本质上还是研究者的主观操作。例如,研究者可能由于某些原因(例如样本量太大而难以分析、研究者认为某些分析策略是无效的)不会进行所有有效的分析(Rijnhart,Twisk et al.,2021;Simonsohn et al.,2020;Steegen et al.,2016)。另外,这也可能引发研究操作的“真正任意性” (truly arbitrary)问题,例如研究者提出的不确定性策略组合(比如两个测量概念上是相似的,但是没有实证证据表明测量的有效性,或者潜在的控制变量对感兴趣效应量的影响没有实证证据),这种真正任意性问题也容易产生偏差,夸大所有可能的策略组合,减弱有意义的效应(Del Giudice &Gangestad,2021;Masur,2021)。针对这种情况,有研究者提出了多元宇宙样分析的分析策略操作框架供研究者参考(Del Giudice &Gangestad,2021)。第四,多元宇宙样分析中效应分布统计推断指标的可靠性仍存在争议。例如,许多研究把效应分布的中位数或均值作为检验稳健性的一个指标,但是有研究者认为这种指标不一定能很好地代表统计结果(Rijnhart,Twisk et al.,2021;Young &Holsteen,2017),所以需要结合多种指标(例如主要方向上的显著结果、p值的Z 分数)进行分析(Simonsohn et al.,2020)。第五,多元宇宙样分析主张报告所有可能策略组合的结果(Simonsohn et al.,2020),但实际上较难实现。研究者在使用该方法时,常常基于已有的数据集,对已有数据集实施所有可能的分析策略并报告其结果是可行的。这提示建立客观有效的数据集的重要性,即在数据收集之前,就应该从已有文献、经验或理论出发,确定相应的指标和潜在的分析方法,并落实预注册从而减少其中的可操作空间。此外,主张报告所有分析策略,也存在过分依赖数据驱动研究取向的问题。但是理论驱动和数据驱动的冲突不是拒绝多元宇宙样分析的理由,研究者应该在讨论分析结果时充分发挥理论的作用,注意辨析为什么不同策略有不同的结果,为什么有些策略产生相同的统计推断而有些产生不同的统计推断,这或许更有助于我们真正理解研究问题。

6 小结与展望

多元宇宙样分析有着独特的优势,也存在一些不足。但该方法未来在以下几个方面有待进一步发展。

第一,应用研究应尽快落实统计推断步骤,最大化发挥多元宇宙样分析的作用。大部分应用该方法的研究在确定研究结果的稳健性时仍停留在描述统计(统计显著结果的占比)水平上(如Black et al.,2021;Patel et al.,2015;Rijnhart,Twisk et al.,2021;Steegen et al.,2016;Wright et al.,2021;Young &Holsteen,2017),有时难以确定效应的真实情况。例如当显著的效应和不显著的效应各占比50%,或者正向或负向的效应各占50%时,研究者难以从描述统计确定应该相信哪种情况,所以应该进一步实施统计推断。此外,该方法可以囊括多种变异(测量、群体、模型估计方法等),但是大部分应用研究通常只发挥其某一方面的作用,比如使用多种测量(行为实验、生物指标、自我报告等)解决不同测量方式存在差异的问题(如Möschl et al.,2021),和使用不同群体解决不同群体差异的问题(如Cosme &Lopez,2020;Orben &Przybylski,2019a)。未来应用研究应该尝试囊括多种变异,以充分发挥该方法的作用,揭示效应结果的可靠性。

第二,不断深化与其他研究方法的融合。尽管现有研究将其与中介效应分析、网络分析和元分析进行融合,但这些融合的方式仍存在主观选择性问题。例如在网络分析中,对于纳入分析的节点(nodes)仍然是主观选择的(Black et al.,2021)。这意味着在与其他方法融合时,也要有相对统一的、适用于不同方法的策略选择标准,如适用于中介效应分析或元分析的纳入标准等。同时,也要尽可能在融合其他方法时实施统计推断,以保证结果更加可靠。此外,未来研究可以考虑将其与更多的其他方法融合(比如运用到结构方程模型中),促进心理科学领域研究方法的创新。

第三,筛选可靠的统计推断指标,融合不同参数估计和模型选择方法,并完善分析软件。许多多元宇宙样分析的方法(如多模型分析,效应颤动分析)并没有涉及统计推断步骤,这就使得现有的统计推断指标非常少。未来研究应该要考虑对更多的指标(例如平均值)进行统计推断。但是,有时多种指标的结果是互相矛盾的(例如Simonsohn等(2020)中的案例2),这增加了研究结果的解释难度,所以未来研究可通过模拟研究筛选出灵敏性和代表性更高的指标。同时,在进行分析策略的选择时,也可以进一步考虑不同策略在不同的参数估计方法、不同抽样算法下的情况,并考虑合适的模型选择指标。这有利于丰富多元宇宙样分析的策略多样性并提升结果的稳健性。另外,许多分析软件的软件包(例如multiverse,rfdanalysis,specr,specification_curve)并没有涉及到统计推断,大多停留在对所有组合进行描述统计的范围内,这使得研究者难以完成第三个步骤,所以未来的研究需要完善该方法的分析软件或分析包。同时,不同的分析软件(或软件包)报告的结果是否存在差异也值得探讨,这对提升结果的稳健性和可重复性同样具有重要意义。

第四,结合多种渠道,共同致力于解决可重复性危机。可疑研究操作可能从研究者设计实验时就开始了,因而多元宇宙样分析无法解决分析策略前端的可疑操作。另外该方法无法完全消除主观偏差的影响,因为研究者在进行分析策略组合时,仍然具有可选择性(Simonsohn et al.,2020)。所以应当结合前人提出的其他方式(例如预注册),共同增加心理学研究结果的透明度和可靠性。例如,心理学研究中不乏将连续变量作为分类变量处理的情况(如实例中的智能手机使用),但可能存在“真正随意性”的问题(比如,量表的选择是否合理、分析模型是否恰当等)。因此研究者可以考虑在预注册中就确定这一系列指标,从而在数据分析前减少此类可疑操作。此外,还有研究者倡导将多元宇宙样分析方法运用于数据收集过程中,以此来减少主观操作(Harder,2020)。

第五,理性看待不同分析策略组合的不同结果。多元宇宙样分析的优势便是告诉研究者所有可能的结果,那么要如何看待不显著或非主要方向上显著的结果呢？是否把他们当作微不足道的“误差”并加以忽视？无论是心理科学研究的可重复性还是多元宇宙样分析,其实都很想强调一个假设——人类的心理与行为之间存在简单的标准化规律(例如,手机使用程度与心理健康水平应存在唯一准确的对应关系、或研究者可以通过平均值代表总体)。但是人类行为可能并不会这么简单,其受诸多因素的影响(例如,基因、个体发展、群体、环境、文化等),正如研究者争论道“研究者通过样本刻画总体,虽然能够告诉许多关于总体的信息,但是还有许多东西没有解释(被认为是误差)……社会科学中的这个误差是一个真实性的、理解性的误差,是知识上的缺陷” (谢宇,2006)。因而,许多研究者反对追求这种简单的“标准化规律”,进而发展出非标准化理论。这提示研究者在使用多元宇宙样分析时应正确看待不同分析策略组合的不同结果,理解不显著或非主要方向上显著的结果的存在意义,并谨慎下结论。

致谢：感谢编委和匿名审稿人对本文提出的宝贵意见,感谢美国田纳西大学儿童和家庭研究系严嘉(Yan Julia Jia)博士(助理教授)对本文英文摘要的阅读与修改。