四入口液-液旋流分离器分离性能数值模拟
2023-02-11李美求陈星黄天成王兆坤
李美求, 陈星, 黄天成, 王兆坤
(长江大学机械结构强度与振动研究所, 荆州 434023)
水力旋流器作为一种常用的分离装置,被广泛应用于化工、石油、煤炭、采矿等领域。它主要是运用离心沉降原理分离混合物中具有密度差异的相[1]。旋流器工作时内部将产生内外两个旋流场,在内外两个旋流场的作用下,大密度和大粒径的相从底流口流出,小密度小粒径的相从溢流口流出,从而实现两相之间的分离[2]。
自1984年首个双锥切向双入口液-液旋流器进行现场应用以来,多入口旋流器开始受到学者们广泛关注[3-4]。近年来,学者们针对多入口旋风分离器和旋流器分离器做了大量研究。Vahedi等[5]研究了四入口对旋风分离器流场、分离性能、以及冲蚀规律的影响,研究结果表明,四入口旋风分离器流场具有良好的对称性和较强的离心力,这使得四入口旋风分离器直径可以进一步减小,同时分离效率得到提高,除此之外,其相较于传统旋流器而言冲蚀率更低。Le等[6]设计了两种四入口旋风分离器,即四入口共面且均匀分布型(C4)以及两两异面均匀分布型(N4),并将其与单入口进行了对比,研究结果发现N4相比于C4分离性能提高0.1%,并得出四入口设计可以提高旋风分离器性能的结论。Nassaj等[7]设计了一种新型的带导流通道的四入口旋流分离器,并将其和传统单入口进行了对比。结果表明带导流通道的四入口旋风分离器,其压降主要发生在导流通道内,同时入口速度对旋流器内部压力、切向速度影响明显,通过提高入口速度可以明显提高旋流器对小颗粒的分离性能。张梓均等[8]研究了旋流器进口数量对于流场对称性以及截面速度分布的影响,研究发现相较于单入口旋流分离器,多入口旋流分离器具有更好的轴对称切向流场分布以及更大的切向速度,同时轴向速度相较于单入口旋流分离器变化明显,其变化趋势为随着高度的增大明显减小。董思捷等[9]对比了不同入口位置分布情况下四入口旋风分离器的分离性能,研究发现当入口在径向上呈对称分布且与旋流器壁面相切,同时轴向上处于与圆柱段上表面相切时,入口布置方案最优。张悦刊等[10]分别对比了单、二、三、四入口对液-固旋流分离器分离性能的影响,研究发现:通过增加入口数量,液-固旋流分离器的分级效率和分离性能都得到了有效改善,尤其偶数入口数量时,旋流器内部径向静压增强效果明显变好。
上述研究都是基于结构参数对四入口旋流分离器性能的影响上开展的,而操作参数对其分离性能影响未见详细研究。在对传统旋流器操作参数研究中发现,溢流口分流比和入口的流速对旋流器分离性能影响最明显。因此现以油水分离作为对象,从溢流口分流比和入口流速两方面对四入口液-液旋流分离器进行数值模拟和流场特性研究,探究其分离效率。
1 数值模型
1.1 数学模型
多相流模型被广泛用于多个速度不同的混合相问题求解中,任何流体的流动都要遵循能量守恒和质量守恒定律的制约,其中连续性方程和动量方程[11]如式(1)和式(2)所示。
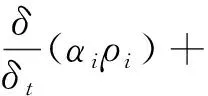
(1)

(2)
式中:下标i表示水相或油相;t为时间,s;α为体积分数;ρ为密度,kg/m3;∇为拉普拉斯算子;u为速度矢量,m/s;τ为应力张量,Pa;p为压力,Pa;Mi为时间动量交换项,kg/(m·s)2;g为重力加速度,m/s2。
在旋流器内部,主相以连续相的形式存在,次要相离散在其中,当旋流器内部混合相的切向速度达到剪切破碎离散相的临界值时,离散相将会发生破碎,同时由于表面张力的存在,离散相之间也会发生聚合作用。因此不可忽略破碎和聚合导致的离散相粒径的变化对旋流器分离性能的影响,特此需要在多相流模型中引入群体平衡方程(population balance model,PBM)[11],表达式为
S(V,t)=BC(V,t)-DC(V,t)+BB(V,t)-DB(V,t)
(3)
式(3)中:S(V,t)为液滴聚并和破碎的源相;BC(V,t)和DC(V,t)分别为聚并导致的液滴生成和破灭;BB(V,t)和DB(V,t)分别为破碎导致的液滴生成和破灭;V为液滴体积,m3。
1.2 物理模型及网格划分
四入口液-液旋流分离器结构如图1所示,尺寸参数见表1,取距离底流口下端面395、375、350、300、250 mm处分别为截面Ⅰ、截面Ⅱ(距离溢流口底部1 mm处)、截面Ⅲ、截面Ⅳ、截面Ⅴ。对四入口液-液旋流分离器进行单元网格划分,单元类型采用四面体和六面体混合,这种划分方式可以在减少网格数量的同时提高网格适应性,全局网格尺寸为2 mm。由于入口管与圆柱段相切处具有较为复杂的相贯曲面,因此针对入口管段选择四面体网格划分,同时进行网格加密,尺寸为1 mm。其具体网格划分图如图2所示。

图1 旋流分离器结构示意图Fig.1 Schematic diagram of hydrocyclone structure
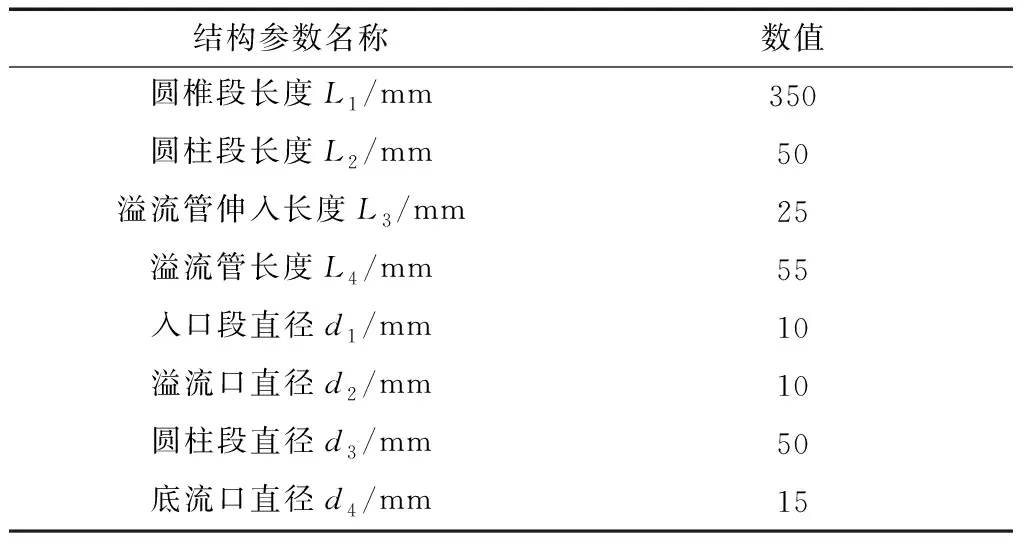
表1 四入口旋流器结构尺寸表Table 1 Table of construction dimensions for four inlet hydrocyclone

图2 旋流器网格划分图Fig.2 Grid drawing of hydrocyclone
1.3 数值计算模型及边界条件
基于上述理论,采用Mixture模型,模拟分流比以及入口速度对其分离效率和流场特性的影响,湍流模型使用雷诺应力模型(Reynolds stress models,RSM),开启群体平衡方程(PBM)[11-12]。将油滴按对数正态形式分布,分为6组,平均直径为80 μm,允许破碎最小直径为10 μm,允许聚合最大直径为150 μm。水相密度设定为998.2 kg/m3,黏度为1.003 mPa·s; 油相参数按照正辛烷进行设定,密度为720 kg/m3,黏度为0.54 mPa·s。边界条件设置为速度入口,含油体积分数0.2。出流边界条件设置为自由出口来允许溢流口和底流口边界的自由流动,残差精度设置为0.001,壁面为无滑移壁面条件。压力速度耦合方式采用SIMPLEC,同时选择二阶迎风格式提高求解精度。
2 分离性能影响因素分析
许多学者针对传统旋流分离器分离性能影响因素做出了大量研究,研究结果表明,旋流器的结构参数、类型、入口管布置和入口管形状都对分离效率有着显著的影响[13-14]。然而除去结构上的影响外,在旋流器操作参数中,处理量和溢流口分流比,即溢流口出流流量与入口流量比值,都是分离效率重要影响因素[15-16]。处理量(即流量)在入口面积一定时,流量越大则流速越快,较快的流速可以提高旋流器离心力并产生较强的涡流,但流速过快旋流器内部离散油滴受到剪切作用增强,不利于分离。分流比过大,则有更多的水相将从溢流口流出,特别是对于考虑油相含水率的情况而言,综合效益下降,而分流比过小,其分离效率又将降低。因此选取上述两个变量对四入口液-液旋流分离器分离性能及流场特性进行研究。
2.1 分流比对分离性能的影响
保持入口流速为8 m/s恒定,改变分流比F并分析其对旋流器分离性能的影响。由图3(a)可知,随着高度的增加,轴向各位置高含油区域面积和油相体积分数逐渐增大,在旋流器内部形成相界面清晰的锥形油柱。由图3(b)可知,油柱随着溢流口分流比的增大逐渐消失,最终油相绝大部分集中在溢流口附近。这是由于随着溢流分流比的提高,底流口背压增大,混合相从底流口排出难度也随之增大,更多的混合相将从溢流口排出,此时油相向溢流口聚集。

图3 不同分流比油相体积分数云图Fig.3 Cloud image of oil phase volume fraction with different split ratio
由图4可知,溢流口含油体积分数随着溢流口分流比的增大明显下降,溢流口分流比为0.18时,其油相体积分数可达95.13%,当溢流分流比为0.26时,此时油相体积分数下降为75.45%。这主要是因为溢流口分流比过大导致较多的水相流入溢流口,使得含油体积分数下降,此时溢流口会出现明显的油夹水现象,严重影响旋流器的分离性能。

图4 溢流口油相体积分数随分流比变化折线图Fig.4 Line chart of oil phase volume fraction in overflow port changing with split flow ratio
由于旋流器内部流场为轴对称状,其内部速度变化趋势相同,为更好反应旋流器内部流场速度变化规律,选择具有一定代表性的截面Ⅱ进行分析。
由图5(a)截面Ⅱ处切向速度随分流比变化折线图可知切向速度呈中心对称分布,在径向距离减小的过程中切向速度出现两个峰值和两个零点,切向速度为零的点分别位于旋流器壁面处和中心处,切向速度峰值分别位于距离旋流器中心5 mm和15 mm处,其在结构上,分别对应溢口半径的1/2处和圆柱段半径与溢流口半径差值的1/2处。这是因为旋流器壁面处切应力大,流体流动所受到的阻力大,从而导致流速较小,而距离旋流器内壁较远处,阻力较小,流速则较大。同时随着分流比的增大,第一个切向速度峰值变化不明显,第二个切向速度峰值呈逐渐增大趋势,说明分流比大小会影响溢流口内壁距离旋流器中心段的内旋流切向速度峰值,而对旋流器溢流管内壁与圆柱段内壁中心处的外旋流峰值影响较小。
由图5(b)可知,轴向速度呈对称分布,随着径向距离的减小,轴向速度方向开始时呈负方向先增大后减小,随后方向发生改变呈正方向增大,在旋流器中心时其轴向速度最大,同时轴向速度最大值随着分流比的增大而增大。证明旋流器外旋流区水相由于密度大受到较大离心力和重力从而向底流口流动,油相由于密度小集中在内旋区向溢流口流动,同时较大的分流比会加快油相向溢流口流动速度,与实际情况相符。
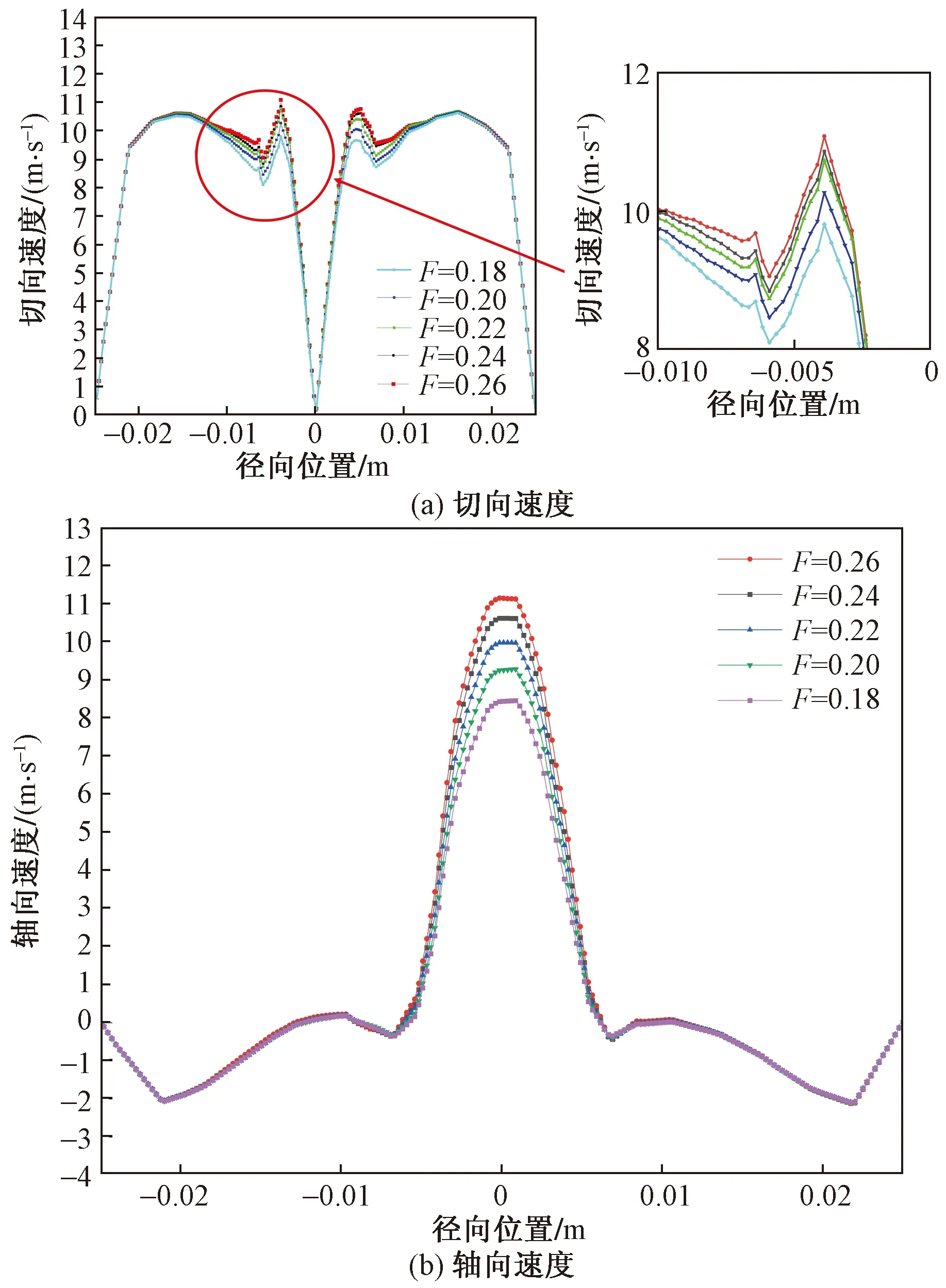
图5 截面Ⅱ速度随分流比变化折线图Fig.5 Line chart of cross section Ⅱ velocity varying with shunt ratio
压降比是通过溢流口压降与底流口压降比值来衡量旋流器分离性能好坏的重要指标,一般在流速相同的情况下更少的压力损失会使旋流器有更好的分离特性。由图6压力随分流比变化云图可以看出,压力分布云图呈中心对称分布,同时径向压力和轴向压力分别随着径向距离和轴向高度逐渐增大。图6中溢流口和底流口数据分别对应该处具体压降数值,当分流比为0.18时,溢流口压降为172 131 Pa,随着分流比的增加,溢流口压降逐渐增加到208 582 Pa,同时底流口压降逐渐减小。由图7可知,压降比随着分流比的增大逐渐增大,对压降比Pr曲线进行拟合可以得到其拟合线性方程为
Pr=0.057 5F+0.756 3
(4)
拟合度R2为0.997 9,通过压降比折线图和拟合方程可知,随着分流比F增大压降比也将增大,此时会因为溢流口压力变小底流口压力变大而产生明显的油相夹带水相现象,不利于油水分离。而当分流比较小时,溢流口压力会变大底流口压力会变小而导致明显的水相夹带油相的现象,严重影响分离效率。因此分流比F应该选取较为合适的值,才能有效提高四入口液-液旋流分离器的分离性能。

图6 静态压力随分流比变化云图Fig.6 Cloud diagram of static pressure varying with split ratio
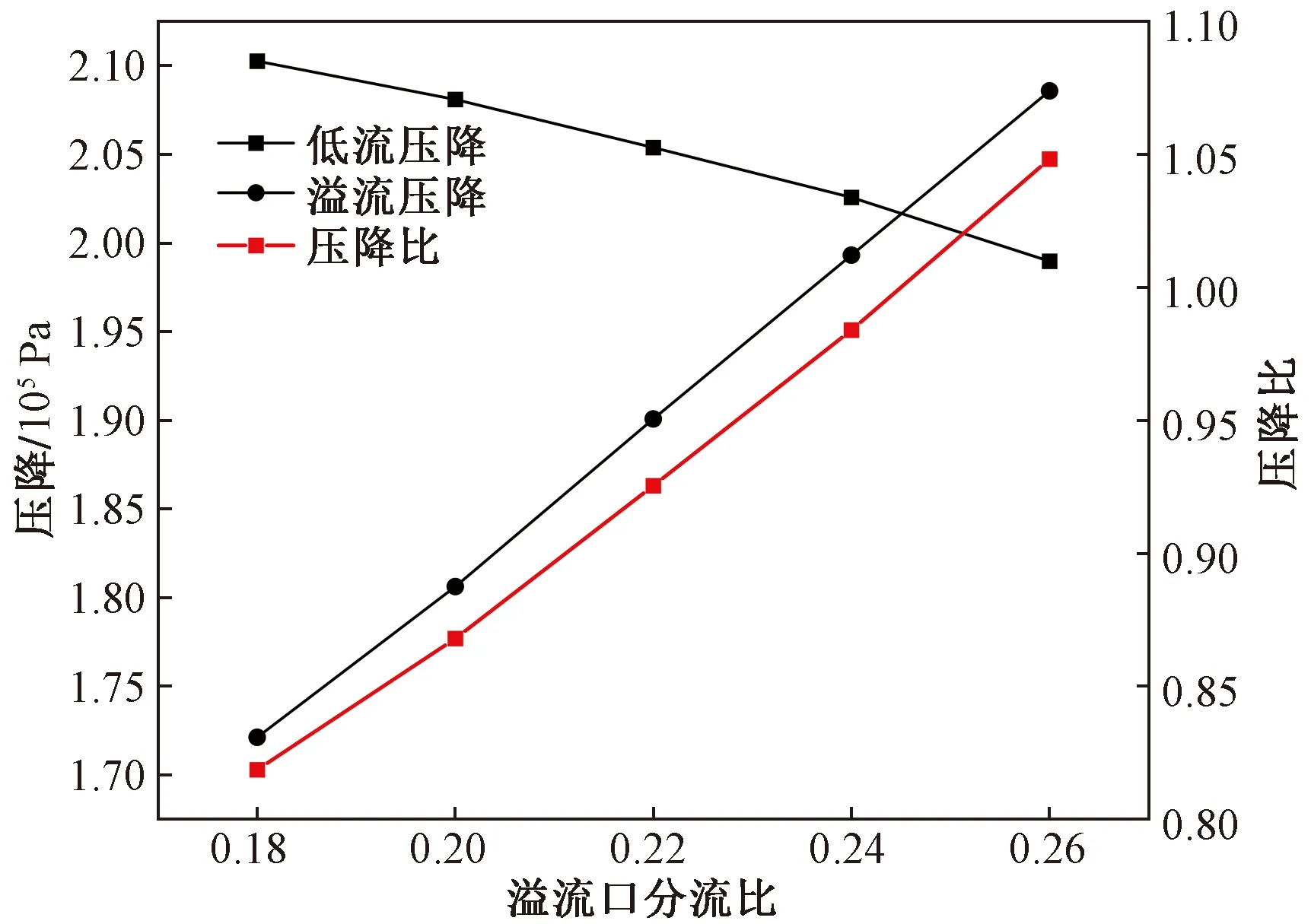
图7 压力降随分流比变化折线图Fig.7 Pressure drop curve with shunt ratio
质量效率、简化效率以及综合效率作为衡量旋流分离器分离效率的3个评价标准,三者之间具有一定的联系[17]。如果单纯从净化方面考虑,则可以把旋流器分离效率定义为旋流器出口质量与入口质量的比值,即公式为
(5)
式(5)中:mo为溢流口流出的油的质量;mi为入口混合液中含油的质量。
然而当溢流口分流比过大时,质量效率相较于实际的情况将会出现较大误差,因此引入简化效率来消除分流比所造成的误差,即不考虑分流比影响[18],公式为
(6)
式(6)中:ηj为简化效率。
以上两种方法在衡量旋流器分离效率时,都有所缺陷,为了较为准确地反映旋流器分离性能,特引入综合效率,其公式为
(7)
式(7)中:ηz为综合效率;Ci为入口混合液含油浓度。
由图8可知,质量效率和简化效率都随着溢流分流比的增大而上升,这是由于溢流分流比的增大,导致溢流口排出的混合相增多,油相更容易从溢流口排出。但是由于分流比过大会产生误差,所以通过计算求出其综合效率,得到其综合效率变化折线图,如图8所示,综合效率随着溢流口分流比增大先上升后下降,在分流比为0.22时达到最大,其值为95.66%。

图8 分离效率随分流比变化折线图Fig.8 Line chart of separation efficiency varying with split ratio
2.2 入口流速对分离性能的影响
通过上述分析,综合考虑设置溢流口分流比为0.22,改变入口流速分析其对分离性能的影响。由图9(a)可知,随着流速的提高,旋流器中间内旋流区油柱逐渐消失,由图9(b)可知,各截面含油体积分数逐渐增大,油相向溢流口运移,主要集中在溢流口附近。由图10可知,溢流口平均油相体积分数随入口流速变化关系,当流速为2 m/s时,溢流口平均油相体积分数为74.14%,流速为4 m/s时,体积分数快速上升到85.36%。此时如果继续提高流速,溢流口平均油相体积分数上升变缓最后趋于稳定。证明在一定范围内提高流速可以有效提高旋流器油相在溢流口附近的油相体积分布,有利于油水分离,但是当入口流速超过该范围后则对油相向溢流口附近聚集的作用下降。
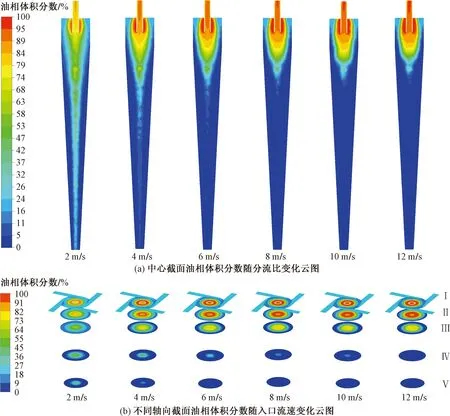
图9 油相体积分数分布随入口流速变化云图Fig.9 Cloud diagram of oil phase volume fraction distribution with inlet velocity
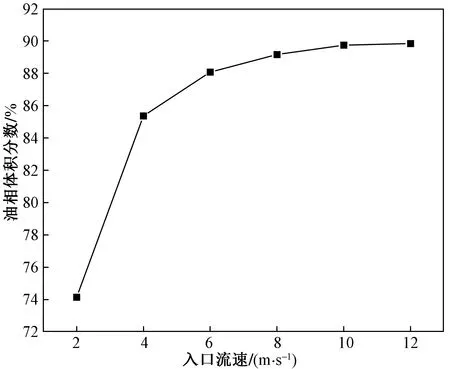
图10 溢流口油相体积分数随入口流速变化折线图Fig.10 Line chart of oil phase volume fraction in overflow port varying with inlet velocity
由图11截面Ⅱ处切向速度和轴向速度随入口流速变化曲线图可知,随着入口速度提高切向速度和轴向速度呈明显上升趋势,在壁面处速度始终为0,同时切向速度两个峰值都始终出现在圆柱段半径与溢流口半径差值的1/2处以及溢流口半径1/2处,轴向速度峰值出现在旋流器轴心处,这表明切向速度峰值和轴向速度峰值位置不会随着入口流速变化发生改变。
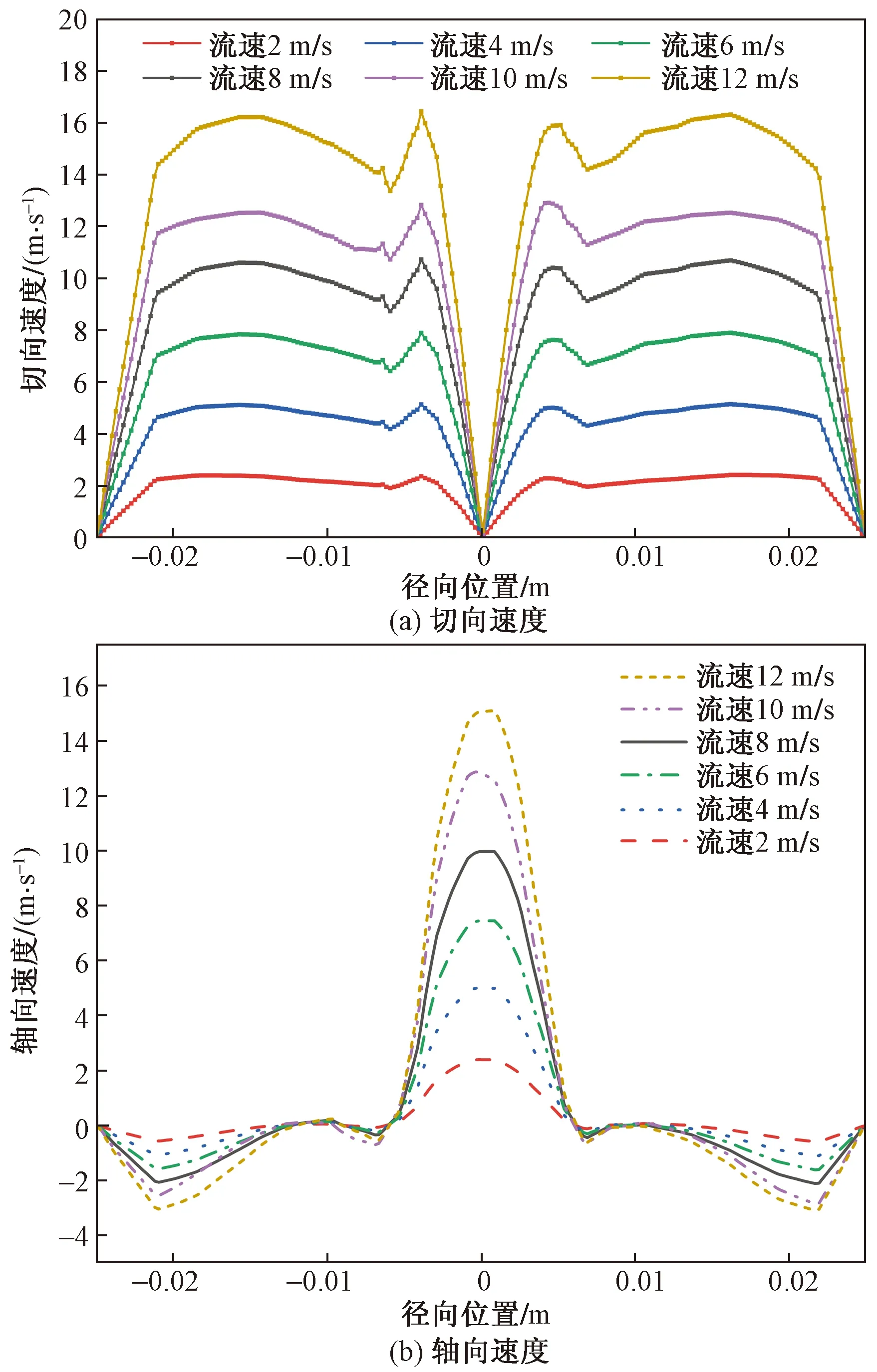
图11 截面Ⅰ切向速度和轴向速度随入口流速变化曲线图Fig.11 Curve of tangential velocity and axial velocity of section I changing with inlet velocity
由图12可知,静压大小不受流速影响,始终保持中心对称分布,且壁面处静压最大,同时在径向上,静压随着径向距离减小而减小,随着入口流速的升高而增大。由图13可知,溢流口压降和底流口压降随着入口流速的提高而增大,当入口流速为2 m/s时,溢流口压降和底流口压降分别为10 578 Pa和10 257 Pa,流速为12 m/s时,其分别为438 805 Pa和475 005 Pa。这是由于随着入口流速的提高,旋流器内压逐渐升高,在流体与壁面接触过程中,流体和壁面发生冲击,同时流体与流体之间产生相互作用,导致旋流器压力损失也提高。
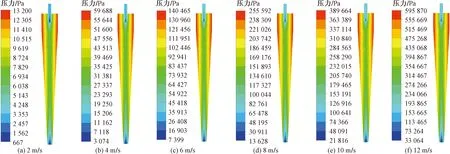
图12 不同入口流速下的静态压力云图Fig.12 Static pressure cloud at different inlet velocities
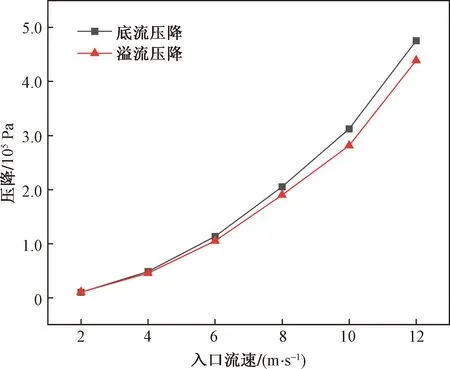
图13 压降随入口流速变化折线图Fig.13 Curve diagram of pressure drop with inlet velocity
由图14可知,旋流器的综合效率随着入口流速增大明显提高,入口流速2 m/s时,综合效率只有75.6%,当入口流速提高到10 m/s时,其综合效率可达96.8%。但此时如果进一步增大入口流速,综合效率出现小幅度下降。这是由于旋流器入口流速达到油滴剪切破碎的临界值,此时大油滴受到剪切应力作用破碎成小油滴,从而导致分离效率降低。
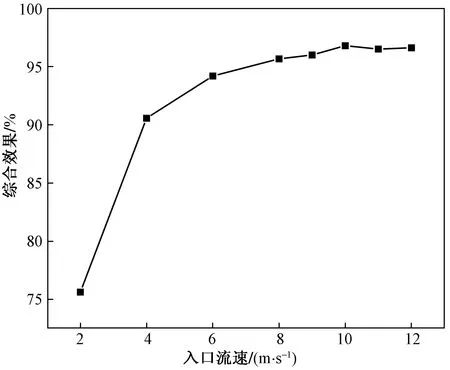
图14 分离效率随入口流速变化折线图Fig.14 Line chart of separation efficiency varying with inlet velocity
3 结论
(1)当入口流速保持8 m/s不变,随着溢流分流比的增大,四入口旋流器溢流口附近出现明显油夹水现象,质量效率和简化效率呈上升趋势,压降比呈线性上升,综合效率呈先上升后下降变化趋势。在溢流分流比为0.22时,综合效率达到最大95.66%,此时分离效率最好。
(2)当分流比为0.22时,随着入口流速的增大,旋流器溢流口油夹水现象逐渐改善,切向速度和轴向速度明显增大,溢流口和底流口压降也呈逐渐增大趋势。旋流器分离效率随着流速的提高表现为先上升后略有下降,当流速达到10 m/s时,油滴发生临界剪切破碎,此时旋流器综合分离效率达到最大96.78%。
(3)分流比和入口流速对四入口液-液分离旋流器分离性能有着显著的影响,针对不同结构尺寸的四入口旋流器存在最佳分流比和入口速度,选择合适的溢流分流比以及入口流速,可以有效地提高四入口旋流器分离性能。
