考虑时空扩散和碳汇的碳捕集-电转气协同优化调度模型

2023-02-11马丽叶朱思宇卢志刚武佳卉梁白雪

电力系统自动化 2023年2期

马丽叶，朱思宇，2，卢志刚，武佳卉，梁白雪

（1. 电力电子节能与传动控制河北省重点实验室（燕山大学），河北省秦皇岛市 066004；2. 国网浙江省电力有限公司湖州供电公司，浙江省湖州市 313000；3. 国网浙江省电力有限公司经济技术研究院，浙江省杭州市 310000；4. 河北省分布式储能与微网重点实验室（华北电力大学），河北省保定市 071003）

0 引言

全球气候变化是当前人类社会面临的挑战之一。为此，中国提出了2030 年前实现“碳达峰”、2060 年前实现“碳中和”的目标［1］。实现“碳中和”，除了从碳排放源减少碳排放，还要从碳去向上考虑增加碳汇、发展碳捕集与封存（carbon capture and storage，CCS）等低碳技术，实现碳排放和碳吸收的平衡［2］。

目前，火力发电仍是中国电力能源的主要来源［3］，将火电机组改造成碳捕集机组成为提高机组灵活性且减少碳排放的重要选择之一。文献［4］基于灵活运行模式，提出了相对捕集度的概念。文献［5］挖掘了碳捕集装置在提供备用服务方面的潜能。与此同时，文献［6-8］建立了碳捕集-电转气（power to gas，P2G）综合能源系统的低碳经济运行模型，以二氧化碳（CO2）为纽带将碳捕集装置与P2G 设备进行耦合，有效提高了可再生能源消纳量。文献［9］提出碳捕集-P2G 协同框架，将碳捕集装置产生的能耗进行负荷需求转移，进一步提高了可再生能源消纳量。然而，CO2的捕集和消耗存在时间上的不同步，为了增强碳捕集装置和P2G 设备的耦合性，使各类资源得到更高效的利用，文献［10］提出了一种以储碳设备为枢纽的碳捕集-P2G 联合运行模式，以解决CO2的捕集和利用存在时间上不匹配的问题，同时减少弃风。

事实上，不同地区的碳汇能力会对净碳排放量造成不同影响，有必要考虑碳排放去向问题。因此，同时考虑碳排放源和碳汇能力的碳浓度控制模式是一种有效的碳减排方法［11］。影响CO2浓度的主要因素除了碳排放位置、高度和排放量等碳排放源因素，还包括风速、风向、大气稳定度等大气环境因素［12］，以及地面植被固碳能力因素。鉴于此，本文在上述研究的基础上，同时考虑碳排放源和碳去向问题，针对不同生态地理环境的碳汇差异，考虑碳汇作用以及CO2的大气扩散时空分布特性，提出自由CO2浓度的概念，并建立考虑时空扩散和碳汇的碳捕集-P2G 协同低碳经济调度模型。

1 碳捕集-P2G 协同运行模式

所构建的碳捕集-P2G 协同运行模式的能流图如图1 所示。当风力发电和光伏发电有盈余时，可通过传输线路给碳捕集装置供电并将多余的电能通过P2G 设备转化为天然气存储起来［9］，提高了供用电的灵活性，进而能够在负荷低谷时期减少弃风弃光量，提高可再生能源利用率。

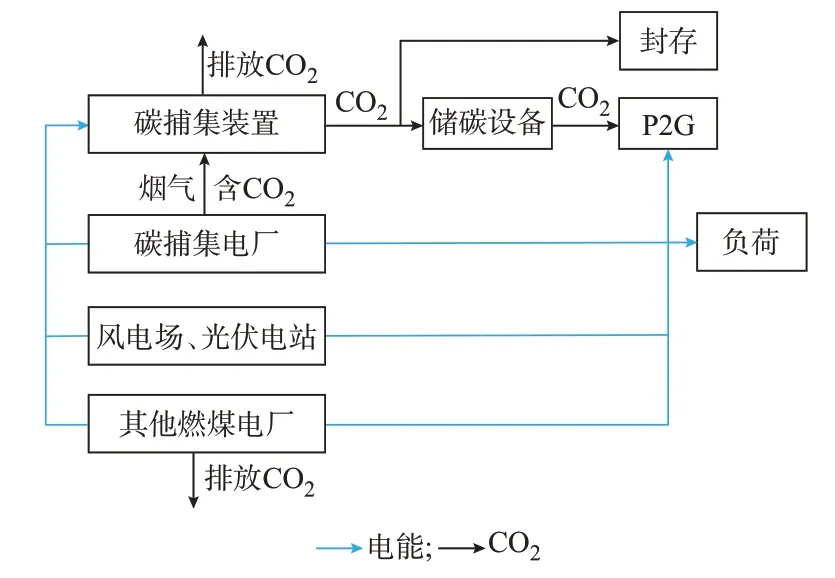
图1 碳捕集-P2G 协同运行模式能流图Fig.1 Energy flow diagram of carbon capture-P2G collaborative operation mode

1.1 碳捕集装置模型

碳捕集装置［13］会产生基准能耗和运行能耗，其模型如式（1）所示［14］。

式中:Qct为时段t碳捕集机组c产生的CO2量；μc为碳捕集机组c的碳排放强度系数；Pct为时段t碳捕集机组c的发电功率；为时段t碳捕集机组c处理的CO2量；αc为碳捕集机组c的烟气旁路系统调节系数，取值为［0，1］；为时段t碳捕集机组c的CO2捕集量；βc为碳捕集机组c的碳捕集率，根据现有技术规范，碳捕集装置的捕集率最大约为90%，故取值0.9；γc为碳捕集机组c捕集单位CO2量所消耗的功率；为碳捕集机组c在时段t的运行能耗。

系统净碳排放总量为:

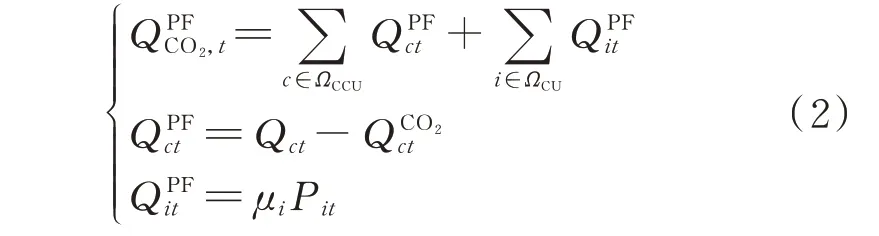
式中:ΩCU为传统燃煤机组集合；ΩCCU为碳捕集机组集合；为时段t所有机组的碳排放总量；为时段t碳捕集机组c的碳排放量为时段t传统燃煤机组i的碳排放量；μi为传统燃煤机组i的碳排放强度；Pit为时段t传统燃煤机组i的输出功率。

1.2 P2G 设备模型

P2G 设备可以将富余电能转化为氢气，并将制取的氢气与CO2通过萨巴蒂埃反应转化为甲烷，如下式所示［15］:

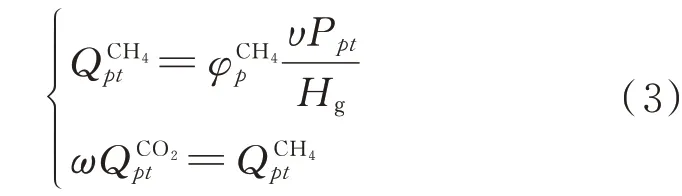
2 自由CO2浓度分布模型

2.1 传统燃煤机组排放CO2的时空扩散模型

由于电力的供应是连续不断的，根据空气污染气象学理论，在均匀、定常湍流场的理想条件下，可采用高架点源的高斯烟羽扩散模型描述传统燃煤机组排放CO2的时空扩散情况［16］。

由于气态CO2密度较空气大而下落，以近地面处空间域作为目标区域，研究水平面上正方体单位域的CO2浓度情况。CO2的实际扩散区域关于x轴对称（见附录A 图A1），每一坐标点的CO2浓度为相应单位域的CO2浓度，可表示为:

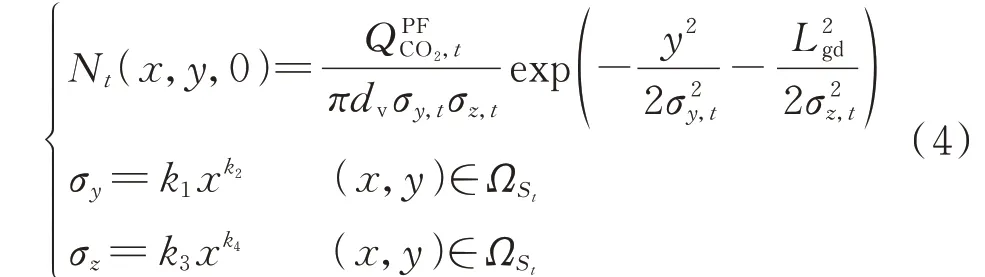
式中:Nt(x，y，0)为时段t目标区域(x，y，0)点的CO2浓度，其中，(x，y，0)为采样点在烟羽扩散坐标系中的坐标；dv为平均风速；σy和σz分别为横向、垂直大气扩散参数；Lgd为有效源高，包含烟囱几何高度h和烟羽的抬升高度Δh，Lgd=h+Δh，取值见文献［12］；St为时段t时CO2扩散覆盖的近地面单位正方体域个数，简化为对应的水平面积，即扩散范围面积；ΩSt为St个坐标点单位域的集合；k1、k2、k3、k4为相应的扩散系数，可通过查表得到，每当大气稳定度、风向与风速等气象条件以及源-荷相对位置确定后，可通过附录A 表A1 获得。

2.2 植物固碳模型

在单位时间和单位面积内，绿色植物利用光合作用固定的有机总碳量称为总初级生产力（gross primary productivity，GPP），GPP 减去植物自养呼吸量（autotrophic respiration consumption，ARC）所得的部分，称为净光合固碳量（net primary productivity，NPP）［17］。三者的关系式如下:

式中:CNPP为NPP；CGPP为GPP；CARC为ARC。

2.2.1 C-FIX 模型

为了得到GPP 和NPP，本文采用C-FIX 光能利用率模型来计算全日的GPP 和NPP［17］。

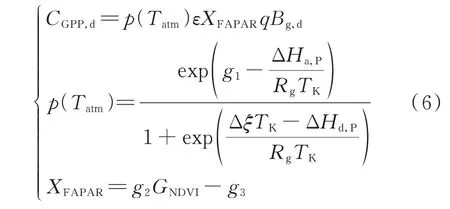
式中:CGPP，d为全日的GPP；p(Tatm)为归一化气温依赖因子，取值［0，1］；Tatm为日平均气温；XFAPAR为植被可吸收的光合作用有效辐射比例系数，一般采用遥感植被指数法推算，取值［0，1］；ε为光能利用率；q为气候效率因子；Bg，d为太阳入射总辐射通量；g1、g2、g3为常数，分别是21.77、1.163 8、0.142 6；ΔHa，P为活力分子能量；ΔHd，P为惰性分子能量；Rg为气体常数；Δξ为CO2动态熵平衡；TK为开尔文温度；GNDVI为归一化植被指数（normalized difference vegetation index， NDVI），取值［-1，1］，当GNDVI不大于0.122 5 时，地表为无植被覆盖的裸土，XFAPAR为最小值0。

由式（5）可知，CGPP包含CNPP和CARC，植被自养呼吸率Yd表示CARC与CGPP的比例，依赖于日温度Ta的Yd为:

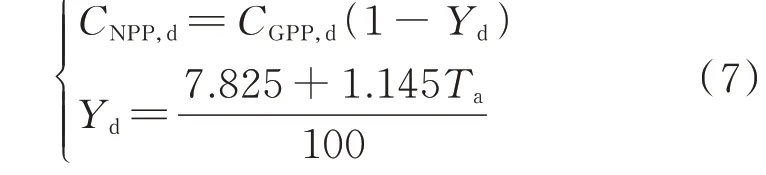
式中:CNPP，d为全日的NPP。

2.2.2 考虑植物碳汇的自由CO2浓度分布模型

为了更好地描述排放的CO2经大气扩散并于近地面处被植物吸收之后，稳定在空气中呈游离态的CO2浓度，本文定义了自由CO2浓度的概念。自由CO2浓度指在化石燃料电厂的大气时空扩散区域内，排放的CO2经当地植被固碳吸收后，剩余CO2以气体形式在近地面空间内自由存在时的浓度，简称自由碳浓度。

由于地面扩散区域范围较广，样本数太多，故而研究每一单位时段的样本平均值，即平均浓度:

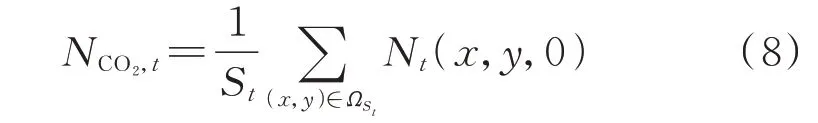
式中:NCO2，t为时段t的平均自由碳浓度。

研究周期Γ=24 h，故选定夏季某日的平均自由碳浓度为研究对象，不必考虑植物碳汇的异养呼吸，通过换算，得到下式:

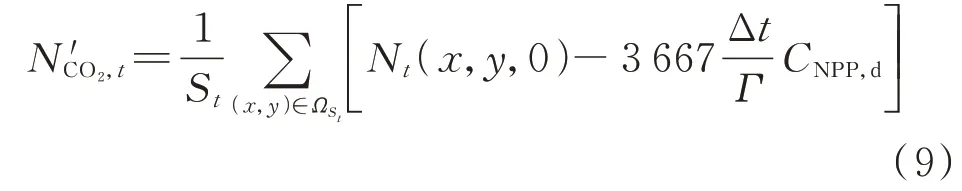
3 调度模型及求解

3.1 目标函数

同时考虑经济指标和环保指标，将平均自由碳浓度最小化和运行成本最小化作为目标函数，通过带权极小模理想点法构造综合目标函数进行求解。

3.1.1 平均自由碳浓度最小化

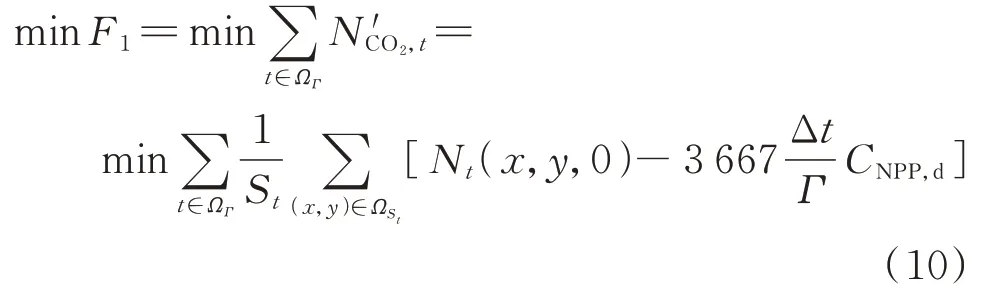
式中:F1为平均自由碳浓度；ΩΓ为运行时间周期的集合。

3.1.2 运行成本最小化

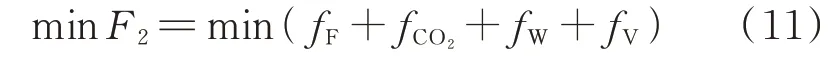
式中:F2、fF、fCO2、fW、fV分别为总成本、燃料损耗成本、综合碳成本、弃风成本和弃光成本。

1）燃料损耗成本，包括所有燃煤机组的发电成本和启停成本，如式（12）所示。

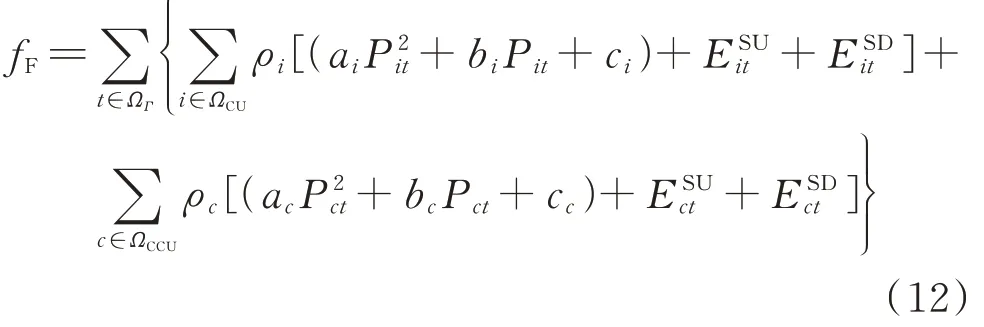
式中:ρi和ρc分别为传统燃煤机组i、碳捕集机组c的燃料价格；ai、bi、ci、ac、bc、cc分别为传统燃煤机组i、碳捕集机组c的燃料损耗系数；、、、分别为时段t传统燃煤机组i、碳捕集机组c的开机和停机能耗。

2）综合碳成本，包括所有燃煤机组在碳交易机制下的碳排放成本和碳捕集机组传输与储存CO2的成本，如式（13）所示。

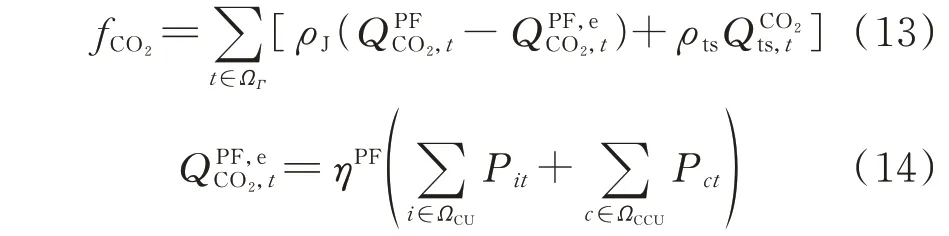
式中:ρJ和ρts分别为碳交易价格、传输储存CO2的价格；为时段t碳排放基准额度；为时段t传输储存的CO2量；ηPF为单位电量的碳排放基准额度系数［18］。

3）弃风弃光惩罚成本如式（15）所示。

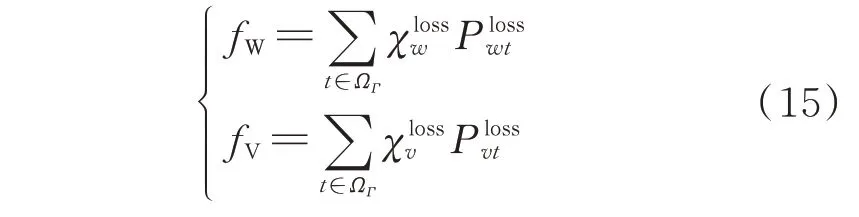
3.2 约束条件

3.2.1 系统约束

高压输电线路一般不计网络有功损耗，为保证传输功率实时平衡，相应的线路传输功率约束和功率平衡约束分别如式（16）和式（17）所示。

式中:ΩWF、ΩPVPS、ΩP2G、ΩTL分别为风电场、光伏电站、P2G 设备和输电线路的集合；Abi、Abc、Abw、Abv、Abp、Abl为与节点b对应的节点关联矩阵元素值；和分别为时段t碳捕集机组c的上网功率和供给P2G 的功率；Pwt和Pvt分别为时段t风电场w、光伏电站v出力预测值；PL，bt为时段t节点b的电负荷；PCSlt为时段t线路l的传输功率；θl1，t和θl2，t分别为时段t线路l首端节点l1和尾端节点l2的电压角度；xl为线路l的电抗和分别为线路l输送有功功率的上限、下限；θb，min和θb，max分别为节点b电压角度的最小值和最大值；θref和θbt分别为参考节点电压角度和t时段节点b的电压角度；ΩB为节点集合；分别为时段t传统燃煤机组i、风电场w、光伏电站v的上网功率；和分别为时段t传统燃煤机组i用于承担碳捕集运行能耗的功率和提供给P2G 的功率。

系统约束还包括正负旋转备用约束、输出功率约束、爬坡约束、开停机能耗约束和最小开停机时间约束，分别见文献［15］。

3.2.2 储碳设备约束

为解决P2G 设备和碳捕集装置运行时间不对等的问题，本文增加储碳设备，保证P2G 设备启动时有充足的碳源去合成甲烷［10］。

储碳设备需要满足储碳平衡约束、储碳量大小约束、注入CO2流量大小约束、取出CO2流量大小约束以及运行周期始末时段存储约束，分别见式（18）至式（22）。

储碳设备的CO2仅来源于碳捕集装置，且满足式（23）。

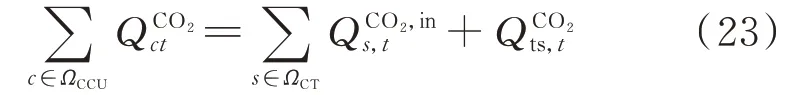
式中:ΩCT为储碳设备的集合。

3.2.3 其他相关约束

在碳捕集-P2G 协同运行模式下，P2G 设备电解过程所耗功率由传统燃煤机组、碳捕集机组、风电场和光伏电站提供［9］，且P2G 设备所消耗的CO2完全来自储碳设备。具体约束如式（24）所示:

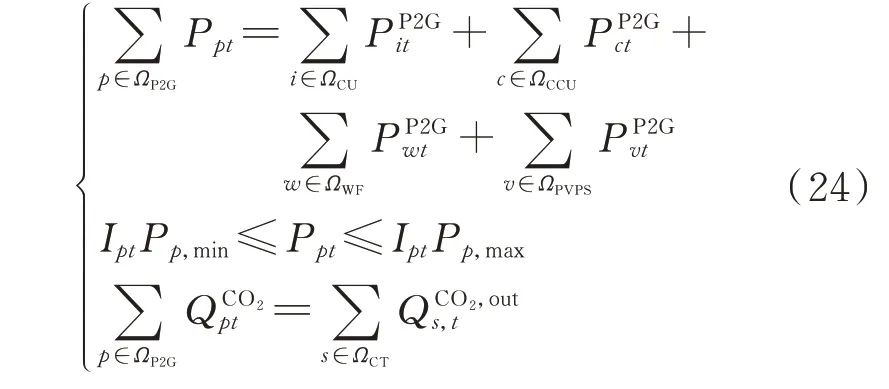
事实上，学生分层、目标分层与作业分层是层层递进、相辅相成的。不同层次的学生有不同层次的目标，通过不同层次的作业巩固才能实现其目标。A类学生在学有余力的情况下可以做一些冲刺题，选题要精，避免无选择性的题海战术，这样只会挫伤其英语学习积极性，同时，教师可以通过课后沟通提供一些学习资源，布置一些有挑战性的开放性任务，以提高其学习兴趣；B类生应选择一些难度较为平实的题目，并且要重视错题的订正，明确自身薄弱点以寻求突破。C类生的首要目标是掌握基础题，平时练习中频繁出现的单词和词组搭配要熟记。结合目标分层将作业分层后，不仅仅有望大幅度提高学生的学习效率，还能减轻教学双方的负担。

碳捕集装置的运行能耗同样由传统燃煤机组、碳捕集机组、风电场和光伏电站出力共同承担［19-20］，故有约束式（25）:

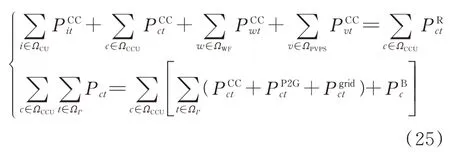
风电场、光伏电站出力平衡约束为:

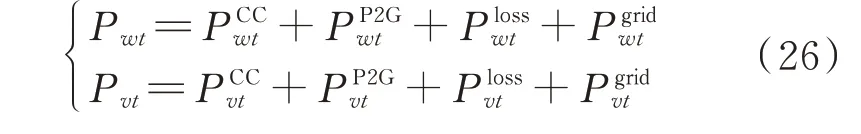
3.3 模型求解

本文所建模型同时包含整数变量和连续变量，并且由式（12）可以看出，燃煤机组的耗量特性为二次方程。因此，首先对非线性方程进行分段线性化处理，将模型转换为混合整数线性规划问题，然后，调用YALMIP 工具箱的Cplex 求解器进行求解。

同时，针对模型的双目标函数，本文使用层次分析法确定各函数权重，并采用带权极小模理想点法构造综合目标函数进行求解［21］，其表达式如下:

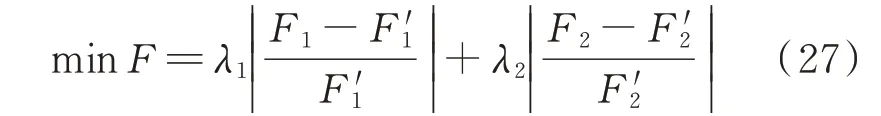
式中:F为综合目标函数；λ1和λ2分别为各相对子目标函数的权重，且满足λ1+λ2=1；F′1和F′2分别为理想点目标值，即各子目标函数最优值。

4 算例仿真

4.1 算例分析

所采用的6 节点电力系统结构如附录A 图A2 所示，包括5 个燃煤机组（G1 至G5）、1 个风电场、1 个光伏电站、1 台P2G 设备、7 条输电线路和3 个电负荷（EL1、EL2、EL3）。燃煤机组G5 被改造为碳捕集机组。机组旋转备用为总负荷的10%。碳捕集装置的固定能耗为机组装机容量的0.5%，碳交易价格和单位CO2传输储存价格分别为14.286 美元/t［18］和5 美元/t［15］。烟气旁路系统调节系数αc取值为0.8，NDVI 数值GNDVI为0.7。风电、光伏和电负荷预测值见附录A 图A3，其余系统参数见附录A 表A2 和表A3。为验证本文模型的有效性，设置以下5种案例。

案例1:不考虑碳捕集装置和P2G 设备；案例2:考虑碳捕集装置；案例3:考虑P2G 设备；案例4:考虑碳捕集装置和P2G 设备；案例5:在碳捕集-P2G 协同运行模式下，考虑时空扩散和碳汇作用。

其中，案例2 和案例4 中捕集的CO2全部被运输储存；案例3 和案例4 的甲烷化过程所需CO2皆来自空气中的捕集；案例5 的碳汇全用于碳排放吸收，且不考虑其他工业民用碳排放的影响。

4.2 仿真结果分析

4.2.1 成本结果分析

5 种案例的成本计算结果如表1 所示。

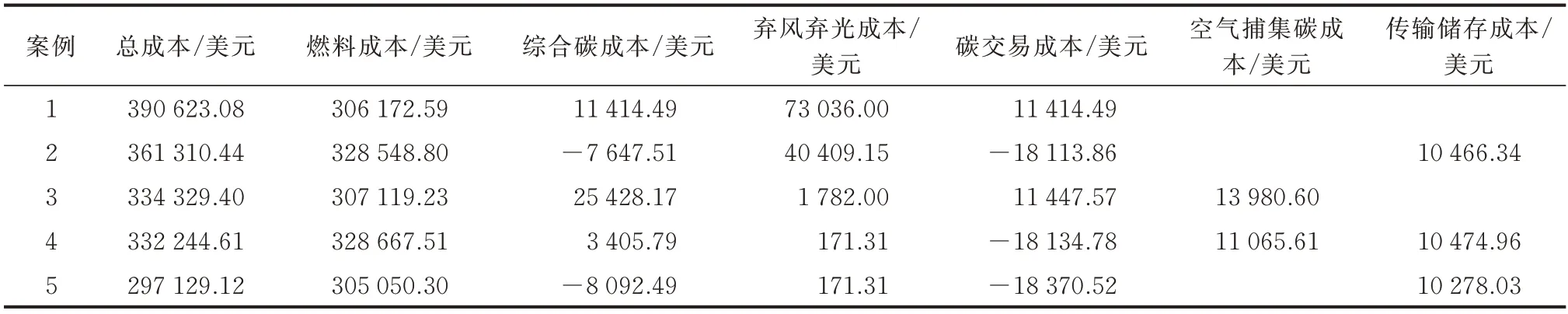
表1 成本计算结果Table 1 Calculation results of costs

由表1 可以看出，与案例1 至4 相比，案例5 的总成本、燃料成本、综合碳成本和弃风弃光成本均有不同程度的减少，说明案例5 的各项经济成本和环保成本皆为最优，验证了考虑时空扩散和碳汇作用的调度模型的优越性。由于碳捕集装置会产生运行能耗和固定能耗，因而案例2 和4 的燃料损耗成本高于案例1 和3。从表1 中弃风弃光成本结果来看，案例4 的弃风弃光成本明显减少，说明在同样的模型和算例中，碳捕集装置和P2G 设备的加入有效实现了燃煤机组、风电场和光伏电站通过各节点之间的输电线路对碳捕集装置、P2G 设备的供电，从而达到了减少弃风弃光的目标。

由于碳捕集装置能减少燃煤机组的碳排放量，因此，案例2 和4 的碳交易成本比案例1 和3 低，而案例5 最低。其中，案例2、4、5 的碳交易成本为负值，说明机组碳排放少于配额，可视作在碳交易市场获得的收益。由于案例3 和4 中P2G 设备的CO2来自空气中的碳捕集，增加了额外的成本，故案例3 和4 的综合碳成本分别比案例1 和2 高。

4.2.2 自由CO2浓度分布情况

案例1 至5 的全天累积平均自由碳浓度计算结果分别为67.33、46.83、65.84、46.84、3.23 g/m3。通过案例5 与案例1 至4 的结果对比可知，植物固碳作用对碳排放区域内平均自由碳浓度影响很大，而在未考虑植物固碳吸收作用时，装设有碳捕集装置的案例2 和4 相比于未装设碳捕集装置的案例1 和3，其平均自由碳浓度明显有所降低，进一步说明碳捕集装置对碳减排的作用。

案例5 的平均自由碳浓度在空间和时间2 个维度上的分布情况分别如附录B 图B1、图B2 所示，进一步说明植物固碳作用对平均自由碳浓度的影响。

4.2.3 弃风弃光量结果分析

与案例1 相比，在增加碳捕集装置或P2G 设备后，案例2 至5 都减少了弃风弃光量（具体结果见附录B）。同时，通过案例2 和案例3 的风光消纳量对比，也能看出虽然P2G 设备会受到输入功率最大容量的限制，但是P2G 设备在消纳清洁能源方面明显比碳捕集装置具备更大的优势。案例4 和案例5 的总弃风弃光量一致且几乎为零，说明同时具备能有效消纳风光的碳捕集装置和P2G 设备，就能达到更理想的风光消纳效果。

4.3 NDVI 对系统运行结果的影响分析

植物固碳作用具有地域差异和季节差异，作为表征区域内植物固碳吸收能力的数值，通过改变NDVI，能得到植物固碳的地域性和季节性差异对系统环保经济效益的影响。故针对案例5，改变NDVI，得到运行结果如图2 所示。

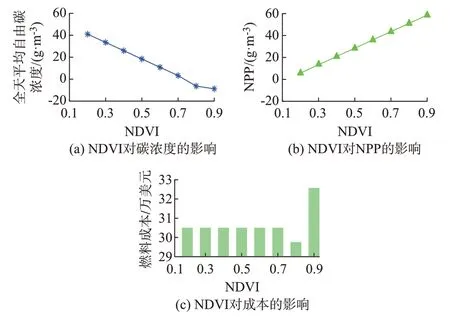
图2 NDVI 对系统运行的影响Fig.2 Influence of NDVI on system operation

由图2 可知，NDVI 与NPP 保持线性正相关关系。当NDVI 为0.2～0.7 时，随着NDVI 的增大，平均自由碳浓度线性减小，而燃料成本基本不变，说明此时碳排放量变化不大，NDVI 主要从碳排放去向方面影响碳浓度；当NDVI 大于0.7 时，燃料成本出现波动变化，此时碳浓度和燃料成本呈相同变化趋势，说明此时NDVI 主要从碳排放源方面影响碳浓度。当NDVI 为0.8 时系统环保经济效益达到最优。

4.4 大气稳定度对碳浓度的影响分析

不同大气稳定度分别对应不同的横向、垂直大气扩散系数，进而使得CO2的扩散范围面积也有所不同。大气稳定度等级分为强不稳定、不稳定、弱不稳定、中性、较稳定、稳定，分别对应A、B、C、D、E、F。假定其他环境气象条件一定，针对案例5 的模型，改变大气稳定度级别，得到碳浓度结果如图3所示。

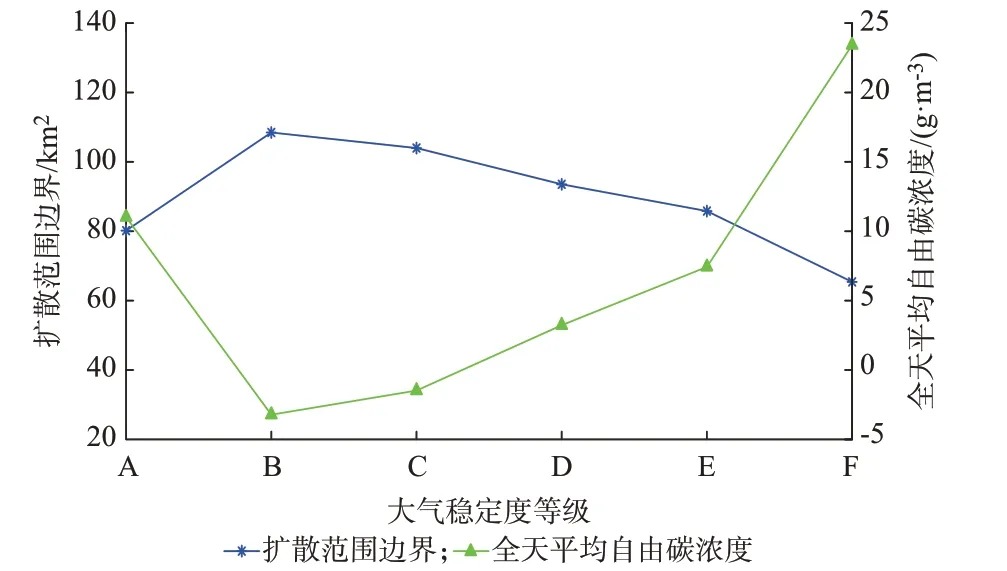
图3 大气稳定度对碳浓度的影响Fig.3 Influence of atmospheric stability on carbon concentration

由图3 可知，系统在不同稳定度级别下运行，能得到不同的扩散范围面积，进而直接导致平均自由碳浓度的改变。同时还可以看出，扩散范围面积大小与平均自由碳浓度大小呈负相关关系。在本文模型中，CO2在大气环境中的扩散强度直接影响其扩散面积，扩散面积的增大一方面能使CO2在地面分布的范围增大进而导致碳浓度减小，另一方面，还能通过新增范围区域的植被固碳作用增强对CO2的吸收，减少地面大气的自由CO2量从而减小碳浓度。从这两方面足以说明CO2的时空扩散环节对最终的碳浓度的影响结果。同时，由于CO2的扩散强度取决于大气稳定度，因此，大气稳定度对碳浓度结果至关重要。从图3 可以看出，当大气稳定度为B 等级时，扩散范围面积达到最大，且碳浓度最小，该等级是最理想的大气稳定度等级。

4.5 烟气旁路系数对系统运行结果的影响分析

在碳捕集装置模型中，烟气旁路系统调节系数αc能够控制进入吸收塔的烟气量比例，直接影响碳捕集机组的CO2捕集量以及净碳排放量，进而影响系统的经济环保效益。针对案例5，仿真得到αc的各项运行结果如图4 所示（具体数值结果见附录B表B1）。

图4 烟气旁路系数对系统运行的影响Fig.4 Influence of flue gas bypass coefficient on system operation

由图4 可知，随着αc的增大，燃料成本和传输储存成本几乎呈线性增长趋势，而碳交易成本几乎呈线性减小趋势，弃风弃光成本总体也呈下降趋势。捕集过程所需的运行能耗随CO2捕集量等比例增加，为满足运行能耗需求，燃料机组将增加发电而风电场和光伏电站将增加风光消纳量，因此，燃料成本增加而弃风弃光成本减小。由于受碳交易成本由正变负趋势的影响，随着αc的增大，系统运行总成本反而大体呈下降趋势。

从图4（e）可以看出，αc与平均自由碳浓度呈负相关关系，且具有线性化趋势。这是因为碳捕集率βc不变，CO2捕集量以αc与βc的乘积为固定比例进行变化。因此，随着αc的增大，CO2净排放量线性减少，在扩散面积和NDVI 不变的情况下，全天平均自由碳浓度也呈线性下降趋势。