基于随机演化动力学的多微网-配电网自组织协同调节策略

陈 中，陈嘉琛，万玲玲

（东南大学电气工程学院，江苏省 南京市 210096）

0 引言

随着《推进并网型微电网建设试行办法》［1］的发布，小规模微网与配电网的耦合程度增加［2-3］。单小微网多点随机入网参与互动后，各利益主体收益结构发生变化，配电网与多微网协同优化的决策变量维数提高。同时，由于多主体优化目标复杂，难以短时间生成控制策略，导致系统优化过程难以收敛，安全性和经济性都得不到保障［4］。因此，提高多微网-配电网对多维可调节资源的主动自发优化能力极其重要。另外，单小微网随机入网互动时，需要提高系统对这类扰动的抗干扰能力［5］，因此，研究基于自发优化调节的抗干扰协同策略也是该领域的难点。

博弈论是处理多利益主体协同优化的常用方法。文献［6］采用合作博弈模型进行分层经济能效建模，将多目标协同优化调度问题映射到合作博弈策略中；文献［7］建立基于主从博弈协同优化的多主体低碳交互机制，并结合自适应差分进化求解；文献［8］针对多主体联合投资单一微网源-储规划场景中的利益分配问题提出基于演化理论的微网容量规划新方法；文献［9］提出含多区域综合能源系统的主动配电网双层博弈优化调度策略以优化多区域综合能源系统与主动配电网协同调度。上述文献多侧重于稳定调度策略下多利益主体的利益博弈，未考虑微网随机接入等一定限度上的不确定性问题。

应对配电网在面对高渗透率可再生能源以不同形式接入电网所带来的不确定性时，现有研究一般采取多层级优化的理念来进行不确定性的处理优化。文献［10］在日前时间层面采取模糊规划理论建立园区综合能源系统可控资源响应的日前不确定性调度模型。文献［11］综合日前-实时两层级，采用场景分析法和结合自适应小波包算法的调度模型平抑不确定性。近年来，微网研究领域也开始采用人工智能算法解决关于可再生能源不确定性的优化调度问题。文献［12-13］通过深度强化学习寻找满足微网源储协同调度和实时在线控制决策问题的最优策略。文献［14］提出计及不确定性因素的深度强化学习算法，以实时求解微网的优化运行问题。上述文章的协同优化研究重点都侧重于将不确定性进行准确的建模，使系统在不确定性条件下得到固定优化策略。这类研究缺乏面对不确定性的自组织主动协同调节能力，调节运行依旧是被动的。

本文提出基于随机演化动力学的多微网-配电网自组织协同调节策略。一方面，以微网及配电网总运行成本最小为目标，将价格响应成本作为演化过程中的公共品建立基于公共品价格响应的多微网-配电网模型，降低了多主体优化的变量维数；另一方面，通过多利益主体二项分布下的演化效用函数将多优化目标转为“合作-非合作”二维目标，并引入计及随机涨落力的演化动力学方程，使多微网和配电网进行自组织演化，获取演化稳定策略后各利益主体具备自发优化协同运行能力以有效应对单小微网随机特性影响。采用改进的IEEE 37 节点系统进行仿真，验证所提优化调度策略的有效性。

1 基于公共品价格响应的多微网-配电网模型

1.1 非线性公共品演化博弈

本文将多微网-配电网协同优化调度问题视为一种非线性公共品演化博弈问题［15］。非线性公共品演化博弈是一种经典多人博弈模型，围绕提出的公共池概念进行演化博弈，最终获得的演化稳定策略具有唯一性。

非线性公共品演化博弈问题的具体规则为:随机抽样N个利益主体参与演化，并随机生成合作与非合作两类策略集，在演化过程中，每个利益主体与其余N−1 个利益主体进行博弈，其中，选择合作策略的利益主体需向公共池中贡献一个固定成本，选择不合作策略的利益主体不需贡献。公共池中积累的固定成本乘以操作系数后平均分配给系统所有利益主体。同时，每轮演化至少需要一定数量的利益主体选择合作策略才能认定为演化有效并进行固定成本分配，即每一轮演化产生公共品，否则停止演化并停止分配。

为了推动微网及配电网各利益主体参与协同优化的积极性，本文考虑以分时电价的方式推动多微网-配电网的价格响应模型，认为贡献公共品可以看作多微网-配电网各主体对调度计划的响应行为，并将该价格响应成本［16］作为演化过程中的公共品。综上，本文所提基于公共品价格响应的多微网-配电网模型架构如附录A 图A1 所示。该协调优化架构分为微网、配电网两个控制层级。微网层级的可控对象考虑自身分布式电源、部分柔性负荷及自身响应行为，配电网的调节对象除可调节负荷以外还考虑接入的微网和自身的响应行为。综合多微网-配电网双层级的调节对象的运行约束条件，以双层级经济性最优为目标，进行基于公共品价格响应的多微网-配电网运行模型的建模。

1.2 微网模型

1.2.1 目标函数

对于微网层级，以微网总运行成本最小为目标的目标函数为:

1.2.2 约束条件

微网层面需考虑功率平衡、设备台数、交互功率以及燃气轮机的可调节功率约束等约束条件，如附录B 式（B1）至式（B4）所示。

1.3 配电网模型

1.3.1 目标函数

对于配电网层级，以配电网总运行成本最小为目标的目标函数如式（10）所示。

配电网在本文演化过程中被假设成一个有充足可调节能力及电能传输能力的利益主体，暂不考虑其他源荷类型。

1.3.2 约束条件

配电网需考虑的功率约束、潮流约束等约束条件［17-19］如附录B 式（B5）至式（B8）所示。

2 计及随机涨落力的多微网-配电网演化动力学自发优化调节策略

本章首先介绍本文所提出的计及随机涨落力的多微网-配电网演化动力学自发优化调节策略的演化博弈理论；接着，以数学模型的方式建立多微网-配电网系统层级的演化动力学模型［20-21］，进而给出在一定涨落力背景下，该模型的演化稳定策略存在且唯一的证明过程；最终，给出对这唯一演化稳定策略的求解流程。

2.1 计及随机涨落力的演化博弈问题

多微网-配电网协同优化调节问题涉及多利益主体的合作与非合作，本文将多微网-配电网各主体的响应行为作为贡献公共品行为，并把价格响应成本作为合作者需向公共池提供的公共品，符合非线性公共品演化博弈问题的定义。

同时，根据协同学对于涨落力的定义［22］:系统随时间演化中受各种因素影响，使系统发生相变的关键因素称为涨落力。多微网-配电网受到系统内外各种因素的影响，而单小微网入网参与互动这一因素变化随机性较强、自由度较高，导致系统优化结果的不确定性增加。因此，数学形式上在演化方程中，本文描述为随机涨落力侵入演化博弈过程，以验证面对小规模微网随机入网互动时演化稳定策略的唯一性及新微网接入后该演化稳定策略使系统具有的自发优化能力。

在此演化过程中，任意时刻加入随机涨落力，该策略都会将随机涨落力视作为一个新的利益主体加入博弈过程，继续演化。

2.2 计及随机涨落力的微网-配电网演化动力学模型

2.2.1 演化效用函数

在此模型中，通过多利益主体二项分布下的演化效用函数将多优化目标转为“合作-非合作”二维目标。本文将合作与非合作策略分别认定为协同调节策略与非协同调节策略，协同调节表现为配电网-微网间、多微网间的功率互动及响应行为。

演化效用函数代表微网与配电网在协同调节与非协同调节策略下的演化经济收益，协同调节者需要提供价格响应成本，非协同调节者无须提供。分别用微网-配电网模型目标函数表示，如式（16）和式（17）所示。经过降维转变，随机演化博弈过程本质上是参与协同调节者与不参与协同调节者两大群组之间的二维目标单层演化策略选取过程而非配电网-微网、微网-微网间的多维目标双层策略选取过程。

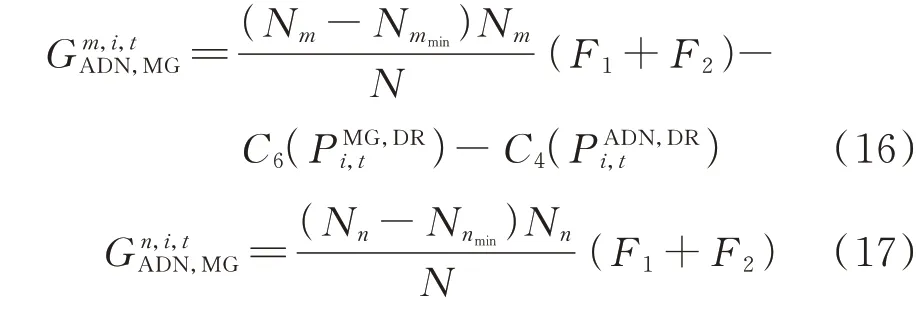
参与演化的利益主体由两类策略随机抽样产生，所以演化群组的构成遵循二项分布，则协同调节和非协同调节策略下利益主体的平均效用函数分别如式（18）和式（19）所示。

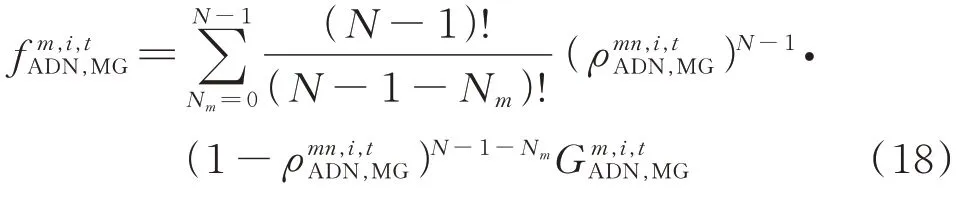
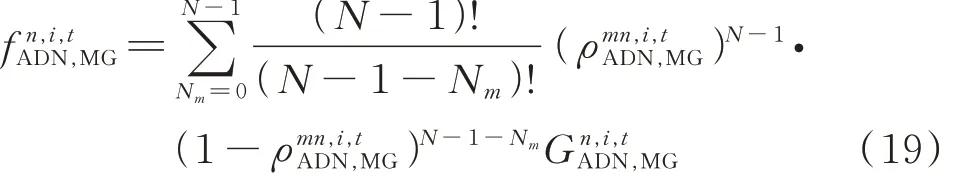
2.2.2 计及随机涨落力的复制动力学方程

根据原始复制动力学方程的定义［23］，它是一种确定性方程，然而，在演化过程中，单小微网入网互动的博弈行为具有较强的随机效应。因此，本文在原始复制动力学方程中，引入标准维纳过程来描述该情况下的随机演化博弈问题。计及随机涨落力的复制动力学方程描述合作的演化动力学如式（20）所示。

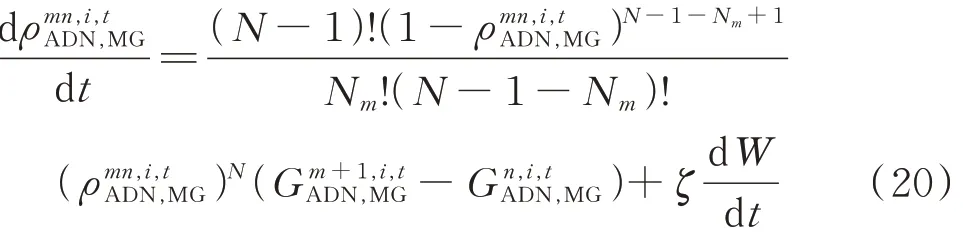
式中:W为标准维纳过程；ζ为随机涨落力强度系数；当/dt>0 时，则根策略转移概率更新演化 策 略；当/dt≤0 时，则 达 到 演 化 稳 定策略。

2.3 演化稳定策略

2.3.1 策略集生成

在演化过程中，先假定存在一个有限的备选策略集合，并将其分为协同调节者策略集S1及非协同调节者策略集S2。本文采取多微网-配电网模型中可调节设备的协同调节能力作为已知有限策略集合，在各约束条件下的表达式为:

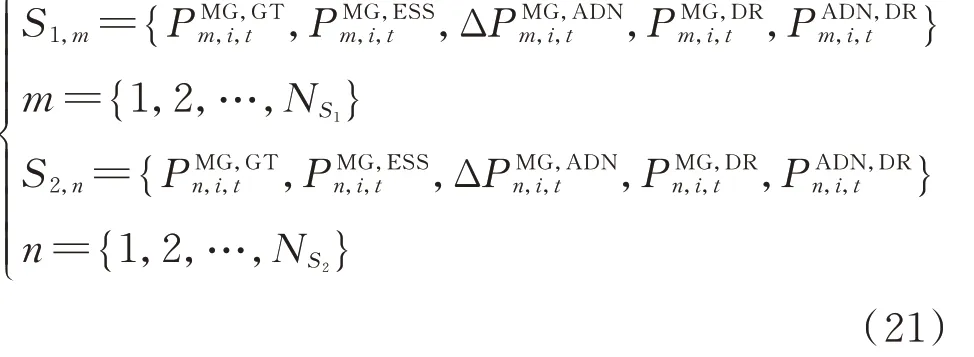
式中:S1，m为选择协同调节策略m的利益主体策略集；S2，n为选择非协同调节策略n的利益主体策略集；NS1和NS2分 别 为S1和S2中 的 策 略 总 数；为协同调节策略m下微网i中燃气轮机的有功出力，其余决策变量根据1.2 节和1.3 节已出现过的变量进行类推。

2.3.2 演化策略稳定性判定

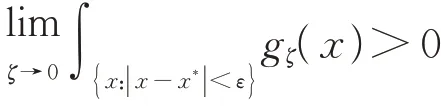
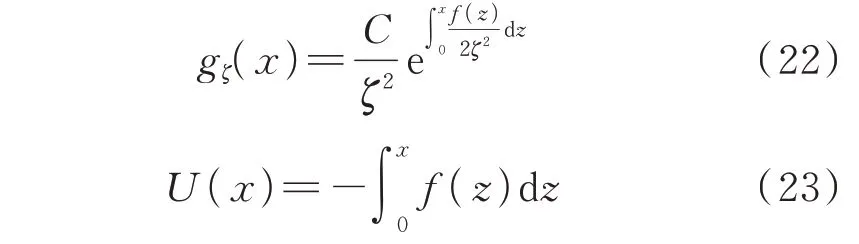
式中:f(z)为一个连续的标量函数；C为在ζ＜0.5情况下，满足gζ(x)dx=1 的常数。

对于本文所述多微网-配电网演化动力学模型，其势函数为:

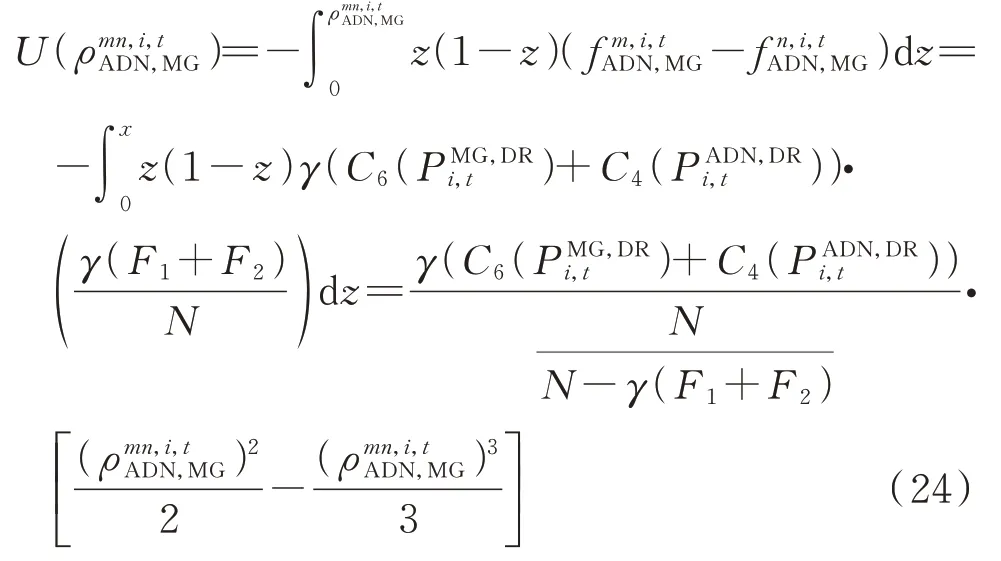
式中:γ为操作系数。

式中:ρmn为转移概率。

2.4 演化求解过程

本文计及随机涨落力的多微网-配电网自发优化调节策略的求解流程如图1 所示，其具体过程为:

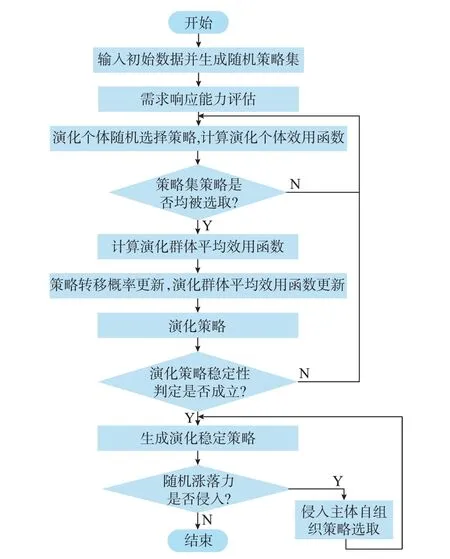
图1 计及随机涨落力的多微网-配电网演化动力学自发优化调节策略求解过程Fig.1 Solving process of MG-ADN cooperative evolutionary model considering random fluctuation force

步骤1:输入初始数据并随机生成协同调节者策略集S1及非协同调节者策略集S2。

步骤3:在演化群体配电网和微网中各随机选取一个个体运营商，并将其选取结果存入策略存储集合后随机在策略集S1和S2中选取一组策略后计算该演化个体的效用函数和。

步骤4:重复步骤2 和3，直至协同调节者策略集S1和非协同调节者策略集S2均被选完。

步骤6:根据计及随机涨落力的复制动力学方程更新策略转移概率ρmn及演化群体在各策略下的平均效用函数和，生成演化策略。

步骤7:根据标准维纳过程生成一定限度内的随机涨落力作为干扰因素侵入演化群体。

步骤8:针对步骤6 提出的演化策略和步骤7 中的随机干扰进行演化策略稳定性判定，若不稳定，重复步骤2 至7；若稳定，则输出为演化稳定策略并结束演化。

3 算例分析

采用如附录A 图A1 所示的多微网-配电网系统对本文所提策略进行分析验证。配电网层面为1 个改进的IEEE 37 节点系统，IEEE 37 节点的参数（线路阻抗、基本负荷）等可以在MATPOWER 软件中获取。微网层面设置为5 个微网MG1～MG5，分别接在配电网的第31、15、18、24、12 节点上，各MG 所含的不同元素如图A1 所示，接入设备详细参数及不确定集合如附录C 表C1 所示。不计及价格响应的微网配电网的基础交互电价为0.5 元/（kW·h）；由于夏季和冬季负荷组成、需求以及可再生能源出力的差距较大，此处将夏季和冬季各作为一类典型日进行算法分析。天然气价格为2.1 元/m3，天然气热值为9.6 kW·h/m3；微网制冷（热）收益为0.1 元/（kW·h），优化时间为24 h。设定微网的响应舒适度系数为1，配电网的响应舒适度系数为2。本文硬件配置如表C2 所示。

3.1 计及随机涨落力的演化稳定策略选取过程

采用本文所述方法进行求解，初始阶段随机生成协同调节和非协同调节策略集各500 组。1 至250 号和751 至1 000 号策略集为非协同调节策略集，251 至750 号策略集为协同调节策略集。策略集内各决策变量均为小范围数值浮动区间，区间大小为±5 kW。设置初次最大演化时间为30 s，演化时间间隔为0.001 s，在演化时间为30 s 时在第37 节点加入一个与MG5 体量相同的微网MG6 作为随机涨落力侵入系统，演化时间间隔为0.001 s，验证一定限度随机涨落力侵入后演化稳定策略的不变性及MG6 策略选择的自组织性，其选取过程如图2 和图3所示。其余演化过程参数设定如附录C 表C3 所示。

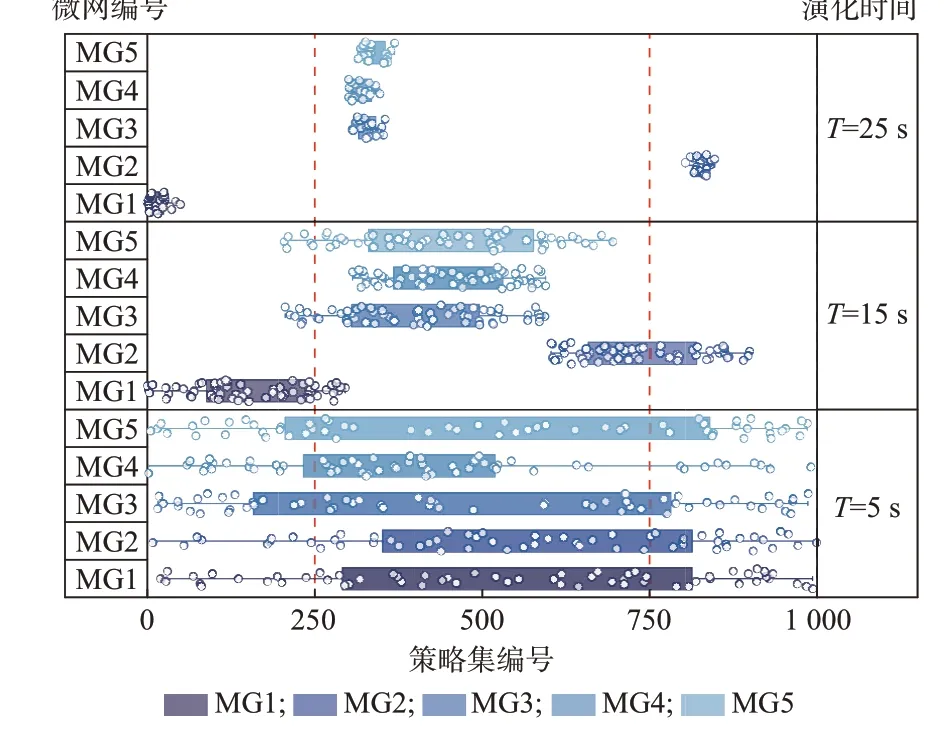
图2 随机涨落力侵入前演化过程Fig.2 Evolution process before invasion of stochastic fluctuation force

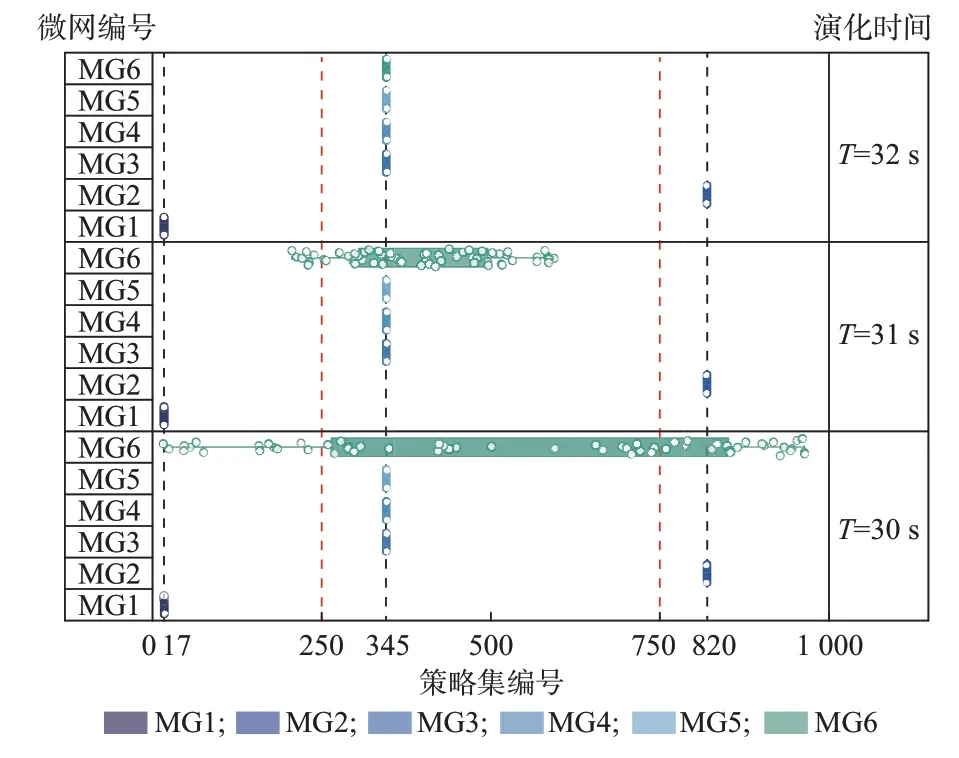
图3 随机涨落力侵入后演化过程Fig.3 Evolution process after invasion of stochastic fluctuation force

在图2 中，由于演化初始阶段所有利益主体的初始策略集为随机选取策略集，与最大演化时间下的演化稳定策略无关，所以从演化时间T=5 s 时记录趋势，实心点代表各利益主体选择的策略集，箱体代表各利益主体选择的策略集收敛趋势。由图2 可知，从5 s 至25 s 的演化期间，MG1 至MG5 这5 个利益主体在配电网利益主体的平均效用函数及各约束条件下选取的策略集分布由发散冗杂向集中单一收敛。其中，MG1 和MG2 在一次稳定时分别选择17号和820 号非协同调节策略集，而MG3 至MG5 在一次稳定时逐渐收敛至同一点，即选择相同的345号协同调节策略集。其选取稳定策略后的24 h 出力分布结果如附录C 图C1 和图C2 所示。

同时，在30 s 时加入一定限度的随机涨落力MG6，如图3 所示，由各利益主体的二次稳定过程可知，在30 s 至32 s 的MG6 自组织策略选取期间，MG1 至MG5 仍按一次演化的演化稳定策略集运行，证明本文计及随机涨落力的演化动力学方程下的演化稳定策略不随一定限度的随机涨落力侵入而改变。同时，随机涨落力MG6 随着其他各利益主体的约束条件，不经过再次演化计算而是自组织性地选择与MG3、MG4、MG5 相同的345 号协同调节策略集进入系统运行，并再次达到稳定。MG6 加入系统且稳定运行后的24 h 出力分布结果如附录C 图C3 所示。

3.2 自发优化能力与抗干扰能力的算法对比分析

为更直观说明本文算法对微网和配电网协同调节自发优化能力与抗干扰能力的影响，本文选取夏/冬典型日前预测负荷曲线以对比本文算法优化曲线与原始负荷曲线；选取粒子群优化（particle swarm optimization，PSO）算法曲线以对比本文优化算法与普通多目标优化算法；选取非合作博弈论（noncooperative game，NCG）算法优化曲线以对比本文优化算法与不计及随机特性影响的传统博弈算法［7］，各算法均以运行成本最小为优化目标。设定以下4 种场景分别对各类型算法进行对比分析:

场景1:夏季典型日无单小微网随机入网互动。

场景2:夏季典型日在当日09:00 有单小微网随机入网互动。场景3:冬季典型日无单小微网随机入网互动。场景4:冬季典型日在当日09:00 有单小微网随机入网互动。

3.2.1 自发优化能力对比

图4 为夏季典型日下采用不同优化算法的协同调节结果对比。从场景1 可以看出PSO 算法曲线针对多峰谷曲线优化效果不佳，NCG 算法优化曲线与本文算法优化曲线结果相近，但优化效果略逊于本文算法。

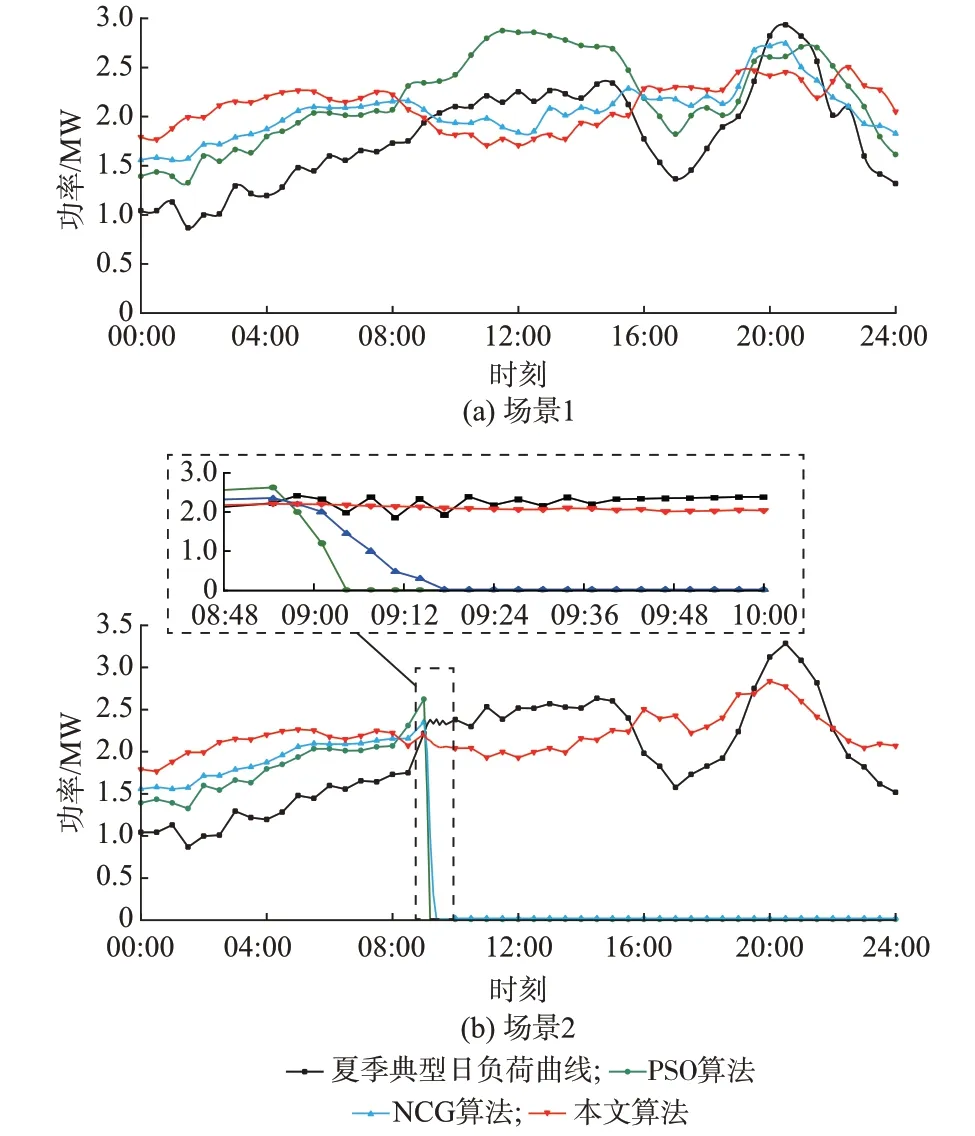
图4 夏季典型日不同算法优化结果Fig.4 Optimization results of different algorithms for typical day in summer

图5 为冬季典型日下采用不同优化算法的协同调节结果对比。从场景3 可以看出，该系统原始日负荷曲线峰谷性相比于夏季典型日有所降低且峰值减小。除PSO 算法优化曲线在10:00—16:00 优化效果不佳外，其余时间，3 类算法优化曲线结果相近，仍以本文算法为最优。

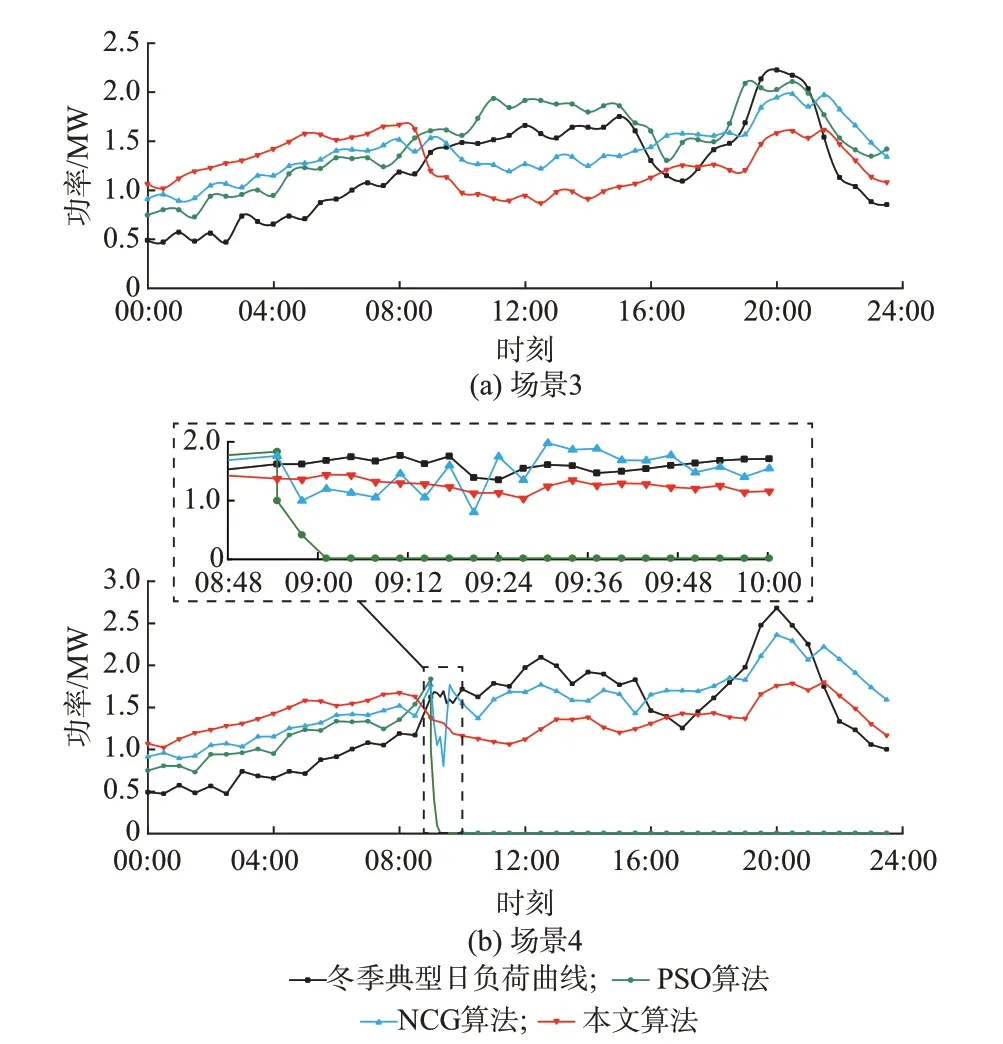
图5 冬季典型日不同算法优化结果Fig.5 Optimization results of different algorithms for typical day in winter

本文方法的优化出力分布如附录C 图C2 和图C3 所示，4 个场景下微网和配电网由价格响应模型优化的交互电价对比如图C4 所示。根据电价及出力分布给出场景1 和场景2 下微网经济性调度收益分别如表1 和表2 所示，场景3 和场景4 下微网经济性调度收益分别如表3 和表4 所示。

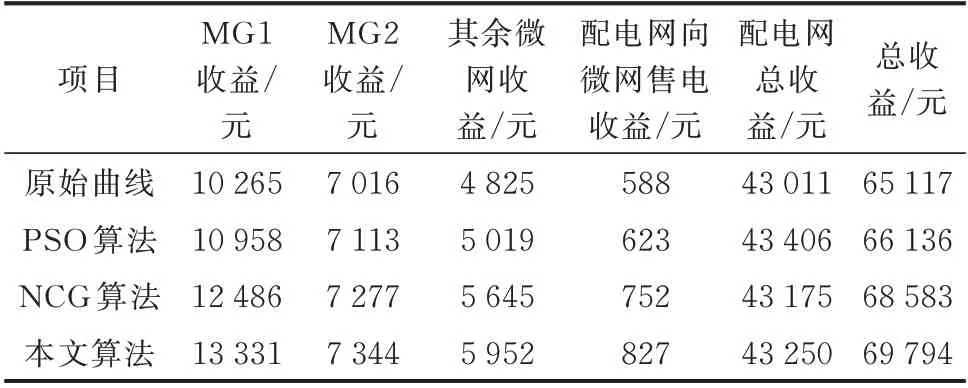
表1 场景1 的经济性调度收益Table 1 Economical dispatching benefit for scenario 1

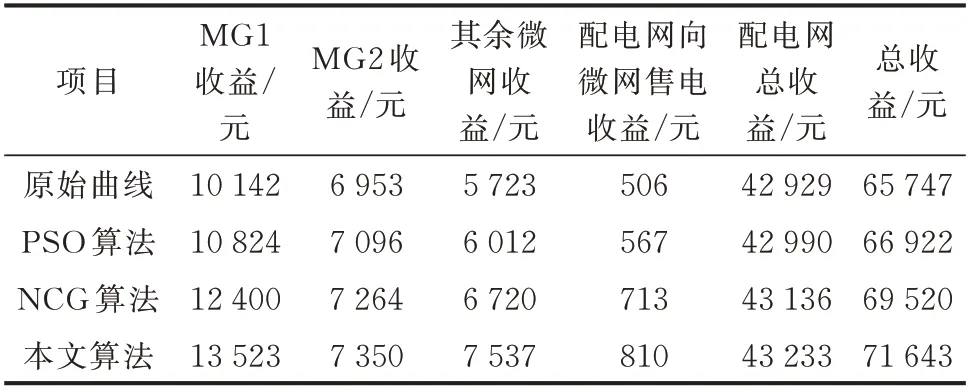
表2 场景2 的经济性调度收益Table 2 Economical dispatching benefit for scenario 2

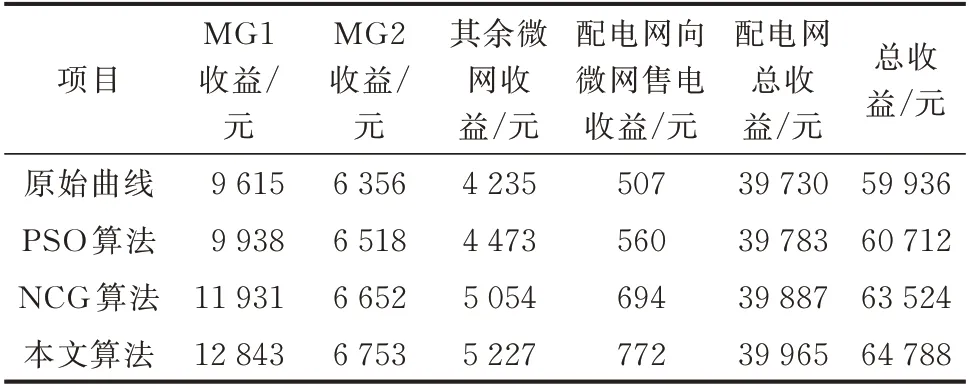
表3 场景3 的经济性调度收益Table 3 Economical dispatching benefit for scenario 3

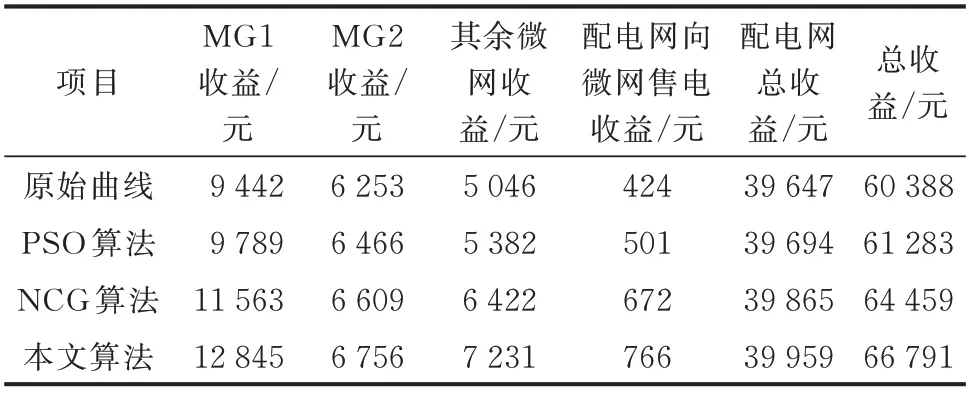
表4 场景4 的经济性调度收益Table 4 Economical dispatching benefit for scenario 4

从表1 和表2 中可以看出，在夏季典型日MG6未接入的情况下，本文提出的算法在微网和配电网方面相较于原始预测经济收益分别提升了20.45%和0.56%；在夏季典型日MG6 接入后，本文所提算法在微网和配电网方面相较于原始预测经济收益分别提升了24.51%和0.71%。

在冬季典型日MG6 未接入的情况下，本文提出的算法在微网和配电网方面相较于原始预测经济收益分别提升了22.85% 和0.59%；在冬季典型日MG6 接入后的情况下，本文提出的算法在微网和配电网方面相较于原始预测经济收益分别提升了29.37%和0.79%。明显看出，在应用本文提出的算法后，无论MG6 是否接入，作为本算法调度的主体微网收益都有明显提高。

进而进行本算法与其他优化算法的经济性对比。由于PSO 算法的优化效果明显差于NCG 算法，因此仅进行本算法与NCG 算法的优化结果对比。在夏季典型日的两种情况下，本文提出的算法在微网方面相较于NCG 算法优化经济收益分别提升了4.80%和7.68%。在冬季典型日的两种情况情况下，本文提出的算法在微网方面相较于NCG 算法优化经济收益分别提升了5.02%和9.10%。

3.2.2 抗干扰能力对比

在图4 场景2 中，当日09:00 有随机涨落力MG6 侵入，可以看出PSO 算法、NCG 算法优化曲线在随机涨落初始侵入阶段，优化结果出现剧烈变化，在重新计算一段时间后趋于稳定。而由于本文算法演化稳定策略的唯一不变性，MG6 迅速形成自组织策略且不影响别的主体运行策略，所以本文算法优化结果趋于平稳。

在图5 场景4 中，当日09:00 有随机涨落力MG6 侵入，优化结果大致趋势与场景2 相同，但由于冬季负荷量小，PSO 算法、NCG 算法重新优化时间略长。由上述对比实验证明，本文算法在一定限度随机涨落力侵入后的优化稳定性高于其余对比算法。其中，本文设置的随机涨落力强度不超过0.2，即随机涨落力容量不超过原各微网总容量的1/5，更大强度随机涨落力下的重新演化情况以作日后研究目标。

4 结语

本文提出了基于随机演化动力学的微网-配电网自组织协同调节策略。以微网及配电网运营利益主体总运行成本最小为目标，建立了基于电价驱动的多微网-配电网模型。其次，考虑利益主体二项分布下的演化效用函数并构建计及随机涨落力的演化动力学方程，建立了基于随机演化策略稳定判据的自组织演化模型并求解。最后，采用多场景下多算法对比实验，证明了基于随机演化动力学的微网-配电网自组织协同调节策略的可行性以及其面对小规模微网随机接入时具有较为优秀的主动调节能力及经济性。主要结论如下:

1）在数学形式上，本文将小规模微网作为新利益主体的随机接入视作一定限度的随机涨落力，搭建了计及随机涨落力演化动力学模型，使得多微网-配电网系统满足形成自组织演化的条件。

2）该模型下的演化稳定策略具有唯一性。在新利益主体接入后，原系统中各利益主体优化策略维持原策略不变，新利益主体的策略选择不需重新迭代，系统具备自发优化能力而不是被动接受指令，策略选择具有自组织性。

3）该模型可提高微网与配电网的总体收益。在新利益主体随机接入的情况下，微网及配电网主体收益不受冲击影响且略有提升。

本文主要针对单小微网随机入网互动，未来会进一步对多类型更大容量微网随机参与互动的演化过程进行研究，采用更复杂的演化动力学数学模型描述策略优化过程，并针对大规模配电网进行验证。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。