煤巷掘进过程中能量转化机制研究

张治伟，王帅锋，樊方正，吴晓龙

(国能神东煤炭集团锦界煤矿，陕西 榆林 719315)

0 引言

在煤巷掘进过程中，在本质上属于“围压卸载”。在卸载的过程中伴随着能量的转移与释放，在煤巷掘进后，储存在深部煤体中的能量会以圆形硐室R0为基点向远离巷道中心的方向转移，同时在转移过程中会伴随着能量的释放。若能量转移不及时，会使储存在煤巷的能量达到煤巷所能承受的极限能量，从而导致煤巷变形甚至造成其他动力灾害。本文讨论在静水压力状态下，在煤巷掘进后，煤巷中应力的状态由相对平衡的原岩应力场转变为重新分布的二次应力状态。在二次应力状态中，由于靠近在煤巷硐室附近的能量较大，所以巷道附近周围的煤岩体会首先进入塑性状态，也就是通常定义的“能量损伤”。在煤巷更远的区域，所受的最小的主应力会更小，煤巷承受的应力更小，所以会由开始的“塑性状态”转变为之后的“弹性状态”。尤其处在塑性状态下的煤巷必须要进行支护，防止煤巷变形甚至煤岩抛出等危害。因此利用弹塑性力学对巷道掘进后的围岩进行塑性区与弹性区分区验算，确定各个分区的范围，计算各分区的应力、应变等量，从能量守恒角度出发，研究巷道掘进后围岩的能量转换规律，建立能量平衡方程，讨论巷道掘进后围岩变形失稳的机理。

在能量耗散与弹性应变能的转化机制研究上，很多学者都进行了大量研究。华安增[1]得出随着围岩所承受的最大主应力的增加，可释放弹性应变能和能量耗散都会相应地增加并且当能量超过岩石所能造成的最大能量极限时，能量会进行转移和释放；金丰年等[2]提出能量损伤的理论公式以及能量损伤阈值的计算方法。通过微分分别求出材料的弹性能、塑性能、流变能以及裂变能各自对应的增量，分别对应为dωe、dωp、dωr、dωf。通过本构方程dψ=dωe+dωp+dωr+dωf计算材料的本构能量；谢和平等[3]得出能量耗散与能量释放是导岩石变形破坏的根本原因，同时岩石在动态加载与静态加载的应用能量准则是有所差别的；黎立云等[4]以加载速率作为自变量，讨论砂岩在循环加载载荷作用下，砂岩内部的可释放弹性应变能和岩石耗散能之间的能量转化机制研究，得出加载速率对砂岩的弹性模量和泊松比影响不大，可弹性应变能与岩石耗散之比随着加载速率的下降而降低；黄达等[5]以大理石为研究材料，并且控制加载应变的速率来研究大理岩的能量耗散与释放的规律，得出在加载速率小于某一个限定值时，岩石表现为塑性流动状态，同时在岩石转化过程中，转化机制与加载应变率有一定的相关性并且岩石的损伤越大，可释放的弹性应变能越高；温韬等[6]研究板岩在不同围压状态下能量转化机制与能量损伤规律，得出在围压应力较低的情况下，围压应力越低，能量损伤越大但是耗散量却越低，反之相反，并且通过能量之比将岩石划分为3个阶段，这3个阶段反映了围岩在卸荷过程中能量的积聚和释放的变化过程。

1 煤巷掘进应力模型

巷道初始应力场处于三向应力平衡，巷道掘进后伴随卸荷破坏了原应力平衡状态，使围岩应力场重新分布实现二次平衡。本模型主要模拟在煤巷掘进过程中，会以巷道r为中心形成弹塑性分区的应力分布，在开挖硐室附近，煤体首先会出现变形损伤所以先形成塑性分布，然后在形成弹性分布，本模型旨在建立静水压力状态下煤巷掘进过程中能量平衡方程[7 -12]。

在实际生产中，巷道所处应力环境复杂多变且受工程扰动影响，很难以数学式表达巷道围岩的应力分布情况，因此，对所建模型作以下简化或假设：①巷道围岩为均质、各向同性煤体。对于厚煤层巷道而言，尤其是留底煤巷道，围岩均是煤体，满足相同介质要求；②在一定开采深度条件下，巷道轴向无限长，将模型简化为轴对称平面应变问题处理；③结合等效开挖理念，巷道断面简化为圆形，其等效半径为r；巷道掘进后，围岩沿径向由浅部至深部依次出现塑性区、弹性区，半径分别为r塑和r弹，当r>r塑是为弹性区，应力分布状态如图1所示。

图1 煤巷掘进过程中的应力分布状态Fig.1 Stress distribution state during coal roadway excavation

1.1 储存能量方程的建立

在静水压力状态下，煤巷掘进之前，煤体所受到的应力值为三向等力状态，即σ10=σ20=σ30=γh(h=开采的深度)。

所以巷道掘进之前煤体储存的能量方程为

因为所考虑的情况为静水压力状态下，所以围压2个方向的力相等，即

1.2 弹性区变形能量方程的建立

弹性区能量方程的建立基于围岩变形与围岩损伤的理论中，围岩弹性区可释放变形能是围岩破坏的主要能量源，可表示为

(1)

式中，re为性区某处至巷道中心距离(3～5r0)。

其中弹性区应力方程为

(2)

(3)

弹性区的半径方程为：由塑性区与弹性区的边界处到无穷远处(实际上原岩应力为5%左右，即3～5r0)

弹性区的应变关系式

(4)

1.3 塑性区耗散能量方程的建立

围岩塑性区可释放变形能为公式

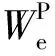
(5)

其中塑性区的应力方程为公式

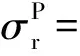
(6)

(7)

塑性区的半径方程为公式

rp=

(8)

塑性区的应变公式为

(9)

因此，巷道围岩能量的方程可以依据热力学能量定律为

(10)

结合实际，建立巷道掘进围岩应力分布力学模型，并根据理论推导围岩分区(塑性区和弹性区)半径及应力与能量方程。基于巷道掘进围岩应力分布力学模型及相关假设，利用弹塑力学推导考虑卸荷扩容的应力分布公式；根据巷道围岩应力边界条件及应力连续条件，推导了各分区径向、环向应力分布公式，弹性区、塑性区巷道围岩储存的可释放变形能表达式，并进行了算例分析；建立了能量的平衡方程，基于应力模型建立弹塑性区的能量平衡机制。

2 三轴加卸载试验方案

试验旨在探索岩石卸荷过程中的力学特性和能量演化特征，试验主要从常规三轴加载、变轴压卸围压和受应力扰动卸围压3方面展开，其中变轴压卸围压包括升、降轴压2种形式，试验方案见表1。常规三轴、升轴压卸围压加卸载路径如图2所示。

表1 试验方案

3 数据分析

将所测数据导入函数绘图软件Origin进行处理分析，得出以下规律。不同围压的应力应变曲线如图3所示。

3.1 围压与煤体储存能量

储存能量=轴压做功+围压做功，分别记为W1，W2，因为轴压做正功，对应的为压缩能，围压做负功，对应的是侧向膨胀变形能。

随着练习我逐渐领悟了要领。熟能生巧，这话在射击时适用，在格斗练习中同样适用，我需要多练了几次，才能悟出怎么控制平衡，怎么移动身体做出动作。踢腿要难得多，尽管他教给我们的还只是一些基本的招式。沙袋弄得我的手脚疼了，皮肤也红肿了，但不管怎么用力击打，它纹丝不动。空气中飘荡的全是击打沙袋的声音。

由公式可得，轴压对应的能量为也就是垂直方向力对煤体做的功即W轴=0.846 249 553 7 kJ≈0.85 MJ，围压所对应的能量也就是水平方向力对煤体做的功即W围-0.288 988 294 4≈-0.29 MJ。

所以围压为5 MPa煤体储存能量为W总=W轴+2W围=0.56 MJ，同理围压10 MPa、15 MPa、20 MPa、25 MPa储存能量分别为1.09 MJ、1.27 MJ、7.8 MJ、28.3 MJ。

所以在静水压力状态下不同围压下煤体储存的能量见表2。

表2 不同围压下煤体储存的能量

能量随围压变化的趋势如图4所示。

图2 常规三轴、并轴压卸围压加卸载路径Fig.2 Conventional three-axis，loading and unloading path of lifting axial pressure and unloading confining pressure

图3 不同围压的应力应变曲线Fig.3 Stress strain curves under different confining prssure

根据不同的围压下煤体对应的能量可得：煤体储存的能量随围压(采深)越大，储存能量越大，储存的能量变化速率越快，与实际煤矿生产中的规律大致相同。

3.2 卸载速率与能量的释放

在煤巷掘进的过程中，对于煤体属于一次卸围压或者多次卸围压的过程，影响煤体稳定性的因素有很多，比如巷道掘进的速度、煤体自身的裂隙构造等，本小结主要讨论在初始围压不变，卸荷速率改变的情况下，煤体的能量演化研究。保持初始围压在20 MPa的情况下，探讨卸荷速率为0.01 MPa/s、0.05 MPa/s、0.1 MPa/s、0.2 MPa/s时的能量演化规律。全应力应变曲线特征如图5所示。

根据图5可知不同卸荷速率下煤体释放能量，见表3。

图4 能量随围压变化趋势Fig.4 Variation trend of energy with confining pressure

根据数据做出能量以及强度随卸荷速率的变化趋势如图6和图7所示。

根据图6可知，在卸载速率逐渐增大的情况下，能量随之下降，体积应变也随之下降，这就表明在煤矿实际生产的过程中，围压卸载速率越快，煤体所释放能量越小，反之亦然，这与实际卸围压过程中能量的演化规律大致相同；由图7可知，煤样的峰值强度和残余强度随卸荷速率的增高而下降，表明在卸荷速率较低的情况下，煤样的峰值强度和残余强度均很大，这就为实际煤矿生产过程提供了一定的参考意义。

图5 不同卸荷速率下全应力应变曲线Fig.5 Full stress strain curve under different unloading rates

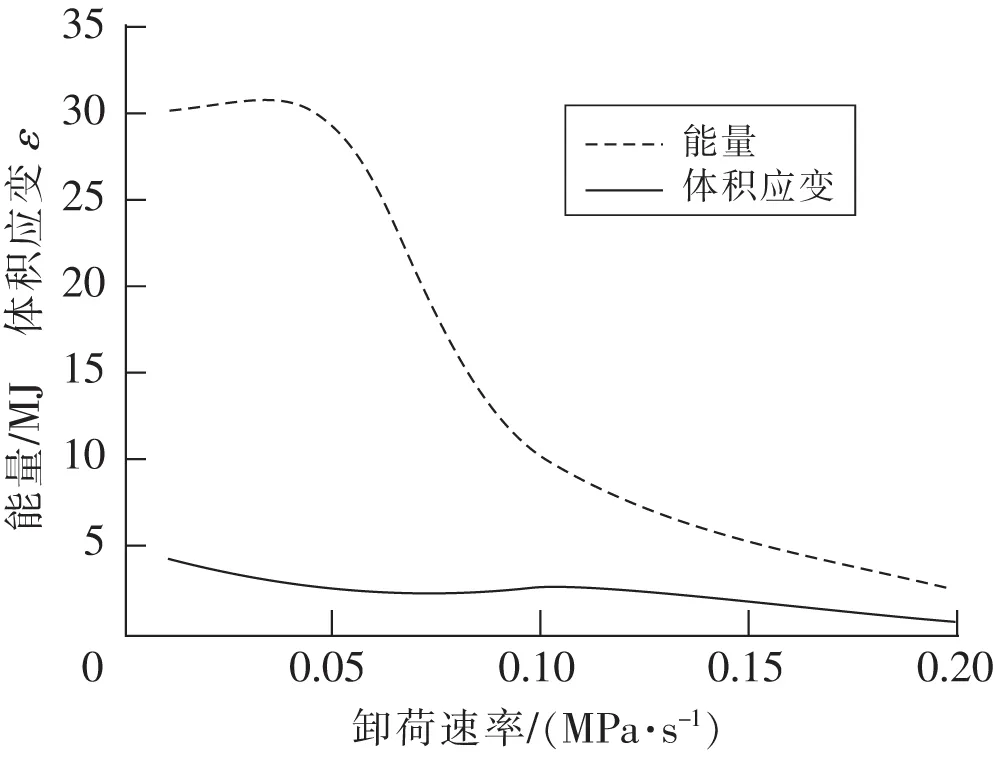
图6 能量与体积应变随卸荷速率的变化趋势Fig.6 Variation trend of energy and volume strain with unloading rate

图7 峰值强度和残余强度随卸荷速率的变化趋势Fig.7 Variation trend of peak strength and residual strength with unloading rate

3.3 升轴压速率与能量的演化规律

实验旨在模拟随着r逐渐增大，轴向载荷逐渐增大，围压逐渐减小的过程。在轴向应力和围压均达到20 MPa时，以不同的加载速率增加轴向荷载，但以相同的卸荷速率降低围压，所对应的全应力应变曲线如图8所示。

图8 不同加载速率下的全应力应变曲线Fig.8 Full stress strain curve under different loading rates

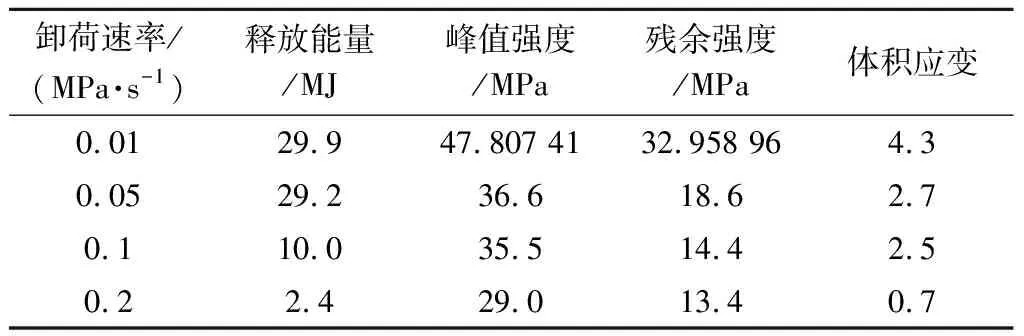
表3 不同卸荷速率下煤体释放能量

在升轴压速率不同的情况下，升轴压所产生的能量与破坏时轴压与围压的载荷见表4。

表4 加载速率变化

根据数据做出能量以及强度随卸荷速率的变化趋势如图9和图10所示。

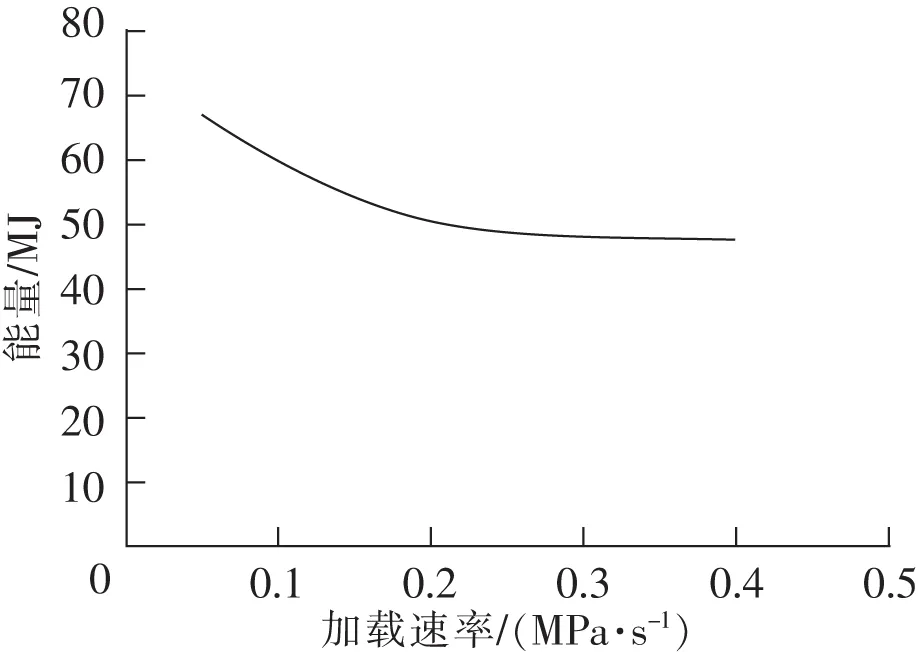
图9 能量随轴压增加速率的变化趋势Fig.9 Change trend of energy with increasing rate of axial pressure

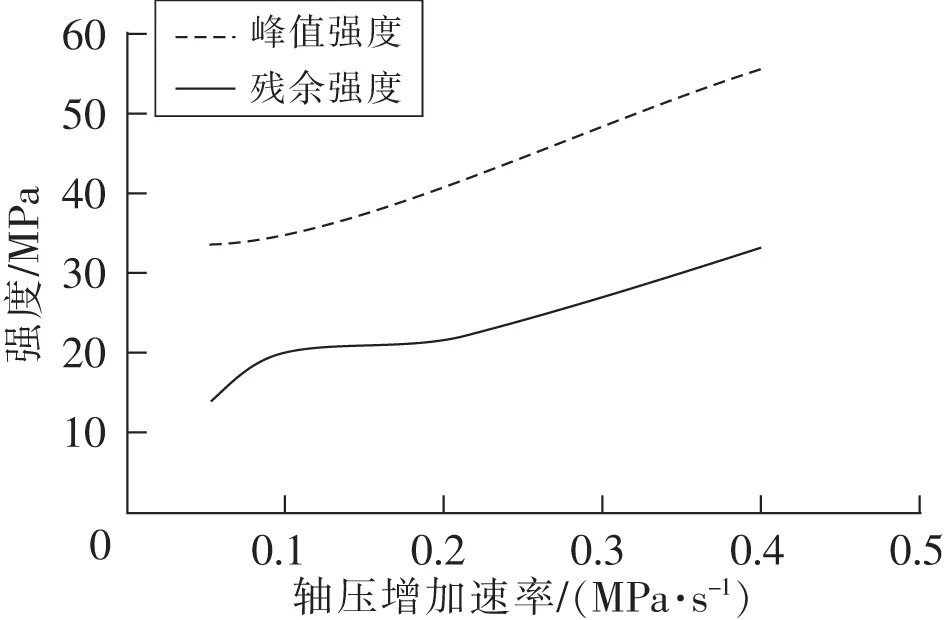
图10 峰值强度和残余强度随增加速率的变化趋势Fig.10 Variation trend of peak strength and residual strength with increasing rate

根据图9可知，在轴压增加速率逐渐增大的情况下，能量随之下降，这就表明在煤矿实际生产的过程中，轴压增加速率越快，煤体所释放能量越大，反之亦然，这与实际过程中能量的演化规律大致相同；由图10可知，煤样的峰值强度和残余强度随增加速率的增高而上升，所以说在轴压增加速率较低的情况下，煤样的峰值强度和残余强度均很小。

4 结论

(1)煤巷在卸围压的过程中，煤巷储存的能量会部分转化成塑性区产生的能量损伤和较大部分弹性区的可释放应变能，煤巷储存的能量与2个分区所产生的能量之差会用来转化成煤体其他形式的做功，比如煤体抛出等动力现象。煤体储存的能量随围压(采深)越大，储存能量越大且围压越大，储存的能量变化速率越快。

(2)在初始围压不变，卸荷速率改变的情况下，煤体卸荷速率越快，煤体释放的能量越小。距离硐室壁越来越远，轴向载荷逐渐增大，围压逐渐减小的过程。以不同的加载速率增加轴向荷载，但以相同的卸载速率降低围压。随着升轴压加载速率的增大，加载速率越大，破坏时的围压和轴压强度越大。在加载和卸载速率不变的情况下，初始围压越大，煤样破坏的峰值轴压强度越大，轴压对煤样产生的能量越多。

(3)煤样的极限强度随着侧限压力б3的增大而增加，根据煤样破坏后的残余强度可知，煤样在发生破坏后仍然可以承受一定的荷载，且大体趋势随着侧限压力б3的增大而增加。

基于以上，可以利用掘巷围岩的能量转换规律，为增加开采速度来减少煤巷变形所产生的矿山动力现象等工程实际提供一些指导。