基于自适应SRUKF算法的电力系统动态谐波状态估计
2023-02-10徐诗露陆东亮夏若平何顺帆
张 明,徐诗露,陆东亮,夏若平,何顺帆
基于自适应SRUKF算法的电力系统动态谐波状态估计
张 明1,徐诗露1,陆东亮1,夏若平1,何顺帆2
(1.武汉纺织大学电子与电气工程学院,湖北 武汉 430200;2.中南民族大学计算机科学学院,湖北 武汉 430074)
针对传统无迹卡尔曼滤波(unscented kalman filter, UKF)谐波状态估计算法存在时变噪声和异常数据时估计准确度较差的情况,提出了一种基于自适应平方根无迹卡尔曼滤波(square- root UKF, SRUKF)的电力系统谐波状态估计算法。首先,针对时变噪声干扰,引入改进的Sage-Husa噪声估计方法实时估计噪声协方差。其次,针对异常数据干扰,引入异常数据修正方法,通过修正系数来降低异常数据对状态估计结果的影响。最后,通过搭建IEEE14节点系统验证自适应SRUKF算法的估计性能,能够有效地应用于电力系统的动态谐波状态估计。仿真结果表明,该算法在时变噪声和异常数据干扰时仍具有良好的估计性能。
动态谐波状态估计;平方根无迹卡尔曼滤波;噪声估计;异常数据修正
0 引言
目前分布式电源逐渐大规模接入电力系统中,并网逆变器等非线性设备作为谐波源会向公共电网中注入谐波电流,由此而产生的谐波污染严重地影响了电力系统的正常运行[1-4]。因此,准确评估电力系统谐波水平是至关重要的。谐波状态估计(harmonic state estimation, HSE)通常用来评估电力系统的谐波状况,为谐波治理和改善电能质量提供依据[5-7]。
电力系统谐波状态估计算法目前主要分为 2类:一类是静态估计算法,通常需要收集一定数量的量测数据,然后计算谐波估计值,其实时性、估计速度及准确性受到一定限制,如加权最小二乘(weighted least square, WLS)算法和奇异值分解(singular value decomposition, SVD)算法[8-10];另一类是动态估计算法,主要是通过系统模型和量测值来确定电力系统运行期间的谐波状况,相比于静态估计算法,更加符合电力系统动态变化的运行特性[11-12]。目前动态谐波状态估计方法主要有卡尔曼滤波(kalman filter, KF)及其改进算法,如扩展卡尔曼滤波(extended kalman filter, EKF)、容积卡尔曼滤波(cubature kalman filter, CKF)和无迹卡尔曼滤波(unscented kalman filter, UKF)等算法,均是利用某一时刻的量测值去估计下一个时刻的状态值。文献[13]考虑到时变系统中噪声协方差的不确定性,提出了一种基于自适应KF谐波状态估计算法,在时变系统中能够自适应改变Kalman增益,从而跟踪系统的快速变化,同时对于噪声协方差,由假设检验方法确定系统状态,在稳态时用零矩阵代替,动态时用单位矩阵代替,所以在噪声发生变化时估计精度必定会下降。文献[14]采用鲁棒EKF算法用于动态谐波状态估计,即使存在异常量测数据,甚至较少的量测数据也能得到很好的估计结果,从而可以减少所需的谐波测量装置,但EKF算法采用基于雅可比矩阵的线性化方法,因而计算量大且估计精度降低。文献[15]提出了一种基于自适应CKF动态谐波状态估计算法,将基于渐消记忆指数加权法的噪声估计算法与坏数据开窗修正算法融入传统CKF算法,克服了传统CKF算法因为时变噪声及坏数据干扰而导致的估计精度降低。虽然CKF算法具有滤波精度好和计算复杂度较低的特性,但对于高维非线性和波动性大的系统,仍然存在滤波精度较差和稳定性较低的问题。UKF算法通过无迹变换(unscented transformation, UT) 采用一组Sigma采样点来获取系统的相关统计参数,计算速度快、计算精度高,文献[16]提出了一种基于粒子群优化的UKF动态谐波估计算法,通过改进粒子群优化算法估计时变噪声的协方差矩阵,提高了传统 UKF 算法针对时变噪声的鲁棒性,动态谐波状态估计的准确性得到提高。
在传统UKF算法的基础上,平方根UKF(square- root UKF, SRUKF)算法在递归运算过程中采用误差协方差的平方根代替误差协方差,保证误差协方差矩阵半正定,能够有效解决由时变噪声导致的滤波器发散问题[17-21]。然而,注入电力系统的谐波电流具有动态特性,为了进一步提高在存在时变噪声和异常量测数据干扰时,电力系统谐波状态估计的准确性和鲁棒性,因此,本文提出一种基于自适应SRUKF动态谐波状态估计算法,通过在SRUKF算法中引入改进的Sage-Husa噪声估计方法和异常数据修正方法,以跟踪系统参数变化,作出精确的动态估计,同时提高动态谐波状态估计的稳定性。
1 自适应SRUKF算法
在系统模型有偏差的情况下,传统UKF算法可能会出现滤波发散或是估计精度降低的问题,本文采用自适应SRUKF算法来进行动态谐波状态估计,正是为了改进这些不足,通过改变误差协方差矩阵的迭代方式来提高传统UKF算法的稳定性,同时将噪声估计环节和异常数据修正环节加入到算法中,自适应系统参数变化提高动态谐波状态估计的精度。
首先,设一般随机离散系统状态方程和量测方程分别为
1.1 SRUKF算法

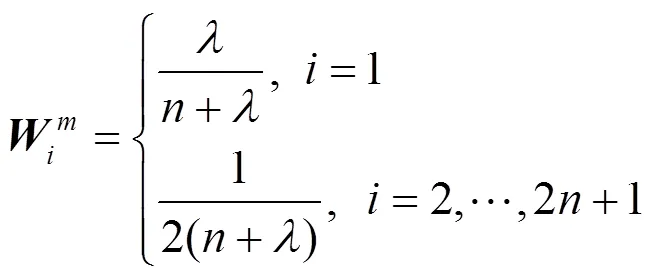


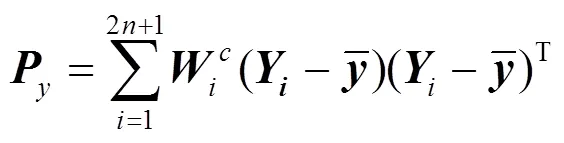
SRUKF算法的具体步骤如下。
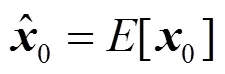

(1) 时间更新

(2) 预测
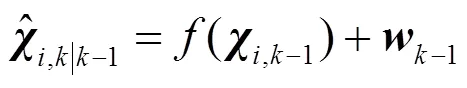


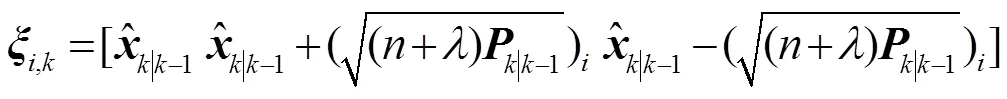
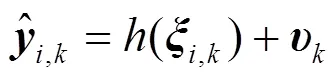
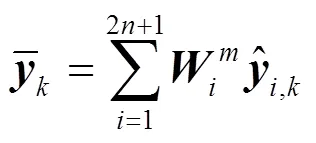
(3) 测量更新




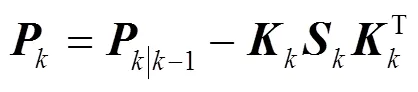
1.2 噪声估计方法
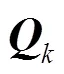
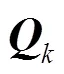




1.3 异常数据修正方法
由于电力系统量测装置故障等往往会带来异常量测数据,将导致SRUKF算法估计谐波参数的准确度降低。
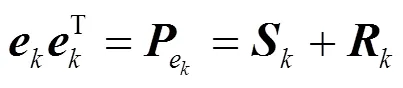

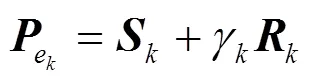
则式(16)中的滤波器增益变为
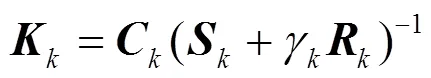
根据式(27)进行测量更新。

整理后得

因此,修正异常量测数据的步骤如下。
2 动态谐波状态估计
2.1 动态谐波状态估计模型
目前动态谐波状态估计所有量测数据均来自同步相量测量单元(phasor measurement unit, PMU)[26],本文以节点处注入的谐波电流为状态量,谐波电压为量测量,结合电力系统的特点,以次谐波为例,将式(1)改写成用于谐波状态估计的状态方程和测量方程。


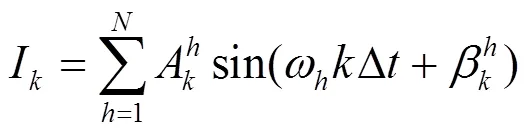
将式(32)可表示为矩阵形式。
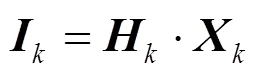

因此,动态谐波状态估计将利用式(30)—式(34)在时刻各节点处的谐波电压量测数据,通过状态方程和量测方程得到各节点处的注入谐波电流状态量,同时估计各次谐波的幅值和相角,从而得到注入谐波电流的位置和参数信息。
2.2 动态谐波状态估计步骤
基于自适应SRUKF算法的动态谐波状态估计流程图,如图1所示,其主要步骤如下:
1) 量测得到各节点谐波电压,然后通过FFT进行频谱分析得到电压谐波的阶次;
2) 采用谐波解耦算法依次设定谐波阶次;
3) 确定电力系统网络拓扑结构,建立系统各谐波阶次阻抗矩阵;
5) 输出各节点注入谐波电流估计结果。
3 仿真分析
为了验证自适应SRUKF算法进行谐波状态估计的性能,本文通过搭建IEEE14节点系统进行验证,如图2 所示。该系统由1、2、3、6、8 接入发电机供电,系统中发电机、变压器、及支路等元件的具体参数可以参见文献[27]。除了10、13上的谐波源外,其余均为非谐波源母线,谐波源采用电流源模型,其谐波频谱如表1所示[5]。在2、4、5、6、7、8、11、12处安装量测装置获取各节点谐波电压,以确保量测方程的能观性。

图2 IEEE14节点接线图包括谐波源位于10 号和13号母线
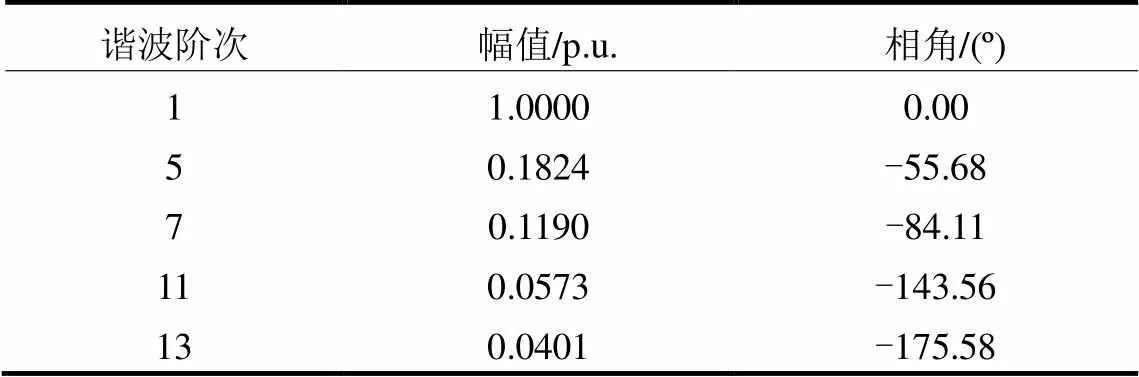
表1 谐波源频谱表
仿真中以900组(3 min)谐波数据作为分析对象,采用[28]中基于BIBC(节点注入电流-支路电流)-BCBV(支路电流-节点电压)的方法建立系统谐波阻抗矩阵,首先输入谐波源负荷注入的谐波电流,执行谐波潮流计算,得到各节点谐波电压,以这些数据作为实际真值,并添加高斯噪声以模拟噪声干扰,采用谐波解耦算法代入自适应SAUKF算法进行状态估计,得到各谐波源注入节点的谐波电流估计结果。
同时为了评估算法性能,引入均方根误差(root mean square error, RMSE)。RMSE可以衡量谐波电流幅值、相角的估计值与实际真值之间的偏差,定义为

仿真分析过程将从三个方面进行:(1) 存在时不变噪声时;(2) 存在时变噪声时;(3) 存在异常数据干扰时。
3.1 存在时不变噪声时的仿真分析
为了验证自适应SRUKF算法存在时不变噪声干扰时的估计准确性,在节点谐波电压中加入信噪比(signal-to-noise, SNR)为30 dB的高斯噪声进行仿真分析,采用本文的自适应SRUKF算法进行谐波状态估计,选取节点 13 注入的谐波电流为例,图3—图6分别为5、7、11、13次谐波电流幅值和相角的比较结果。由仿真结果看出,对于各阶次谐波幅值和相角,自适应SRUKF算法的估计值与实际真值基本接近,说明存在时不变噪声干扰时,该算法可以很好地对谐波电流幅值和相角进行估计。另外,在信噪比为40 dB的噪声干扰下,自适应SRUKF算法与传统UKF算法的各阶次谐波电流幅值、相角估计结果如图7、图8的RMSE直方图所示,自适应SRUKF算法较传统UKF算法误差较小,进一步说明自适应SRUKF算法的估计性能得到了提升。

图3 信噪比30 dB下的5次谐波电流幅值和相角估计
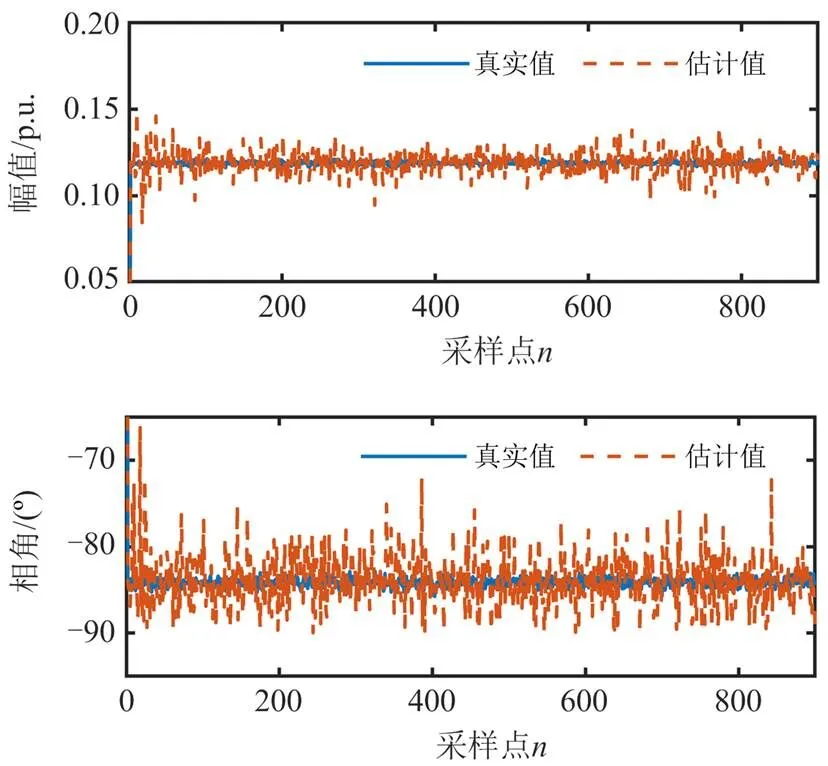
图4 信噪比30 dB下的7次谐波电流幅值和相角估计

图5 信噪比30 dB下的11次谐波电流幅值和相角估计
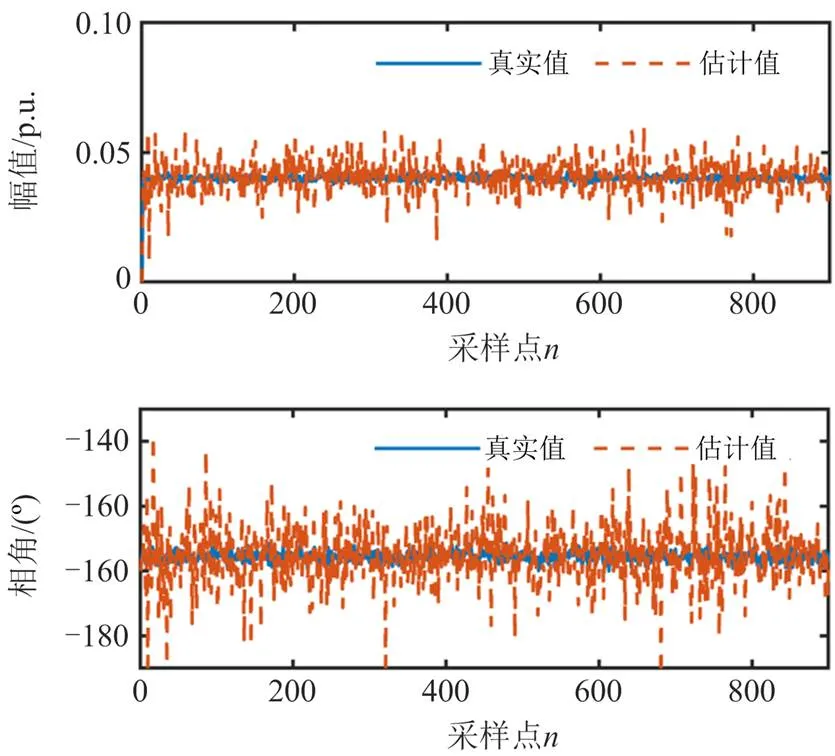
图6 信噪比30 dB下的13次谐波电流幅值和相角估计

图7 信噪比40 dB下的各阶次谐波电流幅值估计RMSE直方图

图8 信噪比40 dB下的各阶次谐波电流相角估计RMSE直方图
3.2 存在时变噪声时的仿真分析


图9 存在时变噪声干扰下估计的5次谐波电流幅值(信噪比递增)
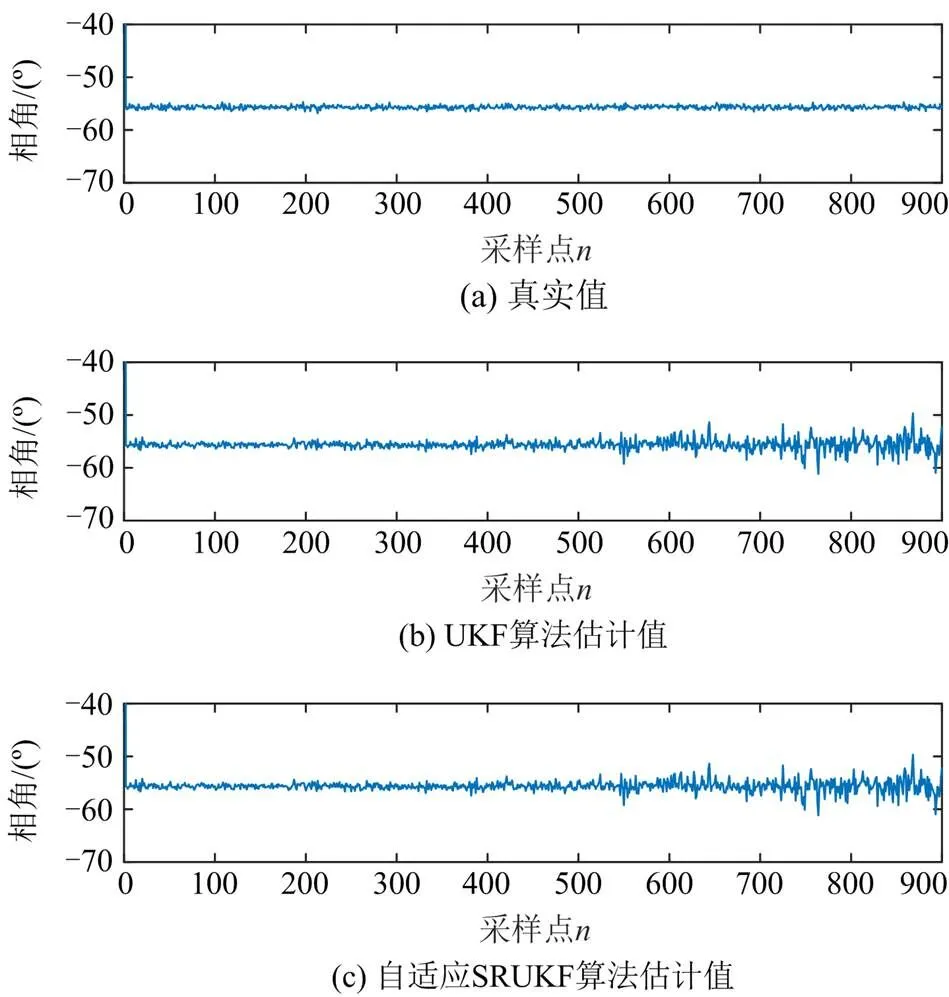
图10 存在时变噪声干扰下估计的5次谐波电流相角(信噪比递增)

图11 存在时变噪声干扰下估计的5次谐波电流幅值(信噪比随机)
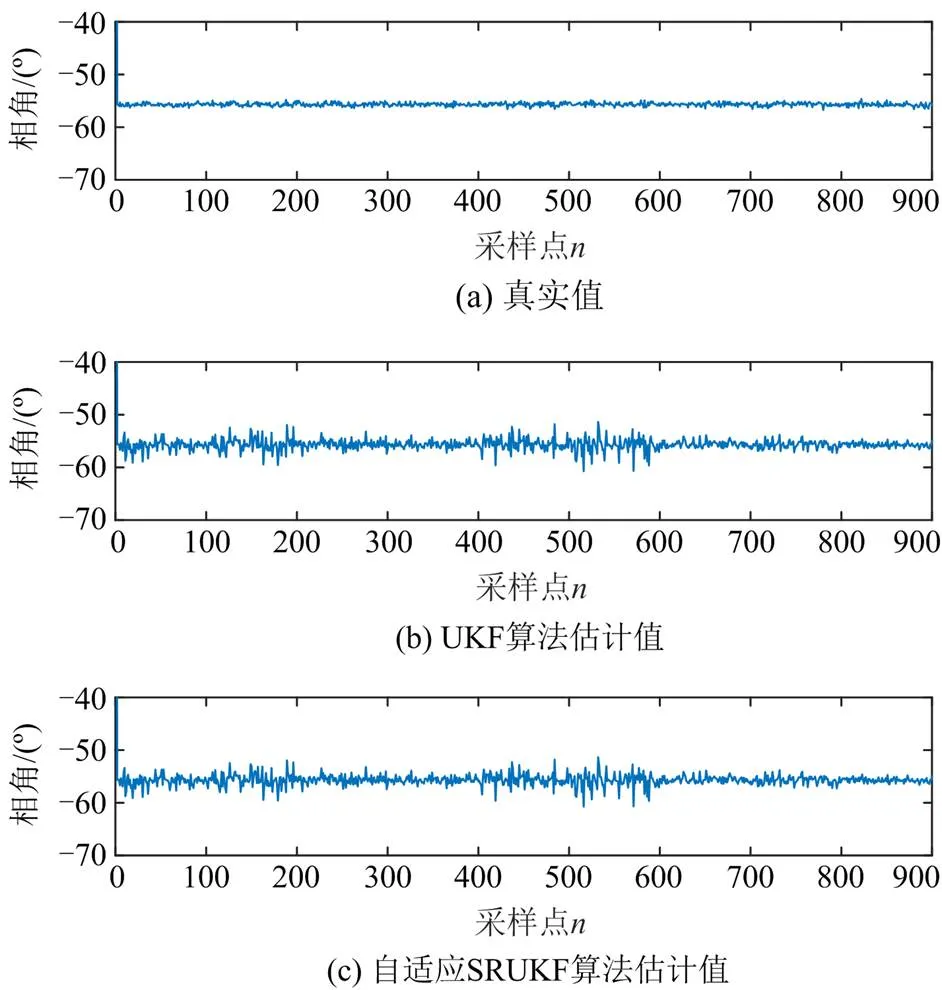
图12 存在时变噪声干扰下估计的5次谐波电流相角(信噪比随机)
3.3 存在异常量测数据时的仿真分析
为了验证自适应SRUKF算法存在异常量测数据时依旧能准确估计出谐波电流参数,并与传统UKF算法的估计结果进行对比,仿真中设置噪声信噪比为40 dB,并设置节点 10 注入的谐波电流在采样点280、650处出现异常数据,其他地方的信号正常。这里以节点 10 注入的5 次谐波电流为例,如图13所示,同时以无异常量测数据为实际真值,在同样仿真条件下采用传统UKF算法与自适应SRUKF算法估计的幅值RSME、相角RSME如表2 所示。由图13 和表2 可以看出,在采样点280、650处出现异常量测数据时,自适应SRUKF算法估计的谐波电流幅值和相角比传统UKF算法准确。
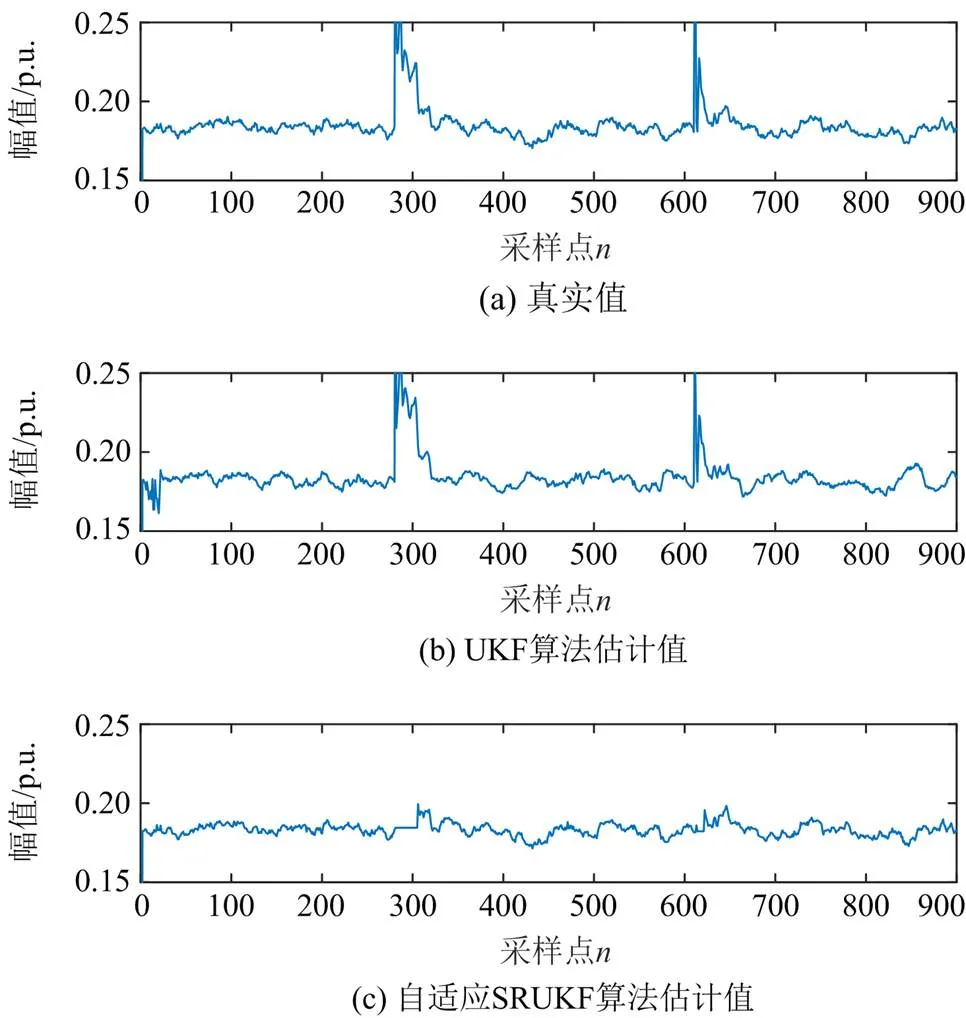
图13 存在异常数据干扰下估计的5次谐波电流幅值

表2 系统存在异常数据时的均方根误差比较
综上可知,在噪声和异常数据干扰下自适应SRUKF算法的估计结果比传统UKF算法更优。
4 结论
为了在存在时变噪声和异常量测数据干扰下准确地进行电力系统动态谐波状态估计,本文提出了一种基于自适应SRUKF的动态谐波状态估计算法,通过在SRUKF算法中引入改进的Sage-Husa噪声估计方法和异常数据修正方法,通过搭建IEEE14节点系统验证自适应SRUKF算法在3种不同情况下的估计效果,并与传统UKF算法进行比较,结果表明自适应SRUKF算法可以很好地克服时变噪声和异常数据的干扰,提高动态谐波状态估计的精度。但如何进一步提高自适应SRUKF算法对谐波电流相角的估计精度,需要进一步的研究工作。
[1] 邵振国, 许昊铂, 肖颂勇, 等. 新能源电网中的谐波问题[J]. 电力系统保护与控制, 2021, 49(4): 178-187.
SHAO Zhenguo, XU Haobo, XIAO Songyong, et al. Harmonic problems in a new energy power grid[J]. Power System Protection and Control, 2021, 49(4): 178-187.
[2] 陈思源, 景巍巍, 史明明, 等. 新能源接入背景下的谐波源建模方法综述[J]. 电力系统保护与控制, 2022, 50(7): 162-175.
CHEN Siyuan, JING Weiwei, SHI Mingming, et al. Review of harmonic source modeling methods with the background of renewable energy access[J]. Power System Protection and Control, 2022, 50(7): 162-175.
[3] 翟晓寒, 丁惜瀛, 姚润宇, 等. 基于径向基神经网络的UPQC 并联侧谐波电流预测与补偿[J]. 电测与仪表, 2021, 58(8): 139-145.
ZHAI Xiaohan, DING Xiying, YAO Runyu, et al. Prediction and compensation of harmonic current in parallel side of unified power quality controller based on radial basis neural network[J]. Electrical Measurement & Instrumentation, 2021, 58(8): 139-145.
[4] 李臻, 曹增新, 蒋程, 等. 应用于光伏发电并网逆变器的有源阻尼控制策略[J]. 电网与清洁能源, 2021, 37(11): 102-108, 114.
LI Zhen, CAO Zengxin, JIANG Cheng, et al. Active damping control strategy applied to grid-connected inverter of photovoltaic power generation[J]. Power System and Clean Energy, 2021, 37(11): 102-108, 114.
[5] 肖先勇, 胡誉蓉, 王杨, 等. 基于非同步电能质量监测系统的谐波状态估计[J]. 中国电机工程学报, 2021, 41(12): 4121-4131.
XIAO Xianyong, HU Yurong, WANG Yang, et al. Harmonic state estimation based on asynchronous power quality monitoring system[J]. Proceedings of the CSEE, 2021, 41(12): 4121-4131.
[6] 王炤宇, 随慧斌. 谐波源责任划分技术的工程应用[J].电力系统保护与控制, 2021, 49(14): 140-148.
WANG Zhaoyu, SUI Huibin. Engineering application of harmonic source responsibility division technology[J]. Power System Protection and Control, 2021, 49(14): 140-148.
[7] LIAO H W. Power system harmonic state estimation and observability analysis via sparsity maximization[J]. IEEE Transactions on Power Systems, 2007, 22(1): 15-23.
[8] RAKPENTHAI C, UATRONGJIT S, WATSON N R, et al. On harmonic state estimation of power system with uncertain network parameters[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4829-4838.
[9] 牛胜锁, 张达, 梁志瑞, 等. 基于抗差总体最小二乘法的电力系统谐波状态估计[J]. 电力系统保护与控制, 2014, 42(11): 106-111.
NIU Shengsuo, ZHANG Da, LIANG Zhirui, et al. Power system harmonic state estimation based on robust total least squares[J]. Power System Protection and Control, 2014, 42(11): 106-111.
[10] 徐志向, 侯世英, 周林, 等. 基于奇异值分解的电力系统谐波状态估计[J]. 电力自动化设备, 2006, 26(11): 28-31.
XU Zhixiang, HOU Shiying, ZHOU Lin, et al. Power system harmonic state estimation based on singular value decomposition[J]. Electric Power Automation Equipment, 2006, 26(11): 28-31.
[11] HEYDT G T. Identification of harmonic sources by a state estimation technique[J]. IEEE Transactions on Power Delivery, 1989, 4(1): 569-576.
[12] BEIDES H M, HEYDT G T. Dynamic state estimation of power system harmonics using Kalman filter methodology[J]. IEEE Transactions on Power Delivery, 1991, 6(4): 1663-1670.
[13] YU K K C, WATSON N R, ARRILLAGA J. An adaptive Kalman filter for dynamic harmonic state estimation and harmonic injection tracking[J]. IEEE Transactions on Power Delivery, 2005, 20(2):1577-1584.
[14] KUMAR A, DAS B, SHARMA J. Robust dynamic state estimation of power system harmonics[J]. International Journal of Electrical Power and Energy Systems, 2006, 28 (1): 65-74.
[15] 连鸿松, 张少涵, 张逸. 基于自适应容积卡尔曼滤波算法的电力系统动态谐波状态估计[J]. 智慧电力, 2020, 48(6): 14-19, 53.
LIAN Hongsong, ZHANG Shaohan, ZHANG Yi. Dynamic harmonic state estimation of power system based on adaptive volumetric Kalman filter[J]. Smart Power, 2020, 48(6): 14-19, 53.
[16] 江辉, 谢兴, 王志忠, 等. 基于优化无迹 Kalman 滤波的电网动态谐波估计[J]. 深圳大学学报(理工版), 2015, 32(2): 188-195.
JIANG Hui, XIE Xing, WANG Zhizhong, et al. Dynamic harmonic estimation based on optimized unscented Kalman filter model[J]. Journal of Shenzhen University (Science and Engineering), 2015, 32(2): 188-195.
[17] ZHOU Y, ZHANG C, ZHANG Y F, et al. A new adaptive square-root unscented Kalman filter for nonlinear systems with additive noise[J]. International Journal of Aerospace Engineering, 2015, 38.
[18] ASLA R M, HAGH Y S, SIMANI S, et al. Adaptive square-root unscented Kalman filter: an experimental study of hydraulic actuator state estimation[J]. Mechanical Systems and Signal Processing, 2019, 132: 670-691.
[19] OUYANG Q, MA R, WU Z X, et al. Adaptive square-root unscented Kalman filter-based state-of-charge estimation for lithium-ion batteries with model parameter online identification[J]. Energies, 2020, 13.
[20] 卫志农, 孙国强, 庞博. 无迹卡尔曼滤波及其平方根形式在电力系统动态状态估计中的应用[J]. 中国电机工程学报, 2011, 31(16): 74-80.
WEI Zhinong, SUN Guoqiang, PANG Bo. Application of UKF and SRUKF to power system dynamic state estimation[J]. Proceedings of the CSEE, 2011, 31(16): 74-80.
[21] 赵洪山, 田甜. 基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J]. 电网技术, 2014, 38(1): 188-192.
ZHAO Hongshan, TIAN Tian. Dynamic state estimation for power system based on an adaptive unscented Kalman filter[J]. Power System Technology, 2014, 38(1): 188-192.
[22] QI J J, SUN K, WANG J H, et al. Dynamic state estimation for multi-machine power system by unscented Kalman filter with enhanced numerical stability[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1184-1196.
[23] 杨韬, 罗萍萍, 龚锦霞, 等. 基于改进无迹卡尔曼滤波的短线路同杆并架双回线参数辨识[J]. 电力系统保护与控制, 2021, 49(5): 36-45.
YANG Tao, LUO Pingping, GONG Jinxia, et al. Parameter identification of short parallel double-lines based on a modified unscented Kalman filter[J]. Power System Protection and Control, 2021, 49(5): 36-45.
[24] XIA Q, RAO M, YING Y, et al. Adaptive fading Kalman filter with an application[J]. Automatica, 1994, 30(8): 1333-1338.
[25] 石勇, 韩崇昭. 自适应 UKF 算法在目标跟踪中的应用[J]. 自动化学报, 2011, 37(6): 755-759.
SHI Yong, HAN Chongzhao. Adaptive UKF method with applications to target tracking[J]. Acta Automatica Sinica, 2011, 37(6): 755-759.
[26] APPASANI B, JHA A V, MISHRA S K, et al. Communication infrastructure for situational awareness enhancement in WAMS with optimal PMU placement[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 124-135.
[27] Harmonic Working Group, Power Quality Subcommittee, T & D Committee, et al. Task force on harmonics modeling and simulation[EB/OL]. http://grouper.ieee.org/groups/ harmonic/simulate/download.htm, link Test System 1: A 14-Bus Balanced Utility Transmission System.
[28] TENG J H. A direct approach for distribution system load flow solutions[J]. IEEE Transactions on Power Delivery, 2003, 18(3): 882-887.
Dynamic harmonic state estimation of a power system based on adaptive SRUKF
ZHANG Ming1, XU Shilu1, LU Dongliang1, XIA Ruoping1, HE Shunfan2
(1. School of Electronic and Electrical Engineering,Wuhan Textile University, Wuhan 430200, China;2. College of Computer Science, South-Central University for Nationalities, Wuhan 430074, China)
Given the shortcomings of the traditional unscented Kalman filter (UKF) algorithm of harmonic state estimation with time-varying noise and abnormal data, an algorithm based on adaptive square root unscented Kalman filter (SRUKF) is proposed for power system harmonic state estimation. First, an improved Sage-Husa noise estimation method is proposed for real-time estimation of noise covariance in view of the time-varying noise. Second, an abnormal data correction method is proposed in view of the abnormal data interference. A correction coefficient is introduced to reduce the influence of abnormal data in state estimation. Finally, an IEEE14-node system is built to validate the estimation performance of the adaptive SRUKF algorithm. It has been applied to the dynamic harmonic state estimation of a power system. The simulation results show that the proposed algorithm has good estimation performance with the interference of time-varying noise and abnormal data.
dynamic harmonic state estimation; square root unscented Kalman filter; noise estimation; abnormal data correction
10.19783/j.cnki.pspc.220514
国家自然科学基金项目资助(61903384,51477124)
This work is supported by the National Natural Science Foundation of China (No. 61903384 and No. 51477124).
2022-04-12;
2022-07-11
张 明(1970—),男,通信作者,博士,副教授,研究方向为电能质量分析与控制;E-mail: zhangming@wtu.edu.cn
徐诗露(1996—),女,硕士研究生,研究方向为电能质量分析与控制。E-mail: 1298370838@qq.com
(编辑 许 威)
