含双馈风电电力系统的采样负荷频率控制

李谟发，张志文，练红海，胡斯佳

含双馈风电电力系统的采样负荷频率控制

李谟发1,2，张志文1，练红海2，胡斯佳1

(1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.湖南电气职业技术学院风能工程学院，湖南 湘潭 411101)

双馈风力发电；负荷频率控制；采样周期；Lyapunov泛函；控制器设计

0 引言

风电等新能源在过去的二十年里得到了广泛的发展和应用[1]。现有新能源一般通过电力电子变换器接入电网，并且，新能源机组主要是按照最大功率跟踪控制向电网输出功率，在系统有功功率扰动下，无法主动为电网提供惯量支撑和参与频率调控[2-3]。因此，新能源的高渗透率，降低了电力系统的转动惯量[4-5]，系统的调频能力降低，电力系统中的功率失衡将导致更快的频率响应和更大的频率偏差[6-7]。另一方面，LFC主要由控制信号的采集与传输、调度中心的调控、指令信号的下发和终端设备的响应三个环节组成。可知，LFC为典型的网络控制系统，其控制信号的固有更新周期可达2~4 s[8]。并且，采样信号在传输过程中会遇到时间延迟、数据丢包和错序等网络问题，对电力系统的稳定性造成很大的威胁[9]。有时，较小的通信时滞对含可再生能源的互联电力系统的动态稳定性有影响[10-11]。可见，含新能源电力系统的频率控制将变得更加复杂和困难[12-13]。

因此，对现有新能源并网方式与采用通信网络的新型电力系统LFC问题进行研究，解决当前系统频率稳定性是新型电力系统进一步发展的当务之急。一些有效并且具有应用前景的智能频率综合控制策略获得了关注。文献[14]利用Lyapunov理论研究了含时滞的电力系统稳定性。文献[15]研究了一类基于无模型算法的含新能源电力系统的频率协调控制方法，但没有考虑系统网络通信问题以及验证系统惯量系数等参数变化后的有效性。文献[16]在具有高风电渗透率的多区域时延电力系统中引入了一种分散的LFC策略。此外，文献[17]研究了基于观测器的鲁棒积分滑模控制策略，可应对建模的不确定性和可变负荷的新能源电力系统。文献[18]解决了基于离散LFC模型的时滞电力系统数字PID控制器的设计问题。为了减少通信负担，节省通信带宽，文献[19]设计了一种基于采样数据的事件触发LFC方案。作为一种改进，文献[20]提出了一种具有补充自适应动态规划的事件触发LFC方案。上述研究在较小的离散周期或采样周期内有效。随着采样周期的增加，LFC的性能会下降甚至不稳定。并且，上述研究没有讨论系统惯量变化对系统频率稳定性能的影响。

为降低系统采样周期、传输时滞与惯性系数等参数变化对系统LFC的影响，采样控制技术在电力系统LFC中的应用受到了关注。文献[21]提出一种时变时滞的离散LFC方法，但将整个系统进行离散化处理，带来了计算负担。并且，对随机扰动负荷没有进行验证。文献[22]针对含风电接入的电力系统，基于Lyapunov理论和线性矩阵不等式(linear matrix inequality, LMI)技术，讨论了不同采样周期对LFC的影响，并在文中验证了系统惯性系数等参数变化后，采用采样控制方法比传统PI控制和连续状态反馈控制的性能更好。但没有充分考虑系统采样的有效信息，导致所得结果仍然具有较大的保守性。

综上所述，本文提出一种基于控制信号变更新周期的采样LFC方法。首先，综合考虑测量/控制信号采样特性，构建了含双馈感应发电机(doubly- fed induction generator, DFIG)接入的电力系统采样LFC模型。其次，利用双边闭环Lyapunov泛函和LMI技术，给出了系统控制信号变更新周期采样的相关稳定准则和控制器设计方法。然后，在单区域和传统两区域电力系统中进行仿真验证。相比已有研究成果，所提方案具有更大的更新周期稳定裕度，可减轻系统的通信负担。并且采样控制在其最大允许更新周期内，通过设置合适的采样周期，能够容忍较大的通信时滞，降低时滞对系统频率稳定性能的影响。对电力系统惯性系数等参数变化也具有更好的鲁棒性，可进一步提升DFIG的渗透率。

1 系统LFC动态模型

1.1 系统LFC连续模型

图1 含DFIG互联电力系统区域i的LFC模型

1.2 基于变更新周期的采样LFC模型

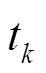
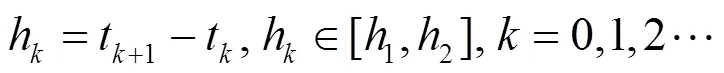
式中，和分别表示更新周期的下界和上界，不同的对应的大小也不同，体现了控制信号更新周期的变周期性。

基于系统的采样特性，网络化电力系统LFC的采样状态反馈控制器可描述如式(3)。

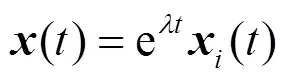
其中：

此时，分析系统(5)的指数稳定问题可转化为分析系统(6)的渐进稳定性问题。

2 基于采样的LFC系统稳定分析与控制

针对含有DFIG电力系统的采样LFC模型(5)，综合考虑电力系统控制信号更新周期的时变性，结合LMI技术，构造能够很好地反映该系统本质的Lyapunonv泛函，推导出该系统变更新周期的相关稳定准则和控制器设计准则。

2.1 采样LFC系统Lyapunov稳定分析判据

下面先给出自由矩阵积分不等式引理1。

用引理1对全采样区间泛函导数的积分项进行估计，能得到更好的求解空间，可有效降低所获结论的保守性。

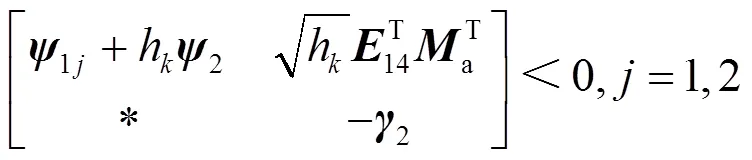
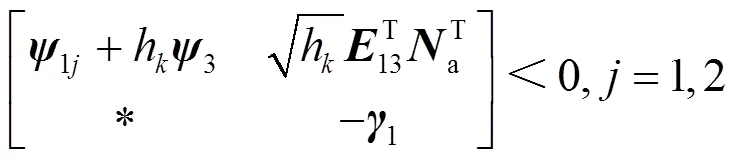
其中：

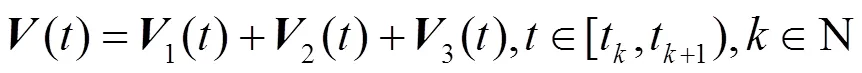
其中：

为了简化定理证明过程中相关式子的描述，定义如下符号：

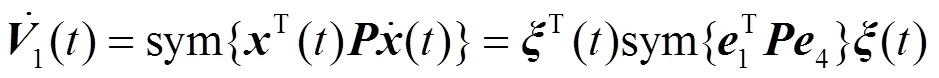
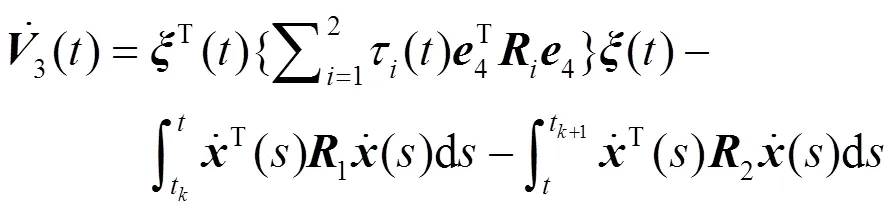
使用引理1估计Lyapunov泛函导数中的积分项，得

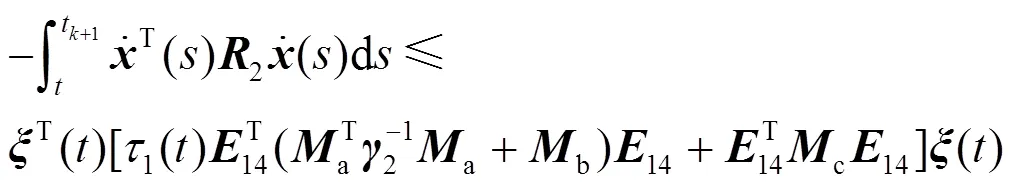
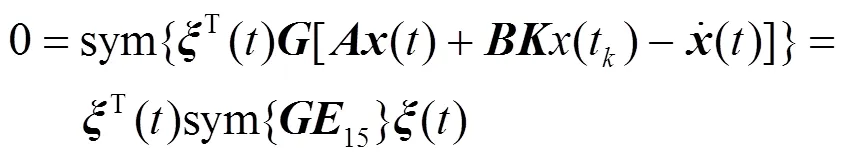
将式(11)—式(16)进行整理可得

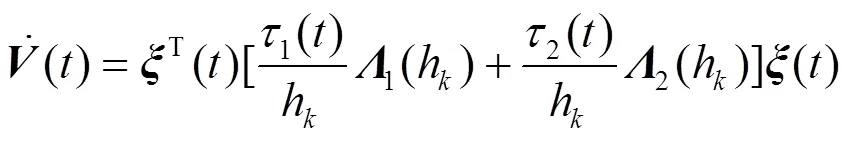
式中：

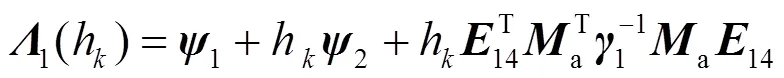
2.2 采样LFC系统控制器设计判据

基于定理1，下面对电力系统采样LFC控制器设计准则以及求解算法进行分析。

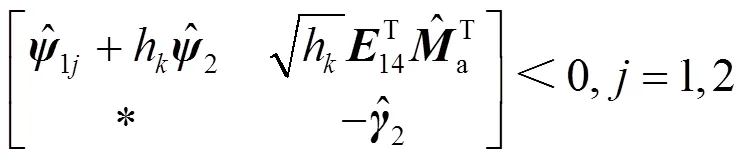
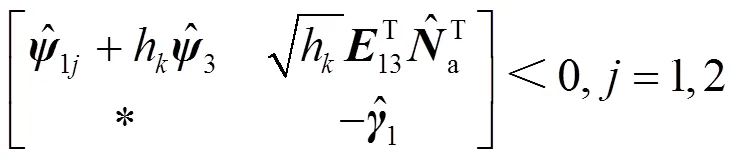
其中：

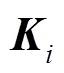
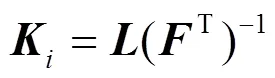
证明：定义如下矩阵变量

2.3 求解步骤

基于定理2，可得两类稳定采样控制器。第一类是给定指数收敛率，获得最大化更新周期的采样控制器；第二类是给定更新周期，获得最大化指数收敛率的采样控制器。这两类控制器可根据实际系统予以选取，并且可以通过仿真验证，得到最优更新周期与指数收敛率下的采样控制器。

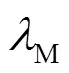
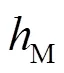
注1若考虑降低系统的硬件成本，减少控制器的计算负担，可预先设定指数收敛率，通过最大化更新周期来设计控制器。若考虑让系统频率偏差以最快的速度恢复到平衡点，可以根据信号传输信道的情况，预先设定更新周期的大小，通过最大化指数收敛率来设计控制器。

3 实例研究

通过对单区域、DFIG接入的两区域系统进行理论计算与仿真分析，验证本文所提方案的有效性和优越性。

3.1 单区域LFC仿真验证与性能分析

基于采样数据网络的单区域LFC模型如图3所示，其参数[22]如附录A中表A1所示，对其进行LFC控制器设计、性能分析与仿真验证。

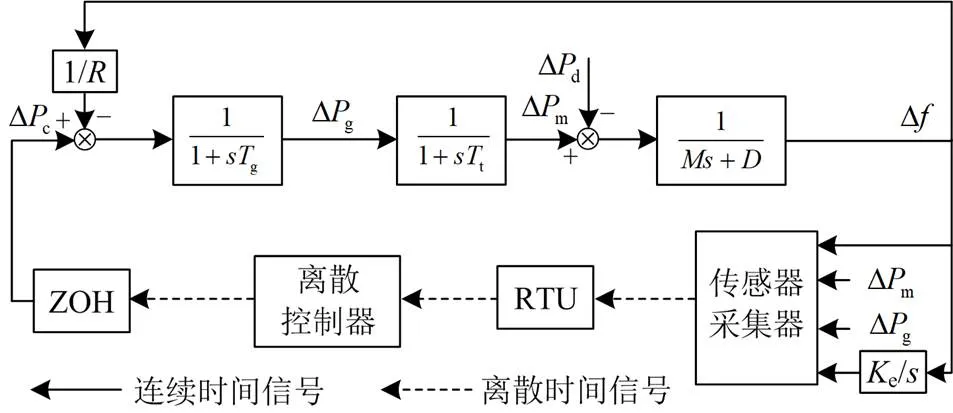
图3 单区域电力系统离散LFC模型

3.1.1控制器设计

表1 单区域LFC的控制器增益

3.1.2控制器性能分析与仿真验证

表2 不同控制器下系统能容忍的最大更新周期

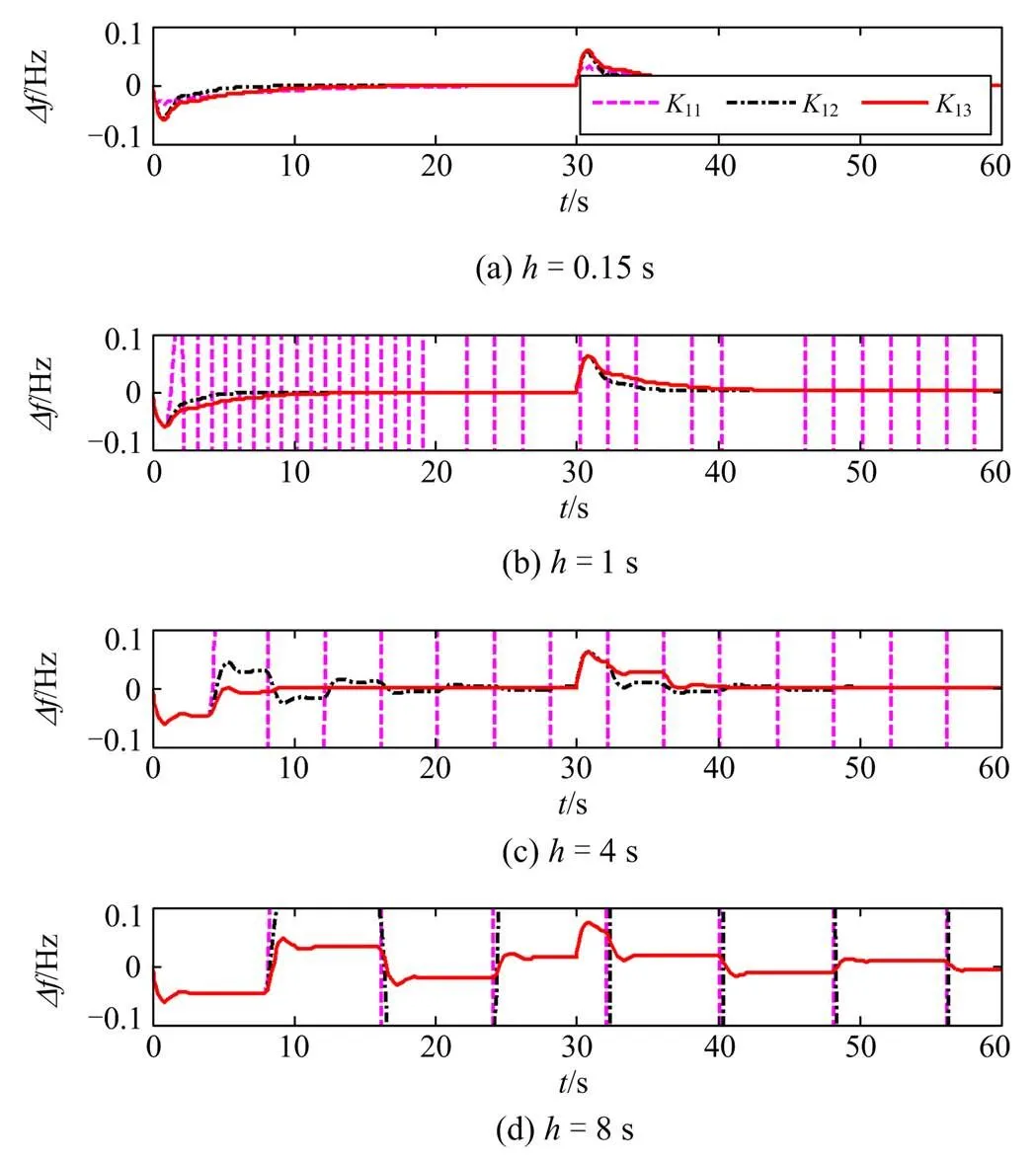
图4 不同h条件下的Df响应曲线

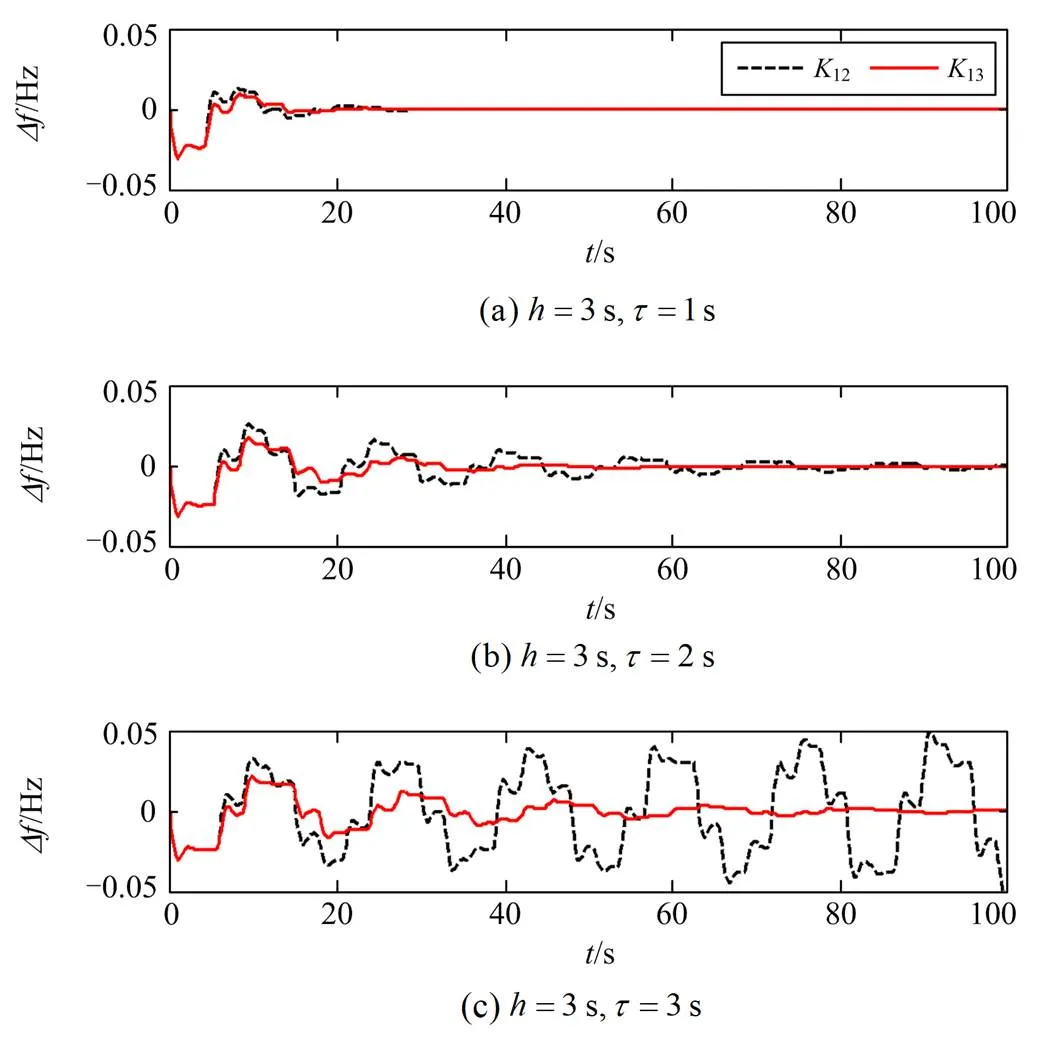
图5 不同t 条件下的Df响应曲线

3.2 两区域LFC仿真验证与性能分析

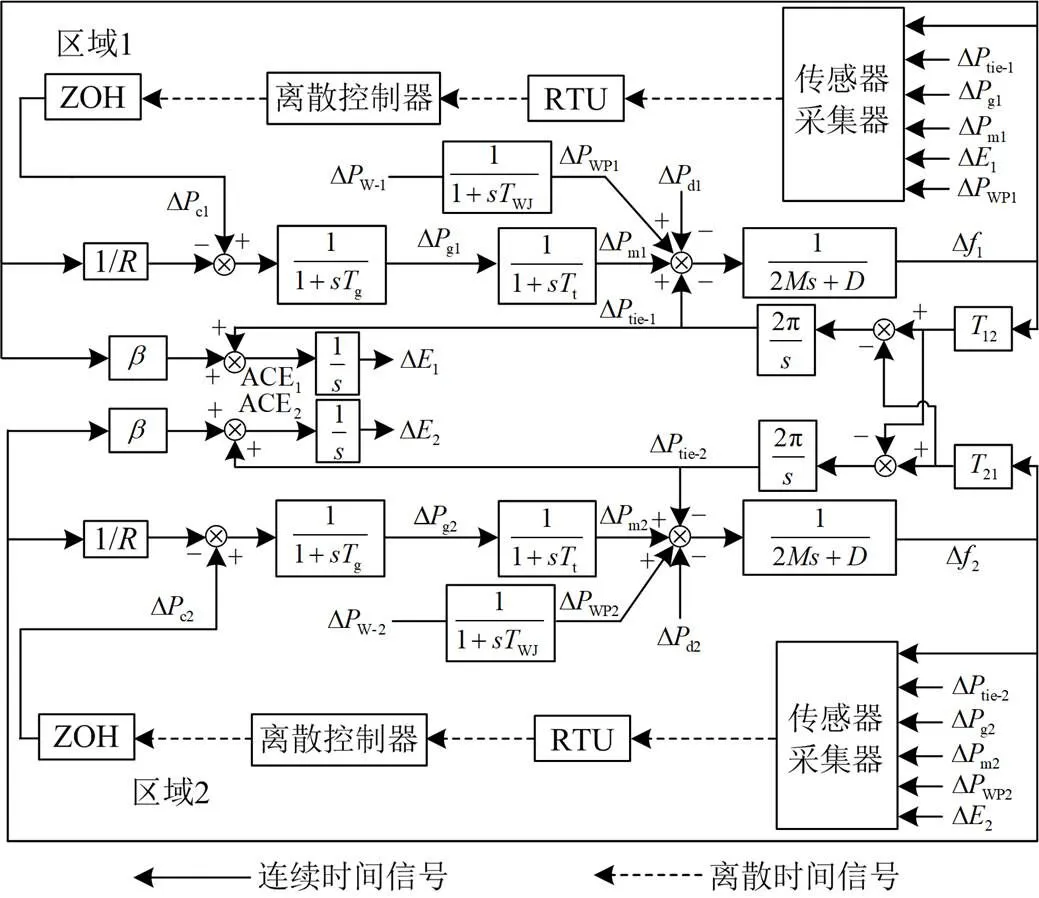
图6 含DFIG接入的两区域电力系统模型

3.2.1控制器设计

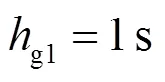
3.2.2控制器性能分析与仿真验证

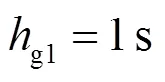
表3 不同给定条件下的负荷频率控制器参数

表4 K24和K28对不同 l 条件下的h上界

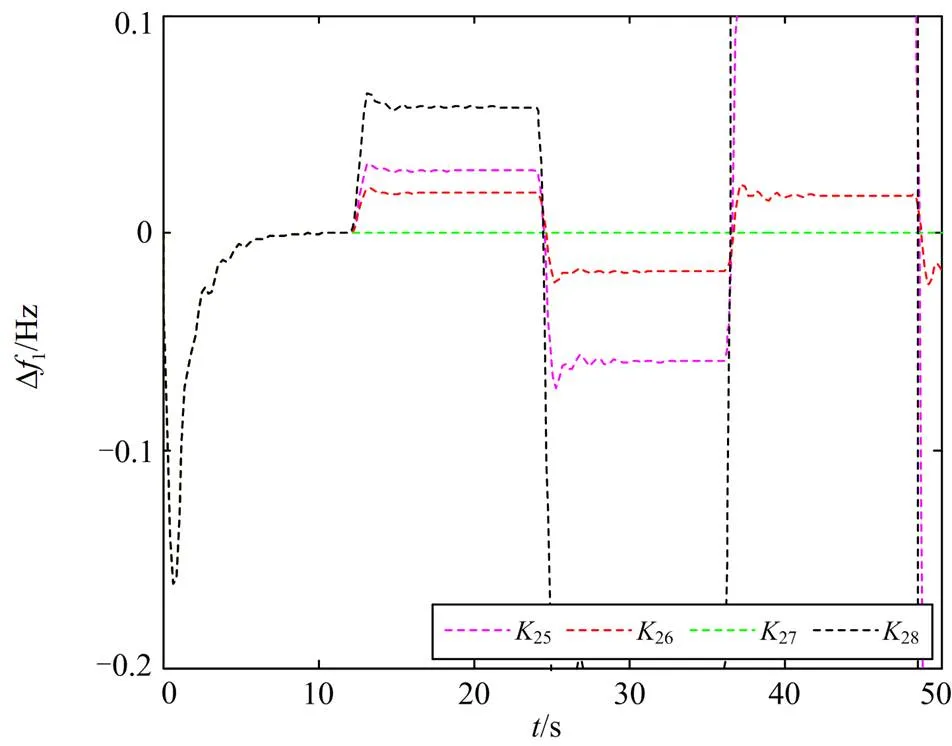
图7 h = 12 s条件下的Df1响应曲线(文献[22])

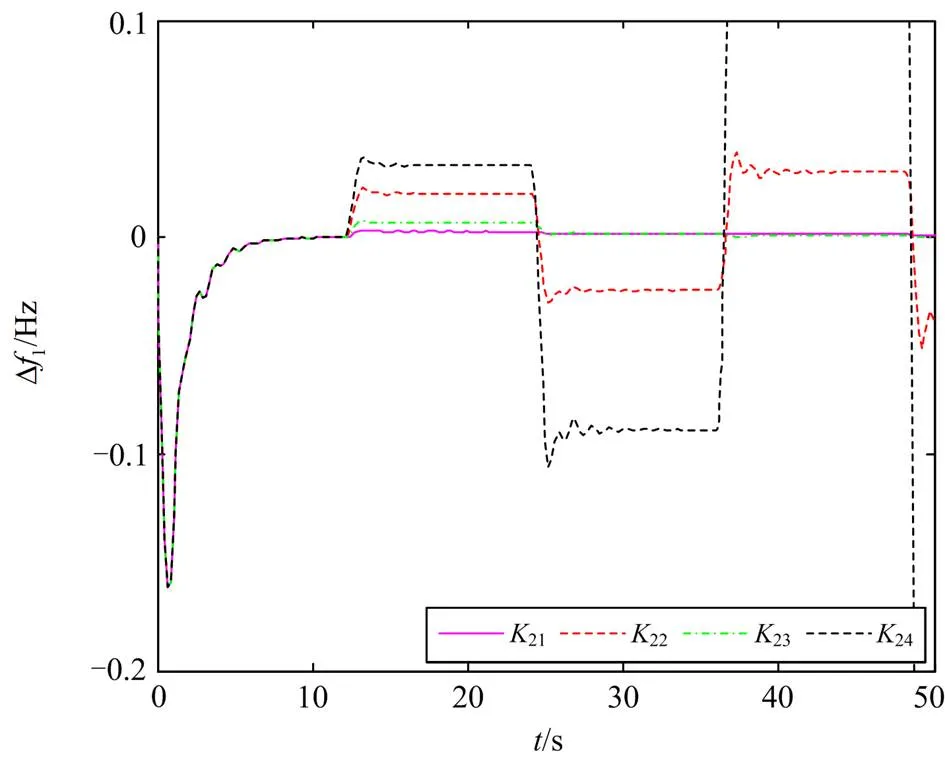
图8 h = 12 s条件下的Df1响应曲线(本文)

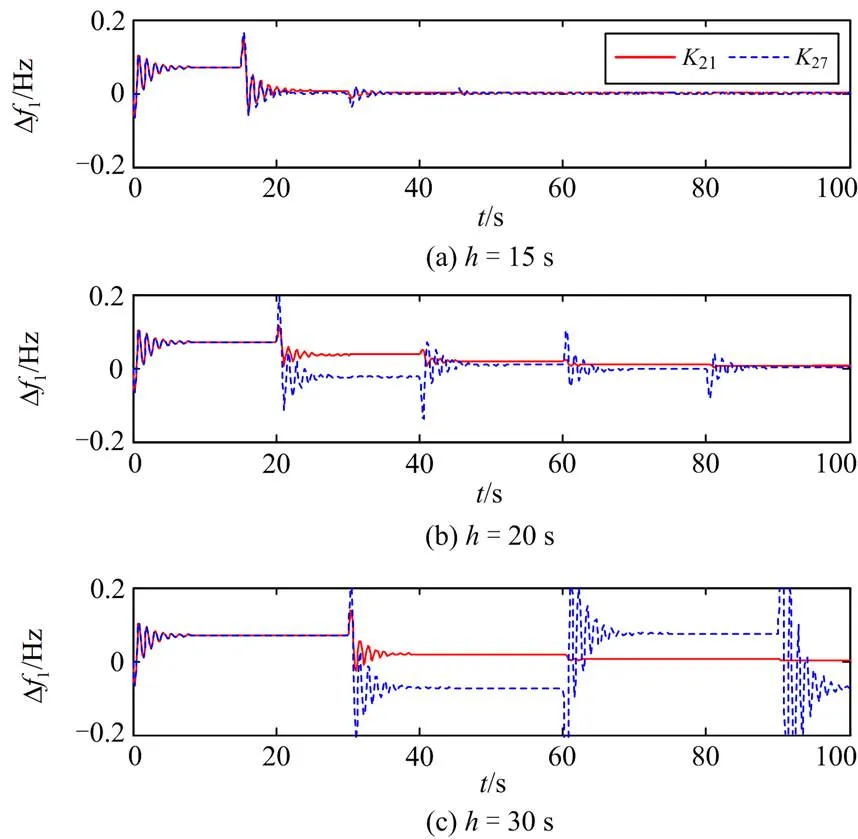
图9 不同h条件下的Df1响应曲线

图10 不同t 条件下的Df1响应曲线

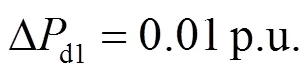
图11 DFIG功率偏差扰动

图12 不同h条件下的Df1响应曲线

图13 惯性常数不同减小比例下的响应曲线

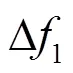
4 结语

本文主要针对DFIG接入电力系统导致系统惯性系数等参数变化，以及采用广域网络通信时，存在数据超时传输、数据丢包或错序等问题，提出了一种考虑控制信号更新周期变化的采样LFC方案。建立了基于采样数据网络的含DFIG的多区域电力系统模型，利用双边闭环型Lyapunov泛函和自由矩阵不等式，给出了系统的稳定性条件以及控制器设计方法。仿真结果表明，相比已有研究成果，所提方案具有更大的更新周期稳定裕度；对电力系统惯性系数等参数变化具有更好的鲁棒性，可进一步提升DFIG的渗透率；验证了采样控制方法在时滞电力系统LFC控制中的有效性。

附录A

表A1 单区域电力系统的参数

Table A1 Parameters of one-area power system

0.300.082.400.08300.1667

表A2 两区域电力系统的参数

Table A2 Parameters of two-area power systems

0.400.081.503.00.0150.16670.34840.20

表A3 惯性常数减少50%时控制区域的仿真参数

Table A3 Simulation parameters of two-area power system with 50% decrease of inertia constants

0.400.081.506.00.0150.08330.18160.20

[1] 付媛, 王毅, 张祥宇, 等. 变速风电机组的惯性与一次调频特性分析及综合控制[J]. 中国电机工程学报, 2014, 34(27): 4706-4716.

FU Yuan, WANG Yi, ZHANG Xiangyu, et al. Analysis and integrated control of inertia and primary frequency regulation for variable speed wind turbines[J]. Proceedings of the CSEE, 2014, 34(27): 4706-4716.

[2] 李东东, 孙雅茹, 徐波, 等. 考虑频率稳定的新能源高渗透率电力系统最小惯量与一次调频容量评估方法[J]. 电力系统保护与控制, 2021, 49(23): 54-61.

LI Dongdong, SUN Yaru, XU Bo, et al. Minimum inertia and primary frequency capacity assessment for a new energy high permeability power system considering frequency stability[J]. Power System Protection and Control, 2021, 49(23): 54-61.

[3] 李志军, 王硕, 张家安, 等. 基于变论域模糊逻辑的互联电力系统负荷频率控制[J]. 电力系统保护与控制, 2021, 49(16): 151-160.

LI Zhijun, WANG Shuo, ZHANG Jiaan, et al. Variable universe fuzzy logic-based load frequency control in an interconnected power system[J]. Power System Protection and Control, 2021, 49(16): 151-160.

[4] 张剑云, 李明节. 新能源高渗透的电力系统频率特性分析[J]. 中国电机工程学报, 2020, 40(11): 3498-3507.

ZHANG Jianyun, LI Mingjie. Analysis of the frequency characteristic of the power systems highly penetrated by new energy generation[J]. Proceedings of the CSEE, 2020, 40(11): 3498-3507.

[5] 张刘杰, 肖仕武, 黄松柏. 基于灵敏度的孤网动态频率偏移峰值分析和调速系统参数优化[J]. 电力系统保护与控制, 2020, 48(2): 137-143.

ZHANG Liujie, XIAO Shiwu, HUANG Songbai. Dynamic frequency offset peak analysis and speed control system parameter optimization of isolated network based on sensitivity[J]. Power System Protection and Control, 2020, 48(2): 137-143.

[6] YAN R, SAHA T K, BAI F, et al. The anatomy of the 2016 south Australia blackout: a catastrophic event in a high renewable network[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5374-5388.

[7] 徐波, 章林炜, 俞向栋, 等. 基于系统辨识的电力系统惯量在线评估改进方法[J]. 电力系统保护与控制, 2021, 49(18): 62-69.

XU Bo, ZHANG Linwei, YU Xiangdong, et al. An improved method of power system inertia online estimation based on system identification[J]. Power System Protection and Control, 2021, 49(18): 62-69．

[8] BEVRANI A H. Robust power system frequency control[M]. New York: Springer, 2014: 82-115.

[9] 赵熙临, 何晶晶, 付波, 等. 考虑双通道随机时延的区域互联电网AGC方法[J]. 电力系统保护与控制, 2018, 46(8): 50-57.

ZHAO Xilin, HE Jingjing, FU Bo, et al. An AGC method for interconnected power grid with two-channel random delays[J]. Power System Protection Control, 2018, 46(8): 50-57.

[10]YAN X G, SPURGEON S K, EDWARDS C. Global decentralized static output feedback sliding mode control for interconnected time-delay systems[J]. IET Control Theory and Applications, 2012, 6(2): 192-202.

[11]ZHANG C K, JIANG L, WU Q H, et al. Delay-dependent robust load frequency control for time delay power systems[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2192-2201.

[12]LIU X, ZHANG Y, LEE K Y. Coordinated distributed MPC for load frequency control of power system with wind farms[J]. IEEE Transactions on Industrial Electronics, 2017, 64 (6): 5140-5150.

[13]YU X, TOMSOVIC K. Application of linear matrix inequalities for load frequency control with communication delays[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1508-1515.

[14]JIANG L, YAO W, WU Q, et al. Delay-dependent stability for load frequency control with constant and time-varying delays[J]. IEEE Transactions on Power Systems, 2012, 27(2): 932-941.

[15]米阳, 伦雪莹, 孟凡斌, 等. 基于无模型算法和电动汽车辅助调节的新能源电力系统频率协调控制[J]. 电力系统保护与控制, 2021, 49(24): 13-20.

MI Yang, LUN Xueying, MENG Fanbin, et al. Frequency coordinated control of a new energy power system based on a model-free algorithm and EV auxiliary regulation[J]. Power System Protection and Control, 2021, 49(24): 13-20.

[16] MI Y, HAO X, LIU Y, et al. Sliding mode load frequency control for multi-area time-delay power system with wind power integration[J]. IET Generation, Transmission, Distribution, 2017, 11(18): 4644-53.

[17] CUI Y, XU L, FEI M, et al. Observer based robust integral sliding mode load frequency control for wind power systems[J]. Control Engineering Practice, 2017, 65(17): 1-10.

[18]ZHANG Y, YUE D. Digital PID based load frequency control through open communication networks[J]. IEEE Control Decision Conference, 2015, 67: 6243-6248.

[19] WEN S, YU X, ZENG Z, et al. Event-triggering load frequency control for multiarea power systems with communication delays[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1308-1317.

[20] DONG L, TANG Y, HE H, et al. An event-triggered approach for load frequency control wit supplementary ADP[J]. IEEE Transactions on Power Systems, 2017, 32(1): 581-589.

[21]周一辰, 覃露, 李永刚. 基于多求和不等式输出反馈Lyapunov 判据的时变时滞电力系统二次调频控制[J]. 电网技术, 2021, 45(8): 3247-3258.

ZHOU Yichen, QIN Lu, LI Yonggang. Secondary frequency modulation control of power with time-delay based on Lyapunov criterion of multi-summation inequality output feedback[J]. Power System Technology, 2021, 45(8): 3247-3258.

[22]SHANGGUAN X C, He Y, ZHANG C K, et al. Sampled-data based discrete and fast load frequency control for power systems with wind[J]. Applied Energy, 2020, 59(2): 114-202.

[23]ZHANG C K, JIANG L, WU Q, et al. Further results on delay dependent stability of multi-area load frequency control[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4465 -4474.

[24]SEURT A, FRIDAM E, RICHARD J P. Sampled-data exponential stabilization of neutral systems with input and state delays[J]. Proceeding of the IEEE Mediterrean Conference, 2005, 70: 1281-1285.

[25]张传科. 时滞电力系统的小扰动稳定分析与负荷频率控制[D]. 长沙: 中南大学, 2013.

[26]NGUYENN, MITRAJ. An analysis of the effects and dependency of wind power penetration on system frequency regulation[J]. IEEE Transactions on Sustainable Energy, 2016, 22(37): 354-363.

[27] MAGDY G, SHABIB G, ELBASET A A, et al. Optimized coordinated control of LFC and SEMS to enhance frequency stability of real multi-source power system considering high renewable energy penetration[J]. Protection and Control of Modern Power Systems, 2018, 3(4): 407-421.

Sampling load frequency control of power systems with doubly-fed wind power

LI Mofa1, 2, ZHANG Zhiwen1, LIAN Honghai2, HU Sijia1

(1. School of Electric and Information Engineering, Hunan University, Changsha 410082, China; 2. School of Wind Energy Engineering, Hunan Electrical College of Technology, Xiangtan 411101, China)

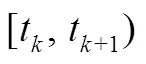
doubly-fed wind power; load frequency control; sampling period; Lyapunov function; controller design

10.19783/j.cnki.pspc.220406

国家自然科学基金项目资助(52061130217)；湖南省科技重大专项资助(2020GK1013)；湖南省教育厅科学研究项目资助(19C0417，20C0425，22B0955)

This work is supported by the National Natural Science Foundation of China (No. 52061130217).

2022-03-24；

2022-06-19

李谟发(1986—)，男，博士研究生，工程师，研究方向为分布式电源接入电网的故障特性分析、保护以及频率稳定性等；E-mail: limofa@126.com

张志文(1963—)，男，通信作者，博士，教授，博士生导师，研究方向为交直流电能变换系统理论与新技术、新型电气装备自动化与控制技术、电力系统谐波抑制、现代电力电子技术及应用等。E-mail: hdzzw@126.com

(编辑 魏小丽)