一种基于MOSA 的低轨卫星星座多波束分配策略

章可钦，林宝军，，5，董明佶，刘迎春2，，李 锐2，

（1.中国科学院空天信息创新研究院，北京 100094；2.中国科学院大学电子电气与通信工程学院，北京 100049；3.中国科学院微小卫星创新研究院，上海 201210；4.上海微小卫星工程中心，上海 201210；5.上海科技大学信息科学与技术学院，上海 201210）

基于LEO 卫星星座的宽带卫星通信系统具备卫星数量多、全球覆盖率高、发射成本低、通信时延小等特点，可为全球用户提供宽带互联网接入，逐渐发展为5G 乃至6G 技术体系中实现全球覆盖的重要解决方案，成为继GEO 宽带卫星之后的研究热点，世界各国的航天业界争相发展LEO 星座互联网技术[1-2]。随着空间宽带卫星通信技术的不断发展，为了提高卫星频谱资源利用率，LEO 宽带卫星系统大都采用多点波束来增加系统容量，如Starlink、OneWeb、Telesat等，其卫星均采用了多点波束，单星设计容量最大超过20 Gbit/s[3]。

针对多波束卫星通信系统中波束分配的问题，国内外研究机构及学者进行了诸多研究，优化内容主要包括单颗卫星波束资源的信道分配方法研究[4-5]、卫星固定波束重叠区切换策略研究[6-7]以及卫星间重叠区波束分配策略研究[8-9]等。随着LEO 宽带卫星星座用户数量和通信容量需求的不断增加，单颗卫星搭载的点波束数量以及地面固定波束体制难以满足大量用户同时接入的要求，航天业界通过增加卫星数量来提高系统容量和对地面用户的覆盖率[10]，因此如何高效合理地分配多卫星同时覆盖情况下的波束资源，提高整个星座通信接入性能成为现如今多点波束分配亟待解决的问题之一。

围绕上述问题，对多卫星多波束分配策略进行了研究，在地面用户小区由多颗卫星同时覆盖条件下，以地面用户接入容量需求和端到端时延最小化为优化目标，建立多目标优化的数学模型，改进模拟退火算法。利用该启发式算法的稳定收敛特性，改善其收敛效率，得到优化的多卫星多波束分配方案。

1 多卫星多波束分配策略

1.1 波束可接入边界条件确立

在研究多卫星多波束分配问题时，首先需确立地面用户接入至LEO 卫星星座的条件。对于地面固定波束体制，地面用户不会面临由于LEO 卫星高速移动而必须切换波束的问题，但其是否具备接入条件仍然同时受到卫星可用波束数量、单波束最大发射功率、最大通信距离、波束覆盖角度范围等因素的约束[11]，只有满足全部接入条件的地面用户才可认为能够接入到相应卫星。

由于低轨卫星相对于地面用户位移速率较快，为了便于分析，将卫星对用户的连续覆盖时间进行离散化，分割为多个时间片，在每个时间片内任意时间点均满足接入条件的用户和波束才被认为可接入。对所有待接入用户依次确立与每颗卫星各波束之间的接入特性，由此得到可接入矩阵L=[lij]，其中i=1,2,3,…,n；j=1,2,3,…,m。n为最大待接入用户数，m为全部用户可见卫星的波束数量之和，可接入矩阵元素定义为：

经过时间分片处理后，假设用户{ui},i=1,2,3,…,M，在某时间片内均在卫星{sj},j=1,2,3,…,N的视场覆盖范围中，每颗卫星有b0波束，每波束可提供的信道容量为xMbps，每个用户通信容量需求为yiMbps，则用户所需的接入波束数量bi为：

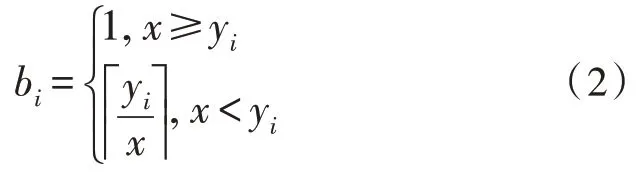
1.2 优化目标

低轨通信卫星网络的拓扑设计既要满足用户对突发大容量数据传输的需求，又要尽可能降低信息交互的时延，因此通信容量和端到端时延是衡量系统拓扑结构的关键性能指标之一[12]。对此，建立了以满足用户通信容量需求和最优端到端时延为优化目标的数学模型，作为设计多卫星对多用户的优化波束分配方案的稳态表征。

在低轨通信网络中，用户i的通信传播时延Di分为两部分，其所接入卫星j与地面关口站的时延f1和用户与卫星空间距离产生的时延f2。假设共有N颗可接入卫星，它们提供的可用波束数量为s={bj|j=1,2,3,…,N}；以及M个用户的波束接入需求为U={ui|0 ≤ui≤b0,i=1,2,3,…,M}，且它们满足可接入边界条件。在满足用户通信容量需求的约束下，针对波束分配方案x，对用户群U的总通信时延D可以描述为：

其中，优化问题(3)为以优化目标集合D尽可能取得最小值的多目标优化问题，其最优解集合称为Pareto 解集。约束函数(4)中第一个约束条件g1(x)＞0为了保证用户群U中每一位用户都能有足够的波束可接入，第二个约束条件g2(x)＞0 为了保证每颗卫星同时负载量不超过最大负载。

考虑到实际场景中各待接入用户的优先级不同，为了使分配方案更为合理化，将问题采用对不同优先级用户进行不同比例的加权和y(x)作为衡量标准更加符合实际情况：

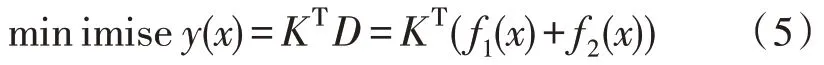
其中，K={kj|j=1,2,3,…,M} 为各用户的权重。

考虑到波束分配优化问题是一个离散多目标约束问题，可采用改进的多目标模拟退火算法来取得约束问题的最优解[13]。

2 基于MOSA的波束分配优化算法

2.1 算法流程

根据约束条件(4)随机设置初始分配方案x(0)，同时设置初始温度t0和用户优先级权重K，由(5)计算初始时延y(0)。外循环中，由初始温度t0逐渐减小至最低温度tmin过程为外循环迭代过程，由预设的温度下降表T决定。内循环中，通过随机扰动产生新分配方案x＇，由Metropolis 准则接受新状态，直到满足内循环终止条件[14]。内循环终止后，判断是否满足外循环终止条件，若不满足，则按照温度下降表T降低温度继续进行外循环，直至满足外循环终止条件，输出最优分配方案和最低时延。具体算法流程图如图1 所示。

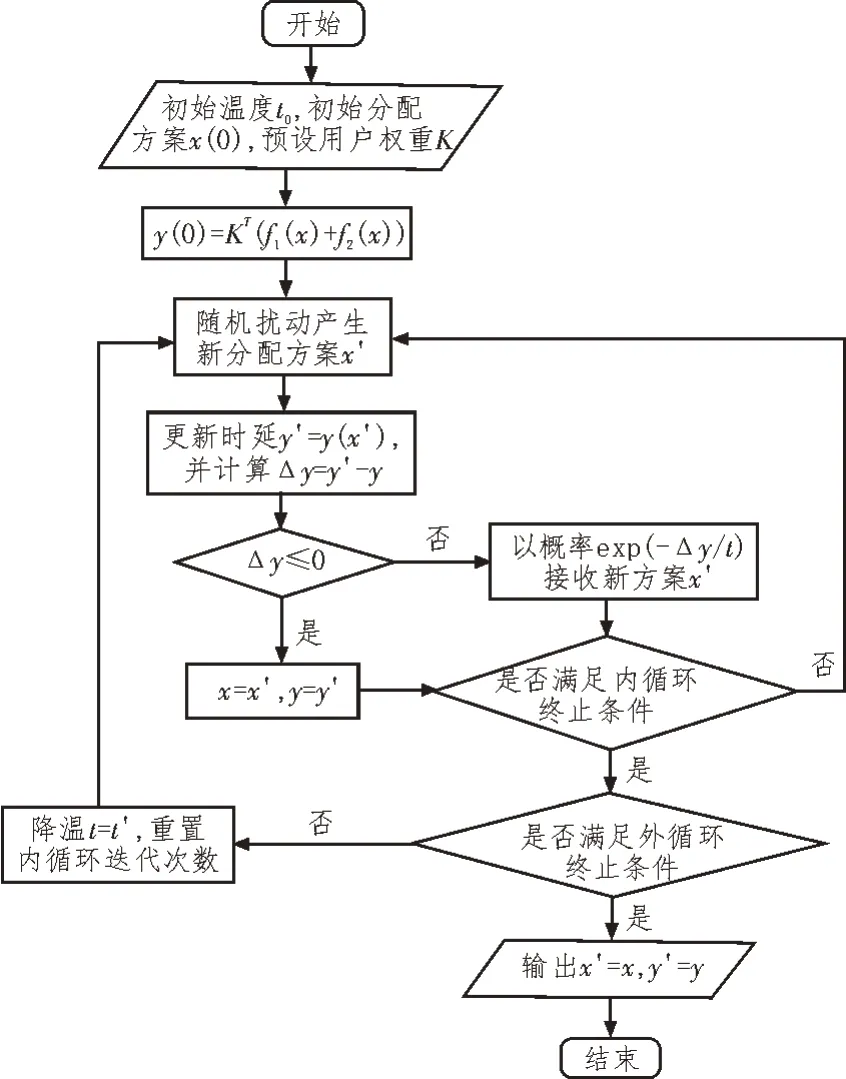
图1 基于MOSA的波束分配优化算法流程图

2.2 算法改进与参数优化

对于算法初始温度t0，其取值越大得到高质量解的几率越大，同时计算时间增加，折衷考虑优化质量和优化效率，算法中采用的方案为：均匀抽样一组状态，以各状态的目标函数y(x)的方差作为初始温度t0；温度下降表T，即温度更新函数，常用的退温函数为指数退温，tk=λtk-1，其中0 ＜λ＜1，该算法中退温指数选择为0.99；状态产生函数，假设随机撤销n个用户Un的链接，在满足约束条件(4)的同时重新进行随机分配，产生新的分配方案x。经过实验发现，n取1 的实验结果收敛性表现最稳定。

MOSA 算法循环终止条件分为内循环终止条件和外循环终止条件，其中内循环终止条件设置为内循环迭代次数阈值lmax，实际中每个温度下可能产生的候选解最多有(Nb) !/b!个，显然在实际应用中很难完全遍历。实验表明，在温度高的时候选择较低的搜索次数，对结果影响很小，但能大幅降低计算时间。该实验中采用指数递增方式，lk+1=ηlk，其中η＞1；对于外循环终止条件，根据反复实验结果，设置足够长的外循环阈值，随着温度降低到一定值后，计算机计算概率在数值上为0，此时的温度t即可作为最低温tmin。

为了进一步提高算法效率和质量，该算法对MOSA 进行了如下改进：内外循环中，当目标函数值保持一定次数不变时，则可认为此时MC(Markov Chain)接近稳态，可提前终止循环，显著提高了算法效率。由于在任意温度下，实际算法均不可能遍历所有候选解，因此在随机游走的过程中，最终输出结果可能从最优解游走到次优解，所以采用带记忆的方法来提高算法结果的质量，即在温度降低过程中，随时更新并保存目标函数得到的最优解，以此来代替循环结束时的输出值，有效提高了算法质量。

3 仿真分析

3.1 仿真环境与参数设置

针对多卫星多波束分配策略优化问题，建立了基于Walker(1440/30/1)的低轨卫星星座[15]，轨道高度为550 km，轨道倾角为55°，如图2 所示。

图2 基于Walker(1440/30/1)星座的低轨卫星星座仿真模型

在美国东部地区共设置49 个地面用户，各地面用户均可被10 颗卫星同时覆盖，地面关口站位于北京，设每颗卫星搭载16 个收发波束，每个用户根据容量需求随机设置需接入1～3 波束，优先级分为三级，如表1 所示。由此可知N=10,M=49,b0=16,Ki∈{1,2,3},i=1,2,3,…,M。算法参数设置：温度下降指数λ=0.99，外循环迭代次数阈值L1=450，内循环l0=10,η=1 500(1450),lk+1=。内外循环均设置为最大循环次数的0.4，最优解保持不变则终止循环。

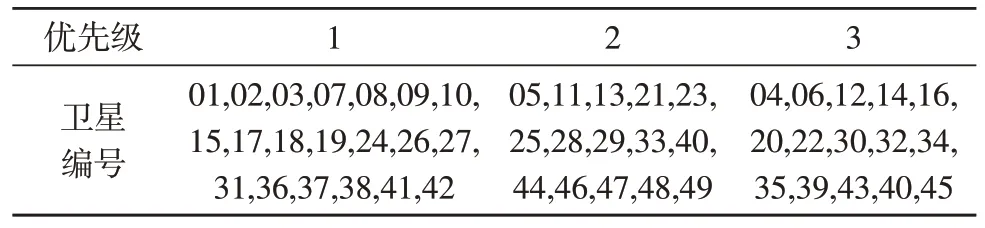
表1 地面用户优先级分配方案

3.2 仿真结果分析

经改进的MOSA 算法优化后，49 个地面用户接入低轨星座的波束分配算法收敛特性如图3 所示。图中实线为温度降低过程中，目标函数y(x)在每个温度下内循环终止时的函数值曲线，该曲线呈振荡收敛趋势，符合MOSA 算法以概率收敛的特征[16]；虚线为加入记忆后的目标函数随温度下降的最小值曲线，有效避免了最优解的丢失情况。收敛后在满足用户容量需求的基础上，低轨星座至地面关口站的加权通信时延由初始状态的6.07 s 降低至5.76 s，其时延性能有显著提升。

图3 基于MOSA算法的LEO卫星网络波束分配算法的加权时延收敛特性图

图4 对比了49 个地面用户在算法优化前后的通信时延情况，每个用户均可根据优先级接入，优化前后通信时延降低约4.1%～20.6%，平均时延较少3.09 ms，其中优先级从高到低的用户平均时延减少量依次为4.82 ms，3.54 ms，1.22 ms。可知算法能够在满足待接入用户通信容量需求的基础上，有效降低用户的通信时延，其中优先级最高的用户优化效果最佳，从而提高用户的总体通信性能。

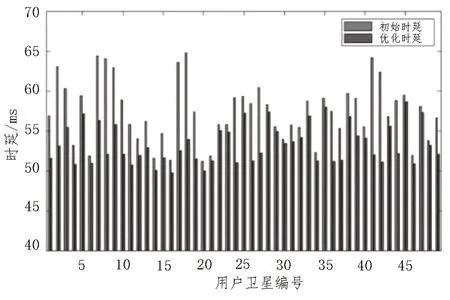
图4 优化前后各用户至关口站通信时延对比

表2 为固定用户需求U和用户优先级表征向量K后，重复多次实验，得到的加权时延。由于该实验中候选解总数达到10100量级，且次优解与最优解之间数值差异极小，因此在迭代次数有限的条件下，难以得到稳定的最优解，得到的次优解仍然可以作为有效解。多次实验结果差异都在微秒级，方差为2.33×10-5，既体现了MOSA 算法对初始状态的不敏感性，也验证了MOSA 算法应用在该问题中的可行性，体现了较好的收敛性质。

表2 多次独立重复实验最优分配方案的加权时延

4 结论

针对地面用户小区由多颗卫星同时覆盖条件下的多卫星多波束分配问题，以地面用户接入容量需求和用户至地面关口站时延最小化为优化目标对多卫星多波束的分配策略展开了分析与研究，采用地面固定波束体制，利用改进的多目标模拟退火算法对多卫星多波束分配方法进行了优化。由于模拟退火算法具有稳定的收敛特性，考虑实际在多目标优化问题中的优先级不同，按相应权重进行线性变换，最终在其Pareto 解集中搜索出具体有效的分配方案，使得多卫星多波束分配问题得到了一个有效的优化解。优化结果表明：改进的MOSA 算法具有良好的收敛特性，优化后的波束分配策略能够在保证待接入用户通信容量需求的基础上有效降低各优先级用户的信息回传时延，从而提高波束分配效率和多卫星覆盖情况下接入用户的通信性能。