重组竹制备过程中温度场变化规律与预测模型

2023-02-09田心池于文吉马红霞林秋琴薛勃杨春梅

林业工程学报 2023年1期

田心池,于文吉,,马红霞,林秋琴,薛勃,杨春梅*

(1.东北林业大学机电工程学院，哈尔滨 150040；2.中国林业科学研究院木材工业研究所，北京 100091；3.广东省林业科学院森林工业研究所，广州 510520)

在重组竹热压过程中，板坯内部的温度场变化与板坯的幅面存在密切关系。根据实际生产经验与相关研究[1-3]，当板材幅面逐渐增大时，由于边界气流通道变长，板材内部的过热蒸汽无法顺利排出，造成板材内部蒸汽压力过大，使得生产过程中具有因“爆板”而产生产能浪费的隐患。为了防止出现“爆板”，实际生产中又会使得通水时间过长，导致再次加热时产生更多能耗。因此，研究幅面对重组竹热压传热的影响具有一定的科学价值和现实意义；同时，由于实验压机与生产压机幅面的差异性，利用实验数据对实际生产中的板材热压传热建立预测模型，对于优化热压工艺，进而减少在实际生产中的热压耗能具有重要意义。

1 材料与方法

1.1 试验材料

纤维化毛竹(Phyllostachyspubescens)单板，购自安徽竹迹新材料科技有限公司，尺寸为200 cm(长)×10 cm(宽)×0.8 cm(厚)，气干密度约0.46 g/cm3，平均相对含水率9.8%。酚醛树脂胶黏剂，购自太尔胶黏剂(广东)有限公司，稀释后的固含量为21%，黏度0.188 Pa·s，pH为10.22。

1.2 仪器设备

小型试验热压机(SDR60*60-20/1.5型，青岛国森)；多路温度巡检仪(JK24UC型，常州金科)，测温范围-100～1 000 ℃，测温精度0.2 ℃，设置温度记录时间为2 s；电热鼓风干燥箱(101-4AB型，常州凯航仪器有限公司)。

1.3 试验方法

由于铺装过程中会在竹束纤维横向边界处放置厚度规，厚度规阻挡了热流与过热蒸汽沿纤维横向的流动，因此认为过热蒸汽流只沿纤维纵向传导。

1)浸胶、干燥：将竹束浸于固含量为21%的酚醛树脂中，浸胶时间10 min，施胶量15%，之后进行二次干燥至含水率为10%。

2)铺装、组坯：干燥后的竹束在模具中按顺纹组坯、铺装，铺装幅面为L(长度)×45 cm，其中，L=10，20，30，40，50，60 cm。铺装层数为6层，将热电偶的测温点放置在表层、底层和芯层竹束靠近中心的位置，共3根热电偶，放置方式如图1所示。

图1 热电偶的放置Fig.1 Layout of thermocouples

3)热压成型：采用“冷进冷出”热压工艺，将板坯送入设定温度140 ℃的热压机中，加压至完全闭合，板坯总体尺寸为L×45 cm×1.8 cm，每隔2 s对各层热电偶温度进行一次记录。热压压力20 MPa，芯层升温至130 ℃后保压10 min，然后通水冷却到芯层温度低于60 ℃后卸板。每种幅面板材6次重复，共36组试验。

2 结果与分析

参考前人的研究结果[4-6]，将竹基纤维复合材料芯层热压曲线分为4个阶段：短暂恒温段、快速升温段、保压升温段、通水冷却段，将短暂恒温段和快速升温段统称为升温段。通过对各段指标的影响来判断幅面对热压传热的影响规律。

2.1 热压幅面对升温段的影响

当芯层温度变化在±0.3 ℃以内时，认为温度曲线处在恒温段；当芯层温度到达130 ℃时，认为到达指定温度，升温段结束。本研究得到不同纵向铺装长度下的恒温时间与芯层升温时间对比结果如图2所示。不同铺装幅面的升温时间方差分析如表1所示。

图2 纵向铺装长度对恒温时间和升温时间的影响Fig.2 Effects of longitudinal pavement length on constant temperature time and heating time

由表1可得，铺装幅面对芯层的升温时间具有极强的显著性，幅面对芯层升温的影响极显著(P<0.001)。由图2可以看出，随着纵向铺装长度的增大，恒温段的持续时间与升温时间都呈现增大趋势，主要有以下2个原因：①热压时由于纤维纵向存在孔隙的影响，当热量传导至边界位置时会沿孔隙流失，因此当幅面较大时，热量会在传导到芯部后继续向中心层平面的其他低温区域传导，当中心层各点温度均达到中心位置温度时，芯部完成向平面内其他位置的热量补偿后才能继续升温，所以幅面越大，恒温段时间越长。②升温段同理，由于中心位置和边界位置受热力学边界条件的影响不同，根据热力学第二定律，当热量到达中心层后，会继续向平面中其他低温位置传导。因此，幅面越大芯层的恒温时间越长，升温越慢。以130 ℃为基准，不同纵向铺装长度下的芯层升温速率对比如表2所示。由表2同样可以得到，幅面越大时，热量需要传导的位置越多，芯层的升温速率越小。

表1 不同铺装幅面的升温时间方差分析Table 1 Variance analysis of heating time of different pavement widths

表2 不同纵向铺装长度下升温速率与升温时间Table 2 Heating rates and heating times of different longitudinal pavement lengths

2.2 热压幅面对“锅炉效应”的影响

在保压阶段会出现中间各层的温度高于上下表面温度的现象，这是由于热压会使芯层的自由水受热汽化为水蒸气，并随蒸汽温度的升高，由饱和状态转化为过热状态[7]。同时，因在高压缩状态下导致的边界气流通道减小，板坯内部的蒸汽无法排出[8-10]，于是在板坯内部的过热蒸汽循环形成了一个小型的“蒸汽锅炉”，水分汽化产生的热量不断增多，压力不断增大，芯层的升温峰值增大。将该现象命名为热压过程中的“锅炉效应”。

为了验证幅面对“锅炉效应”的影响，选择“锅炉效应”的持续时间tc和芯层升温的最高温度Tmax作为因变量，当中间层温度超越T1时，“锅炉效应”产生。T1为板材表面温度Ttop与底面温度Tlower的最小值，即T1=min{Ttop，Tlower}。当芯层温度回落到T1时，“锅炉效应”结束。纵向铺装长度对tc、Tmax的影响见图3，铺装幅面对“锅炉效应”影响的方差分析结果见表3。

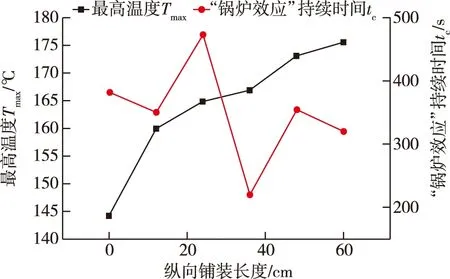
图3 纵向铺装长度对“锅炉效应”的影响对比Fig.3 Comparison of influences of longitudinal pavement lengths on “boiler effect”

表3 铺装幅面对“锅炉效应”影响的方差分析Table 3 Variance analysis of the influence of pavement width on “boiler effect”

由表3可知，铺装幅面对“锅炉效应”的持续时间并无显著的统计学差异，但对芯层最高温度具有极显著的影响；同时由图3可以看出，最高温度随着铺装幅面的增加呈现波动式的上升趋势。这可能有3个原因：①在保压过程中板材内部产生膜态沸腾的区域具有不确定性，在边界气流通道较短的情况下会使得过热蒸汽沿气流通道流出，一定程度上削弱了板坯芯层沸腾气泡的覆盖范围；②由于边界条件的差异，在小幅面热压过程中，压机保压段不再加热时，板坯表面的热量可能从热压板未接触板坯部分流出，一定程度上促进了板坯的冷却；③随着幅面的增大，边界气流通道变长，板坯内部的过热蒸汽范围不断扩大，膜态沸腾的程度更加剧烈，进而对芯层产生更加强大的加热效果。因此，随着幅面增大，板坯芯层的最高温度会持续增大。

2.3 热压幅面对降温的影响

根据工艺要求，通水冷却后，当芯板温度降到60 ℃时才可卸板。以通水时间为起点，当芯板温度达到60 ℃时即压板结束，其中持续时间td为降温时间。纵向铺装长度对降温时间的影响对比见图4，铺装幅面对降温时间影响的方差分析见表4。

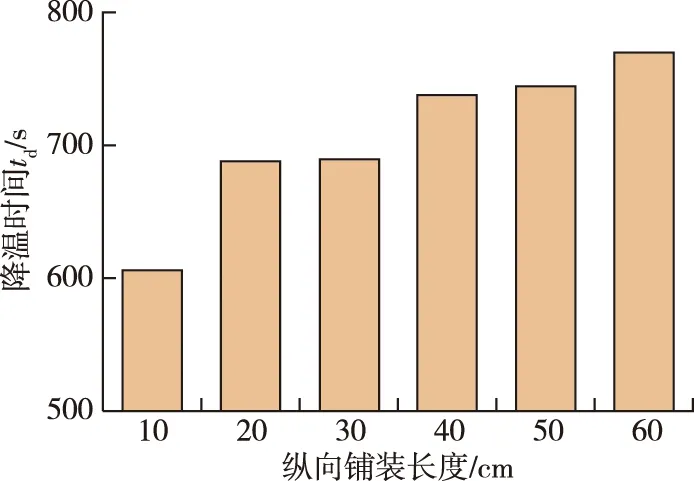
图4 纵向铺装长度对降温时间的影响对比Fig.4 Comparison of influences of longitudinal pavement lengths on cooling time

表4 铺装幅面对降温时间的影响方差分析Table 4 Variance analysis of influence of pavement width on cooling time

根据表4可以得出，铺装幅面对降温时间有极显著影响；通过图4可以看出，降温时间随铺装幅面的增加呈现波动式上升的状态，铺装幅面越大，降温时间越长。这主要有3个原因：①随着铺装幅面的增大，芯层的“锅炉效应”逐渐加剧，膜态沸腾程度更高，芯层的最高温度逐渐递增，其降温的温差范围逐渐增大；②幅面较大时，由于产生膜态沸腾的范围较大，降温需要消耗一定的热量溶解膜态沸腾的边界薄膜，无法直接对芯部进行冷却，因此，降温时间得到了延长；③边界条件促进降温，当幅面较小时，上下压板未与板坯接触的部分快速冷却，与板面接触部分的热量会沿热压板方向流向低温区域，一定程度上促进了冷却效率的提升。

3 预测模型

科学的预测在近年来被广泛应用于林业行业的各个方向[11-13]。在本研究中，由于试验样本较少，样本指标规律性并不显著，含水率、孔隙率、密度等其他因素的影响并不明确，因此采用灰色预测模型GM(1.1)对实际生产的铺装幅面热压规律进行预测，其预测流程如图5所示。灰色预测因其适用于样本少、数据少的研究对象而在近几年被广泛使用[14-16]。

图5 灰色预测流程Fig.5 Grey prediction flow

3.1 模型的建立

3.1.1 指标选择

针对幅面对热压过程各种指标的影响[17]，选择具有一定规律及显著性的指标进行预测，同时根据预测结果绘制出纵向铺装长度200 cm的大幅面板材的芯层升温曲线。选择恒温时间tk、升温时间tr、升温速率vr、最高温度Tmax、降温时间td、热压周期tl6个指标分别进行预测，并基于这些指标得出大幅面板材的芯层升温曲线。

3.1.2 灰色预测模型的建立

1)取L=10～60 cm的纵向铺装长度对应指标建立原始序列，记为：

x(0)=[x(0)(1),x(0)(2),…,x(0)(n)]

(1)

为了弱化原始序列的随机性和波动性，为预测模型提供更加有效的信息，对序列x(0)进行一次累加生成的处理方式，记生成序列为：

x(1)=[x(1)(1),x(1)(2),x(1)(3)，…,x(1)(n)]=

[x(0)(1),x(0)(1)+x(0)(2),…,x(0)(1)+x(0)(2)+…+x(0)(n)]

(2)

2)灰色预测模型是由一个包含单变量的一阶微分方程构成的动态模型：

(3)

对x(1)作紧邻均值生成序列z(1)，即z(1)(k)=0.5[x(1)(k)-x(1)(k-1)],得到：

z(1)(k)=[z(1)(1),z(1)(2),…,z(1)(n)](k=2,3,…,n)

式(3)的白化方程为：

(4)

式中：a为发展系数，其有效区间是(-2，2)；b为内生控制灰数；t为连续化的热压序列次数。应用最小二乘法对参数列a的估计量求解可得：

(5)

3)确定灰色预测模型的响应序列：

(6)

4)求出x(1)的模拟值：

(7)

5)将模拟值还原：

(8)

6)误差检验，为确保所建灰色模型有较高的预测精度和可信程度，需要进行残差检验及后验差检验，主要方法如下。

(9)

(10)

(11)

(12)

(13)

(14)

(15)

C=s2/s1

(16)

(17)

根据灰色系统理论，通常e(0)(k)、Δk、C越小，P越大，则模型精度越好。当发展系数a∈[-0.3,2)时，则GM(1,1)模型的一步预测精度在98%以上，且预测精度都在97%以上，可用于中长期预测。灰色理论模型精度检验见表5[18]。

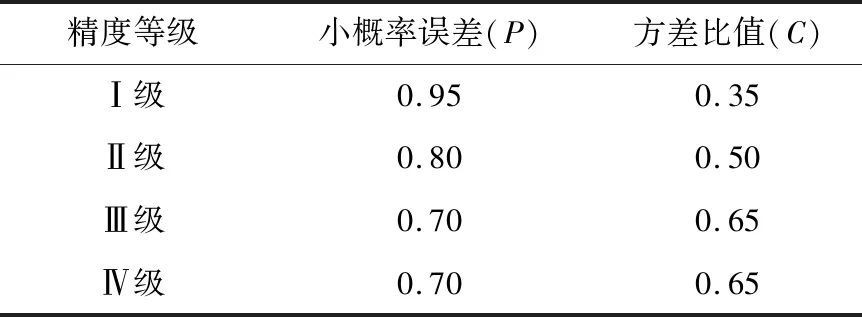
表5 灰色系统理论精度检验Table 5 Accuracy tests of grey system theory

当发展系数a∈(-2,2)时才能保证模型的有效性，不同的a可进行不同情况的预测：当-a≤0.3时，模型可用于中长期预测；当0.3<-a≤0.5时，模型可用于短期预测，中长期预测慎用；当0.5<-a≤1时，模型作短期预测应十分谨慎；当-a>1时，不宜采用GM(1,1)模型。

3.2 模型的求解

3.2.1 升温段预测模型的求解

基于预测模型，得到L=70～200 cm纵向铺装长度的重组竹板材热压恒温时间和升温时间，如图6所示。

图6 纵向铺装长度对升温曲线的预测结果Fig.6 Prediction results of longitudinal pavement lengths on temperature rise curve

由图6可得，随着纵向铺装长度的增大，恒温时间和升温时间均有所升高，当纵向铺装长度为200 cm时，恒温时间和芯层升温时间分别为1 535和2 577 s。不同纵向铺装长度下的升温速率预测结果见表6。

表6 升温速率预测结果Table 6 Prediction results of heating rates

同时，得到恒温时间、升温时间、升温速率的预测模型。恒温时间的预测模型为：

升温时间的预测模型为：

升温速率的预测模型为：

将上述3个模型重新代回原始数据序列，得到预测值与样本值的误差如表7所示。

表7 升温预测模型误差Table 7 Temperature rise prediction model errors

3个模型的后验差比(均方差比)C分别为0.325，0.236，0.211，小概率误差P均为1，因此，3个模型的精度等级为I级。3个模型的发展系数a分别为-0.093 2，-0.031 6，0.032 5，均大于-0.3，因此，3个模型均适用于中长期预测。恒温时间、升温时间、升温速率的预测值残差如图7所示，由图7可知，预测值信度良好，均位于预测阈值的区间内，无明显异常值，因此，该模型具有相当的可信度。

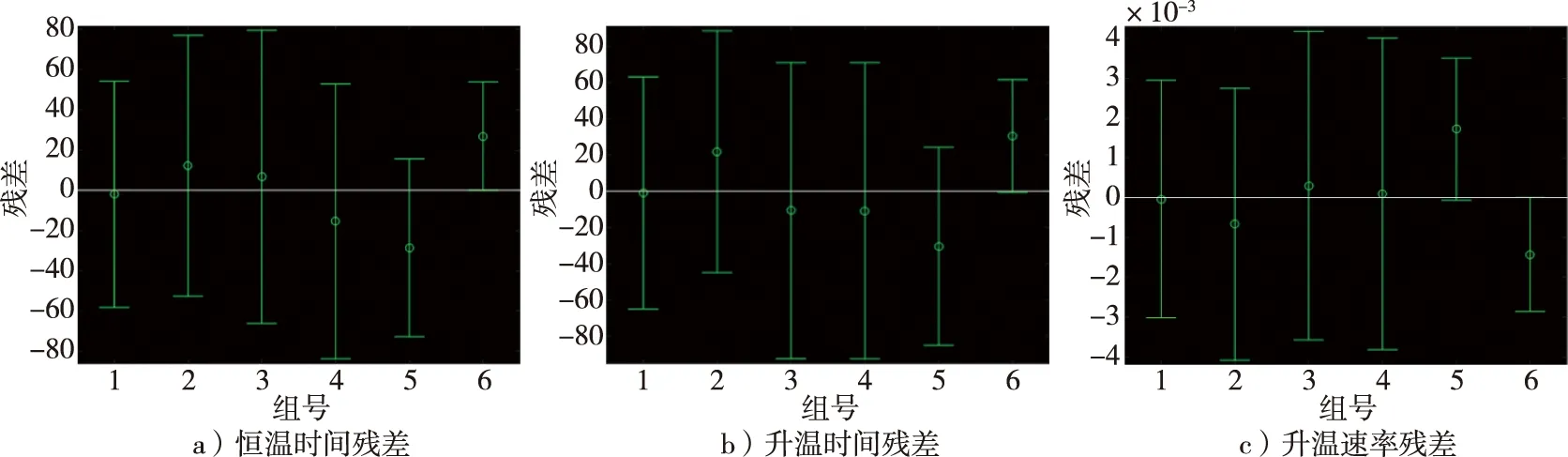
图7 恒温时间、升温时间、升温速率预测值残差Fig.7 Residual errors of predicted values of constant temperature time,heating time and heating rate

3.2.2 最高温度、降温时间、热压周期的预测模型求解

基于灰色系统预测方法，得到L=70～200 cm纵向铺装长度的板材芯层最高温度、降温时间、热压周期预测结果如图8所示。

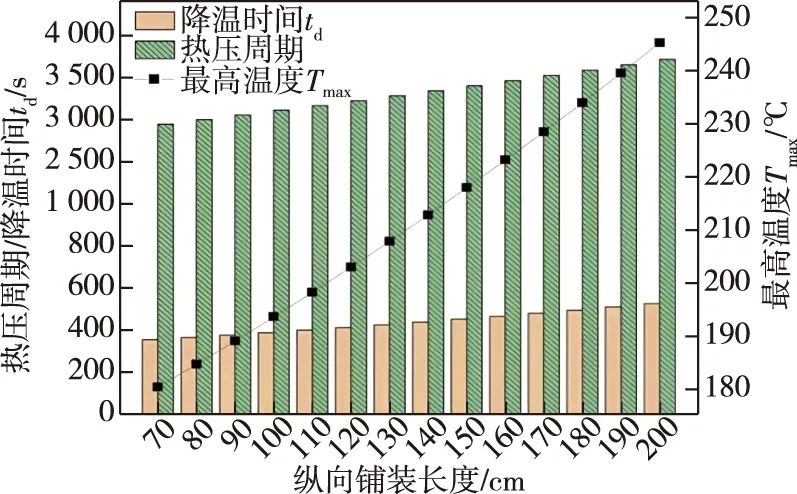
图8 纵向铺装长度对热压周期、降温时间和最高温度的影响预测结果Fig.8 Prediction results of the influence of longitudinal pavement length on hot pressing cycle，cooling time and maximum temperature

由图8可知，随着纵向铺装长度的增大，芯层受“锅炉效应”影响趋于剧烈，芯层升温的最高温度逐渐增大，降温时间和热压周期也随之增大；同时，利用灰色系统可得最高温度、降温时间、热压周期的预测模型。最高温度的预测模型为：

降温时间的预测模型为：

热压周期的预测模型为：

将上述3个模型重新代回原始数据序列，得到预测值与样本值的误差如表8所示。

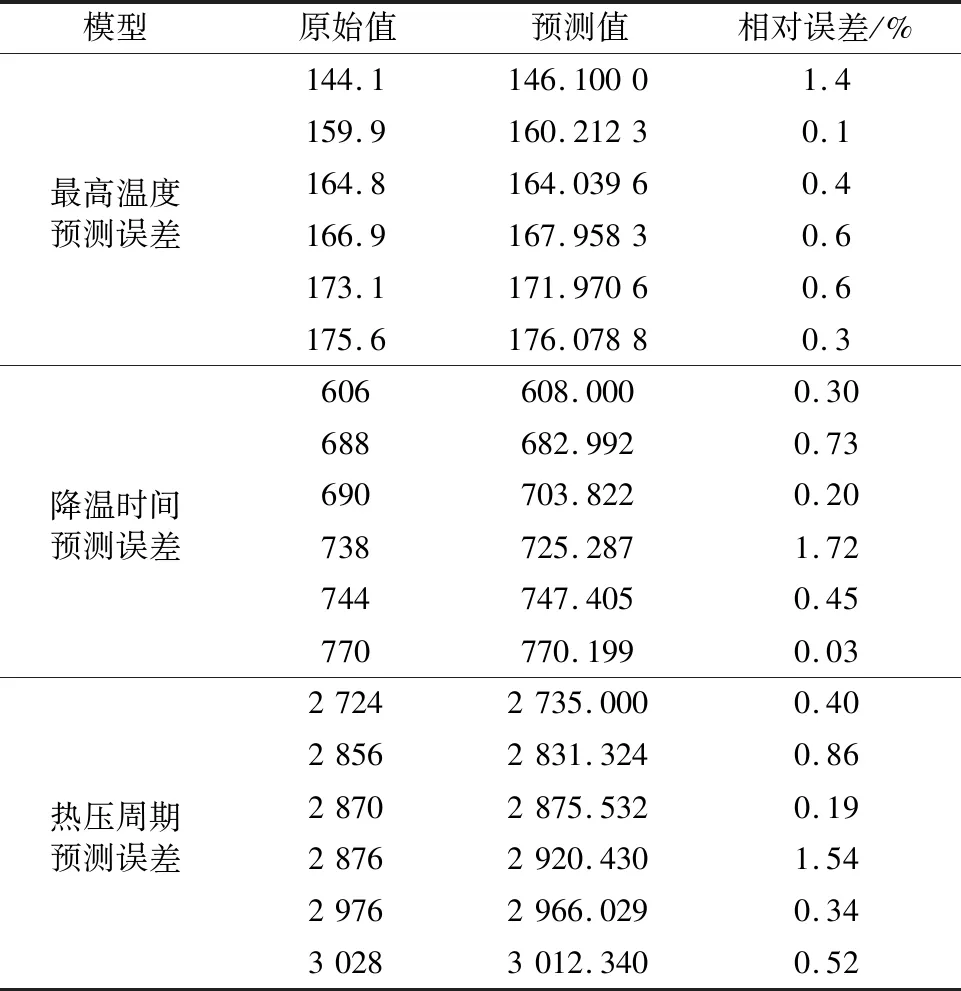
表8 三变量预测模型误差Table 8 Three variables prediction model error

3个模型的后验差比(均方差比)C分别为0.071 80，0.150 71，0.230 39，小概率误差P均为1，因此，3个模型的精度等级为I级。3个模型的发展系数a分别为-0.024 0，-0.030 0，-0.015 5，均大于-0.3，因此，3个模型均适用于中长期预测。最高温度、降温时间、热压周期预测值残差如图9所示。由图9可知，最高温度、降温时间预测值信度良好，均位于预测阈值的区间内，热压周期仅有一个异常值，其预测精度也在合理范围。因此，认为这3种模型均具有较好的预测效果。