Novel moderate transformation of fuzzy membership function into basic belief assignment

Xiojing FAN, Deqing HAN,*, Jen DEZERT, Yi YANG

a School of Automation Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, China

b ONERA, The French Aerospace Lab, Palaiseau 91761, France

c SKLSVMS, School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China

KEYWORDS Basic belief assignment;Belief functions;Fuzzy membership function;Information fusion;Moderate transformation

Abstract In information fusion, the uncertain information from different sources might be modeled with different theoretical frameworks. When one needs to fuse the uncertain information represented by different uncertainty theories, constructing the transformation between different frameworks is crucial. Various transformations of a Fuzzy Membership Function (FMF) into a Basic Belief Assignment (BBA) have been proposed, where the transformations based on uncertainty maximization and minimization can determine the BBA without preselecting the focal elements. However, these two transformations that based on uncertainty optimization emphasize the extreme cases of uncertainty. To avoid extreme attitudinal bias, a trade-off or moderate BBA with the uncertainty degree between the minimal and maximal ones is more preferred.In this paper,two moderate transformations of an FMF into a trade-off BBA are proposed.One is the weighted average based transformation and the other is the optimization-based transformation with weighting mechanism, where the weighting factor can be user-specified or determined with some prior information. The rationality and effectiveness of our transformations are verified through numerical examples and classification examples.

1. Introduction

In multi-source information fusion, the information obtained from different sources usually have different types of uncertainty. Various kinds of uncertainty theories have been proposed including probability theory, fuzzy set theory,1possibility theory,2rough set theory3and theory of belief functions,4etc., for dealing with different types of uncertain information. According to the type of uncertainty, the uncertain information from different sources might be modeled with different theoretical frameworks. Usually, these uncertain information with different representations cannot be directly combined or fused.Therefore,transformations between different frameworks are needed,5and then, one can fuse them under the same framework.

Random set theory is regarded as a unified framework for various frameworks of uncertainty including probability theory,fuzzy set theory,theory of belief functions,etc.5In particular, to fuse the opinion of an expert represented by a Fuzzy Membership Function (FMF) and the output of a sensor expressed by Basic Belief Assignment (BBA), one can transform the FMF into a BBA and then combine two BBAs.One can also transform the BBA into an FMF and then combine two FMFs.In this paper,we focus on the transformation of an FMF into a BBA.Many transformations have been proposed,5-10which can be categorized into two types.

One type of transformation has to preselect the focal elements. For example, Bi et al.6transform an FMF into a BBA by normalizing the given FMF,where the focal elements are preselected as singletons.As a result,the obtained BBA has no compound focal elements.In Ref.5,Florea et al.transform an FMF into a BBA with α-cut approach,where focal elements are preselected to the ‘‘nested in order”. However, a prior selection of focal elements might lead to information loss.The other type of transformation obtains a BBA by solving constrained optimization problems.For example,our previous work7proposed two transformations based on uncertainty optimization, which avoid the subjective preselection of focal elements. The difference between the two transformations is the specific optimization criterion, which is the maximization and minimization, respectively. It has been shown in Ref. 7 that both transformations based on uncertainty optimization are rational and effective. However, these transformations based on uncertainty optimization seem to be ‘‘one-sided” in terms of the uncertainty degrees, since they only focus on the minimal or maximal uncertainty. Either the minimal uncertainty or the maximal uncertainty is an extreme case of uncertainty.If one only pays attention to one of the extreme cases of uncertainty in the process of solving the optimization problem,it would bring the bias of extreme attitudinal on the uncertainty degree, which might bring counter-intuitive results. If we jointly consider two extreme cases of uncertainty, we can obtain the BBA with the degree of uncertainty between the minimal and maximal ones. Such a BBA is more ‘‘balanced”and‘‘moderate”than the BBA obtained by pursuing the maximal or minimal uncertainty. In other words, joint consideration of two extremes of uncertainty corresponds to a better moderate attitude (corresponding to a preferred consensual agreement of behavior) for a transformation of FMF into a BBA, and then we can avoid the bias of extreme attitudinal on the uncertainty degree.

In this paper, we aim to obtain such a trade-off BBA to avoid ‘‘one-sidedness” on the uncertainty degree, which is based on the two BBAs obtained by the two transformations proposed in our previous work.7To transform an FMF into such a trade-off or moderate BBA, a weighting factor is used,which can make the trade-off BBA closer to the BBA obtained with the uncertainty maximization or closer to the BBA obtained with the uncertainty minimization. The weighting factor could be determined by using prior information or user-specified,which reflect the objective situation or meet subjective preferences of users. We propose two ‘‘moderate” (i.e.,balanced) transformations in this paper. One transformation assigns the weighting factors to the two BBAs obtained by optimization-based transformations. Then, the weighted average of these two BBAs is the trade-off BBA. The other transformation is based on a constrained minimization problem with weighting mechanism. The objective function is constructed by the weighting factor and two degrees of dissimilarity between the trade-off BBA (to determine) and the two BBAs obtained by solving the uncertainty minimization and maximization. According to the given FMF and the legitimate conditions of a BBA, the constraints are constructed. Compared with the transformations based on uncertainty optimization, our transformations can avoid the extreme attitudinal bias and allow users to choose the degree of a trade-off BBA according to their preference.

This paper is an extended version our previous preliminary work published in Ref.11.Based on the preliminary work,the main extended work and added value in this paper is as follows. The limitations of available transformations of an FMF into a BBA are analyzed.Examples are given to illustrate the loss of information that might be caused by the preselection of focal elements and the counter-intuitive results that might be caused by the extreme attitudinal of uncertainty.We use another more rational uncertainty measure, which is designed without switching frameworks, to construct the objective function in the transformations proposed in Ref. 7.This is because the uncertainty measure Ambiguity Measure(AM) used in Ref. 7 as the objective function has some disputes and limitations, which is mentioned in Ref. 7. Furthermore, to compare our transformations with the others, some numerical examples and a classification example are provided.Compared with the average classification accuracy of available transformations, the moderate transformation has a better classification performance.

The paper is organized as follows. After a brief introduction of the basics for theory of belief functions and some basic concepts of the fuzzy set theory in Section 2, some traditional transformations of an FMF into a BBA are reviewed and the limitations of them are provided in Section 3.In Section 4,the transformations of an FMF into a trade-off BBA are presented. In Section 5, our transformations are compared with several traditional approaches and related examples are provided. Using our transformations can bring better performances than other transformations in a classification example. Section 6 concludes this paper.

2. Preliminary

2.1. Basics for theory of belief functions

2.2. Uncertainty measure of BBA and distance of evidence

The uncertainty measure is used for evaluating the degree of uncertainty in a BBA. There are two types of uncertainty for a BBA in belief functions including the discord and nonspecificity,which are collectively known as the ambiguity.Various kinds of uncertainty measures in the theory of belief functions have been proposed.31-38

2.3. Fuzzy set theory

Fuzzy set theory1can be used to model the information without a crisp definition or a strict limit (e.g., ‘‘the target is fast”,‘‘the target turns quickly”). A fuzzy set Afis defined on a universe of discourse Θ, which is equivalent to the FOD in belief functions. Afis represented by a Fuzzy Membership Function(FMF)μAf（θ ）.The value of μAf（θ ）denotes the degree of membership for θ in Af.μAf:Θ →［0，1 ］;θ↦μAf（θ ）∈［0，1 ］.The sum of μAfmight be equal to, greater than or less than 1. For

3. Transformations of FMF into BBA

Although fuzzy set theory and the theory of belief functions are two different theoretical frameworks, there are relationships between their basic concepts.52The relationships are between the FMF and the singleton plausibility function or singleton belief function, which are as follows.

3.1. Relationships between FMF and BBA

3.2. Available transformations with preselection of focal elements

3.2.1. Normalization based transformation

3.3. Transformations based on uncertainty optimization

In our previous work,7the multi-answer problem is formulated as a constrained optimization to obtain a unique BBA without preselecting focal elements. We established two transformations based on uncertainty optimization of an FMF into a BBA, where the uncertainty measure AM (see Eq. (5)) is used as the objective function. When an FMF is given, except for m（∅ ）≠0, at most 2n-1 focal elements for the undetermined BBA need to assign the mass. According to the relationships between the given FMF and belief or plausibility function,together with the BBA legitimate conditions, there are n+1 equations, which are used as the constraints. When the given FMF is equivalent to a singleton plausibility function,the corresponding constraint can also use the contour function.As analyzed in Ref.[7],using AM as the objective function has some disputes and limitations because it actually quantifies the randomness of the pignistic probability measure approximating a BBA, so it does not capture all the aspects of uncertainty(specially the ambiguity)represented by a BBA.AM has also been criticized in Ref. 36. TUIis a total uncertainty measure without switching frameworks,36which is based on Wasserstein distance33(a strict distance).Therefore,we replace AM with TUI(see Eq. (8)) as the objective function of the transformations based on uncertainty optimization in this paper.

3.3.1. Transformation based on uncertainty minimization

3.4. Limitations of available transformations

3.4.1. Limitations of transformations with preselection of focal elements

As referred above,to deal with the under-determined problem for the transformation of an FMF into a BBA, preselecting focal elements or solving the optimization problem are used.Compared with solving the optimization problem (Tminand Tmax),preselecting the focal elements without sufficient witness might bring the loss of information. Since the focal elements are preselected, the obtained BBA can only assign the mass to the focal elements specified beforehand (e.g., as with Tnorm, Tα-cutor Ttri). For the BBA obtained by using Tnorm,there are no compound focal elements. The BBA obtained by using Tα-cutor Ttrihas a specific structure of focal elements for the given FMF.In addition,for different FMFs(such as in Example 1),the same BBAs might be obtained by using Tnorm,Tα-cutor Ttri.

3.4.2. Example 1

One can see that m1=m2, m3=m4and m5=m6. This is not that rational. μ1and μ2are completely different FMFs and have different uncertainty degrees. Using Eq. (10) to calculate the degrees of fuzziness for μ1and μ2,one can verify that D（μ1）=0.6907≠D（μ2）=0.7737. That is to say, given two FMFs with different degrees of fuzziness, the obtained BBAs are respectively identical by using Tnorm, Tα-cutand Ttri.

3.4.3. Limitations of transformations based on uncertainty optimization

The optimization-based transformations take every possible focal element into consideration to assign the mass, which avoid preselecting the focal elements and deal with multianswer problem by solving optimization problem. However,in the process of solving optimization problem, the two transformations based on uncertainty optimization consider the minimal and maximal uncertainty degrees respectively, which might lead to extreme attitudinal bias on the uncertainty degree and bring ‘‘one-sided” and counter-intuitive results.

The corresponding pignistic probability is BetP8（θ1）=0.5,BetP8（θ2）=0.25, BetP8（θ3）=0.25. When only emphasizing the minimal uncertainty, BetP8（θ1） is overemphasized.

The optimization-based transformations emphasize the extreme cases of uncertainty and might bring counterintuitive results. In fact, a trade-off, i.e., a more ‘‘moderate”(or balanced) BBA, is more natural than the obtention of BBA based on extreme (min, or max) strategies. To avoid being ‘‘one-sided”, we propose ‘‘moderate” transformations to obtain the trade-off BBA with an uncertainty between the minimal and maximal uncertainty as presented in the next section.

4. Moderate transformations with weighting factor

(1) When β →0,the trade-off BBA becomes closer to mmin.

(2) When β →1,the trade-off BBA becomes closer to mmax.

Meanwhile, the trade-off BBA’s corresponding singleton belief or singleton plausibility should be equivalent to the given FMF. Here, we propose two transformations of an FMF into such a trade-off BBA.

4.1. Weighted average based transformation

According to Eq.(21),the trade-off BBA obtained by using Twaconforms to the conditions aforementioned at the beginning of Section 4. When β →0, mwaapproximates to mmin.When β →1, mwaapproximates to mmax.

Beside the directly weighted approach, we can also use degree of dissimilarity between the trade-off BBA and the BBA obtained by using mminor mmax.Then,the weighting factor can influence the relationship between two degrees of dissimilarity to obtain the trade-off BBA.

4.2. User-specified optimization based transformation

Fig. 1 Illustration of Eq. (24).

We find that using different evidence distances to construct the objective function might transform a given FMF into different BBAs. But the difference between these BBAs is relatively small. Therefore, we use Jousselme’s distance, one of the representative evidence distances,as the objective function of Tuoin this paper.

For convenience, we list all the transformations aforementioned and their abbreviations in Table 1 together with the symbols of corresponding BBAs obtained.

Table 1 Transformations and their abbreviations.

4.3. Example 3 for illustration

5. Examples

We use different approaches to transform an FMF into a BBA in this section.Some numerical examples are provided to illustrate the difference between different transformations (including all the transformations mentioned in Table 1).In addition,a classification example is provided to compare our transformations with other transformations.

5.1. Example 4

In this example, we use the moderate transformations to obtain BBAs from μ3and μ4, respectively. Then, we calculate the corresponding pignistic probability. The trade-off BBAs transformed from μ3and μ4are listed in Table 4 and Table 5,respectively. Here, β=0.7.

As can be seen in Table 4, the three values of the pignistic probability of each trade-off BBA are different instead of BetP7（θ1）=BetP7（θ2）=BetP7（θ3） in Example 2. Using the moderate transformation can obtain a trade-off or balanced BBA to express even a small difference of the given FMF(e.g., μ3) and bring a rational result.

According to the results listed in Table 5, there is no overemphasis on BetP（θ1） (the pignistic probability in Example 2 is BetP8（θ1）=0.5，BetP8（θ2）=0.25，BetP8（θ3）=0.25).One can transform such an FMF like μ4into a trade-off BBA by using the moderate transformations to avoid the overemphasis caused by ‘‘one-sidedness” on the uncertainty degree. Even if the difference of values of μ4is tiny, they are different and there exists μ4（θ1）＞μ4（θ2）＞μ4（θ3）. As can be seen in Table 5, the trade-off BBAs obtained by using Twaand Tuocan represent the tiny difference between the values of μ4, respectively.

5.2. Example 5

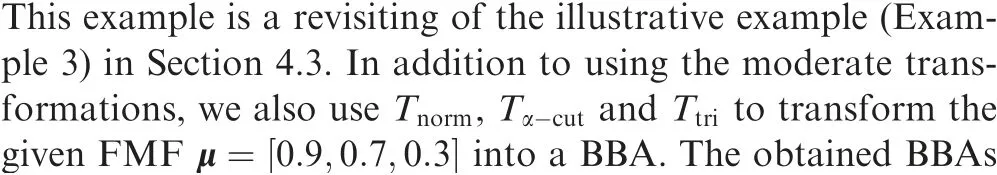
Table 2 BBAs transformed from μ1.

Table 3 BBAs transformed from μ2.

Table 4 Trade-off BBAs transformed from μ3.

Table 5 Trade-off BBAs transformed from μ4.

As shown in Table 6, mnormonly has singleton focal elements. The structure of focal elements for mα-cutis nested and that for mtridepends on the ordering of values of the given FMF. According to the results in Example 3 and Table 6,using the uncertainty optimization based transformations and moderate transformations can consider more focal elements to assign mass. Moreover, the focal element structure of the obtained BBA is not fixed. When the FMF is given,using the transformations with preselection of focal elements can only obtain a BBA with a certain structure of focal element.

Table 6 Obtained BBAs in Example 5.

5.3. Example 6

5.4. Example 7

Table 7 Obtained BBAs in Example 6.

Table 8 Obtained BBAs in Example 7.

In addition,although some of the degrees of uncertainty of the BBAs obtained by using transformations with preselection of focal elements are greater(or less)than the maximal degree of uncertainty(or the minimal degree of uncertainty),the three BBAs mnorm, mα-cutand mtrido not satisfy the relationship as Eq. (13).

5.5. Example 8

To verify the effectiveness for the moderate transformations of an FMF into a trade-off BBA, we compare the average accuracy of 300-run experiments of all the mentioned transformations in a classification problem. Note that we only aim to show the impact of different transformations on the classification results, rather than improve the classification accuracy.

We use three datasets of open UCI database53including iris dataset, wheat seeds dataset and wine dataset. Iris dataset has 150 samples including 3 classes,each of which has 50 samples.Every sample has 4 features and all data of 4 features for 150 samples are complete. Wheat seeds dataset has 210 samples including 3 classes and each of which has 70 samples. Every sample has 7 features and all data of 7 features for 210 samples are complete.Wine dataset has 178 samples including 3 classes,each of which has 59,71 and 48 samples.Every sample has 13 features and all data of 13 features for 178 samples are complete. The transformation process is given.

In this example, only iris dataset is used to illustrate the detailed process of classification and the four features are denoted by f1,f2,f3and f4.We randomly select 70%of samples from each class as samples of the training set and the test set consist of the rest samples.In the training set,the minimal values, average values and maximal values of each feature for each class are used as parameters. Then, the FMF can be defined as follows:where i=1，2，3，4. miniis the minimal value of Class j (θj,j=1，2，3). aveiis the average value of the Class j. maxiis the maximal value of the Class j.

The corresponding BBAs obtained by using transformations with preselection of focal elements, transformations based on uncertainty optimization and moderate transformations are listed in Table 10. We use moderate transformations to determine trade-off BBAs with β=0.2.

When the BBAs of each feature are determined, one can combine the corresponding four BBAs of each transformation.For convenience and simplicity, Dempster’ rule of combination is used. The combined BBAs of each transformation are listed in Table 11.

According to the results of Table 11,the corresponding pignistic probabilities can be calculated by using Eq. (6). As we can see in Table 12,the values of BetP（θ2）for all the transformations are the largest, which means that the classifications are correct.

In order to compare the moderate transformations with the traditional transformations, we provide 300-run experiments on three datasets (including iris dataset, wheat seeds dataset and wine dataset)to obtain the average accuracy,respectively.All the transformations in Table 1 are used and the transformation process is the same as above. We use all the features in iris dataset.In wheat seeds dataset and wine dataset,we randomly select 4 features and 7 features to classify, respectively.Reducing the feature dimensions used for classification is to simplify the experiment process.

Table 9 Parameters of training set.

Fig. 2 FMFs of four features.

On each run, 70% of each class samples of iris dataset and wheat seeds dataset are for training samples,and the rest samples are for testing.For wine dataset,34 samples(the class with the smallest samples contains 48 samples, 70% of which is about 34) of each class samples are for training samples and the rest samples are for testing.The training samples are select randomly. For moderate transformations, we specify β=0.2，0.5，0.8 to obtain the trade-off BBA, respectively.The results for average classification accuracy of three datasets are listed in Table 13.

According to the results in Table 13,there is a gap between the classification accuracy we obtained and the best possible classification accuracy for each dataset (e.g., for iris, the best possible accuracy with other classification approach can be beyond 95%).Here,we only aim to compare the impact of different BBA transformations on the classification performance.

All the results based on optimization-based transformations are better than those based on transformations with preselection of focal elements, i.e., considering more possible focal elements might reduce the loss of information due to the preselection of focal elements, thereby improving the classification accuracy. Meanwhile, the moderate transformations achieve higher classification accuracy than other transformations. The moderate transformations do not pursue the minimal or maximal degree of uncertainty on the basis of considering all possible focal elements, since the extreme attitudinal bias on the uncertainty degree might bring counterintuitive results and a moderate (or balanced) BBA without the minimal or maximal degree of uncertainty is more natural.

Besides, we note two cases of samples of 300-run experiments:

Table 10 Obtained BBAs in Example 8.

Table 11 Combined BBAs in Table 10.

Table 12 Pignistic probabilities in Example 8.

Case 1. the classification results of transformations based on uncertainty optimization are wrong and that of moderate transformations is correct.

Case 2. the classification results of moderate transformations are wrong and that of transformations based on uncertainty optimization is correct.

In this example, the test sets of three datasets have 45, 63 and 76 samples, respectively. Here, we count the number of samples for Case 1 in each run experiment and calculate the average. The average numbers of samples of Case 1 are 2.2167 (4.93%), 1.8833 (3.00%) and 4.08 (5.37%) for three datasets, respectively, i.e., the moderate transformations can bring better results. We find that the samples belonging to Case 1 in each dataset contain at least one dimension feature with small difference in values of different classes. Compared with the transformations based on uncertainty optimization,the moderate transformations can better represent the uncertainty contained in the FMFs obtained according to the samples,e.g.,the samples marked in Fig.3 are the samples of Case 1 in iris dataset after 300-run experiments (repetitive samplesare marked only once). In Fig. 3, samples of Class 1 are marked in red points; samples of Class 2 are marked in blue solid diamonds; samples of Class 3 are marked in cyan solid triangles. We use red circles to mark the samples of Case 1 of Class 1;we use blue diamonds to mark the samples of Case 1 of Class 2;we use cyan triangles to mark the samples of Case 1 of Class 3.

Table 13 Average classification accuracy (%).

Fig. 3 Samples of Case 1 of iris dataset.

Table 14 Obtained BBAs of a sample of Case 1 in Example 8.

We can see that the classification results are correct except for the results obtained using Tminand Tmax.

On the other hand, the average numbers of samples for Case 2 (the moderate transformations bring out incorrect results, while Tminand Tmaxbring out correct results) in 300-run experiment are 0.07 (0.16%), 0.2967 (0.47%) and 0.1433(0.19%) for three datasets, respectively. Compared with the average numbers of samples for Case 1,moderate transformations are better than transformations based on uncertainty optimization. Using moderate transformations can avoid‘‘one-sidedness” in terms of the uncertainty degrees. Meanwhile, the trade-off BBA can represent the small differences between the values of a given FMF.In summary,the moderate transformations can bring better classification results compared with that of the transformations based on uncertainty optimization in a statistical sense.

6. Conclusions

In this paper, we propose two transformations with a weighting factor to transform a given FMF into a trade-off or moderate BBA.The weighting factor could be determined by using prior information or user-specified to reflect the objective situation or meet subjective preferences of users.Numerical examples and classification results validate the effectiveness of the two moderate transformations.Comparing these two transformations, the computational complexity of Twais lower, and Tuocan bring a better classification performance. In practical applications, users can choose Twaor Tuoaccording to the demands of applications.

Note that our transformations have been evaluated through some numerical and classification examples, within which, the design of numerical examples is usually subjective.In fact,the related fields of belief functions, including the generation of a BBA, lack objective and reasonable evaluation criteria. The conclusions obtained by numerical examples are incomplete.An objective evaluation criterion can help to obtain better related tools or approaches of belief functions. Therefore, we will focus on the objective evaluation criteria of the belief functions in our future work.

With the increase of FOD’s cardinality, the possible focal elements in a BBA will grow exponentially, i.e., the unknown variables that need to be determined in our formulated optimization problem will grow exponentially. The exponential growth of computational complexity is a limitation of our transformations. In the future work, we will attempt to use more simple and effective approaches beside the optimization-based transformations to transform an FMF into a trade-off BBA.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 61671370), Postdoctoral Science Foundation of China (No. 2016M592790) and Postdoctoral Science Research Foundation of Shaanxi Province, China(No. 2016BSHEDZZ46).

Because 0 ≤m（A ）≤1（A ⊆Θ）. This means that the focal elements at the left side of Eq. (A3) are 0. Then we have.