正弦波脉动流对微通道内流体流动与传热特性的影响
2023-02-09夏国栋宋殿瑶马丹丹
夏国栋, 宋殿瑶, 马丹丹
(北京工业大学强化传热与过程节能教育部重点实验室暨传热与能源利用北京市重点实验室, 北京 100124)
随着微电子技术与航空航天技术的飞速发展,各种微电子芯片的性能逐渐增强,电子器件的集成度越来越高,其热流密度也在不断提高. 因此,各种微型电子器件的散热问题成为了当今研究的热点问题.
Tuckerman等[1]首次提出微通道散热器,指出将冷却通道的尺寸减小到微尺度可以强化传热效果,由此开始了对微通道散热方面的研究. Gunnasegaran等[2]研究了3种截面形状的微通道,数值模拟结果显示,雷诺数在100~1 000时,矩形微通道的传热系数最大. Xia等[3]对带有三角凹穴的微通道结构进行了数值与实验研究,发现由于通道中凹穴结构的作用使得流体在微通道中的流动与热边界层被破坏,进而导致微通道与流体间换热得到强化. Lee等[4]通过实验研究了硅基矩形微通道在雷诺数为69~800时微通道中层流流动的压降和传热特性. 实验结果显示,压降公式在常规尺度下依然能适用,但是和常规尺度下的传热公式差距较大. 因此,他们在其基础上提出了用于微通道与流体间的传热公式. 周继军等[5]研究了去离子水在硅基微通道中的流动与传热特性. 实验结果显示,微通道的表面粗糙度对流动与传热有重要影响.
流体的流动分为两种状态,分别是稳态流动与非稳态流动. 由于非稳态流动能够使流体的扰动更强,在流体与固体壁面的传热方面有强化作用,因此近年来非稳态流动受到众多学者[6-8]的关注. Glasgow等[9]通过研究也指出了相对于稳态流动,脉动流动对流体的扰动更加强烈. Steinke等[10]还发现在微通道中采用脉动流能够强化单相流的传热效果,在电子器件散热方面有很好的效果. Richadrson等[11]研究了圆管内的脉动流动,得到了脉动流的速度分布,实验结果显示在管道截面上的速度分布相对于稳态流动时要更均匀平缓,将其称之为“速度环效应”. Havemann等[12]研究了水平管道单相脉动流动,实验结果表明,传热效果会随着脉动频率、幅值、波形和雷诺数的改变而变化,并且存在着一个极限频率,高于此极限频率会强化传热,低于该频率就会弱化换热. Ghaddar等[13]采用数值计算方法研究了周期性变化截面通道中流体的对流传热,发现脉动流动能够增加流体的不稳定性,进而使得传热得到强化,并指出脉动流可以在周期性变化截面通道中实现强化传热. Greiner等[14-15]通过实验证明了Ghaddar的结论,在雷诺数为700、脉动振幅为0.2时,对不同脉动频率进行实验,发现传热速率最高提高了160%. Olayiwola等[16]对周期性布置绝热方块的通道进行实验,结果表明,当雷诺数较低时,脉动作用可以使流体与通道的换热效果更好;当雷诺数较高时其强化换热效果就会变弱. 何雅玲等[17]采用数值方法研究了周期性矩形槽通道在脉动流下的换热特性,分别研究了雷诺数、斯特劳哈尔数、脉动振幅等对流体与通道之间换热的影响. 计算结果表明,脉动流能够使通道内的流体相互掺混更强,使得流体与通道的传热得到强化. Valueva等[18]研究了不同高宽比矩形通道的层流脉动流动传热特性,发现只有在较高频率时,努塞尔数才会提高.
综上所述,脉动流的非稳态流动促使了流体之间的互相掺混,使流体的之间的质热交换更加强烈. 并且微通道的特殊结构能够引起流体的扰动,进而强化流体与壁面的换热. 因此,本文对矩形平直微通道与三角形凹穴结构微通道内的脉动流动进行数值计算,将脉动流动状态下与稳态流动状态下的流动与换热特性进行比较,进而得到入口脉动流动参数的变化对微通道内流动和换热的影响规律.
1 数值模拟
1.1 物理模型
图1、2为数值计算区域的三维示意图,因为微通道换热器的每根通道互相对称,所以取单个通道为数值计算区域,包括流体区域与固体侧壁.

图1 矩形微通道模型(单位:毫米)Fig.1 Rectangular microchannel model (unit: mm)

图2 三角凹穴结构通道模型(单位:毫米)Fig.2 Microchannel with triangular reentrant cavities model (unit: mm)
1.2 数学模型
Service等[19]指出,Navier-Stokes方程和无滑移边界条件在克努森数(Kn)小于10-3时仍然能够使用.Kn计算表达式为
(1)
式中:Λ为流体分子平均自由程,m;Dh为微通道的当量直径,m.
由于本文流体部分为去离子水,水分子的平均自由程的数量级为10-10m,而本文所计算微通道当量直径的尺寸数量级在10-4m.通过计算可知,本文中的Kn远小于10-3,因此在常规尺度下使用的无滑移边界条件和Navier-Stokes方程仍然能够使用.
本文数值计算软件为Fluent,采用有限容积法对微通道模型区域进行三维计算.采用SIMPLEC方法对速度压力进行计算.对流项与扩散项分别采用二阶迎风格式和二阶差分格式进行离散.当计算脉动流动时,采用瞬态计算方法.需先计算得到不同入口速度下的稳态计算结果,然后在其基础上,导入速度入口的UDF文件,使入口流速产生正弦形的脉冲变化,然后得到瞬态计算的结果.
本文计算中所用到的控制方程有:
1) 连续性方程
稳态时

(2)
瞬态时
(3)
2) 动量方程
稳态时
(4)
瞬态时
(5)
3) 能量方程
稳态时
(6)
(7)
瞬态时
(8)
(9)
式中:ρf为流体密度,kg/m3;μf为流体动力黏度,kg /(m·s);cp,f为流体比热容,J/(kg·K);λf为流体导热系数,W/(m·K);λs为固体导热系数,W/(m·K);Φ为耗散函数.
本文计算中涉及到的边界条件包括:
1) 速度入口边界条件(入口流体温度为293 K)
稳态时
u=u0;T=Tin
(10)
瞬态时
u=u0[1+Asin(2πft)];T=Tin
(11)
式中:u0为流体的平均速度,m/s;A为量纲为一脉动振幅,表示脉动流的入口速度在平均速度基础上的变化比例;f为脉动频率,Hz;t为流动时间,s.
2) 压力出口边界边界条件
P=Pout=0
(12)
3) 通道底面为恒定热流边界条件q=50 W/cm2,其他壁面为绝热边界
(13)
式中:Ts为固体温度,K;Tf为流体温度,K.
4) 固液接触面无速度滑移
(14)
因计算脉动流动过程为瞬态过程,所以选取时间步长为
(15)
式中T′为脉动流动的一个周期,s.
脉动流动时通道壁面平均温度Tw与最高温度Tmax均为一个周期内的平均值.
为了简化计算过程,做出以下假设:
1) 本文数值计算的Re范围为100~400,流体的流动状态为层流流动且流体不可压缩.
2) 忽略重力、体积力和热辐射对计算过程的影响.
3) 流体的运动黏度随温度改变,如表1所示.流体的其他物性参数与固体的物性参数均为定值,如表2所示.
4) 假设流体为牛顿流体.

表1 去离子水的动力黏度随温度的变化

表2 硅和去离子水的物性参数
1.3 网格无关性验证
数值计算中网格数量的多少会影响计算的准确性和计算速度,数量过少会导致计算误差过大,而数量过多会导致计算时间过长,因此对计算模型网格进行网格独立性检验.对于矩形直通道,分别以31.4万、72.6万和98.4万网格数对通道底面的平均温度和通道的压降进行检验,如表3所示.
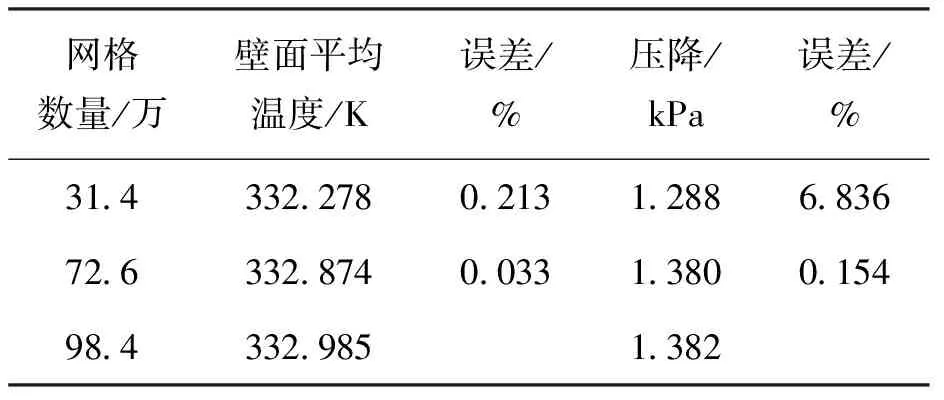
表3 矩形通道网格数量无关性验证
对于三角凹穴结构通道,分别以31.4万、73.6万和102.4万网格数采用同样的方法进行验证,如表4所示.因此,当网格数量为73.6万时,计算得到的各项参数误差均在1%以下.
1.4 数值计算有效性分析
通过进出口流体温差与表观摩擦因数来验证说明数值计算的有效性.通道进出口流体温差由能量方程计算.
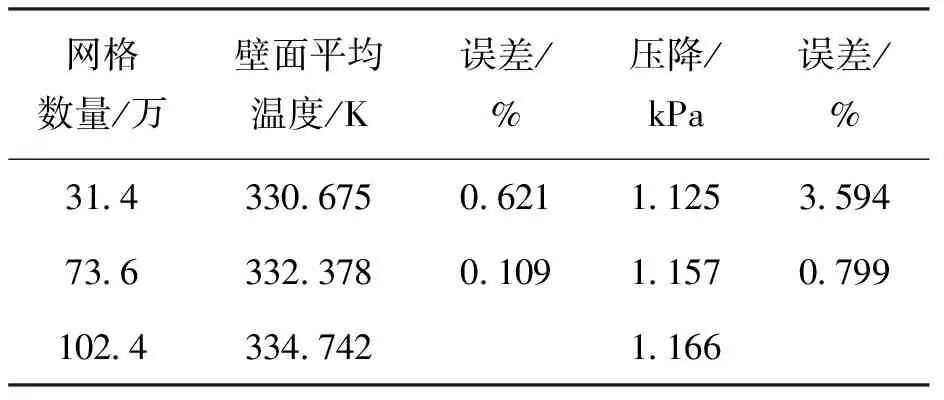
表4 三角凹穴结构通道网格数量无关性验证
(16)
式中:q为通道底面的热流密度,W/m2;Ab为通道底面面积,m2;At为换热总面积,m2.
Shah等[20]对于矩形微通道内发展中的层流流动,提出的表观平均摩擦因数表达式为
(17)
式中:Re为雷诺数;L为通道长度,m;Dh为通道的当量直径,m;泊肃叶数(Po)表达式为
沥青性能优劣直接影响到排水沥青混凝土路用性能及耐久性。本研究选用A型和B型国产沥青改性剂TAFPACK—Seper(简称TPS),改性基质沥青来制备高黏度改性沥青,并参照《公路工程沥青及沥青混合料试验规程》进行相应试验,主要技术性能检测结果见表1。
Po=96[1-1.355 3AR+1.946 7AR2- 1.701 2AR3+0.956 4AR4-0.253 7AR5]
(18)
式中AR为通道宽高比.
经模拟计算得到压降,然后计算得到通道的平均摩擦因数
(19)
式中Δp为通道压降,Pa.
平均换热系数与平均努塞尔数的计算公式分别为
(20)
(21)
式中:Tw,ave为通道底面平均温度,K;Tf,ave为流体平均温度,K.
图3为进出口流体温差理论值与模拟值对比,图4为平均摩擦因数通过理论值与数值模拟计算值对比.计算得到的流体进出口温差和摩擦系数均与理论值趋势相近,证明本文数值计算的结果有效.

图3 进出口流体温差理论值与模拟值对比Fig.3 Comparison between the numerical and theoretical values of the fluid temperature difference between the inlet and outlet

图4 平均摩擦因数理论值与模拟值对比Fig.4 Comparison between the numerical and theoretical value of apparent friction factor
2 结果分析
2.1 脉动频率对流动与传热特性的影响
图5为当雷诺数Re=200,脉动振幅A=1,脉动频率分别为0、10、20、50和100 Hz时,壁面的最大温度与平均温度的变化,其中T1和T2分别代表矩形通道和三角凹穴结构通道壁面温度.从图中可以看出,矩形通道在脉动流动下的壁面平均温度与最大温度都比稳态时要高;而对于三角凹穴结构通道,可以看到随着脉动频率的增加,壁面的最高温度与平均温度均呈现先增大后减小的趋势,说明低频率下的脉动流会使得壁面的温度升高.但是,当脉动频率大于极限频率时,壁面的最大温度与平均温度会低于稳态流动时的壁面温度,且温度会随着频率的增加而减小.这是由于在三角凹穴结构通道中,侧壁面凹穴结构的存在使得凹穴区域的流体与主流区域的流体在脉动流下互相掺混,进而强化了流体与通道间的传热.随着脉动频率的增加,在三角凹穴结构中的这种效果更加明显,因此在高频率时通道的壁面温度更低.当频率f=100 Hz时,壁面平均温度与最大温度分别降低5.63 K和7.59 K.

图5 壁面最大温度与平均温度随脉动频率的变化Fig.5 Variation of the maximum and average temperature of the wall with the pulsation frequency
图6、7分别为Re=200、振幅A=1时,一个周期内不同频率下的平均压降与摩擦因数.从图中可以看出,对于矩形直通道,在脉动频率较低时,微通道压降高于稳态流动时的压降,当脉动频率较高时,通道压降低于稳态流动时的压降;对于三角凹穴结构通道,在脉动流动下通道的压降比稳态流动(f=0)时压降要大,并且压降随着脉动频率的增加而减小.在三角凹穴结构通道中,脉动流在凹穴结构中的流动阻力较大,因此脉动流动时的压降高于稳态流动时的压降.因为在不同频率下流体平均流速不变,所以摩擦因数与通道压降成正比即随着频率的增大而减小.

图6 压降随脉动频率的变化Fig.6 Variation of the pressure drop with the pulsation frequency

图7 平均摩擦因数随脉动频率的变化Fig.7 Variation of the friction factor with the pulsation frequency
图8为雷诺数Re=200、振幅A=1时,一个周期内的平均Nu随频率的变化.通过计算微通道的平均Nu发现,对于矩形通道,在脉动流动下的平均Nu相较于稳态流动时变化不大或略有降低;而对于三角凹穴结构通道,在脉动流动时的平均Nu比稳态流动时要大,并且随着脉动频率的增加,微通道与流体间的平均Nu是不断增大的.在三角凹穴通道中,流体在流经三角凹穴时,其不稳定性和扰动程度随着脉动频率的增大而增强,因而更有利于对流换热.当f=100 Hz时,平均Nu相对于稳态下增加了1.32.

图8 平均努塞尔数随脉动频率的变化Fig.8 Variation of the average Nu with the pulsation frequency
2.2 脉动振幅对流动与传热特性的影响
图9为雷诺数Re=200、脉动频率f=50 Hz时,两种微通道壁面平均温度和最高温度随着脉动振幅变化的趋势.从图中可以看出,对于矩形通道,壁面的平均温度与最大温度略有上升;而对于三角凹穴结构通道,随着脉动振幅的增加,通道壁面的平均温度与最大温度逐渐减小,并且在振幅较大时,脉动流动对微通道壁面的冷却效果较为明显.当振幅A=1时,壁面平均温度与最高温度分别降低了2.61 K和3.82 K.

图9 壁面最大温度与平均温度随脉动振幅的变化Fig.9 Variation of the maximum and average temperature of the wall with the pulsation amplitude
图10、11分别为雷诺数Re=200、脉动频率f=50 Hz时,不同脉动振幅下两种微通道的压降与平均摩擦因数变化情况.可以看到,随着脉动振幅的增大,通道的压降和摩擦因数不断增加.与稳态流动(A=0)时相比较发现,矩形通道的压降大于稳态流动时的压降和摩擦因数.而对于三角凹穴结构通道,当脉动振幅A大于某一振幅值时,通道的压降与摩擦因数比稳态流动时的要大;当A小于这一振幅值时,其压降与摩擦因数要比稳态流动时要小.

图10 压降随脉动振幅的变化Fig.10 Variation of the pressure drop with the pulsation amplitude

图11 平均摩擦因数随脉动振幅的变化Fig.11 Variation of the friction factor with the pulsation amplitude
图12给出了平均Nu随脉动振幅的变化,其中振幅A=0时为稳态流动.图中显示,在脉动流动时,矩形通道的平均Nu相较于稳态流动时变化不大或略有降低;而对于三角凹穴结构通道,其平均Nu均比稳态流动时大,并且随着脉动振幅的增大而增大.在低振幅时,脉动振幅对平均Nu的影响较小;当振幅较大时,平均Nu相对稳态流动时则增加较大.当振幅A=1时,平均Nu值为8.34,相对于稳态流动时增加了0.62.

图12 平均努塞尔数随着脉动振幅的变化Fig.12 Variation of the average Nu with the pulsation amplitude
2.3 雷诺数对微通道传热特性的影响
为了比较在相同平均流速下脉动流动与稳态流动对微通道传热特性的影响,探究了不同雷诺数下的流动与换热特性.图13中,ΔTw为稳态流动与脉动流动壁面平均温度的差值;ΔTmax则为稳态流动与脉动流动壁面最大温度的差值.图13结果显示,对于矩形通道,脉动流动时的壁面温度要大于稳态流动下的壁面温度,且随着Re的增大差值增大.而对于三角凹穴结构通道,在脉动频率f=50 Hz、振幅A=1时,随着Re的增加,ΔTw和ΔTmax均会逐渐减小.当Re=100时,壁面平均温度与最大温度的变化量分别为4.04 K和3.05 K.但是,当Re=400时,壁面平均温度与最大温度变化量分别为2.95 K和1.68 K.因此,随着Re的增加,脉动流动对壁面温度的影响逐渐减弱.

图13 壁面温度降低值随雷诺数的变化Fig.13 Variation of the temperature of wall with the Re
图14为稳态流动与脉动流动下Nu随着Re的变化,其中Nuave,s和Nuave,p分别为稳态流动与脉动流动下的平均Nu.图中显示,对于矩形通道,脉动流动与稳态流动下的平均Nu相差不大,说明脉动流动对矩形通道换热基本没有影响;而对于三角凹穴结构通道,在本文研究的Re范围内,脉动流动的平均Nu均高于稳态流动的平均Nu.
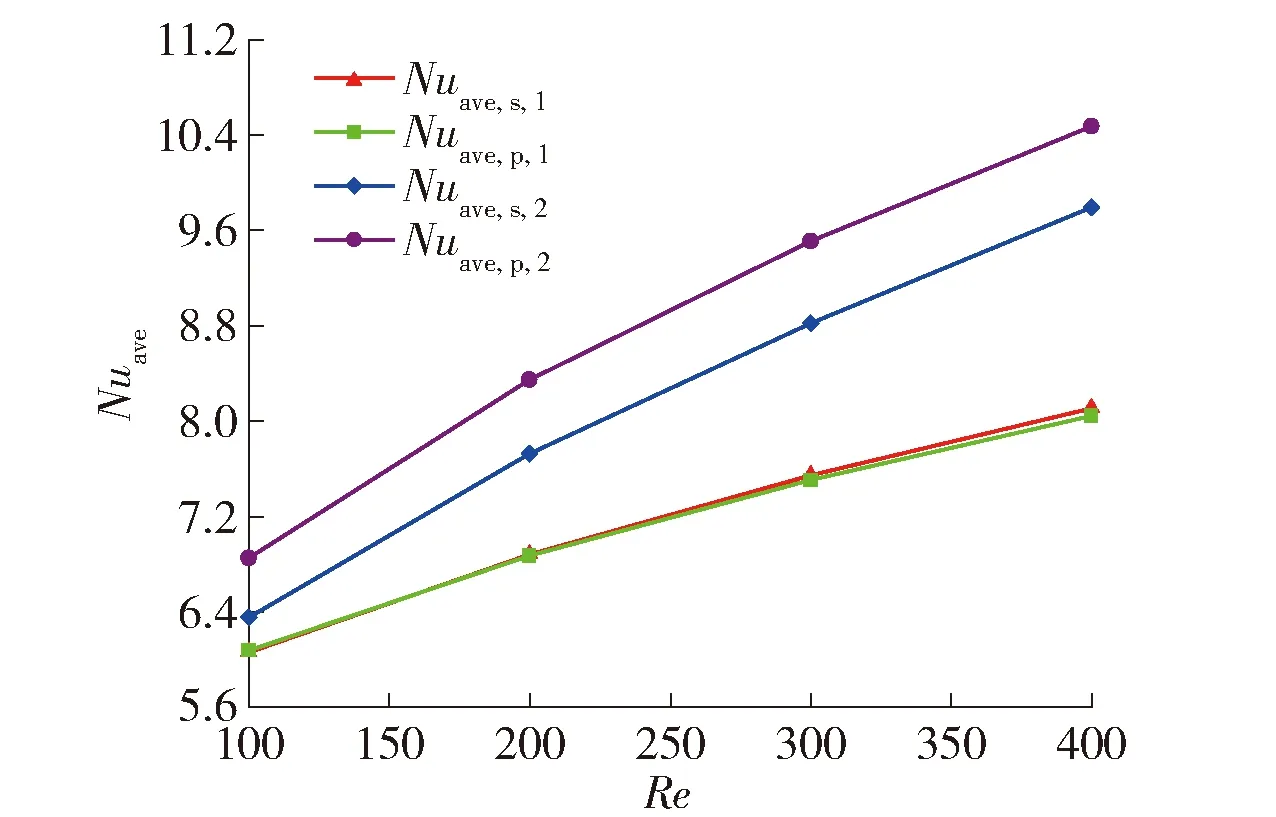
图14 平均努塞尔数随雷诺数的变化Fig.14 Variation of the average Nu with the Re
3 结论
1) 相对于稳态流动,脉动流动对矩形通道内流体流动与传热特性影响不大;而对于三角凹穴通道,脉动频率、脉动振幅和雷诺数等对其流动与传热特性有显著影响.
2) 随着脉动频率增加,三角凹穴结构微通道壁面温度先增大后减小,即存在一个极限频率使得通道壁面温度升高或降低;通道的压降与摩擦因数随着脉动频率的增加而减小,但是比稳态流动下的压降与摩擦因数要大.
3) 三角凹穴结构通道壁面温度随着脉动振幅的增加而减小,压降、摩擦因数和努塞尔数则随脉动振幅的增加逐渐增大;在高振幅时,脉动流动下的压降和摩擦系数要比稳态时大.
4) 随着雷诺数的增加,三角凹穴结构通道壁面温度与稳态流动时的差值逐渐减小,说明脉动流对降低壁面温度的作用随着雷诺数的增大而减弱.
