基于深度学习的粉煤灰混凝土氯离子浓度预测

章玉容， 余威龙， 麻雪晴， 骆天意， 王京京

(1.浙江工业大学土木工程学院， 杭州 310014； 2.浙江省工程结构与防灾减灾技术研究重点实验室， 杭州 310014；3.北京工业大学城市建设学部， 北京 100124)

混凝土中自由氯离子浓度分布是评价氯盐环境下钢筋混凝土结构钢筋锈蚀风险的重要工具[1-2]. 基于菲克第二定律，对测试得到的氯离子浓度分布曲线进行拟合，可得到氯离子扩散系数和表面氯离子浓度等结构服役寿命预测的重要参数[3-6]. 因此，精确预测氯离子浓度对结构耐久性评估与剩余寿命预测意义重大.

氯离子在混凝土中的扩散十分缓慢，且受到混凝土配合比、原材料性质和暴露环境等多种因素的影响[7-9]. 以往研究者多基于试验数据采用统计方法来预测氯离子浓度[10]，但受时间、成本和试验数据质量的影响，预测结果往往很不理想. 近年来，人工智能技术的蓬勃发展为混凝土耐久性能预测提供了新思路，众多学者使用深度学习方法对混凝土中氯盐侵蚀的相关问题展开研究. Liu等[11]通过大量的文献调研建立包含653组氯离子扩散系数的数据库，基于人工神经网络(artificial neural network, ANN)构建混凝土中氯离子扩散系数预测模型，并开展统计分析验证预测模型的性能. Asghshahr等[12]基于162组试验数据，采用ANN和分类与回归树(classification and regression tree, CART)方法开展混凝土不同深度处的氯离子浓度预测，并基于试验结果预测长期的氯离子浓度值.

ANN所构建的结构仅具有1个隐藏层，其在处理简单问题和某些特定问题时表现良好，但在处理复杂问题时会遇到困难，且存在泛化能力不足的问题[13]. 深度神经网络(deep neural networks, DNN)可以解决复杂模式分类问题并泛化能力良好，典型方法包括多层感知器(multi-layer perceptron, MLP)、卷积神经网络(convolutional neural networks, CNN)、长短期记忆(long short-term memory, LSTM)和深度置信网络(deep belief network, DBN)等. 本文基于深度学习的多层感知器模型，结合已有自然潮差环境下粉煤灰混凝土长期暴露试验的3 150组自由氯离子浓度数据，以暴露前期的试验数据预测暴露后期的自由氯离子浓度，并分析不同激活函数和不同隐藏层层数对预测结果的影响. 然后，以MLP模型的预测值和实测的自由氯离子浓度对比，并使用均方误差、平均绝对误差以及决定系数对模型评价得到最优的预测模型. 最后，以最优模型开展基于未测参数(粉煤灰掺量、暴露时间和渗透深度)的自由氯离子浓度预测.

1 试验过程

1.1 原材料

试验采用钱潮P.C32.5复合硅酸盐水泥和比表面积为540 m2/kg的一级粉煤灰作为胶凝材料，试验混凝土的水胶比为0.4. 表1给出试验混凝土的配合比以及标准环境下养护28 d后的混凝土立方体抗压强度.

表1 试验混凝土配合比及28 d抗压强度

试件一次成型浇筑并统一放置到试验现场，按照预定的暴露间隔时间分次取样和测试混凝土中的自由氯离子浓度. 试件尺寸为150 mm×150 mm×550 mm. 在标准环境下养护28 d后，将试件长边的一端4个侧面涂上长度为150 mm的环氧树脂，保证氯离子单向渗入混凝土. 图1给出混凝土氯离子渗透示意图和试验现场的试件照片.

图1 混凝土中氯离子渗透示意图和现场照片Fig.1 Diagram of chloride penetration in concrete and specimens photo

1.2 暴露环境

混凝土试块放置于浙江省嘉兴市乍浦港区一期二号码头D4泊位潮差区. 该地区的多年平均温度为15.6 ℃，年平均降水量99.4 mm. 混凝土试件所放置位置的多年平均日干燥时间约为22 h，浸没时间约为2 h，即多年平均干湿循环时间比例为11∶1.

1.3 自由氯离子浓度测试方法及浓度数据集

将试件分别在现场暴露120、240、360、520、680、840、1 160 d后取回，用混凝土研磨机从试件的表面开始沿着氯离子渗透方向逐层磨粉，每隔2 mm向内研磨至30 mm的深度，经过0.63 mm孔径筛粉后，在(105±5)℃烘箱中放置2 h，最后冷却至室温加蒸馏水配制成溶液以测定其不同深度处的自由氯离子浓度. 为消除试验材料及测试误差，从相同规格的试件中取6个芯样进行自由氯离子浓度测试. 因此，对于5种混凝土配合比、7个暴露时间、15个深度值以及6个芯样，一共可获得3 150组自由氯离子浓度的数据值.

2 MLP模型开发与性能评价

2.1 MLP模型开发

MLP模型由输入层、隐藏层和输出层组成. 输入层参数通过隐藏层的各个神经元传到输出层，然后通过损失函数和梯度下降法反向更新各个神经元的权重，以实现预测值和实际值的最小偏差. 基于深度学习的MLP模型与一般的人工神经网络相比具有更多的层次和神经元，提高了信息特征的提取能力.

工程实践和研究结果表明，混凝土自由氯离子浓度主要与混凝土的组成成分、暴露时间和暴露环境、养护机制以及渗透深度等因素有关. 本文的试验混凝土均采用标准养护并统一放置在相同的暴露环境下，故设置网络模型的输入层为4个节点，分别为渗透深度、粉煤灰掺量、水灰比、暴露时间，设输出层为1个节点，即混凝土的自由氯离子浓度. 基于深度学习的MLP模型网络结构，见图2，其中，xi代表输入变量；wi代表对应的权值；f(x)=∑xiwi+b；b为偏差.

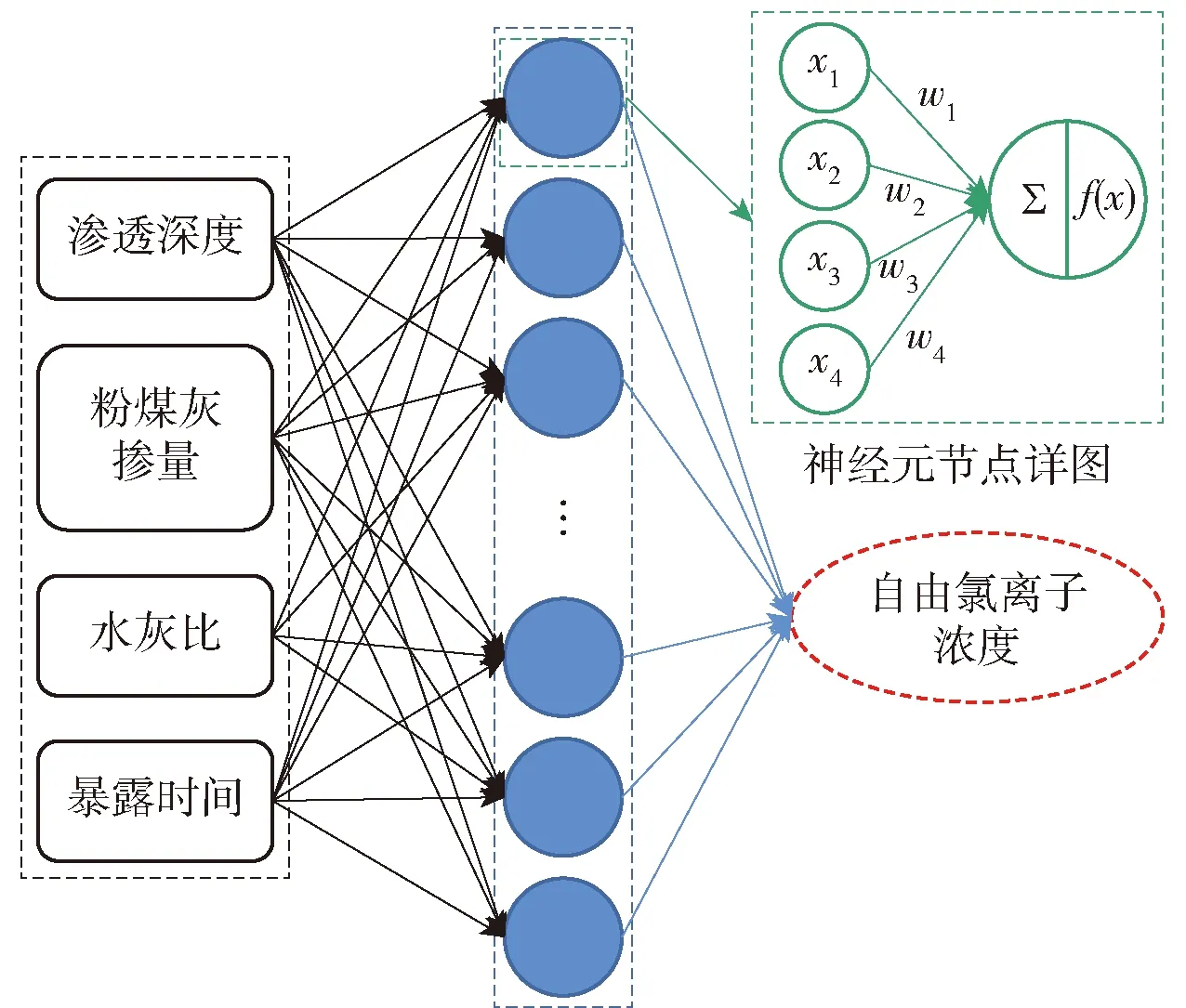
图2 MLP模型网络结构Fig.2 MLP model network structure

不同的激活函数和网络结构会产生不同的拟合结果. 激活函数给MLP加入非线性因素，使网络得以更好地解决复杂的问题，Sigmoid、ReLu和Tanh是最常用的3种激活函数. 增加隐藏层层数可以更好地刻画数据的本质特征，但会增加网络训练时间，甚至产生梯度扩散. 本文选择不同的激活函数和隐藏层层数进行预测模型的构建，探究其对预测结果的影响，以获取最佳的激活函数和隐藏层组合.

此外，氯离子传输具有很强的时变性，根据现有的试验数据进行自由氯离子浓度的长期预测是当前研究热点. 本文取暴露前840 d获得的2 700组自由氯离子浓度数据作为训练集，暴露时间为1 160 d时获得的450组数据作为测试集，即用暴露前840 d的自由氯离子浓度预测1 160 d的自由氯离子浓度，并将预测结果与实测值进行对比分析，以验证MLP模型的有效性.

2.2 数据处理预处理与评价指标

为避免参数值差距过大并提高模型的训练精度，对训练集和测试集的输入变量和输出变量进行归一化，有

(1)

式中：Y表示归一化结果；Xmin为样本中的最小值；Xmax为样本中的最大值；X为需要归一化的样本值.

同时，采用均方误差、平均绝对误差以及决定系数来验证模型预测的有效性，相应的计算公式为

(2)

(3)

(4)

3 结果讨论

3.1 预测效果分析

图3 不同激活函数的测试集预测结果Fig.3 Predict results on the test sets with different activation functions

通过3种激活函数构建的3层隐藏层的MLP模型，对训练样本进行拟合得到测试样本的预测结果，如图3所示. 3种激活函数所构建的MLP模型都能较好地逼近复杂函数，即预测值和实测值比较接近，预测效果良好. 但是ReLu函数的预测输出误差大多处于(-15%，+15%)区间内，而Sigmoid和Tanh函数的预测输出误差只有一部分处于(-15%，+15%)区间内. 表2给出不同激活函数模型预测效果的评价指标，由表2可知，通过ReLu激活函数所构建的MLP模型的预测结果R2最高且Em和Ea最低，Sigmoid次之，Tanh最差. 原因在于ReLu函数小于0时梯度为0，大于0时梯度为常数，不会导致梯度弥散，而Tanh函数和Sigmoid函数只有在0附近具有较好的激活性，在饱和区其梯度接近于0，可能会产生梯度弥散，导致预测效果相对较差. 此外，由图4给出的不同激活函数的数据序列单点相对误差可知，ReLu函数和Tanh函数单点最大相对误差和平均相对误差结果接近，均优于Sigmoid函数，这与上述分析中不同激活函数模型预测效果的评价指标的结果不相符，原因在于3个评价指标都是从整体上判断预测值是否近似于实测值，未开展单个预测点的相对误差评价.

表2 不同激活函数模型预测效果的评价指标

图4 不同激活函数的数据序列单点相对误差Fig.4 Single point relative errors of date order with different activation functions

图5 不同隐藏层层数的测试集预测结果Fig.5 Predict results on the test sets with different hidden layers

图6 不同隐藏层层数的数据序列单点相对误差Fig.6 Single point relative errors of date order with different hidden layers

为分析隐藏层层数对预测结果的影响，以预测效果最好的ReLU函数(3层)为基准，构建不同隐藏层层数的MLP模型，预测结果见图5、6及表3所示，当隐藏层层数为4层时，模型预测效果最好，其中R2最高且Em和Ea最低，预测输出误差基本处于(-15%，+15%)区间内，且平均相对误差仅为3%. 当隐藏层层数大于4层后，预测效果随层数的增加而下降，这可能是因为在误差反向传播时由于层数过多而导致的梯度衰减.

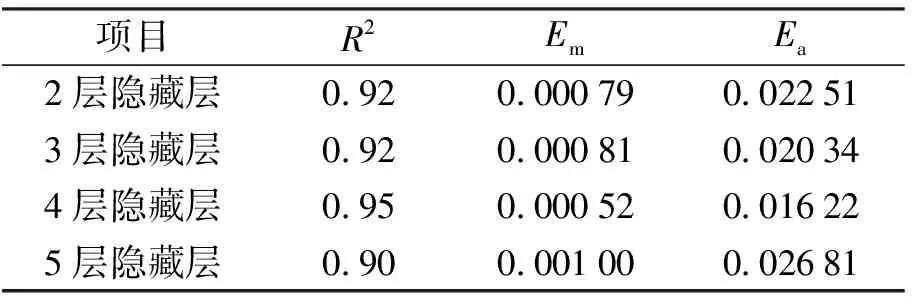
表3 不同隐藏层层数的模型预测效果评价指标

3.2 MLP模型性能评价

损失函数表示单个样本的真实值和模型预测值之间的偏差，通常用于衡量模型的性能[14]，损失函数越小表明模型的拟合程度越好. 由3.1模型预测效果可知，当隐藏层层数为4层、激活参数为ReLu函数时MLP模型的预测效果最优，故对该模型的损失函数进行分析. 采用均方误差作为损失函数，损失函数值与迭代次数的关系见图7. 由图7可知，损失函数值随迭代次数增加先急剧降低而后趋于平稳. 损失函数的训练周期变化可以判断模型的稳定性. 图7表明，该模型在迭代200次左右达到稳定，且不再出现震荡或跳跃的现象，迭代1 000次后，损失值为0.006 9，表明本文所构建的MLP模型具有较好的鲁棒性.

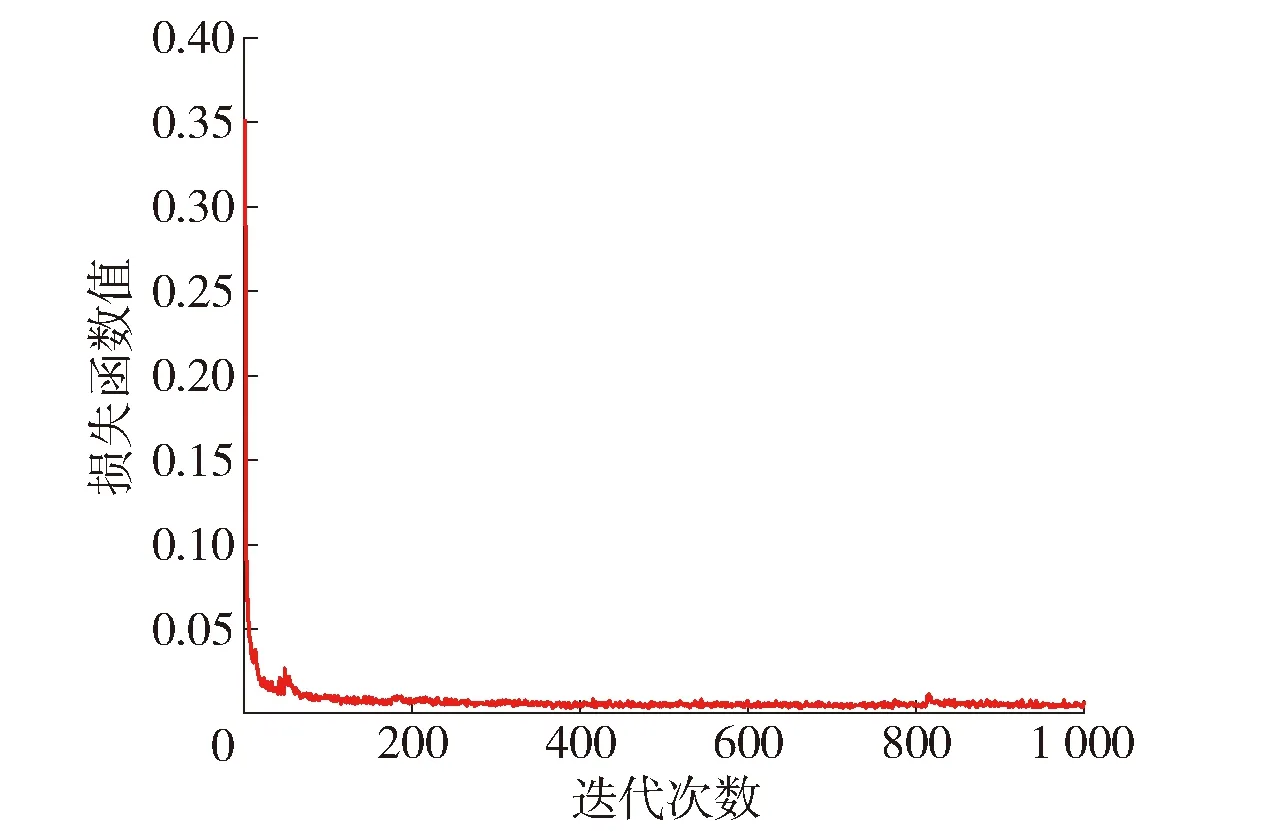
图7 损失函数值与迭代次数之间的关系Fig.7 Relationship between loss value and iteration times

3.3 影响参数敏感性分析

为探究输入参数对输出参数影响程度，采用Python_Salib库中Sobol’方法[15]对模型的4个输入变量进行敏感性分析. Sobol’是一种基于方差的的全局敏感性定量分析方法，能有效分析多个高度非线性变量之间相互作用的敏感性. 4个输入变量对自由氯离子浓度的影响见图8.

图8 输入变量的重要性程度Fig.8 Importance of input variable

图8表明，4个输入变量对自由氯离子浓度影响程度依次为渗透深度、暴露时间、水灰比、粉煤灰掺量. 由于本文的试验采用固定的水胶比，水灰比和粉煤灰掺量是相关变量，因此水灰比对自由氯离子浓度的敏感性在一定程度上反映了粉煤灰的敏感性.

3.4 基于未测参数的自由氯离子浓度预测

基于现有的试验数据，采用所构建的MLP模型预测未知粉煤灰掺量、暴露时间和渗透深度的混凝土中自由氯离子浓度，并与高延红等[16]基于菲克第二定律建立的时变性模型预测结果进行对比.

开展未测深度处的自由氯离子浓度预测时，以暴露时间840 d、粉煤灰掺量20%以及水灰比0.5为例，表4给出渗透深度分别为11 mm和19 mm的自由氯离子浓度预测值，并与邻近深度处的实测值进行对比，结果见表4.

表4 未测深度处的自由氯离子浓度预测结果

众所周知，混凝土中自由氯离子浓度随着渗透深度的增加而逐渐降低. 由表4可知，采用MLP模型预测渗透深度分别为11 mm和19 mm时的自由氯离子浓度值，其预测结果与实际情况相符，而高延红等[16]基于菲克第二定律得出的预测值小于更深渗透深度的自由氯离子浓度实测值，有悖于实际情况，原因在于应用菲克第二定律设定了诸多的假设. 上述结果表明本文所建立的MLP模型能很好地预测混凝土中未测深度处的自由氯离子浓度.

此外，在混凝土自由氯离子浓度的时变性分析中，以渗透深度10 mm、粉煤灰掺量20%以及水灰比0.5为例开展未测暴露时间的自由氯离子浓度预测，预测结果如表5所示. 将预测结果与邻近暴露时间的自由氯离子浓度实测值对比，可知本文所建立的MLP模型预测混凝土中的长期自由氯离子浓度的效果要略优于高延红等[16]建立的时变性模型.

同时采用MLP模型开展基于未知粉煤灰掺量(即未知水灰比)的混凝土自由氯离子浓度值预测，结果见表6.

表5 未测暴露时间的自由氯离子浓度预测结果

表6 未知粉煤灰掺量的自由氯离子浓度预测结果

由表6可知，当粉煤灰掺量低于40%时，MLP模型具有良好的预测效果. 当粉煤灰掺量大于40%时，预测值与实测结果不相符，即不在邻近粉煤灰掺量的实测值区间内，该现象在图6中给出的单点相对误差的后半段曲线中相对误差突然变大也有所体现.

4 结论

本文基于深度学习理论构建了混凝土自由氯离子浓度的MLP预测模型，主要研究结果如下：

1) MLP可以准确预测混凝土自由氯离子浓度，且在隐藏层层数为4层、激活函数为ReLu函数时模型具有最佳预测效果.

2) 由损失函数的训练周期变化可知，所构建的MLP模型具有较强的鲁棒性；由输入参数敏感性分析可知，渗透深度对混凝土中自由氯离子浓度的影响最大.

3) 基于未测参数的自由氯离子浓度预测结果表明，本文所构建的 MLP模型预测效果良好，与实测结果相符，表明MLP模型具有精度高和适用范围广泛的特点，可作为氯盐环境下混凝土中自由氯离子浓度预测的新方法.