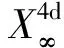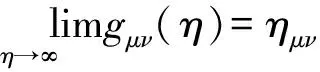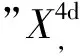广义观测相对论:时空在爱因斯坦广义相对论中为什么弯曲?(上篇)
——GOR理论的建立
2023-02-09阮晓钢
阮晓钢
(北京工业大学信息学部, 北京 100124)
《北京工业大学学报》2020年第1期刊载了笔者的《观测与相对论:光速在爱因斯坦狭义相对论中为什么不变?》[1],报道了物理学一项新的理论:观测相对论(observational relativity, OR). OR理论给予我们关于爱因斯坦狭义相对论全新的认识.
根据OR理论[1-3],物理学一切理论体系皆依赖于观测,不同观测体系导致不同理论体系:伽利略变换和牛顿定律是理想观测体系的产物;而洛伦兹变换和爱因斯坦狭义相对论则是光学观测体系的产物.
OR理论发现,一切相对论性现象皆观测效应,而非客观真实的自然现象,其根源在于观测局域性(observational locality):η<∞.OR理论证明:惯性时空中,信息波速度η(观测媒介传递观测信息的速度)相对于观测者具有观测上的不变性. “光速不变性”是“信息波速度不变性”之特例,仅当光或电磁相互作用担当观测媒介时成立. 观测信息并非只能由光或电磁相互作用传递;理论上,任意物质波皆可为信息波,任意物质运动形式皆可为观测媒介.
OR理论,基于不同于爱因斯坦狭义相对论的逻辑前提,却导出了与洛伦兹变换形式上完全相同的时空变换关系:“广义洛伦兹变换”,其中,时空变换因子Γ=√(1-v2/η2),η具有明确的物理意义,即观测媒介传递观测信息的速度,并非一定是光速c.广义洛伦兹变换概括统一了洛伦兹变换和伽利略变换,在玻尔对应原理下,既与洛伦兹变换严格对应:η=c时约化为洛伦兹变换;又与伽利略变换严格对应:η→∞时约化为伽利略变换.这种严格的对应关系,印证了广义洛伦兹变换既与伽利略变换又与洛伦兹变换具有逻辑上的一致性,同时,也印证了广义洛伦兹变换和OR理论逻辑上的自洽性和理论上的正确性.
物理学历史上,玻尔对应原理(correspondence principle)具有特殊地位[4].玻尔对应原理阐明了量子力学与经典力学的对应关系:普朗克常数h→0时,量子体系同构一致地趋同于经典体系,意味着量子力学与经典力学具有逻辑上的同构一致性,因而,具有某种内在联系和对应关系.更重要地,玻尔对应原理成为发展物理学新理论新模型重要的思想基础和指导原则.正是对应原理,帮助玻尔建立了氢原子模型[5-7],导致矩阵力学建立[8-10],促进量子力学发展[11-12].
OR理论[2-3]发现:普朗克常数h,实为光学观测体系之测量参数,代表光学观测体系之分辨力及其观测上的不确定性.实际上,不同观测体系,其信息波速度η不同,观测分辨率不同,因而,具有不同的普朗克常数:hη,谓之“广义普朗克常数”.OR理论建立了一个极为重要的恒等式:hηη=C(常数C≡hc).这一关系式意味着,普朗克常数h只是广义普朗克常数hη之特例:仅当观测体系为光学体系(η=c)时hη=h.特别值得注意,hηη=C正是玻尔对应原理的形式化表达:广义普朗克常数趋于零(hη→0)时,量子力学情形同构一致地对应变换为经典力学(η→∞)情形.
OR理论揭示了物理学不同理论体系之间的内在联系,同时,揭示了物理学不同观测体系之间的内在联系,赋予玻尔对应原理更为普遍的意义. 理论上或逻辑上,物理学一切理论体系皆应具有其内在的对应关系,因循共同的逻辑前提或公理体系. 实际上,无论是伽利略不变性,还是狭义相对性原理或广义协变原理,甚至等效原理,都是关于物理学不同理论体系之对应关系的原理. 本文基于OR理论和玻尔对应原理,建立“广义对应原理”,概括了玻尔对应原理和相对性原理. 广义对应原理的建立,将有助于物理学新理论的发展和旧理论的统一,并且,有助于物理学理论体系之逻辑上的一致性和自洽性检验.
霍金[13]在其《时间简史》中说:物理学支离破碎,被分割成许多局部理论(partial theory);物理学家们的终极目标是将它们统一起来. 伽利略- 牛顿理论和爱因斯坦相对论,无疑是物理学史上最为伟大的理论;然而,我们并未真正地意识到,无论是伽利略- 牛顿理论还是爱因斯坦相对论,都只是霍金言下的局部理论.
基于广义对应原理,本文将爱因斯坦广义相对论由光学观测体系推广至一般观测体系,将OR理论由惯性时空推广至引力时空,建立“广义观测相对论”(general observational relativity, GOR),概括统一了牛顿万有引力论和爱因斯坦广义相对论.
OR理论之前,关于狭义相对论[14],我们不能理解光速为什么不变. 现在,OR理论告诉我们:光速并非真地不变;所谓“光速不变”,实乃观测效应,与一切观测上的相对论性一样,并非客观真实的自然现象,其根源和本质在于观测局域性. 同样地,GOR理论之前,关于广义相对论[15],我们不能理解时空为什么弯曲. GOR理论将会阐明:时空并非真地弯曲——客观真实的时空是不会弯曲的!所谓“时空弯曲”,实乃观测效应,与一切观测上的相对论性现象一样,并非客观真实的自然现象,其根源和本质同样在于观测局域性. 实际上,无论是狭义的还是广义的相对论性现象,都只是观测局域性所致的表观现象.
GOR理论将会阐明,牛顿万有引力论和爱因斯坦广义相对论同为GOR理论之局部理论,但分属不同的观测体系. 爱因斯坦广义相对论是光学观测体系的产物,服务于光学观测体系,其所描绘的引力时空是物理世界透过光学观测体系呈现给我们的一种光学观测映像,并非完全客观真实的自然世界;而牛顿万有引力论则是理想观测体系的产物,服务于理想观测体系,其所描绘的引力时空是理想化观测情形下的物理世界,乃客观真实的自然世界.
广义对应原理意义下,GOR理论与牛顿万有引力论和爱因斯坦广义相对论具有严格的对应关系:光学观测体系情形,GOR场方程严格地约化为爱因斯坦场方程,GOR运动方程严格地约化为爱因斯坦广义相对论之运动方程;理想观测体系情形,GOR场方程严格地约化为牛顿万有引力定律之泊松方程形式,GOR运动方程严格地约化为牛顿第二定律之运动方程形式. 这种严格的对应关系表明,GOR理论,既与爱因斯坦广义相对论逻辑上一致,又与牛顿万有引力论逻辑上一致;同时,这种严格的对应关系印证了GOR理论逻辑上的自洽性和理论上的正确性.
本文是笔者向北京工业大学学术委员会提交的科学研究报告[16],内容包括:
引言
1 观测与观测代理
2 广义对应原理
3 GOR时空理论:引力时空的观测和度量
4 伽利略时空定理:理想代理对弱场近似
5 GOR场方程的建立
6 球对称引力时空之GOR场方程解
7 GOR理论与行星轨道之旋进
8 GOR理论与光之引力偏折
9 GOR理论与光之引力红移
10 GOR理论与引力波
11 GOR理论与宇宙大爆炸
12 牛顿理论和爱因斯坦理论的统一
GOR后记
人类及其物理学需要重新认识伽利略的思想和牛顿力学,重新认识爱因斯坦的相对论,重新认识引力相互作用及其相对论性现象,重新认识爱因斯坦基于广义相对论所做出的科学预言,重新认识“引力波”论,重新认识“宇宙大爆炸”论,重新认识客观世界,重塑人类的时空观和自然观.
GOR理论将给予我们关于牛顿万有引力论和爱因斯坦广义相对论全新的认识.
1 观测与观测代理
GOR理论试图将OR理论由惯性时空推广至引力时空. OR理论之基本概念和基本定义,以及OR理论之基本前提和基本结论,都将是GOR理论的基础.
OR理论[1]认为:“人类对客观世界的认识,既依赖于观测,又制约于观测. ”然而,我们并未真正地认识到观测和观测媒介在物理学及其理论体系中所扮演的角色及其特殊地位. 人们以为,爱因斯坦相对论是更好的理论,而伽利略- 牛顿理论则只是爱因斯坦相对论的某种近似. 其实,伽利略- 牛顿理论和爱因斯坦相对论分属不同观测代理,其正确性或有效性取决于其所依赖的观测体系和观测媒介.
1.1 观测媒介(observation medium)
观测,即利用我们的感官或观测仪器获取被观测对象的信息. 自然地,被观测对象的信息必须借助于一定的媒介,以一定的方式,传递至我们的感官或观测仪器,方能被我们感知或观测.
20世纪20年代,德布罗意[17-19]杜撰了“物质波”(matter wave)概念,提出德布罗意假设:物质具有波粒二象性,运动起来既似粒子,又似波. 波,具有一种重要特性:可调制性(modulability). 可调制性使波拥有了传递信息的特质. 因此,理论上,作为物质波,任意物质运动形式,皆可扮演观测媒介的角色,为观测者传递被观测对象的信息.
OR理论建立了信息波(information wave)和信息子(informon)的概念[2-3]. 所谓“信息波”,即作为观测媒介的物质波,为观测者传递被观测对象的信息;而所谓“信息子”,即构成信息波的物质粒子. Železnikar[20]曾用Informon指代Informational Entity. 当我们用眼睛看世界的时候,光波即信息波,光子即信息子;而当我们用耳朵听世界的时候,声波即信息波,气体分子即信息子. 理论上,一切物质波,包括声波、水波、光波、电波、地震波、引力波,皆可为信息波;一切物质粒子,包括光子、电子、质子、中子、原子、分子、中微子、引力子,甚至一块岩石,以及被观测对象自身,皆可为信息子.
OR理论[1-3]表明,爱因斯坦相对论是以光为媒的理论体系,其中,信息波即光波,信息子即光子. 然而,在我们的观测活动中,为观测者传递观测信息的观测媒介,并非只能是光波或光子.
或许,将来有一天,“引力波”将会成为“信息波”而“引力子”将会成为“信息子”,为我们传递观测信息. 实际上,“引力波天文学”的概念已经形成[21]. 然而,人们似乎并未认识到,引力波可能会是超光速甚至远超光速的“信息波”.
1.2 观测局域性(observational locality)
自然地,不同观测媒介传递观测信息的速度会有所不同:常温常压之大气声波速度va≈340 m/s;水下超声波速度vs≈1 450 m/s;光速c≈3×108m/s;依拉普拉斯[22]计算,引力或引力波速度vg>7×106c,远超光速. 然而,无论如何,观测媒介传递观测信息的速度是有限的,此即观测上的局域性. 这种观测局域性必然反映在物理学之理论体系或时空模型中.
局域性(locality),或局域性原理,在现代物理学中扮演着重要角色[23]. 爱因斯坦的局域性观念与其光速不变性假设联系在一起[24]:光速不可超越. 1935年,爱因斯坦基于光速不可超越的局域性观念,与同事Podolsky和Rosen一起,构思了一个著名的思想实验:量子纠缠,史称EPR佯谬[25],以质疑量子力学的完备性. 然而,似乎越来越多的EPR实验支持量子纠缠和超光速现象[26-27].
无论光速是否不可超越,有一点是肯定的:宇宙不存在超距作用;物质或信息,跨越空间需要时间. 然而,物理学家们极少将物理世界之相互作用的局域性明确地与观测或观测信息的传递联系起来.
为了明确物理上的局域性对观测的制约,OR理论建立了“观测局域性原理”.
观测局域性原理(The Principle of Observational Locality, POL)[1]:任意观测代理OA(η)之信息波速度η有限,即η<∞;观测信息跨越空间需要时间.
OR理论发现[1-3]:观测局域性是一切相对论性现象的根源和本质. 一切相对论性现象,包括狭义相对论中的“光速不变”效应和广义相对论中的“时空弯曲”效应,皆观测效应,乃观测局域性(η<∞)所致,并非客观真实的自然现象.
1.3 观测代理(observation agent)
OR理论杜撰了一个新的概念:“观测代理”,替代之前使用的“观测体系”概念,以区别于“观测系统”(observation system),以及“观测系”或“参考系”(reference system)的概念;更重要地,“观测代理”有其特定的内涵. 实际上,闵科夫斯基4d时空就是一种特定的观测代理,即光学观测代理.
1.3.1 闵科夫斯基时空
爱因斯坦曾说:“我们应该把自己限定于4d空间和连续的实数坐标变换群.”[28]他所指的是闵科夫斯基时空,即闵科夫斯基专为爱因斯坦狭义相对论打造的4d时空坐标框架[29-30].
开始,爱因斯坦并不认为闵科夫斯基4d时空坐标框架对于相对论有何必要性或重要意义. 然而,开展广义相对论研究之后,爱因斯坦渐渐体会到,自己的广义相对论似乎不得不建立在闵科夫斯基创建的4d时空坐标框架之中,遂将闵科夫斯基时空由狭义相对论之惯性时空扩展至广义相对论之引力时空,并给予闵科夫斯基的4d时空形式化方法高度评价.
闵科夫斯基时空乃一定义了时空度规(metric)gμν(μ,ν=0,1,2,3)和线元ds的4d微分流形(differentiable manifold),因而,乃度量时空(metric spacetime):
(1.1)
式中:OA(c)代表以光或电磁相互作用为观测媒介的观测体系,即光学观测体系;X4d(c)即OA(c)之观测时空:x0代表1d时间,(x1,x2,x3)代表3d空间,可采用笛卡儿坐标(x,y,z).
X4d(c)或为惯性时空或为引力时空:狭义相对论之X4d(c)即“闵科夫斯基时空”,乃惯性时空,是平直的,其中,gμν=ημν=diag(+1,-1,-1,-1)乃不变张量,ημν被称作“闵科夫斯基度规”;广义相对论之X4d(c)乃引力时空,gμν=gμν(xα,c)依赖于时空坐标xα和光速c,因而,引力时空显得有些弯曲.
1.3.2 观测代理之定义
广义相对论中,爱因斯坦将闵科夫斯基4d时空坐标框架由惯性时空扩展至引力时空. 而OR理论却将闵科夫斯基4d时空坐标框架由光学观测体系扩展至一般观测体系.
爱因斯坦并未真正地意识到,自己创建的相对论,包括狭义相对论和广义相对论,都只是借助光观察物理世界的理论,并且,未能真正地理解闵科夫斯基时空的本质意义. 闵科夫斯基时空并不仅仅在于为爱因斯坦相对论提供一种4d时空坐标框架. 实际上,式(1.1)中的OA(c)代表着一种特定的观测体系:光学观测体系,其中,为观测者传递观测信息的观测媒介是光,其传递观测信息的速度乃光速c.
OR理论[1-3]表明:理论上,一切物质运动形式皆可作为观测媒介传递观测信息. 不同的观测媒介,意味着不同的观测体系,OR理论谓之“观测代理”:眼睛是一类观测代理,以光波为观测媒介;耳朵则是另一类观测代理,以声波为观测媒介. 我们的观测可以借助不同的“观测代理”,其中,一切物质运动形式皆可作为传递观测信息的观测媒介.
类比闵科夫斯基4d时空坐标框架OA(c),以“信息波”之速度η替代式(1.1)中的光速c,则“观测代理”的概念可如下定义.
定义1.1(观测代理):以特定观测媒介传递观测信息的观测体系被称为“观测代理”,记作OA(η),定义为如下4d度量时空(metric spacetime):
(1.2)
式中:OA(η)之观测媒介可为任意物质运动形式或任意物质波,η为观测代理OA(η)之“信息波”的速度,即OA(η)之观测媒介传递观测信息的速度;X4d(η)代表OA(η)之4d观测时空:x0代表1d时间,(x1,x2,x3)代表3d空间(可采用笛卡儿坐标(x,y,z));gμν乃时空度规,为一2阶张量:gμν=ημν时X4d(η)为平直时空,gμν=gμν(xα,η)时X4d(η)为弯曲时空;ds乃度量时空之线元.
观测代理OA(η)概括了闵科夫斯基4d时空坐标框架OA(c):η→c时,OA(η)即式(1.1)之OA(c).
正如爱因斯坦广义相对论需要建筑在光学观测代理OA(c)之形式化框架之上,GOR理论需要建筑在一般观测代理OA(η)之形式化框架之上.
1.3.3 理想代理与现实代理
理论上,一般观测代理OA(η)之观测媒介可为任意物质运动形式,而其中的η可为任意值.特定观测代理意味着采用特定观测媒介的特定观测体系.
观测代理可以划分为理想的和现实的2类.
理想观测代理
“理想观测代理”,或称“伽利略代理”,记作:OA∞(OA(∞)),其信息波之速度η被理想化作无穷大,因而,不存在观测局域性(η→∞),观测信息的传递无须时间.
特别值得指出,伽利略- 牛顿理论之观测代理正是“理想观测代理”.然而,理想代理OA∞是可望而不可及的,只能存在于人们的理性之中.
现实观测代理
“现实观测代理”,即客观存在的观测代理,是人类可用于感知或观测客观世界的观测代理.
如表1所示,物理世界存在各种各样的现实的观测代理:陆地机器人之声纳可谓“蝙蝠代理”OA(vS)(vS为大气超声波速度);水下机器人之声呐可谓“海豚代理”OA(vU) (vU为水中超声波速度);以光或电磁相互作用为媒的观测代理可谓“光学观测代理”或“爱因斯坦代理”OA(c)(c为真空光速);
以引力波为媒的观测代理可谓“引力波代理”或“拉普拉斯代理”OA(vG)(vG>7×106c为拉普拉斯的引力速度[22]).

表1 人类感知客观世界可以借助不同的观测代理
一切现实观测代理OA(η)皆存在观测局域性(η<∞). 不同观测代理,采用不同观测媒介,传递观测信息的速度不同,因而,制约于不同程度的观测局域性,呈现不同程度的相对论性现象.
OR理论已经阐明,不同观测代理导致不同理论体系或时空模型(见表1)[1]:洛伦兹变换和爱因斯坦狭义相对论是光学观测代理OA(c)的产物;而伽利略变换和牛顿力学则是理想观测代理OA∞的产物. 因此,不同理论体系或时空模型服务于不同观测代理.
GPS卫星系统采用无线电通信,其观测代理即光学代理OA(c),因而,其时间测定和校准需要依赖爱因斯坦相对论:dτ=dt(c)√(1-v2/c2).
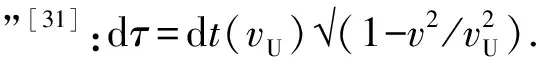
未来,人类或许将会发明超光速观测代理,比如引力波代理OA(vG);或许,正如拉普拉斯的计算,引力波速度远超光速[22]:vG>7×106c. 超光速观测代理将为我们传递更为实时的观测信息,呈现给我们更为真实的客观世界.
爱因斯坦相对论,包括狭义的和广义的,是光学代理OA(c)之理论体系,其呈现给观测者的是客观世界的一种光学映像,并非完全真实的客观世界. 伽利略- 牛顿理论是理想代理OA∞之理论体系,其呈现给观测者的是客观世界之真实写照. 而观测相对论,包括OR理论和GOR理论,则是一般观测代理OA(η)的理论体系,能将伽利略- 牛顿理论和爱因斯坦相对论概括并统一起来.
1.4 观测时空和观测物理量
时间和空间是宇宙的重要属性. 人类对时间和空间的认识,从朴素的绝对时空观到如今占据统治地位的相对时空观,经历着曲折的认知进程.
伽利略和牛顿持绝对时空观[32-35]:空间永恒不变地存在着;而时间则静静地流淌着. 伽利略变换代表着绝对时空观:时间和空间相互独立,空间即空间,时间即时间;不同观测者持相同时间,无须时间变换. 马赫和爱因斯坦持相对时空观[36-38]:空间,是相对的;时间,也是相对的. 洛伦兹变换,或称“菲兹杰拉德- 洛伦兹变换”[39-40],代表着相对时空观:时间和空间相互依存;时间亦空间,空间亦时间. 于是,时间和空间合并形成了“时空”(spacetime)概念.
如今,主流物理学界普遍赞成相对时空观,因为,观测和实验似乎更倾向于支持洛伦兹变换和爱因斯坦相对论. 然而,物理学家们没能意识到,洛伦兹变换和爱因斯坦相对论是光学观测代理OA(c)的产物. 我们的观测和实验大多依赖于OA(c),即光学代理;这正是我们的观测和实验大多支持洛伦兹变换和爱因斯坦相对论的真正原因. 如果我们能借助理想代理OA∞观测客观世界,那么,我们的观测和实验将会倾向于支持伽利略变换- 牛顿理论.
宇宙,包括时空和物质,乃客观存在.
人类必须依赖自己的感官,或者,借助自己发明的观测仪器,方能感知或观测到时空及其物质的存在.然而,制约于观测域性,任意观测代理OA(η)(η<∞)所能呈现给我们的时空X4d(η)都只是一种“观测时空”:客观时空的一个映像而已,并非完全客观真实.
因此,物理学需要将“观测时空”与客观真实的“固有时空”区别开来.
所谓“观测时空”,即观测者借助特定观测代理OA(η)所观测到的时空X4d(η).制约于OA(η)的观测局域性(η<∞),观测时空X4d(η)之物理量的观测值未必等同于其客观真实的物理量.
因此,物理学需要将“观测物理量”与客观真实的“固有物理量”区别开来.
那么,什么是客观真实的物理量呢?
物理量的观测值依赖于观测:相对于不同观测者或不同观测代理,同一物质体系之同一物理量可能具有不同观测值,此即“观测物理量”.然而,客观真实的物理量不依赖于观测,不依赖于观测者,不依赖于观测体系或观测代理,可谓“固有物理量”.
根据OR理论[1],相对论性现象实为观测效应,源于观测局域性,同时,依存于2种因素:第一,相对运动(狭义相对论之情形);第二,相互作用(广义相对论之情形).OR理论有时采用“自由时空”作为“惯性时空”的替代概念.所谓“自由时空”,即不存在任何力或相互作用的时空.我们约定:“自由时空”记作SF;而“观测物理量”的概念和“固有物理量”的概念则可如下定义于自由时空SF.
定义1.2(观测物理量和固有物理量):设有被观测对象P和观测者O及其观测代理OA(η).若O借助OA(η)观测到P之物理量U,则称U为OA(η)或O观测到的P之“观测物理量”;若P和O相对静止于自由时空SF,或OA(η)为理想观测代理OA∞,则称U为P之“固有物理量”,记作Uo.
定义1.2意味着,观测者O观测所得之“观测物理量”U依赖于观测和观测代理OA(η):U=U(η).OR理论已经阐明,GOR理论将会进一步阐明,制约于观测代理OA(η)之观测局域性(η<∞),观测者O通过观测代理OA(η)所观测到的物理量,“观测物理量”,并不等同于P之“固有物理量”.
OR理论已经阐明,GOR理论将会进一步阐明,η→∞时U→Uo:理想观测代理OA∞之一切“观测物理量”趋同于“固有物理量”.理想观测代理OA∞代表着客观真实的物理世界.因而,定义1.2之“固有物理量”代表着客观真实的物理量.
定义1.2对“固有物理量”的测定,要求观测者O与被观测对象P相对静止,更严格地,要求P是静态的,即其物理量不随时间变化,除非,观测者O之观测代理OA(η)即理想观测代理OA∞.
某种意义上,绝对客观真实的“固有物理量”是不可观测的,或者说,是无法测定的. 或许,正因为如此,我们的物理学需要将“观测物理量”与客观真实的“固有物理量”区别开来.
1.5 信息波速度不变性
“观测相对论”理论基于时间定义及其“时频比不变性”导出OR理论之整个理论体系,其中,从某种意义上说,最重要的逻辑结论即“信息波速度不变性”定理[2-3]. 正是“信息波速度不变性”定理,揭示了“光速不变性”的根源和本质.
“信息波速度不变性”不仅是OR理论的逻辑结论,而且,将是GOR理论重要的逻辑前提.
1.5.1 光速不变性与爱因斯坦相对论
众所周知,“光速不变性”假设是爱因斯坦狭义相对论最重要的逻辑前提. 然而,却有许多人,甚至一些职业物理人,不知“光速不变性”假设其实也是爱因斯坦广义相对论的逻辑前提.
关于光速不变性
1887年,因循麦克斯韦[41]的建议,迈克尔逊和莫雷[42]开展了一项旨在捕捉以太(Ether)的实验. 他们没能发现以太,却遇到了一个问题:伽利略速度叠加原理失效了. 迈克尔逊- 莫雷实验显示,光速与地球轨道速度叠加,仍然是光速.
针对迈克尔逊- 莫雷实验所观测到的现象,菲兹杰拉德[39]猜想:空间会收缩;洛伦兹[40]猜想:时间会膨胀. 于是,诞生了菲兹杰拉德- 洛伦兹变换,后人习惯称之为“洛伦兹变换”. 可见,洛伦兹变换原本只是一个唯象模型,而非理论或逻辑结论.
1905年,爱因斯坦[14]提出“光速不变性”假设.
光速不变性假设(The Hypothesis of the Invariance of Light Speed)[14]:惯性时空中,真空光速c相对于任意观测者都是相同的和不变的.
正是基于“光速不变性”假设,爱因斯坦得以从理论上导出洛伦兹变换,最终,建立起爱因斯坦狭义相对论之整个理论体系.
人们以为,爱因斯坦的“光速不变性”假设是正确无疑的,得到包括迈克尔逊- 莫雷实验等观测实验的验证和支持,因而,称其为“光速不变性”原理.
然而,“光速不变性”并不具有作为“原理”所应具备的“不证自明”的特性. 尽管“光速不变性”似乎得到了观测和实验支持,然而,人们知其然而不知其所以然,至今不能真正地理解光速为什么不变.
光速不变性与光学代理OA(c)
闵科夫斯基时空,原本,是惯性时空;后来,爱因斯坦为建立广义相对论将其扩展至引力时空. 实际上,闵科夫斯基时空,无论原本的或扩展的,皆光学观测代理OA(c)之4d时空坐标框架X4d(c),与“光速不变性”原理联系在一起.
惯性时空中,依OA(c)之式(1.1),成立:
ds2=c2g00dt2+2cg0idxidt+gikdxidxk
(1.3)
式中:dt为观测时元;dτ为固有时元.
特别值得注意,dt与dτ的比值γ=dt/dτ即洛伦兹因子,或称“时空变换因子”,且
(1.4)
其中,洛伦兹因子γ隐喻着“光速不变性”.
本质上,光学观测代理OA(c)之4d时空坐标框架X4d(c)是“光速不变性”原理的形式化表达:X4d(c)之时间轴x0=ct代表着“光速不变性”.
特别需要指出,光学观测代理OA(c)之观测时空X4d(c)(式(1.1)),既是爱因斯坦狭义相对论之4d时空坐标框架,也是爱因斯坦广义相对论之4d时空坐标框架.因而,“光速不变性”原理,既是爱因斯坦狭义相对论之逻辑前提,也是爱因斯坦广义相对论之逻辑前提.通过“等效原理”,“光速不变性”即可在爱因斯坦广义相对论中发挥其作为“原理”的作用[15,31].
1.5.2 信息波速度不变性定理
“光速不变性”只是爱因斯坦狭义相对论一个假设性的逻辑前提,而“信息波速度不变性”则是OR理论从理论上导出的逻辑结论.
信息波速度不变性定理(The Theorem of the Invariance of Information-Wave Speed)[1]:惯性时空中,任意观测代理OA(η)之信息波速度η相对于任意观测者都是相同的,具有观测上的不变性.
根据“信息波速度不变性”定理,无论爱因斯坦的“光速不变性”还是OR理论的“信息波速度不变性”,其实,都只是一种观测上的相对论性现象,即“观测效应”,并非客观真实的自然现象.
物理世界并不真地存在“不变的速度”(invariant speed):光速并非真地不变. “光速不变性”只是“信息波速度不变性”一个特例,仅当光作为观测媒介时成立. 任何物质运动形式或物质波,当其作为观测媒介为观测者传递观测信息时,其速度相对于惯性观测者就会呈现出这种观测上的不变性.
实际上,与其说迈克尔逊- 莫雷实验是对爱因斯坦之“光速不变性”假设的支持,不如说是对OR理论之“信息波速度不变性”的支持.
一群大雁从天空中飞过,可以用眼睛看,传递大雁信息的观测媒介将是光波;也可以用耳朵听,传递大雁信息的观测媒介则是声波. 迈克尔逊- 莫雷实验中,被观测对象是光(一群光子). 那么,是什么作为观测媒介在为迈克尔逊和莫雷传递有关光之运动的信息呢?当然,是光自身!换句话说,迈克尔逊- 莫雷实验之观测代理即光学观测代理OA(c),其“信息波”即光波. 因而,光速在迈克尔逊- 莫雷实验中呈现出观测上的不变性.
迈克尔逊- 莫雷实验所呈现出的“光速不变性”现象,其实,正是“信息波速度不变性”的体现.
1.5.3 信息波速度不变性与GOR理论
“信息波速度不变性”,不仅是OR理论的逻辑结论,而且,还将是GOR理论之逻辑前提. 这正是我们在此论述“信息波速度不变性”的原因.
OR时空和GOR观测时空乃一般观测代理OA(η)之4d时空坐标框架X4d(η)(见式(1.2)),与“信息波速度不变性”联系在一起.
OR时空乃惯性时空,依式(1.2),成立:
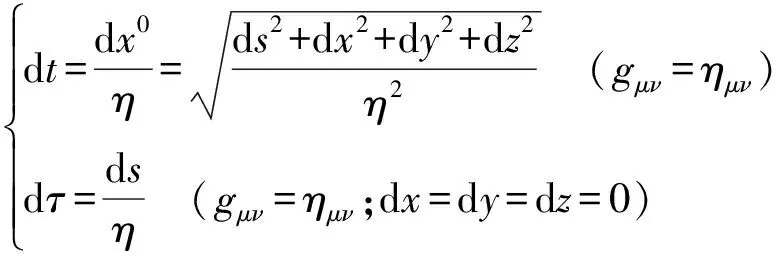
(1.5)
其中,观测时元dt与固有时元dτ的比值Γ(η)=dt/dτ即GOR时空变换因子
(1.6)
其中,时空变换因子Γ隐喻着“信息波速度不变性”.
本质上,OR时空和GOR观测时空,即一般观测代理OA(η)之4d时空坐标框架X4d(η),是“信息波速度不变性”的一种形式化表达.X4d(η)之时间轴x0=ηt代表着“信息波速度不变性”.
如1.5.1所述,“光速不变性”原理,既是爱因斯坦狭义相对论基本的逻辑前提,同时,也是爱因斯坦广义相对论基本的逻辑前提. 同样的逻辑,作为OR理论之逻辑结论的“信息波速度不变性”定理,自然地,也可以作为GOR理论的逻辑前提. 类似“光速不变性”原理在爱因斯坦广义相对论中的情形,通过“等效原理”,“信息波速度不变性”即可在GOR理论中发挥其作为逻辑前提或公理的作用.
将光学代理OA(c)之“光速不变性”对应变换为一般观测代理OA(η)之“信息波速度不变性”,正是GOR理论将爱因斯坦广义相对论由光学代理OA(c)对应变换至一般观测代理OA(η)的重要逻辑途径. 如此,我们将建立起GOR理论之整个理论体系.
1.6 OR时空中的相对论性与观测效应
爱因斯坦以为,呈现在观测中的相对论性现象是时空和物质运动本质特性的体现,这也是目前主流物理学界的认识. 然而,OR理论[1-3]发现,一切相对论性现象,包括“同时性的相对性”“时涨尺缩”“质量扩张”,乃至“光速不变性”,皆观测效应和表观现象,乃观测局域性所致.
如果说“信息波速度不变性”是OR理论最重要的逻辑结论,那么,“一切相对论性现象皆观测效应”则是OR理论最重要的发现.
1.6.1 OR时空变换因子
根据OR理论,观测时空并非客观真实的时空,观测物理量并非完全客观真实的物理量.
任意物理量U皆有其“固有量”Uo,是客观真实的,不依赖于观测.然而,制约于观测代理OA(η)之观测局域性(η<∞),U之“观测量”却依赖于观测,依赖于观测代理OA(η),依赖于OA(η)之信息波速度η:U=U(η).此即所谓“观测效应”.
时间在相对论性现象中扮演着至关重要的角色.
OR时空,乃一般观测代理OA(η)呈现给观测者的惯性观测时空,非固有时空,如式(1.5)所示,其观测时间dt并非客观真实的“固有时间”dτ:
1)固有时间dτ=ds/η.
2)观测时间dt=dx0/η≠dτ.
OR理论有一个重要的物理量,所谓“时空变换因子”:Γ(η)=dt/dτ,即“观测时间”dt与“固有时间”的dτ之比,如式(1.6)所示.
OR时空变换因子Γ(η)=dt/dτ表征惯性时空及其物质运动之相对论性,因而,又称“相对论性因子”.
1.6.2 一切相对论性现象皆观测效应
爱因斯坦狭义相对论中,时空变换因子即洛伦兹因子γ=1/√(1-v2/c2),光速c乃不变量.若v=0,则γ=1而dt=dτ,无相对论性现象;若|v|>0,则γ>1而dt>dτ,此即所谓“时间膨胀”,乃相对论性现象.据此,爱因斯坦和主流物理学界认为,惯性时空之相对论性现象,其根源和本质在于物质运动:|v|>0.
在OR理论中,运动物体同样会呈现出相对论性现象,同样会产生“时间膨胀”效应:若η<∞而|v|>0,则Γ>1而dt>dτ.然而,OR理论显示,相对论性现象,其根源并非物质运动(|v|>0),而在于观测代理OA(η)之观测局域性(η<∞);其本质乃观测效应和表观现象.
根据式(1.5)和式(1.6),如表1所示,不同观测代理,其观测媒介传递观测信息的速度不同,具有不同程度的观测局域性,因而,其观测时间会不同程度地“膨胀”.对于不同观测代理OA(η1)和OA(η2),若η2>η1,则Γ(η2)<Γ(η1),dt(η2) 根据OR理论[1-3],时空和物质运动的相对论性现象可由相对论性因子Γ(η)表征.式(1.6)之相对论性因子Γ(η)=1/√(1-v2/η2)可依泰勒级数分解: (1.7) 其中,Γ∞=Γ(∞)≡1乃伽利略因子,不依赖于观测,不含观测效应,代表客观真实的物理存在;ΔΓ(η) 乃“观测效应因子”,依赖于观测代理OA(η). 特别注意:OR时空变换因子Γ(η)=1/√(1-v2/η2)之泰勒级数中,只有第一项Γ∞≡1不依赖于观测;而其余各项皆依赖于观测,依赖于观测代理OA(η),依赖于OA(η)之观测媒介传递观测信息的速度η.因此,在OR时空变换因子Γ(η)=1/√(1-v2/η2)中,只有伽利略因子Γ∞≡1代表客观真实的存在;而ΔΓ(η)则代表着纯粹的观测效应或表观现象. 不同观测代理具有不同程度的观测局域性,导致不同程度的相对论性.这充分地表明,相对论性现象依赖于观测,乃观测效应和表观现象. Γ(η) =Γ∞+ΔΓ(η)意味着: 第一,我们的观测既包含着客观存在(Γ∞)又包含着表观现象或观测效应(ΔΓ(η)); 第二,相对论性现象乃观测局域性(η<∞)所致,而非时空和物质运动的本质特性. 一切相对论性,包括“光速不变性”,皆观测效应.时间,以及质量和能量,乃最基本的物理量,其相对论性现象,乃最基本的观测效应.解析“光速不变性”,解析“时间膨胀”,解析“相对论性质量”和“相对论性能量”,将有助于我们进一步理解相对论性现象的根源和本质. 1.6.3 光速为什么不变? OR理论[1-3]阐明:“光速不变性”实乃观测效应. “光速不变性”本身是一种相对论性现象.然而,与其他一切相对论性现象不同,“光速不变性”是爱因斯坦相对论之逻辑前提,而其他一切相对论性现象,包括“同时性的相对性”和“时间尺缩”,以及“相对论性质量”和“相对论性能量”,皆爱因斯坦相对论之逻辑结论,源于“光速不变性”假设. 自然地,作为其逻辑前提,爱因斯坦相对论本身并不能解释光速为什么不变.因而,人们至今不能理解“光速不变性”,当然,也就不能解释和理解作为其逻辑结论的其他一切相对论性现象. 爱因斯坦狭义相对论之时空变换因子(洛伦兹因子)γ=1/√(1-v2/c2)意味着:惯性时空中,真空光速c乃宇宙极限速度,是不可超越的,因而,光速具有不变性.然而,洛伦兹因子γ=1/√(1-v2/c2)是由“光速不变性”假设作为逻辑前提导出的;如此循环论证并不能解释“光速为什么不变”. 现在,OR理论阐明(如1.5所述),所谓“光速不变性”只是“信息波速度不变”之特例,仅当光作为观测媒介时成立.根据OR理论,光,并非人类感知客观世界所能借助的唯一的观测媒介;光速,也并非上帝或宇宙为传递观测信息而设置的极限速度. OR时空变换因子Γ=1/√(1-v2/η2)表明,是观测代理OA(η),而不是上帝,为我们设置了观测极限:不能指望借助观测代理OA(η)观测超越OA(η)之信息波速度η的物质运动;当然,也不能指望借助光 或光学代理OA(c)观测超光速物质运动. 洛伦兹因子γ=1/√(1-v2/c2)隐喻着爱因斯坦的“光速不变性”,而OR时空变换因子Γ=1/√(1-v2/η2)则隐喻着“信息波速度不变性”.“光速不变性”乃至“信息波速度不变性”皆观测效应,是观测代理之“信息波”为观测者传递观测信息时的表观现象. 假定惯性观测者O和O′观测光子P之运动,O和O′之相对运动速度为v,O和O′观测到P之运动速度分别为u和u′;如果u′=c,那么u呢?这一问题的现实例子即迈克尔逊- 莫雷实验[42],其中,v为地球围绕太阳之公转速度. 当我们用肉眼观测空中的飞鸟时,被观测对象P是鸟,为我们传递飞鸟信息的是光.迈克尔逊- 莫雷实验中,被观测对象P是光或光子;那么,为迈克尔逊和莫雷传递光或光子之信息的观测媒介是什么呢? 借助不同的观测代理,观测者有不同的观测结论. 根据伽利略速度叠加原理: u=u∞=u′+v=c+3×104>c (1.8) 伽利略速度叠加原理乃伽利略代理(理想代理)OA∞之物理模型,其计算所得速度u是超光速的,既符合人类的直觉,也符合人类的理性. 然而,在迈克尔逊- 莫雷实验中,为光子P传递信息的是光子P自身,相应的观测代理乃爱因斯坦代理(光学代理)OA(c). 根据爱因斯坦狭义相对论之速度叠加公式 (1.9) 其中,光速无速度叠加效应. 此即“光速不变性”,符合迈克尔逊- 莫雷实验. 迈克尔逊- 莫雷实验中,被观测对象P是光,为观测者传递观测信息的也是光:光即“信息波”,光子即“信息子”.这正是迈克尔逊- 莫雷实验中光速表现出“不变性”的原因. 事实上,如果惯性观测者O和O′借助观测代理OA(η)观测OA(η)之“信息波”或“信息子”,且u′=η,那么,根据OR速度叠加公式 (1.10) 其中,信息波速度无速度叠加效应. 此即“信息波速度不变性”的体现,同样地,符合迈克尔逊- 莫雷实验. 特别值得指出:“信息波速度不变性”能更好地诠释迈克尔逊- 莫雷实验:不仅阐明其“光速不变性”现象,而且阐明其“光速不变性”本质. 将来,人类一定会发现超光速观测媒介,发明超光速观测代理,例如,表1中的拉普拉斯代理(引力波代理)OA(vG).如果引力波速度真如拉普拉斯之计算vG>7×106c,那么,依OR理论之速度叠加公式 (1.11) 那时,借助于拉普拉斯代理,我们就会发现,光速并非真地不变.所谓“光速不变性”,实为“信息波速度不变性”,纯属观测效应,乃光学代理OA(c)之观测局域性(c<∞)所致. 1.6.4 时间的膨胀 OR理论是以时间定义为其最基本的逻辑前提而建立起来的[2-3].根据OR理论,客观真实的时间,即“固有时间”(原时)dτ,是不会“膨胀”的;而“膨胀”的只是“观测时间”dt.观测时间的“膨胀”可谓最基本的相对论性现象或最基本的观测效应. (1.12) 客观真实的时间(固有时间或原时)dτ不依赖于观测,不依赖于观测代理OA(η).然而,观测时间dt却依赖于观测,依赖于观测代理OA(η):dt=dt(η).一般地,制约于观测代理OA(η)之观测局域性(η<∞),观测时间dt并不等同于固有时间dτ. 根据式(1.6),若v≠0而η<∞,则 (1.13) 此即所谓“时间膨胀”. 式(1.13)中,Γ∞dτ为观测时间dt中真实的部分(dτ),独立于观测;而ΔΓ(η)dτ则为观测时间dt中“膨胀”的部分(Δdτ),完全依赖于观测代理OA(η): (1.14) 根据式(1.13)和式(1.14),不同的观测代理OA(η),信息波速度η不同,其观测时间dt会不同程度地“膨胀”.而η→∞时,这种“时间膨胀”的现象便会随之消失.这意味着,观测时间dt的“膨胀”实为观测效应,而非客观真实的自然现象,其根源和本质在于观测代理OA(η)之观测局域性(η<∞). 1.6.5 相对论性质量 质量,在相对论(包括爱因斯坦狭义相对论和OR理论)中,也会膨胀,此即“相对论性质量”. OR理论称“相对论性质量”为“观测质量”. 根据OR理论,客观真实的质量,即物体的“固有质量”mo是不会“膨胀”的;而“膨胀”的只是“观测质量”,由OR理论之“质速关系”决定mo. (1.15) 然而,制约于一般观测代理OA(η)之观测局域性(η<∞),OA(η)之观测质量m并不等同于物体或物质体系之“固有质量”mo. 根据OR理论之“质速关系”,v≠0而η<∞时 (1.16) 此即观测质量的“膨胀”. 爱因斯坦狭义相对论中,mo被称作“静止质量”(rest mass),而m=m(c)则被称作“相对论性质量”(relativistic mass).爱因斯坦和主流物理学界认为,物体质量随其运动而膨胀,因而,相对论性质量m大于静止质量mo,并且,具有更强的引力效应.这就导致了一种悖论:同一物体,相对于不同的惯性观测者有不同的质量,进而,呈现出不同的引力效应.如此逻辑悖论意味着:相对论性质量,或观测质量,包含着观测效应,并非完全客观真实. 客观真实的质量mo是不依赖于观测或观测代理OA(η)的.根据式(1.15),观测质量m的“膨胀”依赖于观测代理m=m(η):不同观测代理OA(η)之信息波速度η不同,因而,其观测质量m会不同程度地“膨胀”;η→∞时,这种观测上的“质量膨胀”现象会随之消失.这意味着,观测质量m的“膨胀”实为观测效应,而非客观真实的自然现象,其根源和本质同样在于观测代理OA(η)之观测局域性(η<∞). 式(1.16)中,ΔΓ(η)mo即“膨胀”的质量Δm,完全依赖于观测代理OA(η): Δm(η)=m(η)-mo=ΔΓ(η)mo= (1.17) OR理论[1-3]已经阐明,固有质量mo才是具有引力效应的真实质量;而“膨胀”的质量Δm=ΔΓ(η)mo并非客观存在,自然地,无任何引力效应. 1.6.6 相对论性能量 能量,在相对论(包括爱因斯坦狭义相对论和OR理论)中,也会膨胀,此即“相对论性能量”. OR理论称“相对论性能量”为“观测能量”. 根据伽利略- 牛顿理论,物体的质量和能量是相互独立的:质量即质量,能量即能量.就纯粹能量而言,物质粒子有2种能量:一是动能K,二是势能V.总能量H=K+V,可谓物质粒子之“哈密顿量”.惯性时空中,物质粒子只剩下动能K,依赖于物质粒子的静止质量mo及其运动速度v:K=mov2/2,此即经典力学中经典的动能形式. 然而,依爱因斯坦相对论:物质体系的质量和能量是相互依存的:质量亦能量,能量亦质量. 在爱因斯坦看来,惯性时空之物质粒子,不仅具有动能(kinetic energy)K,而且,还具有静能(rest energy)Eo.爱因斯坦公式是我们熟知的:E=mc2,其中,E=Eo+K即惯性时空中物质粒子总能量,Eo=moc2,K=(γ-1)moc2.爱因斯坦公式又称“质能关系”,意即质量和能量可以相互转化,如此,有物理学家便将所谓“静能”用于解释核能或核爆炸[31]. OR理论从较之爱因斯坦狭义相对论更基本的逻辑前提出发,导出了与爱因斯坦质能关系同构一致(形式上和逻辑上完全相同)的OR质能关系[1-3]: (Eo=moη2;K=(Γ(η)-1)moη2) (1.18) OR质能关系乃一般观测代理OA(η)之质能关系,概括了爱因斯坦公式;而爱因斯坦公式则只是OR质能关系之特例,仅当观测代理OA(η)为光学代理OA(c)时成立. OR质能关系E=mη2揭示了爱因斯坦公式E=mc2之实质,我们因而能理解其中的“静能”Eo=moc2和“动能”K=(γ-1)moc2. 显而易见,OR质能关系中的能量E依赖于观测,依赖于观测代理OA(η):E=E(η).即使对于同一物体和同一观测者,不同的观测代理OA(η)也会有不同的观测能量E(η).这充分表明,OR质能关系E=mη2,包括爱因斯坦质能关系E=mc2,包含着观测效应. 那么,除去观测效应之外,OR质能关系E=mη2中到底存在哪些客观真实的能量成分呢? 将OR时空变换因子Γ(η)=1/√(1-v2/η2)分解为泰勒级数,则OR质能关系E=mη2可表述为 (1.19) 其中,唯一不依赖于观测代理OA(η)的是第二项,即经典力学中的经典动能:K=mov2/2. 特别地,OR质能关系中,“静能”Eo=moη2无独立于观测代理OA(η)的成分,纯属虚拟或表观能量. 实际上,爱因斯坦公式E=mc2和OR质能关系E=mη2,其初衷是相同的:推导物体mo以惯性速度v运动时的动能[1-3].爱因斯坦公式E=mc2原本只是光学代理OA(c)的相对论性动能公式:K=(γ-1)moc2;OR质能关系E=mη2原本只是一般观测代理OA(η)的相对论性动能公式:K=(Γ-1)moη2. 特别值得注意:OR理论之相对论性动能公式K(η)=(Γ-1)moη2概括并统一了爱因斯坦狭义相对论之相对论性动能公式K(c)=(γ-1)moc2和牛顿理论之经典动能公式K∞=mov2/2.如 (1.20) 所示.η→c时,OR动能K(η)即爱因斯坦的相对论性动能K(c);η→∞时,OR动能K(η)即牛顿的经典动能K∞. 式(1.20)表明,OR理论之相对论性动能公式K(η)=(Γ-1)moη2,既与爱因斯坦之相对论性动能公式K(c)=(γ-1)moc2具有逻辑上的一致性,又与牛顿之经典动能公式K∞=mov2/2具有逻辑上的一致性.这从一个侧面印证了OR理论逻辑上的自洽性. 理想观测代理OA∞之情形(η→∞)下,爱因斯坦设想的物质体系之“静止能量”成为无穷大:Eo→∞.这意味着,所谓“静止能量”并非客观真实的物理量. 特别需要指出,观测效应,或者说,观测上的相对论性现象,不仅存在于爱因斯坦狭义相对论,而且存在于爱因斯坦广义相对论:惯性时空之一切相对论性现象,包括“光速不变性”,皆观测效应和表观现象;同样地,引力时空之一切相对论性现象,包括“时空弯曲”,皆观测效应和表观现象. GOR理论将会阐明这一点. OR理论从较之爱因斯坦狭义相对论更为基本的逻辑前提出发[2-3],导出广义洛伦兹变换,不仅概括统一了伽利略变换和洛伦兹变换,并且揭示了不同理论体系之间的对应关系,将对应原理与相对性原理联系起来,赋予玻尔对应原理更为普遍的意义. 本章,旨在发掘一项原理:“广义对应原理”,为GOR理论搭建一座逻辑桥梁,一条逻辑捷径. 玻尔正式地建立对应原理是在1920年[4],后人谓之“玻尔对应原理”. 然而,波尔对应原理的基本思想可追溯至1913年玻尔原子理论和玻尔原子模型的建立[5-6]. 正是基于对应原理的基本思想,玻尔建立了原子模型和原子理论. 实际上,对应原理的基本思想还可以追溯至1900年普朗克黑体辐射定律及其黑体辐射公式的建立[43]. 玻尔对应原理基本思想:量子力学与经典力学之间必定存在某种内在的对应关系,在一定的条件下,二者可以相互转化. 玻尔对应原理有各种不同的解读,其中,最常见的是2种极限表达:1)玻尔量子数(能级)n的极限对应;2)普朗克常数h的极限对应. 2.1.1 玻尔量子数之极限对应:n→∞ 玻尔对应原理(玻尔量子数形式):设n为原子能级(主量子数),n→∞时,量子模型趋同于经典模型,量子物理量趋同于经典物理量—— (2.1) 能量的量子化是量子物理学与经典物理学的分水岭:能量的连续性代表经典物理学,而能量的离散化则代表量子物理学.玻尔认为,大量子数情形下,原子中电子的能量趋于连续,因而,n→∞时,量子物理模型必定趋同于经典物理模型. 一方面,基于经典物理学,假定电子围绕原子核做圆周运动,由牛顿定律和库伦定律可计算电子运行速度v与轨道半径r的关系: (2.2) 式中:K=1/(4πε0)为库伦常数,ε0为真空电容率;Z为原子序数;me为电子质量.以TC=2πr/v为电子轨道运行周期,可计算经典情形之电磁波辐射频率 (2.3) 式中fC即经典电磁辐射频率. 式(2.3)显示,根据经典物理学计算所得结论,原子之电磁辐射频率fC可取连续值. 另一方面,实验显示,原子之电磁辐射频率只能取若干离散值.1889年,里德伯根据实验建立了关于氢原子谱线的经验公式 (2.4) 式中:λQ为氢原子谱线波长;R为里德伯常数,需由实验确定. 1911年,卢瑟福提出原子结构的行星模型,其中,电子像太阳系之行星围绕太阳运行一样围绕原子核旋转.卢瑟福模型存在严重缺陷:依经典电磁理论,卢瑟福模型之电子会因辐射电磁波而损失能量,最终坍缩至原子核.卢瑟福不能解释这一问题. 1913年,玻尔在卢瑟福原子模型的基础上建立玻尔原子模型,其中,玻尔设立了3个假设. 第一,定态条件. 原子只能稳定地存在于离散的能量状态,即所谓“定态”或“能级”,其中,电子只能在特定的能级上围绕原子核做圆周运动,取离散的能量 (2.5) 式(2.5)意味着,原子中的电子可以在特定能级以特定能量稳定地运行. 第二,跃迁条件. 原子中的电子可以通过辐射能量或吸收能量在不同能级之间跃迁.电子由高能级跃迁至低能级时会释放具有一定能量ΔE和频率fQ的光子;反之,电子若吸收一定能量ΔE和频率fQ的光子,则会由低能级跃迁至高能级.被释放的光子或被吸收的光子,其能量ΔE和频率fQ满足 (2.6) 设n′=n-1且n≫1(即大量子数之情形),联立“定态条件”(式(2.5))和“跃迁条件”(式(2.6))可得 (2.7) 式中fQ即量子电磁辐射频率. 式(2.7)意味着:n→∞时,ΔE→0,电子相邻能级之能量趋于连续.依据玻尔对应原理基本思想,这时的量子物理量趋同于对应的经典物理量:fQ=fC,rn=r,vn=v.考虑氢原子(Z=1),联立式(2.2)、式(2.3)和式(2.7)可得电子各能级轨道半径rn和运行速度vn: (2.8) 第三,角动量量子化. 为最终导出原子结构之理论模型,玻尔对其模型中电子之角动量L进行了量子化: (2.9) 联立能级n之电子轨道运行速度vn=√(Ke2/mern)(式(2.8))和“角动量量子化条件”(式(2.9))可得轨道半径rn另一表达式 (2.10) 对照式(2.10)和式(2.8)可得里德伯常数 (2.11) 至此,里德伯公式不再是一个经验公式,而是基于玻尔原子结构理论上的理论模型;里德伯常数R不再是一个经验值,而是玻尔原子结构模型的理论值. 可见,玻尔对应原理的基本思想在玻尔原子模型和玻尔原子理论的建立过程中发挥了重要作用. 然而,值得注意,式(2.7)只是“大量子数”之情形;fQ=fC并非n→∞之极限对应.实际上,经典频率公式(2.3)与量子频率公式(2.7)并不具有同构一致性对应关系:fQ不能由n→∞同构一致地对应变换为fC. 正如Shomar[44]所指出的,大量子数或n→∞情形并不总能代表经典物理体系.这似乎意味着,量子数n→∞之极限对应缺乏一般性和普遍意义. 2.1.2 普朗克常数之极限对应:h→0 玻尔对应原理(普朗克常数形式):普朗克常数h→0时,量子模型趋同于经典模型,量子物理量趋同于经典物理量—— (2.12) 能量量子化源于普朗克方程:E=hf;h≠0意味着能量的离散化,代表着量子物理学.自然地,h→0时能量E趋于连续.然而,需要指出,h→0和n→∞未必具有相同的或等价的效应.Shomar[44]认为,普朗克常数h→0必定代表经典物理学,然而,玻尔量子数n→∞则未必代表经典物理学. 1900年,普朗克以其量子假设E=hf为逻辑前提,从理论上导出普朗克定律[43],其黑体辐射公式 (2.13) 与黑体辐射实验极其吻合,可视为瑞利- 金斯定律[45-46]和维恩近似[47]的融合.更重要地,作为普朗克定律逻辑前提的能量子假设E=hf标志着量子理论诞生[48-49]. 普朗克发现,其黑体辐射定律与瑞利- 金斯定律存在对应关系:h→0时,量子化的黑体辐射公式(2.13)趋同于(或者说,“同构一致”地对应变换为)经典的瑞利- 金斯黑体辐射公式 (2.14) 式中:k为玻尔兹曼常量;T为温度;c即光速. 式(2.14)意味着,普朗克黑体辐射公式与瑞利- 金斯黑体辐射公式具有相同的形式和结构,或者说,具有“同构一致性对应关系”,是“同构一致”的.普朗克将这种“同构一致性对应关系”形式化(参见Shomar之综述文献[44])为 (2.15) 与玻尔量子数n→∞之极限对应不同,式(2.15)显示,普朗克常数h→0之极限对应,不仅体现在物理量的层面上,更体现在物理概念和理论定律的层面上.不同理论体系之间的对应关系,不仅在于其物理量的趋同和结论上的一致性,更在于其形式上和结构上的趋同,以及概念上和逻辑上的一致性. 众所周知,除光速不变性假设之外,爱因斯坦狭义相对论还有一项重要的逻辑前提:相对性原理. 相对性原理是关于时空对称性的原理[50]. 相对性原理基本思想:时空是对称的,因而,一切观测者平权,一切参考系之物理学定律形式相同. 相对性原理最早的论述源于伽利略,所谓“伽利略不变性”[51-52]:经典力学之一切惯性观测者平权,一切惯性参考系之经典力学定律形式相同. 在狭义相对论[14]中,爱因斯坦将伽利略不变性从力学体系推广至任意物理体系,所谓“狭义相对性原理”.之后,在广义相对论[15]中,爱因斯坦又将“狭义相对性原理”从惯性参考系推广至任意参考系,所谓“广义相对性原理”或“广义协变原理”. 于是,相对性原理获得了更为一般的意义. 实际上,相对性原理也是一种对应原理,阐明了不同参考系之物理学定律的内在联系和对应关系,要求不同参考系之物理模型具有相同形式或结构.换句话说,相对性原理要求不同参考系中的物理学定律或物理模型是“同构”的,具有“同构一致性”或“同构一致性对应关系”.因而,基于相对性原理,不同参考系之物理模型,可以进行“同构一致性对应变换”. 基于相对性原理,只需变换不同观测者或不同参考系之间的对应物理量,便可实现其物理模型之间的“同构一致性对应变换”.这种变换只是其对应物理量之间的变换,然而,其物理学定律或物理模型的形式和结构却保持不变. 伽利略变换是不同惯性观测者之间的时空变换模型,阐明了相对性原理,或者说,阐明了不同观测者之物理学定律和物理模型的“同构一致性”: (2.16) 其中,惯性观测者O拥有观测量:t,x,y,z,v;而惯性观测者O′则拥有观测量:t′,x′,y′,z′,v′.v是O′沿O之x轴相对于O运动的速度;而v′则是O沿O′之x′轴相对于O′运动的速度. 式(2.16)显示,时空变换O→O′与O′→O具有完全相同的形式,是“对称”的和“同构”的.根据相对性原理,只需对O→O′中的对应物理变量实施对应变换(tt′,xx′,yy′,zz′,vv′),便能导出O′→O;反之亦然.这既是相对性原理的体现,同时,也是对应原理的体现. 实际上,爱因斯坦狭义相对论有3项原理作为其基本的逻辑前提:1)简单性原理;2)相对性原理;3)光速不变性原理.归纳起来,其演绎过程可谓“三部曲”. 首先,基于简单性原理,将惯性观测者O和O′之间的时空变换关系设定为线性关系: (2.17) 其次,基于相对性原理,对式(2.17)实施“同构一致性对应变换”:tt′,xx′,yy′,zz′,vv′ (v′=-v),则由式(2.17)之O→O′可得O′→O: (2.18) 显然,式(2.18)之时空变换O′→O与式(2.17)之时空变换O→O′具有相同的形式和结构. 最后,基于光速不变性原理,联立式(2.17)和式(2.18),可得洛伦兹变换: (2.19) 并可确定其中的时空变换因子(洛伦兹因子)γ. 爱因斯坦狭义相对论“三部曲”中,基于相对性原理,对惯性观测者O和O′的观测时空进行“同构一致性对应变换”,其中,“相对性原理”扮演着“对应原理”的角色.如此,不仅所得之时空变换O′→O(式(2.18))与O→O′(式(2.17))是“同构一致性的”,而且,所得之洛伦兹变换(式(2.19))与伽利略变换(式(2.16))也具有“同构一致性对应关系”. 相对性原理的核心思想是:“一切观测者平权”.OR理论则进一步阐明:“一切观测代理平权”. 同一物理世界,同一逻辑体系! 作为同一物理世界的形式化模型,物理学之一切理论体系,必定遵循共同的公理体系和逻辑前提,因而,相互之间应该存在某种内在联系和对应关系,具备逻辑上的一致性.不同理论体系之间的内在联系和对应关系是其逻辑一致性的体现或反映. OR理论揭示了物理学不同理论体系(包括爱因斯坦相对论与经典力学、爱因斯坦相对论与量子力学,以及量子力学与经典力学)之间的内在联系和对应关系,同时,揭示了不同观测体系(包括一般观测代理与光学代理 OA(η)、一般观测代理与理想代理OA(c),以及光学代理与理想代理OA∞)之间的内在联系和对应关系,赋予玻尔对应原理更为普遍的意义. 2.3.1 OR物质波论及其广义普朗克常数hη 普朗克常数h→0之极限意义上,玻尔对应原理是关于光学观测代理OA(c)之量子物理学和理想观测代理OA∞之经典物理学内在联系和对应关系的原理:h≠0代表量子物理学,h=0代表经典物理学;而h→0则意味着量子物理学趋同于经典物理学.实际的普朗克常数h由黑体辐射实验测定:h=6.626×10-34J·s. 那么,6.626×10-34J·s=h>0意味着什么呢? 根据OR理论[2-3],普朗克常数h可谓光学观测体系之测量参数,代表着光学代理OA(c)之观测上的分辨力(resolving power)或观测上的不确定性. 普朗克常数h源于普朗克方程E=hf,而E=hf原本为普朗克黑体辐射定律之能量子假设[43],代表单个光子之能量.之后,德布罗意将普朗克方程E=hf由光子推广至任意物质粒子,并且,导出德布罗意关系λ=h/p,建立德布罗意物质波论[17-19].然而,值得注意,德布罗意物质波论乃光学观测代理OA(c)之理论,其中,普朗克方程E=hf只是普朗克定律的一个假设性的逻辑前提,德布罗意对普朗克方程的推广也只是一种启发式推断,而非理论和逻辑结论. OR理论,即基于物质波时间定义及其时频比不变性建立的“观测相对论”,是逻辑和理论的产物,不仅概括了爱因斯坦狭义相对论,而且概括了德布罗意物质波论.OR物质波论乃一般观测代理OA(η)之物质波理论,概括了光学测代理OA(c)之德布罗意物质波论,并与德布罗意物质波论具有“同构一致性对应关系”,其中,包括2个重要的量子关系式:“广义普朗克方程”和“广义德布罗意关系”[2-3]: (2.20) 式中:hη=h(η)为OA(η)之普朗克常数,可谓“广义普朗克常数”;f(η)和λ(η)以及E(η)和p(η)为被观测对象P之于OA(η)的观测物理量,分别为P之“物质波”频率和波长以及能量和动量. OR物质波论概括了德布罗意物质波论,将德布罗意物质波论由光学代理OA(c)推广至一般观测代理OA(η).根据OR物质波论[2-3],不同的观测代理OA(η)具有不同的普朗克常数hη(或“广义普朗克常数”),因而,具有不同观测分辨力和不同观测不确定性.然而,不同观测代理之量子定律或量子模型具有完全相同的形式和完全相同的结构,是“同构一致”的. 故依相对性原理之逻辑:“一切观测代理平权!” 于是,不同观测代理,其量子体系或量子模型可进行“同构一致性对应变换”.对于任意观测代理OA(η1)和OA(η2),成立: (2.21) 根据OR理论之广义普朗克方程E=hηf,广义普朗克常数hη的值取决于观测代理OA(η):不同观测代理具有不同的广义普朗克常数. 这是一个重要的发现! 自然地,η→c时,OA(η)→OA(c),广义普朗克常数hη即普朗克常数h,广义普朗克方程E(η)=hηf(η)即普朗克方程E=hf,广义德布罗意关系λ(η)=hη/p(η)即德布罗意关系λ=h/p.可见,普朗克方程E=hf和德布罗意关系λ=h/p乃光学代理OA(c)之量子模型,仅当其服务于OA(c)时方可成立. 特别地,η→∞时,OA(η)→OA∞,一般观测代理OA(η)之量子物理模型趋同于理想观测代理OA∞之经典物理模型,量子能量E(η)趋于连续,因而:广义普朗克常数hη→0;反之,η→0时hη→∞. 根据广义普朗克方程E(η)=hηf(η)以及2.1.2对普朗克常数之极限对应的分析,玻尔对应原理实际上是光学观测代理和理想观测代理之对应关系的原理,涉及2类物理体系或物理模型. 第一,量子体系:光学代理OA(c),hη=h,OA(η)=OA(c),其信息波速度η=c; 第二,经典体系:理想代理OA∞,hη=0,OA(η)=OA∞,其信息波速度η=∞. 归纳之:hη→0 iffη→∞;hη→hiffη→c. 简单性原理之下,“x→0 iffy→∞”之最简明的数学关系应该是反比例函数:xy=k(k为常数).于是,OR理论建立了一个重要的恒等式 (2.22) 其中,C≡hc由“hη→hiffη→c”确定;hη→0意味着量子物理体系趋同于经典物理体系. OR理论之恒等式hηη=hc(式(2.22))表明:不同观测代理之量子体系或量子模型“同构”,具有“同构一致性对应关系”,或者说,具有相同的形式和结构.如果说,普朗克常数极限意义下的玻尔对应原理(式(2.15))意味着:光学观测代理OA(c)与理想观测代理OA∞“平权”,那么,OR理论之恒等式hηη=hc(式(2.22))则意味着:一切观测代理“平权”! 特别值得指出:式(2.22)中的恒等式hηη=C正是“广义对应原理”的一种形式化表达,并且,概括泛化了玻尔的对应原理. 2.3.2 时空变换之间的对应关系 玻尔对应原理反映了量子物理学与经典物理学之间的内在联系和对应关系.同样地,就逻辑一致性要求而言,洛伦兹变换与伽利略变换之间,乃至相对论与经典力学之间,也应具备内在联系和对应关系. 主流物理学界认为,洛伦兹变换和伽利略变换之间存在近似对应关系:低速情形下(v≪c),洛伦兹因子γ=Γ(c)=1/√(1-v2/c2)≈1近似伽利略因子Γ∞≡1,伽利略变换近似于洛伦兹变换;因而,洛伦兹变换和伽利略变换之间,乃至爱因斯坦狭义相对论与经典物理学之间,具有逻辑上近似的一致性.主流物理学界进而认为:洛伦兹变换更正确,伽利略变换只是个近似;爱因斯坦相对论更正确,经典力学只是个近似. 其实,洛伦兹变换与伽利略变换并不严格对应. OR理论经由不同于爱因斯坦狭义相对论的逻辑前提和逻辑路线,从理论上,导出了更具一般性和普遍意义的微分形式的时空变换关系[2-3]: (2.23) 式中:η具有明确的物理意义,乃观测媒介传递观测信息的速度,即一般观测代理OA(η)之“信息波”速度;Γ=Γ(η)为OA(η)之时空变换因子,O和O′乃OA(η)之惯性观测者. 值得注意:菲兹杰拉德- 洛伦兹变换[39-40]中,光速c并不具有明确的物理意义;爱因斯坦狭义相对论中,光速c只是一个由“光速不变性”假设引入的物理量,其在时空变换过程中所担任的角色并不十分明确. 设定初始条件:t=t′=0时,x=x′=0,y=y′=0,z=z′=0,对微分形式的时空变换关系式(2.23)进行积分,可得如下代数形式的时空变换: (2.24) 显然,式(2.24)之时空变换与洛伦兹变换具有完全相同的形式和结构,并且,概括了洛伦兹变换,因而,被OR理论称之为“广义洛伦兹变换”.实际上,洛伦兹变换只是“广义洛伦兹变换”之特例,即观测代理OA(η)为光学代理OA(c)时的情形. OR时空变换,即“广义洛伦兹变换”,将洛伦兹变换由光学观测代理OA(c)推广至一般观测代理OA(η),其中,观测媒介可为任意物质运动形式,信息波的速度η可为任意值.根据OR理论[2-3],不同观测代理OA(η)具有不同的时空变换因子Γ(η),因而,呈现不同程度的相对论性现象.然而,不同观测代理之时空变换关系,乃至不同观测代理之惯性相对论,具有完全相同的形式和完全相同的结构,或者说,具有“同构一致性对应关系”. 依相对性原理的逻辑:“一切观测代理平权!” 因而,不同观测代理之时空变换关系,乃至不同观测代理之惯性相对论,可进行“同构一致性对应变换”.不同观测代理OA(η1)和OA(η2),成立: (2.25) 即以η2替代η1,OA(η1)之时空变换,乃至OA(η1)整个惯性相对论体系,便可“同构一致地”对应变换为OA(η2)之时空变换,乃至OA(η2)整个惯性相对论体系;反之亦然. 特别地,“广义洛伦兹变换”概括统一了洛伦兹变换和伽利略变换,在“同构一致性对应”的意义上,既与洛伦兹变换严格对应,又与伽利略变换严格对应. η→c时,“广义洛伦兹变换”(式(2.24))严格地约化为洛伦兹变换(式(2.19)): (2.26) η→∞时,“广义洛伦兹变换”(式(2.24))严格地约化为伽利略变换(式(2.16)): (2.27) 根据OR理论[1],爱因斯坦之狭义相对论和伽牛之惯性理论皆霍金言下的局部理论[13]:伽利略变换原本是理想代理OA∞之时空模型;洛伦兹变换原本是光学代理OA(c)之时空模型.然而,现在二者都与“广义洛伦兹变换”具有严格的“同构一致性对应关系”,并且,统一于“广义洛伦兹变换”[1-3]. 如果说,OR理论之恒等式hηη=hc(式(2.22))基于量子理论和对应原理的视角阐明:一切观测代理“平权”,那么,OR理论之“广义洛伦兹变换”(式(2.24))则基于相对论和相对性原理的视角进一步阐明:一切观测代理“平权”! 特别值得指出:式(2.24)中的“广义洛伦兹变换”为“广义对应原理”提供了另一种注解,并且,概括泛化了伽利略的相对性原理. 根据2.1的分析和论述,玻尔之对应原理是关于量子物理模型和经典物理模型之对应关系的原理,是关于光学观测代理和理想观测代理之对应关系的原理,其中蕴含着“不同观测代理之观测者平权”的思想. 根据2.2的分析和论述,伽利略之相对性原理是关于不同参考系时空变换之对应关系的原理,是关于不同观测者时空变换之对应关系的原理,其中蕴含着“不同参考系之观测者平权”的思想. 根据2.3,OR理论及其“广义洛伦兹变换”进一步阐明:一切观测者,无论其参考系,无论其观测代理,是“平权”的,其物理学模型具有“同构一致性对应关系”. 可见,对应原理和相对性原理可以在“一切观测者平权”的理念之下统一起来. 归纳概括2.1~2.3的结论,根据OR理论,我们有理由将玻尔对应原理和伽利略相对性原理联系起来,将其推广为更具一般性和普遍意义的“广义对应原理”. 广义对应原理(The Principle of General Correspondence, PGC):宇宙是对称的,因而,宇宙之一切观测者平权,不同观测体系,包括不同参考系和不同观测代理,其物理学定律或物理模型必定具有相同的形式和结构,或者说,必定是同构一致的,具有同构一致性对应关系. 值得注意,PGC原理中的观测者,不仅包括不同参考系之观测者,而且包括不同观测代理之观测者:不同参考系之观测者“平权”;不同观测代理之观测者“平权”. PGC原理是关于不同观测体系(包括参考系和观测代理)之物理学定律和时空模型对应关系的原理. PGC原理,概括并超越了玻尔对应原理,同时,也概括并超越了相对性原理. 基于PGC原理,可对同一观测代理OA(η)之不同参考系或不同观测者O和O′的物理学定律或物理模型进行同构一致性对应变换: O′→OO→O′:U′U (2.28) 其中,只需对O和O′对应物理量U和U′进行对应变换,正如伽利略变换或洛伦兹变换中O→O′和O′→O之间的同构一致性对应关系. 基于PGC原理,可对同一观测者O之不同观测代理OA(η1)和OA(η2)的物理学定律或物理模型进行同构一致性对应变换 (2.29) 其中,只需对OA(η1)和OA(η2)对应物理量U(η1)和U(η2)进行变换,正如OA(η)之广义洛伦兹变换与OA(c)之洛伦兹变换之间的同构一致性对应关系,以及OA(η)之广义洛伦兹变换与OA∞之伽利略变换之间的同构一致性对应关系. 表2罗列并诠释OR理论之惯性时空中不同观测代理之间基本物理量的同构一致性对应关系. 特别地,根据PGC原理,理想代理OA∞之极限情形(η→∞或hη→0)下,物理学一切理论体系趋同于经典物理学:hη→0意味着量子物理学趋同于经典物理学,正如玻尔对应原理之普朗克常数h→0极限表达;而η→∞则意味着相对论趋同于经典物理学,这正是理想化之观测情形. 表2 OR惯性时空不同观测代理之间基本物理量的同构一致性对应关系 运用PGC原理,对不同观测代理OA(η1)和OA(η2)之时空模型和理论体系进行同构一致性对应变换,可因循2条不同的逻辑路线. PGC逻辑路线1:基于PGC对应原理,直接以OA(η2)之η2替代OA(η1)之η1,则OA(η1)之观测物理量U(η1)将对应变换为OA(η2)之观测物理量U(η2);OA(η1)之物理模型将同构一致地对应变换为OA(η2)之物理模型. PGC逻辑路线2:第一,基于PGC对应原理,将OA(η1)之理论体系的逻辑前提同构一致地变换为OA(η2)之理论体系的逻辑前提;第二,基于OA(η2)之理论体系的逻辑前提,因循或类比OA(η1)之理论体系的逻辑,演绎必定能与OA(η1)之理论体系同构一致的OA(η2)之理论体系. 本文试图运用PGC原理,结合PGC逻辑路线1和PGC逻辑路线2,将OR理论由惯性时空扩展至引力时空,将爱因斯坦广义相对论由光学观测代理OA(c)扩展至一般观测代理OA(η),进而,建立“广义观测相对论”,即GOR理论. GOR理论将阐明广义相对论性现象或引力相对论性现象的根源和本质,最终把牛顿万有引力论和爱因斯坦广义相对论统一起来. PGC原理或许会成为物理学的一件利器,为物理学新理论的发展和旧理论的统一,为物理学理论体系之逻辑上的一致性和自洽性检验,提供重要的思想基础和指导原则. OR理论原本是基于时间定义及其时频比不变性导出的理论体系[2-3]. 然而,OR理论同时也服从PGC原理:以一般观测代理OA(η)之信息波速度η替代光学观测代理OA(c)之信息波速度c,则爱因斯坦狭义相对论即可由OA(c)扩展至OA(η),同构一致地变换为OR理论. 这里,基于PGC原理演绎OR理论,有助于我们对PGC原理及其作用的认识. 如2.4所述,基于PGC原理,无论经由PGC逻辑路线1还是PGC逻辑路线2,我们都能将爱因斯坦狭义相对论同构一致地对应变换为OR理论. 2.5.1 经由PGC逻辑路线1演绎OR理论 爱因斯坦狭义相对论之基本方程式 简单归纳如下. 1)闵科夫斯基时空:光学观测代理OA(c)及其4d惯性时空坐标框架X4d(c)可表述为 3)洛伦兹变换O′→O: 5)爱因斯坦质能关系:E=mc2. OR理论之基本方程式 基于PGC对应原理,经由PGC逻辑路线1,直接以一般观测代理OA(η)之信息波速度η替代光学观测代理OA(c)之光速c,则爱因斯坦狭义相对论之基本方程可同构一致地对应变换为OR基本方程. 1)OR观测时空:一般观测代理OA(η)及其4d惯性时空坐标框架X4d(η)可表述为 3)广义洛伦兹变换O′→O: 5)OR惯性能量公式:E=mη2. PGC对应变换得出的OR理论与基于时间定义及其“时频比不变性”导出的基本方程完全相同[2-3]. 可见,基于PGC对应原理,OR理论整个理论体系,包括其核心关系以及表2列出的OR关系式,皆可通过OA(c)→OA(η)同构一致性对应变换,由爱因斯坦狭义相对论直接变换而来;反之亦然. 如此,基于PGC对应原理,经由PGC逻辑路线1,OR理论之整个理论体系便可建立起来. 2.5.2 经由PGC逻辑路线2演绎OR理论 “光速不变性”原理乃爱因斯坦狭义相对论最重要的逻辑前提. 然而,“光速不变性”并不具备作为“原理”所应具备的“不证自明”特征. 尽管“光速不变性原理”似乎得到了观测和实验支持,然而,人们至今并不理解光速为什么不变. 经由PGC逻辑路线1构建OR理论,简单直接地进行c→η对应变换,即可获得与爱因斯坦狭义相对论同构一致的OR理论. 然而,PGC逻辑路线1无法阐明“光速不变性”的根源和本质,同时,也无法阐明OR理论之关系式或相对论性现象之间的因果联系. OR理论原本以时间定义及其“时频比不变性”为“最基本”的逻辑前提,其导出的理论体系中,有一个重要的逻辑结论——“信息波速度不变性”. “信息波速度不变性”揭示了“光速不变性”的本质:光速并非真地不变;所谓“光速不变性”,其实,只是一种观测效应,是光作为观测媒介为观测者传递观测信息时的一种表观现象,并非客观真实的自然现象. “光速不变性原理”乃爱因斯坦狭义相对论的逻辑前提,因此,爱因斯坦狭义相对论本身并不能解释光速为什么不变. 或许,只有当物理学之理论源于“最基本”的逻辑前提时,我们才能真正地知其然并知其所以然. 然而,无论如何,相对于PGC逻辑路线1,PGC逻辑路线2更有助于我们理解相对论性现象(包括“光速不变性”)的根源和本质. 基于PGC对应原理,通过光学观测代理OA(c)与一般观测代理OA(η)的对应变换:OA(c)→OA(η),作为爱因斯坦狭义相对论之逻辑前提的“三原理”(参见2.2),可同构一致地对应变换为“OR三原理”:第一,简单性原理;第二,相对性原理;第三,信息波速度不变性原理. 在OR理论之逻辑前提中,“简单性原理”和“相对性原理”依然有效;然而,爱因斯坦的“光速不变性原理”,在PGC原理下,对应变换成为“信息波速度不变性原理”,其中,一般观测代理OA(η)之信息波的速度η替代了光学观测代理OA(c)之中的光速c. 如此,基于经PGC逻辑路线2对应变换后的OR理论之逻辑前提,即“OR三原理”,因循或类比爱因斯坦狭义相对论的逻辑,即可演绎OR理论. 我们由此即可建立起与爱因斯坦狭义相对论同构一致的OR理论之整个理论体系[1]. 经由PGC逻辑路线2演绎OR理论,有助于我们阐明OR理论的逻辑思想以及OR关系式之间的因果联系,同时,有助于我们理解“光速不变性”乃至一切狭义相对论性现象的根源和本质. PGC原理可将光学观测代理OA(c)之爱因斯坦狭义相对论同构一致地对应变换为一般观测代理OA(η)之OR理论,即所谓“观测相对论”. 同样地,PGC原理也可将光学观测代理OA(c)之爱因斯坦广义相对论同构一致地对应变换为一般观测代理OA(η)之GOR理论,即所谓“广义观测相对论”. OR理论将爱因斯坦狭义相对论由光学代理OA(c)推广至一般代理OA(η),从而概括了爱因斯坦狭义相对论. 现在,GOR理论试图将爱因斯坦广义相对论由光学代理OA(c)推广至一般代理OA(η),进而概括爱因斯坦广义相对论;并且试图将OR理论由惯性时空推广至引力时空,进而概括OR理论. 本文的中心任务是,基于PGC对应原理,对爱因斯坦广义相对论实施OA(c)→OA(η)同构一致性对应变换,最终建立GOR理论之整个理论体系. 如2.4所述,GOR理论有2条逻辑路线可循. 2.6.1 经由PGC逻辑路线1演绎GOR理论 爱因斯坦广义相对论之基本方程式: 简单归纳如下. 1)4d微分流形之度量时空:光学观测代理OA(c)及其4d引力时空坐标框架X4d(c)可表述为 2)时空变换因子γ(v,χ)=dt/dτ:测定观测时空X4d(c)之时间和空间 3)测地线方程:表征物质运动 4)爱因斯坦场方程:表征时空弯曲 GOR理论之基本方程式(1)GOR理论所有关系式皆采用爱因斯坦求和约定——希腊字母μ,ν,α,β,λ,…求和范围{0,1,2,3};英文字母i,j,k,…求和范围{1,2,3}.: 基于PGC对应原理,经由PGC逻辑路线1,直接以一般观测代理OA(η)之信息波速度η替代光学观测代理OA(c)之光速c,则爱因斯坦广义相对论之基本方程式可同构一致地对应变换如下. 1)4d微分流形之度量时空:表征一般观测代理OA(η)及其4d引力时空坐标框架X4d(η)可表述为 2)时空变换因子Γ(η)=dt/dτ:测定OA(c)之观测时空X4d(η)之时间和空间 3)GOR测地线方程:表征物质运动 4)GOR场方程:表征时空弯曲 PGC逻辑路线1是GOR理论最便捷的逻辑通道. 可以预见,基于PGC原理,即便经由如此简单直接的逻辑通道,也能建立起GOR理论之整个理论体系. 2.6.2 经由PGC逻辑路线2演绎GOR理论 爱因斯坦广义相对论也有“三原理”作为其公理体系或基本的逻辑前提:第一,等效原理;第二,广义协变原理;第三,光速不变性原理. 光速c出现在爱因斯坦狭义相对论中,例如,在惯性时空变换因子γ中:γ(v)=1/√(1-v2/c2),是“光速不变性原理”作为其逻辑前提导致的结果.同样地,光速c出现在爱因斯坦广义相对论中,如引力时空变换因子:γ(χ)= 1/√(1+2χ/c2),也是“光速不变性原理”作为其逻辑前提导致的结果.正如1.5.3所述, “光速不变性原理”,既是爱因斯坦狭义相对论的逻辑前提,也是爱因斯坦广义相对论的逻辑前提.借助于“等效原理”,“光速不变性”即可在爱因斯坦广义相对论中发挥其作为“原理”和逻辑前提的作用. 光学观测代理OA(c)(式(1.1))与一般观测代OA(η)(式(1.2))具有同构一致性对应关系.基于PGC对应原理,OA(c)可同构一致地变换为OA(η).根据1.5,OA(c)隐喻着“光速不变性”,而OA(η)则隐喻着“信息波速度不变性”.因此,基于PGC原理,通过同构一致性对应变换:OA(c)→OA(η),作为爱因斯坦广义相对论之逻辑前提或公理体系的“三原理”即可同构一致地对应变换为“GOR三原理”并成为GOR理论的逻辑前提或公理体系:第一,等效原理;第二,广义协变原理;第三,信息波速度不变性原理. 在GOR理论之逻辑前提中,爱因斯坦设立的“等效原理”和“广义协变原理”依然有效,并且,在PGC广义对应原理的意义下,具有了更普遍的意义:其观测者不仅可以是不同参考系之观测者,而且可以是不同观测代理之观测者. 与OR理论之情形相同,爱因斯坦的“光速不变性原理”,在PGC原理下,对应变换成为“信息波速度不变性原理”,其中,一般观测代理OA(η)之信息波的速度η替代了光学观测代理OA(c)之中的光速c. 如此,基于PGC原理对应变换后的GOR理论之逻辑前提(“GOR三原理”),经由PGC逻辑路线2,因循或类比爱因斯坦广义相对论的逻辑,即可演绎GOR理论,最终导出与爱因斯坦广义相对论同构一致的GOR理论之整个理论体系. 经由PGC逻辑路线2演绎GOR理论,将有助于我们理解爱因斯坦广义相对论,理解引力时空“弯曲”现象乃至一切广义相对论性现象或引力相对论性现象的根源和本质,同时,有助于我们阐明GOR理论的因果关系和逻辑思想. 引力时空如何观测和度量是GOR理论首要问题. 人类所感知的时空,依赖于观测,可谓“观测时空”,是物理世界透过某种观测代理OA(η)呈现给观测者的时空X4d(η),并非客观时空.一切现实的观测代理,包括爱因斯坦相对论之光学代理OA(c),皆存在观测局域性(η<∞),令我们所观测到的时空呈现相对论性效应,“观测起来”显得些弯曲. 那么,引力时空之时间和空间当如何定义和度量?广义相对论性现象或引力相对论性效应,包括“时空弯曲”,究竟是物理世界之本质特性呢,还是观测代理之局域性所致之观测效应呢? 关于引力,物理学存在两大理论体系:一是牛顿万有引力论[53];二是爱因斯坦广义相对论[15]. 无论牛顿万有引力论还是爱因斯坦广义相对论,均涉及2类局域性问题:一是引力局域性;二是观测局域性. 3.1.1 引力局域性:引力波速度是有限的 作为物理世界的形式化模型,物理学一切理论皆具有某种理想化特征. 实际上,无论牛顿万有引力论或爱因斯坦广义相对论,皆隐喻着一项重要的理想化假设:引力乃超距作用,辐射速度无穷. 牛顿万有引力定律未计引力局域性:物质体系之物质分布变化时,其泊松方程所描述的引力场会随之瞬时变化[54],引力跨越空间无须时间. 如果我们称牛顿万有引力定律为理想代理OA∞之引力定律,则爱因斯坦场方程可谓光学代理OA(c)之引力定律:依广义相对论[15],“弱场近似”条件下,爱因斯坦场方程约化为泊松方程形式的牛顿万有引力定律. 这意味着,爱因斯坦广义相对论中的引力,与牛顿之万有引力一样,也是超距作用,其引力辐射速度无穷. 但不能设想,弱场之引力速度更快. 根据“物理可观测性原理”[1-3],物理世界不存在超距作用:一切物理量(包括引力辐射速度)都必定是有限的. 1859年,法国天文学家Verrier[55]发现水星椭圆轨道以不同于牛顿定律预测的速率旋进,引发了人们对引力速度的关注. 1805年,Laplace[22]通过计算得出结论:引力辐射速度大于7×106c. 美国物理学家Flandern[56]认为:引力辐射速度远高于光速,否则,宇宙之星系将会失去现有的稳定结构;1998年,他通过计算得出的引力辐射速度为2×1010c. 基于其广义相对论[15],爱因斯坦导出了一个所谓的引力波方程,其中,引力波的速度恰为光速. 然而,逻辑上,或者说,就逻辑而言,无论牛顿万有引力论还是爱因斯坦广义相对论,皆无关于引力波和引力辐射速度的任何先验信息,根本无法计算引力速度或导出引力波方程. 那么,爱因斯坦广义相对论之引力波方程究竟意味着什么呢?其中的引力波速度为何恰恰是光速呢? GOR理论将为我们揭示其中的奥妙. 需要特别指出,与牛顿万有引力论和爱因斯坦广义相对论一样,GOR理论也无关于引力波和引力辐射速度的任何先验信息. GOR理论同样蕴含着这一重要的理想化假设:引力乃超距作用,辐射速度无穷. 3.1.2 观测局域性:信息波速度是有限的 牛顿万有引力论是理想观测代理OA∞的产物,其中,信息波之速度无穷:理想化观测时空不存在观测局域性(η→∞),信息跨越空间无须时间. 然而,爱因斯坦广义相对论却是光学观测代理OA(c)的产物,其中,信息波之速度即光速c,是有限的:光学观测时空存在观测局域性(c<∞),信息跨越空间需要时间. 与惯性时空之狭义相对论性现象(包括“光速不变性)一样,引力时空之广义相对论性现象(包括“时空弯曲”),其根源和本质,仍然在于光学观测代理OA(c)之观测局域性(c<∞). OR理论[1-3]基于Schwarzschild度规[57]的分析显示:所谓“时空弯曲”,实则观测效应. 存在观测局域性的光学代理OA(c)犹如广角镜,令引力时空看起来有些弯曲或变形. GOR理论将进一步阐明:如果我们能够借助理想代理OA∞(η→∞)观测物理世界,那么,引力时空将会呈现出客观真实的面貌:平直,而非弯曲. 在牛顿万有引力论[53]中,引力,与电磁力以及弱力和强力一样,乃物质间4种基本相互作用(力)之一,是一种“力”(force),而非时空弯曲之几何效应. 然而,在爱因斯坦广义相对论[15]中,引力被去除,只剩下了几何化的引力效应:时空弯曲. 爱因斯坦广义相对论将引力几何化,将引力效应等效为时空弯曲:物质的存在导致时空弯曲,物质密度越大时空曲率越大. 于是,地球围绕太阳运转,不再是万有引力之作用,而是弯曲的时空所致. 将引力效应几何化,不失为物质相互作用的一种形式化方法;实际上,这一方法将通过PGC对应原理渗入GOR理论及其逻辑演绎进程. 然而,这种将引力效应几何化的方法,终究只是一种形式化手段,并不代表引力作为基本相互作用真实的物理特性,更不意味着万有引力不存在. 否则,我们应该将电磁力以及弱力和强力一并几何化. GOR理论将会告诉我们,所谓“时空弯曲”,并非因为物质堆积,而是一种观测效应和表观现象. 基于PGC对应原理论述GOR时空理论之前,我们需要首先理解爱因斯坦广义相对论之时空理论,理解光学观测代理OA(c)及其观测时空X4d(c). 爱因斯坦广义相对论是光学观测代理OA(c)的产物,其中,OA(c)的基本任务,是以光或电磁相互作用为观测媒介,量化和测定引力时空X4d(c),包括其时间的测定和其空间的测定. 值得指出的是,爱因斯坦广义相对论之引力时空X4d(c)的测定,运用了“等效原理”和“光速不变性原理”.在广义相对论中,爱因斯坦基于“等效原理”引入局部惯性时空,其目的和作用在于,令“引力时空”局部等效于“惯性时空”或“自由时空”SF,于是,“光速不变性原理”在局部惯性时空中成立,从而: 第一,测定X4d(c)之时间——将“观测时间”dt变换为“标准时间”dτ; 第二,测定X4d(c)之空间——用“标准时间”dτ和不变的真空光速c计算“物理空间”dl. 3.2.1 爱因斯坦时间概念 闵科夫斯基4d时空坐标框架(式(1.1)),实为光学观测代理OA(c),蕴含着爱因斯坦相对论之时空理论,其中,X4d(c)乃OA(c)之4d观测时空——1d时间+3d空间. 1)X4d(c)之1d时间坐标:x0=ct; 2)X4d(c)之3d空间坐标:x1=x,x2=y,x3=z. 其中t=x0/c隐喻着“光速不变性”. 设运动物体或被观测对象P在X4d(c)中运动,其时空轨迹(包括时元dt和线元ds)可基于X4d(c)之4d时空坐标框架之定义(式(1.1))描述: (3.1) 式中:dt乃OA(c)之观测者O的“观测时间”;xμ(μ=1,2,3,4)为X4d(c)之时空坐标;gμν(c)为X4d(c)之时空度规;ds为P之时空轨迹之线元;而xi(t)(i=1,2,3)则是P特定时刻t=x0/c之空间坐标. OR理论和GOR理论称观测时空X4d(c)之时间t为光学观测代理OA(c)之“观测时间”.然而,爱因斯坦在其相对论中并未明确观测的地位及其作用.我们并不十分清楚,OA(c)之观测时空X4d(c)(式(3.1))中,计量时间t或时元dt的时钟何在,观测时间t或时元dt的观测者何在. 那么,X4d(c)之dt究竟意味着什么呢? 设想被观测对象P本身即一部钟,或者,TP为P之“固有时钟”.依照定义1.2,当观测者O与被观测对象P相对静止于惯性时空SI或“自由时空”SF时,O观测P或TP所得之时间即客观真实的“固有时间”:dτ=ds/c;否则,O观测P或TP所得之时间则只能是O之“观测时间”:dt=dx0/c. 爱因斯坦狭义相对论之惯性时空的时间: 爱因斯坦狭义相对论之观测时空X4d(c)乃惯性时空:gμν=ημν=diag(+1,-1,-1,-1). 因此,依式(3.1),成立: (3.2) 式中:v为光学代理OA(c)之惯性时空X4d(c)中观测者O与被观测对象P或TP之间的相对运动速度. 根据爱因斯坦狭义相对论之关系式(3.2): 1)v=0时dt=dτ,这表明,爱因斯坦狭义相对论之“固有时间”(原时dτ)概念服从OR理论和GOR理论之定义1.2; 2)v≠0时dt>dτ,此即惯性时空之“时间膨胀”,不同惯性速度导致不同程度的“时间膨胀”. 惯性时空中,运动是相对的,静止也是相对的.就爱因斯坦狭义相对论关系式(3.2)之时元dt而言,可以设想,O是静止的,而P则以惯性速度v相对于O运动,如此,dt则应为静止的观测者O观测“动钟”TP所得时间;也可以设想,P是静止的,而O则以惯性速度v相对于P运动,如此,dt则应为运动的观测者O观测“静钟”TP所得时间. 爱因斯坦狭义相对论中,静止于惯性时空SI的时钟被视为“标准钟”,其向静止之惯性观测者所指示的时间即“标准时间”,也即原时:dτ. 人们通常以为:“原时”dτ乃惯性时空之“静钟”时间速率,“观测时间”dt乃惯性时空之“动钟”时间速率.然而,如果将dt诠释为“动钟”时间速率,那么,dt>dτ则意味着“动钟快”,有悖于爱因斯坦狭义相对论之“动钟慢”的认知!因此,dt实为运动的观测者观测静止的标准钟所得观测时间. OR理论[1-3]已经阐明,实际上,光学代理OA(c)之惯性时空X4d(c)中,被观测对象P之“固有时钟”TP应视为静止于“自由时空”SF之“标准钟”,而观测时间dt则为运动的观测者O借助OA(c)观测静止的“标准钟”TP所得时间. 广义相对论引力时空之时间: 爱因斯坦广义相对论之观测时空X4d(c)乃引力时空,其时空度规gμν=gμν(xi)依赖于X4d(c)之空间坐标xi(i=1,2,3):不同坐标之时间速率可能不同. 关于时间,爱因斯坦广义相对论有2个概念. 1)标准时间:dτ=ds/c; 2)坐标时间:dt=ds/(c√(g00)). 人们通常以为:“标准时间”即“标准钟”之时间;“坐标时间”即“坐标钟”时间.如此,依照式(3.1),“坐标钟”应静止于观测时空X4d(c)之空间坐标xi(dxi=0),而“标准钟”则应静止于惯性时空SI或“自由时空”SF(gμν=ημν, dxi=0). 根据闵科夫斯基4d时空坐标框架或光学观测代理OA(c)的定义(式(1.1)),观测时空X4d(c)之时间速率dt(式(3.1))应为:dt=dx0/c.而实际上,爱因斯坦广义相对论之时间dt=dx0/c,服从定义1.2之“观测物理量”的定义,可谓OA(c)之“观测时间”;而爱因斯坦广义相对论之“标准时间”dτ=ds/c,服从定义1.2之“固有物理量”的定义,可谓“固有时间”或“原时”,可谓真实的时间. 可见,一般地,OA(c)之“观测时间”dt=dx0/c并不等同于X4d(c)之“坐标时间”dt=ds/(c√(g00)).仅当P静止于观测时空X4d(c)时,OA(c)之“观测时间”方为X4d(c)之“坐标时间”. 需要特别注意:正因为如此,爱因斯坦在其广义相对论中基于“等效原理”将P在引力时空X4d(c)中的邻域局部惯性化,其中,P瞬态静止. P静止于X4d(c) 时,dxi=0;依式(3.1),成立: (3.3) 式中χ(=-GM/r≤0)为引力时空X4d(c)特定空间位置xi(i=1,2,3)之引力势. 根据爱因斯坦广义相对论之关系式(3.3): 1)χ=0时dt=dτ,这表明,爱因斯坦广义相对论之“标准时间”的概念等同于OR和GOR理论中的“固有时间”概念; 2)χ≠0时dt>dτ,此即引力时空之“时间膨胀”,不同的引力势导致不同程度的“时间膨胀”. 引力时空中,观测者O和被观测对象P可能存在一定势差.就爱因斯坦广义相对论之关系式(3.3)中的时元dt而言,可以设想,O静止于“自由时空”(χ=0)SF,而P则处于引力时空X4d(c)之势位χ(≠0),如此,dt应为零势位观测者O观测χ势位之势钟TP所得时间;也可以设想,P静止于“自由时空”(χ=0)SF,而O则处于引力时空X4d(c)之势位χ(≠0),如此,dt则应为χ势位之观测者O观测零势位之“标准钟”TP所得时间. 爱因斯坦广义相对论中,静止于“零势位”的时钟被视为“标准钟”,其向静止于“零势位”之观测者所指示的时间即“标准时间”,也即原时:dτ. 人们通常以为:“原时”dτ乃“零势钟”之时间速率,“观测时间”dt乃“势钟”之时间速率.然而,如果将dt诠释为“势钟”时间速率,那么,dt>dτ则意味着“势钟快”,有悖于爱因斯坦广义相对论之“势钟慢”的认知!因此,dt实为势场的观测者观测“零势位”的标准钟所得观测时间. GOR理论将会阐明,实际上,光学代理OA(c)之引力时空X4d(c)中,被观测对象P之“固有时钟”TP应视为静止于“自由时空”SF(处于“零势位”:χ=0)之“标准钟”,而观测时间dt则为势场的观测者O借助OA(c)观测零势位之“标准钟”TP所得时间. “标准时间”和“坐标时间”概念乃爱因斯坦广义相对论之重要概念,不仅用于计量或测定光学代理OA(c)之引力时空X4d(c)的时间,而且,用于计量或测定光学代理OA(c)之引力时空X4d(c)的空间. 3.2.2 广义相对论之标准时间的测定[15,58-59] 如3.2.1所述,惯性时空中,不同惯性速度(v)之观测者,其时间速率dt不同;引力时空中,不同引力势(χ)之观测者,其时间速率dt也不同. 爱因斯坦狭义相对论中的时空乃惯性时空,属光学代理OA(c)之观测时空X4d(c).如式(3.2)所示,dτ乃v=0时的时间,爱因斯坦将其理解为时钟静止于惯性时空的时间速率;dt乃v≠0时的时间,爱因斯坦将其理解为时钟运动于惯性时空的时间速率.dt依赖于被观测对象P在X4d(c)中的惯性速度v,然而,并不依赖于P在X4d(c)中的空间坐标.因此,在其狭义相对论中,爱因斯坦似乎更愿意使用dt而不是dτ描述P之运动,并且,依据并非客观真实的dt解释其“时涨尺缩”和“同时性之相对论性”观念,渲染其“相对论性乃时空和物质运动本质特性”的思想. 爱因斯坦广义相对论中的时空乃引力时空,也属光学代理OA(c)之观测时空X4d(c).如式(3.3)所示,dτ乃χ=0时的时间,爱因斯坦将其理解为时钟静止于“零势位”的时间速率;dt乃χ≠0的时间,爱因斯坦将其理解为时钟静止于χ势位的时间速率.就引力时空而言,不同空间坐标有不同的引力势χ,因而,其时间速率dt不同.如此,爱因斯坦广义相对论便不能直接地运用闵科夫斯基4d时空坐标框架之时间速率dt描述被观测对象P之运动.或许,正因为如此,爱因斯坦意识到,闵科夫斯基4d时空坐标框架之时间速率dt并不代表客观真实的时间. 爱因斯坦广义相对论需要统一时间.于是,“标准时间”(dτ)的概念出现在了爱因斯坦广义相对论中,以区别于其“坐标时间”(dt)的概念. 自然地,“标准时间”,应该独立于时空和物质运动,不依赖于v和χ.或许,这让爱因斯坦想到了狭义相对论中静止于惯性时空的时钟和时间dτ(式(3.2)).爱因斯坦广义相对论的“标准钟”静止于“零势位”(χ=0),等效于爱因斯坦狭义相对论的“标准钟”静止于惯性时空(v=0).这意味着,对于“标准中”,gμν=ημν且dxi=0(i=1,2,3).因此,依据式(3.1)即可得出不依赖于v和χ的“标准时间”dτ: (3.4) 图1 观测时空的度量Fig.1 Measurement of observational spacetimes 显然,式(3.4)之“标准时间”dτ乃定义1.2的“固有物理量”,可谓“固有时间”,即客观真实的时间. 爱因斯坦狭义相对论需要将依赖于惯性速度v的观测时间dt变换为“标准时间”dτ;而爱因斯坦广义相对论则需要将依赖于引力势χ的观测时间dt变换为“标准时间”dτ. 若被观测对象P之“固有时钟”TP静止于“自由时空”SF,则TP即“标准钟”,其时间便是“标准时间”.然而,在爱因斯坦看来,P处于引力势场(χ≠0),TP并非“标准钟”,其时间并非“标准时间”;若P静止于X4d(c)特定空间坐标xi(i=1,2,3),则TP便是xi(i=1,2,3)之“坐标钟”,而时间dt则是xi(i=1,2,3)之“坐标时间”.因此,爱因斯坦需要对广义相对论实施“时间标准化”:将引力时空X4d(c)变换为惯性时空,将时钟TP变换为“标准钟”,将“坐标时间”dt变换为“标准时间”dτ. 设D0(xi(t) (i=1,2,3))为被观测对象P之特定时刻t=x0/c的空间坐标.D0之观测者O原本属于引力时空SO=X4d(c);SO即OA(c)之观测时空.如图1(a1)所示,基于“等效原理”,可在D0处引入瞬时静止的局部惯性时空SI,其中,P和O静止于D0,“光速不变性”原理成立. 于是,“等效原理”体现出其特殊的价值和意义:经由“等效原理”之等效变换,引力时空SO瞬时局部地变换为或等效于惯性时空SI. 根据式(3.4),“标准时间”dτ正比于被观测对象P在光学代理OA(c)之观测时空X4d(c)中的线元ds.如图1(a1)所示,设LO为P在OA(c)之引力时空SO中的世界线,LI为P在等效惯性时空SI中的世界线.合理地,SO之标准时间可定义为dτO=dsO/c;SI之标准时间可定义为dτI=dsI/c.显然,根据式(3.4)之“标准时间”定义,惯性时空SI之dτI即客观真实的“固有时间”(原时)dτ:dτI=dτ. 根据微分几何,曲线LO之线元dsO与其切线LI之线元dsI相等:dsO=dsI;故有 (3.5) 式(3.5)具有重要寓意:光学代理OA(c)之不同观测时空X4d(c)(包括SO和SI)具有相同的“标准时间”,皆客观真实的“固有时间”(原时)dτ. 经“等效原理”对引力时空SO=Xμ(c)的惯性化处理,被观测对象P和X4d(c)之空间坐标D0(xi)的观测者O瞬时静止于SI:dxi=0(i=1,2,3).故依式(3.1)和式(3.4)、式(3.5),爱因斯坦广义相对论之“标准时间”dτ可依其“坐标时间”dt测定: (3.6) 式中χ为X4d(c)空间坐标xi之“牛顿引力势”. 爱因斯坦广义相对论之关系式(式(3.6))表明:“标准时间”是可以测定的;更重要地,客观真实的时间,即“原时”,是可以由观测和测量测定的. 特别需要指出,“光速不变性”假设在爱因斯坦广义相对论之时间测定中同样发挥着重要作用. 如1.5.1所述,闵科夫斯基时空,或者说,光学代理OA(c)之观测时空X4d(c),是“光速不变性原理”的一种形式化表达,其时轴x0=ct代表着“光速不变性”.爱因斯坦的“标准时间”dτ(式(3.6))正是基于被观测对象P在闵科夫斯基4d时空中的时元dt=dx0/c(式(3.1))和线元ds=gμνdxμdxν(式(3.1))导出的. 3.2.3 广义相对论之物理空间的测定[15,58-59] 爱因斯坦广义相对论之物理空间的测定既需要“标准时间”dτ,也需要“光速不变性”假设,同时,还需要借助“等效原理”,将引力时空SO=X4d(c)瞬时局部地变换为或等效于惯性时空SI. 如图1(a2)所示,设D为观测时空SO=X4d(c)中足够接近D0的相邻空间点;光信号由D0射向D,再由D返回D0,其所需时间服从 (3.7) 若D0至D之空间位移为dxi(i=1,2,3),则D至D0之空间位移为-dxi(i=1,2,3).光学代理OA(c)情形之下,光之时空线元ds2=0,因而 (3.8) 特别地,依“等效原理”,D0点之局部惯性时空SI必定各向同性,其中,“光速不变性”假设成立.因而,D0和D之间的“物理空间距离”dl可基于原时dτ和真空光速c定义为dl=cdτ/2. 依式(3.6),“原时”dτ=√(g00)dx0/c. 于是,“物理空间距离”dl可如下测定: 或 (3.9) 式中γik(i,k=1,2,3)被称为“物理空间度规”. 3.2.4 广义相对论之时空变换因子[15,59-60] 在爱因斯坦相对论中,“时空变换因子”γ=dt/dτ,即“观测时元”dt与“固有时元”dτ的比,是一个重要的物理量:γ越大,被观测对象之相对论性现象越显著.因此,γ又可称作“相对论性因子”,表征时空和物质运动的相对论性效应. 爱因斯坦狭义相对论中,“时空变换因子”γ=dt/dτ乃惯性时空变换因子,即洛伦兹因子: (3.10) 其中,γ依赖于被观测对象P之惯性速度v,|v|越大,则惯性相对论性效应越显著. 爱因斯坦广义相对论中,“时空变换因子”γ=dt/dτ乃“引力时空变换因子”;单纯引力情形(v=0)之下: (3.11) 其中,γ依赖于P所处空间坐标之引力势χ,|χ|越大,则引力相对论性效应越显著. 如果考虑被观测对象P在引力场中运动,那么,爱因斯坦广义相对论之时空变换因子γ应为 (3.12) 然而,式(3.12)中的χ是标量,只代表“标量引力势”,简称“标势”.爱因斯坦设想,引力场或许也像电磁场那样,既有标势,又有矢势.仿照静电场场强定义,引力场任意一点之场强g可定义为 (3.13) 式中:Δm乃质量,依“等效原理”,不区分引力质量和惯性质量;引力场强g等效于点xi(i=1,2,3)处的引力加速度a(a1,a2,a3). 根据爱因斯坦广义相对论之计算和分析: (3.14) 式中γi(i=1,2,3)即“矢量引力势”. 若矢量引力势γi(i=1,2,3)果真存在,则∃i∈(1,2, 3)g0i≠0;根据式(3.9),在光学代理OA(c)之观测时空X4d(c)中,空间度规γik(i,k=1,2,3)与X4d(c)之时间轴x0相关.这将意味着,X4d(c)之时间轴x0与空间轴xi(i∈(1,2,3))可以是非正交的. 反之,若矢量引力势γi(i=1,2,3)不存在,则g0i=0(i=1,2,3);根据式(3.9),X4d(c)之空间度规γik=-gik(i,k= 1,2,3)与X4d(c)之时间轴x0无关.这将意味着,X4d(c)之时间轴x0与空间轴xi(i∈(1,2,3))正交:时间与空间相互独立,相应的X4d(c)坐标系可谓“时空正交系”. 引力场真地存在“矢量引力势”吗?这涉及四维时空中“时间轴和空间轴是否正交”的问题.更重要地,这引发了“时间和空间是独立”的问题. 依光学代理OA(c)(式(1.1)):dt=dx0/c和dτ=ds/c;考虑引力场之标势χ和矢势γi(i=1,2,3),则 (3.15) 将式(3.15)与式(3.6)以及式(3.9)和式(3.14)对照,可得爱因斯坦广义相对论之时空变换因子 (3.16) 式中:v=dl/dt;vi=dxi/dt(i=1,2,3). 爱因斯坦广义相对论之时空变换因子(式(3.16)),概括了惯性时空和引力时空的相对论性效应:无引力场(χ=0,γi=0)时,式(3.16)约化为惯性时空变换因子γ=1/√(1-v2/c2);无相对运动(v=0)时,式(3.16)约化为引力时空变换因子γ=1/√(1+2χ/c2). 3.2.5 相对论性现象的根源和本质问题 最早观测到相对论性现象或许可追溯到迈克尔逊- 莫雷实验[42],由此,诞生了菲兹杰拉德- 洛伦兹变换[39-40].基于迈克尔逊- 莫雷实验,爱因斯坦建立“光速不变性”原理,从理论上导出洛伦兹变换,进而,建立狭义相对论[14]乃至广义相对论[15].然而,无论菲兹杰拉德或洛伦兹,还是爱因斯坦,并不真正地理解光在菲兹杰拉德变换[39]或洛伦兹变换[40]中扮演什么角色.直到今天,主流物理学界仍然并不十分理解光在爱因斯坦相对论中究竟扮演着什么角色. 光速c为什么会出现在爱因斯坦相对论中?特别地,光速c为什么会占据着爱因斯坦相对论之“时空变换因子”γ=dt/dτ之特定位置? 自然地,光速c出现在爱因斯坦相对论中,特别是出现在其“时空变换因子”γ=1/√(1+2χ/c2-v2/c2)中,乃“光速不变性”假设所致.然而,作为爱因斯坦相对论之逻辑前提,“光速不变性”假设本身并不能解释光速在爱因斯坦相对论中扮演着什么角色. 爱因斯坦认为,如今,主流物理学界也这么认为:光速乃宇宙极限速度,是不可超越的;因而,光速c相对于任意惯性观测者是不变的或相同的.如此,式(3.16)之“时空变换因子”γ=γ(v,χ)取决于物质运动速度v和引力相互作用χ:v=0且χ=0时,γ=Γ∞≡1,无相对论性现象;而v≠0或χ≠0时,则γ>Γ∞≡1,时空和物质运动便会呈现出相对论性现象. 据此,爱因斯坦认为,如今,主流物理学界也这么认为:相对论性现象,包括“光速不变性”和“时空弯曲”,乃时空和物质运动的本质特性,其根源在于物质运动(v)以及物质间的相互作用(χ). 然而,OR理论已经阐明,爱因斯坦狭义相对论中的惯性相对论性效应的根源并非物质运动,其本质在于光学代理OA(c)之观测局域性(c<∞).GOR理论将进一步阐明,爱因斯坦广义相对论中的引力相对论性效应的根源并非物质相互作用,其本质同样在于光学代理OA(c)之观测局域性(c<∞). 时间是最基本的物理概念和最基本的物理量. 正是从时间的定义出发,OR理论从逻辑上和理论上导出具有重要意义的“时频比不变性”,进而,建立起OR理论之整个理论体系[2-3]. OR理论不仅概括并统一了爱因斯坦狭义相对论和伽利略- 牛顿之惯性理论,而且概括并统一了爱因斯坦狭义相对论和德布罗意物质波论. 实际上,OR理论之时间定义及其时频比不变性,并不局限于惯性时空和OR理论,可推广至引力时空和GOR理论. 需要指出,时间的定义以及“时频比不变性”,并非源于爱因斯坦相对论,而是OR理论. 3.3.1 时间的定义 时间的定义需要借助周期性物理现象. 任意周期性物理现象之周期皆可作为时间单位用于计量时间:1年乃地球绕日运行1周,1月乃月亮圆缺变化1周,1天乃昼夜交替1周. 最基本的时间单位是秒(s). 依照现行的国际单位制(SI),1 s乃铯- 133原子基态2个超精细能级之间跃迁辐射或震荡9 192 631 770周所持续的时间. 爱因斯坦在其广义相对论中引入了“标准钟”和“标准时间”的概念;所谓“标准钟”,即静止于惯性时空的时钟. 然而,无论SI之原子钟或爱因斯坦之“标准钟”都没有明确观测者的地位和作用:谁在观测时间,谁在观看 “标准钟”,或者,谁在测定铯- 133之辐射;特别地,谁作为观测媒介或信使在为观测者传递有关时间的信息? 国际单位制(SI)中定义的时间自然可视为“标准时间”,相应的原子钟自然可视为“标准钟”. 然而,SI之原子钟作为“标准钟”是有条件的. OR理论引入“自由时空”作为“惯性时空”的替代概念. 如1.4所述,所谓“自由时空”,即不存在任何力或相互作用的时空,记作:SF. 特别注意,SI基于铯原子辐射周期定义时间单位“s”,要求铯原子静止于温度绝对零度和零磁场状态. 实际上,理论上,这要求铯原子静止于“自由时空”SF. 正是基于“自由时空”概念,OR理论定义了“固有物理量”和“观测物理量”(定义1.2). 如果GOR理论将“标准钟”定义为静止于“自由时空”SF的时钟,那么,国际单位制(SI)定义的原子钟,以及爱因斯坦的“标准钟”,将成为一致的和等价的概念,皆可指示“标准时间”. 那么,“标准钟”所指示的时间就是“标准时间”吗?这取决于观测者的观测代理,取决于观测者的运动状态,取决于观测的物理环境. 我们必须认识到: 第一,任意周期信号源皆可作为“标准钟”,但必须静止于“自由时空”SF; 第二,任意观测者皆可直接测定“标准时间”,但必须相对于“标准钟”静止于“自由时空”SF,除非观测者能借助理想观测代理OA∞为其传递“标准钟”之时间信息. OR理论明确了观测和观测者在时间计量中的地位和作用,引入了“观测时间”概念,以区别于客观真实的“固有时间”或“原时”. 理论上,任意周期性物理现象皆可用于定义时间;任意周期性物理现象之固有周期To或固有频率fo皆可作为计量时间的基本单位. 定义3.1(时间):设有周期信号源P和观测者O及其观测代理OA(η),To和fo分别为P之固有周期和固有频率.若O借助OA(η)在时段Δt内观测到P之N个周期,则Δt=NTo=N/fo,并称其为P相对于O或OA(η)的 “观测时间”;特别地,若Δt乃O和P相对静止于自由时空SF之观测值,则称Δt为P之“固有时间”,记作Δτ(=NoTo=No/fo),其中,No乃P静止于SF时固有时段Δτ内的周期数. 周期信号源P静止于“自由时空”SF时即“标准钟”,其所指示的时间即“固有时间”.(注意:静止于SF等同于静止于惯性时空或“零势位”.) 或者,更正式地,“标准钟”的概念可如下定义. 定义3.2(标准钟):设有周期信号源P,To和fo分别为P之固有周期和固有频率.若To或fo被定义为计量时间之基本单位,则当P静止于“自由时空”SF时,P即“标准钟”. 对照定义3.1之时间速率Δt和闵科夫斯基4d时空之时间速率dt(式(3.1)和式(3.3))可知: 1)Δt=Δx0/c乃观测者O借助光学代理OA(c)所得之“观测时间”; 2)O和P静止于观测时空X4d(c)特定空间坐标时,Δt即爱因斯坦之“坐标时间”; 3)O和P相对于静止于“自由时空”SF时,Δt=Δτ即爱因斯坦之“标准时间”. 可见,OR和GOR之“固有时间”概念与爱因斯坦之“标准时间”的概念是一致的;而爱因斯坦之“坐标时间”乃“观测时间”之特定情形. 定义3.1意味着,观测者O观测所得之“观测时间”Δt依赖于观测和观测代理OA(η):Δt=Δt(η).OR理论已经阐明,GOR理论将会进一步阐明,制约于观测代理OA(η)之观测局域性(η<∞),观测者之“观测时间”未必等同于“固有时间”. OR理论已经阐明,GOR理论将会进一步阐明,η→∞时Δt→Δτ:理想观测代理OA∞之“观测时间”Δt趋同于“固有时间”Δτ.理想观测代理OA∞代表着客观真实的物理世界.因而,定义3.1之“固有时间”(原时)代表着客观真实的时间,不依赖于观测,不依赖于观测者,不依赖于观测代理. 3.3.2 时频比不变性 定义3.1隐喻着时间观测上的一个重要性质:时频比不变性(The Invariance of Time-Frequency Ratio). 时频比不变性:设观测代理OA(η)之观测时空X4d(η)有物理周期信号源P和观测者O,fo为P之固有频率,依定义3.1和定义3.2,将P定义为“标准钟”,则P相对于O之“观测时元”dt与O之“观测频率”f的比dt/f乃一不变量,恒等于P之“固有时元”dτ与P之“固有频率”fo的比:dτ/fo. 证明: 固有物理量(包括固有时间Δτ)乃不变量,是一切观测者共同遵循的计量标准. 依定义3.1,时钟P之“固有频率”fo=No/Δτ;相应地,O之“观测频率”为f=N/Δτ.故有:f/fo=N/No. 依定义3.1,N/No=Δt/Δτ.故有:f/fo=Δt/Δτ. 令Δ→d,成立: (3.17) 故:基于定义3.1,时频比不变性成立. (证毕) 特别需要指出:“时频比不变性”中的“频率”乃时钟频率,而非任意被观测周期现象之频率;“时频比不变性”是时间之观测上的相对论性效应,而非一般周期性物理现象之多普勒效应.同时要指出:一般地,多普勒效应之观测代理,既非理想代理OA∞,也非光学代理OA(c),而是周期性物理现象自身. 时频比不变性具有深刻寓意:相对论性效应和量子效应可以通过“时频比不变性”联系在一起. 正是基于“时频比不变性”,OR理论统一了爱因斯坦狭义相对论和德布罗意物质波论,将爱因斯坦公式E=mc2和普朗克方程E=hf两个原本分属不同理论体系的伟大公式纳入了同一理论体系[2-3]. 主流物理学界一些学者怀疑甚至批判OR理论及其“时频比不变性”,以维护爱因斯坦狭义相对论. 实际上,“时频比不变性”原本就存在于爱因斯坦相对论和经典量子论中.爱因斯坦狭义相对论中的质速关系意味着“时质比不变性”: (3.18) 式中:mo乃被观测对象P之固有质量;m乃P之相对论性质量(OR谓之“观测质量”). “时质比不变性”与“时频比不变性”是等价的.结合爱因斯坦公式E=mc2和经德布罗意推广的普朗克方程E=hf,即可检验或验证光学观测代理OA(c)情形下的“时频比不变性”: (3.19) 这印证了OR和GOR理论之“时频比不变性”. 在GOR理论中,“时频比不变性”将为广义相对论性效应(例如“引力红移”现象)注入新的见解,并且把引力论与量子论自然地联系起来. 或许,这将有助于量子力学扩展至引力时空,进而促进“量子引力论”或“引力量子论”的发展. “时频比不变性”,是“固有时间”和“观测时间”所遵循的法则,可表述为物理学一项基本原理. 广义相对论中,爱因斯坦基于“等效原理”将引力时空变换为惯性时空,其中,“光速不变性”假设成立. 于是,“坐标时间”可变换为“标准时间”,因而,引力时空之时间可测定;“引力空间”可变换为“惯性空间”,因而,引力时空之空间可测定. 现在,基于PGC对应原理,我们拟将爱因斯坦广义相对论中的“标准时间”和“坐标时间”概念,以及爱因斯坦度量引力时空之时间和空间的方法,由光学观测代理OA(c)推广至GOR理论之一般观测代理OA(η). 爱因斯坦借助光学代理OA(c)度量时空;而OR和GOR理论度量时空可借助任意观测代理OA(η). 3.4.1 PGC逻辑路线:OA(c)→OA(η) 理论上,观测代理OA(η)之观测媒介可为任意物质运动形式,未必一定是光;其观测信息之传播速度η可为任意值,未必一定是光速c. 客观世界中,物质运动速度必定是有限的.因此,与光学代理OA(c)一样,一切现实的观测代理OA(η)皆存在观测局域性(η<∞).制约于观测局域性,OA(η)之观测时空X4d(η),与OA(c)之观测时空X4d(c)一样,也会显得有些“弯曲”.然而,如图1(b1)所示,不同观测代理OA(η),其信息波速度η不同,存在着不同程度的观测局域性,其观测时空X4d(η)会呈现出不同程度的“弯曲”. 基于PGC对应原理,不同观测代理之间,包括光学代理OA(c)与一般观测代理OA(η)之间,皆可进行“同构一致性”对应变换.实际上,正是基于PGC对应原理,式(1.1)中的光学观测代理OA(c)被同构一致地变换为定义1.1之一般观测代理OA(η). 如2.4所述,基于PGC对应原理,演绎GOR引力时空度量关系,有2条逻辑路线可循. 经由PGC逻辑路线1: 基于PGC对应原理,将光学观测代理AO(c)同构一致地对应变换为一般观测代理OA(η),则爱因斯坦广义相对论之光学观测时空X4d(c)随之变换为GOR观测时空X4d(η). 如此,爱因斯坦广义相对论测定引力时空的度量关系式便可同构一致地对应变换至GOR理论. 第一,以η替代光速c,则爱因斯坦广义相对论测定“标准时间”的式(3.6)可直接变换为GOR理论测定“标准时间”的逻辑关系: (3.20) 式中g00=g00(η)为OA(η)之观测时空X4d(η)的时空度规元素(区别于OA(c)之光学时空X4d(c)的g00(c)). 于是,一切观测代理OA(η)(而不仅仅是OA(c))之观测时空X4d(η),其“标准时间”皆可测定. 第二,以η替代光速c,则爱因斯坦广义相对论测定“物理空间”的式(3.9)可直接变换为GOR理论测定“物理空间”的逻辑关系: (3.21) 式中γik=γik(η)为OA(η)之观测时空X4d(η)的空间度规(区别于OA(c)之光学时空X4d(c)的γik(c)). 于是,一切观测代理OA(η)(而不仅仅是OA(c))之观测时空X4d(η),其“物理空间”皆可测定. 经由PGC逻辑路线2: 或许,基于PGC对应原理,经由PGC逻辑路线2,更有助于我们对爱因斯坦广义相对论之时空理论的理解,进而,更具逻辑性地演绎GOR时空理论. 实际上,定义1.1所因循的正是PGC逻辑路线2: 光学代理OA(c)中,x0=ct代表着“光速不变性”;而一般观测代理OA(η)中,x0=ηt则代表着“信息波速度不变性”.因此,OA(η)与OA(c)之间的同构一致对应变换,并非简单地以信息波速度η替代光速c,实则是“信息波速度不变性”替代了“光速不变性”. 如3.2所述,爱因斯坦广义相对论中,引力时空的度量,包括时间的测定和空间的测定,依赖于爱因斯坦广义相对论之“三原理”:1)等效原理;2)广义协变原理;3)光速不变性原理.基于PGC对应原理,经由PGC逻辑路线2,以“信息波速度不变性”替代“光速不变性”,则GOR理论也将拥有“三原理”:1)等效原理;2)广义协变原理;3)信息波速度不变性原理.自然地,以此“三原理”为逻辑前提,因循爱因斯坦广义相对论的逻辑,则GOR理论必能导出与爱因斯坦广义相对论同构一致的引力时空度量关系. 基于“等效原理”,一般观测代理OA(η)之“弯曲的引力时空”SO=X4d(η)被局部惯性化,等效于“平直的惯性时空”SI,或“自由时空”SF,其中,“广义协变原理”和“信息波速度不变性原理”成立.于是,第一,如3.4.3,GOR引力时空X4d(η)之“标准时间”dτ可测定,因循爱因斯坦的逻辑可自然地导出时间测定关系(3.20);第二,如3.4.4,GOR引力时空X4d(η)之“物理空间”dl可测定,因循爱因斯坦的逻辑可自然地导出空间测定关系式(3.21). 3.4.2 GOR时间 根据定义1.1,一般观测代理OA(η)之观测时空X4d(η)与光学代理OA(c)之闵科夫斯基时空X4d(c)同构一致,具有同样的1d时间+3d空间的时空结构: 1)X4d(η)之1d时间坐标:x0=ηt; 2)X4d(η)之3d空间坐标:x1=x,x2=y,x3=z. 其中,时间坐标t=x0/η隐喻着“信息波速度不变性”. 设有被观测对象P和观测者O∶P存在于“固有时空”;O借助观测代理OA(η)观测P.从O之观测角度看,P在OA(η)之观测时空X4d(η)中运动.根据定义1.1,P的时空轨迹可用OA(η)之观测时空X4d(η)的时元dt和线元ds描述: (3.22) 式中:dt乃观测者O利用OA(η)观测所得时间;xμ(μ=1,2,3,4)为X4d(η)之时空坐标;xi(t)(i=1,2,3)为P之特定时刻t=x0/η的空间坐标;ds为P之时空轨迹的线元;而gμν(η)则为X4d(η)之时空度规. 定义3.1或式(3.22)之时元dt可称:“GOR时间”. 那么,GOR时间与定义1.1之时间以及爱因斯坦之“坐标时间”和“标准时间”有什么关系呢? GOR时间是定义1.1之一般观测代理OA(η)的时间,与定义3.1之时间概念是一致的.依3.2.1和3.3.1,GOR时间dt=dx0/η,乃一般观测代理OA(η)之“观测时间”,同时,也是定义3.1之“观测时间”;一般地,dt=dx0/η既非“标准时间”也非“坐标时间”. 定义3.1之时间概念概括了爱因斯坦广义相对论之“坐标时间”和“标准时间”:无论“坐标时间”或“标准时间”,都只是定义3.1之“观测时间”的特定情形.特别地,定义3.1之“固有时间”与爱因斯坦之“标准时间”是一致的或等价的,皆“标准钟”静止于“自由时空”SF之时间. 然而,爱因斯坦没有明确观测者在时间之观测或度量中的地位和作用.基于定义3.1,OR理论和GOR理论的时间概念需要与观测和观测者联系起来:任意观测代理OA(η)之观测时空X4d(η)中,时间dt即定义3.1中O之“观测时间”;特别地,根据定义1.2,定义3.1之“固有时间”乃客观真实的时间,仅当O相对于“标准钟”静止于“自由时空”SF,或借助于理想观测代理OA∞,方可测定. 可以设想:定义1.1(式(1.2)或(3.22))之dt乃“标准钟”呈现给OA(η)之观测者O的“观测时间”. 那么,就P之时空轨迹(式(3.22))而言,问题是: 谁是“标准钟”或“标准钟”在哪里? 谁是观测者O或观测者O在哪里? 依定义3.2,“标准钟”乃静止于“自由时空”SF的时钟;所有静止于SF的周期信号源,包括P或其“固有时钟”TP,皆可作为“标准钟”. 观测者O的基本任务是测定被观测对象P之时空坐标xμ(μ=1,2,3,4),即测定P之特定时间t=x0/η,同时,测定P之特定时刻t的空间坐标xi(t)(i=1,2,3).GOR时间dt=dx0/η的测定需要明确OA(η)之观测者O与被观测对象P的相对关系. 观测意味着时空变换:观测者O借助观测代理OA(η)将被观测对象P由其“固有时空”变换至OA(η)之观测时空X4d(η).原本,被观测对象P属于“固有时空”,静止于“自由时空”SF;P本身或其“固有时钟”TP即“标准钟”.因此,定义1.1(式(1.2)或(3.22))之dt乃TP作为“标准钟”呈现给OA(η)之观测者O的“观测时间”. 特别注意,引力场中,不同空间坐标之观测者有不同“观测时间”dt.那么,定义1.1(式(1.2)或(3.22))之dt所对应的观测者O在哪里?作为观测者,O观测P之时空轨迹如式(3.22)所示:特定时刻t=x0/η,P到达或位于特定空间坐标xi(t)(i=1,2,3);相应的dt必定是P或TP位于xi(t)(i=1,2,3)的“观测时间”速率.因此,观测者O应该定位于P之空间坐标:特定时刻t=x0/η,P之时空轨迹(式(3.22))之相应的dt,乃与P或TP瞬时定位于同一空间坐标xi(t)(i=1,2,3)之观测者O的“观测时间”. 就空间位置而言,“标准钟”TP永远地静止于P.自然地,若t=x0/η时刻O和P瞬时相对静止于“自由时空”SF,则O之“观测时间”dt=dx0/η(gμν=ημν,dxi=0;i=1,2,3)便是“标准时间”;若t=x0/η时刻O和P瞬时相对静止于X4d(η)特定空间坐标xi(t)(i=1,2,3),则O之“观测时间”dt=dx0/η(dxi=0;i=1,2,3)便是xi(t)(i=1,2,3)之“坐标时间”. 归纳起来,GOR时间,包括其标准时间和观测时间,服从定义3.1,GOR标准时间与爱因斯坦的“标准时间”是一致的,GOR坐标时间与爱因斯坦的“坐标时间”是一致的,皆可由定义1.1或被观测对象P的时空轨迹之式(3.22)导出. GOR标准时间:若O和P相对静止于“自由时空”SF,则gμν=ημν且dxi=0(i=1,2,3),应成立: (3.23) 其中,O之“观测时间”dt即“固有时间”或“标准时间”dτ,与定义3.1之“固有时间”概念以及爱因斯坦广义相对之“标准时间”概念一致. GOR坐标时间:若O和P静止于X4d(η)特定空间坐标xi(t)(i=1,2,3),则dxi=0(i=1,2,3),应成立: (3.24) 其中,GOR理论一般观测代理OA(η)之“坐标时间”dt(η)与爱因斯坦广义相对论之光学观测代理OA(c)的“坐标时间”同构一致:dt(c)=dτ/√(1+2χ/c2). GOR观测时间:O和P瞬时位于X4d(η)同一空间坐标xi(t),未必意味着其相对静止;dt=dx0/η乃O之“观测时间”dt最一般情形,服从定义3.1.若仅考虑时空正交情形:g0i=gi0=0(i=1,2,3),则成立: (3.25) 其中,涉及O相对于P运动之情形(v乃O相对于P之瞬时运动速度). 值得注意,GOR理论的一般观测代理OA(η)之式(3.25)与爱因斯坦广义相对论的光学代理OA(c)之式(3.11)同构一致:dt(c)=dτ/√(1+2χ/c2-v2/c2). 观察式(3.23)~式(3.25)可知,GOR时间,即GOR观测时间(式(3.25)),概括了GOR标准时间和GOR坐标时间:v=0时,式(3.25)约化为式(3.24),GOR观测时间dt=dx0/η即GOR坐标时间;而v=0且χ=0时,则式(3.25)约化为式(3.23),GOR观测时间dt=dx0/η即GOR标准时间dτ=ds/η. “观测时间”概念乃OR理论和GOR理论重要的时间概念.定义3.1的GOR“观测时间”概念,乃一般观测代理OA(η)之时间,适用于一切观测代理,包括光学代理和理想代理.GOR观测时间(式(3.25))dt乃一般观测代理OA(η)之观测时空X4d(η)的观测者O观测“标准钟”所得时间.与爱因斯坦相对论之情形一样,GOR观测时间dt也会“膨胀”:v≠0或χ≠0时,dt>dτ;在观测者看来,“标准钟”变快了. 特别地,根据式(3.25)可知: 第一,惯性时空(χ=0):dt=dτ/√(1-v2/η2)≥dτ. 这意味着,运动的观测者(v≠0)观测静止于“自由时空”SF的“标准钟”,其“观测时间”dt大于“标准时间”dτ.换句话说,在惯性观测者看来,静止于惯性时空的时钟走得更快.这符合爱因斯坦狭义相对论关于“动钟慢”的认知或判断. 第二,引力时空(v=0):dt=dτ/√(1+2χ/η2)≥dτ. 这意味着,势场之观测者(χ≠0)观测“零势位”的“标准钟”,其“观测时间”dt大于“标准时间”dτ.换句话说,在势场观测者看来,处于“零势位”的时钟走得更快.这符合爱因斯坦广义相对论关于“势钟慢”的认知或判断. GOR时间与爱因斯坦广义相对论之时间具有一致性对应关系.因而,爱因斯坦广义相对论之“标准时间”和“坐标时间”可基于PGC原理由光学代理OA(c)对应变换至一般观测代理OA(η);特别地,爱因斯坦广义相对论度量或测定光学观测时空X4d(c)的逻辑方法,可推广至GOR理论,度量或测定一般观测时空X4d(η). 3.4.3 GOR标准时间的测定 实际上,3.2.2已阐明:GOR时间,即式(3.22)之dt=dx0/η,应为GOR观测时间,式(3.23)之dτ=ds/η为GOR标准时间,而式(3.24)之dt=dx0/(η√(g00))则为GOR坐标时间. 与爱因斯坦广义相对论之观测时空X4d(c)一样,GOR观测时空X4d(η)也是引力时空:不同空间坐标有不同的引力势χ;因而,不同空间坐标之时间速率dt不同.如此,GOR理论不能直接地运用OA(η)之“观测时间”dt或“坐标时间”dt描述或测定被观测对象P的运动.因此,如同爱因斯坦广义相对论,GOR理论也需要统一的“标准时间”. 基于PGC对应原理,经由PGC逻辑路线1,以η替代光速c,则爱因斯坦之“标准时间”dτ=ds/c可变换为GOR“标准时间”:dτ=ds/η.或者,基于PGC对应原理,经由PGC逻辑路线2,因循爱因斯坦广义相对论的逻辑:“标准钟”静止于SF,gμν=ημν且dxi=0(i=1,2,3),则由式(3.22)可得客观真实的时间,也即GOR“标准时间”dτ: (3.26) 依定义3.2,静止于“自由时空”SF的时钟即“标准钟”.设想被观测对象P之“固有时钟”TP原本静止于SF,那么,TP便是“标准钟”,相对静止于SF(“零势位”)的观测者O,O之“观测时间”便是“标准时间”.然而,GOR理论中,OA(η)之观测时空X4d(η)乃引力时空,其任意空间坐标之观测者O皆处于引力势场(χ≠0);因而,O之“观测时间”dt并非“标准时间”dτ.若P静止于X4d(η)特定空间坐标xi(i=1,2,3),而O为xi(i=1,2,3)坐标处之观测者,则其“观测时间”dt便是O之“坐标时间”. 因此,GOR理论需要对观测代理OA(η)之“观测时间”dt=dx0/η实施“标准化”.基于PGC对应原理,经由PGC逻辑路线2,因循爱因斯坦广义相对论之逻辑,借助“等效原理”和“信息波速度不变性”,GOR理论便可将引力时空X4d(η)之观测者O的“观测时间”dt=dx0/η(式(3.22))变换为“标准时间”dτ. 设D0(xi(t) (i=1,2,3))为被观测对象P特定时刻t=x0/η的空间坐标.D0之观测者O乃引力势位χ之观测者,借助特定观测代理OA(η)测定GOR引力时空SO=X4d(η)之时间,如上所述,其“观测时间”dt并非“标准时间”dτ.如图1(b1)所示,基于“等效原理”,在D0处引入瞬时静止的局部惯性时空SI,其中,P和O静止于D0,“信息波速度不变性”成立. 如同爱因斯坦广义相对论,“等效原理”体现出其特殊的价值和意义:经由“等效原理”之等效变换,GOR引力时空SO瞬时局部等效于惯性时空SI. 式(3.26)意味着,“标准时间”正比于被观测对象P在观测代理OA(η)之观测时空X4d(η)中的线元ds.如图1(b1)所示,设LO为P在OA(η)之引力时空SO中的世界线,LI为P在等效惯性时空SI中的世界线.合理地,SO之标准时间可定义为dτO=dsO/η;SI之标准时间可定义为dτI=dsI/η.显然,根据式(3.26)之“标准时间”定义,惯性时空SI之dτI即客观真实的“固有时间”(原时)dτ∶dτI=dτ. 根据微分几何,曲线LO之线元dsO与其切线LI之线元dsI相等:dsO=dsI;故有 (3.27) 式(3.27)具有重要寓意:给定观测代理OA(η),其任意观测时空X4d(η)(包括SO和SI)具有相同的“标准时间”,皆客观真实的“固有时间”(原时)dτ. 经“等效原理”对GOR观测时空SO=Xμ(η)的惯性化处理,被观测对象P和X4d(η)之空间坐标D0(xi)的观测者O瞬时静止SI:dxi=0 (i=1,2,3).依式(3.22)和式(3.27),GOR之“标准时间”dτ可依GOR 之“坐标时间”dt测定: (g00=1+2χ/η2) (3.28) 式中χ为X4d(η)空间坐标D0(xi)之“牛顿引力势”. 显然,GOR“标准时间”(式(3.28))与爱因斯坦广义相对论之“标准时间”(式(3.6))是同构一致的. 式(3.28)表明:“标准时间”,即客观真实的“原时”dτ,不仅可以借助光学代理OA(c)测定,而且,理论上,任意观测代理OA(η)皆可测定之. 特别需要指出,“信息波速度不变性”在GOR时间测定中发挥了重要作用. 如3.4.2所述,一般观测代理OA(η)之4d时空坐标框架X4d(η)是“信息波速度不变性”的形式化表达,其时轴x0=ηt代表着“信息波速度不变性”.式(3.28)之“标准时间”dτ正是基于被观测对象P在一般观测代理OA(η)之观测时空X4d(η)中的时元dt=dx0/c(式(3.22))和ds=gμνdxμdxν(式(3.22))导出的. 3.4.4 GOR物理空间的测定 基于PGC对应原理,经由PGC逻辑路线2,因循爱因斯坦广义相对论的逻辑,则GOR理论可借助“等效原理”将OA(η)之引力时空SO=X4d(η)惯性化作局部等效于SO的惯性时空SI.于是,基于“信息波速度不变性”,用信息波速度η和“标准时间”dτ定义并测定GOR引力时空X4d(η)之“物理空间距离”dl. 因循爱因斯坦广义相对论之空间测定的逻辑,如3.2.3所述和图1(b2)所示,设D为观测时空SO=X4d(η)中足够接近D0的相邻空间点,D0之观测者O向D发射“信息波”;“信息波”由D0射向D,再由D返回D0,其所需观测时间为 (3.29) 若D0至D之空间位移为dxi(i=1,2,3),则D至D0之空间位移为-dxi(i=1,2,3).一般观测代理OA(η)情形之下,“信息子”之时空线元ds2=0,因而 (3.30) 特别地,依“等效原理”,D0点之局部惯性时空SI必定各向同性,其中,“信息波速度不变性”成立.因而,D0和D之间的“物理空间距离”dl可依“原时”dτ和“信息波”速度η定义为dl=ηdτ/2. 依式(3.28),“原时”dτ=√(g00)dx0/η. 于是,GOR“物理空间距离”dl可如下测定: 或 (3.31) 式中γik=γik(η)(i,k=1,2,3)乃一般观测代理OA(η)之观测时空X4d(η)的“物理空间度规”. 显然,GOR“物理空间”关系(式(3.31))与爱因斯坦广义相对论之“物理空间”关系(式(3.9))是同构一致的. 需要明确指出:爱因斯坦广义相对论之观测时空Xμ(c)的时空度规gμν=gμν(c)和空间度规γik=γik(c)是光学观测代理OA(c)之观测时空X4d(c)的度规,依赖于光速c;而GOR观测时空Xμ(η)之时空度规gμν=gμν(η)和空间度规γik=γik(η)则是一般观测代理OA(η)之观测时空X4d(η)的度规,依赖于或取决于观测代理OA(η)及其信息波之速度η. 观测,意味着时空变换. GOR时空,即一般观测代理OA(η)之观测时空X4d(η),属引力时空.设有物体或被观测对象P:1)P静止于引力场;2)P在标量引力场中运动;3)P在矢量引力场中运动. 让我们从惯性时空开始吧. 3.5.1 惯性时空变换因子 一般观测代理OA(η)之惯性时空变换因子可称OR时空变换因子,或OR因子,即OR理论之广义洛伦兹因子[1-3],概括了光学代理OA(c)之爱因斯坦狭义相对论的洛伦兹因子[14]. 设有观测者O借助观测代理OA(η)观测物体P∶P之“固有时钟”TP即“标准钟”;O相对于P以惯性速度v运动.这意味着:观测者O借助OA(η)将被观测对象P由其静止的“自由时空”SF变换至O运动的惯性时空SI=X4d(η). 爱因斯坦狭义相对论中,时空变换因子即洛伦兹因子:γ=dt/dτ=1/√(1-v2/c2),是光学代理OA(c)之惯性时空变换因子,表征P在OA(c)之惯性时空X4d(c)中呈现给O的惯性相对论性效应.实际上,洛伦兹因子γ=Γ(c)只是OR时空变换因子的一个特例. OR理论中[1-3],时空变换因子乃一般观测代理OA(η)(包括光学代理OA(c))的惯性时空变换因子: (3.32) 表征P在一般观测代理OA(η)之惯性时空X4d(η)中呈现给O的惯性相对论性效应. 原本,OA(η)之时空变换因子Γ(η)(式(3.32))是由OR理论之基本逻辑前提导出的逻辑结论[1-3],却同时服从PGC对应原理,与爱因斯坦狭义相对论之洛伦兹因子γ=Γ(c)(式(3.10))同构一致.这既反映了PGC对应原理逻辑上的有效性,也反映了OR理论与爱因斯坦狭义相对论之逻辑上的一致性. 实际上,基于PGC对应原理,经由PGC逻辑路线1,以信息波速度η替代光速c,便可直接将洛伦兹因子γ=1/√(1-v2/c2),由光学代理OA(c)变换至一般观测代理OA(η),由爱因斯坦狭义相对论变换至OR理论:Γ(η)=1/√(1-v2/η2)(式(3.32));反之亦然. 显然地,基于PGC对应原理,经由PGC逻辑路线2,将“光速不变性”变换为“信息波速度不变性”,并因循爱因斯坦狭义相对论的逻辑,同样能导出式(3.32)之OR时空变换因子.特别地,经由PGC逻辑路线2,更有助于我们理解OR理论之一般观测代理OA(η)之惯性时空变换因子. 3.5.2 引力时空变换因子:静态场 引力时空变换因子即GOR理论之时空变换因子,可称作GOR因子,概括了爱因斯坦广义相对论中的引力时空变换因子[15]. 设有观测者O借助观测代理OA(η)观测物体P∶P之“固有时钟”TP即“标准钟”;O位于静态引力时空SG=X4d(η)之χ势位,相对于P静止;SG是一静态场.这意味着:观测者O借助OA(η)将被观测对象P由其静止的“自由时空”SF变换至观测者O所处的引力时空SG=X4d(η)之χ势位. 爱因斯坦广义相对论中,时空变换因子γ=dt/dτ=1/√(1+2χ/c2),是光学代理OA(c)之引力时空变换因子,表征P和O在OA(c)之静态引力时空X4d(c)中相对静止时P呈现给O的引力相对论性效应. 基于PGC对应原理,经由PGC逻辑路线1,以信息波速度η替代γ=Γ(c)之光速c,即可由爱因斯坦广义相对论之公式(3.11)直接地获得GOR引力时空变换因子:Γ(η)=dt/dτ=1/√(1+2χ/η2),表征P和O在一般观测代理OA(η)之静态引力时空SG=X4d(η)中相对静止时P呈现给O的引力相对论性效应. 基于PGC对应原理,经由PGC逻辑路线2,将 “光速不变性”变换为“信息波速度不变性”,因循爱因斯坦广义相对论的逻辑,同样能导出GOR引力时空变换因子.特别地,因循PGC逻辑路线2,更有助于我们理解GOR理论之中一般观测代理OA(η)的引力时空变换因子. 自然地,因循PGC逻辑线路2,同样可将光学代理OA(c)变换为定义1.1之一般观测代理OA(η);根据式(3.22),即可演绎推导O和P相对于O静止(dxi=0(i=1,2,3))时的GOR引力时空变换因子: (3.33) 显然,GOR理论之式(3.33)与爱因斯坦广义相对论之关系式(3.11)是同构一致的.可见,PGC逻辑路线2的结论与PGC逻辑路线1的结论相同. 3.5.3 引力时空变换因子:标量场 设有观测者O借助观测代理OA(η)观测物体P∶P之“固有时钟”TP即“标准钟”;O位于引力时空SG=X4d(η)之χ势位,相对于P以速度v运动;SG乃标量场.这意味着:观测者O借助OA(η)将被观测对象P由其静止的“自由时空”SF变换至观测者O所处的引力时空SG=X4d(η)之χ势位. 爱因斯坦广义相对论中,若P和O在光学代理OA(c)之标量引力时空SG=X4d(c)中相对运动,则其时空变换因子为:γ=1/√(1+2χ/c2-v2/c2),表征P和O在光学代理OA(c)之标量引力场X4d(c)中相对运动时P呈现给O的引力相对论性效应. 基于PGC对应原理,经由PGC逻辑路线1,以信息波速度η替代γ=Γ(c)之光速c,即可由爱因斯坦广义相对论之公式(3.12)直接地获得标量场之GOR引力时空变换因子:Γ(η)=1/√(1+2χ/η2-v2/η2),表征P和O在一般观测代理OA(η)之标量引力场SG=X4d(η)中相对运动时P呈现给O的引力相对论性效应. 基于PGC对应原理,经由PGC逻辑路线2,将 “光速不变性”变换为“信息波速度不变性”,因循爱因斯坦广义相对论的逻辑,同样能导出P和O在一般观测代理OA(η)之标量引力场SG=X4d(η)中相对运动时的GOR引力时空变换因子. OA(η)之观测时空SG=X4d(η)为标量场时,其“矢量引力势”γi=0(g0i=gi0=0(i=1,2,3)).根据定义1.1之式(3.22),成立: (i=1,2,3)) (3.34) 对照式(3.28)以及式(3.31)和式(3.34),可得 (3.35) 式中:v=dl/dt为O相对于P的运动速度;dl为P在观测时空X4d(η)之时间dt内移动的物理空间距离. 显然,GOR理论之公式(3.35)与爱因斯坦广义相对论之关系式(3.12)是同构一致的.可见,PGC逻辑路线2的结论与PGC逻辑路线1的结论相同. 3.5.4 引力时空变换因子:矢量场 或许,真如爱因斯坦所设想的那样:引力场如同电磁场,既有“标势”,又有“矢势”. 设有观测者O借助观测代理OA(η)观测物体P∶P之“固有时钟”TP即“标准钟”;O位于引力时空SG=X4d(η)之χ势位,相对于P以速度v运动;SG乃矢量场.这意味着:观测者O借助OA(η)将被观测对象P由其静止的“自由时空”SF变换至观测者O所处的引力时空SG=X4d(η)之χ势位. 爱因斯坦广义相对论中,若P和O在光学代理OA(c)之矢量引力时空SG=X4d(c)中相对运动,则其时空变换因子为:γ=1/√(((1+2χ/c2)1/2-γivi/c)2-v2/c2),表征P和O在光学代理OA(c)矢量引力场X4d(c)中相对运动时P呈现给O的引力相对论性效应. 基于PGC对应原理,经由PGC逻辑路线1,以信息波速度η替代γ=Γ(c)之光速c,即可由爱因斯坦广义相对论之公式(3.12)直接地获得矢量场之GOR引力时空变换因子:Γ(η)=1/√(((1+2χ/η2)1/2-γivi/η)2-v2/η2),表征P和O在一般观测代理OA(η)之矢量引力场SG=X4d(η)中相对运动时P呈现给观测者O的引力相对论性效应. 基于PGC对应原理,经由PGC逻辑路线2,将 “光速不变性”变换为“信息波速度不变性”,因循爱因斯坦广义相对论的逻辑,同样能导出P和O在一般观测代理OA(η)之矢量引力场SG=X4d(η)中相对运动时的GOR引力时空变换因子. 仿照静电场场强之定义,引力场任意空间坐标xi(i=1,2,3)之场强g可定义为 (3.36) 式中:Δm乃质量,依“等效原理”,不区分引力质量和惯性质量;引力场强g等效于该点引力加速度a. 基于PGC原理,爱因斯坦广义相对论之公式(3.14)可进行同构一致地变换为 (3.37) 其中,γi=γi(η)(i=1,2,3)乃一般观测代理OA(η)之“矢量引力势”,依赖于OA(η)之信息波速度η. 根据一般观测代理OA(η)之定义1.1:“观测时间”dt=dx0/η,“固有时间”dτ=ds/η;被观测对象P在OA(η)之观测时空X4d(η)中运动,其时空轨迹,包括P之时元dt和线元ds,依式(3.22)描述.考虑式(3.37)中引力场之“标量引力势”χ和“矢量引力势”γi(i=1,2,3),则依式(3.22),成立: (3.38) 对照式(3.28)和式(3.31)以及式(3.37)和式(3.38),可得OR和GOR理论之一般时空变换因子 (3.39) 式中:η为OA(η)之信息波速度;dt=dx0/η为OA(η)之观测者O的“观测时间”,即被观测对象P之“固有时钟”TP作为“标准钟”呈现给O的时间;dτ=ds/η为“固有时间”(原时),即客观真实的时间;v=dl/dt为P相对于O的运动速度,vi=dxi/dt(i=1,2,3);χ为牛顿引力势,即“标量引力势”;而γi=γi(η)=-g0i/√(g00) (i=1,2,3)则为“矢量引力势”,依赖于观测代理OA(η). 显然,GOR理论之关系式(3.39)与爱因斯坦广义相对论之关系式(3.16)是同构一致的.可见,PGC逻辑路线2的结论与PGC逻辑路线1的结论相同.特别值得指出的是,式(3.39)之GOR时空变换因子Γ(η)乃一般观测代理OA(η)之时空变换因子,是时空变换因子Γ(η)最一般的形式. 首先,GOR时空变换因子Γ(η)概括了不同观测代理OA(η)(包括光学代理OA(c)和理想代理OA∞)之时空变换因子:η→c时,式(3.39)严格地约化为式(3.16)之爱因斯坦之时空变换因子;η→∞时,式(3.39)严格地约化为伽利略因子Γ∞(≡1). 其次,式(3.39)之GOR时空变换因子Γ(η)概括了惯性时空变换因子和引力时空变换因子:无引力相互作用(χ=0,γi=0)时,式(3.39)严格地约化为OR理论之惯性时空变换因子Γ(η)=1/√(1-v2/η2);无相对运动(v=0)时,式(3.39)严格地约化为GOR理论之引力时空变换因子Γ(η)=1/√(1+2χ/η2). 同时,式(3.39)之GOR时空变换因子Γ(η) 概括了标量引力势(χ)和矢量引力势(γi(i=1,2,3))之时空变换因子.当γi=0(i=1,2,3)时,式(3.39)严格地约化为式(3.35)之“标量引力时空”的时空变换因子:Γ(η)= 1/√(1+2χ/η2-v2/η2). GOR时空变换因子具有重要寓意,给予我们不同于爱因斯坦广义相对论之新的认识. OR时空变换因子[1-3]已经阐明,一切惯性相对论性效应皆观测效应;GOR时空变换因子将进一步阐明,一切相对论性效应,包括惯性相对论性效应和引力相对论性效应,皆观测效应和表观现象. 爱因斯坦相对论中,真空光速c乃宇宙常量,是宇宙速度上限,是不变的,是不可超越的.因此,根据式(3.11):γ=1/√(1+2χ/c2-v2/c2),爱因斯坦广义相对论之时空变换因子γ=γ(v,χ)并不取决于c,而取决于物质运动速度v和牛顿引力势χ:仅当v≠0或χ≠0时,γ>Γ∞≡1,此时,被观测对象P呈现相对论性现象.据此,爱因斯坦乃至当今主流物理学界皆认为,相对论性乃时空和物质运动之本质特性,其根源在于物质运动(|v|>0)以及物质间的相互作用(|χ|>0). 爱因斯坦相对论诞生之后,人们对于相对论性效应或相对论性现象,既充满好奇,又充满疑惑.尽管主流物理学界坚持认为,相对论性是时空和物质运动的本质特性,人们至今仍然不能理解时空和物质运动为什么会呈现相对论性效应,不能理解光速为什么不变,不能理解时空为什么弯曲. 相对论性效应的根源和本质究竟是什么呢? 3.6.1 相对论性现象的根源和本质 相对论性并非时空和物质运动的本质特性. 根据GOR时空理论,相对论性并非如爱因斯坦和主流物理学界所主张的那样:其根源在于物质运动(|v|>0)或物质间的相互作用(|χ|>0). 实际上,爱因斯坦广义相对论之时空变换因子γ=γ(c)仅表征光学代理OA(c)之相对论性,乃光学观测代理OA(c)之时空变换因子,是GOR时空变换因子之特例,即一般观测代理OA(η)之时空变换因子Γ=Γ(η)之特例,并不意味着相对论性取决于物质运动(|v|>0)或物质间的相互作用(|χ|>0). OR理论[1-3]已经阐明,惯性相对论性现象的根源和本质在于观测代理存在观测局域性.现在,GOR理论将进一步阐明:引力相对论性效应的根源和本质同样在于观测代理存在观测局域性(η<∞). 不同观测代理呈现不同程度的相对论性: GOR理论显示,不同观测代理呈现不同程度的相对论性.依式(3.35):Γ=1/√(1+2χ/η2-v2/η2),GOR时空变换因子Γ=Γ(η)依赖于观测代理OA(η).不同观测代理OA(η),观测媒介不同,信息波有速度η不同,相应地,GOR时空变换因子Γ=Γ(η)取值不同,代表不同程度的相对论性效应. 设有观测代理OA(η1)和OA(η2)(η2>η1),给定的v和χ,则OA(η1)和OA(η2)之时空变换因子有不同取值:Γ(η1)>Γ(η2)≥Γ∞≡1.可见,不同观测代理OA(η)之观测时空X4d(η)中,同一物质运动(v)或同一物质相互作用(χ)呈现出不同程度的相对论性效应:η越小,其呈现出的相对论性效应越显著. 这表明,相对论性依赖于观测,依赖于观测代理,依赖于观测媒介,依赖于观测媒介传递观测信息的速度.因此,所谓“相对论性现象”,只是观测代理呈现出的观测上的相对论性效应,乃“观测效应”. 客观真实的时空并不存在相对论性现象: 观察式(3.35)之GOR时空变换因子可知: 可见,就客观真实的物理世界而言,时空和物质运动并无“相对论性效应”或“相对论性现象”. 这就充分地表明,客观真实的时空并不存在相对论性;所谓的“相对论性效应”或“相对论性现象”,并非客观真实的自然现象,而是“观测效应”或“表观现象”,其根源和本质在于观测代理OA(η)存在观测局域性(η<∞). 我们应该认识到,光虽然极快,然而,光速仍然是有限的:c<∞,因而,光学观测代理OA(c)仍然存在观测局域性.正是光学观测代理OA(c)之观测局域性(c<∞)造就了爱因斯坦相对论. 观测信息既是客观的也是表观的: 如1.6.2所述,我们的观测(以时空变换因子Γ(η)表征),既包含着关于时空和物质运动之客观真实的信息(以伽利略因子Γ∞表征),又包含着观测代理OA(η)之观测局域性所致的观测效应或表观现象(以相对论性因子ΔΓ(η)=Γ(η)-Γ∞表征). 因此,我们的观测并不完全客观真实. OR理论中,OR时空变换因子Γ(η)=1/√(1-v2/η2)可依泰勒级数分解为伽利略因子Γ∞和观测效应因子ΔΓ(η):Γ(η)=Γ∞+ΔΓ(η).这意味着,任意观测代理OA(η)对惯性时空的观测,既包含着客观真实的惯性运动信息(Γ∞),也包含着观测代理OA(η)之观测局域性(η<∞)所致的观测效应或表观现象(ΔΓ(η)). 同样地,GOR理论中,GOR时空变换因子Γ(η)= 1/√(1+2χ/η2)也可依泰勒级数分解为伽利略因子Γ∞和观测效应因子ΔΓ(η): (3.40) 式中:α=-2χ≥0;ΔΓ(η)≥0. 与式(1.5)中的OR观测效应因子ΔΓ(η)一样,式(3.40)中的GOR观测效应因子ΔΓ(η)代表着观测上的相对论性效应,实属观测效应或表观现象,并非客观真实的自然现象;而伽利略因子Γ∞,正如OR理论所阐明的,则代表着客观真实的物理存在. 与式(1.5)中的OR时空变换因子Γ(η)=Γ∞+ΔΓ(η)类似,式(3.40)中的GOR时空变换因子Γ(η)=Γ∞+ ΔΓ(η)意味着:任意观测代理OA(η)对引力时空的观测,既包含着客观真实的引力相互作用信息(Γ∞),也包含着观测代理OA(η)之观测局域性(η<∞)所致的观测效应或表观现象(ΔΓ(η)). 3.6.2 时空真地会弯曲吗? 时空,是不会“弯曲”的. 实际上,“时空弯曲”是一种相对论性现象,一种引力相对论性效应.与一切相对论性效应一样,“时空弯曲”也是一种观测效应和表观现象,其根源和本质同样在于观测代理OA(η)之观测局域性(η<∞). 如3.1.2所述,引力,与电磁力以及弱力和强力一样,乃物质间最基本的相互作用之一,是一种力(force),而非时空弯曲之几何效应.将引力效应几何化,将引力时空等效为弯曲时空,不失为描述引力相互作用的一种形式化方法. 然而,时空并不真地弯曲. 我们并不确定,爱因斯坦真地以为引力时空是弯曲的,或爱因斯坦广义相对论需要弯曲的时空.依照爱因斯坦广义相对论[15],物质和能量的聚集导致“时空弯曲”,因而,地球在太阳弯曲的时空中围绕太阳旋转.然而,令我们感到一丝疑惑的是,太阳又当如何在地球弯曲的时空中运动呢? 现在,GOR理论告诉我们,爱因斯坦广义相对论之所谓“时空弯曲”,并非因为物质和能量聚集,而是一种观测效应,乃光学代理OA(c)之观测局域性(c<∞)所致,恰如我们透过广角镜所观测到或拍摄到的弯曲景象,实属“广角镜效应”. OR时空变换因子Γ(η)=1/√(1-v2/η2)代表一般观测代理OA(η)之惯性时空X4d(η),其时空度规gμν乃闵科夫斯基度规:ημν=diag(+1,-1,-1,-1).显然,ημν不依赖于惯性时空坐标xα(α=1,2,3,4)和信息波速度η,因而,OR惯性时空X4d(η)是平直的而非弯曲. GOR时空变换因子Γ=1/√(1+2χ/η2-v2/η2)代表一般观测代理OA(η)之引力时空X4d(η),其时空度规gμν=gμν(xα,η)依赖于引力时空坐标xα(α=1,2, 3,4)和信息波速度η,因而,GOR引力时空X4d(η)显得有些弯曲.特别值得注意,时空是否“弯曲”以及“弯曲”到何等程度,并不真地取决于引力势χ,而取决于观测代理OA(η),取决于信息波速度η. 由此可见,客观真实的时空是不会弯曲的.所谓“时空弯曲”,本质上,只是一种“观测效应”,与一切相对论性效应一样,其根源在于观测代理OA(η)之观测局域性(η<∞).理想观测代理OA∞之下,观测时空将会呈现出其客观真实的自然面貌. 3.6.3 引力场真地存在矢量引力势吗? 引力场,并非矢量场,并不存在矢量引力势. 如3.5.4所述,因循爱因斯坦广义相对论之逻辑, GOR理论也能导出包含矢量引力势γi=-g0i/√(g00) (i=1,2,3)的时空变换因子,即一般观测代理OA(η)之时空变换因子:Γ(η)=1/√(((1+2χ/η2)1/2-γivi/η)2-v2/η2). 若引力场果真存在矢量引力势γi=-g0i/√(g00) (i= 1,2,3),则必定∃i∈(1,2,3)g0i≠0;根据式(3.31),X4d(η)之空间度规γik=g0ig0k/g00-gik(i,k=1,2,3)必定依赖于X4d(η)之时间轴x0.这意味着,一般观测代理OA(η)之观测时空X4d(η)的时间轴x0与空间轴xi(i∈ (1,2,3))可以是非正交的:时间和空间相互依存. 反之,若引力场不存在矢量引力势,则必定g0i=0(i=1,2,3);根据式(3.31),X4d(η)之空间度规γik=-gik(i,k∈(1,2,3))与X4d(η)之时间轴x0无关.这意味着,一般观测代理OA(η)之观测时空X4d(η)的时间轴x0与空间轴xi(i∈(1,2,3))正交:时间和空间相互独立. 因此,GOR时空理论同样存在着“时空是否正交”(或者说,“时间和空间是否正交”)的问题. 时空是否正交,原本,是一个哲学问题. 正如1.4所述,伽利略和牛顿持绝对主义时空观[32-35]:时间与空间相互独立;时间静静地流淌着,空间永恒不变地存在着.这意味着,时空原本是正交的,或者说,时间与空间是正交的. 然而,如果真如爱因斯坦所设想的那样,引力时空,不仅存在“标量引力势”χ,还存在“矢量引力势”γi=-g0i/√(gi0)(i=1,2,3),那么,引力时空之时间和空间可以是非正交的.这符合马赫和爱因斯坦的相对主义时空观[36-38]:时间亦空间,空间亦时间;时间和空间相互依存,并且在一定的条件下相互转化. 据说,的确有实验观测到引力场之“矢量引力势”.然而,GOR理论表明:所谓“矢量引力势”并非客观存在.如果矢量势呈现在观测中,那只能是特定观测代理的观测效应或表观现象. GOR时空变换因子(式(3.39))之“标量引力势”χ乃牛顿引力势,是客观真实的“固有物理量”.毫无疑问,牛顿引力势χ乃客观存在:无论我们观测与否,地球表面一切物质必定受其作用. 第一,客观真实的引力场并无“矢量引力势”; 第二,时间与空间原本是正交的,相互独立的. 可见,根据GOR时空理论:客观真实的引力时空是牛顿为我们描绘的标量引力场;爱因斯坦设想的矢量引力场并非客观存在.时间和空间是绝对的,正交的,相互独立的,符合伽利略和牛顿之绝对主义时空观,而非马赫和爱因斯坦之相对主义时空观. 3.6.4 理想观测代理和超光速观测代理 GOR理论表明,牛顿引力论和爱因斯坦引力论分属不同观测体系:爱因斯坦广义相对论是光学观测体系的产物,服务于光学观测代理,其所描绘的引力时空是物理世界透过光学观测体系呈现给观测者的一种光学观测映像,并非完全客观真实的引力世界;而牛顿万有引力论则是理想观测体系的产物,服务于理想观测代理,其所描绘的引力时空则是理想观测体系中的物理世界,乃客观真实的引力世界. 然而,自然世界并不存在理想观测代理OA∞. 根据OR和GOR理论,一切现实的观测代理OA(η)皆存在观测局域性(η<∞),其呈现给观测者的自然景观,永远只能是客观世界的一种映像,永远也不可能等同于客观真实的自然世界. 限于目前的科学技术水平,我们的观测和实验大多依赖于光学观测代理OA(c).这是爱因斯坦相对论,包括狭义相对论和广义相对论,得到大多数观测和实验支持的原因.实际上,与其说这些观测或实验是对爱因斯坦相对论的支持,不如说是对观测相对论的支持.自然地,这些观测和实验验证了光学代理情形下的OR理论和GOR理论. 当然,光学观测代理OA(c)或其观测局域性未必是人类不可逾越的观测屏障[31].根据OR理论[1-3],光速不变性只是光作为观测媒介时的一种观测效应;光速并非真地不变或不可超越.随着科学技术的不断进步,人类将会发现甚至发明超光速的物质运动.实际上,越来越多的量子纠缠实验已经呈现出超光速物理现象[61-66],其鬼魅般的超距作用似乎正在越来越强烈地挑战爱因斯坦以光速为极限的局域性观念. 可以设想,人类未来将会掌握“超光速观测代理”[31],令我们观测到更为真实的自然世界.那时,我们将会观测到不同于光学观测代理呈现给我们的自然景象,观测到不同于爱因斯坦广义相对论所能预测的“引力偏折”和“引力红移”以及“水星进动”.那时,“超光速天文学”,比如“引力波天文学”[21],或许,将会替代传统的光学天文学,包括射电天文学. 逻辑上,作为描述统一物理世界之引力相互作用的物理学理论,爱因斯坦广义相对论与牛顿万有引力论应该具有内在的对应关系和逻辑上的一致性. 根据其广义相对论之时空变换因子,爱因斯坦设想:类同于“低速”时狭义相对论之洛伦兹变换近似对应伽利略变换,“弱场”时广义相对论之场方程应近似对应牛顿万有引力定律之泊松方程形式.爱因斯坦广义相对论中,“弱场近似”(weak-field approximation),既是一个重要的概念,又是一种逻辑技巧,在爱因斯坦广义相对论的建立过程中,发挥了重要作用. 原本,基于PGC对应原理,因循爱因斯坦之“弱场近似”逻辑,无论经由PGC逻辑路线1或PGC逻辑路线2,GOR理论都能将爱因斯坦广义相对论由光学代理OA(c)推广至一般观测代理OA(η),导出与爱因斯坦场方程同构一致的GOR场方程,即GOR理论之引力场方程. 然而,PGC对应原理之下,无论PGC逻辑路线1或PGC逻辑路线2,乃逻辑捷径;走捷径是需要付出代价的.完全依赖于PGC原理对爱因斯坦广义相对论施行同构一致性对应变换,可能会令GOR理论丧失对于引力相对论性效应之本质和根源的认识. 爱因斯坦场方程属光学代理OA(c),牛顿万有引力定律属理想代理OA∞,二者并不具有直接的对应关系.因此,爱因斯坦只能通过“弱场近似”法,将其场方程与牛顿万有引力定律近似对应.GOR理论属一般观测代理OA(η),因此,GOR理论可通过“理想代理”法将GOR场方程与牛顿万有引力定律严格对应,即通过理想代理OA∞(η→∞)“逼近”牛顿万有引力定律.因此,GOR引力场方程的推演和标定需要“理想代理”法,而非“弱场近似”. 本章力求阐明GOR理论之“理想代理”法的逻辑和思想,同时,将会有一个重要的定理诞生:所谓“伽利略时空定理”. 在论述GOR理论之“理想代理”法之前,首先需要解析爱因斯坦之“弱场近似”法的逻辑和思想.类比爱因斯坦之“弱场近似”法,将有助于我们阐明GOR理论之“理想逼近”的逻辑思想. 4.1.1 弱场近似之逻辑思想 在爱因斯坦广义相对论中,所谓“弱场近似”,指引力场强g(式(3.13))较弱之时,爱因斯坦场方程近似牛顿万有引力定律. 爱因斯坦广义相对论之引力时空是弯曲的,而牛顿万有引力时空是平直的.爱因斯坦设想:弱场,即引力场之引力势较弱的情形,广义相对论之弯曲的引力时空近似平直;如此,爱因斯坦广义相对论便可与牛顿万有引力定律联系或对应起来. 爱因斯坦之“弱场近似”法的基本思想源于爱因斯坦对于相对论性效应之根源和本质的认识.在爱因斯坦看来,相对论性现象,无论惯性效应或引力效应,乃物质运动和物质相互作用之本质特性. 爱因斯坦广义相对论之“弱场近似”可类比爱因斯坦狭义相对论之“低速近似”.或者,更准确地说,爱因斯坦之“弱场近似”的逻辑源于爱因斯坦之“低速近似”的思想. 爱因斯坦狭义相对论中,光速c是不变的;惯性时空变换因子γ=γ(v)=1/√(1-v2/c2)依赖于物质运动速度v:惯性速率 |v|越大,则惯性因子γ=γ(v)越大,惯性相对论性效应就会越显著. 据此,爱因斯坦和主流物理学界认为:惯性相对论性的根源和本质在于物质运动. 低速之情形(|v|≪c)之下,洛伦兹因子γ近似于伽利略因子Γ∞:γ=1/√(1-v2/c2)≈1=Γ∞,洛伦兹变换近似于伽利略变换.于是,爱因斯坦以及主流物理学界认为:洛伦兹变换与伽利略变换,乃至狭义相对论与经典力学,逻辑上是一致的,具有“低速近似”对应关系.并且,主流物理学界认为:洛伦兹变换是更正确的时空变换,而伽利略变换则只是个近似,仅在“低速”情形下近似成立. 类似地,爱因斯坦广义相对论中,光速c是不变的;引力时空变换因子γ=γ(χ)=1/√(1+2χ/c2)依赖于引力势χ:引力势|χ|越大,则引力因子γ=γ(χ)越大,引力相对论性效应越就会显著. 据此,爱因斯坦和主流物理学界认为:广义相对论之引力相对论性的根源和本质在于物质相互作用. 弱场之情形(|χ|≪c2),引力时空变换因子γ近似于伽利略因子Γ∞:γ=1/√(1+2χ/c2)≈1=Γ∞,引力时空近似平直.爱因斯坦认为,如此,爱因斯坦场方程应近似于牛顿万有引力定律之泊松方程形式;爱因斯坦广义相对论与牛顿万有引力论便具备了逻辑上的一致性,此即“弱场近似”对应关系.并且,在主流物理学界看来,爱因斯坦广义相对论是更正确的引力论,而牛顿万有引力论则只是个近似,仅在“弱场”情形下近似成立. 特别注意:无论“低速近似”或“弱场近似”,实则,要求时空变换因子γ近似于伽利略因子Γ∞.伽利略因子Γ∞≡1,代表着平直的伽利略时空,其中,“观测时间”dt即“固有时间”dτ∶dt=dτ;时空度规gμν即闵科夫斯基度规ημν∶gμν=ημν=diag(+1,-1,-1,-1).(我们将在4.2之“伽利略时空定理”中专门讨论“伽利略时空”这一问题.) “弱场近似”条件下:γ≈Γ∞.这意味着:弱引力场近似平直,其中,牛顿之万有引力论近似成立.于是,借助“弱场近似”法,爱因斯坦广义相对论可与牛顿万有引力论近似对应,爱因斯坦场方程可与牛顿万有引力定律之泊松方程形式近似对应.如此,爱因斯坦场方程之系数可标定. 4.1.2 弱引力场之时空度规 一般地,如第3章之3.5所述,爱因斯坦广义相对论之时空变换因子γ与物质运动速度v以及引力时空之“标量引力势”χ和“矢量引力势”γi(i=1,2,3)相关:γ=γ(v,χ,γi). 爱因斯坦广义相对论(式(3.16))中,时空变换因子 欲令γ≈Γ∞(“弯曲”的引力时空近似“平直”的伽利略时空),除假设:1)弱场(|χ|≪c2且|γi|足够小(i=1,2,3));还需假设:2)低速(|v|≪c);并且,还常常假设:3)时空正交(g0i=0(i=1,2,3)).实际上,g0i=0即意味着γi=0;或者,反过来,|γi|足够小即意味着时空正交(g0i≈0). “弱场近似”法,实为爱因斯坦广义相对论之线性化理论.爱因斯坦广义相对论之引力时空是弯曲的或非线性的:γ>Γ∞;而“低速弱场”情景下,γ≈Γ∞,引力时空趋于平直或线性,引力时空度规gμν近似闵科夫斯基度规ημν=diag(+1,-1,-1,-1):gμν(xα,c)≈ημν. 观察爱因斯坦广义相对论之时空变换因子γ,欲令gμν(xα,c)≈ημν,需营造“弱场”情景.|χ|≪c2且|γivi|≪c时,引力时空度规gμν(xα,c)可线性化作 |χ|≪c2和|γivi|≪c:gμν(xα,c)=ημν+hμν(xα,c) (|hμν|≪|ημν|) (4.1) 式中:hμν及其各阶导数皆无穷小量;ημν可称作“平度规”而hμν则可称作“曲度规”. 式(4.1)乃爱因斯坦广义相对论之“弱场度规”,即弱引力场之度规,是爱因斯坦“弱场近似”法的核心关系式.式(4.1)之“弱场度规”是爱因斯坦广义相对论引力时空度规gμν之线性化方程,是“弱场近似”的结果,是“弱场近似”法的形式化表达. 特别注意,依照爱因斯坦的“弱场近似”逻辑:“弱场”时|hμν|≪|ημν|;无引力场时gμν=ημν而hμν=0.如此,爱因斯坦认为:式(4.1)中的“曲度规”hμν即“弱引力势”,代表着引力辐射,代表着“引力波”.这为爱因斯坦之后演绎“引力波”方程并对“引力波”做出预测埋下伏笔. GOR理论将会阐明,式(4.1)之“曲度规”hμν并不代表引力辐射,更非“引力波”. 4.1.3 弱场近似条件 实际上,“弱场近似”法所涉及的假设条件不仅仅是“弱场”和“低速”,以及“时空正交”. 爱因斯坦试图通过“弱场近似”法将其广义相对论之引力场方程与牛顿万有引力定律或其泊松方程形式近似对应,进而,标定爱因斯坦场方程之系数.而爱因斯坦场方程之系数标定的过程,涉及若干线性化假设,均与“弱场近似”相关. 爱因斯坦“弱场近似”法涉及5项假设. 第一,弱场(weak field): 牛顿引力势χ=0时,时空平直:gμν=ημν;故而“弱场”(|χ|≪c2)时,时空近似平直,应成立: gμν=ημν+hμν(|hμν|≪|ημν|) 第二,低速(slow motion): 被观测对象P相对于观测者O的速率|v|≪c,或 第三,静态场(stationary field): 度规gμν或hμν不随时间变化,即 (α,β=0,1,2,3) 在爱因斯坦广义相对论中,静态场条件是“近似的”,只是要求度规gμν或hμν不“显著”地随时间t变换.并且,特别注意,静态场条件在应用时,并非∂hαβ/∂t=0;而是hμν,0=∂hαβ/∂x0≈0. 第四,时空正交(space-time orthogonality): 时间轴x0与空间轴xi(i=1,2,3)正交,即 gi0=g0i=0 (i=1,2,3) 需要说明:“时空正交”假设似乎有些多余. 第五,调和坐标(harmonic coordinates): (μ=0,1,2,3) 式中:g=det(gμν)乃度规gμν之行列式;调和坐标条件之极端情形为√(-g)=1或gμν=ημν. 我们将会阐明,GOR理论(包括爱因斯坦广义相对论),其引力场方程之逻辑演绎(包括线性化处理),无须“弱场近似”逻辑或“弱场近似”法. 正如我们反复强调的,GOR理论与牛顿万有引力论的对应关系,并非“弱场近似”,而是一般观测代理OA(η)与理想观测代理OA∞之间的对应关系.因此,GOR理论不应通过“弱场近似”与牛顿万有引力论近似对应;而应通过“理想代理”与牛顿万有引力论严格对应,即通过理想代理OA∞(η→∞)“逼近”牛顿万有引力论. GOR理论将会阐明,爱因斯坦广义相对论之所谓“弱场近似”条件,包括弱场、低速、静态场、时空正交,以及调和坐标,皆可通过“理想逼近”逻辑得到满足:观测代理OA(η)之η→∞时,爱因斯坦之“弱场近似”条件都能成立. 4.1.4 牛顿万有引力场景 爱因斯坦之“弱场近似”法,其“近似”的对象是牛顿万有引力定律,或者,严格地说,是牛顿万有引力定律之泊松方程形式[54]. 自然地,为了爱因斯坦广义相对论之引力场方程能与牛顿万有引力定律对应,场方程理应设定与牛顿万有引力定律同样的引力相互作用场景. 这里,所谓“牛顿万有引力场景”,即牛顿万有引力定律所设定的引力场景:平直的引力时空中,静静地存在2个质点M和m(相距r),M乃引力源和引力中心(形成一球对称引力场),m乃受引力作用之物体(物质密度ρ).令m所处引力势为χ,依牛顿万有引力定律:χ=-GM/r.不失一般性,令M位于引力时空之空间坐标原点,则其半径为r的球面上,引力势处处相等. 特别值得指出,牛顿万有引力场景,并不意味着其引力场为“弱场”:M和m质量均可任意大,同样可以设想为引力无穷的“黑洞”.(就此而言,爱因斯坦广义相对论与牛顿万有引力论并不必然地具有“弱场近似”之对应关系.) 实际上,无论“牛顿万有引力场景”是否为弱引力场,伽利略时空之牛顿引力场景都是平直的时空.为了将广义相对论与牛顿万有引力论对应,爱因斯坦必须将广义相对论之引力时空平直化.然而,就广义相对论对应牛顿引力场景而言,爱因斯坦所能采用的逻辑和方法,只能是“弱场近似”的逻辑方法:χ→0或r→∞时,广义相对论之观测时空X4d(c)的度规gμν(xα,c)→ημν,因而,X4d(c)近似平直. 这里特别需要指出,GOR理论并不需要“弱场近似”逻辑或“弱场近似”法;GOR理论可以采用的逻辑方法是“理想逼近”,即通过理想代理OA∞“逼近”牛顿万有引力场景:η→∞时,GOR观测时空X4d(η)之度规gμν(xα,η)→ημν,因而,X4d(η)趋于平直. 对照4.1.3之“弱场近似”条件可知,5项假设包括弱场、低速、静态场、时空正交,以及调和坐标,在牛顿万有引力场景中自然成立. 第一,弱场:牛顿引力场景中,时空平直,自然地,gμν=ημν+hμν(|ημν|≫|hμν|=0). 牛顿引力场景中,gμν=ημν+hμν(|hμν|≪|ημν|)依然成立;然而,并非因为“弱场”(牛顿引力场景并非必然地意味着“弱场”),而是因为,牛顿万有引力场景乃平直时空. 第二,低速:牛顿场景中m相对于M静止. 第三,静态场:牛顿场景中χ不随时间改变. 第四,时空正交:gμν=ημν,自然地,g0i=gi0=0. 第五,调和坐标:gμν=ημν,自然地,□xμ= 0. 可以说,爱因斯坦广义相对论设立的“弱场近似”条件正是比照牛顿万有引力场景而设置的.反过来说,当我们比照牛顿万有引力场景设置爱因斯坦场方程的引力场景时,爱因斯坦广义相对论之“弱场近似”条件(见4.1.3)自然成立. 这一问题涉及“伽利略时空定理”. 爱因斯坦认为,牛顿万有引力场景是平直时空;反之,平直时空中,牛顿万有引力论必定成立.正是基于这样的认识,爱因斯坦构造了“弱场近似”逻辑和“弱场近似”法,进而,将其广义相对论与牛顿万有引力论对应,建立起爱因斯坦场方程. 需要特别指出,牛顿万有引力论并非弱引力场论;伽利略时空,其平直的时空特征也非弱场所致,而是理想观测代理OA∞呈现给观测者的客观景象. 4.2.1 理想代理与伽利略时空 OR理论已阐明,观测者观测自然世界,必须借助“观测代理”.理论上,任意物质运动形式皆可作为观测媒介为观测者传递观测信息.根据第1章1.3之定义1.1,一般观测代理OA(η)可形式化地表述为 式中:η乃OA(η)之信息波速度;X4d(η)即OA(η)之观测时空:x0为1d时间,(x1,x2,x3)为3d空间;gμν=gμν(xα,η)乃观测时空X4d(η)之度规. GOR理论基于定义1.1导出了GOR时空变换因子Γ(η)(参见第3章3.5),即一般观测代理OA(η)之观测时空X4d(η)的时空变换因子(式(3.39)): 伽利略时空定理:设有观测代理OA(η),其观测时空X4d(η)之时空度规为gμν=gμν(xα,η),其中,η为OA(η)之信息波速度.η→∞时gμν→ημν. 这里需要证明:η→∞时gμν(η)→ημν. 4.2.2 引理 伽利略时空定理的证明,可由若干引理构成. 引理A及其推论 引理A:设有观测代理OA(η),η为OA(η)之信息波速度.η→∞时,OA(η)之观测时空X4d(η)中,任意观测者O之“观测时间”dt皆“标准时间”dτ:dt=dτ;而dτ=ds/η. 证明: 如图2所示,观测者O借助观测代理OA(η)观测“标准钟”TP;TP之“固有周期”为To. 根据“标准时间”定义:O和TP相对静止于“自由时空”SF(gμν=ημν且dxi=0(i=1,2,3))时,O之“观测时间”dt即“标准时间”dτ. 依定义1.1和gμν的对称性,观测代理OA(η)之观测时空X4d(η)线元ds公式为 ds2=gμνdxμdxν=η2g00dt2+2ηg0idxidt+gikdxidxk=η2η00dt2(gμν=ημν;dxi=0(i=1,2,3))=η2dτ2(η00=1) (4.2) 故:“标准时间”dτ=ds/η. 假设“标准钟”TP于时刻τ1和τ2分别向外发射时钟周期之0-相位和2π-相位信号,那么,自然地,TP之“固有周期”To=Δτ=τ2-τ1.假设O于时刻t1和t2分别接收到TP之时钟周期0-相位和2π-相位信号,那么,O所观测到的时钟周期则为T=t2-t1. η→∞时,观测代理OA(η)无观测局域性,观测媒介传递观测信息不需要时间.因此,t1=τ1且t2=τ2,O所观测到的时钟周期T即标准钟TP之“固有周期”To:T=t2-t1=τ2-τ1=To. 如此,η→∞时,OA(η)之观测时空X4d(η)中,任意观测者O之“观测时间”dt皆“标准时间”dτ:dt=dτ;而dτ=ds/η. (证毕) 图2 观测者O与观测时间dtFig.2 Observer O and observed time dt 因此,由引理A可得如下推论: 推论A:设有观测代理OA(η),η为OA(η)之信息波速度.η→∞时,OA(η)之观测时空X4d(η)的度规gμν,其0i和i0元素为零:g0i=gi0=0(i=1,2,3). 推论A具有重要意义. 1)推论A表明,客观真实的物理世界,其时间和空间原本是正交的:时间只是时间,静静得流淌着;空间只是空间,静静地存在着. 2)推论A表明,客观真实的物理世界,并不存在爱因斯坦所设想的“矢量引力势”:γi=g0i/√(g00)=0(i=1,2,3). 然而,值得注意,引理A中,γi=0(i=1,2,3)要求η→∞;这意味着,当观测代理OA(η)存在观测局域性(η<∞)时,“矢量引力势”γi(i=1,2,3)作为一种纯粹的“观测效应”,可能会呈现在观测中. 引理B及其证明 引理B:设有观测代理OA(η),η为OA(η)之信息波速度.η→∞时,OA(η)之观测时空X4d(η)度规gμν的00元素为1:g00=η00=1. 证明: 观测代理OA(η)之观测时空X4d(η),其时空度规gμν不依赖于观测者O和被观测对象TP.因此,我们可以设定O和TP相对静止的场景:dxi=0(i=1,2,3). 根据定义1.1,以及引理B之条件,成立: ds2=gμνdxμdxν=η2g00dt2+2ηg0idxidt+gikdxidxk=η2g00dt2(dxi=0(i=1,2,3)) (4.3) 根据引理A:η→∞时,dt=dτ;而dτ=ds/η. 对照引理A和式(4.3)即得:g00=η00=1. (证毕) 引理C及其证明 引理C:设有观测代理OA(η),η为OA(η)之信息波速度.η→∞时,X4d(η)之时空度规gμν的ii元素为-1:gii=ηii=-1(i=1,2,3). 证明: 观测代理OA(η)之观测时空X4d(η),其时空度规gμν不依赖于观测者O和被观测对象TP;因此,我们可以设定TP相对于O沿x1匀速运动的场景:dx1≠0,dx2=dx3=0. 根据定义1.1,根据引理A及其推论,根据引理C之给定条件以及设定的运动场景,应成立: (4.4) 式中dl乃OA(η)之观测者O测定被观测对象TP在观测时空X4d(η)中时段dt=dτ内所移动的“物理空间距离”或“纯空间距离”. 同理:η→∞时,g22=g33=-1. 故有:η→∞时,gii=-1(i=1,2,3). (证毕) 引理D及其证明 引理D:设有观测代理OA(η),η为OA(η)之信息波速度.η→∞时,X4d(η)时空度规gμν的ik元素为零:gik=ηik=0(i,k=1,2,3;i≠k). 证明: 观测代理OA(η)之观测时空X4d(η),其时空度规gμν不依赖于观测者O和被观测对象TP;因此,我们可以设定TP在x1-x2平面内匀速运动的场景:dx1≠0和dx2≠0,dx3=0. 根据定义1.1,根据引理A及其推论,根据引理D之给定条件以及设定的运动场景,应成立: (4.5) 式中dl乃OA(η)之观测者O测定被观测对象TP在观测时空X4d(η)中时段dt=dτ内所移动的“物理空间距离”或“纯空间距离”. 根据引理C,η→∞时,gii=-1(i=1,2,3);故 (4.6) 对照式(4.6)可知:η→∞时,g12=g21=0. 同理:η→∞时,g23=g32=0. 故有:η→∞时,gik=ηik=0(i,k=1,2,3;i≠k). (证毕) 4.2.3 伽利略时空定理的证明 基于引理A~D即可证明伽利略时空定理. 证明: 1)“观测时间”dt即“标准时间”dτ:dt=dτ; 2)“时空正交”:时空度规gμν之0i和i0元素g0i=gi0=0(i=1,2,3). 3)gμν之00元素即闵科夫斯基度规ημν之00元素:g00=η00=1. 4)gμν之ii元素即闵科夫斯基度规ημν之ii元素:gii=ηii=-1(i=1,2,3). 5)gμν之ik元素即闵科夫斯基度规ημν之ik元素:gik=ηik=0(i,k=1,2,3;i≠k). 归纳起来,伽利略时空定理成立: η→∞时gμν→ημν. (证毕) 4.2.4 伽利略时空定理的验证 爱因斯坦广义相对论中,爱因斯坦采用“弱场近似”法求解场方程,得到了爱因斯坦场方程的第一个解[15]:爱因斯坦近似解,其中,光学观测代理OA(c)之观测时空X4d(c)的度规gμν(xα,c)为 (4.7) 式(4.7)中,χ=-GM/r为牛顿引力势;r→∞时,χ→0,gμν(xα,c)→ημν.这符合爱因斯坦“弱场近似”逻辑和“弱场近似”法的预期. 然而,正如GOR理论于3.6所阐明的:引力相对论性效应的根源和本质并不在于引力相互作用,而在于观测代理OA(η)之观测局域性(η<∞).基于PGC对应原理,经由PGC逻辑路线1,以η替代gμν(xα,c)之光速c,即可获得一般观测代理OA(η)之观测时空X4d(η)的度规gμν(xα,η): (4.8) 令η→∞,则 (4.9) 可见,对于爱因斯坦场方程近似解,伽利略时空定理成立:η→∞时gμν(xα,η)→ημν. 类似地,Schwarzschild度规[57],即爱因斯坦场方程第一个精确解,也可用于验证“伽利略时空定理”,并且,得出类似爱因斯坦场方程近似解的结论. 4.2.5 伽利略时空定理的意义 “伽利略时空定理”令第1章和第3章中模糊的伽利略时空图像变得更加清晰.实际上,伽利略时空定理与第1章1.4中有关“观测时空”和“固有时空”的论述,以及第3章3.5、3.6中有关GOR时空变换因子的论述,是一致的. 根据“伽利略时空定理”,OR和GOR理论之一般观测代理OA(η),概括了一切观测代理,包括光学代理OA(c)和理想代理OA∞,将爱因斯坦相对论之闵科夫斯基4d时空和伽利略- 牛顿理论之笛卡儿4d时空(独立的1d时间和独立的3d空间)统一起来. 一般观测代理OA(η)之观测时空X4d(η)之度规gμν依赖于观测代理OA(η):gμν=gμν(η),可分解为 (4.10) 其中,闵科夫斯基度规ημν(平度规)不依赖于OA(η),而曲度规hμν则依赖于OA(η):hμν=hμν(η);特别地,根据“伽利略时空定理”,η→∞时,hμν→0. 根据第1章“观测代理”之定义1.1及其式(1.2),一般观测代理OA(η)之观测时空X4d(η)之线元ds为 (4.11) 式中:dt为“观测时间”;dl为“纯空间距离”. 将式(4.11)改写作 (4.12) 根据“伽利略时空定理”,η→∞时,hμν→0. (4.13) 式中:“观测时间”dt即客观真实的“固有时间”dτ;而“纯空间距离”dl则是笛卡儿3d空间距离. 第一,时间处处一致:不同的观测者有相同的时间,同时性是绝对的; 第二,时间和空间相互独立:时间静静地且均匀地流淌着,空间永恒不变地存在着. 基于“伽利略时空定理”,可以建立“理想逼近”条件:η足够大时,gμν(η)=ημν+hμν(η)(|hμν| ≪|ημν|);进而,编制GOR理论之“理想逼近”逻辑. “伽利略时空定理”为GOR理论之“理想代理”法以及GOR引力场方程的确立奠定了理论基础. “同一物理世界,同一逻辑体系”乃PGC对应原理之基本思想.与爱因斯坦广义相对论一样,GOR理论也需要与牛顿万有引力论保持逻辑上的一致性;与爱因斯坦场方程一样,GOR引力场方程也需要与牛顿万有引力定律或其泊松方程形式保持逻辑上的一致性.然而,与爱因斯坦广义相对论不同,GOR理论所因循的是“理想逼近”逻辑和“理想代理”法,而非“弱场近似”逻辑和“弱场近似”法. OR理论之广义洛伦兹变换与伽利略变换的逻辑一致性,并非“低速近似”对应关系,而是“理想逼近”逻辑,系一般观测代理OA(η)与理想代理OA∞之间的同构一致对应关系,乃严格的逻辑一致性:η→∞时,广义洛伦兹变换严格地约化为伽利略变换. 同样地,GOR理论之引力论与牛顿万有引力论的逻辑一致性,并非“弱场近似”对应关系,而是基于PGC对应原理的“理想逼近”逻辑,系一般观测代理OA(η)与理想观测代理OA∞之间的同构一致对应关系,乃严格的逻辑一致性:η→∞时,GOR引力场方程严格地约化为牛顿万有引力定律之泊松方程. 4.3.1 理想逼近之逻辑思想 局限于光学观测代理OA(c),爱因斯坦以为,相对论性的本质在于物质运动和物质相互作用,只能通过“低速”将狭义相对论之洛伦兹变换与伽利略变换近似对应,只能通过“弱场”将广义相对论之场方程与牛顿万有引力定律之泊松方程近似对应. 然而,OR和GOR理论发现:一切相对论性效应皆观测效应,其本质在于观测代理OA(η)之观测局域性(η<∞):不同观测代理存在不同观测局域性,呈现不同程度的相对论性效应.牛顿万有引力论乃理想观测代理OA∞(η→∞)之理论.因此,逻辑上,GOR理论只能通过理想代理OA∞(而非爱因斯坦之“弱场近似”)“逼近”牛顿万有引力论. 此即所谓“理想逼近”逻辑或“理想代理”法. GOR理论反复强调:牛顿万有引力论并非爱因斯坦广义相对论之“弱场近似”理论;爱因斯坦广义相对论与牛顿万有引力论分属不同的观测代理,并不具有直接的对应关系.爱因斯坦广义相对论是光学观测代理OA(c)的理论,仅当光担当观测媒介之角色时成立;牛顿万有引力论是理想观测代理OA∞的理论,代表客观真实的引力相互作用,只能借助理想观测代理OA∞方可“逼近”. 如此,GOR引力论便可“逼近”牛顿万有引力论;GOR引力场方程便可“逼近”牛顿万有引力定律. 4.3.2 准伽利略时空之度规 基于一般观测代理OA(η)之定义1.1,GOR理论导出与爱因斯坦广义相对论时空变换因子γ(式(3.16))同构一致的GOR时空变换因子(式(3.39)). GOR时空变换因子Γ=Γ(η)依赖于观测代理OA(η),η乃信息波速度,可为任意物质运动速度;而爱因斯坦广义相对论之时空变换因子γ则只是GOR时空变换因子Γ=Γ(η)之特例,其中,η只能是光速c:γ=Γ(c). 然而,正如OR和GOR理论已经阐明的,爱因斯坦广义相对论与牛顿万有引力论并不具有直接的对应关系,并且,牛顿引力场并非一定为弱引力场. (4.14) “理想代理”法,也是一种线性化理论. 一般观测代理OA(η)存在观测局域性(η<∞).因而,依爱因斯坦广义相对论之逻辑,OA(η)之GOR引力时空也应视为弯曲的或非线性的:Γ(η)>Γ∞.而理想代理OA∞情景下:η→∞,Γ(η)→Γ∞.此时,GOR引力论理当“逼近”牛顿万有引力论. (4.15) 其中,hμν及其各阶导数皆无穷小量;根据“伽利略时空定理”:η→∞时gμν(xα,η)→ημν,故而hμν→0. 显然,式(4.15)与爱因斯坦广义相对论之“弱场近似”条件(式(4.1))同构一致.式(4.15)可称“理想逼近”条件;式(4.15)之gμν(xα,η)即“准伽利略时空度规”,ημν即“平度规”,hμν即“曲度规”. 式(4.1)乃爱因斯坦“弱场近似”法的核心关系式;而式(4.15)则是GOR理论之“理想代理”法的核心关系式,是GOR理论之引力时空度规gμν(xα,η)的线性化方程,是“理想逼近”的结果,是“理想代理”法的形式化表达. 特别注意,曲度规hμν=hμν(η)依赖于观测代理OA(η):不同观测代理OA(η)下,同一引力场景,却呈现出不同的弯曲状和曲度规hμν(η).这一事实表明,hμν并非所谓“弱引力势”,并不代表引力辐射,更不是什么“引力波”;而是一种“载波”(carrier wave),一种加载了物质运动信息(v)和引力相互作用信息(χ)的“信息波”(information wave). GOR理论将在第9章揭示“引力波”的奥秘. 4.3.3 理想逼近条件和理想代理法 GOR理论之“理想逼近”条件可与爱因斯坦广义相对论之“弱场近似”条件对应和类比. 如4.1.3所述,爱因斯坦“弱场近似”法涉及5项假设;而GOR理论之“理想逼近”条件则仅仅意味着:观测代理OA(η)之信息波速度η足够大或η→∞.基于“伽利略时空定理”,η足够大或η→∞时,“理想代理”法之线性化方程(4.15)成立,爱因斯坦之“弱场近似”法中的5项假设自然地成立. 对应于爱因斯坦之“弱场近似”法之五条件,GOR理论之“理想逼近”条件也可引申为五条件. 第一,时空平直条件(对应“弱场”假设). GOR理论之观测时空,乃一般观测代理OA(η)之观测时空X4d(η),其度规gμν(η)可分解为“平度规”ημν和“曲度规”hμν(η):gμν(η)=ημν+hμν(η). 根据“伽利略时空定理”:η→∞时gμν=ημν.因此,对于任意引力场景(设牛顿引力势χ),η足够大(η≫√|χ|)时,引力时空皆趋于平直,可视为爱因斯坦之“弱场近似”法中的“弱场”情形,成立: gμν(xα,η)=ημν+hμν(xα,η) (|hμν|≪|ημν|) 第二,低速条件. η→∞时,一切被观测对象P相对于观测者O的速度v皆可视为“低速”;因而,η足够大(η≫|v|)时,“低速”条件成立: 第三,静态场条件. η→∞或η足够大时,依照爱因斯坦“弱场近似”法之“静态场条件”的逻辑,此时之引力时空可视为不随时间变化的“静态引力场”,即度规gμν(η)或hμν(η)不“显著”地随时间t变化,成立: (α,β=0,1,2,3) 然而,特别注意,GOR理论之“理想代理”法中,所谓“静态场条件”,并非要求gμν(η)或hμν(η)不“显著”地随时间t变化,而是要求gμν(η)或hμν(η)不“显著”地随时间线x0=ηt变化,只需η足够大. 第四,时空正交条件. 在“伽利略时空定理”中,引理A之推论已经证明,η→∞时,时空度规gμν(η)之0i和i0元素为零:g0i=gi0=0(i=1,2,3).这已经表明,OA(η)之观测时空X4d(η)的时间轴与空间轴是正交的:客观真实的物理世界之时空原本就是正交的.(这与第3章3.6.3之相关论述是一致的.) 第五,调和坐标条件. 根据“伽利略时空定理”:η→∞时gμν=ημν,因而,η足够大时|hμν|≪|ημν|或gμν≈ημν或√(-g)≈1.于是,如下调和坐标关系式成立: (μ=0,1,2,3) 式中g=det(gμν)乃度规gμν之行列式. 实际上,归纳起来,GOR理论之“理想代理”法的“理想逼近”条件仅剩下一项:观测代理OA(η)之信息波速度η足够大或η→∞. η→∞或η足够大时,GOR理论之“理想逼近”条件,包括时空平直条件、低速条件、静态场条件、时空正交条件,以及调和坐标条件,皆成立;并且,爱因斯坦广义相对论之“弱场近似”条件皆成立. 于是,可以设想:基于“理想逼近”条件“η→∞或η足够大”,因循和类比爱因斯坦广义相对论之“弱场近似”法的逻辑路线,GOR理论即可将GOR引力场方程与牛顿万有引力定律之泊松方程形式对应,并且,最终确立GOR理论之场方程. 这便是GOR理论之“理想代理”法. GOR理论将基于“伽利略时空定理”,因循“理想逼近”逻辑,运用“理想代理”法,标定GOR场方程系数,确立GOR引力场方程. 爱因斯坦场方程是爱因斯坦广义相对论最基本和最重要的关系式.从某种意义上说,爱因斯坦场方程就代表着爱因斯坦广义相对论.同样地,GOR场方程,或GOR引力场方程,将代表GOR理论,成为GOR理论最基本和最重要的关系式. 本章,旨在建立GOR理论之引力场方程. 我们可以基于PGC原理,经由PGC逻辑路线1,以η替换c,直接将爱因斯坦场方程由光学代理OA(c)同构一致地对应变换至一般观测代理OA(η),即GOR场方程.然而,完全依赖于PGC逻辑路线1,我们可能错失对于引力相对论性效应之本质的认识. 我们也可以基于PGC原理,经由PGC逻辑路线2,因循和类比爱因斯坦广义相对论之逻辑,演绎GOR场方程;进而,因循和类比爱因斯坦“弱场近似”逻辑和“弱场近似”法,标定和确立GOR场方程.然而,完全依赖于PGC逻辑路线2,我们可能会错失对于爱因斯坦“弱场近似”法之逻辑缺陷的认识,并且,类同于爱因斯坦广义相对论,形成关于牛顿万有引力论以及关于爱因斯坦“引力波”论的错误认识. 因此,一方面,我们力求,基于PGC原理,结合PGC逻辑路线1和PGC逻辑路线2,因循和类比爱因斯坦广义相对论之逻辑,演绎GOR场方程;另一方面,我们力求基于“伽利略时空定理”,运用第4章所阐明的GOR理论之“理想逼近”逻辑和“理想代理”法,标定和确立GOR场方程. 在基于PGC原理演绎GOR场方程之前,在运用“伽利略时空定理”和“理想代理”法标定GOR场方程之前,我们需要解析爱因斯坦广义相对论之“弱场近似”逻辑和“弱场近似”法.这将有助于我们理解GOR理论之“理想逼近”逻辑和“理想代理”法,同时,有助于我们重新认识牛顿万有引力论,重新认识爱因斯坦广义相对论. 爱因斯坦场方程,即爱因斯坦广义相对论之引力场方程,其形式确定之后,剩下的问题便是如何标定场方程之系数.爱因斯坦希望通过某种逻辑途径,能将其场方程与牛顿万有引力定律之联系或对应起来. 5.1.1 牛顿万有引力定律及其泊松方程 毫无疑问,万有引力是牛顿的伟大发现;万有引力定律是人类物理学一座伟大的丰碑,是牛顿对人类及其物理学做出的伟大贡献. 牛顿[53]认为:万物皆相互吸引,任意2个物体M和m之间存在引力相互作用,其引力F与其质量M和m的乘积成正比,与其距离r的平方成反比: (5.1a) (5.1b) 自然地,物理学一切理论皆客观物理世界之理想化模型,其中,必定包含着理想化的假设或前提条件.牛顿万有引力定律也不例外. 正如第3章3.1“引力时空之局域性问题”所指出的,牛顿万有引力论存在2项理想化的假设: 第一,引力乃超距作用,辐射速度无穷; 第二,信息波乃超距媒介,传播信息速度无穷. 第一项假设,可谓“超距作用”条件. 实际上,牛顿从一开始就意识到,自己的万有引力定律存在引力超距作用问题.而理性告诉牛顿,超距作用是非物理现实的,万有引力一定存在有限的辐射速度.虽然,牛顿(乃至其后的物理学家们)未能解决引力超距作用问题,而直觉告诉牛顿,以及后来的像拉普拉斯[22]和Flandern[56]等人,引力辐射速度一定超奇地快,远远地超过光速,否则,光子当如何被引力作用,宇宙之天体又当如何保持其如此稳定的运行结构(参见Flandern之研究[56]). 第二项假设,可谓“超距媒介”条件. 牛顿并未意识到,物理学之理论模型需要与观测联系在一起,依赖于观测代理,依赖于观测媒介,依赖于观测媒介传递观测信息之信息波速度,制约于观测局域性.然而,“超距媒介”假设却隐喻在了牛顿的万有引力定律之中.当然,“超距媒介”假设,不仅隐喻在牛顿万有引力定律中,实际上,隐喻在古典物理学之一切定律或理论模型之中,包括开普勒三大定律,以及伽利略变换和牛顿三大定律. “超距媒介”假设赋予了古典物理学一种理想化的观测体系——“理想观测代理”OA∞.正如OR和GOR理论已经阐明的,伽利略- 牛顿理论,乃理想观测之理论,属理想观测代理OA∞.牛顿万有引力定律(式(5.1))也不例外:严格意义上,当且仅当其服务于理想观测代理OA∞时,才是正确的或有效的. 5.1.2 爱因斯坦场方程和运动方程 爱因斯坦认为:地球围绕太阳运转,乃“时空弯曲”所致;而“时空弯曲”则乃物质和能量的堆积或分布所致.因此,爱因斯坦设想,自己的广义相对论应该包含2个基本的方程: 第一,场方程:描述时空如何弯曲——其后被赋予“时空弯曲=能量动量”的形式 (5.2) 式中:Gμν称作“爱因斯坦张量”;Rμν(即里奇张量)为时空曲率;R为高斯曲率;gμν为时空度规;Tμν为能动张量;而κ则为场方程系数.式(5.2)未含宇宙项Λgμν(我们暂不讨论爱因斯坦场方程之宇宙项问题). 第二,运动方程:描述弯曲的时空中物体如何运动——其后被确定为测地线方程 (5.3) 后来,爱因斯坦等[67]和Fock[68]先后证明:场方程(5.2)可由运动方程(5.3)导出.这意味着,爱因斯坦广义相对论实际上只有一个基本方程:爱因斯坦场方程.然而,这并不意味着对运动方程之价值和意义的否定,只意味着运动方程与场方程具有内在的关联性或等价性.并且,特别值得我们注意,场方程系数κ的标定,既需要依赖于爱因斯坦场方程(5.2),也需要借助于运动方程(5.3). 作为客观物理世界之理想化模型,爱因斯坦广义相对论,包括其场方程和运动方程,同样存在理想化特征和假设性的前提条件. 正如第3章3.1之“引力时空之局域性问题”所指出的,爱因斯坦广义相对论也存在2项假设: 第一,引力乃超距作用,辐射速度无穷; 第二,信息波乃光波,传播信息速度即光速. 第一项假设,同样,乃“超距作用”条件. 关于第一项“超距作用”假设,爱因斯坦并未意识到,与牛顿万有引力论一样,自己的广义相对论同样包含着“引力乃超距作用”的理想化假设.实际上,正如第3章之3.1所指出的:爱因斯坦之引力论,包括其场方程和运动方程,隐喻着引力超距作用的假设条件,并无任何关于引力波和引力辐射速度的先验知识或先验信息,逻辑上或理论上,根本不能预测引力波的存在,更不能预测引力波之速度. 第二项假设,可谓“光学代理”条件. 与牛顿一样,爱因斯坦也未意识到,物理学之理论模型需要与观测联系在一起,需要依赖于观测代理.然而,“光学代理”假设却隐喻了在爱因斯坦广义相对论中,隐喻在其“光速不变性”假设之中.(或许,在爱因斯坦看来,鉴于光速不变或不可超越,观测信息以光速传递可谓理所当然的事情.或许,爱因斯坦从未考虑过光在自己的理论中扮演着观测媒介或信息使者的角色,也从未设想过非光观测媒介之情形;甚至,从未考虑过自己的理论依赖于观测媒介.) “光速不变性”假设赋予爱因斯坦相对论一种人类感知客观世界最常用的观测体系——“光学观测代理”OA(c).闵科夫斯基将光学观测代理OA(c)形式化作光学4d时空坐标框架,即所谓“闵科夫斯基时空”[29-30].虽然闵科夫斯基时空是专为爱因斯坦狭义相对论打造的,之后,却又被爱因斯坦推广至广义相对论.可见,正如OR和GOR理论已经阐明的,爱因斯坦相对论,包括狭义相对论和广义相对论,皆光学观测理论,属光学观测代理OA(c),当且仅当其服务于光学观测代理OA(c)时,才是正确的或有效的. 那么,“弯曲”时空中的爱因斯坦场方程,当如何与“平直”时空中的牛顿万有引力定律对应呢? 5.1.3 弱场近似逻辑与弱场近似法 就逻辑而言,作为描述同一物理世界之引力相互作用的物理学理论,爱因斯坦广义相对论与牛顿万有引力论理当具有某种内在的联系或对应关系. 爱因斯坦设想:类同于“低速近似”情形下狭义相对论之洛伦兹变换近似于伽利略变换,“弱场近似”情形下,广义相对论之引力场方程应近似对应牛顿万有引力定律或其泊松方程形式. 然而,正如第4章所阐明的,爱因斯坦场方程(光学观测理论模型)与牛顿万有引力定律(理想观测理论模型),并不具有直接的对应关系.然而,就标定爱因斯坦场方程之系数而言,爱因斯坦广义相对论之“弱场近似”逻辑和“弱场近似”法似乎是奏效的:通过“弱场近似”,爱因斯坦场方程和牛顿万有引力定律之泊松方程联系并对应起来,进而,爱因斯坦成功地标定和确立了广义相对论之引力场方程. 爱因斯坦场方程是一个复杂的非线性偏微分方程组,难以标定和求解.爱因斯坦不得不采用线性化和近似的手段对其进行处理:最基本的任务是确定场方程系数κ;最基本的手段则是“弱场近似”法. 为了能将“弯曲时空”之爱因斯坦场方程与“平直时空”之牛顿万有引力定律或其泊松方程形式联系并对应起来,爱因斯坦需要将其场方程所处的“弯曲时空”平直化,令引力时空变换因子γ近似伽利略因子:γ≈Γ∞.观察爱因斯坦广义相对论之引力时空变换因子:γ=1/√(1+2χ/c2),其中,真空光速c乃常数,欲使γ≈Γ∞≡1,只能令χ≈0或|χ|≪c2,即令牛顿万有引力场为所谓“弱引力场”. Γ∞≡1代表着平直的伽利略时空,其中:dt=dτ.(爱因斯坦的“弱场近似”法隐含着了一主张;而严格的理论证明则来自“伽利略时空定理”.) 就爱因斯坦广义相对论时空变换因子γ之一般形式而言,如式(3.15)和式(3.16)所示: (5.4) 除标量引力χ势外,还需考虑矢量引力势γi(i=1,2,3)和物质运动速度;欲令γ≈Γ∞,除了假设:1)弱场(|χ|≪c);还需假设:2)低速(v≪c);3)时空正交(g0i=gi0=0或γi=0(i=1,2,3)). 弱场近似情形之下,γ≈Γ∞,意味着“弱场”之时空近似平直.爱因斯坦设想:既然弱引力场之时空近似平直,则牛顿万有引力定律在弱场条件下近乎成立;那么,“弱场”时的广义相对论之场方程和运动方程可近似对应牛顿万有引力定律或其泊松方程形式.如此,场方程系数κ便可与牛顿引力势χ联系起来,并由牛顿万有引力定律或其泊松方程之参数确定. 如第4章所述,“弯曲”的引力时空度规gμν可分解成为“平度规”ημν(闵科夫斯基度规)和“曲度规”hμν;“弱场”情形下,必定成立或满足“弱场近似”条件: gμν=ημν+hμν(|hμν|≤|ημν|) 自然地,无引力或无引力场时,gμν=ημν,hμν=0;因此,爱因斯坦广义相对论中,或在爱因斯坦看来,“弱场近似”条件中的“曲度规”hμν代表着“弱引力势”. 特别注意,时空正交条件下(g0i=gi0=0(i=1,2,3)),广义相对论之时空变换因子γ(式(5.4))约化为 (g00=η00+h00;η00≡1) (5.5) 如此,爱因斯坦广义相对论之引力时空的“弯曲”状态便只依赖于“曲度规”hμν之00-元素h00. 由时空正交情形之时空变换因子(5.5)可知:依爱因斯坦之“弱场近似”逻辑,若|h00|≪1(弱场)并且|v|≪c(低速),则γ≈Γ∞,“弯曲”的引力时空近似“平直”,牛顿万有引力定律近似成立.因而,“弯曲时空”之爱因斯坦场方程和运动方程可与“平直时空”之牛顿万有引力定律或其泊松方程形式近似对应. “弱场近似”法可视为爱因斯坦广义相对论之“线性化理论”.实际上,“弱场近似”法,即爱因斯坦场方程和运动方程之线性化处理方法. 依据式(5.5),“弱场近似”法可如下设计. “弱场近似”法程序 以标定爱因斯坦场方程之系数κ为目标,根据弱场情形之时空变换因子(式(5.5)),基于“弱场近似”逻辑,将h00与牛顿引力势χ和场方程系数κ联系起来,其逻辑演绎程序可分为2步. 第一步,运动方程之弱场近似:将式(5.3)之曲度规00(元素h00)与牛顿引力势χ联系起来(h00~χ). 第二步,场方程之弱场近似:将式(5.2)之曲度规00(元素h00)与场方程系数κ联系起来(h00~κ). 最终,在牛顿万有引力定律场景之下,对照弱场近似关系式h00~χ和h00~κ,即可确定场方程系数κ. “弱场近似”条件 实际上,作为爱因斯坦广义相对论的一种“线性化”理论,爱因斯坦之“弱场近似”法涉及一组线性化条件.根据第4章之4.1.3所论述的爱因斯坦“弱场近似”法条件,除了弱场假设之处,还需4个假设—— 第一,弱场:gμν=ημν+hμν(|hμν|≪|ημν|); 第二,低速:v≪c; 第三,静态场:gμν,0=∂gαβ/∂x0=0或hμν,0=∂hαβ/∂x0=0; 第四,时空正交:g0i=gi0=0(i=1,2,3); 牛顿万有引力场景 如第4章4.1.4所述,牛顿引力场景,即牛顿万有引力定律所设定的场景:平直的时空中仅存2个质点M和m(相距r),M为引力源,乃一球对称引力场之引力中心;m为被引力作用之物体(物质密度ρ).令m处引力势为χ,依牛顿万有引力定律:χ=-GM/r.距离M半径为r的球面上,引力势χ处处相等. 自然地,为了爱因斯坦广义相对论之场方程或运动方程能与牛顿万有引力定律或其泊松方程近似对应,场方程和运动方程理应设定与牛顿万有引力定律同样的引力相互作用场景. 特别值得指出,牛顿万有引力场景,并不意味着其引力场为“弱场”:M和m质量均可任意大,同样可以被设想为引力无穷或任意大的“黑洞”. 然而,正如第4章4.1.4已经阐明的,在牛顿万有引力场景中,爱因斯坦广义相对论之“弱场近似”条件或“线性化”条件自然成立;或者说,爱因斯坦广义相对论之“弱场近似”条件或“线性化”条件正是为了对应牛顿万有引力场景而设立的.这里,特别需要说明,爱因斯坦之“弱场近似”条件第一项“弱场:gμν=ημν+hμν(|hμν|≪|ημν|)”依然成立,并非因为“弱场”(牛顿引力场景并非必然地意味着“弱场”),而是因为牛顿万有引力场景乃平直时空.(在“弱场近似”条件之第一项中,爱因斯坦理所当然地将|χ|≪c2替换为了gμν=ημν+hμν(|hμν|≪|ημν|);在爱因斯坦看来,“弱场”即意味着“平直”时空.) 5.1.4 运动方程之弱场近似 爱因斯坦广义相对论之运动方程(5.3)可写作 (5.6) 设想运动方程之“弱场近似” 可以设想:“弱场近似”条件下,时空近似平直; “弯曲时空”中的“短程线”(式(5.6))将约化为牛顿引力场之欧几里得空间中的“直线”: (5.7) 式中χ即牛顿引力势.式(5.7)左右两端同乘m,既得牛顿第二定律,又得牛顿万有引力定律. 于是,“弱场近似”条件下的“弱势度规”hμν可与牛顿引力势χ联系起来. 运动方程之“弱场近似”操作 运动方程之“弱场近似”的过程,是其线性化过程:非线性的“短程线”化作线性的“直线”. (gμν=ημν-hμν;ημν=ημν,hμν=ημαηβνhαβ) (5.8) 已知弱场近似情形下,dt≈dτ.依“低速”条件|vi|=|dxi/dt|≪c以及x0=ct,|dxi/dτ|≪|dx0/dτ|.因而,成立: (5.9) 式(5.6)约化为 (5.10) 基于“静场”条件hαβ,0=0,由式(5.8)可得 (5.11) 因为η0i=0,ηii=-1(i=1,2,3),所以 (5.12) 于是,弯曲时空之“短程线”方程(5.6)在平直时空中“分裂”(split into)为时间和空间2组方程: (5.13) 这种时间与空间的“分裂”令我们想到了伽利略变换.在伽利略变换中,时间和空间便是“分裂”的:时间与空间相互独立,互不依赖. 式(5.13)之时间方程意味着,“弱场”中,“坐标时间”dt与“标准时间”dτ没有区别;解之可得 t=aτ+b (5.14) 适当选取单位(令a=1)并校准时间(令b=0),则t=τ. 其实,根据式(5.4)和式(5.5),我们已经知道,“弱场”和“低速”以及“时空正交”条件下,时空变换因子Γ(c)≈Γ∞≡1,即dt=dτ. 因此,式(5.13)之空间方程组约化为 (5.15) 对照弱场近似情形下的“短程线”(式(5.15))和牛顿引力场中的“直线”(式(5.7))可知 (5.16) 如此,引力时空之“弱势度规”00(元素h00)便与牛顿引力势χ联系起来(h00~χ). 5.1.5 场方程之弱场近似 爱因斯坦场方程(5.2):Gμν=κTμν,左端Gμν代表引力时空的弯曲,右端Tμν代表物质能量的分布;Gμν通过场方程系数κ与能量分布Tμν联系在一起. 设想场方程之“弱场近似” 可以设想:“弱场近似”条件下,随着“弱势度规”hμν的弱化,时空曲率Rμν与度规张量gμν的非线性关系将退化为关于“弱势度”hμν的线性关系,非线性的爱因斯坦场方程将退化为线性化场方程. 于是,“弱场近似”条件下的“弱势度规”hμν可与爱因斯坦场方程之系数κ联系起来. 场方程之“弱场近似”的操作 以gμν乘以爱因斯坦场方程(5.2)左右两端可得 (5.17) 式中:R为高斯曲率;T为能动张量Tμν的迹. 于是,R=κT,爱因斯坦场方程(5.2)可改写作 (5.18) 依定义,式(5.18)之时空曲率(里奇张量)Rμν为 (5.19) 可见,爱因斯坦场方程是关于度规张量gμν的非线性偏微分方程;这是其难以处理和难以求解的原因. 如同运动方程之“弱场近似”的情形,经“弱场近似”法处理,去除hμν二阶及以上高阶小量,只保留一阶无穷小,时空曲率Rμν乃至爱因斯坦场方程可约化为关于“弱势”hμν的线性方程. 对照式(5.8),忽略hμν高阶小量,Rμν近似为 (5.20) (5.21) (5.22) 于是,式(5.20)可改写作 (5.23) (5.24) 因而,“弱场近似”条件下,Rμν可进一步约化为 (5.25) 根据式(5.25),非线性场方程(5.18)最终线性化作 (5.26) 如此,引力时空之“曲度规”00(元素h00)与爱因斯坦场方程之系数κ便联系在了一起(h00~κ). 5.1.6 标定场方程系数κ 爱因斯坦希望,其“弱场近似”之线性化场方程(5.26)能与牛顿万有引力定律之泊松方程近似对应. 牛顿万有引力定律场景中,物质粒子M作为引力源构成引力场;而物质粒子m受M之引力作用,在引力时空中运动.设物质粒子m之三维速度v=(v1,v2,v3)(vi=dxi/dt(i=1,2,3)),而四维速度u=(u0,u1,u2,u3)(uμ=dxμ/dτ(μ=0,1,2,3)). 在“弱场”和“低速”条件下,dt≈dτ,gμν≈gμν,|v|≪c2;于是: (5.27) 其中,引力时空属光学观测代理OA(c)之观测时空X4d(c),其时间轴x0=ct;ρ为物质粒子m之物质密度,Tμν则为物质m在光学代理OA(c)之观测时空X4d(c)中的能动张量,而T则为Tμν的迹. 特别需要说明,“四维速度”的概念来自爱因斯坦狭义相对论,乃“三维速度”概念由3d笛卡儿空间至4d闵科夫斯基时空的扩展.实际上,爱因斯坦狭义相对论中的“四维速度”概念只是光学代理OA(c)之4d观测时空X4d(c)中的速度概念.OR和GOR理论进一步将其扩展为一般观测代理OA(η)之4d观测时空X4d(η)中的速度概念,可应用于OR和GOR理论[16]. “弱场”和“低速”条件下,物质粒子m之四维速度u≈(c,0,0,0),故如式(5.27)所示,m之能动张量Tμν退化为标量T00. 于是,场方程(5.18)和式(5.26)可改写作 (5.28) 式中δμν为Kronecker张量. “弱场”和“低速”条件下,光学代理OA(c)之达朗贝尔算子“□”为 (5.29) 对照式(5.16)和式(5.28)以及式(5.29)可知: □h00=-κρc2 或 Δh00=κρc2(h00=2χ/c2) 故 (5.30) (5.31) 爱因斯坦基于“弱场近似”法对其场方程和运动方程进行线性化处理,通过与牛顿万有引力定律之泊松方程形式的近似对应,标定了场方程系数κ,最终,确立了广义相对论之场方程. “弱场近似”法在爱因斯坦广义相对论中扮演了重要角色,在爱因斯坦场方程的标定和确立过程中发挥了重要作用.之后,爱因斯坦又运用“弱场近似”逻辑和“弱场近似”法求其场方程之近似解. 爱因斯坦场方程是爱因斯坦广义相对论最重要的关系式,乃爱因斯坦广义相对论之核心.同样地,GOR场方程,即GOR理论之引力场方程,乃GOR理论最重要的关系式,是GOR理论的核心. GOR场方程的建立,与爱因斯坦建立其广义相对论之引力场方程的一样,涉及2项工作: 第一,推演GOR场方程; 第二,标定GOR场方程之系数. 5.2.1 GOR场方程 基于PGC对应原理,经由PGC逻辑路线1,直接地将爱因斯坦广义相对论之场方程及其场方程系数κ中的光速c变换为信息波速度η,即可将爱因斯坦场方程(式(5.2))由光学代理OA(c)推广至一般观测代理OA(η),成为GOR场方程: (5.32) 式中κη乃GOR理论之引力场方程系数. 特别注意,与爱因斯坦场方程不同,GOR场方程中的里奇张量Rμν=Rμν(η),时空度规gμν=gμν(η),高斯曲率R=R(η),能动张量Tμν=Tμν(η),以及场方程系数κη=κη(η),皆依赖于观测代理OA(η)之信息波速度η,而非真空光速c. 我们甚至不需要再耗费时间对式(5.32)之GOR场方程中的系数κη进行标定. 自然地,我们也可以基于PGC对应原理,经由PGC逻辑路线2,因循或类比爱因斯坦广义相对论之逻辑,从“信息波速度不变性”原理出发,对GOR理论之引力场方程进行严谨的逻辑推导,并且,必然地得出与式(5.32)完全相同的结果. 显然,式(5.32)之GOR场方程与式(5.2)之爱因斯坦场方程是同构一致的;并且,特别值得注意:η=c时,GOR场方程即爱因斯坦场方程,其中,κη=κ即爱因斯坦场方程系数. 可见,GOR场方程将概括爱因斯坦场方程. 5.2.2 GOR运动方程 我们已经知道,爱因斯坦曾设想,自己的广义相对论应该包含2个基本的方程:一是场方程,二是运动方程.后来发现,场方程与运动方程是等价的[67-68].既然是等价的,那么,爱因斯坦运动方程与爱因斯坦场方程应该具有同样的价值和意义.特别地,正如5.1所述,爱因斯坦场方程之系数κ的标定,需要借助爱因斯坦广义相对论之运动方程. 同样的逻辑,GOR理论也应该具备2个相互等价的重要关系式:一个是GOR场方程,而另一个则是GOR运动方程. 自然地,如同GOR场方程,基于PGC对应原理,经由PGC逻辑路线1,直接将爱因斯坦广义相对论之运动方程中的光速c变换为“信息波”速度η,即可将爱因斯坦运动方程(5.3)由光学代理OA(c)推广至一般观测代理OA(η),成为GOR运动方程: (5.33) 自然地,我们也可以基于PGC对应原理,经由PGC逻辑路线2,因循或类比爱因斯坦广义相对论之逻辑,从“信息波速度不变性”原理出发,对GOR理论之运动场方程进行严谨的逻辑推导,并且,必然地得出与式(5.33)完全相同的结果. 显然,式(5.33)之GOR运动方程与爱因斯坦广义相对论之运动方程(式(5.3))是同构一致的;并且,特别注意:η=c时,GOR运动方程即爱因斯坦广义相对论之运动方程. 可见,GOR运动方程将概括爱因斯坦运动方程. 5.2.3 GOR场方程系数的标定问题 现在,基于PGC原理,我们已经建立起GOR理论之引力场方程和GOR理论之运动方程.剩下的问题便是,如何标定GOR场方程之系数:κη=κη(η),最终,确立GOR理论之引力场方程. 最简单便捷的自然是,基于PGC对应原理,经由PGC逻辑路线1,直接地将爱因斯坦场方程之系数κ= 8πG/c4中的真空光速c变换为信息波速度η,即可得到GOR场方程系数:κη=8πG/η4. 然而,特别需要指出,那样,我们可能会为逻辑上的简单和便捷而付出代价,丧失对于爱因斯坦场方程和GOR场方程的正确认识,丧失对于爱因斯坦之“弱场近似”逻辑和“弱场近似”法的正确认识,丧失对于牛顿万有引力论和爱因斯坦广义相对论的正确认识,丧失对于引力相对论性效应的正确认识. 为避免“知其然而不知其所以然”,GOR理论并不打算盲目地沿用或照搬PGC逻辑路线1毫不费力得来的GOR场方程之系数:κη=8πG/η4. GOR理论力求基于PGC原理,经由PGC逻辑路线2,类比爱因斯坦广义相对论之逻辑,重新标定GOR场方程,重新确定式(5.32)中GOR场方程的系数:κη=κη(η),并最终确立GOR场方程. 特别强调,在经由PGC逻辑路线2标定GOR场方程之系数κη=κη(η)时,我们并不打算沿用爱因斯坦广义相对论之“弱场近似”逻辑或照搬爱因斯坦之“弱场近似”法.GOR场方程系数κη=κη(η)的标定,将基于“伽利略时空定理”,运用第4章所论述的“理想逼近”逻辑和“理想代理”法. 无论爱因斯坦广义相对论,还是GOR理论,其引力场方程的标定和确立,都需要借助某种逻辑途径,将其引力场方程与牛顿万有引力定律或其泊松方程形式联系或对应起来.爱因斯坦广义相对论采用“弱场近似”逻辑和“弱场近似”法;而GOR理论则采用“理想逼近”逻辑和“理想代理”法. 第4章曾基于“伽利略时空定理”专门就爱因斯坦广义相对论之“弱场近似”法和GOR理论之“理想代理”法进行研究和论述.这里,我们对其做进一步梳理,特别地,对“弱场近似”法之逻辑缺陷做近一步分析,正确地认识爱因斯坦广义相对论之“弱场近似”逻辑和“弱场近似”法;对“理想代理”法之“理想逼近”条件做近一步分析,正确地运用GOR理论之“理想代理”法,进而,确立GOR场方程. 5.3.1 弱场近似法的逻辑缺陷 在爱因斯坦广义相对论中,为了将“弯曲”时空中的爱因斯坦场方程与“平直”时空中的牛顿万有引力定律或其泊松方程形式对应,爱因斯坦构思设计了“弱场近似”逻辑和“弱场近似”法,意在将其广义相对论之“弯曲”的引力时空“平直”化:令时空度规gμν=ημν或时空变换因子γ=Γ∞.如此,爱因斯坦场方程方可与牛顿万有引力定律之泊松方程对应. 观察爱因斯坦广义相对论之时空变换因子: (5.34) 式中:光速c乃宇宙常量;γ=γ(v,χ,γi)代表爱因斯坦广义相对论之“弯曲”的引力时空,依赖于物体运动速度v以及引力时空之“标量引力势”χ和“矢量引力势”γi(i=1,2,3);而伽利略因子Γ∞则代表“平直”的伽利略时空,包括“平直”的牛顿万有引力场. 式(5.34)显示,欲令γ=Γ∞,要求v=0和χ=0.然而,v=0且χ=0是平凡的;因此,只能令γ≈Γ∞.于是,对于广义相对论之引力时空,爱因斯坦只能如下假设.1)弱场:|χ|≪c2;2)低速:|v|≪c;3)时空正交:g0i=gi0=0 (i=1,2,3).如此,γ≈Γ∞,爱因斯坦广义相对论之“弯曲”的引力时空得以“平直”化. 这便是爱因斯坦之“弱场近似”法的逻辑. 爱因斯坦广义相对论之“弱场近似”逻辑和“弱场近似”法似乎是有效的和成功的.运用“弱场近似”法,爱因斯坦得以将其场方程与牛顿万有引力定律之泊松方程对应,由此,标定场方程之系数:κ=8πG/c4,最终,确立了爱因斯坦场方程. 然而,爱因斯坦“弱场近似”法所存在的逻辑缺陷却误导了物理学和爱因斯坦本人. GOR理论反复强调,爱因斯坦广义相对论为光学代理OA(c)之理论,而牛顿万有引力论则为理想代理OA∞之理论,二者并不具有直接的对应关系.通过“弱场近似”法,将光学代理OA(c)之理论模型与理想代理OA∞之理论模型牵强地联系在一起,这正是爱因斯坦“弱场近似”法逻辑缺陷之所在. 正如第4章4.1“弱场近似之逻辑思想”所述,无论“低速近似”还是“弱场近似”,实际上皆反映了爱因斯坦对相对论性效应之本质的错误认识. 局限于光学代理,爱因斯坦错误地以为:惯性相对论性效应乃时空和物质运动之本质特性;引力相对论性效应乃物质相互作用之本质特性. 正是基于这种对相对论性之本质的错误认识,相对论被视为更符合客观物理世界的“正确”理论;而非相对论性的伽利略- 牛顿理论则被视为“近似”理论.至今,主流物理学界仍然坚持认为:伽利略变换是洛伦兹变换的“低速近似”理论;而牛顿万有引力论则是爱因斯坦广义相对论的“弱场近似”理论. 正是这种对相对论性之本质的错误认识,催生了爱因斯坦广义相对论之“弱场近似”逻辑和“弱场近似”法.反过来,“弱场近似”逻辑和“弱场近似”法又进一步强化了物理学界对引力相对论性之本质的错误认识.至今,主流物理学界仍然坚持认为:牛顿万有引力论只是“弱场近似”理论,仅适用于“宏观”以及“低速”和“弱场”之情形. “弱场近似”法的逻辑缺陷在爱因斯坦广义相对论中被进一步地放大:加载引力场信息的“信息波”被视为“引力波”.无任何关于引力辐射的先验知识或先验信息,爱因斯坦广义相对论,仅凭其弱引力场方程,便预测得出似是而非的“引力波”;并且,令人称奇的是,爱因斯坦预测的“引力波”,其引力辐射速度或“引力波”速度恰好就是光速! GOR理论力求引力论能回到正确的逻辑轨道上,力求因循正确的逻辑路线,正确地演绎GOR引力场方程,进而,正确地认识引力相对论性效应,包括:“引力偏折”效应、“引力红移”效应,以及“水星进动”效应,乃至“引力波”或“引力波”效应. 5.3.2 理想代理法之逻辑程序 GOR理论乃一般观测代理OA(η)之理论.爱因斯坦广义相对论乃光学观测代理OA(c)之理论,而牛顿万有引力论则为理想观测代理OA∞之理论. 光学代理OA(c)之爱因斯坦广义相对论与理想代理OA∞之牛顿万有引力论并不具有直接的对应关系. 在PGC对应原理的意义上,一般观测代理OA(η)之GOR理论,既可与光学观测代理OA(c)之爱因斯坦广义相对论严格对应:η=c时,观测代理OA(η)即光学代理OA(c),GOR理论即爱因斯坦广义相对论;同时,也可与理想观测代理OA∞之牛顿万有引力论严格对应:η→∞时,观测代理OA(η)即理想代理OA∞,GOR理论即牛顿万有引力论. 这便是GOR理论之“理想代理”逻辑和“理想代理”法的基本思想或思想基础. 据此,GOR理论在第4章中基于“伽利略时空定理”构思设计了“理想逼近”逻辑和“理想代理”法,其中,基于“理想逼近”逻辑设立了“理想逼近”条件:观测代理OA(η)之信息波速度η足够大或η→∞.这里,简单归纳,进一步将GOR理论之“理想代理”法与爱因斯坦之“弱场近似”法类比,以便我们将其应用于标定并确立GOR场方程. 观察一般观测代理OA(η)之时空变换因子: (5.35) 其中,Γ=Γ(η)本质上依赖于OA(η)之信息波速度η,而非(v,χ,γi). 自然地,“伽利略时空定理”之结论:η→∞时gμν(η)=ημν,与式(5.35)之结论:η→∞时Γ(η)=Γ∞,是一致的,或者说,是等价的. “伽利略时空定理”之引理A有一个重要的推论(第4章4.3.2):η→∞时,OA(η)之观测时空X4d(η)的度规gμν,其0i和i0元素为零:g0i=gi0=0(i=1,2,3).这意味着,在理想代理OA∞下,或者说,在“理想逼近”条件下(η→∞),时空是正交的;也就是说,伽利略时空(包括牛顿万有引力场),其时间和空间原本就是相互正交或相互独立的. 特别注意,时空正交情形下(g0i=gi0=0(i=1,2,3)),GOR时空变换因子Γ(式(3.38))约化为 (g00(η)=η00+h00(η);η00≡1) (5.36) 如此,GOR引力时空的“弯曲”状态便只依赖于“曲度规”hμν之00-元素h00. 特别注意,爱因斯坦广义相对论中,“时空正交”乃爱因斯坦“弱场近似”法或其线性化方法之假设性条件;然而,在GOR理论中,“时空正交”乃“伽利略时空定理”和“理想逼近”条件的逻辑结论. 基于“伽利略时空定理”,“理想逼近”条件下,必定成立:|h00|≪1而|v|≪η.结合时空正交情形之时空变换因子(5.35)可知,η→∞时Γ(η)→Γ∞,因而,观测代理OA(η)之“弯曲”的引力时空X4d(η)趋于“平直”,牛顿万有引力定律成立.因而,“弯曲时空”中的GOR场方程和GOR运动方程可与“平直时空”之牛顿万有引力定律或其泊松方程形式对应. “理想代理”法乃GOR理论之“线性化理论”,是GOR场方程和GOR运动方程的线性化处理方法. 依据式(5.36),类比爱因斯坦之“弱场近似”法,GOR理论之“理想代理”法可如下设计. “理想代理”法程序 以标定GOR场方程之系数κη为目标,根据理想情形之时空变换因子(5.36),基于“理想逼近”逻辑,将h00与牛顿引力势χ和场方程系数κη联系起来,其逻辑演绎程序可分为2步. 第一步,运动方程之理想逼近:将式(5.33)之曲度规00(元素h00)与牛顿引力势χ联系起来(h00~χ). 第二步,场方程之理想逼近:将式(5.32)之曲度规00(元素h00)与场方程系数κη联系起来(h00~κη). 最终,在牛顿万有引力定律场景之下,对照“理想逼近”关系式h00~χ和h00~κη,即可标定GOR场方程之系数κη,确立GOR理论之引力场方程. “理想逼近”条件 “伽利略时空定理”和式(5.35)意味着,GOR理论只需设定η→∞,即可满足:Γ(η)=Γ∞和gμν(η)=ημν.因而,GOR理论无须“弱场近似”假设.正如第4章4.3“GOR理想代理法”所述,GOR理论之“理想代理”法基于“伽利略时空定理”所设定的假设条件仅有一项,即所谓“理想逼近”条件. “理想逼近”条件:观测代理OA(η)之信息波速度η足够大或η→∞. 因此,仅需“理想逼近”条件:η足够大或η→∞,GOR理论即可因循或类比爱因斯坦“弱场近似”法之逻辑程序,标定GOR场方程之系数κη. 牛顿万有引力场景 类似爱因斯坦广义相对论,为了将GOR场方程和GOR运动方程与牛顿万有引力定律或其泊松方程形式对应,GOR场方程和GOR运动方程理应设定与牛顿万有引力定律同样的引力相互作用场景. 第4章4.1.4定义了牛顿万有引力场景,即牛顿万有引力定律所设定的引力相互作用场景. 特别需要指出,正如我们一再强调的,牛顿万有引力场景是理想代理OA∞之引力论,是客观物理世界的真实写照;牛顿万有引力场景是真实的引力相互作用场景,并非“弱引力场”. 现在,无须限定于“弱引力场”,GOR理论将因循“理想逼近”逻辑,运用“理想代理”法,基于“伽利略时空定理”和“理想逼近”条件(η足够大或η→∞),将GOR场方程与牛顿万有引力定理或其泊松方程形式联系或对应起来,标定GOR场方程之系数κη,最终,确立GOR理论之引力场方程. GOR运动方程(5.33)可写作 (5.37) 与爱因斯坦广义相对论之运动方程一样,GOR运动方程代表物质在引力场之“弯曲时空”中运动的测地线,即所谓“短程线”.所不同的是,爱因斯坦广义相对论之运动方程属于光学代理OA(c),而GOR运动方程则属于一般观测代理OA(η). 设想GOR运动方程之“理想逼近” GOR运动方程之“理想逼近”,实则基于“理想逼近”条件(η足够大或η→∞),导出一般观测代理OA(η)之运动方程的理想代理OA∞形式. 自然地,“理想逼近”条件下,即η足够大或η→∞时,引力时空趋于平直;“弯曲时空”中的“短程线”(式(5.37))将约化为牛顿引力场之欧几里得空间中的直线(式(5.7)): 直线(式(5.7))左右两端同乘m,既得牛顿第二定律F=ma,又得牛顿万有引力定律: (5.38) 式中:χ即牛顿引力势;V即牛顿引力势能;F即力. 于是,“理想逼近”条件下的“曲度规”hμν可与牛顿引力势χ联系起来. GOR运动方程之“理想逼近”操作 GOR运动方程概括了爱因斯坦广义相对论之运动方程,而爱因斯坦广义相对论之运动方程仅当观测代理为光学代理OA(c)时成立. (gμν=ημν-hμν;ημν=ημν,hμν=ημαηβνhαβ) (5.39) η足够大或η→∞时,dt=dτ,|vi|=|dxi/dt|≪η;又x0=ηt,故|dxi/dτ|≪|dx0/dτ|.因而,成立: (5.40) 式(5.37)之“短程线”约化为 (5.41) η足够大或η→∞时,∂/η∂t=0,gαβ,0=∂gαβ/∂x0=∂hαβ/∂x0=∂hαβ/η∂t0=0;因而,由式(5.39)可得 (5.42) 因为η0i=0,ηii=-1(i=1,2,3),所以 (5.43) (5.44) 式(5.44)之时间方程意味着,在伽利略时空中,观测时间dt与固有时间dτ没有本质区别;解之可得 t=aτ+b (5.45) 适当选取单位(令a=1)并校准时间(令b=0),则t=τ;这与伽利略变换中,不同观测者O和O′之时间相同(t=t′)具有同样的含义. 这与“伽利略时空定理”的结论相同:dt=dτ. 因此,式(5.44)之空间方程组约化为 (5.46) 对照理想代理OA∞之GOR“短程线”(式(5.46))和牛顿引力场中的“直线”(式(5.7))可知 (5.47) 如此,GOR引力时空之“曲度规”00(元素h00)与牛顿引力势χ便联系在了一起(h00~χ). GOR场方程与爱因斯坦场方程(5.32)是同构一致的:Gμν(η)=κηTμν(η);同样,可类似爱因斯坦广义相对论之逻辑理解:左端Gμν(η)代表一般观测代理OA(η)之GOR时空的弯曲,右端Tμν(η)代表物质能量在GOR时空中的分布;Gμν(η)通过场方程系数κη与能量分布Tμν(η)联系在一起. 所不同的是,爱因斯坦场方程属于光学代理OA(c),而GOR场方程则属于一般观测代理OA(η).GOR场方程概括了爱因斯坦场方程,而爱因斯坦场方程则只是GOR场方程之特例,仅当观测代理OA(η)为光学代理OA(c)时成立. 设想GOR场方程之“理想逼近” 于是,“理想逼近”条件下的“曲度规”hμν可与GOR场方程之系数κη联系起来. 场方程之“理想逼近”的操作 以gμν乘以GOR场方程(5.32)左右两端可得 (5.48) 式中:R为高斯曲率;T为能动张量Tμν的迹. 于是,R=κηT,GOR场方程(5.32)可改写作 (5.49) 依定义,式(5.49)之时空曲率(里奇张量)Rμν为 (5.50) 这意味着,一般观测代理OA(η)之GOR场方程是关于度规张量gμν的非线性偏微分方程. “理想逼近”条件下,即η足够大或η→∞时,代表时空弯曲状态的“曲度规”hμν为一小量;去除hμν高阶小量,保留一阶小量,时空曲率Rμν乃至GOR场方程可约化为关于hμν的线性方程. η足够大或η→∞时,对照式(5.40),忽略hμν之高阶小量,时空曲率Rμν(η)为 (5.51) (5.52) (5.53) 于是,式(5.51)可改写作 (5.54) 如此,时空曲率Rμν与hμν呈线性关系. (5.55) 因而,η足够大或η→∞时,Rμν进一步约化为 (5.56) 特别需要说明,式(5.56)中的“□”是OR和GOR理论扩展的“达朗贝尔算子”,即一般观测代理X4d(η)之达朗贝尔算子[16]. 于是,在理想代理OA∞情形下,一般观测代理OA(η)之非线性场方程(5.49)最终退化为线性场方程: (5.57) 如此,GOR引力时空之“曲度规”00(元素h00)与GOR场方程之系数κη便联系在了一起(h00~κη). 5.6 标定GOR场方程系数κη GOR理论设想,理想代理OA∞情形下,GOR场方程与牛顿万有引力定律之泊松方程严格对应. 牛顿万有引力定律场景中,物质粒子M作为引力源构成引力场;而物质粒子m受M之引力作用,在引力时空中运动.设物质粒子m之三维速度v=(v1,v2,v3)(vi=dxi/dt(i=1,2,3)),而四维速度u=(u0,u1,u2,u3)(uμ= dxμ/dτ(μ=0,1,2,3)). “理想逼近”条件下,即η足够大或η→∞时,dt=dτ,gμν=ημν;于是 (5.58) 式中:引力时空属一般观测代理OA(η)之观测时空X4d(η),其时间轴x0=ηt;ρ为物质粒子m之物质密度;Tμν则为物质m在观测代理OA(η)之观测时空X4d(η)中的能动张量;而T则为Tμν的迹. 特别需要说明,式(5.58)中的“四维速度”是OR和GOR理论对爱因斯坦相对论之“四维速度”概念的扩展,即一般观测代理OA(η)“四维速度”的概念[16]. 在“理想逼近”条件下,即η足够大或η→∞时,物质粒子m之四维速度u=(η,0,0,0),故如式(5.58)所示,物质粒子m之能动张量Tμν退化为标量T00. 于是,场方程(5.49)和式(5.57)可写作 (5.59) 式中δμν为Kronecker张量. η足够大或η→∞时,一般观测代理OA(η)之达朗贝尔算子“□”为 (5.60) 对照式(5.47)和式(5.59)以及式(5.60)可知 □h00=-κηρη2或Δh00=κηρη2(h00=2χ/η2) 故 (5.61) (5.62) 这一结果正是式(5.32)基于PGC对应原理,经由PGC逻辑路线1,由爱因斯坦场方程同构一致地对应变换所得到的GOR场方程系数. 至此,GOR场方程得以确立,代表着一种新的引力论诞生——所谓“广义观测相对论”:GOR理论. 引力场方程乃引力论之核心关系式. GOR场方程代表着GOR理论,爱因斯坦场方程代表着爱因斯坦广义相对论;而牛顿万有引力定律之泊松方程形式,可谓牛顿引力论之场方程,或称“牛顿场方程”,代表着牛顿万有引力论. 牛顿万有引力论[53]和爱因斯坦广义相对论[15],是物理学有关引力相互作用的两大理论体系.GOR理论反复强调,牛顿万有引力论并非爱因斯坦广义相对论之近似理论,并非只适用于“宏观”“低速”“弱场”之引力场景.牛顿万有引力论和爱因斯坦广义相对论分属不同观测体系:牛顿引力论乃理想观测理论,是理想观测代理OA∞的产物;爱因斯坦引力论乃光学观测理论,是光学观测代理OA(η)的产物.从某种意义上说,牛顿引力论是“正确”理论,其所表达的是客观物理世界;而爱因斯坦引力论则是“近似”理论,其所表达的只是客观物理世界的光学映像. GOR场方程,即GOR理论之引力场方程,乃一般观测代理OA(η)之引力场方程,其最重要的价值和意义在于,它概括了归属理想观测代理OA∞的牛顿万有引力论之场方程和归属光学观测代理OA(c)的爱因斯坦广义相对论之场方程.实际上,这意味着牛顿万有引力论和爱因斯坦广义相对论的统一. GOR场方程最一般的形式(5.32)可重写作 (κη=κ(η)=8πG/η4) (5.63) 其中,里奇张量Rμν=Rμν(η),高斯曲率R=R(η),时空度规gμν=gμν(η),能动张量Tμν=Tμν(η),乃至场方程系数κη=κ(η),皆依赖于一般观测代理OA(η). 自然地,当观测代理OA(η)之信息波速度η为光速c时,GOR场方程即爱因斯坦场方程: (κ=κ(c)=8πG/c4) (5.64) 其中,里奇张量Rμν=Rμν(c),高斯曲率R=R(c),时空度规gμν=gμν(c),能动张量Tμν=Tμν(c),乃至场方程系数κη=κ(c),皆依赖于光学观测代理OA(c). 可见,爱因斯坦场方程乃光学代理之引力场方程,乃GOR场方程之特例,仅当观测代理OA(η)之观测媒介为光,或OA(η)之信息波速度η为光速c时,才是有效的. 特别地,考虑理想代理OA∞之情形(η→∞). 将GOR场方程(5.63)重新写作 (5.65) 式中χμν为扩展牛顿引力势.可以证明,当η→∞时,χμν→0(μ≠0或ν≠0)而χ00→χ(牛顿引力势). 依“理想逼近”式(5.48)和式(5.49)以及式(5.57)和式(5.59):η→∞时,GOR场方程(5.63)中,能动张量Tμν退化为标量T00,而Tμν之迹T=T00,相应地,高斯曲率R为 (5.66) 式中χ乃牛顿引力势. 依式(5.59)以及式(5.65)和式(5.66): (5.67) 原本,GOR场方程由10个独立的偏微分方程组成,然而,理想代理OA∞情形(η→∞)时,随着能动张量Tμν的退化,GOR场方程相应地退化,仅剩下对应T00的唯一一个非平凡式: (5.68) 实际上,式(5.68)即“牛顿场方程”,与牛顿万有引力定律之泊松方程(式(5.1b))是等价. 如此,η→∞时,GOR场方程(5.66)严格地约化为牛顿场方程(5.68).或者说,理想代理OA∞情形(η→ ∞)时,GOR理论之引力场方程严格地约化为牛顿万有引力定律之泊松方程形式. 可见,牛顿万有引力定律之泊松方程形式,作为“牛顿场方程”,也只是GOR场方程之特例,仅当理想观测代理OA∞情形时,才是有效的. 古老的泊松方程,作为牛顿万有引力定律的一种偏微分方程形式,作为“牛顿引力场方程”,居然与GOR理论之引力场方程和爱因斯坦广义相对论之引力场方程同构一致.这一现象值得我们深思. 归纳起来,GOR引力场方程概括并统一了牛顿引力场方程和爱因斯坦引力场方程.PGC对应原理下,GOR场方程与牛顿场方程和爱因斯坦场方程具有严格的同构一致性对应关系:η→c时,GOR场方程严格地约化为爱因斯坦场方程;η→∞时,GOR场方程严格地约化为牛顿引力场方程.这种严格的同构一致性对应关系反映了GOR场方程与牛顿引力场方程和爱因斯坦场方程之逻辑上的一致性,同时,印证了GOR场方程乃至GOR理论逻辑上的自洽性. GOR理论这一涉及爱因斯坦广义相对论的结论可与OR理论涉及爱因斯坦狭义相对论的结论进行类比——OR理论中,广义洛伦兹变换概括并统一了洛伦兹变换和伽利略变换:η→c时,广义洛伦兹变换严格地约化为洛伦兹变换;η→∞时,广义洛伦兹变换严格地约化为伽利略变换. GOR场方程的标定和确立,意味着GOR理论的建立.如此,我们能基GOR理论,站在一个更高的视角,正确认识牛顿引力论和爱因斯坦广义相对论. 物理学,既是思辨的,又是实证的.一个新的物理学模型或物理学理论,既需要具备逻辑上的合理性和理论上的正确性,同时,还需要经受观测和实验的检验,符合观测实验,符合客观自然现象. 本章,旨在求解GOR场方程,为后续测试和验证GOR场方程乃至GOR理论,解析爱因斯坦广义相对论,揭示引力相对论性效应之本质做准备. 因循和类比爱因斯坦验证或测试其广义相对论的逻辑途径,GOR理论的验证和测试可如下设置. 1)测试内容:爱因斯坦三大著名预测; 2)测试场景:静态球对称引力场,其度规乃球对称物质分布之GOR场方程外部真空解; 3)测试途径:求解GOR场方程,确定一般观测代理OA(η)之观测时空X4d(η)的度规gμν(η),计算预测值,对照观测值. 实际上,一切对于爱因斯坦广义相对论的验证和测试,即是对于GOR理论的验证和测试;一切支持爱因斯坦广义相对论的观测和实验,即支持GOR理论的观测和实验.然而,对于引力相对论性效应,GOR理论将给予我们不同于爱因斯坦广义相对论的诠释和解读,进而,揭示引力相对论性效应之根源和本质,纠正爱因斯坦广义相对论的错误认识. 6.1.1 爱因斯坦之三大预测 为了验证其广义相对论,爱因斯坦构思了3项测试,即爱因斯坦著名的三大预测: 第一,引力红移(Gravitational Redshift):光在引力场中穿行,其频率会呈现红移; 第二,引力偏折(Gravitational Deflection):光线在引力场中会呈现弯曲; 第三,行星进动(The Precession of Planets):水星和金星近日点会呈现反常进动. 爱因斯坦著名的三大预测,为引力论,包括爱因斯坦广义相对论和牛顿万有引力论,乃至GOR理论,提供了验证和测试的途径及方法. 实际上,牛顿万有引力论和GOR理论也能预测“引力红移”和“引力偏折”以及“行星进动”. 爱因斯坦设想和构思的测试,无论“引力红移”或“引力偏折”或“行星进动”,其广义相对论所计算的预测值都依赖于时空度规,而时空度规的计算则需要求解爱因斯坦场方程,其中,引力场景皆理想化的天体“二体问题”和“球对称物质分布之静态引力时空”.实际上,这与牛顿万有引力定律之泊松方程形式中的引力场景相同. 人们总是在为牛顿还是爱因斯坦正确而纠结. “引力红移”和“引力偏折”是爱因斯坦在其广义相对论正式建立之前基于“等效原理”提出的.而“水星进动”或水星轨道旋进的计算和预测则是爱因斯坦广义相对论正式建立之后提出的. 爱因斯坦广义相对论计算和预测的“引力红移”量与牛顿万有引力论之计算似乎是相近的,观测上难以分辨.(需要指出:基于牛顿万有引力论的“引力红移”计算尚存疑点,有待商榷.)广义相对论正式建立之前,爱因斯坦计算和预测的“引力偏折”量与牛顿引力论之计算相同.然而,广义相对论正式建立之后,爱因斯坦重新计算“引力偏折”,得出的预测值较牛顿万有引力论之计算值大1倍. 理想化的引力场景下,基于理想化的天体“二体系统”理论模型,爱因斯坦广义相对论所能计算和预测的水星进动值为每100年43角秒,而牛顿万有引力论所能计算和预测的水星进动值则为零.并非牛顿万有引力论不能预测行星进动;实际上,如果考虑天体运动体系之非理想化因素,牛顿万有引力论也能预测行星之进动或行星轨道之旋进.水星轨道实际旋进率为每100年5 600.73角秒,扣除坐标系之“岁差”导致的进动大约5 000角秒;而考虑金星和地球以及木星对水星的“摄动”,牛顿万有引力论所预测的水星进动值达到了约557角秒,远远地大于爱因斯坦广义相对论所能预测的水星进动量.GOR理论将会阐明,爱因斯坦广义相对论所预测的水星每100年43角秒进动,并非水星客观真实的轨道旋进. 6.1.2 GOR理论之测试场景 自然地,爱因斯坦著名的三大预测也可用于验证或测试GOR理论,包括GOR场方程及其运动方程. GOR理论也能预测“引力红移”和“引力偏折”以及“行星进动”.特别地,GOR理论对于光在引力场中运动的预测,以及对于天体运动的预测,是一般观测代理OA(η)所呈现的观测现象,包括理想代理OA∞和光学代理OA(c)所呈现的观测现象.换句话说,GOR理论,既能做出爱因斯坦广义相对论之预测,也能做出牛顿万有引力论之预测. 无论“引力红移”或“引力偏折”或“行星进动”,皆可归结为理想化的天体之“二体问题”(two-body problem):(M,m),其中,M乃形成引力场的物质体系(比如太阳系中的太阳);m乃被观测运动对象(常理想化作物质粒子),既可以是“引力红移”和“引力偏折”中的光子,也可以是“行星进动”中的行星,例如:太阳系中的水星或金星或地球. 理想化的测试场景:设有天体之“二体系统”(M,m),M乃一半径为R的球体,物质呈中心对称分布,形成静态之球对称引力场,不计m,M之外部乃无物质分布的真空;运动物体m(≪M)在M之引力场中运动.(更理想化地,M和m皆为质点.) 与爱因斯坦基于其广义相对预测“引力红移”和“引力偏折”以及“水星进动”时所进行的操作一样,GOR理论的首要任务是,求解GOR理论之引力场方程,确定天体“二体系统”(M,m)之理想化引力时空的度规gμν(η).基于时空度规gμν(η),方可构造天体或运动物体m之GOR运动方程,进而,计算光之红移或光之偏折或水星进动等天象的预测值. 实际上,爱因斯坦所得其场方程之近似解,以及Schwarzschild 所得爱因斯坦场方程之精确解,乃至牛顿万有引力之泊松方程形式,皆“二体系统”(M,m)之物质体系M的外部静态真空解. 为便于类比,我们首先简要地回顾并解析爱因斯坦场方程之解,包括其近似解和精确解. 爱因斯坦场方程是一个关于时空度规gμν的非线性偏微分方程组,共有10个独立关系式.求解爱因斯坦场方程,即确定光学观测时空X4d(c)之度规gμν=gμν(c),计算时空度规gμν中的10个独立元素. 6.2.1 爱因斯坦场方程之近似解 鉴于场方程的非线性和复杂性,爱因斯坦在求解其场方程时,沿袭了“弱场近似”逻辑和“弱场近似”法,即“弱场近似”的线性化方法. 参照太阳系中太阳的尺度,以M为太阳质量,RS为太阳半径,则太阳表面之牛顿引力势|χ|=GM/RS≈1.9×1011m2/s2≪c2.因此,太阳表面之外无物质区域的牛顿引力势χ可视为“弱引力势”.另一方面,r足够大时,距离M质心r处的牛顿引力势χ=-GM/r自然地也可视为“弱引力势”. 考虑一种特定的符合爱因斯坦“弱场近似”逻辑的情形:gμν(c)≈ημν,相应地,gμν之行列式g=det(gμν)满足√(-g) =1.依黎曼几何和张量微积分公式,成立: (6.1) 根据所设定的球对称引力场景,M之外部物质密度ρ=0,能动张量Tμν=0,爱因斯坦场方程(5.18)退化为:Rμν=0.依式(5.19)之里奇张量Rμν(c)定义和式(6.1),爱因斯坦场方程(5.18)可约化作 (6.2) 如此约化后的场方程(6.2)仍然是一个非线性偏微分方程组,难以求解.爱因斯坦基于其“弱场近似”之线性化条件(第4章4.1.3),对引力场方程(6.2)进行线性化处理并求解. 基于“弱场近似”条件(第4章之4.1.3),包括:弱场、低速、静态、时空正交,以及调和坐标条件,结合运动方程之“弱场近似”的结论(式(5.16)),求解场方程(6.2),可得光学观测代理OA(c)之引力时空X4d(c)的度规gμν(c): (i,k=1,2,3;χ=-GM/r) (6.3) 其中,hμν被爱因斯坦视为平直时空背景ημν下的“弱引力势”(|hμν|≪|ημν|). 式(6.3)显示,正如GOR理论所阐明的,爱因斯坦场方程属光学代理OA(c),其观测媒介为光,其传递观测信息的速度为光速c,其引力时空X4d(c)之时空度规gμν依赖于光速c:gμν=gμν(c)和hμν=hμν(c). 相应地,引力时空X4d(c)之线元ds为 (6.4) 式中引力时空X4d(c)之时间轴x0=ct. 早在广义相对论正式建立之前,爱因斯坦便基于“等效原理”做出了“引力红移”和“引力偏折”预测.广义相对论及其场方程正式建立之后,有了场方程近似解(式(6.3)和式(6.4)),爱因斯坦便将其应用于光之“引力红移”和光之“引力偏折”的理论计算,建立行星运动方程,解析水星近日点之进动,甚至还预测了“引力波”及其辐射速度(恰好即真空光速c). 6.2.2 爱因斯坦场方程之精确解 1916年,爱因斯坦广义相对论正式发表之后不久,德国天文学家及物理学家Schwarzschild[57]便在第一次世界大战前线的战壕里得出了爱因斯坦场方程第一个精确解,史称Schwarzschild解. 与爱因斯坦场方程近似解一样,Schwarzschild解所设定的引力场景也是天体“二体系统”(M,m)之静态球对称引力场,M外部无物质分布.根据牛顿万有引力定律,与M相距r(>R)的引力势χ=-GM/r.Schwarzschild解即M外部真空解,其中,空间坐标采用球坐标而非笛卡儿坐标.相应地,光学代理OA(c)及其观测时空X4d(c)之定义1.1可改写作 (6.5) 式中空间坐标(x1,x2,x3)=(r,θ,φ)乃球坐标. 值得注意:式(1.1)和式(6.5)所定义的观测代理皆为光学观测代理OA(c).无论笛卡儿坐标之定义式(1.1)或球坐标之定义式(6.5),其时间轴x0之定义是相同的,即:x0=ct;并且,其线元公式之形式相同,即 (6.6) 自然地,球坐标度规gμν=gμν(r,θ,φ,c)与笛卡儿度规gμν=gμν(x,y,z,c),其表现形式有所不同.特别地,笛卡儿坐标中,“平直时空”即闵科夫斯基时空,相应的度规gμν即闵科夫斯基度规ημν=diag(+1,-1,-1,-1);而球坐标中,ημν=diag(+1,-1,-r2,-r2sin2θ). Schwarzschild所得球坐标之时空度规gμν[57]为 (6.7) 相应的Schwarzschild线元ds为 (6.8) 借助Schwarzschild解(式(6.7)和式(6.8)),基于其更为精确的时空度规gμν(c),可构建更为理想的天体运动方程(爱因斯坦广义相对论之“短程线”),进而,对光之“引力红移”和光之“引力偏折”,乃至“行星进动”或水星轨道旋进,做出更为精确的计算和预测. 与爱因斯坦场方程一样,GOR场方程也是一个关于时空度规gμν的非线性偏微分方程组,包含10个独立的关系式.求解GOR场方程,即确定一般观测代理OA(η)之观测时空X4d(η)之度规:gμν=gμν(η),计算时空度规gμν中的10个独立元素. 基于PGC对应原理,经由PGC逻辑路线1,将式(6.3)和式(6.4)中的光速c变换为η,爱因斯坦场方程之近似解,即光学代理OA(c)之场方程近似解(式(6.3)和式(6.4)),便可同构一致地变换为一般观测代理OA(η)之场方程近似解.然而,为了解析时空度规gμν及其曲度规hμν的本质,我们更愿意经由PGC逻辑路线2,由更基本的逻辑前提出发,求解GOR场方程. 6.3.1 近似解之GOR场方程 GOR场方程近似解因循和类比爱因斯坦求解其场方程近似解的逻辑途径.然而,与爱因斯坦采用的“弱场近似”逻辑和“弱场近似”法不同,GOR理论采用“理想逼近”逻辑和“理想代理”法(第4章4.3)求解GOR场方程,基于“理想逼近”条件:η足够大或η→∞,求取GOR场方程之近似解. 第4章4.3之“理想代理法”已经阐明:基于“伽利略时空定理”,η足够大或η→∞时,“理想代理”法之线性化方程(式(4.15))成立,爱因斯坦之“弱场近似”法中5项假设,包括:弱场、低速、静态、时空正交,以及调和坐标条件,皆自然地成立.换句话说,GOR理论之“理想代理”法可取代爱因斯坦之“弱场近似”法:经由PGC逻辑路线2,基于“理想逼近”条件,可得GOR场方程之近似解. 在“理想逼近”条件下:η足够大或η→∞,根据“伽利略时空定理”,gμν(η)→ημν;对于度规gμν之行列式g=det(gμν),√(-g)=1自然成立. 于是,依黎曼几何和张量微积分公式,成立: (6.9) 注:爱因斯坦场方程近似解中,√(-g)=1是强行设置的假设或条件,以满足“调和坐标”条件之要求. 根据设定的球对称引力场景,M外部物质密度ρ和能动张量Tμν为零:ρ=0,Tμν=0;GOR场方程(5.49)退化为:Rμν=0.根据式(5.50)之里奇张量Rμν(η)定义以及式(6.9),GOR场方程(5.49)可约化作 (x0=ηt;μ,ν,ρ,σ,α=0,1,2,3) (6.10) 6.3.2 基于理想逼近条件的近似解 求GOR场方程之近似解,即在“理想逼近”条件(η足够大或η→∞)下,确定场方程(6.10)中的时空度规:gμν=gμν(η)和hμν=hμν(η). 如此约化后的GOR场方程(6.10),与约化后的爱因斯坦场方程(6.2)一样,仍然是一个非线性偏微分方程组,难以求解.爱因斯坦继续沿用其“弱场近似”法求解其场方程(6.2);而GOR理论则继续采用“理想代理”法求解GOR场方程(6.10). 第一,求时空耦合之度规元素g0i(i=1,2,3). 第4章4.2之“伽利略时空定理”中,引理A之推论已经证明,“理想逼近”条件之下:η足够大或η→∞,“时空正交”条件自然成立.即引力时空之度规gμν(η)的0i和i0 (i=1,2,3)元素为零: g0i(η)=gi0(η)=0h0i(η)=hi0(η)=0 (i=1,2,3) (6.11) 注:爱因斯坦场方程近似解中,“时空正交”是强行设置的假设或条件,而非逻辑结论. GOR线元ds,乃一般观测代理OA(η)之观测时空X4d(η)的线元;“理想逼近”条件下,X4d(η)呈现“时空正交”,因而,线元公式约化为 ds2=g00(η)(dx0)2+gik(η)dxidxk (x0=ηt;i,k=1,2,3) (6.12) 第二,求解时间之度规元素g00. “理想逼近”条件下,“时空正交”,时间与空间相互独立,GOR场方程(6.10)分裂为“时间方程”和“空间方程”2个独立的部分,其中,“时间方程”为 (x0=ηt;ρ,σ,α=0,1,2,3) (6.13) 第4章4.3之“GOR理想代理法”已经阐明,“理想逼近”条件下:η足够大或η→∞,“弱场”条件(曲度规hμν足够小),以及“静态”条件(度规gμν不随x0显著变化)和“低速”条件(m之运动速度v远小于“信息波”速度η)自然成立. 弱场: gμν(η)=ημν+hμν(xα,η)(|hμν|≪|ημν|) 低速: 静态: 注:爱因斯坦场方程近似解中,“弱场”,以及“低速”和“静态”是强行设置的假设或条件,而GOR之“理想逼近”条件并不要求引力场真的“弱场”或“静态”,也不要求运动物体真的“低速”,而只是要求观测代理OA(η)之“信息波”速度η足够大. (6.14) 这一结果与第5章5.4之“GOR场方程之理想逼近”的结果(式(5.47))相同. 第三,求解空间之度规元素gik(i,k=1,2,3). GOR场方程(6.10)之“空间方程”为 (x0=ηt;i,k=1,2,3;ρ,σ,α=0,1,2,3) (6.15) (i,k=1,2,3;χ=-GM/r) (6.16) 归纳式(6.11)、式(6.14)和式(6.16),静态球对称引力场外部真空之GOR场方程(6.10)的解为 (i,k=1,2,3;χ=-GM/r) (6.17) 其中,hμν=hμν(η)依赖于观测代理OA(η),任意hμν皆包含着因子|χ|/η2. 依式(6.17),引力时空X4d(η)之线元ds为 (6.18) 其中,引力时空X4d(η)之时间轴x0=ηt,而空间轴系笛卡儿坐标轴:x1=x,x2=y,x3=z. GOR场方程之解(式(6.17)和式(6.8))是近似解,要求观测代理OA(η)之信息波速度为η足够大. 基于GOR场方程之近似解(式(6.17))以及GOR线元公式(6.18),GOR理论也能对光之“引力红移”和光之“引力偏折”进行理论计算和理论预测;并且,可建立GOR理论之行星运动方程,解析行星近日点之进动,包括“水星进动”,可建立GOR理论之“信息波”方程,解析爱因斯坦广义相对论之“引力波”的实质. 基于GOR场方程之近似解(式(6.17)和式(6.8)),对于“引力红移”和“引力偏折”,以及“水星进动”等相对论性天象,乃至“引力波”,GOR理论将给予我们不同于爱因斯坦广义相对论的观点和认识. 基于PGC对应原理,经由PGC逻辑路线1,将式(6.7)和式(6.8)中的光速c变换为η,爱因斯坦场方程之Schwarzschild精确解[57],即光学代理OA(c)之场方程精确解(式(6.7)和式(6.8)),便可同构一致地变换为GOR理论之一般观测代理OA(η)的场方程精确解. 然而,为了知其所以然,更好地理解GOR场方程之精确解的逻辑思想,我们依然经由PGC逻辑路线2,力求由更基本的逻辑前提出发,求GOR场方程之精确解.特别地,基于“理想逼近”逻辑和“理想代理”法,以“理想逼近”条件,而不是“弱场近似”条件,作为GOR场方程的边界条件. 6.4.1 球对称引力场之度规与GOR线元 与Schwarzschild精确解一样,GOR场方程之精确解所设定的引力场景也是静态球对称引力场:设有 “二体系统”(M,m),其中,M乃一半径为R的球体,物质呈中心对称分布状态,形成球对称引力场;不计m,M外部乃无物质分布之真空.依牛顿万有引力定律,与M相距r(>R)的引力势为:χ=-GM/r. GOR场方程之精确解与Schwarzschild解一样,也是M之外部静态真空解,其中,空间坐标采用球坐标而非笛卡儿坐标.相应地,一般观测代理OA(η)及其观测时空X4d(η)之定义1.2可改写作 (6.19) 式中空间坐标(x1,x2,x3)=(r,θ,φ) 乃球坐标. 值得注意:式(1.2)和式(6.19)所定义的观测代理OA(η)皆为一般观测代理.无论笛卡儿坐标之定义式(1.2)还是球坐标之定义式(6.19),其时间轴x0之定义相同的:x0=ηt;并且,其线元公式之形式相同,即 笛卡儿坐标: ds2=gμν(x,y,z,η)dxμdxν (x0=ηt,x1=x,x2=y,x3=zημν=diag(1,-1,-1,-1)) 球坐标: ds2=gμν(r,θ,φ,η)dxμdxν (6.20) 其中,一般地,球坐标之度规gμν=gμν(r,θ,φ,η)和笛卡儿坐标之度规gμν=gμν(x,y,z,η),不仅是各自空间坐标(r,θ,φ)和(x,y,z)的函数,而且是一般观测代理OA(η)之信息波速度η的函数. 如式(6.20)所示,球坐标和笛卡儿坐标,其时空度规有不同的表达形式.特别地,笛卡儿坐标式(1.2)中,“平直时空”即闵科夫斯基时空,度规gμν即闵科夫斯基度规ημν=diag(+1,-1,-1,-1);而球坐标式(6.19)中,ημν=diag(+1,-1,-r2,-r2sin2θ). 球对称引力场,其时空度规也是球对称的.根据Birkhoff定理[70],真空球对称度规gμν必定是静态的,不随时间而变化:∂gμν/∂t=0.如此,真空球对称时空之度规gμν及其线元ds最一般的形式可为 ds2=W(r)η2dt2-U(r)dr2-r2dθ2-r2sin2θdφ2 (6.21) 式中g00=W(r)和g11=-U(r)乃待求解之度规元素. 实际上,式(6.21)还意味着,球对称引力时空之时间和空间是正交的:g0i=gi0=0(i=1,2,3). 特别地,在GOR理论中,一般观测代理OA(η)之时空度规gμν=gμν(η)依赖于OA(η)之信息波速度η;对应式(6.21),g00=W(r,η)和g11=-U(r,η),不仅是r的函数,而且也是η的函数.因此,GOR理论中,一般观测代理OA(η)之真空球对称时空度规gμν及其线元ds最一般的形式可为 (6.22) 式中g00=W(r,η)和g11=-U(r,η)乃待求解之度规元素;或者说,一般观测代理OA(η)之真空球对称时空度规gμν待求解的参数即式(6.22)中的ξ(r,η)和ζ(r,η). 6.4.2 球对称引力场之GOR场方程 依照真空解所设定的球对称引力场景,能动张量Tμν=0.如此,爱因斯坦场方程(5.2)可借助于“弱场近似”法由式(5.18)的形式约化为式(6.2):Rμν(c)=0,解之可得爱因斯坦场方程之近似解;GOR场方程(5.32)可借助于“理想代理”法由式(5.49)的形式约化为式(6.10):Rμν(η)=0,解之可得GOR场方程之近似解. 然而,如同Schwarzschild精确解并不借助于“弱场近似”法,GOR场方程之精确解也不借助于“理想代理”法.因而,GOR场方程(5.32)不能由式(5.49)的形式约化为Rμν(η)=0(式(6.10)). 鉴于真空解所设定的球对称引力场景:Tμν=0,依GOR场方程之式(5.32),一般观测代理OA(η)之真空球对称引力时空X4d(η)的场方程可写作 (6.23) (6.24) 进一步计算可得 (6.25) 利用公式: (6.26) 并依时空曲率Rμν之定义(式(6.23)),计算可得 (6.27) 利用式(6.27)可得曲率标量R: (6.28) 整理后,一般观测代理OA(η)之真空球对称时空X4d(η)的场方程(6.23)剩下4个非平凡式: (6.29) 6.4.3 理想代理法与GOR场方程精确解 Schwarzschild精确解属式(6.29)之观测代理OA(η)为光学代理OA(c)(即η=c)之情形.Schwarzschild为求解相应的光学代理OA(c)之场方程而设置的边界条件是:r→∞时,g00=1,g11=-1.其中仍然沿袭了爱因斯坦“弱场近似”的逻辑思想:r→∞时,引力势χ→0,时空趋于平直,因而,gμν→ημν. 根据第4章之“伽利略时空定理”:η→∞时gμν→ημν.因此,GOR场方程的边界条件,可基于“理想代理”法的逻辑和思想,依“理想逼近”条件(η→∞时gμν→ημν)设置: 或 (6.30) 无论r→∞,还是χ→∞,或η→∞,时空度规gμν都将退化为“平直时空”之度规:gμν→ημν.可以预计:gμν=gμν(r,χ,η).换句话说,W=W(r,χ,η)和U=W(r,χ,η)皆为r和χ以及η的函数. 基于PGC对应原理,因循Schwarzschild解之逻辑,采用“理想代理”法之边界条件(6.30),结合式(6.24)和式(6.28),求解GOR场方程(6.29),可得 (6.31) 式中χ=-GM/r乃牛顿引力势. 相应地,GOR球对称引力时空X4d(η)之线元ds及其精确的时空度规可表述为 ds2=(1+2χ/η2)η2dt2- (6.32) 其中,r=0(代表M质心)以及r=2GM/η2(代表M球面)均为式(6.32)之奇点;引力时空X4d(η)之时间轴x0=ηt,而空间轴系球坐标轴:x1=r,x2=θ,x3=φ. 基于GOR场方程之精确解(式(6.31))以及GOR线元公式(6.32),GOR理论便可对光之“引力红移”和光之“引力偏折”做出更为精确的理论计算和理论预测;并且,建立更为准确的和更具有可信度的GOR理论之行星运动方程,解析行星近日点之进动或行星轨道之旋进,包括“水星进动”;进而,建立更为准确和更具有可信度的GOR理论之“信息波”方程,解析爱因斯坦广义相对论之“引力波”的实质. 基于GOR场方程之精确解(式(6.31)和式(6.2)),对于“引力红移”和“引力偏折”,以及“水星进动”等相对论性天象,乃至“引力波”,GOR理论将给予我们不同于爱因斯坦广义相对论的新的观点和新的认识. 如式(4.10)所示,GOR引力时空X4d(η)之度规gμν(η)可分解为“平度规”ημν和“曲度规”hμν(η): gμν(η)=ημν+hμν(η) 式中:ημν即闵科夫斯基度规,表征“平直时空”,包括伽利略时空和闵科夫斯基时空;而hμν=hμν(η)则表征“弯曲时空”,代表时空之“弯曲”状态. GOR观测时空,即一般观测代理OA(η)之引力时空X4d(η),其度规gμν=gμν(η)及其曲度规hμν=hμν(η)具有深刻寓意.而GOR场方程之解,包括其近似解和精确解,则反映了X4d(η)之时空度规gμν=gμν(η)及其曲度规hμν=hμν(η)所具有的深刻寓意. 6.5.1 概括不同观测代理之时空度规 第5章已经阐明,GOR理论之引力场方程,概括统一了爱因斯坦场方程和牛顿场方程.GOR观测时空之度规,乃一般观测代理OA(η)之观测时空X4d(η)的度规:gμν=gμν(η),自然地,概括了一切观测代理之观测时空的度规;GOR场方程之解,自然地,概括了爱因斯坦场方程之解和牛顿场方程之解. 显然地,GOR场方程之近似解,既概括了光学代理OA(c)之爱因斯坦场方程近似解,又概括了理想代理OA∞之牛顿场方程之解:η→c时,GOR场方程之近似解(式(6.17))约化为爱因斯坦场方程之近似解(式(6.3));η→∞时,GOR场方程之近似解约化为牛顿场方程之解的笛卡儿形式gμν(∞)=diag(+1,-1,-1,-1).可见,基于“理想代理”法的GOR场方程近似解,既与基于“弱场近似”法的爱因斯坦场方程之近似解同构一致,又与牛顿场方程之解同构一致. 同样地,GOR场方程之精确解,既概括了光学代理OA(c)的爱因斯坦场方程之Schwarzschild解,又概括了理想代理OA∞之牛顿场方程的解:η→c时,GOR场方程之精确解(式(6.31)和式(6.2))约化为爱因斯坦场方程之Schwarzschild解(式(6.7)和式(6.8));而η→∞时,GOR场方程之精确解则约化为牛顿场方程之解的球坐标形式gμν(∞)=diag(+1,-1,-r2,-r2sin2θ).可见,GOR理论之一般观测代理OA(η)的场方程精确解,既与爱因斯坦场方程之Schwarzschild解同构一致,又与牛顿场方程之解同构一致. GOR理论之场方程作为一般观测代理OA(η)之引力场方程的一般性,以及GOR场方程之解与爱因斯坦场方程之解和牛顿场方程之解的同构一致性对应关系,再次反映了GOR场方程与爱因斯坦场方程和牛顿场方程逻辑上的一致性,同时,进一步体现了GOR理论逻辑体系的自洽性. 6.5.2 时空并不真地弯曲 第3章3.6.2之“时空真地会弯曲吗?”曾基于GOR时空变换因子Γ=Γ(η)阐明:时空并非真地弯曲;所谓“时空弯曲”,实际上,只是一种观测效应,依赖或取决于观测代理OA(η),其根源和本质在于观测代理OA(η)本身存在观测局域性(η<∞). 实际上,根据第4章之“伽利略时空定理”,理想代理OA∞情形下,观测时空之“曲度规”hμν为零: (6.33) 这同样意味着,客观真实的时空是不会弯曲的. 现在,我们可以换一个视角,基于GOR场方程之解,包括其近似解(式(6.17)和式(6.8))和精确解(式(6.31)和式(6.2)),进一步验证这一结论:“时空并不真地弯曲”. 任意观测代理OA(η)之观测时空X4d(η),其度规gμν(η)为常值张量(如闵科夫斯基度规ημν)时,X4d(η)为“平直时空”;反之,则为“弯曲时空”. 观察爱因斯坦场方程之解(式(6.3)和式(6.7))可知,光学代理OA(c)之引力时空X4d(c)的度规gμν=gμν(xi,c)依赖于空间坐标xi(i=1,2,3):不同空间坐标,其度规不同,因而,光学观测中的引力时空X4d(c)呈现“弯曲”状.在爱因斯坦广义相对论中,真空光速c是不变的宇宙常数.局限于光学观测代理OA(c),爱因斯坦只能将“时空弯曲”的根源归咎于引力势χ=χ(xi),归咎于引力时空中物质和能量的分布. 观察GOR场方程之解(式(6.17)和式(6.32))可知,一般观测代理OA(η)之引力时空X4d(η)的度规gμν=gμν(xi,η)仍然依赖于空间坐标xi(i=1,2,3):不同空间坐标,其度规不同,因而,GOR引力时空X4d(η)也会呈现“弯曲”状.然而,根据GOR场方程之解(式(6.17)和式(6.32)),一般观测代理OA(η)之引力时空X4d(η)的度规gμν=gμν(xi,η),本质上,依赖于观测代理OA(η),依赖于OA(η)之信息波速度η:不同观测代理之下,同一引力场景会呈现出不同程度的“弯曲”. 这一事实表明,本质上,一般观测代理OA(η)之引力时空X4d(η)的“弯曲”,并非物质和能量分布所致,而是观测代理OA(η)之观测局域性(η<∞)所致,属观测效应,乃表观现象;相应地,爱因斯坦广义相对论之引力时空的“弯曲”,则为光学代理OA(c)之观测局域性(c<∞)所致之观测效应. η→∞时,GOR场方程之近似解式(6.17)约化为 即 (6.34) 式中:gμν=gμν(xi,η)(x1=x,x2=y,x2=z)为笛卡儿时空度规;ημν为闵科夫斯基度规之笛卡儿坐标形式. η→∞时,GOR场方程之精确解式(6.32)约化为 (6.35) 式中:gμν=gμν(xi,η)(x1=r,x2=θ,x2=φ)为球坐标时空度规;ημν为闵科夫斯基度规之球坐标形式. 如此,若能借助理想观测代理OA∞观测引力时空,η→∞,没有了观测局域性,则GOR场方程,无论近似解或精确解,无论笛卡儿坐标或球坐标,其时空度规皆趋同于“平度规”:gμν→ημν;而“曲度规”则趋于零:hμν→0. 可见,客观真实的时空是不会弯曲的.理想代理OA∞之下,客观时空将会呈现出真实而平直的面貌. 6.5.3 曲度规hμν并不代表引力辐射 爱因斯坦相对论,无论狭义的或广义的,皆与光和光速c联系在一起.然而,主流物理学界并未真正理解真空光速c为什么会出现在爱因斯坦相对论中. 爱因斯坦场方程之解,包括近似解(式(6.3))和精确解(式(6.7)),其引力时空之度规gμν=gμν(c)及其“曲度规”hμν=hμν(c),不出意料地与真空光速c联系在一起.然而,爱因斯坦未能正确解读其场方程之解中的时空度规gμν及其“曲度规”hμν为什么会出现真空光速c. 实际上,这正是光学观测代理OA(c)之体现. 的确,观测和实验显示,引力时空“看起来”有些“弯曲”.然而,爱因斯坦并未真正意识到,我们的观测和实验大多借助光学代理OA(c);而所谓“时空弯曲”,正是光学代理OA(c)之观测局域性(c<∞)所致,乃观测效应或表观现象.在爱因斯坦看来,引力时空的“弯曲”乃物质之引力相互作用所致,是物质和时空的本质特性.在爱因斯坦广义相对论中,“曲度规”hμν代表着引力势χ,被视为“平直”时空背景ημν下客观存在的引力辐射或“引力波”. 然而,GOR场方程之解(式(6.17)和式(6.32))却显示:本质上,一般观测代理OA(η)之观测时空X4d(η)的度规gμν=gμν(η)及其“曲度规”hμν=hμν(η),依赖于观测代理OA(η),依赖于OA(η)之信息波速度η.因而,“曲度规”hμν=hμν(η)并不代表引力势,更不能解释为引力辐射或“引力波”. GOR场方程之近似解(式(6.17))中的“曲度规”: (x0=ηt,x1=x,x2=y,x3=z;i,k=1,2,3) (6.36) GOR场方程之精确解(式(6.32))中的“曲度规”: (x0=ηt,x1=r,x2=θ,x3=φ;i,k=1,2,3) (6.37) 观察式(6.36)和式(6.37)可知,无论笛卡儿坐标或球坐标,无论近似解或精确解,GOR场方程之解中的“曲度规”hμν之非零元素,皆包含着个一重要的量纲一的因子:CW=|χ|/η2,即引力势|χ|与信息波速度η之平方的比,可谓“载波因子”(The Factor of Carrier Wave).当观测代理OA(η)为光学代理OA(c)时,即爱因斯坦场方程之近似解(式(6.3))和Schwarzschild解(式(6.7))中的情形:CW=|χ|/c2. 特别值得注意,正是“载波因子”CW导致引力时空观测起来或“看起来”有些弯曲. 从广义相对论的角度看:CW=|χ|/c2;其中,真空光速c乃宇宙常量,是不变的.因而,爱因斯坦将“时空弯曲”归咎于引力势χ:引力越强,|χ|越大,CW越大,|hμν|=|hμν(c)|越大,引力时空越“弯曲”. 然而,GOR理论发现:CW=|χ|/η2;引力时空之所以观测起来或“看起来”有些弯曲,本质上,并非物质间的引力相互作用(χ),而在于观测代理OA(η)存在观测局域性(η<∞).GOR场方程之解(式(6.17)和式(6.32))显示,同一引力场景(χ),不同的观测代理(η),引力时空观测起来或“看起来”,其“弯曲”的程度不同.观测代理OA(η)之信息波速度η越小,“载波因子”CW便会越大,|hμν|=|hμν(η)|越大,引力时空观测起来或“看起来”就会越“弯曲”.反之,η→∞时,“载波因子”CW→0,GOR场方程之解中的“曲度规”皆趋于零:hμν→0. 引力时空之“曲度规”hμν依赖于观测代理OA(η)之“信息波”速度η,这一事实表明:“曲度规”hμν并不代表引力场客观存在的引力或引力势,更非引力辐射或“引力波”. 可以设想:“曲度规”hμν=hμν(χ,η)乃引力相互作用信息(χ)之“载波”,即经引力辐射信号χ调制后的OA(η)之“信息波”,以信息波之速度η传递引力辐射信号或引力势χ之信息. 关于曲度规hμν究竟意味着“引力波”还是“信息波”的问题,我们将在第10章中进一步论述. (未完待续)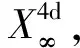
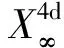
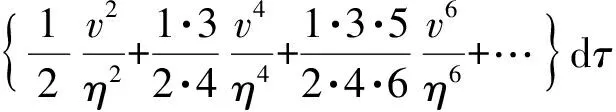
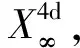
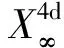
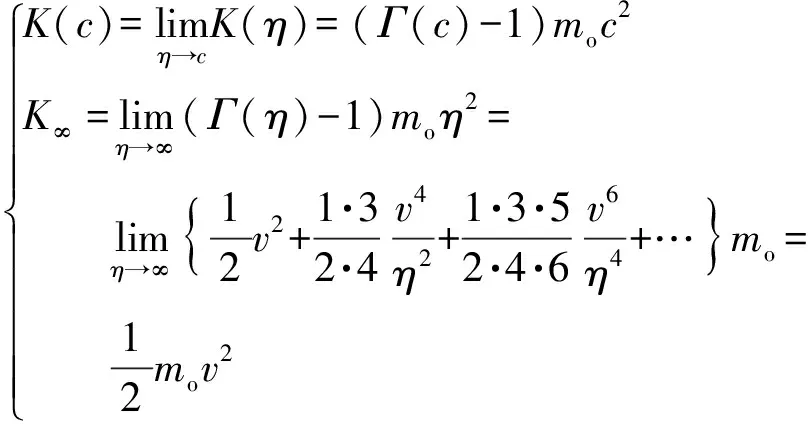
2 广义对应原理
2.1 玻尔对应原理

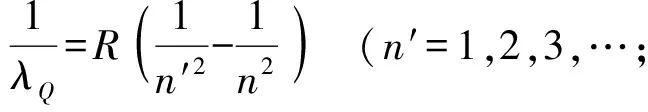
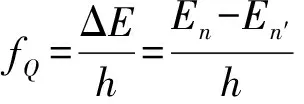
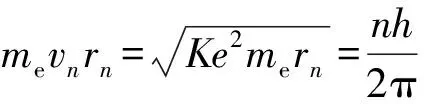
2.2 相对性原理与对应原理

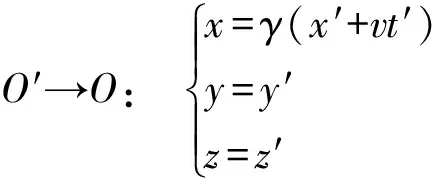
2.3 OR理论与对应原理
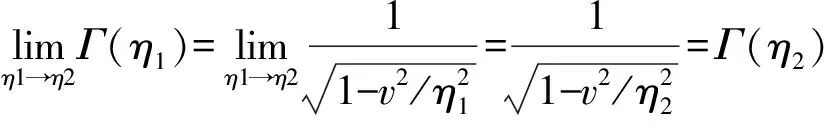
2.4 对应原理和相对性原理的统一
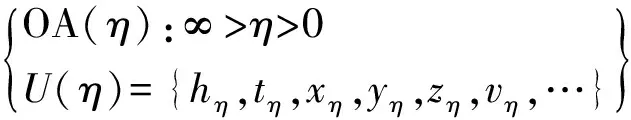

2.5 OR理论对狭义相对论
2.6 GOR理论对广义相对论
3 GOR时空理论:引力时空的观测和度量
3.1 引力时空之局域性问题
3.2 爱因斯坦广义相对论之时空理论

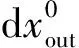
3.3 时间与时频比不变性
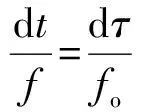
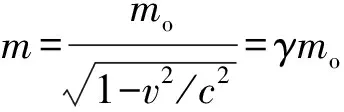
3.4 GOR时空的度量
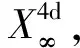

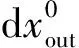
3.5 GOR时空变换因子
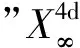
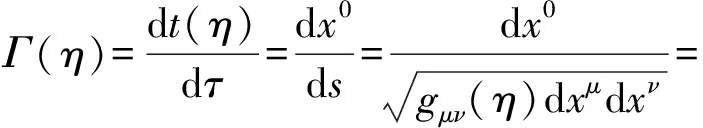
3.6 一切相对论现象皆观测效应和表观现象
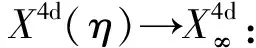
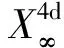
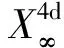
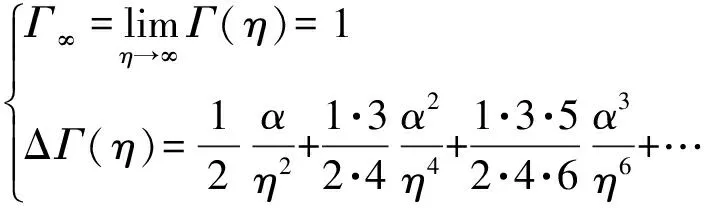
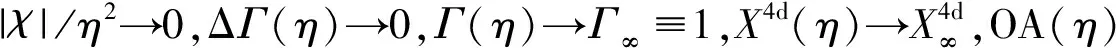
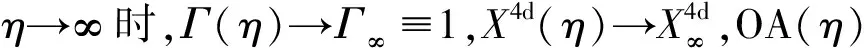

4 伽利略时空定理:理想代理对弱场近似
4.1 爱因斯坦之弱场近似法

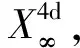
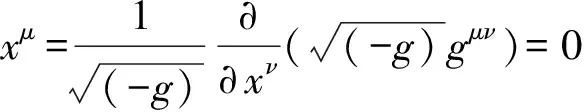
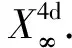
4.2 伽利略时空定理
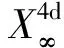
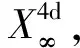
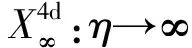
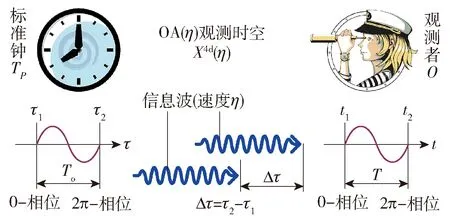

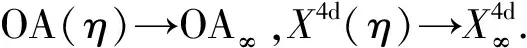
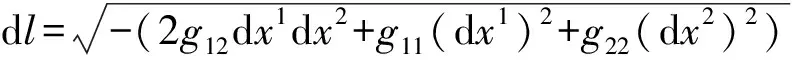
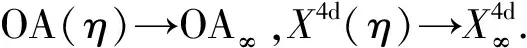
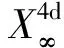

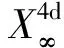
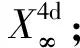
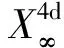
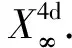
4.3 GOR理想代理法
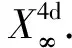
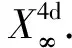
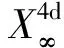
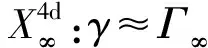
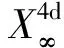
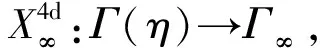
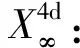
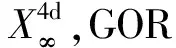
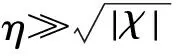

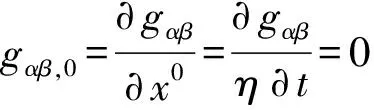
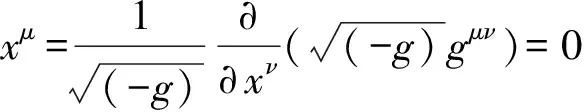
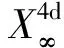
5 GOR场方程的建立
5.1 爱因斯坦场方程的确立
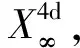
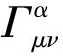
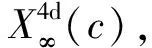
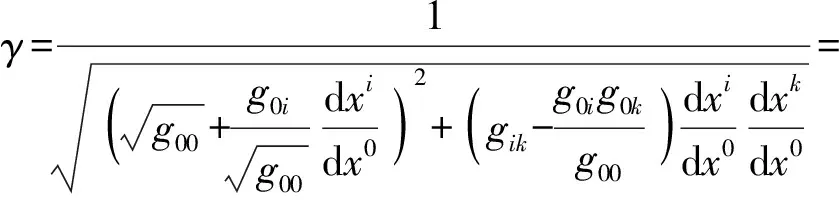
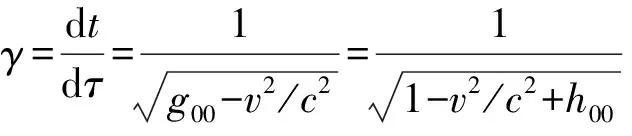
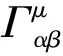
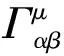
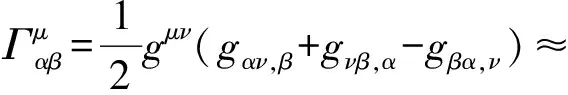

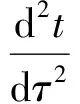
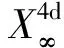
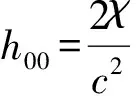
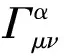
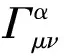
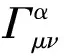



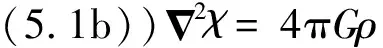
5.2 GOR场方程与GOR运动方程
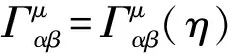
5.3 理想代理对弱场近似
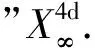
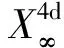
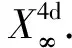
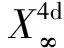
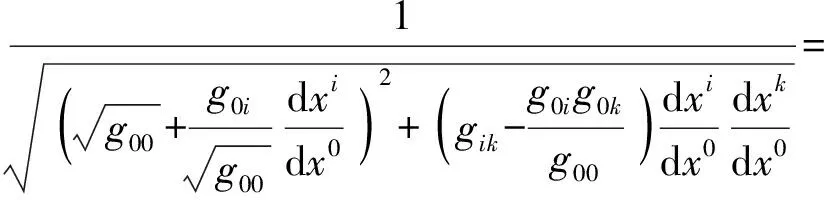
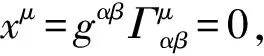
5.4 GOR运动方程之理想逼近

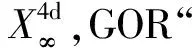
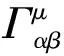
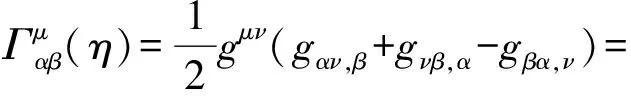

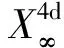
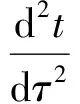
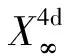
5.5 GOR场方程之理想逼近
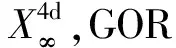
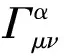
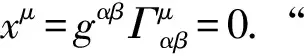


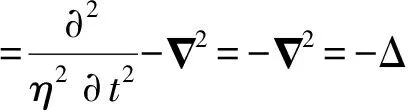

5.7 GOR场方程与引力论的统一
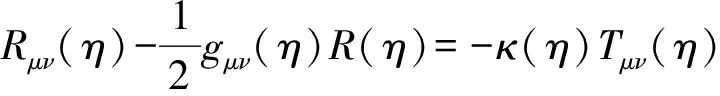
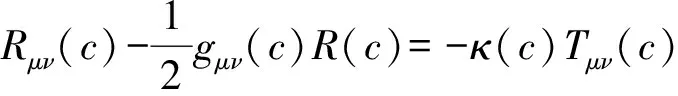
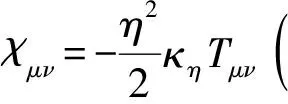
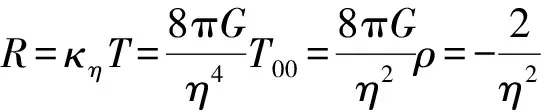
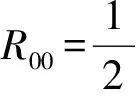
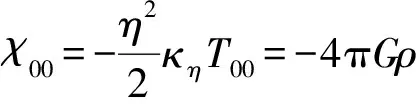
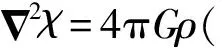
6 球对称引力时空之GOR场方程解
6.1 GOR理论与爱因斯坦预测
6.2 爱因斯坦场方程之解
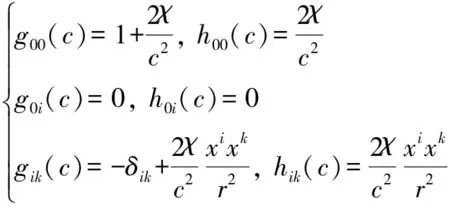
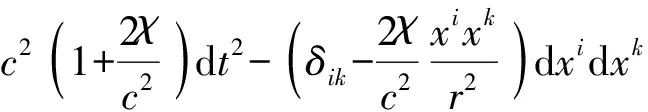
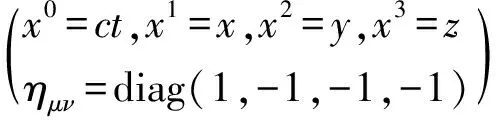
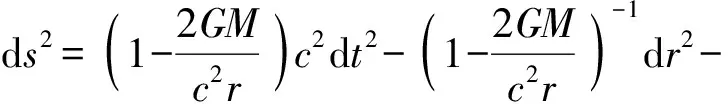
6.3 GOR场方程之近似解
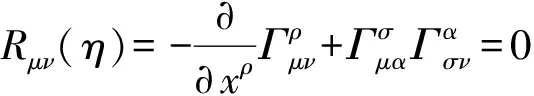
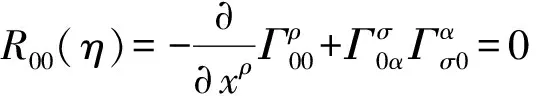
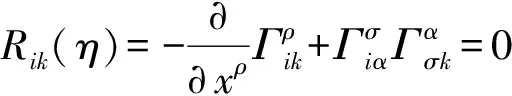
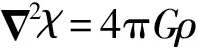
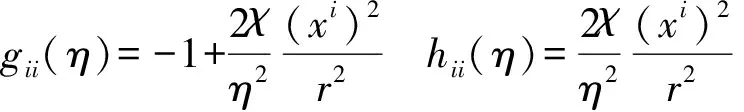

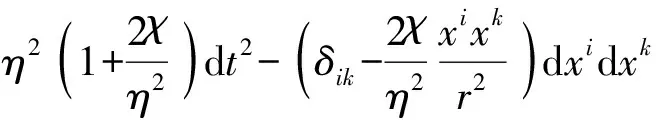
6.4 GOR场方程之精确解
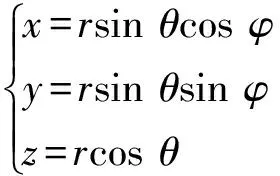

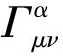
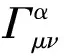

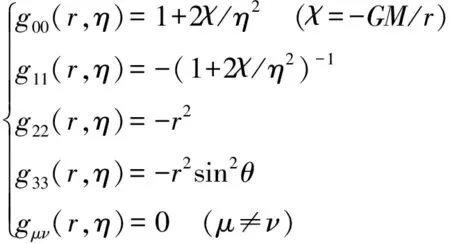
6.5 GOR场方程解之寓意