基于点融合系统的多目标进场排序与调度

张军峰，游录宝，周铭，杨春苇，康博

(1. 南京航空航天大学 民航学院，南京 210016； 2. 中国民用航空中南地区空中交通管理局，广州 510403)

终端空域资源受限，且进离场交通交织，随着终端空域进离场交通需求的激增，导致终端空域交通流量增长，从而造成管制工作负荷增加。为提高进场运行效率、缓解管制工作负荷，点融合系统（point merge system，PMS）[1]应运而生。该系统是一种新型仪表进场程序结构，通过融合到达交通流的新方法，相对于传统的雷达引导，能够标准化进场管制运行、增强飞行员情境意识。从实际运行来看，PMS 主要解决管制指挥标准化的问题，而进场运行效率提升的根本依旧需要借助进场排序与调度领域的研究及进场管理系统的应用。

Liang 等[2-3]研究了基于PMS 的进场调度问题，利用滑动时间窗机制、采用模拟退火算法动态优化进场运行。Hong 等[4]将PMS 引入进场调度，同时采用混合整数线性规划（mixed integer linear programming,MILP）建模，通过最小化PMS 中所有航空器的总运行时间来优化着陆时间。在后续研究中，Hong 等[5]考虑了连续下降期间的不确定性，并依据不确定性规划[6]提出了带有鲁棒特性的解决方案。You 等[7]考虑了PMS 并联形式，并通过带精英策略的遗传算法实现并联PMS 的进场排序与调度优化。

空中交通领域中空管、航司、机场和民众等各利益相关方往往秉持不同的诉求，于是，进场排序与调度也需要综合考虑安全、效率、容量、准点运行、环境等多个方面目标，因此，多目标进场排序与调度近年来逐渐引起重视。Hong 等[8]在PMS 运行情况下，以运行时间和序列改变次数为目标进行进场排序优化。Zhang 等[9-10]通过等效进场调度问题与机器调度问题，利用已有研究成果，梳理并精简了进场排序与调度问题的优化目标，以总延误时间、总飞行时间和最大飞行时间构建多目标进场排序与调度模型。

因此，本文面向多目标进场排序与调度问题，构建基于PMS 的多目标优化模型，设计多目标优化算法，借助蒙特卡罗模拟[11]验证算法可行性。为了实现管制决策支持，引入四维航迹预测[12]协助解决进场调度问题。最后以长沙黄花国际机场的PMS运行为场景，考察融合四维航迹预测和PMS 的多目标进场排序与调度效果。

1 点融合系统与四维航迹预测

1.1 点融合系统

PMS 的结构示意图如图1 所示。航空器进入系统后在排序支路上匀速平飞，直到管制员发布转弯指令，然后从排序支路到合并点执行连续下降进近。

图1 PMS 结构示意图Fig. 1 Schematic diagram of PMS

内外排序支路平行但不等高，用来实现必要延误。为使内外支路上的航空器不发生冲突，支路的水平和垂直方向都配备间隔。航空器在排序支路上匀速平飞时，可以在任意点经由管制员引导转向融合点。航空器进入PMS 之前，为确保与同一定序航段中的前序航空器安全分开，可以通过等待程序或速度调整加以实现。

在PMS 中，除了必要转向指令，不再使用开环雷达引导，从而有助于节约燃油消耗、减少污染排放、降低噪音影响。因此，PMS 一方面可以确保飞行管理系统充分使用水平导航模式，发挥基于性能导航的优势；另一方面能够帮助飞行管理系统优化垂直剖面，实现连续下降进近。

1.2 四维航迹预测

引入PMS 后的进场排序与调度，进场航空器的四维航迹预测是前提和基础。一方面，通过四维航迹预测获得预计到达时间；另一方面，经过排序与调度获得优化到达时间的同时，也可通过四维航迹预测反推航空器在排序支路上的飞行时间，给出航空器在排序支路上转弯的决策建议。如图2 所示各部分之间的逻辑关系。

图2 航迹预测与排序调度的关系Fig. 2 Relation between trajectory prediction and arrival sequencing

航空器四维航迹预测是指根据当前航空器的位置、环境状态和航空器性能参数，基于航空器动力学与运动学模型，（见式（1）），以及航空器意图，预测航空器未来四维航迹的过程[12]。

式中：(ς，η，h)为空间位置；VTAS为真空速；γ、ψ和φ分别为航径角、航向角和转弯坡度；mg、T和D分别为航空器飞行时受到的重力、推力和阻力；w1和w2分别为飞行时受到风的正东向分量和正北向分量。本文中各种机型性能参数均来自航空器基础性能资料数据库(base of aircraft data，BADA)，计算过程详见文献[12]。

在PMS 中，航空器在排序支路平飞，管制员发布转弯指令后，航空器向融合点执行连续下降运行指令。因此，整个过程中航空器意图明确，能够保障四维航迹预测的准确性。

2 多目标进场排序与调度模型

2.1 多目标选择

在航空器进场着陆的过程中，有诸如机场、航司、管制、民众等利益相关方，通过对其诉求进行类比，得出表1 中5 个具有代表性的目标。

表1 排序目标汇总Table 1 Multi-objective arrival sequencing and scheduling

文献[9，13]研究结果表明，表1 中的5 个目标可以用3 个目标函数涵盖，分别为：最小化总延误、最小化总飞行时间、最小化最大飞行时间；对于PMS 来说，航空器在排序支路上的飞行时间即代表其延误时间。故当连续下降时间接近时，最小化总延误与最小化总飞行时间可缩减为一个目标，即本文的多目标为最小化总飞行时间和最小化最大飞行时间为

2.2 约束条件

1) 进入点时间窗。航空器在进入点的时间窗约束：

规定了排序支路上航空器的飞行时间约束，也限制了到达融合点时航空器的飞行时间范围。

3) 安全间隔。

不管在进入点还是融合点,在保证安全距离间隔的情况下一次只允许一架航空器通过。

5) 位置转换约束。

位置转换约束通过限定航空器在先到先服务序列的基础上移动位置不超过z位次，从而确保了公平，以及限制了管制工作负荷。

6) 专机约束。

当航空器为专机时，要保证航空器要在预定的时间内落地，即着陆时间限定为预计到达时间。

3 多目标进场排序与调度算法

3.1 帝国竞争算法

作为一种新型的社会仿生进化算法，帝国竞争算法(imperialist competitive algorithm, ICA)[14]包含帝国(Emp.)、殖民国家(Imp.)和殖民地(Col.)等元素，是将初始解分组成若干个帝国，每个帝国中包含一个殖民国家（帝国内最优解）和多个殖民地，通过对帝国内殖民地和殖民国家不断更新迭代达到产生最优解的目的。该算法的优点在于：通过帝国内竞争和帝国间竞争，加强深度搜索和广度搜索，从而提升邻域搜索和全局优化的能力[13]。

3.2 多目标帝国竞争算法

在PMS 进场排序与调度中，设计多目标帝国竞争算法，其特点在于引入非支配排序。多目标帝国竞争算法流程如图3 所示。图3 中算法的参数imax为最大迭代次数。

图3 多目标帝国竞争算法流程Fig. 3 Flowchart of multi-objective ICA

步骤 3 革命。为防止陷入局部最优，本文主要采用子段逆序、单点变异和2 点交换3 种算子进行革命。子段逆序：随机选择部分连续航空器进行逆序操作，获得相反序列。单点变异：随机选择某架航空器，分配新的优化时间；2 点交换：满足最大位置转换约束限制下，随机交换2 航空器优化时间；为确保新解均为可行解，需要考虑连续落地航空器之间的尾流间隔。

步骤 4 帝国内竞争。更新帝国内殖民国家与殖民地的成本值，成本值最小成为新殖民国家。

步骤 5 帝国间竞争。帝国间竞争实现了帝国间殖民地的再分配，势力强大的帝国逐步吞并势力弱小的帝国。帝国势力值计算过程如下：

4 案例仿真与验证

4.1 四维航迹预测验证

为验证四维航迹预测模型与方法，将预测航迹与真实数据作对比。选用某航班的快速存取数据（quick access recorder, QAR），该航班机型为B737，与预测数据对比得出结果如图4 和图5 所示，其中图4为三维航迹对比，图5 中表示的是过点时间对比，其中，横坐标为航路点。

由图4 和图5 发现，预测航迹与真实航迹在水平轨迹与高度剖面高度吻合，且在过点时间上精度也较高，证明了四维航迹预测模型与方法的可用性。

图4 预测轨迹与实际三维轨迹对比Fig. 4 Comparison between three dimensional predicted and actual trajectory

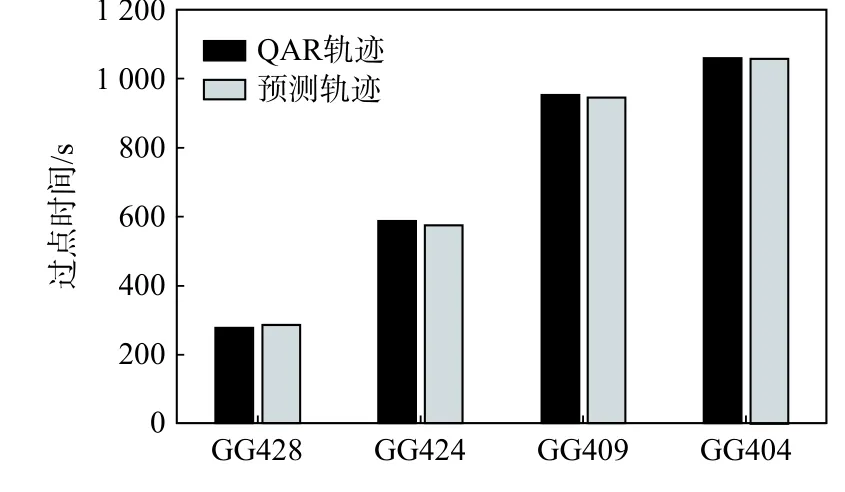
图5 预测轨迹与实际轨迹过点时间对比Fig. 5 Comparison of flight time at each fix between predicted and actual trajectory

4.2 参数值确定

为研究序列改变对多个目标造成的影响，Hong等[5]采用序列偏差（order deviation，OD），Jung 等[15]使用斯皮尔曼秩，评价进场排序与调度模型和算法的优化结果。本文拟用序列变化来量化常规的先到先服务（first come first service, FCFS）序列和优化序列之间的差异。若航空器改变其与相邻航空器的位置，则序列变化的数量增加1。例如，如果FCFS序列和优化序列分别为1-2-3 和3-2-1，那么序列差异为3。1-2-3 →1-3-2 →3-1-2 →3-2-1

考虑10 架进场航空器，PMS 期间的连续下降飞行时间设定为290 s，整个排序支路可供水平飞行时间为310 s（上述数值的确定考虑了实际运行的历史数据分析）。

可以预期，所提算法的性能与交通密度存在较大关系。因此，考虑高、中、低3 种不同的交通密度。记2 架航空器之间的标准尾流间隔为Sijrr′A。在高交通密度下，2 个航班之间的初始相对距离在Sijrr′A和 1.5 倍 的Sijrr′A之 间 随 机 产 生。对 于 中 和 低交 通 密 度，范 围 在1.5 倍Sijrr′A和 2 倍Sijrr′A及2 倍Sijrr′A和 2.5 倍Sijrr′A之 间。对 于 每 种 交 通 密 度 采 用蒙特卡罗模拟各生成500 个初始位置序列，分配的每个航班初始位置用到达PMS 的初始点的时间来表示。

通过MATLAB2014b 编程实现模型及算法， 如图6 所示交通密度情况下，Pareto 解位置转换趋势，图6 中每个点为500 次模拟的平均结果。通过重复增加序列改变次数的上限，随之优化总延误、最大飞行时间的目标。

图6 目标随序列改变趋势Fig. 6 Trend of objectives with different sequences

如图6 所示，横坐标为0 时表示FCFS 的序列，当序列次数从0 变化到1 时，2 个目标都可以观察到最大的斜率。说明序列的改变相对于FCFS 来说各个目标都有优势。从大趋势来看，各个目标（纵坐标）随着序列改变次数的增加而减少，在序列改变次数为6 时，最大飞行时间和总延误达到最优。序列的最终决定权取决于空中交通管制员，其根据目前的态势及整体情况从获得的Pareto 最优解中选择最合适的解来做决定。

尽管空中交通管制员通常根据FCFS 顺序做出决定，但由分析表明，与FCFS 序列之间略有偏差，可以实现总延误与最大飞行时间的显著减少。因此，经多目标算法优化的解决方案更适合于空中交通管制员。

4.3 排序与调度优化算法验证

本节采用真实数据对PMS 的排序与调度优化算法进行验证。以长沙黄花国际机场进场运行为例，图7 显示了一天的进场航空器的综合航迹，机场共有5 个进港点：DAPRO、OVTAN、LIG、LLC、BEMTA。

图7 长沙终端航班进场轨迹Fig. 7 Arrival trajectories within Changsha terminal area

利用Qt 平台构建长沙黄花国际机场的PMS 进场排序与调度仿真系统，通过处理实际雷达轨迹数据得到如表2（部分数据）所示的飞行计划。将处理好的飞行计划输入到PMS 进场排序与调度仿真系统中进行仿真，仿真场景如图8 所示。

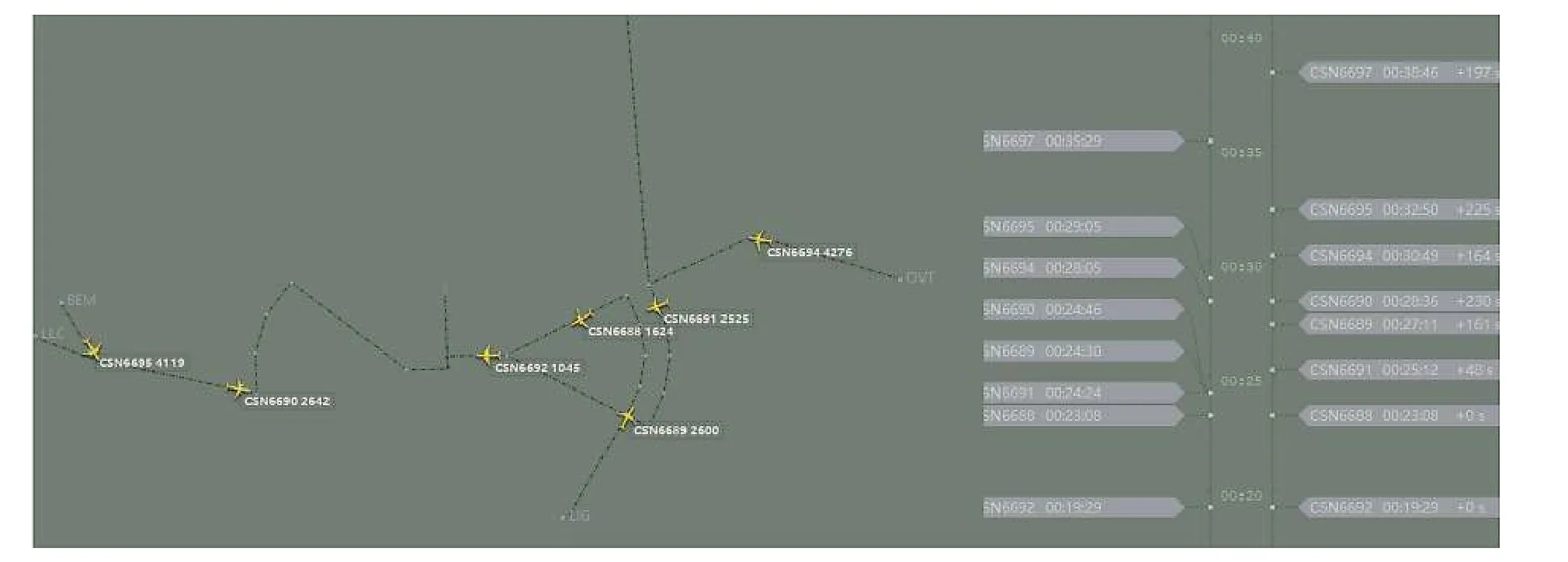
图8 系统仿真界面示意图Fig. 8 Interface of simulation system

表2 基于实际进场数据的飞行计划（部分）Table 2 Flight plan based on actual operation (part)

选取繁忙时段20 架航空器进行优化，由于航空器从不同进港点到PMS 进入点的飞行时间不同，因此需同时考虑总飞行时间和总延误时间。尾流间隔分别取标准间隔的1.2 倍和1.5 倍，仿真优化结果如表3 所示。

表3 仿真结果Table 3 Simulation results

由表3 可知，利用PMS 结合多目标优化算法的方法可以有效提升航空器进场的运行效率和效益。初步引进新技术时，往往需要优先保证安全第一，因此容易采取更为保守的安全间隔，所以本文适当扩大尾流间隔限制。

1.2 倍标准尾流间隔时，多个目标的效益都有较大幅度提升，其中总延误时间减少了70.8%，总飞行时间减少了13.2%，最大飞行时间减少了11.8%。1.5 倍标准尾流间隔时，在不增加其他指标的同时，总延误仍能缩短23.4%，说明PMS 确实能提升效率和效益。

图9 以时序图的形式展示了实际着陆次序与1.2 倍标准间隔下优化着陆序列的对比。图10 是实际和优化序列的航迹对比。表4 提供了基于PMS 的进场排序与调度的航空器在排序支路上总的飞行时间。图9 中蓝色菱形表示通过PMS 优化的着陆时间，红色方框表示实际着陆时间，绿色三角表示航空器预计着陆时间。从图9 可知，经PMS的航班序列与预计到达序列较相似，说明优化算法在保证优化目标的前提下优先考虑公平性。反观实际运行到达序列，与预计到达序列有较大的差距，究其原因，在于常规进场管制员对于航班的引导没有既定路线，航班密度较大情况下可能有较多的盘旋等待、侧向偏离等调配策略，如图10 真实轨迹所示，容易造成既定序列的改变，也会影响运行的效率和效益。

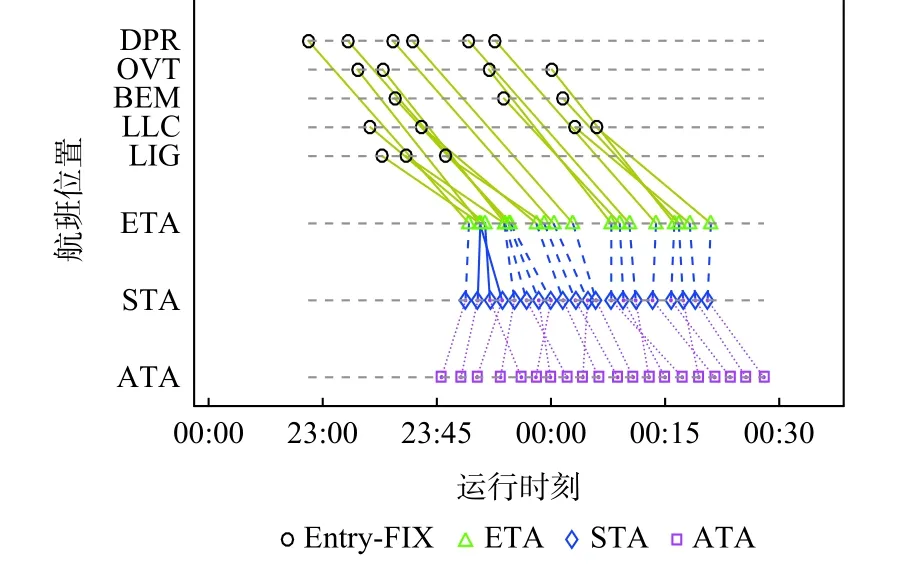
图9 PMS 与实际数据时序对比Fig. 9 Comparison of scheduling results between PMS and actual operation

图10 中在标准尾流间隔1.2 倍的情况下，PMS仍然不需要通过等待进行航班延误。在长沙PMS进场程序中，最短的一条排序支路是西向进港（LLC/BEM）的部分，航班在支路上最长可飞行290 s，而由表4 可以看出，20 架航空器在排序支路上等待的最长时间为275 s，还未达到溢出的状态，说明PMS不仅能在延误及飞行时间等方面有效能的提升，还在容量方面有相应的利用价值。而常规情况下管制员引导航空器主要依赖经验，兼之飞行员具体操控航空器时对管制员指令的依从度无法预知，最终导致无法充分利用终端空域及跑道的容量。

图10 PMS 仿真轨迹与实际轨迹对比Fig. 10 Comparison of trajectories between PMS simulation and actual operation

表4 仿真案例航空器在排序支路飞行时间Table 4 Aircraft flight time on sequencing leg of simulation case

综合4.3 节可以得出，将PMS 与进场排序与调度结合有诸多优点：①排序与调度的结果可达性，根据优化结果直接在PMS 程序上以转弯时机的形式表现，为管制员提供决策建议；②结合优化算法，从空管、航司、机场、民众等多方面进行了效能提升；③PMS 的特殊固定路线，增强了管制员与飞行员的态势感知；④飞行轨迹更为规整有序，有效降低了终端空域进场运行的复杂性。

5 结 论

本文研究了PMS 的运行，从实际运行角度出发，基于四维航迹预测，结合以非支配排序的多目标帝国竞争算法，对航空器进场排序与调度做出优化。

1） 基于非支配排序的多目标帝国竞争算法可行性较好，解决方案能为空中交通管制员提供决策支持。

2） 结合四维航迹预测的多目标优化算法在模拟实验中有良好的反馈，在较为保守的安全间隔限制下仍能获得比实际运行更好的效果。

3） PMS 在航空器进场过程中发挥了显著的优势，从管制的角度来说降低了相关工作人员的工作负荷；从机场的角度PMS 合理利用了空域，对提升有限终端区内的进场容量有很大的发展潜力。

本文主要解决了单跑道航空器进场排序与调度问题，结合PMS 的优势，未来在多跑道机场跑道分配和进离场协同运行等方面值得后续深入研究。