体育拉力训练器拉伸最大阻尼力预估模型

郭志浩，何 标，王 虹

（1.武汉体育学院体育工程与信息技术学院，湖北武汉 430079；2.安徽师范大学体育学院，安徽芜湖 241002）

1 引言

体育拉力训练器作为体育训练项目及生活运动领域中的重要器材设备，其主要用于训练背部肌肉或舒展筋骨，是维护身体健康的重要辅助工具。但由于器械的老化或其内部器件的损坏，会影响阻尼力的变化，进而导致减振效果下降，在实际使用过程中器械会出现抖动现象，一方面影响作用效果，另一方面容易出现安全隐患。所以为了保证运动的质量及安全，需要构建预估模型来检测计算在各种拉伸力下阻尼力的变化，并将数值变化控制在可调节或可承受范围之内，在最大程度上减少因阻尼力不稳定变化带来的影响及损失，减少器械耗用，延长使用寿命。在工程学和物理学的范畴上，阻尼力主要表示振动速度与外力大小的正比关系。

有研究人员针对这一现象，提出基于PLC的液压健身器阻力控制系统设计。根据健身器材液压阻尼系统的结构原理，设计了阻力控制系统，能够有效的读液体压力进行调节，方便健身器材的应用。虽满足了阻尼力当前的需求，但是该系统忽略了对阻尼力系数的计算，并不会减少器材的抖动现象[1]。

有研究人员提出了约束阻尼结构阻尼效果的有限元预测方法研究。通过基于模态应变能给出的复杂结构的阻尼有限元计算方法，对总阻尼效果进行评价，通过谐波响应分析验证该方法的有效性，虽然该方法消振效果较好，但是未计算多种拉伸力下阻尼力的变化，从而在实际的应用中效果不佳[2]。

所以文章结合该特点建立了关于阻尼力系数的预估模型。通过外界拉力的发力特点，对比分析在水平方向及竖直方向的拉伸位移及拉力速度，增加后续计算的可参考性。该模型直观性较强、算法过程较为简单，具有较高的实用性和可实施性。能帮助实现连续可调的阻尼计算过程，并且整体预估的准确性较高，计算误差较小，对于异常数据也能够完成高效解决。保证预估过程的稳定性及高效性。

2 拉伸最大阻尼力特性系数计算

根据体育训练器材进行拉伸时的发力特点[3]，分析其中拉伸力、拉伸位移、阻抗数值[4]以及阻尼力系数[5]之间的线性关系，帮助实现阻尼力的有效预估，计算公式如下所示：

式中：K()—在x或y方向上的拉伸力；C()—在x或y方向上的拉伸位移；F()—在x或y方向上的阻尼力系数。经过FFT（Fast Fourier Transform 傅里叶变换）[6]就可得到拉伸过程中拉力频率参数与运动位移之间的关系，表达公式为：

式中：H()—在x或y方向上的阻抗数值；D()—拉力频率系数（该系数为复数），阻尼变动系数的计算公式为：）

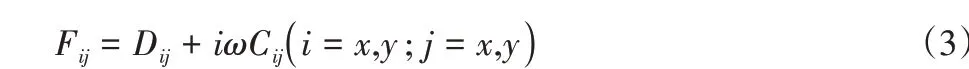
式中：Fij—阻尼力在i和j频率下的变动参数；Dij—拉力变动参数。如式（2）所示，如果仅靠2个方程组是不能求出所有的未知参数，所以需要分别设置在x和y方向上的2个独立方程进行目标求解为：

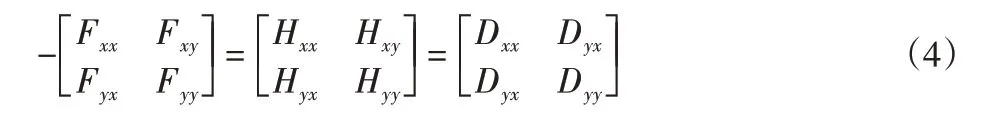
通过上述过程中，利用傅里叶变换得出的阻尼力在x、y方向上以及各个拉伸频率下的变动参数。以此为判断基准，将阻尼力变动参数Fij与拉力变动参数Dij代入到式（4）中，就能计算在x和y方向上的阻抗数值，公式为：

在x方向上的直接阻抗[7]数值为：

根据式（5）～式（8）可得出体育拉力训练器中，出现拉伸力时阻尼力的阻抗数值，根据该动力特性就能得出在x、y拉伸力方向上的刚度及阻尼系数，Re直接评价参数；Im直接评价参数；ω为权重因子，在x方向上的直接刚度[9]和直接阻尼系数为：

在x方向上的交叉刚度[10]和交叉阻尼系数为：

在y方向上的直接刚度和直接阻尼系数为：

在y方向上的交叉刚度和交叉阻尼系数为：

根据上述公式就能准确计算出，体育拉伸训练器的直接阻尼及交叉阻尼系数，帮助建立最大阻尼力的预估模型，实现精准计算。

3 基于切向载荷的最大阻尼力预估模型建立

考虑到体育拉力训练器在进行拉力动作时，其训练器内部关节的接触面之间会出现干摩擦力[11]，而干摩擦是运动阻尼的一种特殊表现形式。

所以结合阻尼系数并利用干摩擦概念以及切向载荷[12]表现，就可以建立最大阻尼力的预估模型，通过模型预测训练器在受到各种拉力系数下的最大阻尼力数值。

由于阻尼力接触面的边界法向力过小，所以任意大小力的出现都有可能引起切向载荷的变动。

当切向载荷数值大于训练器内部出现的干摩擦力时，受力面以及接触边界区域就会出现滑动现象，影响阻尼力的计算；而切向载荷数值小于内部干摩擦力时，就不会出现完全滑动现象，阻尼力的预测准确性就会增加。

因此，需要计算切向载荷在训练器中出现拉伸位置的滑动位移，表达公式为：

式中：δstick—阻尼力的插入数值；r—无滑动区域内的边界距离；p0—训练器受力面的最大压力，且该压力数值为一般情况下的1.5 倍；μ—干摩擦力系数；Gs—等效力的切向载荷模量。

体育训练器中，拉伸最大阻尼力切向载荷示意图，如图1所示。

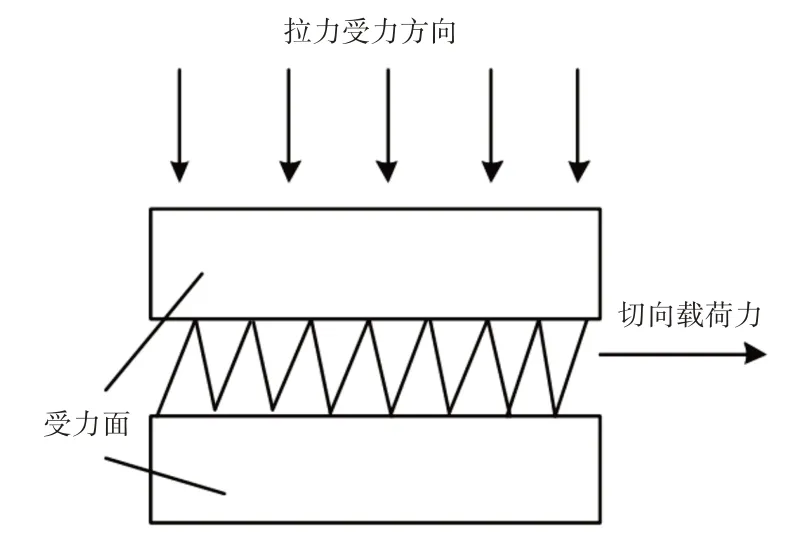
图1 拉伸最大阻尼力切向载荷示意图Fig.1 Schematic Diagram of the Maximum Tensile Damping Force Tangential Load

图中：Qn—训练器内部受力接触面的法向载荷；Qt—周期—力的作用幅值。

一般情况下，当受到拉力作用（即Qn <μQ）时，预估其内部的周期能耗为：

式中：ed—周期能耗的预估值；Λ—摩擦因数，表达公式为：

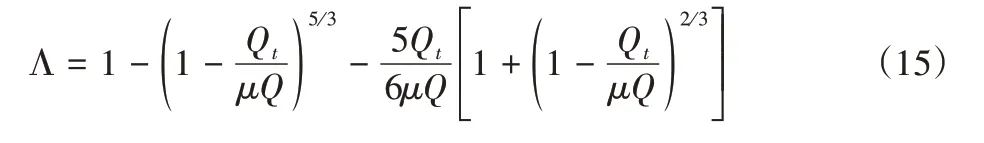
根据训练器受力面的能耗机理，可推算出阻尼力在整个周期内的能耗数值：

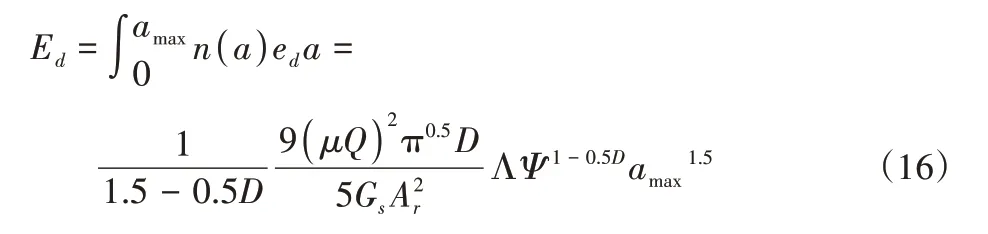
式中：Ψ—等效阻尼力系数；amax—拉力a最大状态；在该状态下阻尼力预测点的分布n(a)将满足以下关系：

根据此关系式就可得出在最大拉力状态下，同等拉伸力的阻尼力数值：

将式（16）和式（13）计算得出的最大值，代入到式（18）中，可得：

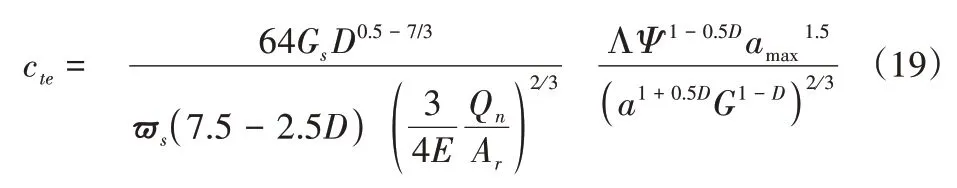
式中：Ar—在r状态值下的阻尼统一参数；训练器内受拉力作用的接触点出现了整体滑移现象即a=amax*，那么所有相等的最大拉力状态下的阻尼预估公式为：

式中：G*=G2/Ar，Qn*—结合摩擦因数、受拉力接触面的载荷情况，amax—最大拉力状态，基于此，就能有效预估出的相关阻尼力数值。

4 仿真实验

4.1 实验背景

为验证所提体育训练器拉力最大阻尼力预估模型的有效性及准确性，将采用以下器械作为实验的主要设备，分别为：BH（LL500）型号体育训练器、MR型阻尼力检验器、Easy Data数据采集系统以及拉力器。部分实验器材，如图2所示。

图2 部分实验设备器材Fig.2 Some Experimental Equipment

为提高实验结果的真实性及可对比性，将拉力器的出力大小设置为200N、拉伸动作的振幅设置为100mm、150mm 以及200mm，阻尼力的预估频率设置为1Hz。本次实验主要通过阻尼力位移及时间两个方面来进行具体分析，并采用控制正弦波加载方式表达可以准确直观地判定出阻尼力波频变化与原始数据的吻合程度，帮助有效分析。

通过使用拉力器模拟正常使用体育训练器时的外界拉力，根据不同的拉力，使用阻尼力检验器测试体育训练器拉力最大阻尼力，以此来验证设计模型的实用性能。

4.2 基于位移变化的拉伸最大阻尼力预估分析

这里给出了BH（LL500）拉伸训练器在频率为（1～10）Hz、动作振幅为150mm下阻尼力原始位移曲线，如图1所示。基于位移预估的拉伸最大阻尼力原始曲线，如图3所示。将二者曲线进行对比分析得出具体实验结论。

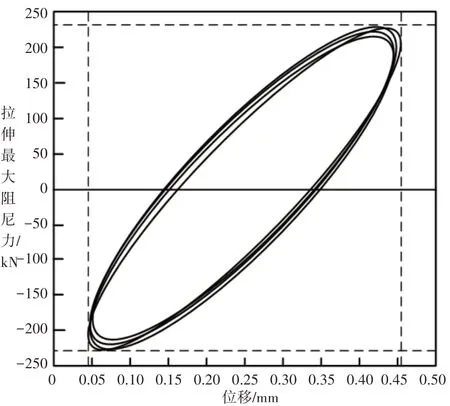
图3 基于位移预估的拉伸最大阻尼力原始曲线Fig.3 The Original Curve of the Tensile Maximum Damping Force is Based on Displacement Estimation

这里设计方法的位移阻尼力预估曲线，如图4所示。

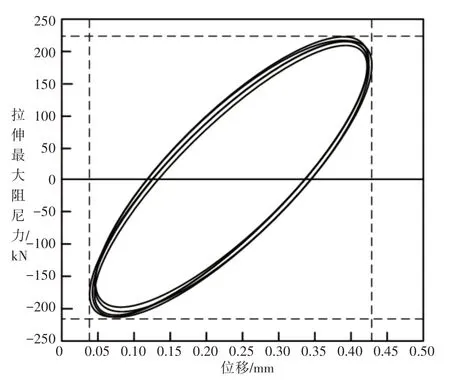
图4 文章方法的位移阻尼力预估曲线Fig.4 Estimating Curve of the Displacement Damping Force in this Method

从图3 和图4 中可以看出，二者的阻尼力曲线相差并不明显，其形状和大小基本保持一致，整体吻合度较高，二者都出现随着位移的增加、内部塑性区逐渐扩张现象。并且这里设计方法的预估曲线没有出现断连现象，整体形态饱满，这说明设计方法对训练器阻尼力的预估准确性较高，预估模型实施的稳定性较强、没有出现计算误差或其他干扰现象。这主要是因为，在进行阻尼力的具体预估前，先对阻尼特性系数完成了有效计算，这样就可以根据拉力的大小判定直接阻尼和交叉阻尼系数，并以此为依据，可减少一定的计算误差，实现预估数值的准确判定。

4.3 基于速度变化的拉伸最大阻尼力预估分析

基于速度变化，将这里设计预估方法与原始阻尼数值进行有效对比，基于速度预估的拉伸最大阻尼力原始曲线，如图5所示。

图5 基于速度预估的拉伸最大阻尼力原始曲线Fig.5 The Original Curve of the Tensile Maximum Damping Force Based on the Velocity Estimation

从图5 中可以看出，原始数据的阻尼数值主要分布，在（−125～75）kN范围内，在低速区域表现出较为明显的滞回特性且整体曲线呈密集分布。这说明在恒定增长的拉伸速度下，该训练器的阻尼变化较为稳定，但如果速度增长不规律，阻尼的变化也会受到一定程度的影响。这里设计方法的阻尼力速度预估曲线，如图6所示。

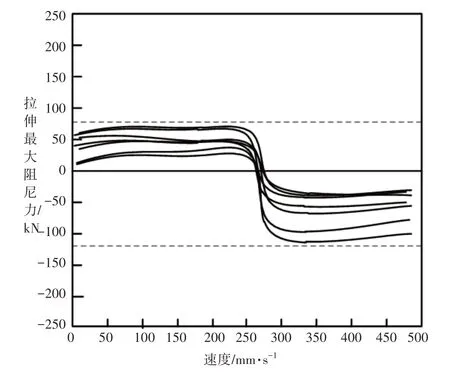
图6 设计方法的阻尼力速度预估曲线Fig.6 Damped Force Speed Estimation Curve of this Method

从图6中可以看出，设计方法的阻尼预估曲线与原始曲线的变化范围相差无异，整体分布在（−120～75）kN之内，并且曲线中没有出现任何突出点或异常点，与原始数据相比，阻尼差值变化了15kN。这是因为在进行阻尼力预估时，由于不同拉力速度的变化会引起受力面干摩擦力的增减，导致预估差值增大。说明设计方法对初始拉伸力带来的阻尼饱和现象实现了有效处理，解决了一些常见问题，在一定程度上减少了预估误差，提高了计算的准确性及效率，改善了数值饱和现象，并有效处理了其他干扰因素的影响。

5 结论

通过分析体育训练器在拉伸时的动作发力特点，给出其拉力速度、位移与阻尼力系数的线性关系，建立直接阻尼和交叉阻尼预估模型。利用模型计算训练器材受力面的干摩擦力及切向载荷系数，进而减少阻尼力的计算量、提高整体速度。根据拉力最大状态下阻尼力的预测点的分布情况，减少预估误差并对阻尼饱和现象实现一定处理。提出阻尼力与拉伸力系数成正比增长的关系，通过分组研究来提升预估的准确性。仿真实验证明，这里设计方法具有一定的优越性和可实用性，无论是基于拉伸位移及拉速度的变化下，整体预估数据都与原始数据表达无异，吻合度较高、准确性较强。并且对异常及噪声数据的处理效果较好，在预估过程中没有出现任何的计算误差或数据饱和现象，可以高效实现训练器材的阻尼力预估。