计及间隙耦合效应机械臂关节振动特性的研究
2023-02-09张发军宋爱林何孔德
张发军,宋爱林,何孔德
(1.机器人与智能系统市重点实验室,湖北宜昌 443002;2.三峡大学机械与动力学院,湖北宜昌 443002)
1 引言
随着科技的快速发展,机器人直接影响着人们生活的各个方面,特别是在精密制造,航空航天等领域中机械臂关节间隙的耦合效应极大地带来了机械臂作业末端的动态振动从而影响其运行精度的稳定性[1−2]。机械臂是通过含有间隙的运动副链接而成的多体系统,间隙的存在不仅会使定位出现偏差,还会使两元素发生冲击碰撞,引发振动,从而影响机械臂的稳定性和可靠性[3−6]。目前,对于多体机构的振动研究有许多,但是都是在理想状态下去进行的,而间隙的影响又是不可忽视的,因此开展含铰间隙机械臂振动特性的研究,对机械臂系统动力学特性的提高具有重要的意义[7]。
针对含间隙机械臂在间隙处发生了接触碰撞问题,这里以ABB机械臂系统作为研究对象,抽取其分析模型,运用Adams/Vi‐bration振动分析模块对含间隙机械臂作了振动模态分析。
研究各阶振型及其振动特性,得到了对应的频率值,为避免在其共振频率附近作业给出了参数依据,为整体响应分析提供了重要的模态参数,同时也为改进机械臂的结构设计奠定了一定的理论依据。
2 实验振动模型建立
这里基于虚拟样机技术,以ABB 机械臂为例,通过Solid‐works建立含间隙机械臂的振动仿真模型。首先是通过三维软件建立各部分构件的模型,并装配;利用软件之间的接口将其导入Adams/View 中;最后通过Vibration 振动模块对含间隙机械臂进行振动模态分析,如图1所示。在模型中,铰间隙大小通过设计精度来得到,在此模型中,由于轴的直径是50mm,选取孔和轴的精度分别为IT8,得到此设计精度下的铰间隙为0.092mm。分析过程中,对与理想情况的旋转副采用Revolute约束定义,而对有间隙的铰链则通过Contact来定义接触[11−12]。通过Contact能够将组成运动副的两个构件之间的传动定义为接触力传动,并设定接触部位的等效刚度值为(1.0×108)N/m、等效阻尼值为175Ns/m、摩擦系数为0.1。

图1 虚拟实验模型Fig.1 Virtual Experimental Model
实验振动模型的建立,首先通过对系统进行相关计算,一方面是为了避免系统在工作时发生共振,另一方面是为了对系统作进一步的动力学分析打下基础[8]。
通过前期计算并查阅相关资料,设定ABB机械臂底座尺寸为(180×180)mm,机械臂高度为700mm,重量约为25kg,工作范围580mm,有效荷重为(3~4)kg,手臂荷重为0.3kg。
3 含隙机械臂的振动分析
机械臂系统的振动是导致精度降低和稳定性降低的主要因素[13−14]。因此,通过对含铰间隙的机械臂进行动力学和振动仿真分析,揭示了含间隙机械臂系统发生振动的现象与固有频率及主振型的关系,将直接关系到我们含间隙机械臂动态响应的认识和理解。在这里中主要是研究运动副间隙对机械臂末端所产生的振动分析。因此在输出通道中选择了机械臂末端的X、Y方向位移、速度以及加速度作为该振动系统的输出通道。
3.1 自由振动仿真分析
首先对模型进行自由振动分析,计算系统的固有频率,并对系统各阶模态的主振型进行求解。由于在模型中有阻尼的存在,因此得到的模态是复数模态,如图2所示。
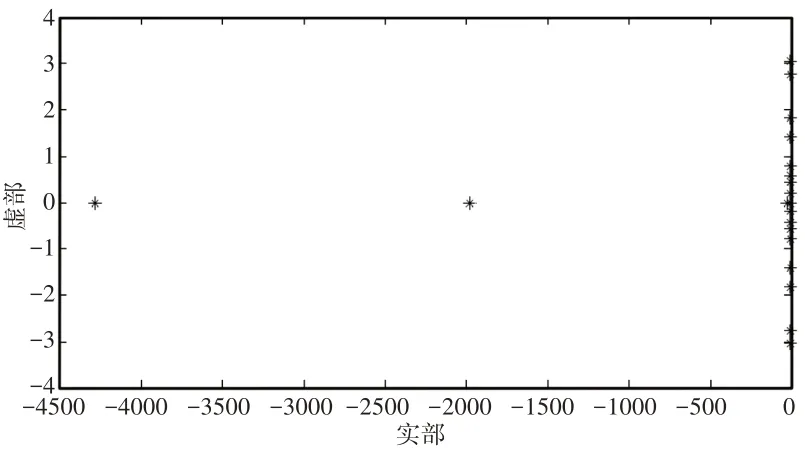
图2 机械臂系统特征根图Fig.2 Characteristic Root Diagram of Robot−Arm
可得出每个特征值点的实部值和虚部值以及其所对应的频率,通过查看各阶模态数据可得,如表1所示。
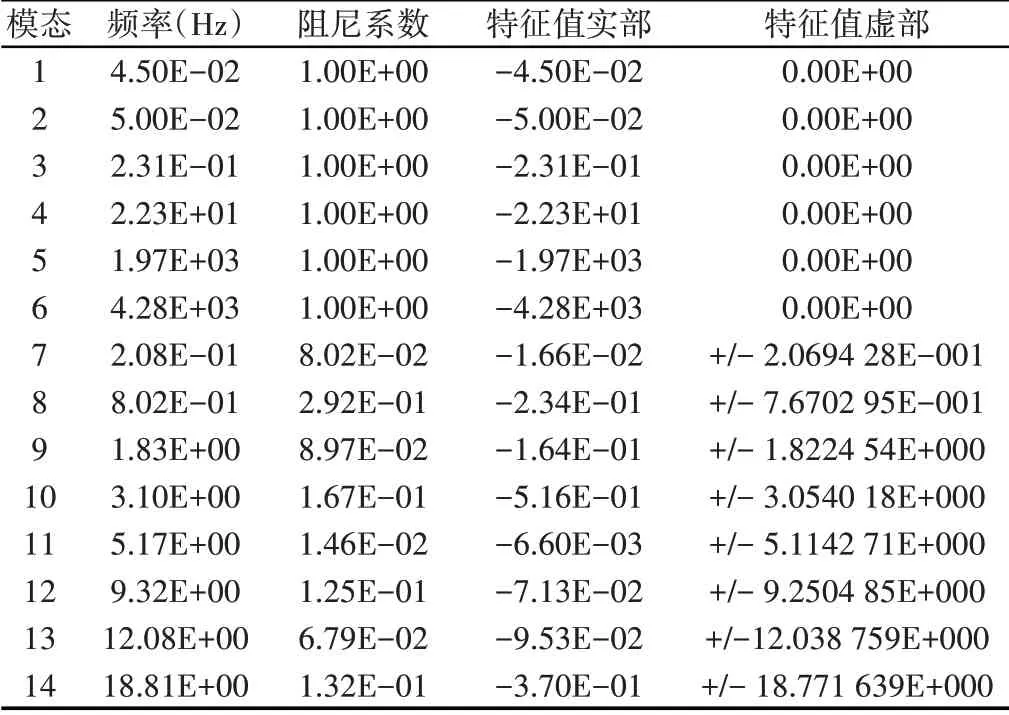
表1 各阶模态参数表Tab.1 Each Order Modal Parameters
通过查看系统振动模态的分布情况,可对系统振动情况的分布有具体的了解。
该系统共有14阶模态,其中前6阶为过阻尼,其余为欠阻尼模态应该对其进行考虑。
机械臂摆臂的工作频率大于4Hz,其中(7~9)阶,频率都低于4Hz属于低频区域,不会引起共振现象。
当达到的第10阶是,频率达到3.1Hz,比较接近与机械臂的工作频率范围,阻尼系数为0.167,因此需要注意,以防止共振情况的出现。
当超过第10阶以后,频率基本都在机械臂的工作频率范围之内,会发生一定的共振,而且振动较为强烈,伴随整机做大幅度的振动,此时需要通过其他减振方式来防止机器发生共振现象。
为了找到对系统影响最大的振动模态,可以通过绘制模态坐标图来判断各阶模态对系统振动的影响,如图3所示。
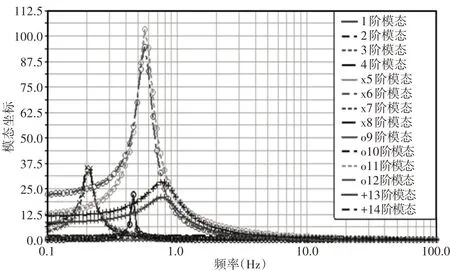
图3 振动各阶模态坐标图Fig.3 Coordinate Diagram of Vibration Modes
从图中可以看出,在含间隙机械臂振动系统中,第11阶和第12阶模态对模型的振动影响较大,其次是第7阶和第8阶,其它阶模态的模态频响曲线没有较大波动,影响不大。
由上面振动模态分析可以知道,在超过第10阶以后系统会有共振情况的出现,因此在第11阶与第12阶模态的振型是机械臂手腕、小臂关节间隙相互作用的振动,振动较为明显,整机的振动幅度也较大。因此需要引起较大的重视。
3.2 强迫振动仿真分析
由于机械臂系统的规模并不太大,因此在进行机械臂受迫振动分析的时候,采用单点激励的方式,这里中的机械臂最大载荷大约为3kg,因此给机械臂建立一个Y方向的激振器,其大小设置为29.4N。在定义了输入通道与输出通道以后就可以对模型进行受迫振动分析。
3.2.1 模态参与因子分析
振动系统具有N个最少独立不相关正交模态,系统的任何振动都是这N个模态中对应的模态振型的加权,那么所谓的模态参与因子就是各个模态的加权系数。通常所指的系统自身频率其实就是每一阶模态所对应的共同频率,而这个频率会使得模态参与因子达到最大值。即,在固有频率和激振频率相互对应的时候,参与因子就达到了最大。但是,输入通道以及输出通道选取不同的时候,其贡献量也会随着发生改变。由此这样的通道就可以通过仿真分析来得到,并对影响这一通道的结构进行改进,从而降低该模态的贡献量,以减小振动。
含间隙机械臂X方向振动模态参与因子图分析可知,第7阶模态的模态参与因子最大,是影响含间隙机械臂X方向振动的主要模态,如图4所示。第7阶模态的频率为0.208Hz,没有较强的振动,而且振动幅度也不大,表明X方向振动并不明显。
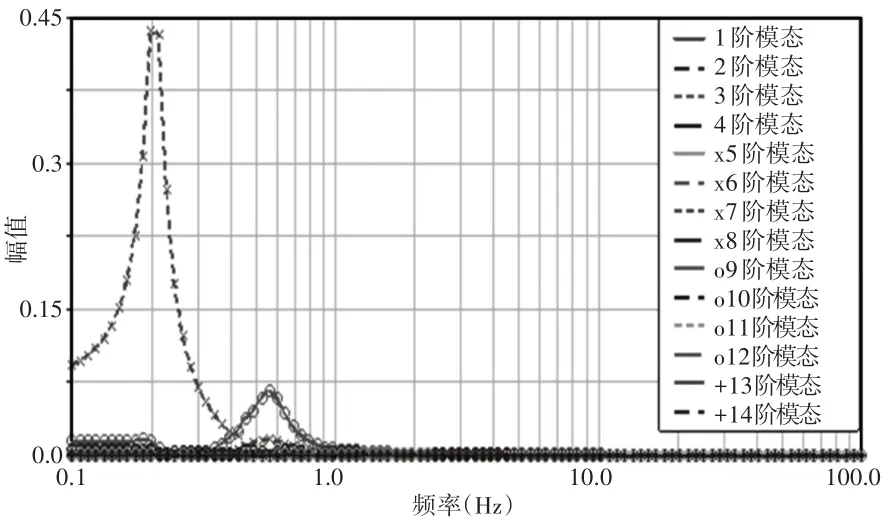
图4 X方向位移模态参与因子幅频特性Fig.4 Modal Participation Factor Amplitude−Frequency Characteristics in X Direction
如图5所示,含间隙机械臂Y方向振动模态参与因子图分析可知,第7阶和第9阶的模态参与因子较大,是影响含间隙机械臂Y方向振动的主要模态。虽然第7阶与第9阶没有达到共振的情况,但是在第9阶的时候已经接近与共振条件了,所以需要对其加以注意。
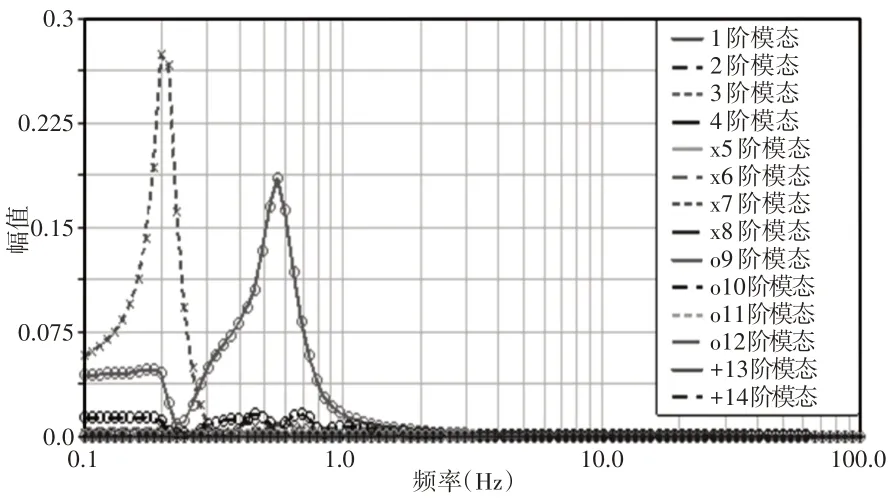
图5 Y方向位移模态参与因子幅频特性Fig.5 Modal Participation Factor Amplitude−Frequency Characteristics in Y Direction
经过对含间隙机械臂在末端X方向和Y方向的模态参与因子的分析可知,第7阶模态含间隙机械臂末端X方向和Y方向振动的模态参与因子最大,但是其频率并不在机械臂工作频率之内,因此不会引发共振的出现。但第9阶模态对含间隙机械臂Y方向的振动参与模态也较为明显,而且接近工作频率,所以需要引起注意。
3.2.2 振动频率响应分析
为进一步分析含间隙机械臂的振动情况,本节中将对机械臂末端X和Y方向的位移、速度、加速度进行频率响应函数的分析,通过对得到的幅值以及相位相互对照,分析系统振动的响应特性。为得到的几个测试通道的相位和幅值分析图,如图6~图9所示。

图6 X方向频率响应相位分析图Fig.6 Frequency Response Phase Analysis in X Direction
X方向频率响应的相位分析图,三条曲线分别为位移、速度和加速度的响应曲线,如图6所示。从X方向位移曲线可以看出,在频率(0.1~0.2)Hz的过程中,相位角从负最大值达到正向最大值175°,然后随着频率增大,逐步回归到0°,但是在0.45Hz时出现了一次波动;从X方向速度曲线可以看出,在频率(0.2~0.6)Hz过程中,相位角在负最大值和正最大值之间有过几次波动,而后在80°达到平稳;从X方向加速度曲线可以看出,频率在(0.1~0.9)Hz时,相位角从最大值有减小的趋势,而后又达到最大相位角,并在(0.9~2)Hz之间出现了相位角在正负最大之间转换,最后又达到最大相位角。
Y方向频率响应的相位分析图,如图7所示。从Y方向位移曲线可以看出,在频率小于1Hz时,其相位角从0开始随着频率的增大,在零线一下出现负向增大的趋势,而后趋于最大值;从Y方向速度曲线可以看出,其相位角从正向最大值随着频率增大最后达到负向最大值。

图7 Y方向频率响应相位分析图Fig.7 Frequency Response Phase Analysis in Y Direction
从Y方向加速度曲线可以看出,在小于0.7Hz时,其相位角开始向着负向增大而后转向正向增大,后又回归到0°。
X方向频率响应的幅值分析图,如图8所示。从X方向位移曲线可以看出,随着频率的增大,幅值在0.2Hz时达到最大值,而后逐渐减小并反向增大,但在0.73Hz和4Hz时各出现了一次波动。从X方向速度曲线可以看出,幅值同样在0.2Hz左右达到最大值,而后逐渐减小后反向增大,但是相比位移曲线则较为平稳。从X方向加速度曲线可以看出,在频率为0.2Hz时出现了峰值,但是在达到4Hz时又一次出现了峰值,而后逐渐减小趋近于0。
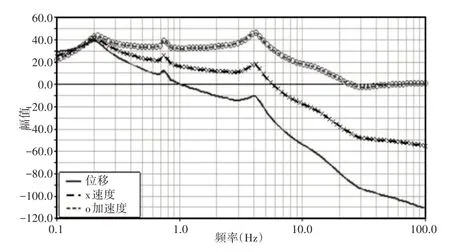
图8 X方向频率响应幅值分析图Fig.8 Frequency Response Amplitude Analysis in X Direction

图9 Y方向频率响应幅值分析图Fig.9 Frequency Response Amplitude Analysis in Y Direction
如图9所示,Y方向频率响应的幅值分析图。从Y方向位移曲线可以看出,在0.2Hz 时出现了一次跳动,而后逐渐增大,到0.73Hz时达到最大值,但随着频率逐渐增大,幅值也开始减小而后反向增大,并在中途发生了一次突变;从Y方向速度曲线可以看出,在频率达到0.73Hz时出现了最大值,而后随着频率增大出现了两次波动后逐渐减小;从Y方向加速度曲线可以看出,在频率小于4Hz的时候出现了几次波动,并出现了最高值,而在频率大于4Hz以后则不在变化,趋于稳定。
通过分析给定输出通道的频率响应,分别得到了相位与频率、幅值与频率之间的关系,对于本含间隙机械臂模型而言,由于在这里中所研究的含间隙机械臂的工作频率大于4Hz,从图中可以看出在频率大于4Hz时幅值波动均很小,而在其他频率时,模型的振动情况就会有很大程度上的区别。因此可以通过其响应曲线对模型的结构进行改进,起到提高含间隙机械臂的精度和减小振动的作用。
4 结论
由于间隙的存在使得机械臂的振动增大,提出了一种利用Adams/Vibration 软件研究机械臂振动性能的方法。通过建立含铰间隙机械臂的振动模型,对其进行自由振动分析和受迫振动分析。
(1)通过自由振动分析得到了含间隙机械臂系统的各阶模态主振型,发现系统共有14阶模态,其中前6阶为过阻尼,其余为欠阻尼模态,分析中应对其充分注意。
并通过仿真研究获得可以看出对系统影响最大的模态坐标图。
(2)通过受迫振动分析分别得出了X和Y方向的位移、速度、加速度相位和幅值与频率之间的对应关系,对于本文中所研究的机械臂模型来讲,其含间隙机械臂的工作频率大于4Hz,而从研究结果中也可以看出在频率大于4Hz是振动幅值波动很小。
可见,机械臂设计中参考所得响应曲线对模型结构进行改进与优化,能有效避开共振频率,极大提高机械臂运行的稳定性与可靠性。
