应用比例导引法的探测机器人机械臂路径规划
2023-02-09刘莹,邵彧
刘 莹,邵 彧
(郑州西亚斯学院电子信息工程学院,河南郑州 451150)
1 引言
近几年,中国制造向着更智能、更精密的方向快速发展,机器人行业逐渐成为重点研究领域之一。机械臂作为探测机器人行动的主要载体,依靠机器人可以实现自主感知、规划路径以及完成各类作业等操作。在地质勘探、煤矿探测中都起到了非常重要的作用,可执行人工无法完成的作业。因此,对探测机器人机械臂的路径规划研究十分有必要。
当机械臂在作业时,一个合理的预作业位姿对于机械臂的探测作业非常重要。通常情况下,工作人员会在机器人到达现场后再进行位姿的调整,以实现最短路径的探测。但当作业空间相对较小时,调整机器人的位姿十分困难。如果改变这种策略,直接在机器人到达现场时调整好位姿,那么可直接进行作业,在一定程度上提高了工作效率。将这种思想应用到实际的作业空间内,演变成如何实现机械臂从一个位姿到另一个位姿的最短路径研究,不少行业专家进行了深入研究。
文献[1]提出了绿篱修建机器人机械臂与目标之间的路径规划方法。首先,确定作业环境内障碍物位置信息,输入到机器人内部,建立简易执行模型;然后计算机械臂在到达目标时,所遇到的障碍物的碰撞条件,以此获得机械臂的避碰空间,即可活动范围;最后,构建优化模型,通过引入斥力场调节策略剔除计算过程中影响因素,再引入扰动人工势场法实现机械臂的作业路径规划。运用该方法可使机械臂灵活避碍,找出最优路径,但计算过程较为复杂,计算量较大;文献[2]对于分拣机器人提出了多目标多机械臂协同作业路径规划方法。首先,对矸石目标建立位置信息坐标系,确定其具体位置信息;然后,在算法中引入机器人的反馈机制,目的是使多机械臂处于协同作业下;最后,将影响多机械臂作业效率的因素综合考虑在内,并对矸石模型进行部分改进,使得机械臂在作业时避碍能力更强、行驶路径更短。该方法有效提高了多机械臂协同工作的效率,但是并未考虑到所抓取的矸石是否满足分拣需求。
基于此,这里在比例导引法的基础上,提出了探测机器人机械臂最优路径规划方法。通过对机器人的作业环境进行自主探测,在确定边界点信息后,对机械臂与探测目标之间的位置关系展开研究。由于探测目标处于不断运动中,与机械臂的位置存在前后、平行的关系,确定二者之间的相对运动方程,同时引入比例导引法,跟踪目标运动轨迹,在控制机械臂动态跟踪时间最短的前提下实现探测,此时运动路径为最短路径。实验验证了这里方法具有较强的通用性,可在时间、路径成本最少的前提下实现对目标的精准探测。
2 机器人机械臂自主环境探测
2.1 前沿点探索
在机器人机械臂规划路径之前,需要对周围环境进行自主探测,这里通过RRT(Rapidly−Exploring Random Trees,快速扩展随机树)算法实现。RRT算法的主要作用是在机器人作业现场周围不断检测、更新边界点[3],实现过程,如图1所示。

图1 RRT算法探索前沿点实现过程Fig.1 Implementation Process of RRT Algorithm Exploration Frontier
首先,利用RRT算法遍历树的所有节点信息,找到与Xrand距离最近的点Xnearest,并以点Xnearest 为起始点,顺着点Xrand 的方向,以增长速率为η的恒定速度增长,直至树节点的末端接触到未知环境停止,将末端节点Xfrontier 作为作业环境的边界点。
2.2 前沿点过滤
根据上述探索到的前沿点进行过滤。首先,对探索到的所有前沿点进行聚类处理,提取聚类中心,并分类存储。然后,将完成分类的点传送至分配模块,将重复和无用的点删除掉,由此完成对前沿点的过滤处理。
2.3 前沿点分配
接收到来自过滤模块的前沿点后,分配模块对所有前沿点进行评估[4−5],确定哪些点可以作为机械臂下一步的运动目标点F。对筛选目标点的过程建立一个数学模型,计算每个点的收益E,计算过程,如式(1)、式(2)所示:

式中:Xfp—接收来自过滤模块的前沿点;Xr—机器人所处位置;i—点Xfp的信息增益,也可以用来表示在点Xfp处初期探测到的未知环境范围。i值的计算方法为:以点Xfp为圆心,在其半径范围内获得的单元个数即为i的值。N—路径规划成本,也就是机械臂到目标点所消耗的距离成本;λ—为一个常数项,用来表示信息收益在整个算法中所占的权重[6]大小;h—为一个函数项。
根据前沿点与机械臂之间的距离大小,设定增益系数值,将前沿点与机械臂的距离控制在hrad范围内,增益hgain>1,其他情况hgain=1。这样可以避免机器人探索重复的前沿点,降低运动成本。E—点Xfp的收益,算法的目的是找出具有最大E值的点Xfp,该点即为机械臂运动最佳目标点。
3 比例导引法下探测机器人机械臂路径规划
当机械臂对探测目标作业时,机械臂的运动路径与探测效率呈正相关。通过应用比例导引法,实时勘探探测机器人的作业环境以及机械臂的运动路径,实现最小成本的探测作业。
假设探测目标在水平向右方向上匀速直线运动,那么机械臂与目标的相对运动,如图2所示。
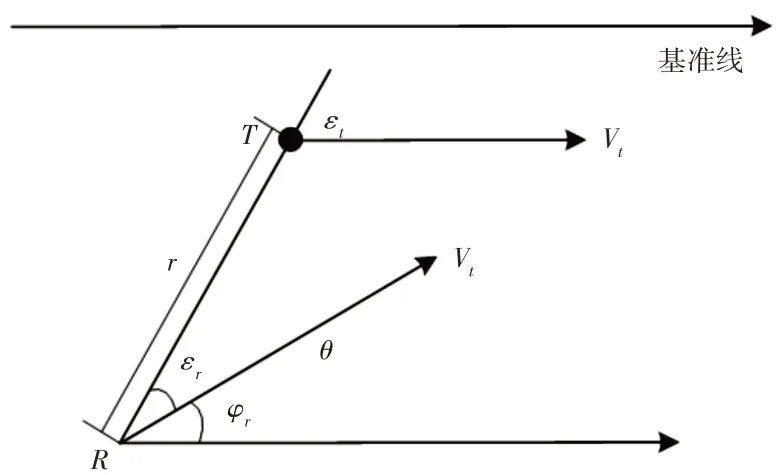
图2 机械臂与探测目标的相对运动Fig.2 Relative Motion between Manipulator and Detection Target
图中:R—机械臂末端;T—探测目标。
为了进一步验证机械臂与动态目标之间的距离变化,这里分别对垂直方向和视线方向上的速度向量进行分解计算[7],由此获得机械臂与目标之间的距离变化值和视线角变化值为:
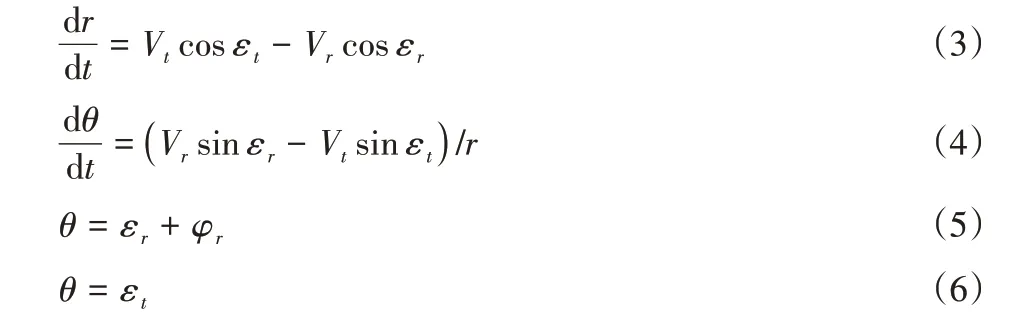
式中:dr/dt—探测机器人机械臂与目标之间距离的变化值;dθ/dt—目标视线角的变化值;Vr、Vt—机械臂末端和探测目标运动状态下的速度值,单位为m/s;εr、εt—机械臂末端和探测目标在运动状态下的前置角,单位为(°);r—机械臂末端与目标运动状态下距离的变化值,单位为m;φr—机械臂末端作业状态下方向角的值,单位为(°);θ—探测目标运动状态下视线角的值,单位为(°)。
在确定机械臂与目标之间的距离变化值和视线角变化值后,引入比例导引方程,计算探测目标的动态轨迹[8],得到:

然后,将式(3)~式(7)合并,即可得到机械臂与探测目标之间的相对运动方程组。
在实际作业环境中,运用比例导引法对探测机器人机械臂进行路径规划时,为了达到理想的作业效率[9],会尽可能控制机械臂的动态跟踪时间,使得机械臂通过最短路径到达目标处。此时,视线角的变化,也就是视线角速度为0,则:

由式(10)可得,在Vt已知的前提下,可计算得到εt的值,在Vr已知时,可求得εr的值。
实际上,机械臂的运动是通过机器人电机驱动,电机在启动过程中存在一个加速度的过程,这个过程可有效控制因启动速度过大而导致的堵转。所以机械臂在加速运动过程中,速度随时变化,也就是εr的值时随时变化,而在机械臂匀速运动时,εr的值为一个固定值[10]。
机器人机械臂探测目标的最优路径规划过程为:
(1)在完成上一轮的探测任务后,机器人内部控制器会根据机械臂关节角确定机械臂当前所处的位置,通过目标运动方程确定探测目标的位置信息,计算得到视线角θ;
(2)通过求解机械臂加速度方程,得到εr的变化方程式;
(3)通过εr,计算得到φr;
(4)计算任意时刻下机械臂关节角的值和加速度;
(5)通过操控机器人,使机械臂按期望路径对目标完成探测任务。
4 实验分析
4.1 实验数据
为了验证这里方法在实际的探测作业中是否合理有效,进行了实验分析。将实验用的机械臂至于某车间的操作台上,通过程序控制机械臂的运动,发送机械臂关节指令到关节控制器,机械臂运行的轨迹数据通过中央控制器与总线通信协议,传输机械臂运行的轨迹数据。其中,传输的机械臂传输数据包括运行速度、运行时间、运行轨迹数据以及运行成本数据。在实验中,探测机器人的机械臂从初期的匀加速转换为后期匀速,初期阶段,速度从0迅速提升到2m/s,加速度为4m/s,时间为0.5s。这个阶段中,机械臂的方向角时刻发生变化,到后期,速度方向角为固定值,机械臂只会按照直线方向运动,直到探测到目标为止。
将目标的运动速度设为0.7m/s,实验用机械臂,如图3 所示。

图3 实验用机械臂Fig.3 Mechanical Arm for the Experiment
4.2 探测路径规划分析
在实际作业中,机械臂与探测目标之间存在三种状态关系,实验对此均进行了研究。
(1)追踪式探测路径规划
此种状态下,机械臂处于探测目标后方的位置。定义机械臂的初始位置坐标为(0,0.5,0),探测目标的初始位置坐标为(0.5,1.5,0.4),探测到目标所花费的时间为1.070s,实验中的路径规划,如图4所示。
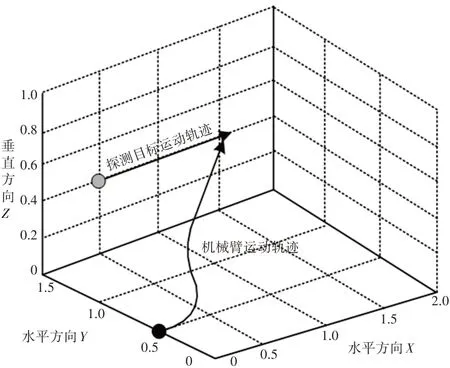
图4 追踪式探测轨迹Fig.4 Tracking−Type Detection Trajectory
(2)平行式探测路径规划
当机械臂与探测目标处于水平方向上时,称为平行式探测。定义机械臂的初始位置坐标为(0,0.5,0),探测目标的初始位置坐标为(0,1.5,0.4),探测到目标所花费的时间为0.873s。实验路径规划,如图5所示。
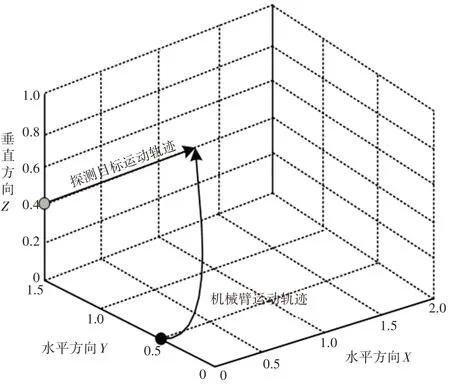
图5 平行式探测轨迹Fig.5 Parallel Detection Trajectory
(3)拦截式探测路径规划
拦截式探测指机械臂处于探测目标前方的位置。定义机械臂的初始位置坐标为(0.5,0.5,0),探测目标的初始位置坐标为(0,1.5,0.4),探测到目标所花费的时间为0.791s。实验路径规划,如图6所示。
从图4~图6中可以看出,三种状态下的机械臂运动路径,在初期匀加速阶段,存在一小部分的曲线,曲率较大,但是弯曲程度较低,整体路径较为光滑。
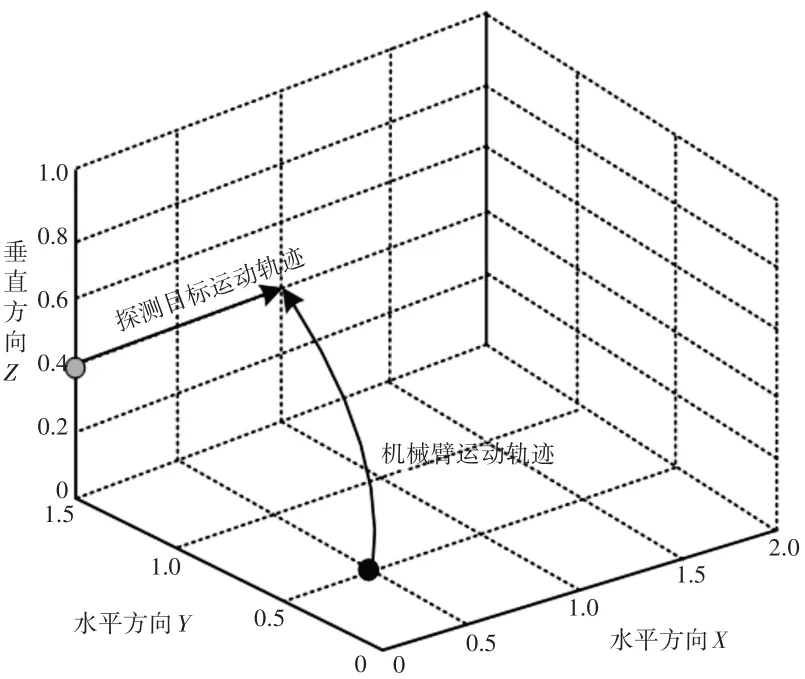
图6 拦截式探测实验轨迹Fig.6 Blocking Detection Experiment Trajectory
在后期加速阶段,机械臂的运动轨迹逐渐成为一条直线,运动时间也相对较短,消耗的能量也就越小,机械臂的稳定性也就越高。
不仅如此,从这三幅图中还可以看出,通过引入比例导引法对机械臂进行路径规划,不管机械臂与探测目标的位置关系如何变化,机械臂都能以最短路径探测到目标,由此也可以证明,这里方法的通用性较强。
4.3 空间大小对规划成本影响分析
考虑到探测机器人的作业环境为小范围环境时,可能对作业效率、运动路径产生一定的影响,因此,将这里方法与扰动人工势场法和多机械臂协同策略两种方法在路径成本和时间成本上进行实验对比。
实验中选择了一个相对较大的空间和一个狭小的空间,大空间为182m2,小空间为49m2。
经过统计后得到路径距离和时间成本的直方图,如图7、图8所示。
从图7、图8中可以得出,与扰动人工势场法和多机械臂协同策略两种方法对比,这里方法路径距离和时间成本最小,这是由于这里方法分别对机械臂与探测目标之间的垂直方向与水平方向进行了相对运动方程计算,精准定位了探测目标所在位置,所以运用这里方法,即使在小范围环境中同样可以取得理想效果。
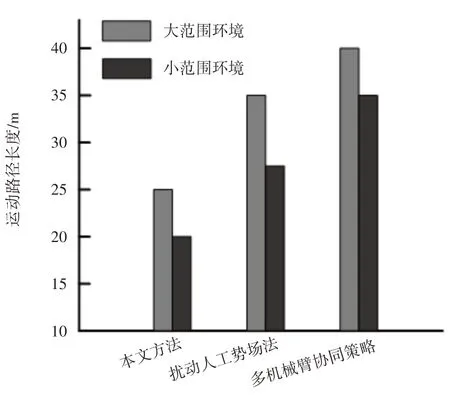
图7 三种方法下路径规划距离对比图Fig.7 Comparison of Path Planning Distance Under Three Methods

图8 三种方法下路径规划时间对比图Fig.8 Comparison of Path Planning Time Under Three Methods
5 结论
这里针对探测机器人提出了一种机械臂路径规划方法,使机械臂实现了合理、高效的作业。
实验也验证了这里方法通用性较强。这里方法具有以下优势:
(1)通过分析探测目标与机械臂的位置关系,给出了机械臂实现探测的路径规划步骤。实验中设定了三种位置关系,验证了这里方法可以平滑、快速地跟踪到探测目标。
(2)考虑到探测机器人的作业空间大小,设定大范围环境和小范围环境的实验,结果表明,这里方法依然可以很好地探测到目标,基本不受空间大小的影响。
