触土曲面准线形式对推土铲切削性能的影响

邓利军，刘 朋，姚鹏华，王书贤

（1.湖北文理学院纯电动汽车动力系统设计与测试湖北省重点实验室，湖北襄阳 441053；2.湖北文理学院汽车与交通工程学院，湖北襄阳 441053）

1 引言

构形仿生是触土部件节能减阻设计的重要方法之一，仿生原型的选取是该方法的关键所在。目前，一些研究常以各种土壤动物爪趾作为仿生原型。

文献［1］以棕熊爪趾为仿生原型设计了仿生深松铲，试验结果表明仿生深松铲的工作阻力明显低于国标圆弧形深松铲。

文献［2］以蝼蛄爪趾为仿生原型设计了挖掘机斗齿，仿真分析和试验结果均表明仿生斗齿切削性能优于JL80 原型斗齿。文献［3］设计了仿鼹鼠爪趾的旋耕机刀片，其切削性能和作业效果均优于常规刀片。文献［4］为降低振动深松机的牵引阻力，设计了以家鼠爪趾为仿生原型的仿生深松铲。

由此可见，将各种土壤动物爪趾作为仿生原型设计仿生触土部件的研究较多。然而，对于各种不同仿生原型的切削性能有何差异以及是否存在某种能适应各种工作条件（工作深度、切削角等）的仿生原型等一系列深层次的问题，目前国内外鲜有文献进行深入研究。

现有文献中，仅文献［5］对比了以公鸡、小家鼠、田鼠、蝼蛄等动物爪趾为仿生原型的几种切削工具的切削性能。这为触土部件的仿生设计提供了一定的参考。然而，该研究并非在相同切削角的条件下进行的对比，且未考虑工作深度的影响。因此，其结论可能并不能真实地反映不同仿生原型之间切削性能的差异。

综上所述，现有文献很少针对不同仿生原型的切削性能差异以及准线形式、切削角对仿生触土部件切削性能的影响等方面开展研究，而仅有的少量研究所采取的方法有待改进。为探寻切削性能优良的仿生原型，探索不同仿生触土部件之间切削性能的差异及准线形式、切削角对触土部件切削性能的影响，采用有限元法对比几种触土部件的切削性能，探索其在不同切削角、不同工作深度条件下的切削阻力规律，以期为触土部件的高效节能设计提供指导。

2 材料与方法

2.1 仿生原型的选取与触土部件的设计

选取具有代表性的棕熊、狗獾及蝼蛄三种动物共7个爪趾作为仿生原型，各爪趾内轮廓曲线方程，如表1所示。

表1 动物爪趾及其内轮廓曲线方程Tab.1 The Claw Toes of Animals and Their Inner Contour Curve Equation

由于仿生曲线的特殊性与复杂性，其切削角往往难以定义。为此，提出一种定义仿生曲线切削角的方法：对各仿生曲线进行适当缩放、旋转，使其凹向一致且首尾端点重合，用直线连接各仿生曲线首尾两个端点，将该直线与水平线的夹角定义为各仿生曲线的切削角。

7条仿生曲线及其切削角的示意图，如图1所示。图中各仿生曲线首尾两个端点A与O的连线与水平线的夹角为60°，则定义各仿生曲线的切削角为60°。显然，这种定义仿生曲线切削角的方式不受爪尖形态的影响，且具有普遍适应性。此外，该方法还便于直观地比较各仿生曲线的曲率半径大小。

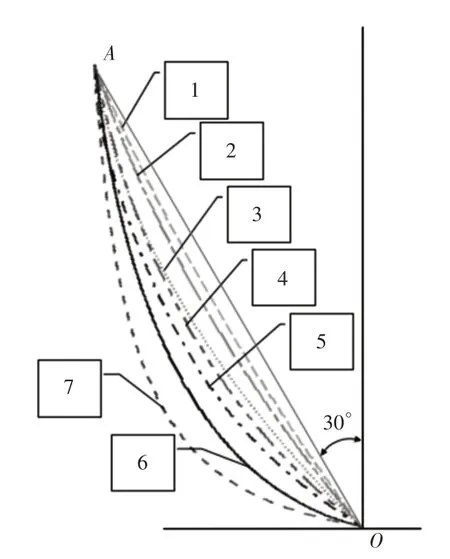
图1 7条仿生曲线及切削角Fig.1 Seven Bionic Curves and Cutting Angles

因推土铲应用广泛且结构简单，触土部件类型选择推土铲。推土铲的主要设计参数包括切削角δ、后角γ、铲尖尖角β、前翻角βk、斜装角ε、高度H及准线形式等，其结构及主要设计参数，如图2所示。

图2 推土铲结构及参数示意图Fig.2 Schematic Diagram of the Structure and Parameters of the Bulldozer

将图1中的7条仿生曲线进行适当旋转和缩放后分别作为推土铲的准线，保持其他结构形式不变，共设计7 种仿生推土铲。同理，以直线作为准线设计直线型推土铲。为消除后角γ、铲尖尖角β等参数对切削性能的影响，在仿真试验中以各推土铲准线代替对应的推土铲，且仅考虑对切削阻力影响较大的三个参数：准线形式、切削角δ和高度H。其中，准线形式分别为图1所示的7条仿生曲线及直线，切削角δ（与斜装角ε相等）的取值范围为（75～80）°，切削角为90°时的高度H为200mm。

2.2 有限元模型及仿真试验设计

一些研究者采用有限元法研究了土壤－工具相互作用过程，均取得了较为理想的结果［8］。因此，有限元法是一种可靠的模拟土壤－工具相互作用的方法。有限元模型的建立及相应的仿真试验包括两部分：第一部分为直线型推土铲有限元模型的建立及试验，主要将几种不同宽度的直线型推土铲的切削力与文献［8］的结果进行对比，以验证有限元建模的准确性；第二部分为仿生推土铲有限元模型的建立及试验，对比7种仿生推土铲和直线型推土铲在不同切削角、工作深度下的切削性能。

首先在ABAQUS环境下建立土壤－直线型推土铲的有限元模型。目前应用较多的土壤本构模型包括Mohr－Coulomb、Drucker－Prager 和Cam－Clay 等。因扩展的Drucker－Prager 模型已被一些研究人员用来模拟土壤－工具相互作用过程中土壤的力学行为，该模型非常适用于颗粒状土壤和岩石［8］。因此，土壤本构模型采用扩展的线性Drucker－Prager 模型，其屈服面函数为：

式中：F、t、p、β、d、q、r、K—屈服函数、偏应力、等效压应力、内摩擦角、粘聚力、米塞斯等效应力、偏应力第三不变量、流应力比。

虽然三维有限元模型能更精确地模拟切削过程，但求解效率较低。研究证明，二维有限元仿真也能取得较为理想的结果［9−10］。为减小包括推土铲后角γ在内的一些参数对仿真结果的影响，以各推土铲准线代替对应的推土铲。土壤－推土铲有限元模型，如图3所示。整个土壤模型共划分为7867个单元、6125个节点。推土铲与土壤的接触形式设置为面－面接触，接触算法选择罚函数法。接触面法向行为设置为硬接触，切向行为设置为罚函数。推土铲沿X轴负方向（切削方向）的速度设置为1m/s。为尽量保持与文献［8］一致的初始条件，有限元模型中大多数参数均与其相同。土壤特性参数［8］，如表2所示。推土铲的宽度分别取30mm、60mm和90mm，工作深度为100mm，切削角为90°。

表2 土壤特性参数Tab.2 Soil Characteristic Parameters

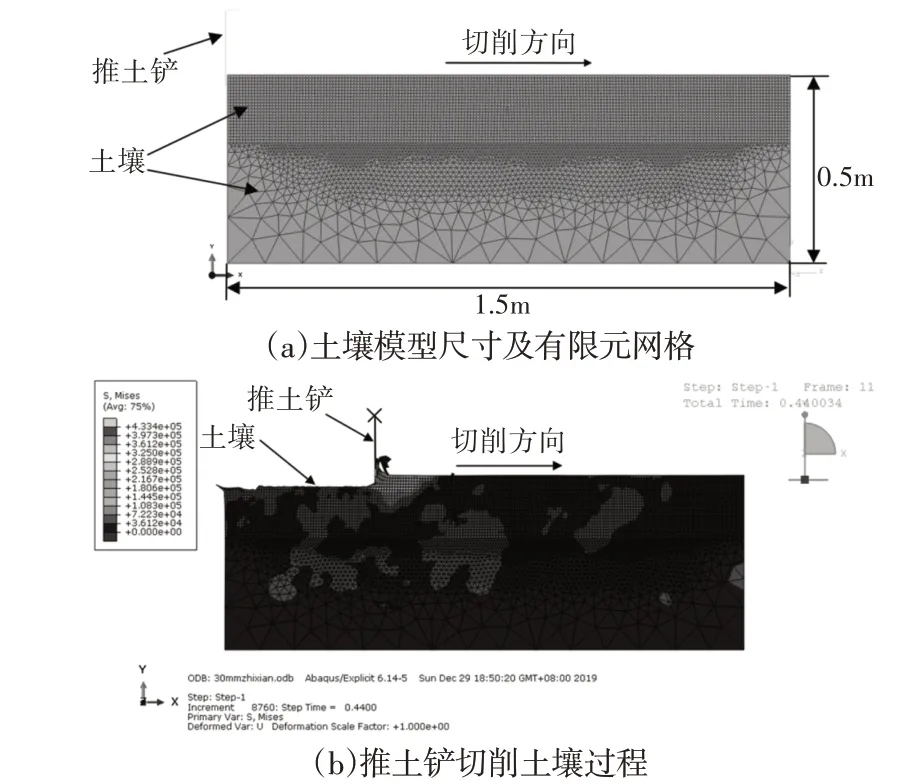
图3 土壤−推土铲二维有限元模型Fig.3 Two－Dimensional Finite Element Model of Soil−Bulldozer

同理建立土壤−仿生推土铲有限元模型，并进行仿真试验。仿真试验中的工作深度分别为30mm、60mm和90mm。虽然按照推土铲的设计要求，切削角δ的取值范围为（75～80）°，为较全面地研究各推土铲的切削阻力与切削角之间的变化规律，将切削角的范围扩大至（60～90）°。

3 结果与分析

3.1 直线型推土铲的切削阻力

对于几乎所有的触土部件而言，水平方向的阻力决定了动力系统的功率需求［8］。因此，仅考察切削过程中推土铲在水平方向的阻力。

直线型推土铲在有限元试验中输出的水平方向的阻力曲线，如图4所示。其中，推土铲宽度为30mm。从图4可以看出，推土铲在水平方向的阻力呈现持续波动的特征，这与实际情况较为符合［1］。从图中可知，该推土铲水平方向的切削阻力大约为2299.4N。限于篇幅，省略了其他宽度推土铲的切削阻力曲线。3种宽度的直线型推土铲在水平方向的切削阻力与文献［8］的对比结果，如图5所示。可以看出，仿真结果与文献［8］的结果符合良好，说明二维有限元建模的准确性。

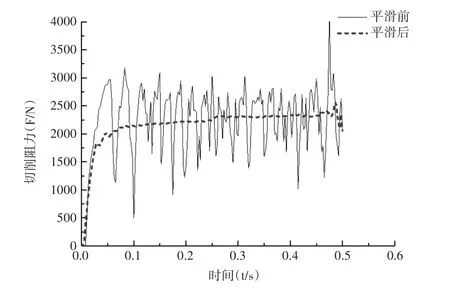
图4 直线型推土铲切削力曲线Fig.4 Cutting Force Curve of Straight Bulldozer

图5 直线型推土铲二维有限元仿真值与文献值对比Fig.5 Comparison of Two－Dimensional Finite Element Simulation Results of Straight Bulldozer with Those of Reference

3.2 工作深度与切削角对推土铲切削性能的影响

各推土铲在30mm工作深度下的切削阻力随切削角变化的规律，如图6所示。可以看出，所有推土铲的切削阻力均随切削角的减小逐渐递减。

图6 推土铲在30mm工作深度下的切削阻力Fig.6 Cutting Resistance of Bulldozers at 30mm Working Depth

以棕熊爪趾为仿生原型的仿生推土铲在所有切削角下都具有最小的切削阻力，直线型推土铲的切削阻力最大，其余仿生推土铲的切削阻力大小顺序视切削角范围的不同而不同。

各推土铲在60mm工作深度下的切削阻力随切削角变化的规律，如图7所示。可以看出，棕熊、狗獾2号、狗獾3号、蝼蛄3号和直线型推土铲的切削阻力均随切削角的减小逐渐递减。狗獾1号、蝼蛄1号和蝼蛄2号对应的仿生推土铲的切削阻力随切削角的减小呈现先减小后增大的趋势。以棕熊爪趾为仿生原型的仿生推土铲在所有切削角下都具有最大的切削阻力，其余推土铲的切削阻力大小顺序视切削角范围的不同而不同。当切削角相对较小（60～75）°时，大多数仿生推土铲的切削力均低于直线型推土铲。当切削角较大（80～90）°时，仅有少数仿生推土铲的切削阻力低于直线型推土铲。

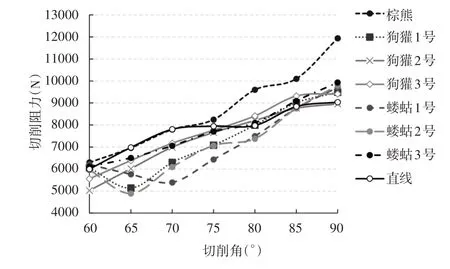
图7 推土铲在60mm工作深度下的切削阻力Fig.7 Cutting Resistance of Bulldozers at 60mm Working Depth

各种推土铲在90mm工作深度下的切削阻力随切削角变化的规律，如图8所示。

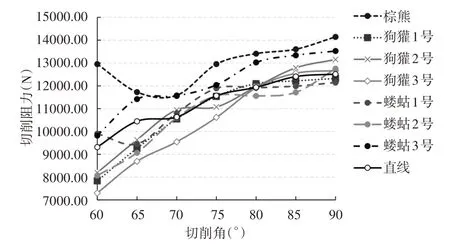
图8 推土铲在90mm工作深度下的切削阻力Fig.8 Cutting Resistance of Bulldozers at 90mm Working Depth

可以看出，除棕熊和蝼蛄1号外，其他推土铲的切削阻力均随切削角的减小逐渐递减。棕熊和蝼蛄1号对应的仿生推土铲的切削阻力随切削角的减小呈现先减小后增大的趋势。以棕熊爪趾对应的仿生推土铲在所有切削角下都具有最大的切削阻力，其余推土铲的切削阻力大小顺序视切削角范围的不同而不同。

在某些切削角下，部分仿生推土铲的切削阻力高于直线型推土铲。

对比图6～图8可看出，在不同的工作深度下，推土铲之间切削性能的差异各不相同。工作深度较小时，仿生推土铲的切削性能普遍优于直线型推土铲。随着切削深度的提高，直线型推土铲与仿生推土铲的切削性能差距逐渐减小，部分仿生推土铲的切削性能甚至比直线型推土铲更差。

3.3 推土铲准线曲率半径对切削性能的影响

按照斜装角为75°的设计要求，各推土铲分别在不同工作深度下的切削阻力与推土铲触土曲面准线曲率半径之间的关系，如图9所示。

图9 切削角为75°时推土铲切削阻力与准线曲率半径的关系Fig.9 Relationship Between Cutting Resistance and Curvature Radius of Bulldozer′s Directrix at Cutting Angle of 75°

从图中可知，当工作深度为30mm时，各推土铲切削阻力大小顺序刚好与各推土铲准线的曲率半径大小顺序一致（直线的曲率半径可认为是无穷大），即推土铲的切削阻力随准线曲率半径的增大而增大，切削阻力最小的推土铲是准线曲率半径最小的棕熊爪趾对应的仿生推土铲。这说明在30mm的工作深度下，准线曲率半径最小的棕熊爪趾是最为理想的原型。

当工作深度为60mm时，各推土铲的切削阻力随各准线曲率半径的增大先减小后增大，切削阻力最小的推土铲是准线曲率半径大小适中的蝼蛄1号爪趾对应的仿生推土铲，即蝼蛄1号爪趾是最为理想的原型。

当工作深度为90mm时，各仿生推土铲的切削阻力随准线曲率半径的增大而减小，切削阻力最小的仿生推土铲是准线曲率半径最大的狗獾3号爪趾对应的仿生推土铲，即狗獾3号爪趾是最为理想的原型。

从图9可知，推土铲准线曲率半径对切削阻力有重要影响，且在不同工作深度下，切削性能最佳的仿生原型也各不相同。

在所选取的7种仿生原型中，未发现任何一种能在所有切削角和工作深度下均具有最佳的切削性能。

这一结论与文献［11］的研究结果一致。因此，可能并不存在某种仿生原型能在各种工作条件下都具有最小的切削阻力，或者说可能并不存在“最佳”的仿生原型。

4 结论

采用有限元法对比了几种推土铲在不同切削角、不同工作深度条件下的切削性能，得到以下结论：

（1）定义仿生曲线切削角的方法具有普遍适应性，适用于对各种触土部件切削性能的对比。（2）大多数推土铲切削阻力随切削角的减小逐渐递减，少部分仿生推土铲切削阻力随切削角的减小先减小后增大。（3）工作深度不同时，各推土铲切削阻力随切削角的变化规律不同，切削性能最佳的仿生原型也不相同。随着工作深度的增大，直线型推土铲与仿生推土铲的切削性能差距逐渐减小，部分仿生推土铲的切削性能甚至比直线型推土铲更差。（4）推土铲准线曲率半径对切削阻力有重要影响，为获得较为理想的减阻效果，推土铲触土面准线曲率半径应随工作深度的增大而增大。