考虑裂纹闭合效应的疲劳裂纹扩展有限元分析
2023-02-09赖森华孙维光田洪雷于洋洋
赖森华,孙维光,田洪雷,于洋洋
(中车青岛四方机车车辆股份有限公司,山东青岛 266111)
1 引言
周期性载荷下结构疲劳失效机理和寿命预测一直是工程领域的研究热点和难点。当工程结构承受典型循环拉伸载荷时,将导致结构内部损伤的产生和疲劳裂纹扩展,此时裂纹尖端会形成两种不同的塑性区,其中,裂尖后端的反向塑性区将阻止低应力下裂纹面的闭合,使外载不再对裂纹尖端做功,即塑性诱发的裂纹闭合效应。文献[1]最先提出此概念,并给出有效应力强度因子对裂纹扩展速率进行预测。
裂纹面闭合后,仅当外载大于裂纹张开应力时,裂纹才能张开并发生裂纹扩展,因此裂纹扩展速率和寿命预测与裂纹张开应力密切相关。对于此方面的研究众多学者采用经验公式[2−3]、理论分析[4−5]和数值计算[6−7]的方法给出裂纹张开应力。文献[7]对铸造钛合金ZTC4进行了疲劳试验,结合断口分析研究了裂纹扩展行为,基于小裂纹理论对ZTC4的疲劳寿命进行了预测,但经验公式容易受限于试验条件以及一定的材料和应力比范围。理论分析虽然可获得精确的张开应力,但需要基于假设条件,局限于较为简单的裂纹几何构型上的应用。
对于复杂裂纹几何或外载条件,采用有限元法分析塑性诱发的裂纹闭合效应是一种有效手段[9]。其基本流程是通过建立一个带有初始裂纹的有限元模型,外加载荷作用于模型的远端。在恒幅加载条件下,载荷循环于最大外加载荷和最小外加载荷之间,在循环外载作用下,裂纹按照某种指定的方式向前扩展,导致在裂纹尖端后方形成一条塑性尾迹区。
现有的分析方法大都采用此流程,但影响裂纹闭合效应的因素很多,例如,文献[5]对网格精细程度进行了详细探讨,给出了建议网格尺寸;对裂纹闭合效应的处理也有节点约束和上下表面建立接触等方式模拟[10−11]。
对于裂纹扩展时机,文献[12]的研究表明扩展时机不同会导致张开应力明显不同,也有学者研究发现减小裂纹尖端网格尺寸对不同裂纹扩展时机影响很小。
针对紧凑拉伸试样,通过构建其平面有限元模型,同时考虑塑性诱发的裂纹闭合效应,研究了网格尺寸、裂纹扩展时机、裂纹张开点的确定等关键因素对裂纹张开应力的影响,并采用节点反力线性插值的方法,给出了稳定的裂纹张开载荷判断方式,为复杂疲劳裂纹扩展行为分析和寿命预测提供有益参考。
2 有限元模型及分析流程
对于紧凑拉伸试样(CT,Compact Tension),由于裂纹贯穿试件并且试样几何尺寸和边界条件具有对称性,因此,采用二分之一对称平面模型,并对裂纹尖端网格进行加密处理以满足塑性区要求,如图1所示。其中,模型中材料本构为理想弹塑性模型,具体参数为:E=200GPa,μ=0.3,σ0=230MPa。

图1 CT试样有限元模型Fig.1 Numerical Model of CT Specimen
考虑裂纹闭合效应的疲劳裂纹扩展分析是一个非线性的分析过程,需采用等幅循环外载,在每一次循环外载内为等值增量加载,裂纹扩展计算过程具体为:在每一次循环外载的最大载荷处释放一个节点约束,此时裂纹尖端扩展一个单元格长度Δa,形成新的裂纹面;裂纹发生扩展后,监测每一增量步裂纹扩展区域内裂纹尖端后的节点y向位移值,当节点位移为负时,则约束节点y向位移以阻止裂纹面的穿透,此时对应的外载为裂纹闭合载荷;在随后的加载过程中,监测闭合节点的反力,当节点反力由压力转变为拉力时,去除该节点y向约束,当裂纹扩展区域内距离裂纹尖端最近的节点y向约束解除时,此时外载对应为裂纹的张开载荷;当相邻循环外载下,裂纹张开载荷基本保持不变,此时确定为稳定扩展阶段的裂纹张开载荷,获得稳定的裂纹扩展张开载荷或裂纹扩展一定长度后,程序结束。疲劳裂纹扩展的计算分析流程图,如图2所示。

图2 疲劳裂纹扩展分析流程图Fig.2 The Flow Chart of Fatigue Crack Growth Analysis
3 结果与讨论
3.1 模型验证与网格划分尺寸
由于应用有限元法来分析疲劳裂纹扩展是在每一次外载循环过程中,裂纹扩展一个单元格长度Δa,因此有限元网格划分的精细化程度对计算结果有很大的影响。为了提高计算效率,不适宜把网格划的过分精细,但是,如果网格质量比较粗糙,将会造成不准确的计算结果。
参考文献[5]中给的建议,以裂纹尖端塑性区尺寸为参照,讨论网格尺寸对稳定的裂纹扩展张开载荷影响,塑性区尺寸rf计算公式为:

式中:平面应力α=1,平面应变α=3,Kmax—峰值载荷时最大应力强度因子。
在上述验证有限元计算流程的基础上,对CT试样进行分析,归一化的裂纹张开外载随载荷循环次数的变化,如图3所示。由图可见,随着循环次数的增加,导致裂纹张开的外载逐渐增大并趋于稳定,并且由计算结果与文献[5]所得结果相比较,彼此符合良好,说明了所采用计算方法的有效性。下面进一步对CT试样进行参数讨论。

图3 裂纹张开外载随循环次数变化Fig.3 Crack Opening Load Varies with Number of Cycles
给出CT试样的裂纹张开载荷随网格尺寸变化规律,图中不同曲线为裂尖网格尺寸与塑性区的比值,如图4 所示。由图可见,网格尺寸相对较大时,稳定的裂纹张开载荷较小,随着网格尺寸的减小,稳定的裂纹张开载荷逐渐增加并趋于稳定,此时继续增加网格密度不但增加整体网格数量,同时由于单元格长度较小,需要更多的循环次数才能达到裂纹张开载荷的稳定状态。

图4 裂纹张开载荷随网格尺寸变化Fig.4 Crack Opening Load Varies with Mesh Size
3.2 黏连节点释放
疲劳裂纹扩展是在外加循环外载下裂纹尖端按某种规律逐步向前扩展。有限元分析中最常见的处理方法是逐步释放裂尖节点约束,使裂纹每次以一个网格宽度的增量向前扩展。
当采用释放裂尖节点约束的方式来实现裂纹扩展时,究竟应该在循环外载的什么时机释放节点对还是一个有待明确的问题。
目前,针对节点释放时机,主要有如下三类处理方式:
(1)在最大外载时刻释放节点;
(2)在最小外载时刻释放节点;
(3)在第二次循环中最大外载时刻释放。
上述三种情况下裂纹张开载荷的变化情况下的计算结果,如图5所示。由图可知,裂尖节点在最小外载时释放,张开载荷略小于节点在最大外载释放的值;节点在第二次循环中释放,此时对应的裂纹张开载荷变化不大,但需要指出的是节点在第二次循环中释放增加了一倍的计算量。
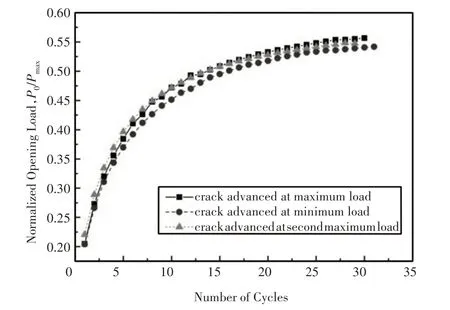
图5 不同时刻节点释放对比Fig.5 Comparison Diagram of Node Release at Different Time Points
3.3 裂纹张开/闭合点的确定
对于裂纹张开/闭合载荷的确定是通过对裂纹扩展区域内的节点反力/位移进行判断,目前大多数学者在有限元分析中是在每次载荷循环对裂尖后的第一个节点进行反力/位移的监测,为了对比监测不同节点时对裂纹张开载荷的影响,同时对裂纹尖端后第二个节点进行了监测,将所确定的裂纹张开载荷与监测裂尖后第一个节点确定的裂纹张开载荷进行对比,如图6所示。
由图6可见,当监测裂纹尖端后第二个节点时,所得到的裂纹张开载荷要明显小于监测第一个节点时得到的值,说明当裂尖后第二个节点张开时,已扩展裂纹仍处于闭合状态,因此监测第二个节点不能真实描述裂纹张开/闭合点的位置。
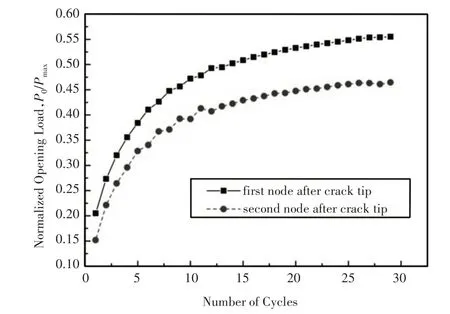
图6 监测不同节点对裂纹张开载荷的影响Fig.6 The Influence of Different Monitored Node on Crack Opening Load
3.4 稳定的裂纹张开载荷
在恒幅加载情况下,裂纹张开载荷随着裂纹扩展的进行而逐渐趋于一稳定的数值,此时裂纹需完全穿透初始的裂纹尖端单调塑性区才能形成一个稳定的塑性尾迹区,得到稳定的裂纹张开载荷。
在此需要进一步探讨的是对于稳定的裂纹张开载荷的判断,由于每一次循环外载是通过等值增量步进行加载,在研究中发现,所确定的裂纹张开载荷和加载增量步数相关。
对于前后两次循环外载,通常将裂纹张开载荷为相同增量步数时确定为稳定的裂纹张开载荷,但在后续的循环外载作用下,裂纹张开载荷又有所增加,此时难以对稳定的裂纹张开载荷进行精确判断。
为了获得更加精确真实的稳定裂纹张开载荷,可采用2种方案以改善计算结果,具体为:
(1)增加增量步数,可以对每次循环外载下裂纹张开载荷进行更加精确的判断,但此方法将导致计算量大幅增加且增量步数仍无统一标准;
(2)采用线性插值的方法,即对裂尖后节点的监测时,当节点反力由压力转变为拉力,认为节点反力呈现线性变化,通过线性插值来确定节点反力为0时所对应的裂纹张开载荷。
相同增量步数时,线性插值与普通增量步对裂纹张开载荷的影响,如图7所示。
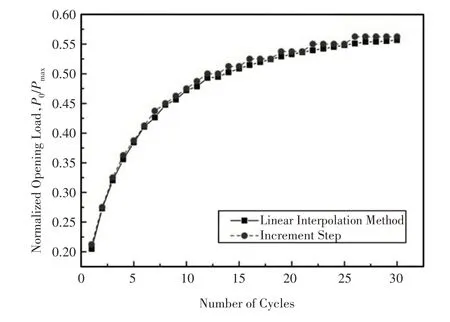
图7 裂纹张开载荷计算Fig.7 Crack Opening Load Calculation
由图可知随着外载循环次数的增加,当采用普通增量步进行计算时,裂纹张开载荷呈现一定的阶跃状态,容易出现几个相邻循环步均为相同裂纹张开载荷,无法精确判断稳定的裂纹张开载荷。
当采用线性插值后,裂纹张开载荷曲线更加平滑,此时稳定的裂纹张开载荷判断将更加精确。
不同增量步数对裂纹张开载荷的影响,每一次循环加载增量数分别为80、120和160,即当每次循环加载增量步数为160时,每增量步加载/卸载为0.0125Pmax,如图8所示。

图8 增量步数对裂纹张开载荷的影响Fig.8 Effect of Increment Step Number on Crack Opening Load
由图可见,当采用线性插值方法时,不同加载子步数对裂纹张开载荷影响不大。
为了得到稳定的裂纹张开载荷,于分析过程中,在保证裂纹完全穿透初始的裂纹尖端的单调塑性区后,当前后两次裂纹张开载荷计算结果之间的相对差别不超过1%时为稳定的裂纹张开载荷,即若网格尺寸Δa/rf=0.05,外载循环次数需超过20次后再进行稳定的裂纹张开载荷判断。
4 结论
针对紧凑拉伸试样,采用有限元法对其考虑裂纹闭合效应的疲劳裂纹扩展进行分析,研究了网格尺寸、节点释放时刻、监测不同的节点等对裂纹张开载荷的影响,得到以下结论:
(1)裂纹张开载荷随着网格尺寸减小逐渐增加,并趋于稳定,但过小的网格尺寸会显著降低计算效率;
(2)在研究闭合效应时,无论在最大还是最小外载处释放节点都不会导致结果产生明显不同;裂纹扩展区域内监测距裂尖最近的节点更加符合实际裂纹张开/闭合状态;
(3)对监测节点的反力采用线性插值可以使裂纹张开载荷曲线更加平滑,能够更精确地判断稳定的裂纹张开载荷。
