永磁同步驱动电机温度场研究进展综述

靳永春 ，陈俐 ，邹宇晟 ，段诚武 ，姚健

（1.上海交通大学船舶海洋与建筑工程学院动力装置与自动化研究所，上海 200240；2.上海交通大学海洋工程国家重点实验室，上海 200240；3.通用汽车研发中心，上海 201206）

面对能源以及环保提出的双重挑战，节能减排成为汽车行业研究的重要课题。当前，我国汽车行业正积极向电动化转型，预计到2035年，节能汽车与新能源汽车销售量占比将达到50%[1]。永磁同步电机具有效率高、转速范围宽、功率密度大、控制性能好等优点，在电动汽车驱动系统中得到了广泛应用[2-3]。

然而，随着电机尺寸的减小以及功率密度的不断提高，电机损耗而引起的温升问题成为制约车用永磁同步电机发展的瓶颈。温升对永磁同步电机的影响主要有两个方面：一是定子绕组线圈过热，大的热应力加速绕组绝缘层的老化、脱落[4-6]；二是引起转子永磁体高温退磁甚至不可逆退磁[7-9]。传统的电机设计方法多从电磁设计的角度出发，运用冗余设计应对电机温升问题[10-11]。然而，电机电磁场与温度场相互耦合，电机温度场分析具有复杂性与挑战性。

因此，对永磁同步驱动电机温度场的研究具有重要意义。本文将从损耗来源与计算方法、热量传递路径与传热形式、温度场分布规律、温度场建模与测试方法四个方面对永磁同步驱动电机温度场研究进行梳理，并分别总结了目前研究与应用中存在的问题，最后指出永磁同步驱动电机温度场研究中亟待解决的关键问题。

1 损耗来源与计算方法

永磁同步驱动电机损耗包括绕组铜耗、定子铁耗、转子及永磁体涡流损耗、机械损耗。

1.1 绕组铜耗

绕组铜耗是指定子绕组通电时产生的电阻损耗，根据焦耳定律，总的绕组铜耗可由下式计算：

式中：m为电机相数；I为定子相电流的有效值；Rdc为电机每相的直流电阻值。

温度升高引起绕组电阻值增加，可以利用修正公式进行计算[12]：

式中：R0为绕组初始电阻值；α为铜的温度系数，α=3.93×10-3/K；Ts为绕组温度；T0为绕组初始温度。

研究表明，绕组铜耗不仅受温度变化的影响，还受集肤效应与临近效应的影响[13]。通常，集肤效应的影响可以用集肤深度δ表示，δ可由下式计算[14]：

式中：f为电流频率；σ为导线的电导率；μ为导线的磁导率。

若导体集肤深度δ小于其半径r，导体有效面积减小，集肤效应引起的附加损耗PCu_skin可由下式计算[15]：

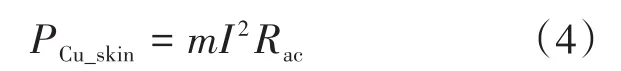
其中

式中：kR为集肤效应系数，与导体半径以及电流频率有关；Rac为集肤效应引起的等效交流电阻值。

同样，电机高速运行时临近效应引起的附加损耗PCu_pr可由下式计算[16]：

式中：Bw为绕组磁密；d为导线直径；l为导线长度；ρ为导线电阻率。

随着电机转速的升高，集肤效应与临近效应引起的附加损耗不断增加。附加损耗与电流频率、绕组形状、尺寸、排布方式等多种因素有关，解析计算方法复杂且计算参数难以获得，可以采用有限元方法对绕组建模计算铜耗[17-18]。

1.2 定子铁耗

定子铁耗包括磁滞损耗、涡流损耗和附加损耗，由定子铁心中随时间和空间变化的磁场产生。

1.2.1 Bertotti分离铁耗计算模型

目前最常用的定子铁耗计算模型是Bertotti分离铁耗计算模型，该模型将电机定子铁耗分为磁滞损耗Ph、涡流损耗Pc、附加损耗Pe进行计算[19]：

式中：kh，kc，ke分别为磁滞损耗系数、涡流损耗系数和附加损耗系数；α为Steinmetz系数，可以通过对铁磁材料损耗测试数据进行拟合得到；Bm为磁密幅值。

高频交变磁场加剧定子铁心的集肤效应，导致铁心叠片上涡流分布不均，涡流损耗不再正比于频率磁密乘积的平方，此时可采用变涡流损耗系数对Bertotti分离铁耗模型中涡流损耗项进行修正[20]：

其中

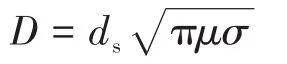
式中：ds为硅钢片厚度；μ，σ分别为硅钢片的磁导率和电导率。

考虑时间谐波与空间谐波的影响，为提高计算精度，可以对磁密波形进行傅里叶分解得到基波与各次谐波，分别带入式（8）进行计算，累加得到总的定子铁耗[21-23]。

1.2.2 椭圆旋转铁耗计算模型

除Bertotti分离铁耗计算模型外，椭圆旋转铁耗计算模型是另外一种广泛使用的定子铁耗计算模型。定子铁心中同时存在交变磁化与旋转磁化两种磁化方式，不同位置的磁化方式不同，可统称为椭圆旋转磁化，椭圆旋转铁耗计算模型如下[24-25]：

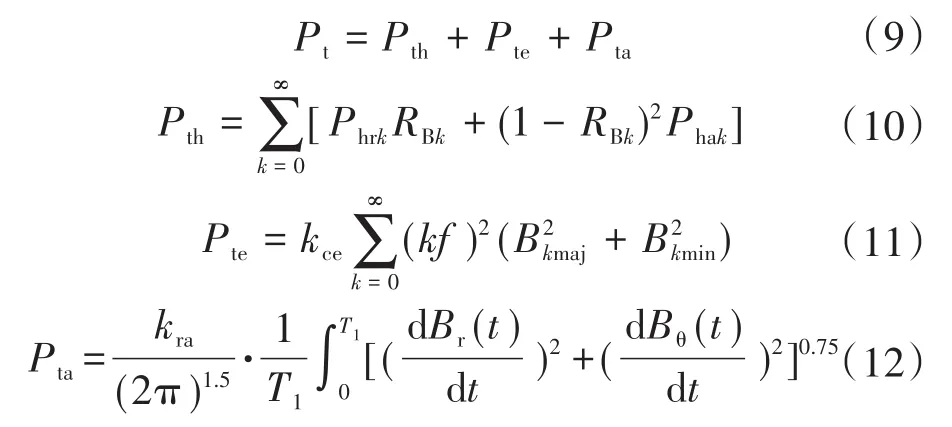
式中：Pth为总磁滞损耗；Pte为总涡流损耗；Pta为总附加损耗；Bkmaj为k次磁密谐波椭圆磁场的长轴；Bkmin为k次磁密谐波椭圆磁场的短轴；RBk为k次磁密谐波椭圆形轨迹中的短轴与长轴之比；Phrk为k次磁密谐波按旋转磁化计算的磁滞损耗；Phak为k次磁密谐波按交变磁化计算的磁滞损耗；kce为交变磁化涡流损耗系数；kra为圆形旋转磁化附加损耗系数；t为时间；T1为基波磁场周期；Br（t），Bθ（t）分别为定子椭圆磁场B的径向与切向分量。

研究发现，定子铁心的制造工艺（冲片、热处理、叠压）、铁心的温度均会对定子铁耗造成影响[26]。文献[27]考虑谐波、旋转磁化效应、温度变化、应力的影响，提出一种考虑多物理场影响的铁耗计算模型，但是该模型存在大量的变化系数，计算复杂。

上述基于解析法的定子铁耗计算模型均需要确定模型中的各项系数，这些系数一般通过对损耗测试数据进行拟合得到，实验工作量较大，可以利用有限元方法直接对电机进行建模计算定子铁耗[28-29]。

1.3 转子及永磁体涡流损耗

定子铁心开槽引起的气隙磁密不均匀分布、绕组非正弦分布等会产生磁势空间谐波，PWM供电会产生电流时间谐波，这两种谐波是引起转子及永磁体涡流损耗的主要原因[30-31]。

永磁同步电机转子铁心及永磁体涡流损耗可用下式计算[32]：

式中：σre为材料的电导率；Jec为涡流电流密度；Vre为体积。

涡流电流密度可以通过解析法[33-34]或有限元法[29，35，36]计算得到。

1.4 机械损耗

永磁同步电机中的机械损耗主要有轴承摩擦损耗和空气摩擦损耗。

轴承的摩擦损耗与摩擦面之间的压力、摩擦系数以及相对运动速度有关，其中摩擦系数受润滑条件、温度、加工质量等因素影响[37]。

对于滑动轴承常用下式计算[38]：

式中：μf为摩擦系数；db为轴颈直径；lb为轴颈长度；ωn为轴的圆周速度；Gb为轴承的载荷；Sn为轴颈对轴直径平面的投影面积。

对于滚动轴承，常采用下式计算[38]：

式中：dnr为滚珠中心处直径；ωnr为滚珠中心的圆周速度。

电机工作时转子的空气摩擦损耗主要由转子表面空气摩擦损耗和转子端部空气摩擦损耗组成。气隙空气摩擦损耗与电机转速的三次方成比例，可用下式计算[39]：

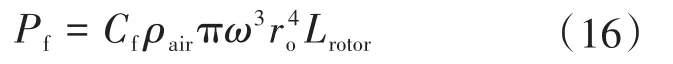
式中：Cf为空气摩擦系数，其值与空气的流动状态和流动速度有关；ρair为空气密度；ω为转子角速度；ro为转子外径；Lrotor为转子长度。

转子表面的空气摩擦损耗与电机转速、转子表面形状、粗糙度等多种因素有关，还受电机冷却结构的影响，难以利用理论分析与解析方法进行准确计算。利用计算流体力学（computational fluid dynamics，CFD）计算电机空气摩擦损耗是一种常用的方法，该方法能够对电机及其周围流体进行建模，得到比传统解析方法更加准确的结果[40-42]。

1.5 存在的问题

准确计算电机损耗是电机热分析的基础，通过前面的分析，目前电机损耗计算方法存在以下问题：

1）定子铁耗的计算模型。目前解析计算模型含有较多损耗系数，这些系数受电机磁化方式、谐波、温度、机械应力等多种因素的影响，难以准确地确定这些损耗系数。

2）永磁体涡流损耗的计算模型。随着电机的高速化，永磁体中的涡流损耗也越来越大，而目前研究多忽略永磁体的特性，而将其与转子铁心视为一体，这样无法反映永磁体涡流损耗引起的局部过热问题。

2 热量传递路径与传热形式

永磁同步驱动电机的传热形式包括热传导、对流换热、辐射换热。大多数工况下，最高温度不超过300℃，可忽略辐射换热。

观察电机内部的传热路径，定子绕组和铁心产生的热量主要以热传导的方式传递到机壳，然后在机壳表面以对流换热方式传递到周围环境，或在机壳内部冷却水道以对流换热方式将热量传递到冷却系统中[43]。转子铁心和转轴产生的热量则主要通过热传导传递到电机端部表面，然后在端部表面以对流换热形式散发到周围环境[44]。

2.1 热传导路径中的关键因素

2.1.1 不同部件间的接触热阻

电机中存在多种接触热阻，如定子铁心与机壳之间、永磁体与转子铁心之间、绕组与定子槽绝缘之间的接触热阻。接触热阻受接触面之间的不规则性、粗糙度、材料硬度、压紧力和气压等因素的影响。对定子铁心与机壳之间的接触热阻，可采用经验公式进行计算[45]：

式中：Lair为部件之间的界面间隙；Kair为空气导热系数；rsy为定子轭半径；Ls为定子铁心长度。

界面间隙Lair可使用经验公式进行估算：

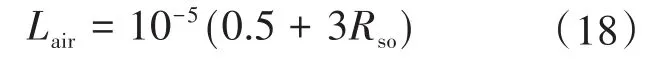
式中：Rso为定子铁心外径。

针对界面间隙的计算，文献[46]给出了几种电机的部件间平均界面间隙取值，文献[47]给出了不同功率的全封闭扇冷式感应电机的平均界面间隙。文献[48]给出了接触面的等效界面间隙，如表1所示。

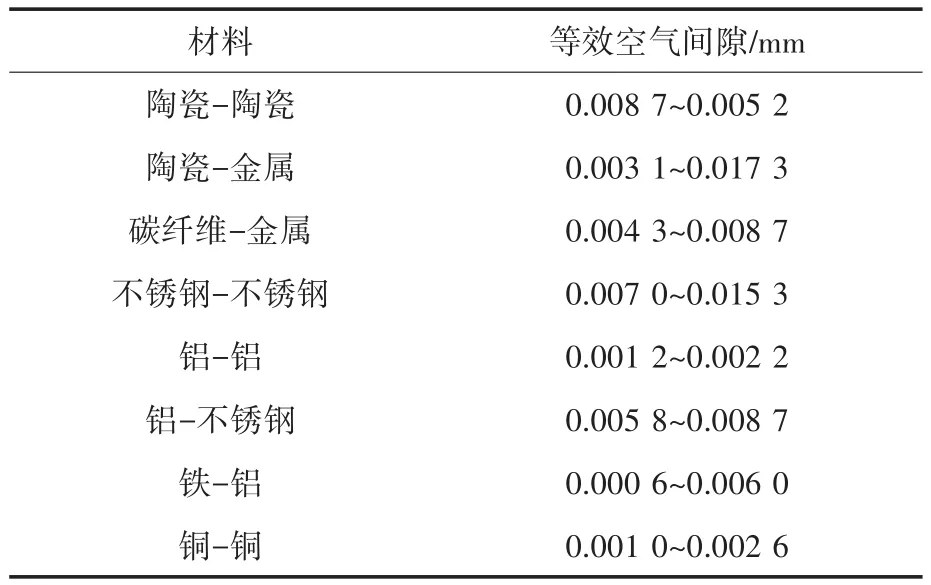
表1 不同的材料之间接触面的等效界面间隙Tab.1 Equivalent interface gap between different materials

2.1.2 定子槽的等效导热系数

定子槽内包含绕组和绝缘层，绝缘层包括灌封胶层、铜线浸渍漆层和空气，这些材料都有不同的热阻值，给定子槽的热分析带来困难。此外，绕组多采用多股细线并绕而成，每根导线在槽中的位置具有不确定性，难以对每根导体进行精细化建模[47]。目前多数研究采用等效导热系数的方法来克服这个问题，将槽内所有铜线集中等效为一个导热体，所有绝缘层等效为一个导热体，如图1所示，其等效导热系数可用下式计算[49]：

式中：δi为各种绝缘材料的等效厚度；λi为各种绝缘材料的导热系数；n为材料层数。

图1 采用定子槽集中等效的电机三维温度场模型Fig.1 3-D temperature field model with concentrated equivalent stator slot

上述方法简单易行，但由于铜具有良好的导热性，该方法会忽略绕组中存在的温度梯度。另一类研究建立了定子槽分层等效模型[49]，如图2所示。基于定子槽分层等效假设，文献[50]提出了一种定子槽椭圆分层计算模型，如图3所示，每一铜线层的厚度等于绕组直径，绝缘层分布在铜线层之间，试验验证了该模型的准确性。相较于前面的方法，绕组分层模型能够反映定子槽中的温度梯度，但是划分的层数以及温度相同的导体难以确定。

图2 采用定子槽分层等效的电机三维温度场模型Fig.2 3-Dtemperaturefieldmodelwithlayeredequivalentstatorslot

图3 定子槽椭圆分层模型Fig.3 Layered elliptical model of stator slot

2.1.3 定子和转子铁心导热系数的各向异性

定、转子铁心通常由硅钢片叠压而成。相邻叠片之间存在接触热阻，使铁心的轴向热阻高于径向热阻。为简化计算，多做各向同性假设，忽略了铁心导热系数的各向异性。文献[51]指出，径向方向的导热热阻可以按照叠片材料的热阻计算；轴向的导热热阻受材料、接触面粗糙度、压紧力等因素的影响，其等效导热系数可按下式计算：

式中：td为叠片厚度和界面间隙之和；NL，NC分别为叠片和接触面的数量；RL，RC分别为叠片热阻和接触热阻。

2.2 对流换热路径中的关键因素

2.2.1 电机端部空间的对流换热

电机端部区域流体的流动状态受多种因素的影响，如绕组末端形状、转子端面的粗糙度、风扇的转动等，难以确定该区域的对流换热系数[46]。目前，常用的计算电机端部对流换热系的数经验公式如下[52]：

式中：k1，k2，k3为曲线拟合系数；v为空气流动速度。

k1项表示自然对流的影响，k1k2vk3项表示强制对流换热的影响。

2.2.2 机壳与外界的对流换热

机壳表面的对流换热系数与其结构形状紧密相关，目前已有文献中提出了多种基于无量纲数的经验公式[53]。例如，对于强制风冷式电机，机壳的对流换热系数可以近似按照下式计算[54]：

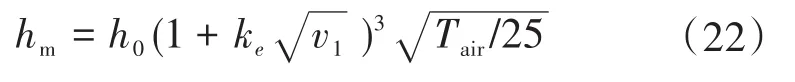
式中：h0为发热表面在静止空气中的换热系数，近似值为14 W/m2；ke为经验系数；v1为机壳表面空气流速；Tair为空气温度。

2.2.3 定转子间气隙的等效计算

电机气隙中的对流换热十分复杂。为了简化计算，引入等效导热系数对气隙对流换热问题做简化处理[55]。

电机气隙中空气流动状态受电机转速的影响，空气的雷诺数Re可由下式计算[56]：

式中：ωo为转子外径处的线速度；δ为气隙长度；υ为空气动力粘度。

若气隙中的雷诺数小于临界雷诺数，气体的流动状态为层流，反之则为紊流。气隙中气体的等效导热系数可按下式计算[56]：

其中η=ro/rI

式中：ro为转子外径；rI为定子内径。

2.3 存在的问题

在传热路径以及传热形式方面，目前存在的问题有：

1）定、转子铁心导热系数的各向异性未得到充分考虑。铁心轴向的导热热阻明显高于径向导热热阻，这一现象在目前的研究中较少考虑，大部分研究做各向同性假设。

2）气隙间对流换热忽略了空气的流动。由于流体流动状态的复杂性，流固界面的换热系数受多种因素的影响，不同等效模型的经验公式往往仅考虑其中部分因素，因此会带来计算误差。

3 温度场分布规律

对永磁同步驱动电机，温度过高将引起永磁体的不可逆退磁和定子绕组绝缘的老化脱落，这是电机中的两个薄弱环节。因此研究永磁同步电机温度场的分布，关键在于转子永磁体和定子绕组的温度场分布及其温度变化规律。

在目前的研究中，大部分结果都表明，电机工作过程中温升从高到低依次为：定子绕组、定子铁心、转子铁心，永磁体与转子铁心温度相当[44，57-61]，这是由于在大部分电机中，绕组铜耗远大于转子及永磁体上的涡流损耗，因此定子绕组部分的温度最高。但也有文献的结果与这个规律不同，文献[30，62-63]中的实验结果和仿真结果均显示永磁体的温度高于定子铁心的温度，甚至高于绕组线圈的温度。造成这一现象的原因有三：第一是由于PWM波供电的情况下，会在电机空间中产生高次谐波，随着电流频率的增加，永磁体涡流损耗迅速增加，造成永磁体温度急剧上升[30，63]；第二是永磁同步电机在定子铁心的外径处往往采用风冷或水冷，因此散热条件较转子更好，所以引起定子铁心温度低于转子的温度[62]；第三是定子铁心材料采用非晶合金，可以降低定子铁心损耗[63]。

此外，也有文献对永磁同步电机温度场的影响因素进行研究。文献[30]研究了PWM时间谐波对电机温度场的影响，发现当PWM占空比越小，引起永磁体及转子涡流损耗越大，电机温升越明显。文献[44]研究了电机损耗对其各部位温度的影响，结果表明对定子及绕组温度，铜耗影响最大，定子铁耗次之，永磁体涡流损耗最小；对转子及永磁体温度，永磁体涡流损耗影响最大，铜耗次之，定子铁耗最小。文献[64]使用热网络模型分析了转速对电机定子和转子温度的影响，发现当转速降低时，定子和转子上的发热功率均明显减小，且在转速较高时，定子温度较高，而在转速较低时，则为转子的温度较高。文献[65]建立电机的有限元模型，对正弦波供电以及PWM逆变器供电下永磁体温度分布进行了研究，结果表明PWM逆变器供电将会引入大量时间谐波，导致永磁体温度明显增加。文献[66]针对集中绕组电机设计了一种新的水冷盘结构，仿真与试验结果表明，相比于传统的冷却水套结构，所提出的新型水冷盘结构可以使电机定子温度再下降20℃。文献[62]分析了电机外接水套中流体流速对于电机温度的影响，结果表明在将流量从2 L/min增加到9 L/min时，各部分温度显著降低。然而，当冷却剂到达全湍流时，冷却系统的散热能力的增长受限，冷却效果改善不再明显。

综上所述，电机的供电方式、运行工况、冷却条件等因素均会对其温度场产生影响，在电机热分析的过程中，需要综合考虑各方面的影响。

4 温度场建模与测试方法

4.1 集总参数热网络法

集总参数热网络法（lumped parameter thermal network，LPTN）具有计算量小、计算速度快的优点，该方法基于集中参数假设，忽略物体内部的导热热阻，将物体在空间连续分布的质量和热容量汇总到一点，用该点温度代表物体平均温度。将热流传递路径及原件与电路模型进行类比，如表2所示，从而建立描述各节点温度的热网络模型[67-68]。

表2 等效热电路与电路的类比Tab.2 Analogy between equivalent thermal circuit and electric circuit

LPTN模型的温度计算精度取决于网络节点划分的数量，根据节点的数量，可以将LPTN模型分为两类[69]：灰箱热网络模型（grey-box LPTN）、白箱热网络模型（white-box LPTN）。

灰箱热网络模型一般包含2～15个节点，每个节点代表电机的一个主要部件，例如转子、定子绕组、定子铁心等。由于每个部件的结构比较复杂，相邻两个部件之间的热阻计算困难，因此灰箱热网络模型中导热热阻值可由实验数据辨识得到[70-72]。白箱热网络模型一般包含15个以上的节点，对于同一部件，可划分多个节点，反映该部件的温度分布。相邻节点之间的导热热阻，可以根据电机的几何尺寸和物性参数，由导热热阻的计算公式得到[73-76]。

4.2 数值方法

数值方法可分为两类，即：有限元分析（finite element analysis，FEA）和CFD。

FEA是电机热分析中一种常用的方法，该方法用二维或三维有限单元对电机几何模型进行离散化，在每个节点建立热平衡方程，在离散模型边界设定不同的边界条件，对整个离散方程组进行求解获得各点的温度值，进而得到电机的温度场分布[77]。其中，三维FEA可以真实描述电机的几何结构，得到电机详细的温度场分布。然而，三维FEA所需计算量较大，此时可根据电机对称性取部分结构进行计算，从而降低计算量[78-79]。但是，FEA只能分析固体导热，不能考虑流体流动的影响，对于对流换热等边界可通过经验公式或CFD计算确定[10]。

CFD可以用来模拟复杂区域的流动，通过设置流固耦合边界条件，考虑流体流动对固体散热的影响，获得准确的电机温度场以及流场分布[80-82]。此外，CFD还可用于分析外接冷却流体对电机温度场的影响和计算流固界面的换热系数[65，83]。但是，CFD建模工作量大，需要对模型进行合理简化，且无法考虑电机装配间隙对导热的影响，计算量大，计算时间较FEA长。

4.3 温度场测试方法

为了验证电机热模型的准确性，需要测量电机实际的温度对热模型进行验证。对永磁同步驱动电机，根据运动状态可将其部件划分为旋转件和非旋转件，旋转件主要指转子、转子轴，非旋转件主要指定子及壳体。

非旋转件测温相对比较容易，可以直接在该部件安装温度传感器测量其温度，常用的温度传感器有热电阻、热电偶、布拉格光栅传感器。文献[66]在电机槽内绕组、端部绕组、定子齿部、定子轭部分别布置PT100热电阻测量电机不同部位的温度，对仿真结果进行验证。文献[84]在电机端部绕组埋置PT1000热电阻测量绕组温度，验证了电机在动态工况下的温升计算结果。文献[85]在电机端部绕组的内层与外层分别埋置环形布拉格光栅传感器阵列，每个传感器阵列有6个温度探头，通过测量端部绕组12个测点的温度来监测其热状态。

针对电机旋转部件的温度测量方法，根据温度传感器与被测件是否接触可分为非接触式测温和接触式测温。非接触式测温包括霍耳元件测温法和红外测温法。霍耳元件测温法通过测量永磁体剩磁密度来确定永磁体温度，由于定子磁场对永磁体的磁场存在影响，所以使用该方法需要设法补偿定子磁场引起的干扰[86]。红外测温法需要安装红外探头和光电感应器，使用较多的温度传感器会引起较大误差[87-89]。此外，霍耳传感器法测得的是永磁体的平均温度，红外测温法只能测量部件的表面温度，而永磁体内部温度分布不一定均匀，因此当需要分析部件内部的最高温度时，这两种非接触式测温的方法均不能满足要求。

接触式测温指在测温点处安装温度传感器进行温度测量，并通过一定方式将温度信号从旋转件中传输出来。接触式测温中常见的信号传输方式有红外传输，无线电传输，滑环传输3种[90-92]。红外和无线电传输都是在旋转件中安装信号发射装置，将热电偶的测量信号以无线方式传输到信号接收端。区别在于无线电传输的频率为特高频（433 MHz），容易受到磁场的干扰造成数据丢失，而相比较而言，红外传输具有很高的可靠性和抗噪声性[90]。滑环传输，信号由滑环的旋转端传递到固定端，工作过程中两端直接接触，过高的转速容易引起滑环的接触面温度升高过快，从而损坏滑环本身或引起信号失真[50]。随着滑环技术的成熟，目前市场上已有可在转速20 000 r/min条件下连续稳定工作80小时以上的电滑环[93]。

4.4 存在的问题

在温度场建模与测试方法方面，目前存在如下问题：

1）对集总参数热网络模型，网络热参数识别是关键。采用集中参数假设的参数取值，合理性值得推敲。基于试验数据进行参数辨识是可行的思路，但是试验工况的选择对参数辨识的结果具有重要影响，因此参数辨识的工况适应性应该重视。

2）有限元模型中计算精度与建模精细化程度相关，对定子槽、端部绕组、气隙等均做等效处理，虽然可以降低计算难度，但是会引入相应的误差，尤其在高速永磁同步电机中，面临如何平衡计算负荷与计算精度的问题。此外，有限元模型准确程度与边界条件的设定密切相关，选取准确的边界条件是一个需要考虑的重要问题。

3）电机高速化给旋转部件的温度测量带来了新的挑战，如何提高滑环的转速适用范围与寿命需要进一步研究。

4）仿真计算结果与实际测量值之间的差异需要客观对待，为提高仿真结果的说服力，需要合理设计试验方案，对仿真结果进行充分验证。

5 结论与展望

车用永磁同步驱动电机的温度场研究是电机设计的重要参考，准确计算电机的温度场分布及其演变规律有助于提高驱动系统的可靠性。通过对损耗来源与计算方法、热量传递路径与传热形式、温度场分布规律、温度场建模与测试方法四个方面的梳理，本文将从以下五个方面总结当前永磁同步驱动电机温度场研究中亟待解决的关键问题并做研究展望：

1）定子铁耗和永磁体涡流损耗的精细化建模。经验公式对不同的电机适合程度不同。基于仿真或试验数据对现有的损耗计算模型进行改进，或利用智能算法建立基于数据驱动的损耗计算模型，实现复杂工况下损耗准确高效地计算是未来研究的重点与难点。

2）铁心导热各向异性的建模与影响分析。其轴向导热热阻远高于径向导热热阻，相较于各向同性假设，各向异性引起温度场的不同分布和演变过程。建立考虑叠压系数、接触面粗糙度、材料热阻等因素的铁心轴向导热系数计算模型，在电机热分析中考虑铁心导热系数各向异性的影响，是未来研究的重点。

3）流固接触界面上的对流换热系数的精细化建模。目前对电机中的对流换热过程有多种不同的等效模型，但等效处理过程容易忽略一些因素的影响，带来计算误差。CFD方法可以准确计算流固边界上的对流换热系数，利用CFD方法对经验公式进行修正，或将CFD方法与FEA、LPTN结合进行耦合分析，可以提高电机温度场的计算精度。

4）热网络模型中热参数的辨识问题。全面考虑电机运行工况，基于试验数据，采用智能优化算法对模型热参数的辨识过程进行优化，提高热网络模型的工况适应性与预测精度。

5）电机高速化之后的旋转件温度测量技术。相比于滑环信号传输，无线信号传输方法不存在高转速下寿命迅速缩短的问题，未来研究可以集中于提高无线信号传输的抗干扰能力和可靠性。