无线充电最优匹配下最大输出功率自适应选择

刘鸿，徐诗豪，杨凌升

（南京信息工程大学电子与信息工程学院，江苏 南京 210044）

近年来，电动汽车（electric vehicle，EV）市场增长迅速，对如何提供方便、安全的充电服务的需求也越来越高。电动汽车无线充电技术因其有节省材料、无触电危险、恶劣天气环境可使用性强等优点，越来越受到汽车制造商的关注。目前汽车工程师学会（society of automotive engineers，SAE）制定的标准J2954中有五个可供无线充电使用的频带[1]，分别为：21.05～38.10 kHz，42.00～56.19 kHz，69.93～71.43 kHz，81.38～90.00 kHz及140.91～148.50 kHz。围绕这些频带，产学研界展开了大量的研究，而如何能实现高能量传输效率[2-5]和高输出功率[6-8]是这些研究所需解决的主要问题。例如参考文献[9]，讨论了耦合系数对于整个无线充电系统的影响，并提出了最优耦合系数区间的概念，通过选择最优耦合区间，保证了整个系统在线圈出现水平偏移的情况下仍可以保持高传输效率。而文献[10-11]主要研究了汽车线圈一侧的补偿电路中负载电阻对于整个电路效率的影响。

上述研究及其他相关研究[12-14]都是基于频带内固定工作频率下的讨论，没有考虑在工作频带内调整工作频率点的供能方式。

在电动汽车无线充电系统（wireless power transfer，WPT）电路中，存在着零电抗频率（zero reactance frequency，ZRF）[15]。即从电路输入端看，整个电路的电抗为零，在该频率下初级侧电流相位差为零，此时整个系统可以实现高效率下大功率传输。因为现阶段研究中最常用的频段为81.38～90.00 kHz，所以本文将在此工作频带内，在输出端加入最优负载的基础上，对电路分频现象加以讨论，并找到输出功率最大的ZRF频点，进而明确该频点对应的耦合系数k。从而可通过对充电频率实时调整，实现整个电路系统在高能量传输效率下维持最高的输出功率。

1 WPT电路的理论研究

图1为电动汽车无线充电系统示意图和等效电路图。

图1 电动汽车无线充电系统示意图、等效电路图Fig.1 Schematic and the equivalent circuit of EV＇s wireless charging system

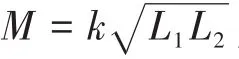
系统根据基尔霍夫定律[17]可以得到以下公式：

式中：ω为电流的角频率。

设置如下变量等式：

将式（2）代入式（1）求解可得i1，i2如下：

通过电路各个值的定义，可以得到如下公式：

式中：Pin为输入功率；Pout为输出功率；η为传输效率；Zin为输入阻抗。

利用公式（5）中的值可以得到后面讨论的频率与阻抗、传输效率、输出功率的关系。

2 分析分频现象

本文线圈由直径1.5 mm规格的Litz线绕制而成，主从线圈匝数都为33匝，利用电流相位差为零可以确定3个ZRF点的位置。实际操作中可以根据需求进行调整。

根据线圈规格可以得到线圈的自感L1，L2和线圈电阻rl1，rl2，谐振电容取常见的10 nF，负载电阻和并联电容根据参考文献的最优负载[14]相应调整，电源电压就是正常的220 V，电路中的各个指标取值设置如下：L1=L2=395µH，C1=C2=10 nF，rl1=rl2=0.04 Ω，Rout=37 Ω，Vin=220 V，C3=10µF。

在Matlab中进行仿真测试，得到式（8）定义的输入阻抗值Zin与工作频率f之间的关系图如图 2～图 4所示，其中，f0，f1，f2为 3个 ZRF频率点。

从图2～图4输入阻抗与频率的关系曲线可以看出，当k值逐渐变大时，电路产生了分频现象，并且从图3可以判断出，当k值高于某个临界的点，整个电路会出现分频现象。从图4可以明显得到在81.38～90.00 kHz频段中存在一个ZRF频率点。代入式（5）～式（8）可得到输出效率η和输出功率Pout与频率f的关系图如图5～图7所示。

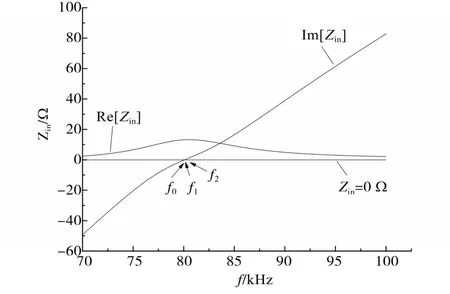
图2 k=0.1时Zin实部与虚部与f的关系Fig.2 The relationship between the real and imaginary parts of Zinand f when k=0.1

图3 k=0.16时的Zin实部与虚部与频率的关系Fig.3 The relationship between the real and imaginary parts of Zinand f when k=0.16

图4 k=0.22时的Zin实部与虚部与f的关系Fig.4 The relationship between the real and imaginary parts of the Zinand the f when k=0.22

图5 k=0.1时η和Pout与频率的关系Fig.5 The relationship between η，Poutand f when k=0.1

在图5中，3个ZRF点都在80.1 kHz处，传输效率为99.56%，输出功率为3.65 kW，在图6中，3个频点分别为77.4 kHz，0.1 kHz和84.5 kHz，传输效率分别为99.69%，99.73%和99.68%，输出功率分别为1.835 kW，1.432 kW和1.895 kW。在图7中，3个频点分别为75.0 kHz，80.1 kHz和87.8 kHz，传输效率分别为99.72%，99.79%和99.71%，输出功率分别为1.510 kW，0.758 kW和1.566 kW，对比之后可以得到，k值的变化对于3个ZRF点（f0，f1，f2）上的传输效率影响很小，但对于3个点上的输出功率影响很大。f1，f2频点上的输出功率明显高于f0，所以当k值确定时，将频率设置为f1，f2，整个电路将会达到99.7%的高传输效率以及1.8 kW左右的高输出功率，此时的充电效果将达到最优。

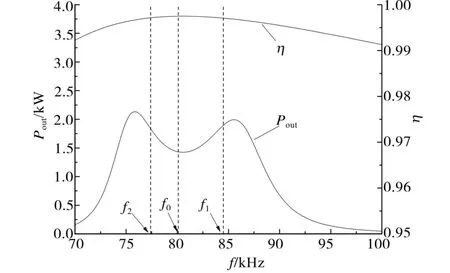
图6 k=0.16时η和Pout与频率的关系Fig.6 The relationship between η，Poutand f when k=0.16

图7 k=0.22时η和Pout与频率的关系Fig.7 The relationship between η，Poutand f when k=0.22

由于ZRF是零电抗频率，所以可以通过Im[i1]=0，将式（5）的i1提取虚部可以得到下列公式：

依据上述公式，可得f与k值的关系如图8所示。

图8 f0，f1，f2与k值关系Fig.8 Relationship between f0，f1，f2and k value

图8中，三条线分别对应式（9）～式（11）中的f0，f1，f2，由于k值的变化，从最初的3个点在同一个值上，到产生了3个不同的值，即当k值大于kth=0.150 8时，电路就产生了分频现象，当k值小于kth时，电路不发生分频现象。而对于给定的工作频段81.38～90.00 kHz内，明显存在着对应的ZRF点。在上面的分析中对于分频现象产生3个ZRF点，当电路频率取k值对应的f1，f2时，电路的传输效率高且输出功率最高。所以81.38～90.00 kHz频段内，k值在0.152～0.248时，都可以取得对应的ZRF点。

3 针对分频自适应频率选择

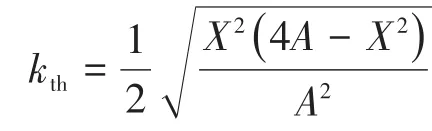
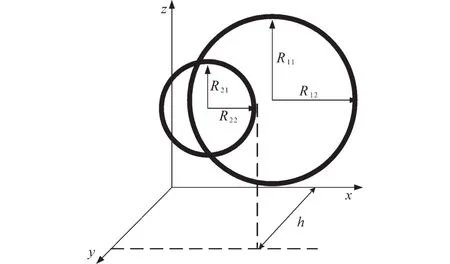
图9 圆形线圈尺寸和相对位置参数Fig.9 The size and relative position parameters of the circular coil

根据文献[18]中的讨论可以根据两个线圈的空间位置得到两线圈之间的互感。方形线圈之间的互感参照研究文献[19]也可以得出。

利用互感和已知的L1，L2可以得到充电线圈与汽车线圈的耦合系数k，先比较k与kth的关系，若k值未大于kth，则通过调整充电线圈的位置（垂直位置的变化）使k值大于kth，此时整个电路会产生分频现象，利用式（9）～式（11）可以得到k值相对应的ZRF点f1的频率大小，调整供能电路的频率使之达到f1，整个电路将会达到高传输效率下高输出功率的充电效果。具体的自适应流程如图10所示。

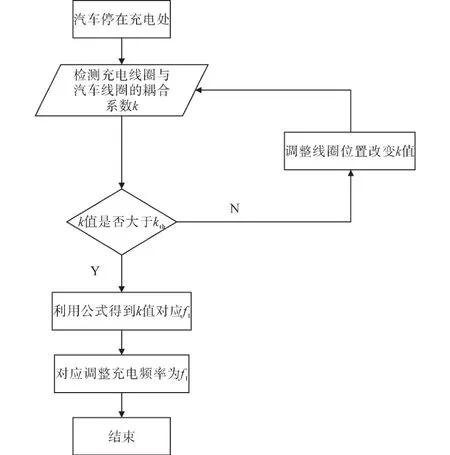
图10 频率选择自适应流程图Fig.10 Frequency selection adaptive flow chart

表1为本文提案方法与近期研究的比较。可以看出提案方法同时兼顾传输效率和输出功率，与传统方法相比，线圈设计简单，无需原副边实时通信，实现起来更为方便。

表1 各研究比较Tab.1 Comparison of studies

4 实验验证

为了验证磁耦合谐振电路的分频现象，我们搭建相应的实验平台进行验证，如图11所示。

图11 磁耦合谐振电路实验搭建示意图Fig.11 Schematic of the experimental construction for magnetic coupling resonant circuit

本文设计的实验参数如下L2=10µH，发射端谐振电容C1=8 nF，接收端谐振电容C2=8 nF，发射线圈内阻r1=0.2 Ω，接收线圈内阻r2=0.2 Ω，负载Rout=5 Ω，输入电压Vin=5 V，平滑电容C3=10 µF。此时电路的耦合系数临界值kth为0.146 7。

耦合线圈形状大小确定，自感固定，可以根据线圈的位置调整改变两个耦合线圈之间的耦合系数，并在不同的条件下进行测试，仿真数据结果如图12～图14所示。

图12 k=0.1时η和Pout与f的关系Fig.12 The relationship between η，Poutand f when k=0.1

图12中并未产生分频现象。仿真结果在558 kHz取得最大输出功率为8.596 W，传输效率为88.56%；实测结果在560 kHz取得最大的输出功率为8.283 W，此时的传输效率为85.62%。

图13中电路产生了分频现象，仿真结果在536 kHz时取得5.676 W的输出功率与90.83%的传输效率；在597 kHz时取得5.339 W的输出功率与91.21%的传输效率；在562 kHz时得到4.144 W的输出功率与92.71%的传输效率。实测结果在535 kHz取得最大的输出功率为5.548 W，此时的传输效率为88.64%；另一个较大的输出功率在595 kHz时取得，输出功率为5.192 W，此时的传输效率89.34%；而此时560 kHz时输出功率为4.095 W，传输效率为90.66%。三者相比，前两个点的传输效率相对较低一点，但相差不大。而输出功率则高于后者。

图13 k=0.15时η和Pout与f的关系Fig.13 The relationship between η，Poutand f when k=0.15

图14中分频现象更加明显。仿真结果在521 kHz时取得5.001 W的输出功率与91.36%的传输效率；在620 kHz时得到4.779 W的输出功率与91.83%的传输效率；在562 kHz时得到2.405 W的输出功率与94.18%的传输效率。实测结果在520 kHz处取得的最大输出功率为4.891 W，此时传输效率为89.32%；在620 kHz处产生了另一个高输出功率为4.675 W，此时的传输效率为89.84%；与中间频率560 kHz时的2.378 W输出功率及92.18%的传输效率相比，传输效率变化不大，输出功率有明显提高。

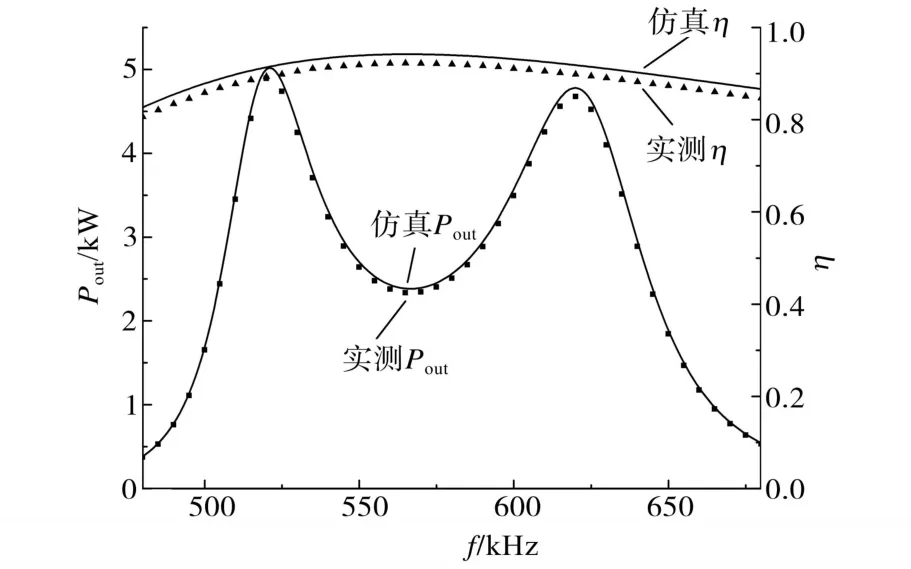
图14 k=0.2时η和Pout与f的关系Fig.14 The relationship between η，Poutand f when k=0.2

根据上述三图可以得出，在线圈之间耦合系数逐渐增大的情况下，整个电路的分频现象会如前面仿真分析的一样逐渐趋于明显。但实验结果和仿真结果比较都有一定程度的下降，分析原因可能有：1）系统中实际使用的电器元件与仿真中的理想模型存在一定误差。2）电路运行过程中会产生发热现象，导致能量的消耗。3）利用铁氧体磁芯对线圈进行辐射抑制，未加入铝片加强磁屏蔽，导致了部分能量辐射损耗。

5 结论

本文在81.38～90.00 kHz频段，以最优负载阻抗为前提，对电磁互感电路的零电抗频率展开讨论，得出了电路分频现象产生的条件。在仿真模型中，当k值在0.152～0.248内时，都可得相应的ZRF频点。通过对比3个ZRF点相应的传输效率和输出功率，可实现99.7%的传输效率及1.8 kW左右的高输出功率。论文还在此基础上搭建了实验平台进行测试，验证了分频现象。这也从侧面证实了在目标频段内，基于最优负载阻抗，利用耦合系数k和ZRF频点，在实现高传输效率下，得到最大输出功率频率选择方法的可行性。