基于STAR CCM+的轴流叶片弯掠对气动性能影响的研究

常智豪，徐尧天

（1.200093 上海市 上海理工大学 机械工程学院；2.201400 上海市 上海应用技术大学 机械工程学院）

0 引言

轴流风机作为一种应用广泛的流体机械，其工作性能一直是高校、研究机构和企业的研究重点。叶轮是风机做功转换能量的直接部件，叶形设计对风机工作性能具有相当重要的影响。

计算流体力学（Computational Fluid Dynamics，CFD）理论结合高性能计算机通过数值模拟仿真得到风机性能指标，从而提高风机设计、优化和选型的效率和成本。上官文斌等[1]用Fluent 软件求解了风机的静压、流量和效率等性能指标，结果表明，叶尖间隙过大将导致风机效率低下，故应减小叶尖间隙或安装圆环以提高风机性能；刘涛等[2]构建了发动机冷却风机的CFD 性能数值模拟模型，通过STAR CCM+软件求解，仿真与实验的性能变化趋势基本一致。

20 世纪80 年代以来，弯掠技术越来越多地应用在轴流风机叶形设计上，这增加了叶形设计的自由度，有利于高性能叶形的开发。利用轴流风机的弯掠技术可以良好地解决速度分离和失速裕度等流体机械领域的重要问题[3]。茅晓晨[4]用数值方法对弯掠设计前后的压气机气动性能进行了对比实验分析，结果表明压气机轴流叶形弯掠可以重新分配叶轮载荷，改善压气机内部流场；盛建萍[5]以最大效率为目标函数，掠角为自变量，运用CFD 技术研究了潜水轴流泵效率和扬程与叶轮掠角的关系，并且分析了掠角对水力性能的影响。

本文首先采用平面翼型设计和弯掠设计相结合的参数化方法建立了轴流风机的三维模型，利用STAR CCM+数值仿真软件对多种弯掠组合的轴流风机的气动性能进行求解，并对比分析了轴流叶片叶形弯掠设计对风机气动性能的影响。

1 弯掠的定义

由于不同学者之间的研究领域以及关注重点存在一定的差异，致使对于弯掠设计的定义方式有差异[3]，所以在对叶形进行参数化之前有必要对弯掠进行说明。弯掠分为周向和轴向2 种，即沿着叶高方向翼型向着轮毂周向偏移和向着轮毂轴向偏移2 种[6]，下文简称周向弯掠为弯叶片，周向偏移为掠叶片。图1 为叶片弯掠示意图。

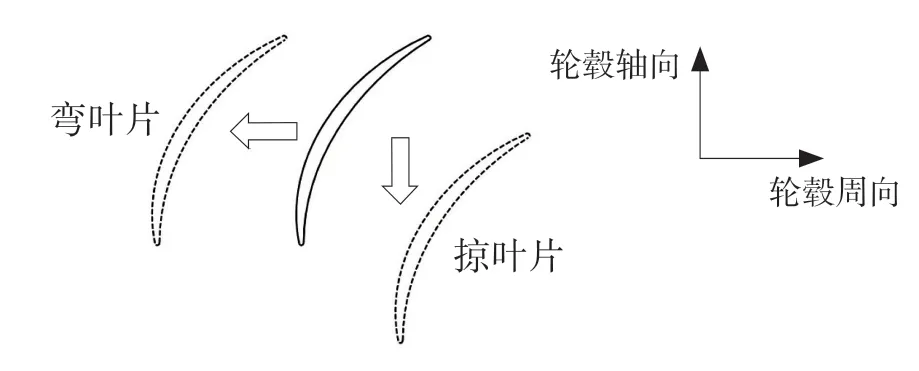
图1 叶片弯掠示意图Fig.1 Skewing and sweeping of blade

2 叶形参数化

轴流风机叶形的参数化包括不同叶高处的翼型截面参数和不同叶高处的翼型弯掠值2 个部分。翼型截面的参数包括翼型的前、后缘方向角、翼型安装角和翼弦长。不同叶高处的弯掠值包括周向偏移（弯）值和轴向偏移（掠）值。理论上，通过调整4 个翼型参数和2 个弯掠参数的控制曲线，就可以完全控制整个叶形。

如图2 所示为平面翼型的示意图，α和β分别是翼型的前、后缘方向角；θ为翼型的安装角；L为翼弦长。翼型轮廓是按照翼型截面厚度分布将翼型中线向两侧偏置得到的。

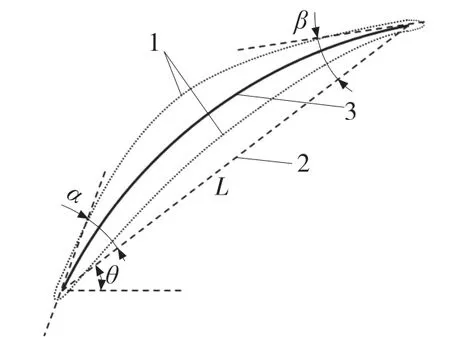
图2 平面翼型示意图Fig.2 Plane airfoil

使用叶根处的截面参数计算得到的平面翼型截面经过柱面变换可以得到叶根处的空间翼型截面，将此空间曲面变化拉伸就可以得到完整的叶形。采用参数控制曲线来描述翼型截面参数与弯掠参数沿着叶高的变化规律。由于叶形在叶高方向的变化要连续且光滑，所以参数控制曲线采用5 个控制点控制的B 样条曲线，横坐标表示叶片高度百分比，纵坐标表示参数的取值。

3 轴流叶轮几何模型

采用未经过叶形弯掠设计的轴流风机作为原型机，控制变量设计3 组弯掠组合的叶形作为比较模型，原型机和比较模型的基本参数和翼型参数控制曲线均相同，如表1 和图3 所示。

表1 风机基本参数Tab.1 Basic parameters of fan

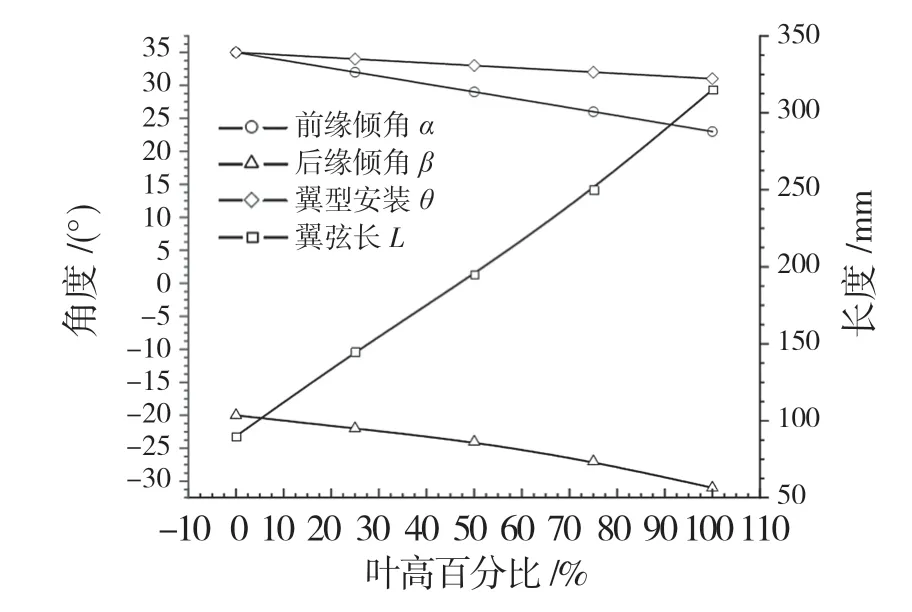
图3 翼型参数控制曲线Fig.3 Control curves for airfoil parameters

3 种比较模型的弯掠设计组合分别为：①弯叶片；②掠叶片；③弯掠叶片。原型机和比较模型的弯掠参数控制曲线如图4所示，三维模型如图5所示。

图4 弯掠参数控制曲线Fig.4 Skewing and sweeping parameter control curve

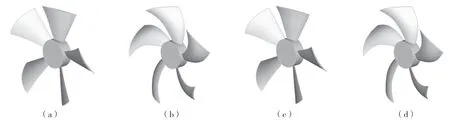
图5 叶轮三维模型Fig.5 Three-dimensional impeller model

4 轴流叶轮几何模型

4.1 控制方程及湍流方程

不可压缩流体的质量守恒方程为

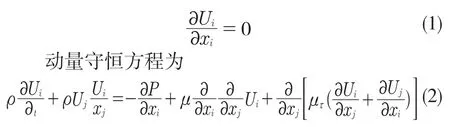
式中：P——流体静压；xi，xj——位移分量；Ui，Uj——速度分量；μ——动力粘度；μτ——湍流粘度。K-ε湍流模型为

式中：K——湍动能；ε——湍流耗散比；c1，c2——两个常数；στ，σs——湍动能和湍流耗散比的普朗特常数。

4.2 CFD 模型建立

本文采用在风机流场计算领域应用广泛的STAR CCM+软件，选用流体旋转机械常用的K-ε模型对轴流风机流场进行稳态求解，壁面处理选用Two-Layer All y+类型，轴流风机的流场气体属于低马赫数流动，空气在轴流风机流场内密度不发生改变，定义流体介质为恒密度分离流类型，密度和动力粘度分别设置为1.18 kg/m3和1.855×10-5Pa·s。

如图6 所示，轴流风机的流场分为旋转区域、中间区域、入口区以及出口区等4 个部分。为了保证整个风机流场的入口和出口的相对大气压力为0 Pa，流场入口和出口区域的长度应不少于旋转区域直径的6 倍[7]。设置计算区域的入口边界类型为Stagnation Inlet（停滞入口），为出口边界指定Pressure Outlet（压力出口），并在出口处设置风机的工作静压。将旋转区域与中间区域的交界面设置为数据交换面（Interface）以保证流场的相通性，其余边界的类型均设置为壁面（Wall）。为旋转区域指定旋转参考坐标系，这相当于风机运动所引起的动量源效果被定义为相对于风机轴具有给定转速的一个转动惯量，实现了叶轮的旋转运动。

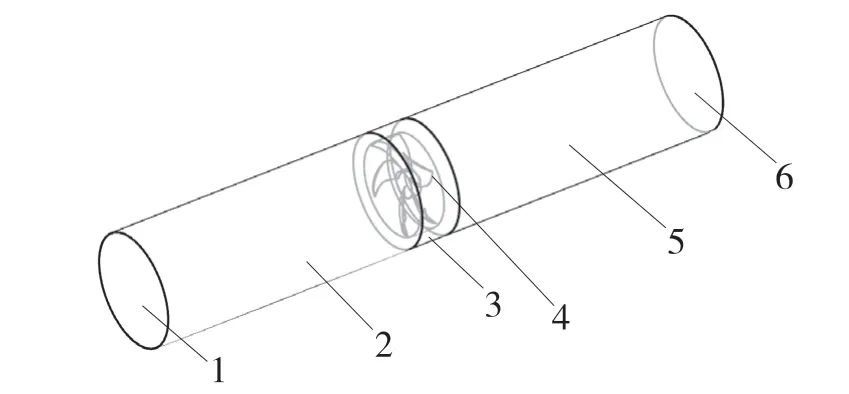
图6 计算区域示意图Fig.6 Calculation region

4.3 模型求解及对比分析

对流场区域划分多面体网格。由于中间区域中包含叶轮表面，曲面比较复杂，为了能够精确模拟曲面表面的流体流动，对叶轮表面的网格进行局部加密的处理。图7 所示为原型机网格划分结果。利用STAR CCM+软件的网格划分算法对网格进行划分，最终网格总量约为142 万，其中进、出口区域网格量约为59 万，中间区域的网格量约为83 万。

图7 叶轮网格Fig.7 Impeller grid

对CFD 模型进行迭代求解，如图8 所示。迭代到1 758 步时，连续性方程和动能方程等迭代计算方程的数值计算残差均在1×10-4之下，判定为求解收敛并停止迭代。

图8 残差收敛曲线Fig.8 Residual convergence curve

图9 为原型机和3 个比较模型的叶片表面静压分布云图。由图9 可以看出，4 种叶片的最大压力均出现在压力面前缘中部偏叶顶的位置，最小静压均出现在吸力面的前缘和尾缘处，这与实际情况相符，证明了数值模拟的正确性。这些区域的压力波动较为剧烈，产生的噪声能量损失也较大，不同的是，比较模型①和比较模型③在叶顶靠近前缘处也出现了绝对值较大的静压，且压力的变动范围小于其他2 个模型，这说明弯叶片设计有助于降低叶片的表面压力波动，从而减少能量损失。

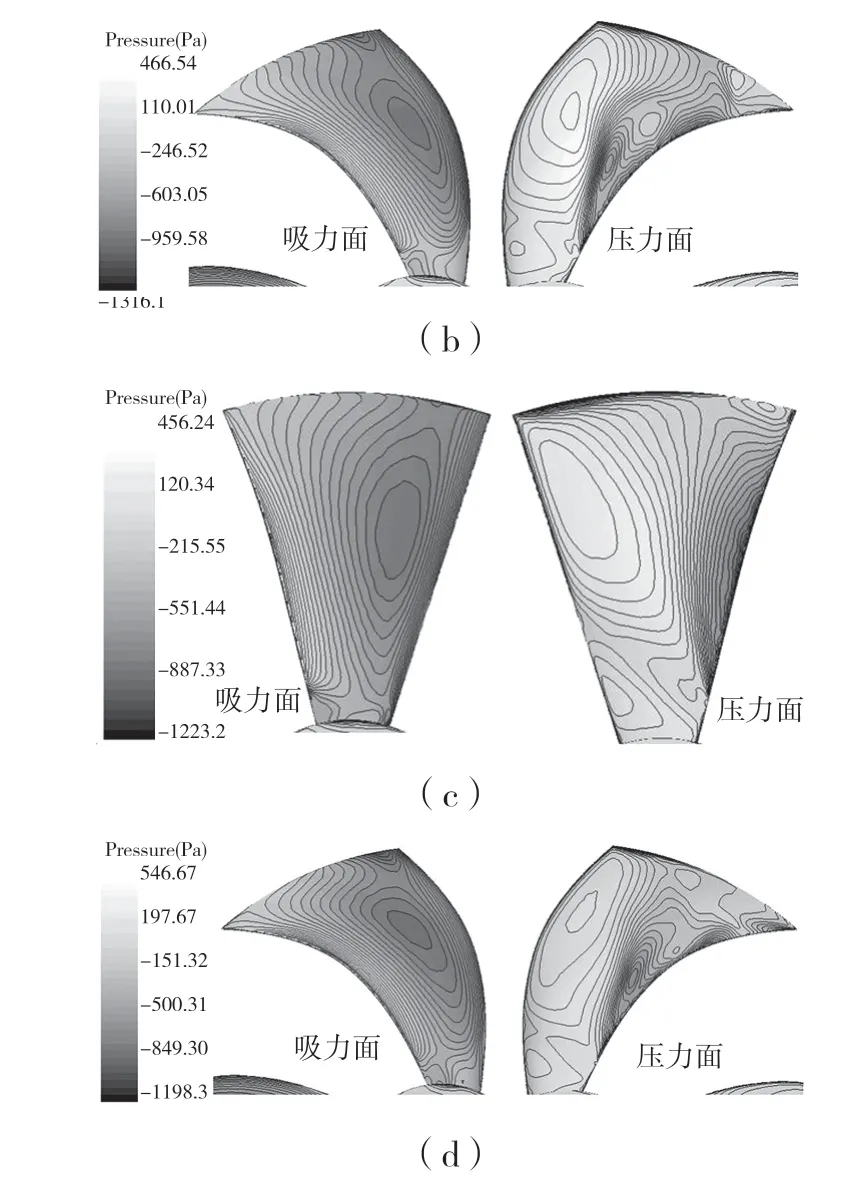
图9 叶片压力分布Fig.9 Pressure distribution of fan surface

由图9 可见，原型机的压力面最大压力为579.22 Pa，吸力面最小压力为-1 417.7 Pa；比较模型②的压力面最大压力为456.24 Pa，吸力面最小压力为-1 223.2 Pa。比较模型②的压力绝对大小较原型机大幅度减小，叶轮轴向力也相应减小，说明掠叶片设计有助于改善叶轮轴向受力。

图10 为原型机和3 种比较模型的风量-静压性能曲线。由图10 可以看出，在各个静压下，风量由大到小排序是：比较模型①（弯叶片）＞比较模型③（弯掠叶片）＞原型机（直叶片）＞比较模型②（掠叶片）。

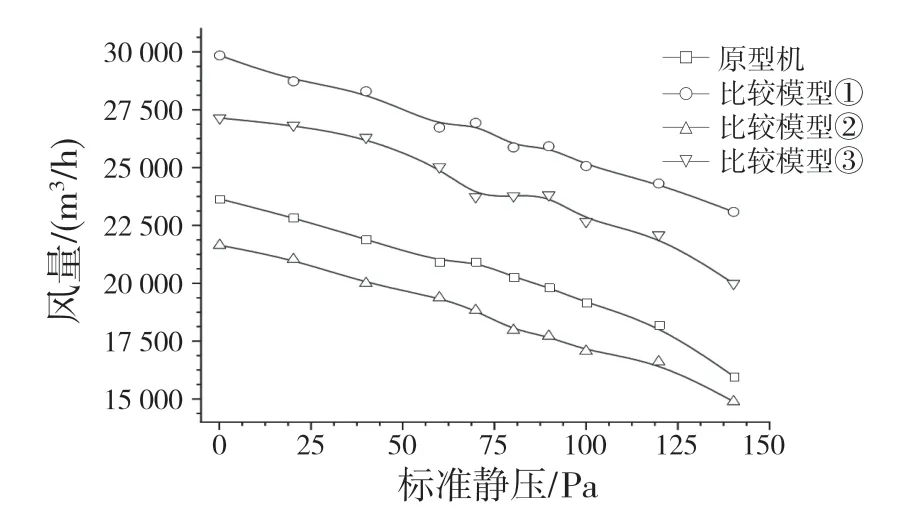
图10 风量-静压性能曲线Fig.11 Air volume-hydrostatic performance curve

风量性能较优的2 种模型都采用弯叶片设计，说明弯叶片设计可以提高风机的风量，而风量性能较差的2 种模型中，采用掠叶片设计的比不采用掠叶片设计的风量性能还差，这说明掠叶片设计会降低风机的风量。

5 结论

本文用控制曲线控制不同叶高处的翼型截面参数和不同叶高处的翼型弯掠值参数，得到了参数化表达的轴流叶轮叶形，可以通过改动翼型截面控制曲线和翼型弯掠控制曲线实现对轴流叶形的控制。在STAR CCM+软件中建立轴流风机的CFD 模型，对不同弯掠组合的轴流风机的流场进行仿真，得到叶片表面静压分布云图以及风机风量-静压性能曲线，通过对比得到以下结论：

（1）叶片表面的最小和最大静压分别出现在吸力面和压力面，符合实际情况，证明了数值模拟的正确性；

（2）比较模型①和比较模型③在叶顶靠近前缘处也出现了绝对值较大的静压且压力的变动范围小于其他两个模型，这说明弯叶片设计有助于降低叶片的表面压力波动；

（3）比较模型②的压力绝对大小较原型机大幅度减小，叶轮轴向力也相应减小，说明掠叶片设计有助于改善叶轮轴向受力；

（4）风量性能较优的两种模型都采用弯叶片设计，说明弯叶片设计可以提高风机的风量；采用掠叶片设计的比不采用掠叶片设计的风量性能还差，说明掠叶片设计会降低风机的风量。