基于逆向增广Burgers 方程的声爆反演技术

2023-02-07顾奕然黄江涛陈树生刘德园高正红

航空学报 2023年2期

顾奕然，黄江涛，陈树生，3，*，刘德园，高正红

1.西北工业大学航空学院，西安 710072

2.中国空气动力研究与发展中心，绵阳 621000

3.航空工业第一飞机设计研究院，西安 710089

受到诸多工程技术因素的影响，超声速客机自20 世纪70 年代出现以来发展极其缓慢，而声爆带来的地面噪声问题是超声速客机发展的重要障碍之一［1］。以欧洲联合研发的超声速客机协和号为例，其巡航状态下地面感觉噪声约为105 dB［2-3］，这会对航线下方的生物和建筑造成难以忽视的影响。

飞行器在超声速飞行下于近场产生的扰动波经过大气传播，会在远场演化成形如英文字母“N”的远场波形［4］，如图 1 所示。声爆在远场演化的N 形声波直接影响着地面，因此低声爆设计工作的最终目的即通过对声爆产生的N 形波进行修型，降低地面感觉噪声。依据NASA 在SSBD（Shaped Sonic Boom Demonstrator）［5］项目中的研究成果，认为对超声速飞行器的外形进行优化设计能够改变其对应的地面声爆波形，这为声爆的设计优化提供了基础和参考，意味着在低声爆设计工作中引入气动外形优化的相关方法是行之有效的。

图1 声爆传播过程示意图Fig.1 Schematic diagram of sonic boom propagation

低声爆设计方法依据其推进的方向，可以大致分为正设计［6-9］和反设计［10-13］两类。正设计通过针对超声速飞行器外形的优化设计，经过多次迭代计算从而得到符合要求的远场声爆波形；反设计则是通过选择一个符合要求的远场声爆波形，利用相应的反演技术反向推演出超声速飞行器的气动外形。通常情况下，人为设计一个理想波形然后反向寻找其对应的飞行器气动外形，比使用正向算法搜索最优的地面波形更加高效，因此反设计方法在低声爆设计领域受到极大重视。

有关声爆反设计的方法通常可以分为地面目标波形匹配［14-15］和近场目标波形匹配［16-17］两类。地面目标波形匹配方法通过指定一个目标地面声爆波形，并使用反演技术将地面声爆波形反向传播至近场，以完成反设计任务；近场目标波形匹配方法指定一个目标近场过压分布，然后通过反设计算法来寻找其对应的气动外形。由于飞行器的气动外形和近场过压分布是紧密耦合的，因此通常情况下，实现近场目标波形匹配更为容易。但倘若考虑大气传播过程，一个优化后的较好的低声爆近场波形未必能对应一个较好的远场波形，这限制了近场目标波形匹配方法的应用。与此相比，地面目标波形匹配方法能够更准确地反映地面声爆波形与飞行器外形的关联性，但其对声波大气传播过程的模拟技术要求更为苛刻。

对于模拟声波在大气层内的传播过程，通常可以由3 种方式实现：一为基于弱激波理论的波形参数法［18］；二为基于时频域分析技术的Pestorius-Anderson 方法［19］；三为基于非线性声学的增广Burgers 方程方法［20］。3 种方法中，前2种方法由于需要引入经验公式［21］和需要交替进行时域频域变换，模拟精度往往难以达到工程应用的需求，因此增广Burgers 方程方法使用更为广泛［22］。

反设计工作的重心在于寻找与目标波形相对应的近场波形。基于相波形参数法，Seebass 和George［23］提出了一种相对较为粗糙的反设计方法。基于增广Burgers 方程方法，Li 等［24］提出了一种基于逆向增广Burgers 方程的方法来反向传播声波并以此完成反演计算。Rallabhandi［25］发展了基于反向等效面积目标的离散伴随方法。张绎典和高正红等［26］提出了基于本征正交分解（Gappy Proper Orthogonal Decomposition，GPOD）的声爆反设计方法。各方法均能在一定程度上使设计外形的地面波形接近目标波形，从而降低地面声爆强度。

本文基于一种逆向增广Burgers 方程的数值反演方法展开研究，对求解过程中的各影响因素进行探索，并在已有研究成果的基础上，进一步对基于此方法的中场反设计方法进行了研究，对声爆传播过程中高频分量的演化及其对反设计方法的影响进行了讨论。

1 增广Burgers 方程

增广的Burgers方程由Pierce［27］于20世纪80年代提出，在经典Burgers 方程中引入了额外的几何扩散、大气分层及分子弛豫项，能够更好地模拟声压信号在大气中的传播。逆向增广Burgers 方程可用于模拟声爆信号的反向传播，能够将中场压力分布反向传播到近场位置。本节描述逆向增广Burgers 方程及其求解方法。

1.1 经典正向增广Burgers 方程

增广Burgers 方程包括非线性、经典耗散、分子弛豫现象等效应。无量纲的Burgers 方程如式（1）所示：

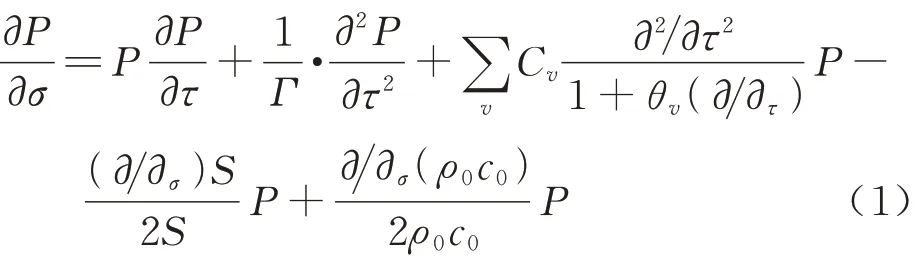
式中：P为无量纲压力；τ为无量纲时间；σ为无量纲声管距离；Γ、Cv、θv分别为无量纲气体耗散参数、无量纲松弛系数和无量纲松弛时间；S、c0与ρ0为声管面积、声速和大气密度。

方程（1）右侧5 项分别为非线性效应项、经典耗散效应项、分子弛豫效应项、几何扩散效应项和大气分层效应项，分别表示对应的物理效应对声压信号的影响。

1.2 逆向增广Burgers 方程

经典正向增广Burgers 方程中，非线性效应项、经典耗散效应项和分子弛豫效应项与时间有关，而几何扩散效应项和大气分层效应项只与声管路径有关。构建逆向方程可以看作令时间反向流动，因此只需要修改非线性效应项、经典耗散效应项和分子弛豫效应项。

对于波形的反向传播，增广Burgers 方程可以修改为

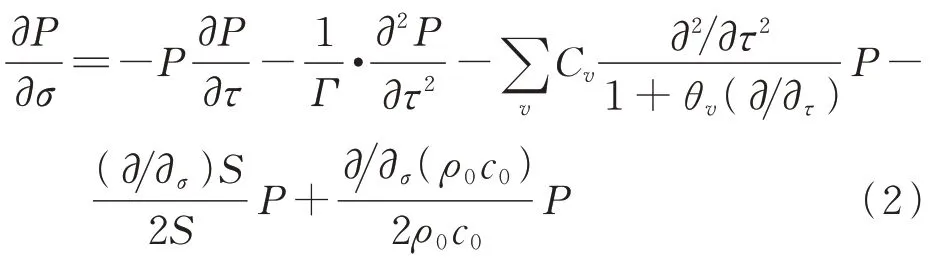
逆向增广Burgers 方程与正向方程类似，在形式上只有非线性效应项、经典耗散项和分子弛豫项的正负发生了变化［24］。

1.3 数值求解方案

在对逆向增广Burgers 方程进行求解之前，首先需要对时间和空间进行离散。时间维度上需要对过压信号进行离散处理；空间维度上需要对声管传播路径进行离散处理。使用均匀的网格对时间和空间进行离散，并使用参考时间1/ω0，参考长度为时间采样频率，β为非线性系数）和参考压力p0进行无量纲化，无量纲化过程由式（3）～式（5）所示：

使用算子分裂法［28］对逆向增广Burgers 方程进行求解。式（2）可由算子分裂法分裂成以下5 项：

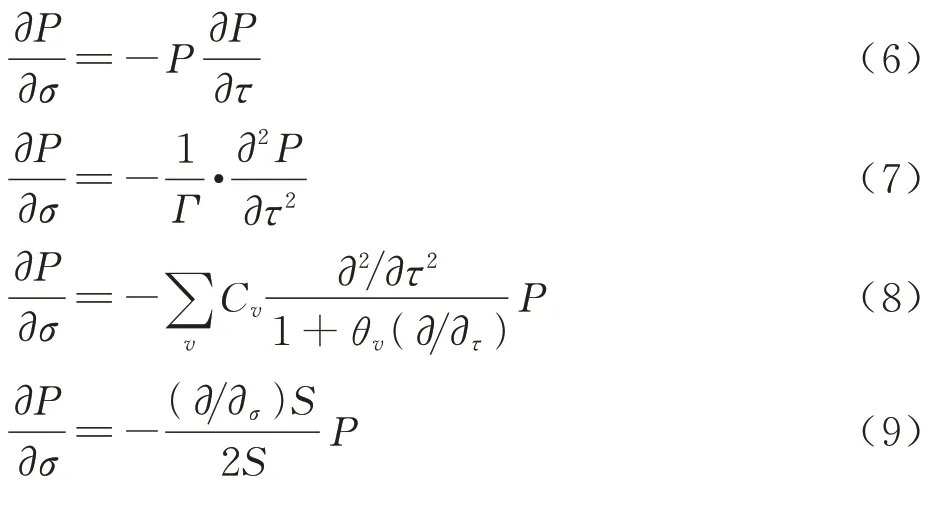
求解过程中，依次使用式（6）～式（10）更新无量纲压力P，推进至下一高度后继续循环上述过程，直至高度推进至目标高度，从而完成求解。

对于式（6），其等价于：

使用以下离散方法进行求解：

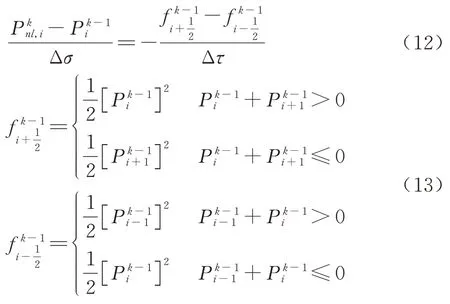
式（7）与式（8）是病态方程，为稳定方程求解过程，可以引入伪抛物线型正则化方法改写方程，其形式如式（14）所示：

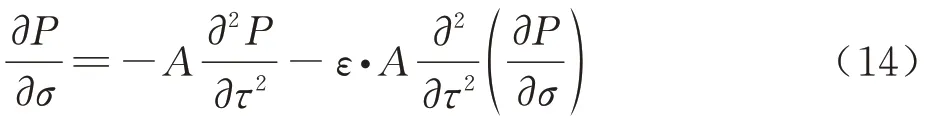
正则化参数ε是一个正的标量，使得式（14）数值可解，可以通过试错法选取ε=10-4。使用伪抛物线型方程改写经典耗散项和分子弛豫项，能够较好的稳定数值求解的过程。

使用待定系数法改写经典耗散项，可以写为

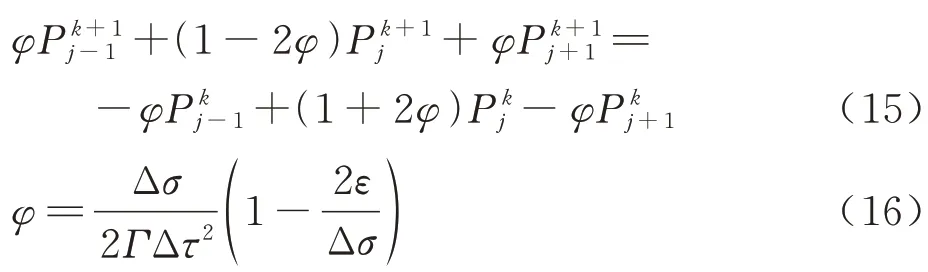
分子弛豫项也可使用类似的方法写为

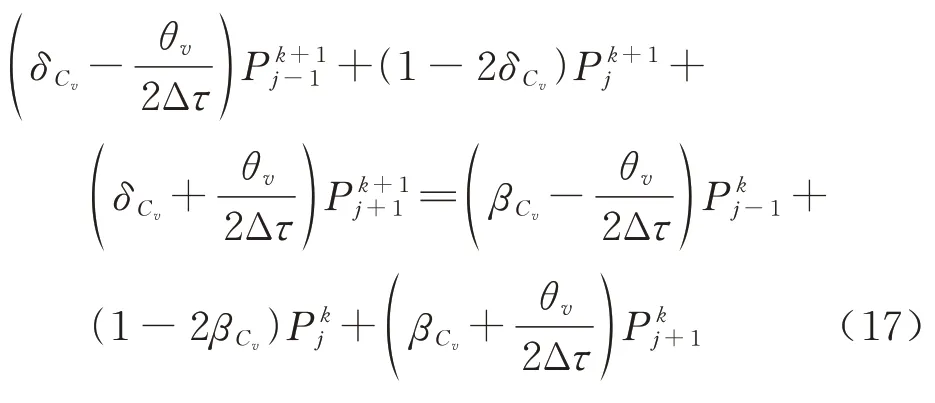
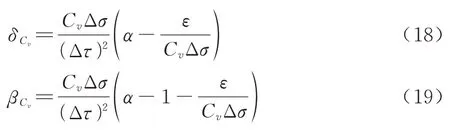
式中：α取0.5。

式（15）与式（17）均为三对角方程，可以使用TDMA 方法（Tridiagonal Matrix Algorithm）高效率求解。

式（9）与式（10）本质是一个守恒方程，可以分别使用式（20）与式（21）进行求解。

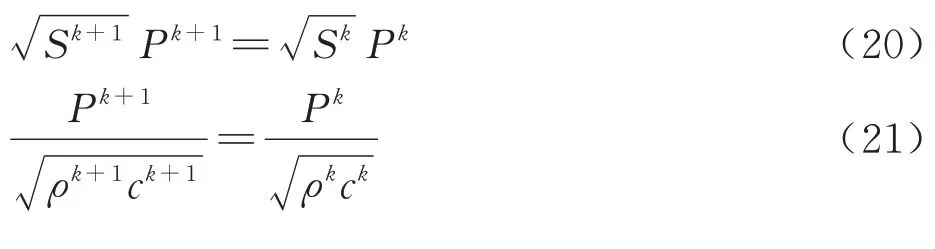
1.4 反向等效面积求解

通过使用前文中讨论的反向传播方法，中场位置的压力信号分布可以反向传播到近场位置，近场过压分布可以逆变换为等效面积分布，称为反向等效面积Ae，r。使用以下等式［24］：

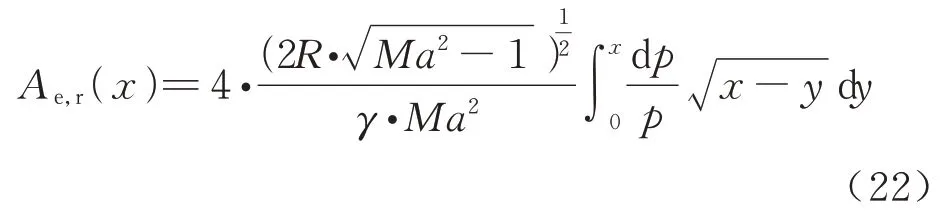
式中：Ma为巡航马赫数；R为近场位置到飞行器的距离；γ取1.4。需要注意的是，只有当飞行器满足细长体假设［29］时式（22）才成立。

2 计算程序验证

基于增广Burgers 方程及逆向增广Burgers方程，可以编写计算程序对声爆过压信号在近场与远场之间的传播进行研究。

正向增广Burgers 方程计算程序参考笔者所在实验室自研声爆程序［22］，图 2 展示了正向增广Burgers 方程计算程序的主要框架。过压信号由近场传播向远场，首先使用声管计算程序输出对应的声管路径和大气参数，并将其提供给求解器。求解器使用算子分裂法求解，输入过压信号依次通过非线性效应项求解器、经典耗散项求解器、分子弛豫项求解器、几何扩散项求解器和大气分层效应项求解器，然后推进至下一高度，继续以上述顺序进行迭代，直至高度推进至目标高度。

图2 正向程序结构Fig.2 Forward program structure

图3 展示了逆向增广Burgers 方程计算程序的主要框架。与正向求解程序类似，在声管计算程序输出相应计算参数后，使输入过压信号依次通过逆向非线性效应项求解器、逆向经典耗散项求解器、逆向分子弛豫项求解器、几何扩散项求解器和大气分层效应项求解器，然后推进至下一高度，继续以上述顺序进行迭代，直至高度推进至近场高度。求解获得近场过压信号后，通过Abel 逆变换计算得到对应的逆向等效面积分布，完成计算任务。

图3 逆向程序结构Fig.3 Reverse program structure

为验证计算程序的有效性，选取第2 次AIAA 声爆预测研讨会（SBPW-2）提供的官方算例Axibody 来进行验证工作。Axibody 是一个几何回转体，其外形大致如图 4 所示［30］。

图4 Axibody 外形［30］Fig.4 Appearance of Axibody［30］

2.1 正向计算程序验证

选取飞行高度H=15 849.6 m，飞行马赫数Ma=1.6，近场与机体距离R=128.93 m。Axibody 在周向角0°时的标准近场过压信号如图 5所示。

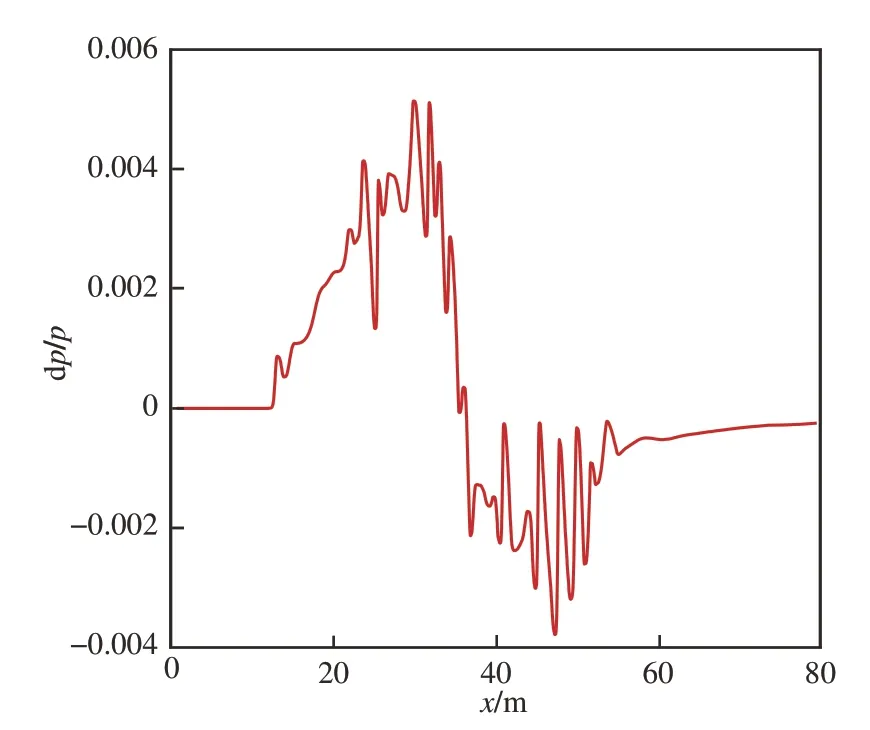
图5 Axibody 近场过压分布Fig.5 Near-field over-pressure distribution of Axibody

由正向增广Burgers 计算程序计算所得的地面波形和NASA 的sBOOM 软件的计算结果对比图如图 6 所示，验证了编写的正向增广Burgers计算程序计算准确度符合要求。

图6 地面信号对比Fig.6 Ground signal comparison

2.2 逆向计算程序验证

由于经典耗散效应和分子弛豫效应的影响，近场过压信号中的部分分量在向远场传递的过程中会不可避免地出现耗散和消亡的现象［31］；此外，在逆向求解数值方法中，逆向过程会趋向于抹平波形，这使得使用逆向增广Burgers 方程难以将远场信号准确地反演至近场［24］。但倘若缩减逆向计算程序的反演距离，从一个距离近场较近的中场过压信号开始反演，也可以获得大致准确的近场过压信号。

选取3 个不同的中场高度Hm=15 500 m、15 000 m、14 000 m 进行验证。使用正向增广Burgers 计算程序计算获得对应的中场过压信号如图 7 所示，再使用逆向增广Burgers 计算程序反演至近场，其计算结果与标准数据对比图如图 8 所示，反演过压信号对应的等效面积分布与标准近场过压信号的等效面积分布的对比图如图 9 所示。可以观察到，虽然随着反演距离的增长计算精度有所降低，但逆向增广Burgers 方程计算程序的计算结果与标准近场数据大致相同，可以认为逆向Burgers 方程反演得到的信号在一定精度范围内可以代表近场信号。

图7 中场过压信号Fig.7 Mid-field over-pressure signal

图8 近场过压分布对比Fig.8 Comparison of near-field over-pressure distributions

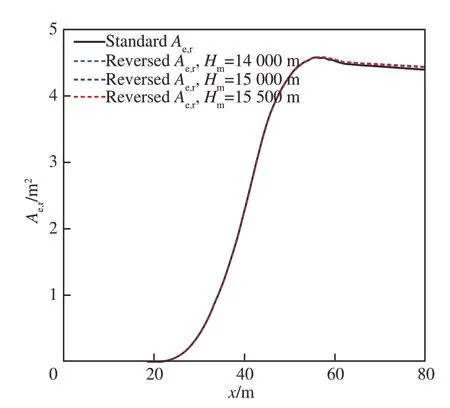
图9 等效面积分布对比Fig.9 Comparison of equivalent-area distributions

2.3 逆向计算程序网格收敛性

在进行逆向增广Burgers 方程计算时，不仅需要对声管传播路径进行离散，还要对过压信号进行离散，即在空间和时间上各有一个离散维度。

采用控制变量法对网格收敛性进行研究。选取中场高度Hm=14 000 m，首先固定空间网格数为10 000，使用不同的网格数量离散时间维度，其对应的计算结果对比图如图 10 所示。然后固定时间网格数为10 000，使用不同的网格数量离散空间维度，其对应的计算结果对比图如图 11所示。

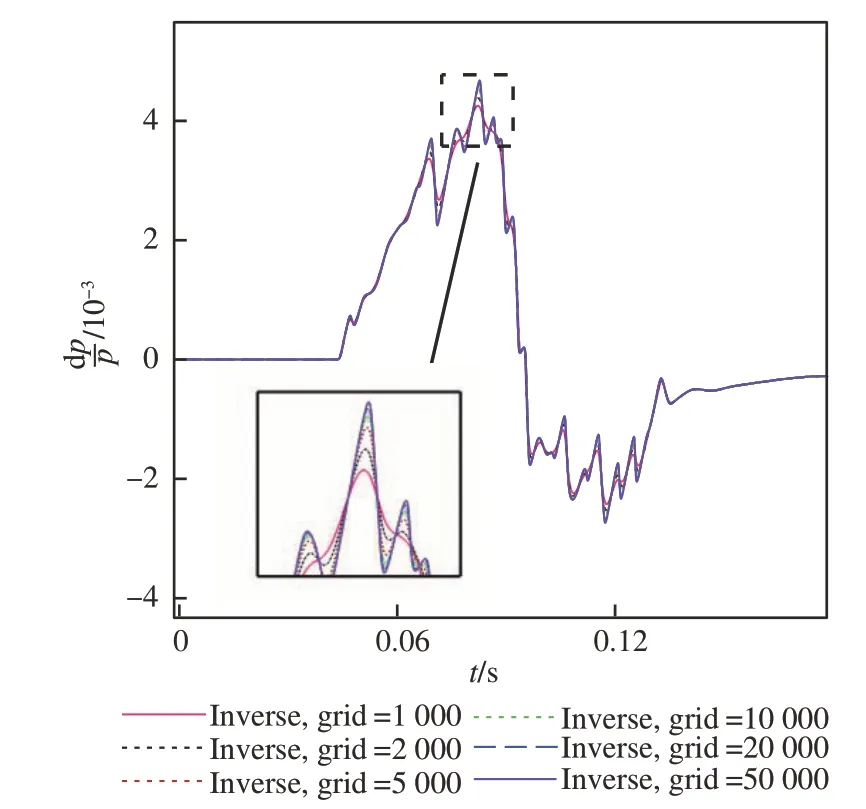
图10 不同时间网格数量计算结果对比Fig.10 Comparison of results with different grid numbers in time dimension

图11 不同空间网格数量计算结果对比Fig.11 Comparison of results with different grid numbers in spatial dimension

观察计算结果，认为时间采样率提升至25 kHz 时，计算结果趋向于收敛，而空间网格的密度对结果无显著影响。比较两组计算结果，可以发现时间网格密度对计算结果的影响较大，而空间网格密度对计算结果影响较小。这和正向Burgers 方程离散求解的特点相似［22］。

3 数值结果

在第2 节中，研究已经针对正向和逆向的增广Burgers 方程计算程序进行了准确度验证和网格收敛性研究，认为正向和逆向的计算程序均能较为准确地完成计算任务。基于上述计算程序，本节对方程求解实际问题中各因素的影响进行了较为系统的研究，对在不同中场高度与不同周向角条件下使用逆向增广Burgers 方程计算程序进行反演计算，并对计算结果进行分析。

3.1 反演距离

前文已经提到，由于近场过压信号在向远场传递的过程中，不可避免地受到经典耗散效应和分子弛豫效应的影响，使得逆向增广Burgers 方程难以准确地将远场声压波形反演为对应的近场过压信号。而若缩短反演距离，则中场过压信号中因经典耗散效应与分子弛豫效应而消亡的频率分量将减少，因此从一个距离较近的中场利用逆向增广Burgers 方程进行反演计算能够取得更高的准确度。反演距离对于逆向增广Burgers方程的反演具有重要影响。

研究采用LM1021、C608 两个标准算例进行研究。其外形如图 12［30］与图 13［32］所示。LM1021为SBPW-1 的可选算例和SBPW-2 的标准算例之一，是洛克希德·马丁公司设计的新一代超声速客机；C608 是SBPW-3 的标准算例之一，是NASA的低声爆试验飞行器X59的初步改形方案。

图12 LM1021 飞行器［30］Fig.12 LM1021 aircraft［30］

图13 C608 飞行器［32］Fig.13 C608 aircraft［32］

对于LM1021 算例，选定的计算条件为飞行高度H=16 764 m，近场与机体距离R=222.59 m，飞行马赫数Ma=1.6。图 14 与图 15展示了LM1021 算例在不同中场高度开始反演计算所得到的近场过压信号对比与对应的等效面积分布。

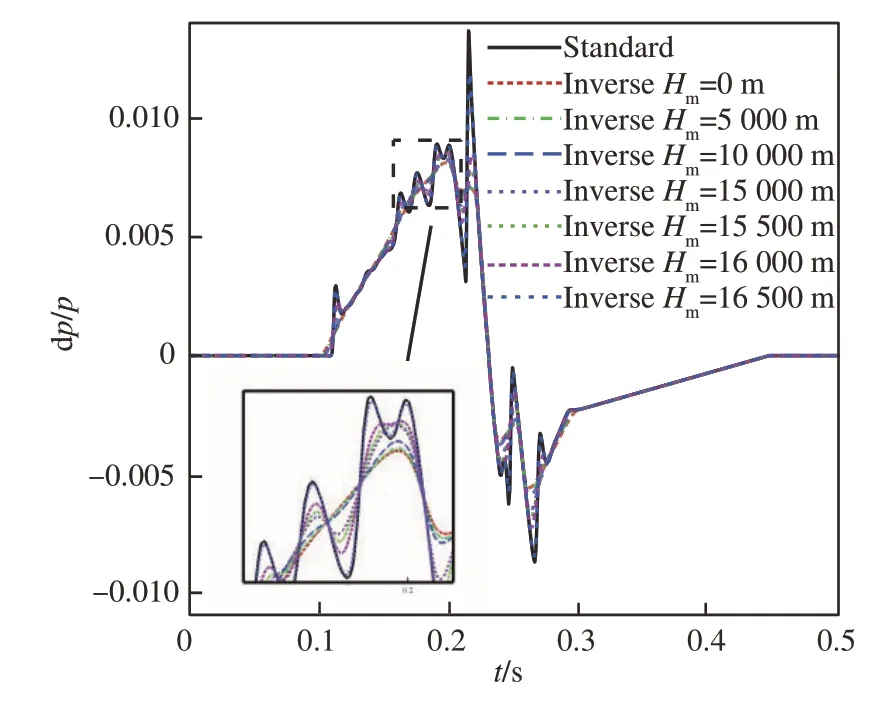
图14 不同中场高度反演结果对比（LM1021）Fig.14 Comparison of inversion results at different mid-field heights（LM1021）

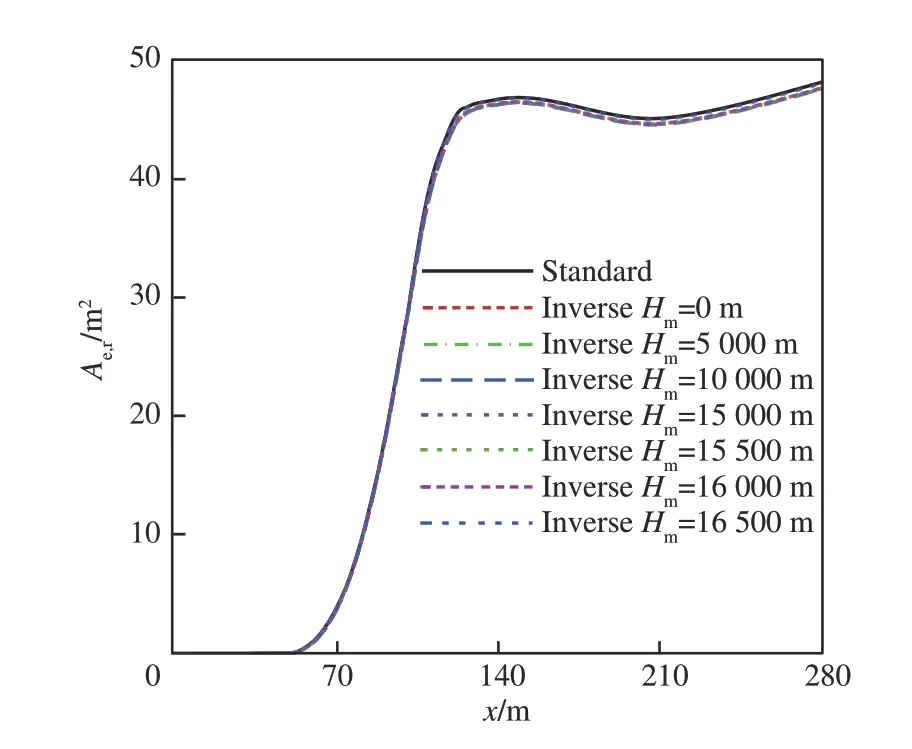
图15 不同中场高度反演等效面积对比（LM1021）Fig.15 Comparison of equivalent-areas at different mid-field heights（LM1021）

对于C608 算例，选定的计算条件为飞行高度H=16 215.36 m，近场与机体距离R=82.296 m，飞行马赫数Ma=1.4。图 16 与图 17展示了C608 算例在不同中场高度开始反演计算所得到的近场过压信号对比与对应的等效面积分布。

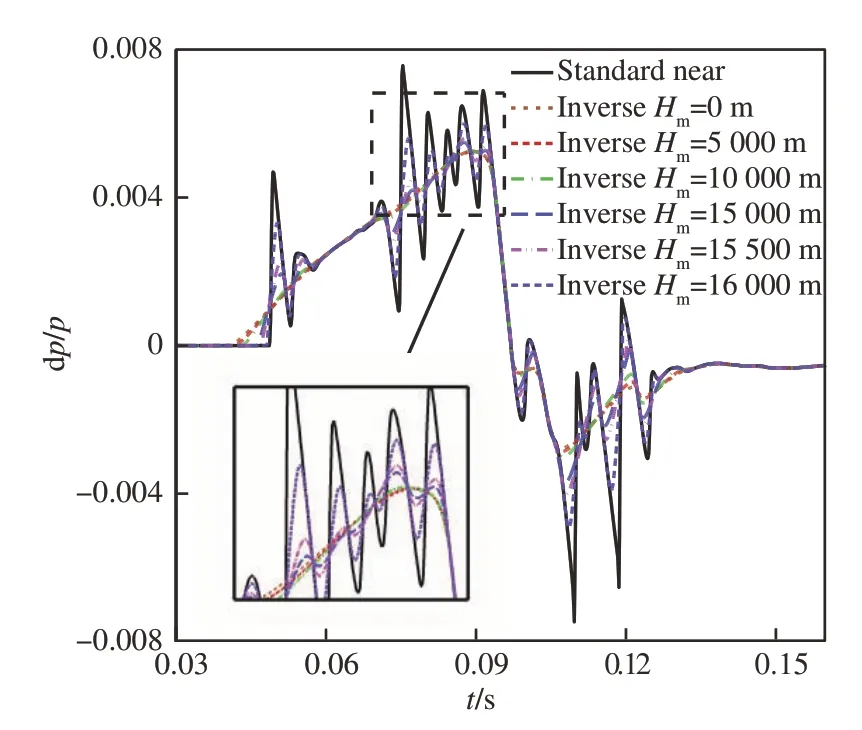
图16 不同中场高度反演结果对比（C608）Fig.16 Comparison of inversion results at different mid-field heights（C608）

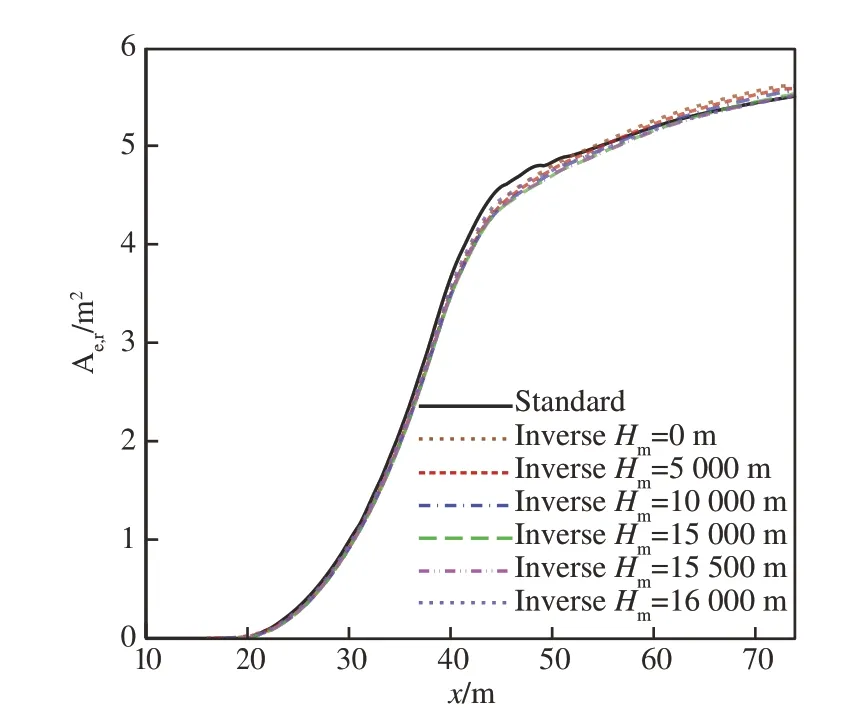
图17 不同中场高度反演等效面积对比（C608）Fig.17 Comparison of equivalent-areas at different mid-field heights（C608）

观察计算结果，可以观察到随着中场高度的增大，逆向增广Burgers 方程计算程序的计算结果越来越逼近标准近场过压信号，这与理论分析的结果相一致。同时可以注意到，虽然不同中场高度的选取对反演的近场过压信号波形有较大影响，但相应的等效面积分布变化相对较小，这使得基于逆向增广Burgers 方程的低声爆反设计方法能够提供较为准确的低声爆等效面积分布。

此外，从图 14 与图 16 中可以观察到，反演结果的误差主要来自于无法对过压信号中的高频分量进行准确的还原，且当中场位置靠近机体时，反演准确度会迅速增大。图 18 与图 19 展示了由正向增广Burgers 方程计算程序得出的LM1021 与C608 算例距离近场约1 000 m 内声爆过压信号的演变过程。可以观察到，在声爆传播过程初期，非线性效应的扭转作用和大气分层效应的作用效果尚不明显，过压信号的演化主要受经典耗散和分子弛豫效应对高频分量的耗散作用以及声管几何扩散对声爆信号的线性衰减作用的影响。由于逆向增广Burgers 方程计算程序和正向程序在处理几何散布效应的方式相同，不会对准确度产生较大影响，因此可以认为在距离机体较近的情况下，中场位置对反演精度的影响主要是由经典耗散效应和分子弛豫效应引起的。

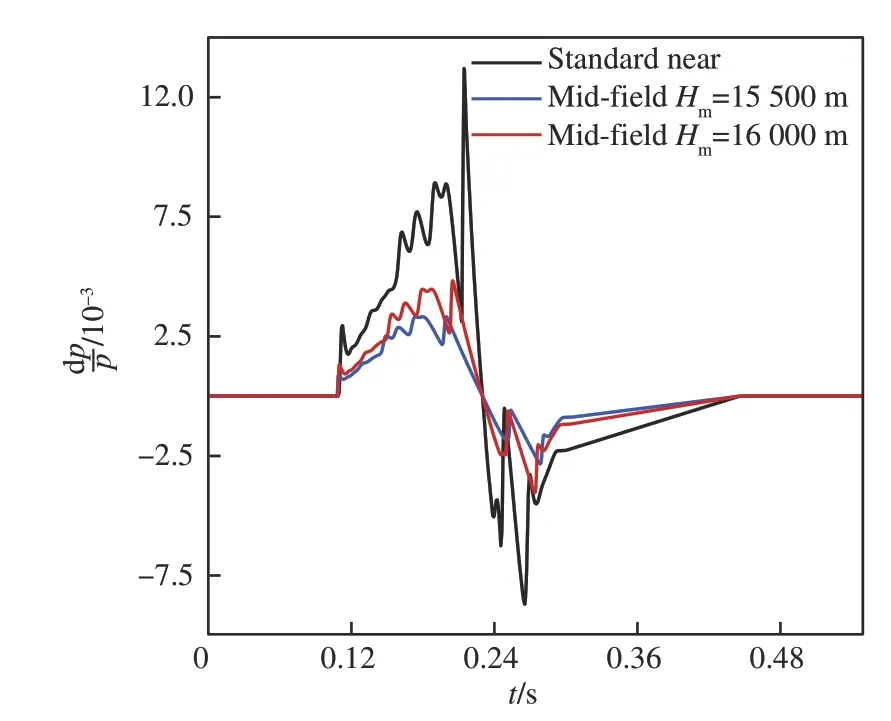
图18 LM1021 机体附近过压信号演化过程Fig.18 Evolution process of over-pressure signals near LM1021 body

图19 C608 机体附近过压信号演化过程Fig.19 Evolution process of over-pressure signals near C608 body

3.2 不同周向角下反演效果

周向角用以表示近场过压信号位置相对于机体的位置，其示意图如图 20 所示。通常情况下，飞机在不同周向角下的近场过压信号是不同的，且其向远场传播的声管路径也不同。但值得注意的是，若飞机的外形为轴对称的回转体，则其不同周向角下的近场过压信号相同。研究选取LM1021 与Axibody 两个标准算例进行研究。

图20 周向角相对于机体位置Fig.20 Rolling angles relative to body position

图21～图 25 展示了LM1021 算例在不同周向角下逆向增广Burgers 方程计算程序的反演结果。飞行高度、近场距离和飞行马赫数与3.1 节中相同，选取的中场高度为Hm=16 400 m。

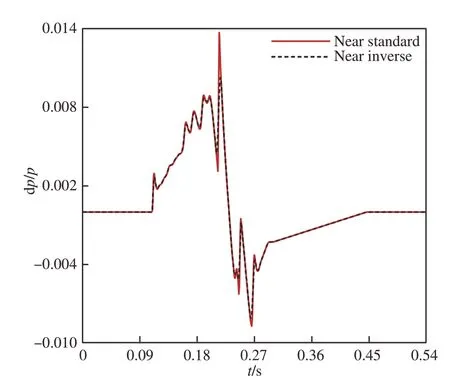
图21 周向角0°下近场波形对比（LM1021）Fig.21 Comparison of near-field waveforms at rolling angle 0°（LM1021）

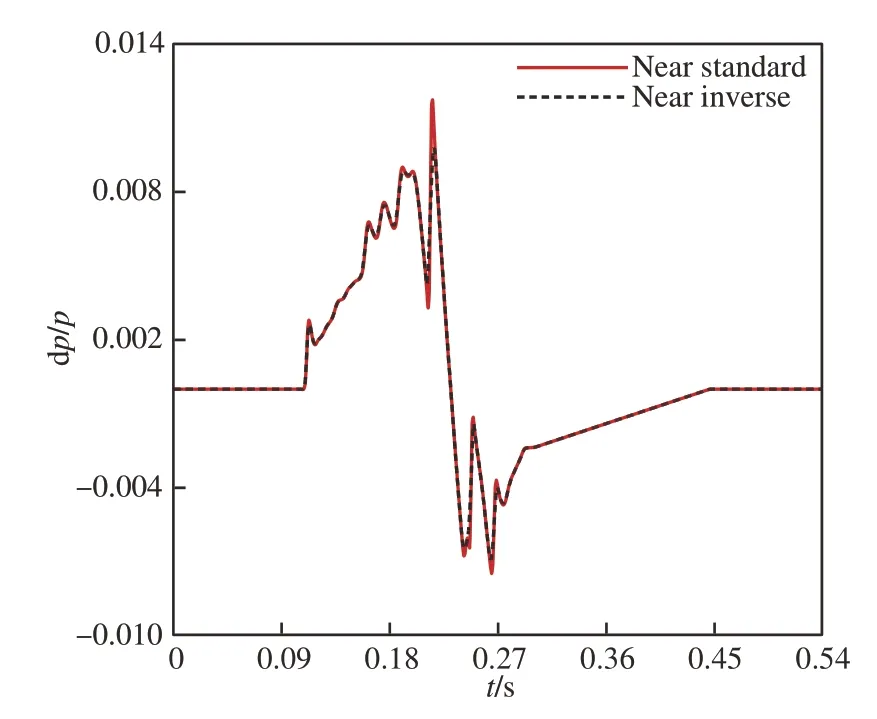
图22 周向角10°下近场波形对比（LM1021）Fig.22 Comparison of near-field waveforms at rolling angle 10°（LM1021）

图23 周向角20°下近场波形对比（LM1021）Fig.23 Comparison of near-field waveforms at rolling angle 20°（LM1021）

图24 周向角30°下近场波形对比（LM1021）Fig.24 Comparison of near-field waveforms at rolling angle 30°（LM1021）

图25 周向角50°下近场波形对比（LM1021）Fig.25 Comparison of near-field waveforms at rolling angle 50°（LM1021）

图26 展示了Axibody 算例在不同周向角下逆向增广Burgers 方程计算程序的反演结果。飞行高度、近场距离和飞行马赫数与第2.1 节中相同，选取的中场高度为Hm=15 500 m。由于Axibody为回转体外形，其不同周向角下的近场过压信号相同，因此可以直接比较不同周向角方向反演过压信号的不同。

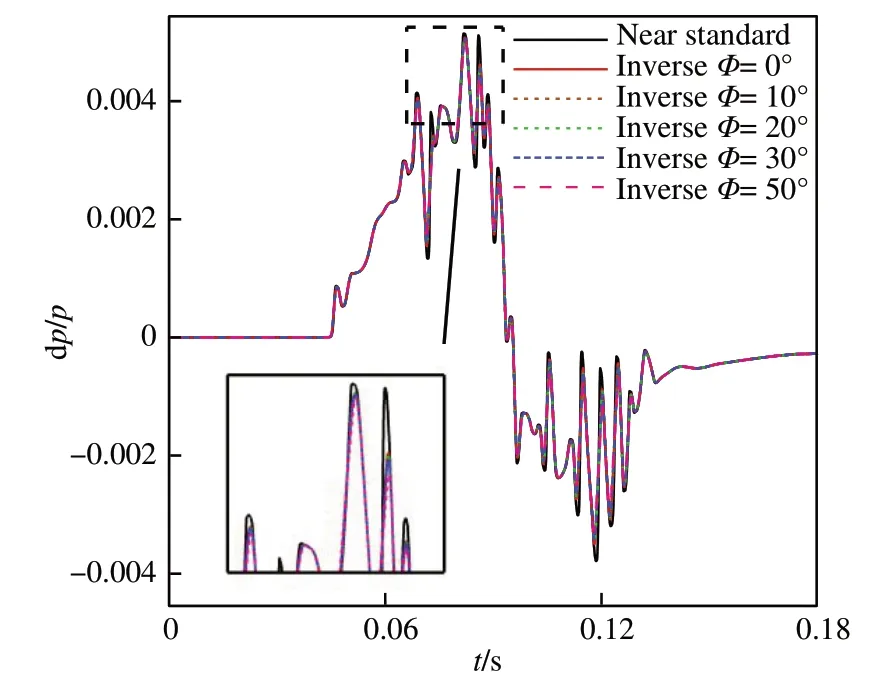
图26 不同周向角下近场波形对比（Axibody）Fig.26 Comparison of near-field waveforms at different rolling angles（Axibody）

由结果可以观察到，逆向增广Burgers 方程计算程序的反演准确度随着周向角的减小而有少量的提升，在周向角为0°时反演准确度最高。考虑到在低声爆反设计过程中，往往更为关注低周向角下声爆波形的传播，因此认为周向角对反演准确度的影响并不会对反设计任务造成过大的影响。

4 基于中场目标波形的优化设计方法可行性

在低声爆反设计方法中，通常先选取一个低噪声的地面远场目标波形，然后寻找到与其对应的近场波形，再利用Abel 逆变换获得对应的等效面积分布，并以此来指导飞行器的外形优化，其流程图如图 27 所示。由于前文提到的原因，逆向增广Burgers 方程难以将地面声压波形准确地反演至近场。因此，可以尝试在中场设计目标波形，以减轻反演过程带来的误差，其流程图如图 28 所示。本节对基于增广Burgers 方程的中场目标波形方法展开研究，验证中场目标波形方法的可行性，并对声爆信号中的高频分量对优化设计过程的影响进行了探讨。

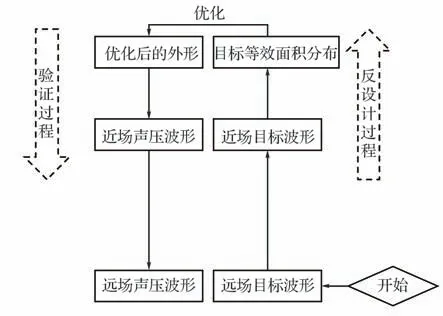
图27 基于地面目标波形的设计方法Fig.27 Design method based on ground target waveform

图28 基于中场目标波形的设计方法Fig.28 Design method based on mid-field target waveform

基于Plotkin 等［33］的研究成果，将低声爆地面目标波形修改为一个类正弦波形，能够有效地抑制声波中的高频分量的能量，从而降低人耳听觉频率范围内的噪声分量。研究尝试将这一结论用于中场目标波形的设计，使用一个类正弦的中场波形作为目标波形。选取LM1021 作为算例，飞行高度、近场与机体距离和飞行马赫数的选取与3.1 节相同，选取中场高度为Hm=14 500 m。利用正向增广Burgers 方程计算程序获取LM1021 在中场高度的声压波形，在此基础上设计了一个类正弦的目标中场波形，如图 29 所示。并将中场目标波形使用逆向增广Burgers 方程反演至近场，生成近场目标波形。

图29 中场目标波形Fig.29 Mid-field target waveform

由于物理约束的限制，通常很难通过对飞行器外形的优化设计，将对应的近场过压信号波形优化至和近场目标波形一致。通常情况下，近场过压信号在峰值附近会出现不可避免的高频振荡。为研究这一特性对优化过程的影响，研究在目标近场信号的峰值附近添加了频率约为100 Hz、200 Hz 和300 Hz 的振荡信号，以及200 Hz下最大振幅为1.8×10-3、2.7×10-3与3.6×10-3的振荡信号。将合成后的新波形作为假想的优化后近场波形，合成近场波形和目标近场波形如图 30 与图 31 所示。

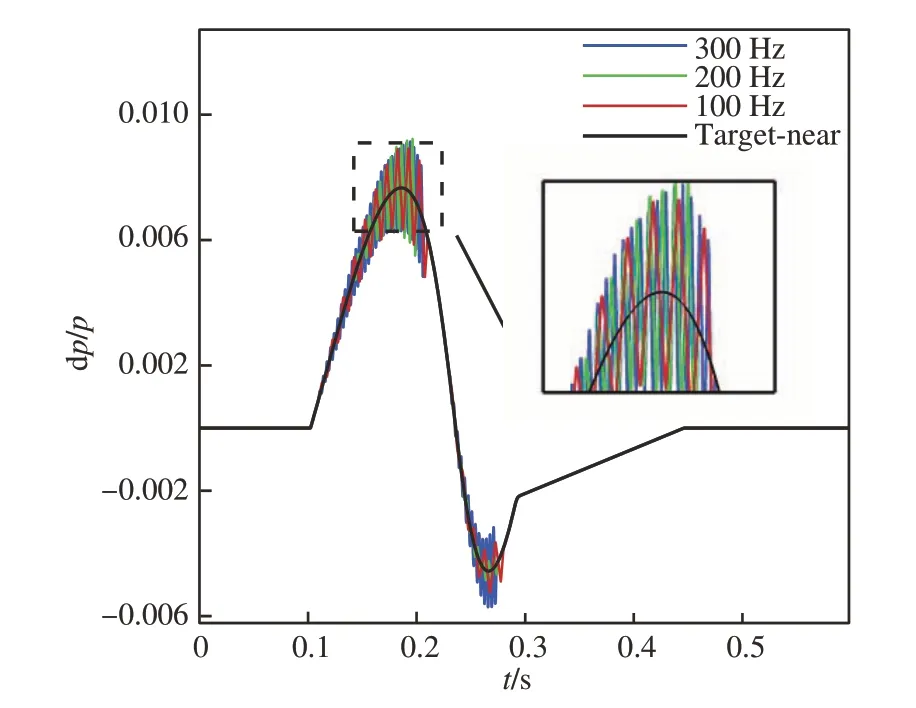
图30 不同频率的合成近场波形Fig.30 Synthetic near-field waveforms of different frequencies

图31 不同幅值的合成近场波形Fig.31 Synthetic near-field waveforms of different amplitudes

将合成近场波形和目标近场波形使用正向增广Burgers 方程计算程序传播至远场，其计算结果如图 32～图 34 所示。观察计算结果，可以发现中场目标波形在传递至远场后，其形状依然是一个类正弦波形，说明Plotkin 等［33］的研究结论也可用于中场目标波形的设计。而合成近场波形经过传播，可以发现同频率不同幅值的附加信号也并非按照相同的比例线性衰减，由于非线性效应对波形的扭转作用，大振荡幅度的高频分量会改变波形的整体形状。此外，也能观察到波形信号内高频分量的衰减幅度远大于低频基波分量，由于经典耗散效应和分子弛豫效应的存在，大气对高频声波分量的吸收作用更为明显，使得大气具有类似低通滤波器的性质［34］，而程序计算结果也与这一理论分析相吻合。