故障机理与领域自适应混合驱动的机械故障智能迁移诊断
2023-02-07于功也蔡伟东胡明辉刘文才马波
于功也,蔡伟东,胡明辉,刘文才,马波,*
1.北京化工大学 发动机健康监控及网络化教育部重点实验室,北京 100029
2.北京化工大学 高端机械装备健康监控及自愈化北京市重点实验室,北京 100029
3.中国科学院 工程热物理研究所,北京 100190
4.中国石油集团安全环保技术研究院,北京 102249
航空发动机作为机械工业“皇冠上的明珠”,其运行可靠性直接影响着整个飞行器的安全可靠运行[1-3]。中国航空发动机暂未实现地面试车、机载环境下的故障智能分析,其中主要原因之一为:针对单个型号航空发动机的各类故障案例样本较少,学者们研究以简化实验台为主,研究所得故障智能诊断方法由于迁移能力不足,难以在实际试车、飞行过程中应用。
经过多年发展,支持向量机[4]、神经网络[5]、聚类分析[6]等机器学习算法对特定场景下的故障诊断取得了很高的准确率。然而,以上算法受待测设备故障样本缺失及旋转机械个性化差异的影响,存在因设备个性化模型构建困难导致诊断准确率低的问题[7-8]。
近年来,领域自适应(Domain Adaptation)被众多学者认为是解决该困境的有效途径[9-10]。在机械故障诊断中,包含待测设备正常样本及未知状态样本的空间构成目标域,其他设备各类健康状态样本空间构成源域[11]。Chen 等[12]提出采用迁移成分分析(Transfer Component Analysis,TCA)的方法进行轴承故障诊断,该方法通过非线性变换使源域与目标域间的特征差异最小;雷亚国等[13]提出基于深度残差网络的诊断方法,该方法通过对网络施加领域适配正则约束缩小各设备间样本数据的差异;康守强等[14]采用子空间对齐算法将源域特征与目标域特征映射至高维空间,然后在高维空间进行特征对齐;Liao 等[15]提出领域泛化网络对变转速下的旋转机械进行诊断,该方法通过生成对抗网络和半监督学习的方法实现领域自适应,完成诊断网络搭建。此外,Shen 等[16]提出一种变工况故障诊断方法,采用TrAdaboost 算法选择与目标域数据类似的源域数据,并将其用于目标域诊断模型的训练;邵海东等[17]提出提升深度迁移自编码器的方法,该方法以源域数据的模型参数作为诊断模型的初始化参数,并采用目标域的少量样本对模型进行微调,即Fine-tune。
综上可知,现有的故障诊断方法均需目标域设备各类健康状态数据(包括正常数据和故障数据)才能实现诊断模型的构建,在实际应用中往往因目标域故障数据的缺失导致诊断模型构建困难,诊断准确率低。
针对目标域故障样本数据缺失的问题,样本生成是一种可行的解决思路。罗嘉宁[18]提出基于赫兹碰撞理论进行动力学仿真的虚拟故障样本生成方法,并采用SqueezeNet 架构的模型实现轴承故障程度评估;董韵佳[19]在轴承仿真模型的建立过程中考虑了滚动体打滑等随机因素,基于仿真数据训练的故障诊断模型对真实场景中轴承故障状态的识别准确率达到80%以上。基于动力学仿真的方法能够为机械设备建立较为准确的物理模型,然而仿真模型均是在一定简化条件下建立,未考虑实际设备的运行状态。对此,马波等[20]提出基于故障机理生成设备个性化虚拟故障样本的方法(Mechanism Character Generative Model,MCGM),MCGM同时结合了故障机理和设备的个性特征,最终在轴承故障诊断上取得了不错效果。然而该项研究存在2 个问题:①MCGM 中存在的不确定性参数依据经验设定,受人为因素影响较大;②仅验证了MCGM 在多种工况和故障尺寸下的诊断效果,未对其在不同设备间的泛化性能进行验证分析。
为此,在文献[20]研究基础上提出故障机理与领域自适应混合驱动的机械故障智能迁移诊断方法(Domain Adaptive Fault Diagnosis Based on MCGM,DA-MCGM)。该方法依据源域数据对MCGM 中的共性参数分布模型进行估计,将该分布模型和目标域正常数据共同用于MCGM 的自适应。最后,通过实验对提出方法在不同设备轴承间的诊断性能进行了验证。
1 相关理论
1.1 领域自适应

1.2 MCGM 原理
对基于状态数据进行设备故障诊断的系统而言,设备的故障状态数据由个性特征和共性特征组成。例如初始不平衡量、初始不对中量、环境噪声等均属于该台机械设备的个性特征,MCGM 原理认为,机械设备的正常数据反映了其个性特征;机械设备由于发生故障所体现的信号特征为机械设备的共性特征,例如周期性冲击所出现的特定故障频率。基于以上分析,通过对包含机械设备个性特征的正常数据添加共性特征即可生成相应故障的个性化虚拟样本,此即为MCGM 的原理[20]。故障状态频域数据的生成方法可表示为
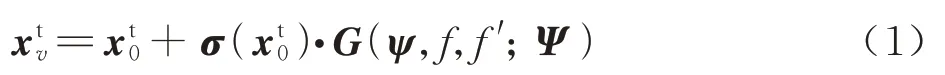
2 DA-MCGM 诊断方法
DA-MCGM 诊断方法依据旋转机械故障机理明确适用于不同设备的共性特征,基于不同样本的源域数据确定共性参数分布模型,并结合目标域正常数据和MCGM 原理生成目标域个性化故障虚拟样本,依据各状态样本实现目标域的故障诊断模型训练。
2.1 领域自适应
当轴承、齿轮、轴等转动部件发生故障时往往会产生激励源,导致机器在旋转过程出现周期性激励信号,在频谱上表现为特定的频率成分,即故障频率。MCGM 给出了个性化故障样本生成方法,然而受真实场景中噪声、装配误差等各类复杂因素的影响,故障频率幅值大小的分布难以确定。
以滚动轴承为例对提出方法进行论述,以内圈故障为例,在无噪声干扰的理想情况下,依据故障机理分析其理论上频域分布如图1 所示,存在内圈缺陷频率fIR,同时会伴有fIR的倍频及边带,以上3 种频率即轴承内圈故障频率成分。轴承内圈故障的MCGM 中存在3 项共性参数无法确定:

图1 轴承内圈故障频谱示意图Fig.1 Frequency diagram of bearing inner ring fault
1)缺陷频率fIR的幅值大小k未知,即图1 中的A1,令其服从分布Κ。
2)缺陷频率倍频幅值的相对变化系数为θ未知,即图1 中θ1~θ4,令θ服从分布Θ。
3)边带出现在缺陷频率及其倍频的左右两侧,令其相对变化系数为φ,即图1 中φ1、φ2,令φ服从分布Φ。
共性参 数k、θ、φ组成共 性参数向量ψ=(k,θ,φ),ψ服从Κ、Θ、Φ组成的联合概率分布Ψ=(Κ,Θ,Φ)。在源域数据足够充足的理想情况下,目标域共性参数向量分布Ψt应属于源域共性参数向量分布Ψs的子集,即Ψt⊆Ψs,因此将源域数据的共性参数向量用于建立目标域的MCGM 具备可行性。
2.2 方法流程
DA-MCGM 诊断方法应用流程如图2所示。
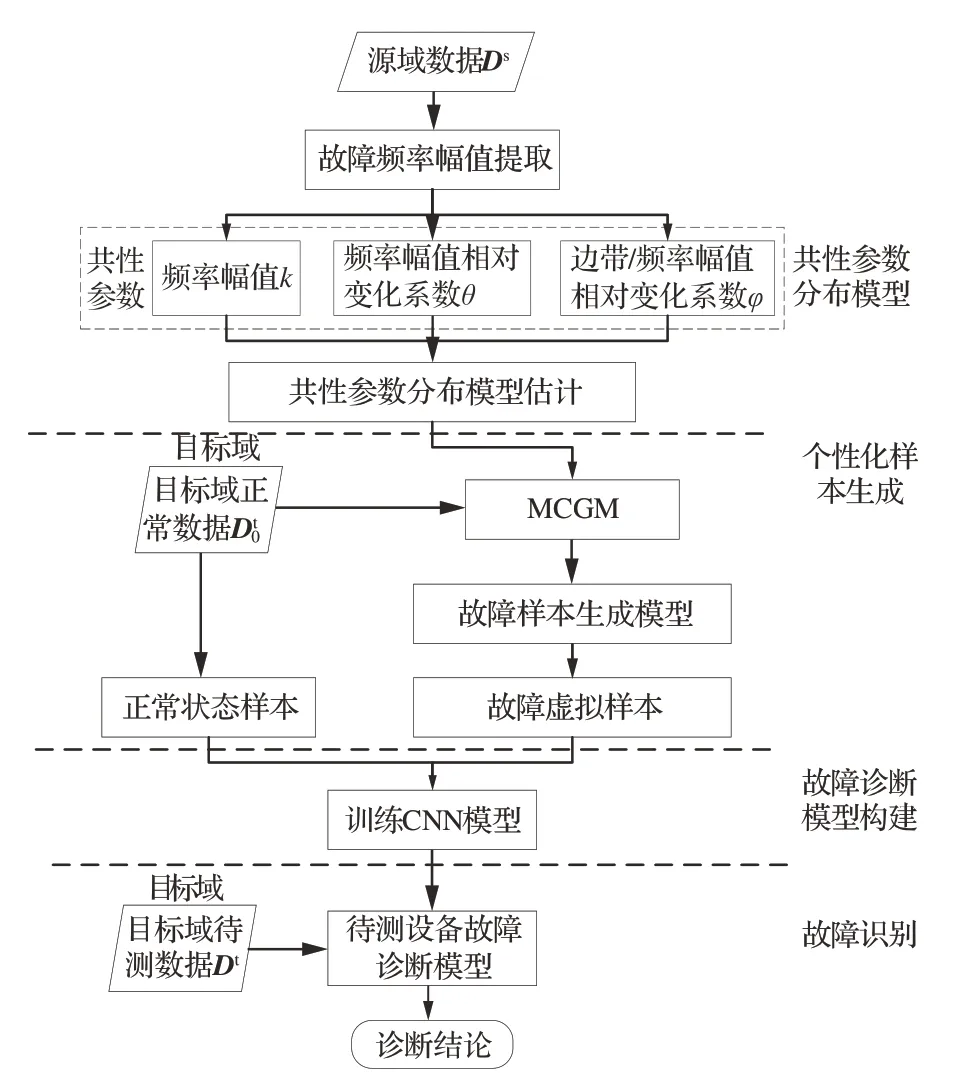
图2 DA-MCGM 诊断方法应用流程Fig.2 Fault diagnosis method application process of DA-MCGM
方法具体步骤如下:
步骤1 共性参数分布模型计算。将源域数据Ds的时域数据转换至频域,基于不同缺陷的故障机理,从Ds中提取各故障缺陷频率、倍频及边带的幅值,计算可反映故障类别的共性参数k、θ、φ,并计算其服从的分布模型。
步骤2 个性化样本生成。基于故障虚拟样本生成模型及正常状态样本,完成目标域训练样本生成。
2)依据故障样本生成模型获取故障虚拟样本,结合正常状态样本完成诊断模型训练样本生成。
步骤3 故障诊断模型构建。利用个性化样本训练卷积神经网络(Convolution Neural Network,CNN)得到目标域设备故障诊断模型。
步骤4 故障识别。依据目标域待测数据Dt与诊断模型识别故障类别,完成故障诊断。
2.2.1 共性参数的分布模型
基于故障机理生成目标域故障状态频域数据,依据式(1)可推导源域共性参数ψ=(k,θ,φ)的计算方法,鉴于k反映的是频谱的整体特征A1,而θ、φ反映的是局部特征,因此先计算k,进而依次计算θ和φ。令为源域中故障j的Q'个样本,为源域中正常数据的Q''个样本。对于任一,其共性参数的计算方法如下:
1)计算k。任取一正常数据,依据式(1)可得k的计算式为
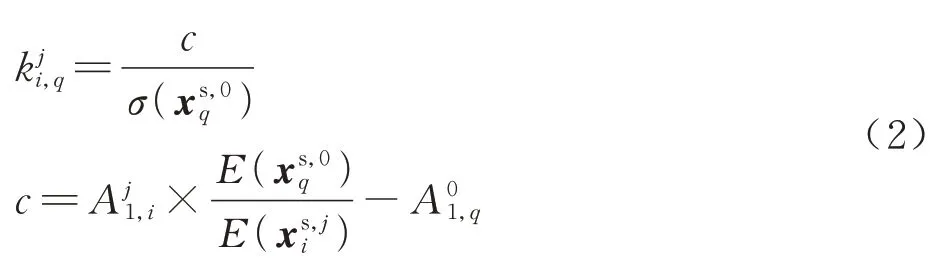
式中:E(·)和σ(·)分别为计算均值和标准差;分别为在故障频率处幅值;c为故障状态相对于正常状态时故障频率幅值的变化值。
2)计算θ。令在m(m≥2)倍故障频率处的幅值为,依据图1 可得m倍故障频率处的变化系数为

3)计算φ。令在m(m≥1)倍故障频率处边带的幅值为,依据图1 可得m倍故障频率处边带变化系数为

4)共性参数向量集合。对于故障j的任一数据和任一正常数据,可计算得到共性参数向量,则Q'组故障数据与Q''组正常数据形成共性参数向量集合为

对Ψ'的分布进行估计得到共性参数分布模型Ψs。考虑到狄利克雷过程高斯混合模型(Dirichlet Process Gaussian Mixture Model,DPGMM)能够拟合任何数据的分布并依据数据自动确定子成分数的优势[21]。且设备在出现相同故障时,其特定频率成分的频域分布存在一定的聚类性[22-23]。因此本文采用DPGMM 对共性参数服从的分布进行估计,参数估计方法为最大期望(Expectation Maximum,EM)算法,基于DPGMM 和EM 算法确定MCGM 的共性参数分布模型。
2.2.2 个性化样本生成
依据MCGM 的原理,样本生成方法如式(1)所示。通过旋转机械故障机理和相应部件的结构尺寸信息,可求取不同故障的理论故障频率,令f为故障频率理论值,f'为边带频率理论值,因此样本生成的关键在于G(·)的确定,G(·)为故障数据的缺陷频率幅值相对于正常状态发生变化的系数向量,基于2.2.1 节迁移参数ψ=(k,θ,φ)的计算方法可得到G(·),G(·)的计算方法伪代码如算法1 所示。由式(1)和算法1 伪代码可生成目标域设备的个性化故障样本。

算法 1 G(·)计算方法伪代码Algorithm 1 Pseudo code of calculation method for G(·)
2.2.3 故障诊断模型构建
基于CNN 的故障诊断模型结构及其结构参数分别如图3 和表1 所示[24]。表1 中M为P8 层的输出展开为一维向量后的维度,V为旋转机械源域故障类型数目,1 为机械设备的正常状态。鉴于旋转机械的故障频率集中在低频段,因此选取频域数据的前1 024 个样本点作为诊断模型的输入,即式(1)中xtv、xt0的频域数据长度L=1 024。
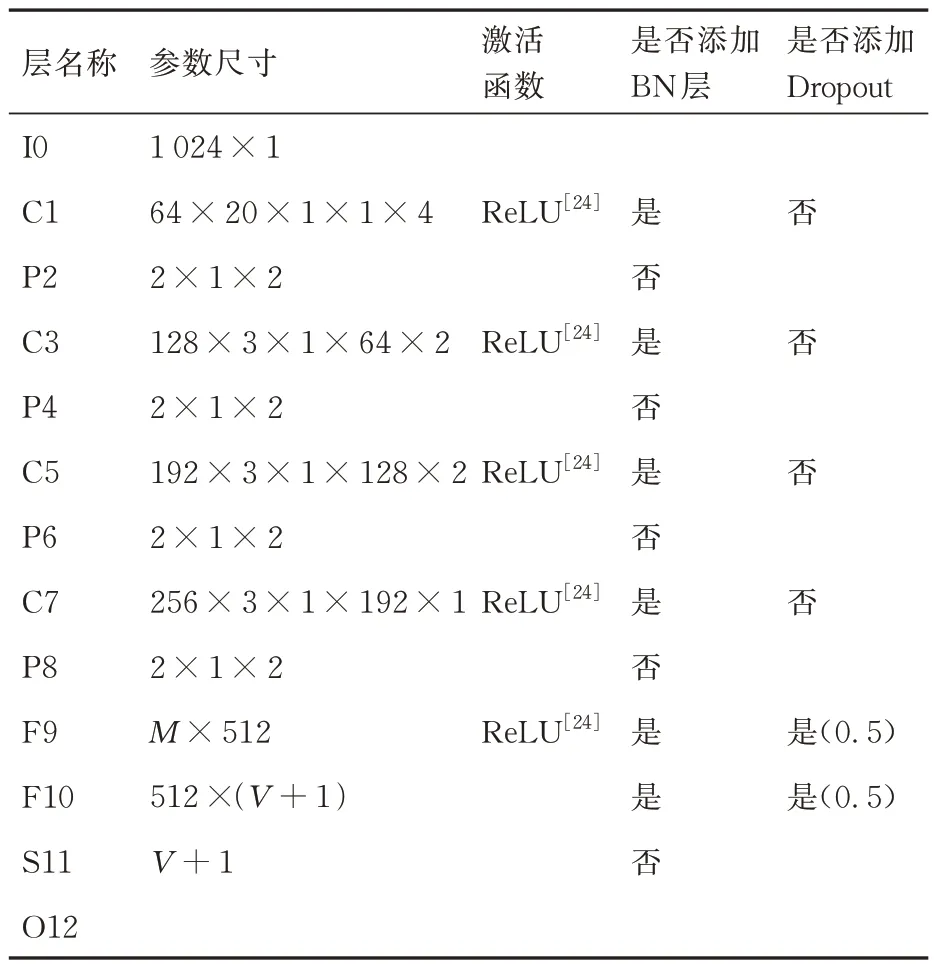
表1 故障诊断模型的结构参数Table 1 Structural parameters of fault diagnosis model

图3 CNN 故障诊断模型结构Fig.3 Structure of CNN fault diagnosis model
2.2.4 故障诊断
输入实测数据Dt至待测设备故障诊断模型中,完成故障诊断。
3 实验验证
以滚动轴承为例,基于CWRU[25]、MFPT[26]公开数据集和故障模拟实验台数据,对提出的DA-MCGM 方法有效性进行验证,同时与TCA[27-28]、测地流核函数(Geodesic Flow Kernel,GFK)[29]、领域对抗神经网络(Domain Adaptive Neural Network,DaNN)[30]、Finetune[17]4 种领域自适应方法以及未做任何改变的CNN 模型[31]的分析结果进行对比。方法验证环境使用Python 3.7 语言、PyTorch 1.6 机器学习框架和CUDA 10.1 GPU 加速库,计算机操作系统为Windows 10。
3.1 数据描述
基于上述数据组成表2 所示的数据集A、B、C和D,其中数据集A、B 和C 的实验数据为一段连续数据,故采用重叠采样的方法分割得到多组数据,每组数据基于希尔伯特变换的包络谱频域分辨率为1 Hz,数据集D 的分辨率则为1.562 5 Hz(25 600 Hz/16 384)。
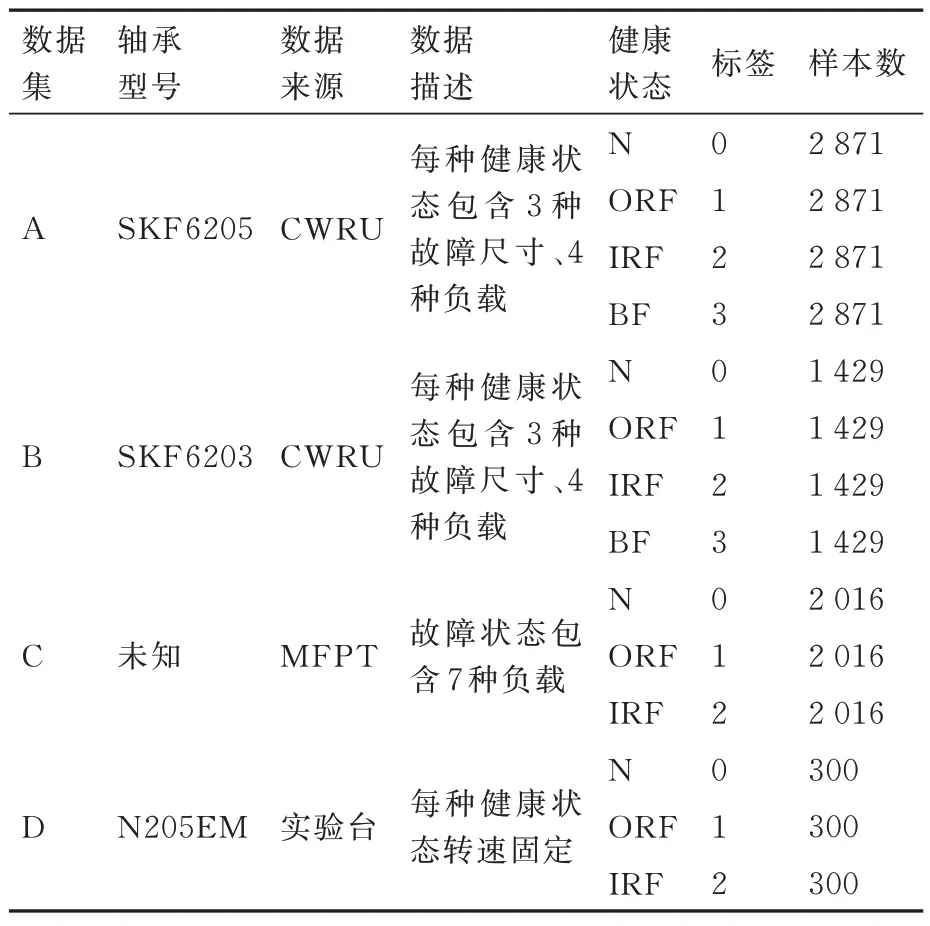
表2 轴承数据集Table 2 Bearing datasets
实验室搭建的轴承故障模拟实验台(以下简称实验台)如图4 所示,实验台由电机、增速箱、平衡盘、轴承等部件组成。实验轴承安装于右侧轴承座内,轴承型号为N 205 EM 圆柱滚子轴承。通过实验模拟了轴承正常、外圈故障和内圈故障共3 种健康状态。轴转速为1 200 r/min,采用右侧轴承座上的传感器分别采集3 种健康状态的加速度信号,每种健康状态采集300 组,每组采样点数为16 384,采样频率为25 600 Hz。

图4 轴承故障模拟试验台Fig.4 Simulation test bench for bearing failure
3.2 方法验证
方法应用前提为目标域数据状态标签集合为源域数据状态标签集合的子集,即yt⊆ys,以各数据集作为源域,组成表3 所示的8 项诊断任务对方法进行验证。其中训练样本中故障样本均为依据目标域正常状态数据生成的个性化故障虚拟样本,目标域的真实故障数据均为测试样本。

表3 诊断任务列表Table 3 List of diagnostic tasks
依据轴承故障机理模型[32],ORF 不存在边带,IRF 和BF 存在边带,故轴承故障的共性参数如表4 所示。

表4 轴承故障共性参数Table 4 Common parameters of bearing failure
以数据集A、B 为例,分别计算ORF、IRF 和BF 的共性参数,其分布如图5 所示,从图可看出:①相同故障的共性参数分布相似,但数值存在差异;②共性参数间存在一定相关性(若不相关其分布应为圆形或圆球形),例如ORF,当Κ取值较大时,Θ的取值较小,反之亦成立。
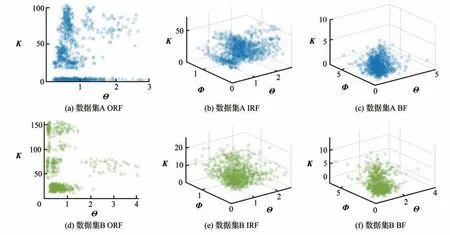
图5 数据集A、B 共性参数分布Fig.5 Distribution of common parameters of datasets A and B
依据源域数据集A 的共性参数分布模型与目标域数据集B 的正常数据,生成的数据集B 中3 类个性化故障虚拟样本及真实样本如图6 所示。图中fB为电机旋转频率,fOR、fIR和fBF分别为轴承外圈、内圈和滚动体缺陷频率。图6 所示真实样本受噪声中各频率成分干扰及设备个性特征的影响,其频域分布与图1 所示理想状态下的频域分布存在一定区别。由图6 可看出,虚拟样本与真实样本频率分布相近,其中虚拟样本更加突出故障频率,某些真实样本甚至无法观察到明显的故障频率,例如BF。
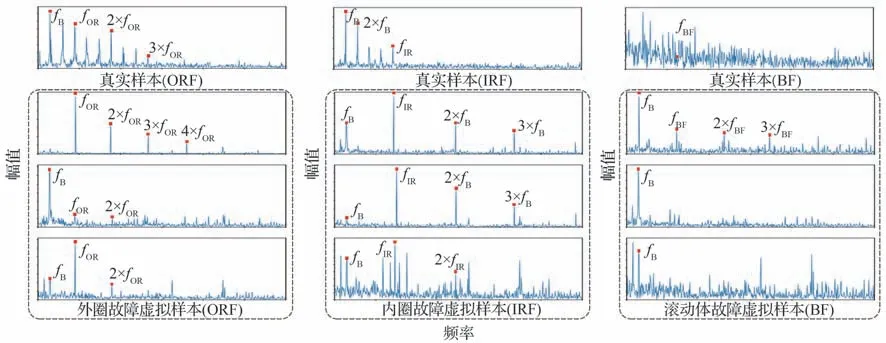
图6 故障虚拟样本与真实样本Fig.6 Fault virtual samples and real samples
3.3 结果分析
采用十折交叉实验对DA-MCGM 方法进行测试,8 项诊断任务的实验诊断准确率如表5 所示,可看出不同诊断任务的准确率存在较大差异,其中诊断任务A →B 与B →A 的准确率均较低,而其余6 项诊断任务的准确率均高于90%。这与数据集A 和B 的工况类型较为复杂有关,其每种健康状态的数据均由3 种故障尺寸和4 种负载组成。为进一步分析方法的有效性,以下从共性参数分布的影响和对比方法对实验结果进行分析。
3.3.1 共性参数分布影响
通过控制变量法研究共性参数对诊断准确率的影响。表6 为共性参数服从不同分布模型的情况下8 项诊断任务的平均准确率,表中Κ、Θ和Φ为采用2.2.1 节方法得到的共性参数分布模型,N(μ,σ2)代表均值为μ标准差为σ的正态分布。
由表5 数据可得到DA-MCGM 方法对8 项诊断任务的平均准确率为88.61%,此时共性参数(k,θ,φ)∈Ψ=(Κ,Θ,Φ),对比表6 中的实验结果可看出,不同共性参数分布下的准确率均低于提出方法。
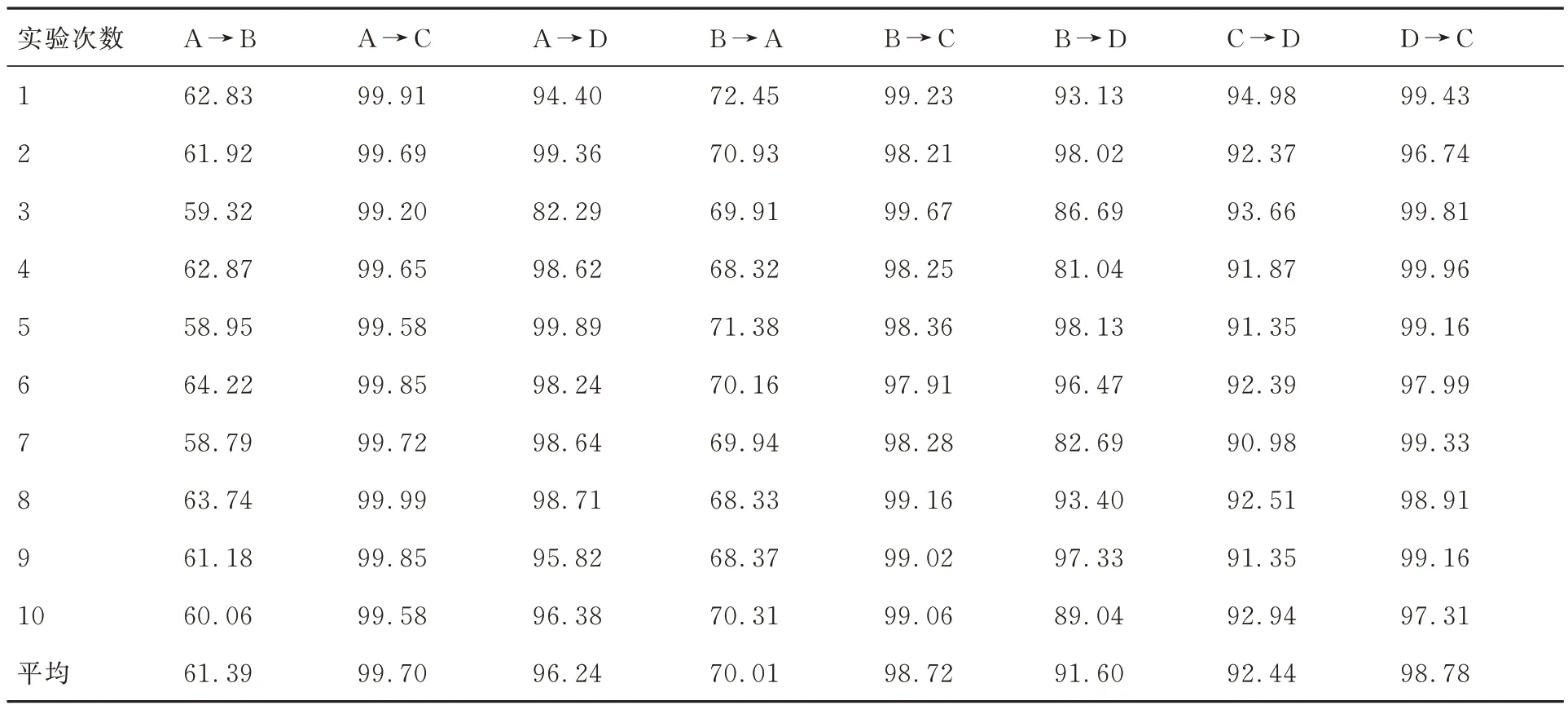
表5 十折交叉实验诊断准确率(%)Table 5 Diagnostic accuracy of ten-fold crossover experiment(%)
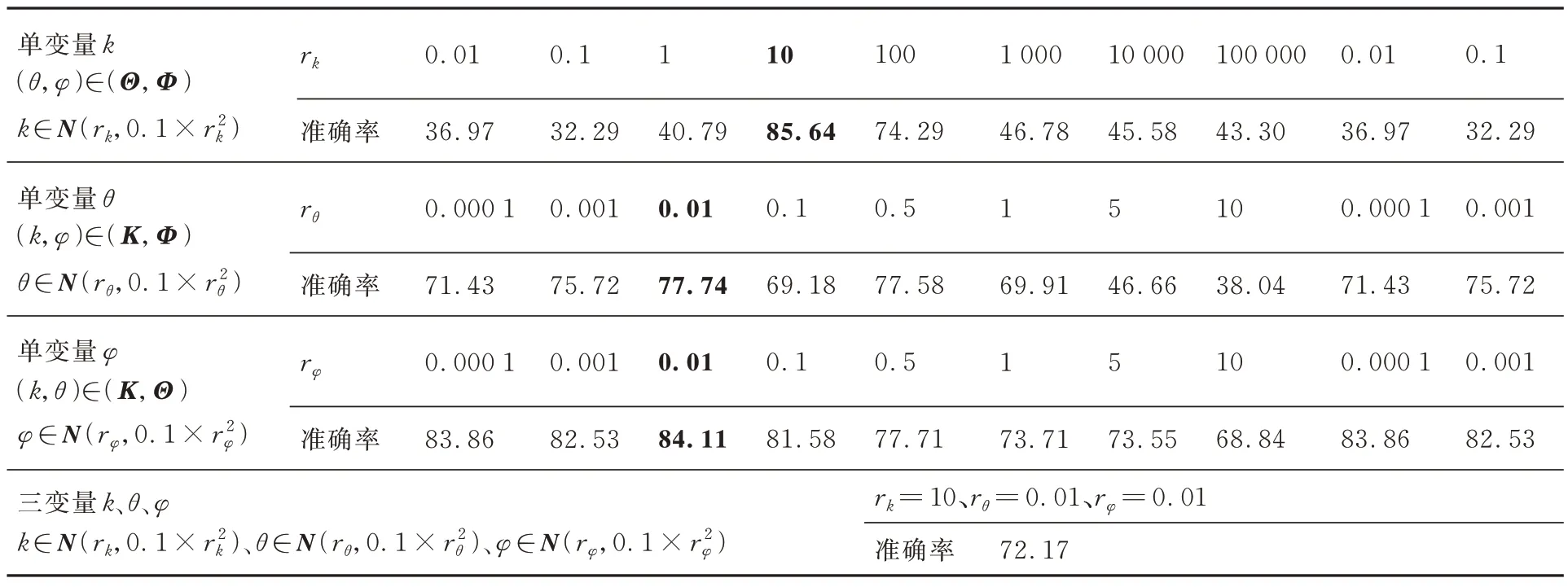
表6 不同共性参数分布下的诊断准确率(%)Table 6 Diagnostic accuracy under different common parameter distributions(%)
在单变量情况下,不同共性参数对准确率的影响存在差异,例如,k在10 左右取得最大值,而φ在小于0.5 时依旧有较高准确率,这与k影响频谱整体而φ仅影响边带有关。选取单变量情况下的最佳分布组合进行三变量实验,实验结果表明准确率为72.17%,相比DA-MCGM 方法低16.44%。
以上结果表明共性参数分布模型对提出的DA-MCGM 方法准确率存在较大影响,共性参数分布的确定是基于MCGM 的故障诊断方法应用的关键,本文提出的基于源域数据建立共性参数分布模型的方法取得了较好的效果。
3.3.2 对比分析
提出的DA-MCGM 方法和对比方法的描述见表7,6 种方法在8 项诊断任务中的实验结果见表 8。由对比方法实验结果可看到:DA-MCGM方法的平均准确率最高,为88.61%,对比方法中DaNN 的平均准确率最高,为47.39%,相比DA-MCGM 方法低41.22%。该结果表明提出方法具有明显优势,在解决不平衡样本问题时基于故障机理生成虚拟样本的思路具有明显的优越性。

表7 方法描述Table 7 Method description
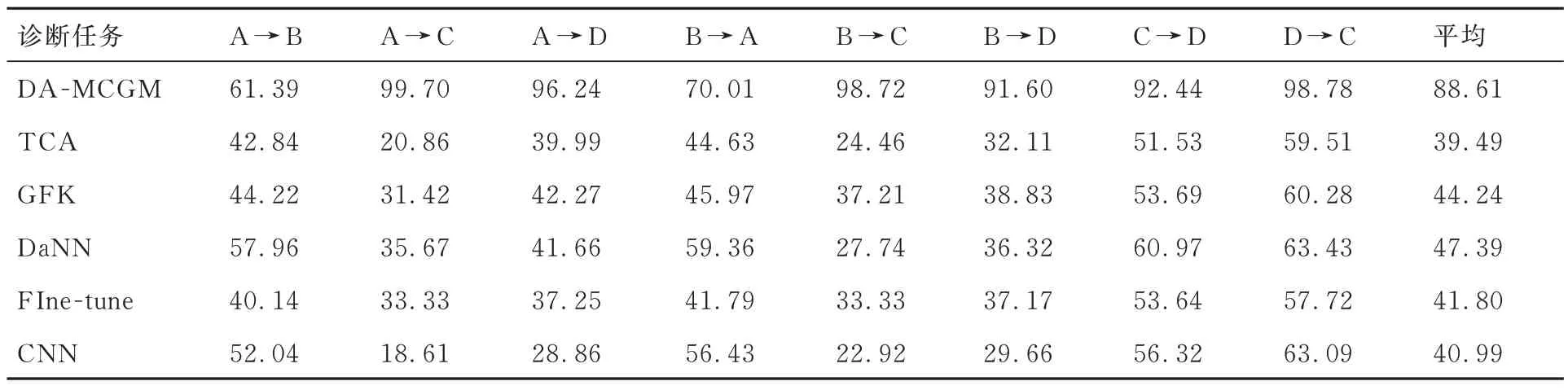
表8 试验结果准确率对比(%)Table 8 Comparison of test results accuracy(%)
以CNN 方法的准确率作为基准值进行分析:
1)从单个诊断任务分析。提出的DAMCGM 方法在8 项诊断任务中的准确率均高于对比方法,达到了较好的诊断效果;对于对比方法,DaNN 在8 项诊断任务的准确率均高于基准值,TCA、GFK 和Fine-tune 在部分诊断任务的准确率高于基准值,但总体而言均表现出一定的诊断效果。
2)从单个方法的实验结果分析。对比方法在诊断任务A →B 与B →A 中的准确率明显较高,而DA-MCGM 方法恰恰相反,在诊断任务A →B 与B →A 中准确率较低。结合数据集的特点可发现,数据集A、B 的工况种类更为复杂,每类故障包含3 种故障尺寸4 种负载。以下对两者差异的原因进行分析。
对于对比方法,数据集A、B 均来自CWRU,两个数据集工况相同,轴承型号类似,相较于其余6 项诊断任务而言,诊断任务A →B 与B →A中源域与目标域的相似度更高。由于对比方法完全基于数据实现领域适应,因此数据的相似度越高,从源域到目标域的领域适应效果越好,因而在诊断任务A →B 与B →A 取得了更高的准确率。
对于DA-MCGM 方法,表9 为方法对各类别故障的诊断准确率,可看到BF 的准确率较低。由图6 所示的BF 包络频谱可看到,其它频率成分远高于BF 的缺陷频率fBF,fBF被淹没,而DA-MCGM 方法基于机理模型建立,导致其诊断准确率较低。因此,如何实现提出方法与对比方法的优势互补值得进一步研究。
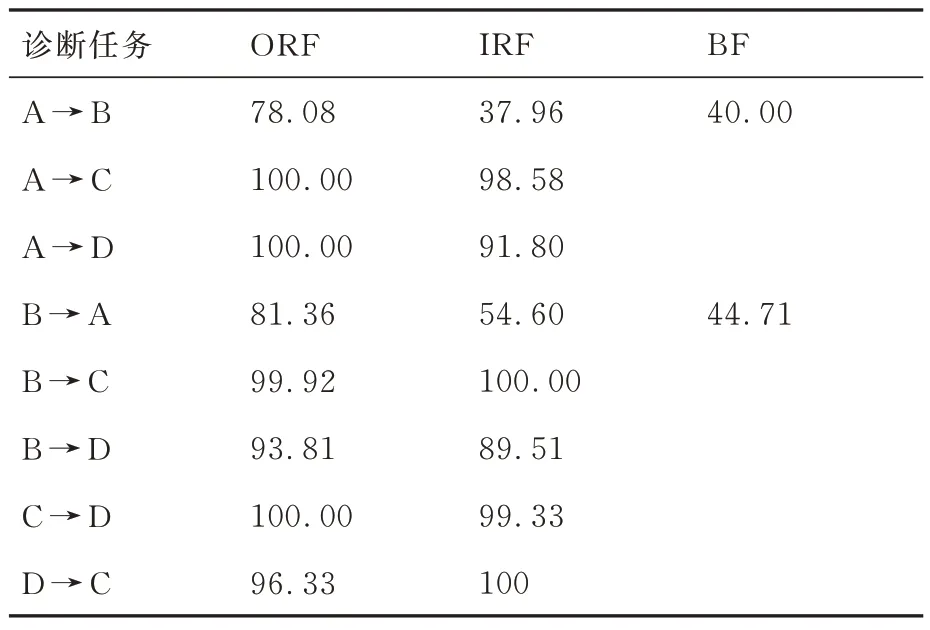
表9 DA-MCGM 方法对各类别故障诊断准确率(%)Table 9 Diagnostic accuracy of DA-MCGM method for various types of failures(%)
4 结论
1)DA-MCGM 方法考虑了每类设备的共性故障机理和该类每台设备的个性特征,依据领域自适应,较好实现了诊断模型的构建,相比现有诊断模型构建方法具有明显优势。
2)实验证明了共性参数分布模型对MCGM 的影响,提出的共性参数分布模型建立方法取得了很好的效果。
3)丰富了旋转机械故障样本生成方法,进一步证明了基于故障机理生成的个性化虚拟样本可代替真实样本,对其他领域中小样本问题的解决具有借鉴意义。
