基于月球借力的低能DRO 入轨策略
2023-02-07张晨张皓
张晨,张皓
中国科学院 空间应用工程与技术中心,北京 100094
随着航天技术的发展,人类的生存空间逐渐由近地空间拓展到地月空间,2017 年美国国家航空航天局(National Aeronautics and Space Administration,NASA)提出的“ 阿尔忒弥斯(Artemis)”任务[1]将首次实现人类在月球及其轨道上的长期居留,并为未来复杂的载人火星任务奠定基础。2021 年中国与俄罗斯就建设国际月球科研站达成了合作协议[2]。可以预见在未来很长一段时间内,地月空间都将是人类航天活动的主要内容。在地月空间部署大型月球轨道站可以显著降低月球开发成本并作为其他深空任务的跳板[3-5],停泊轨道的选择不能以单方面性能作为评价指标,而应权衡各种任务场景以达到综合性能最优。其中近直线晕轨道(Near Rectilinear Halo Orbit,NRHO)和远距离逆行轨道(Distant Retrograde Orbit,DRO)是两类适合部署月球轨道站的三体周期轨道族,这两类轨道具有一定的相似性,但侧重点略有不同,NRHO 适合用于载人登月任务,而DRO 更能兼顾后续的小行星及火星任务,本文仅对基于DRO 的月球轨道站部署策略展开研究。
近年来多个任务围绕地月三体系统中的DRO轨道展开,这类轨道具有长期稳定性好和入轨代价低的特点。例如“小行星重定向任务(Asteroid Redirect Mission,ARM)[6]”计划从小行星上抓取一块巨石并拖曳至DRO 轨道上,DRO 当中的某些轨道具有长达100 a 的稳定性而不需要进行频繁的轨道维持。Artemis 的首星[7]将把猎户座飞船送入25.5 d 的任务轨道,其中6 d 将位于DRO轨道。面向未来DRO 月球轨道站的在轨建造和货物补给任务,提高DRO 入轨质量是重要问题。
1987 年Belbruno[8]提出的弱稳定边界(Weak Stability Boundary,WSB)转移技术在深空任务中获得巨大成功,WSB 转移依靠多个引力体的相互作用,利用混沌区域所展现的一些新的动力学特性降低飞行器入轨脉冲。WSB 转移最早用于奔月轨道设计,通过选择合适的地球发射条件,卫星首先抵达日地引力混沌的弱稳定边界(大约3~5 倍地月距),卫星在这个区域无动力飞行时,太阳引力将近地点从地球附近抬升至月球轨道附近,当卫星从外部返回月球时被低能捕获[9],尽管这种方法需要80~120 d 的飞行时间,但是能够节省大约25%的月球制动脉冲。1991年WSB 转移首次应用于日本Hiten[10]卫星的营救任务,随后GRAIL(Grarity Recovery and Interior Laboratory)[11]、ESMO(the European Student Moon Orbiter)[12]、CAPSTONE(Cislunar Autonomous Positioning System Technology Operations and Navigation Experiment)[13]、KPLO(Korea Pathfinder Lunar Orbiter )[14]等任务都采用或计划采用WSB 转移技术。
国内外学者围绕WSB 转移轨道的设计方法展开了内容丰富的研究,Koon 等[15]通过平动点附近的不变流形对WSB 的转移机理进行了解释,并采用双三体流形拼接方法构建了低能奔月轨道。Yagasaki[16]在四体简化模型下将地月WSB 转移问题转换成非线性规划问题,通过数值迭代求解了地月低能转移轨道。WSB 转移不仅适用于地月低能转移,也适用于DRO、NRHO、L4/5等地月空间典型周期轨道。Xu M 和Xu S J[17]、Tan 等[18]利 用L1/2附近不变流形设计了基于WSB 转移的DRO 入轨策略。Scheuerle等[19]基于多步打靶和和数值延拓在四体简化模型下计算了地球至DRO 的低能转移轨道。Zhang 和Hou[20]在双圆四体模型下设计了地球至L4/5的低能转移轨道。
为了最大化飞行器入轨质量,一些学者指出在WSB 转移轨道的地球出发段增加月球借力(Lunar Gravity Assist,LGA)能够有效降低火箭发射能量。为方便描述,将这种类型的转移轨道称为“LGA+WSB”转移方式。“LGA+WSB”最早出现于Belbruno 和Miller 在1993 年发表的文章[10]。Topputo[21]在双圆四体模型下探索了两脉冲地月低能转移轨道的全局解空间,并对不同转移方式进行了分类,指出“LGA+WSB”转移方式具有较低的火箭发射脉冲。Parrish 等[13]针对“CAPSTONE”任务对2 种NRHO 入轨方案进行了对比,其中“WSB”方案火箭发射脉冲较高但是发射窗口宽松(每天都有发射窗口),“LGA+WSB”方案火箭发射脉冲较低但是发射窗口紧张(一个月一次)。上述研究没有针对敏感的月球借力进行单独设计和优化,转移轨道中仅有很少一部分呈现“LGA+WSB”的转移方式,数值计算效率较低。Scheuerle 等[19]在双圆四体模型下从“WSB”延拓得到“LGA+WSB”转移轨道,但没有在星历模型下进行修正。Tselousova 等[22]在双圆四体模型下基于轨道拼接的思路设计了“LGA+WSB”转移轨道,设计过程较为繁琐且没有在星历下实现。
为了提高星历模型下的“LGA+WSB”转移轨道设计效率,为了避免复杂动力学环境对转移轨道收敛性所带来的影响,使用“近月点庞加莱图”和“v无穷匹配”获得转移轨道初值,再通过“多步打靶”在星历下修正转移轨道。改进的方法充分优化了月球借力参数,有效改善了“LGA+WSB”转移方式的计算效率,所得到的转移轨道满足地球发射约束和高精度动力学约束。
本文结构如下:第1 节介绍火箭发射能量和载荷质量的关系;第2 节为动力学模型和状态转移矩阵;第3 节介绍DRO 轨道;第4 节介绍“LGA+WSB”转移方式的特点;第5 节介绍LGA 至DRO 轨道段的设计方法;第6 节介绍近地球轨道(Lwo Earth Orbit,LEO)至LGA 轨道段的设计方法;第7 节介绍多步打靶技术;第8 节为数值仿真;第9 节为结论。
1 火箭发射能量和载荷质量
假设卫星初始位于近地圆形停泊轨道,沿切向施加脉冲抬升远地点高度。卫星在近地点的速度模表示为
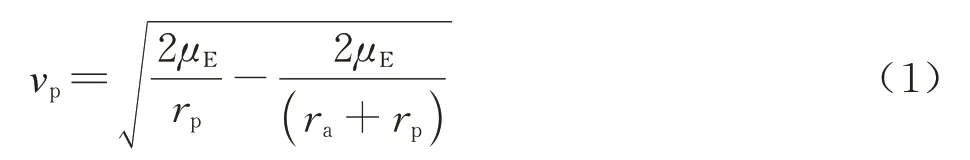
式中:ra和rp分别为远地点和近地点地心距;μE为地球引力常数。卫星在近地点的脉冲为

发射能量C3表示为

假设卫星近地点高度为200 km,图 1 展示了LEO 发射脉冲Δνdep和发射能量C3随远地点地心距ra的变化曲线。当发射脉冲Δνdep=3.131 3 km/s时远地点能够抵达月球(ra约为4×105km),发射能量C3约为-2.03(km)2/s2。发射脉冲为[3.194 3,3.206 3] km/s 时远地点抵达WSB 区域ra约为[1.2,2.0]×106km,发射能量C3约为[-0.66,-0.39](km)2/s2。
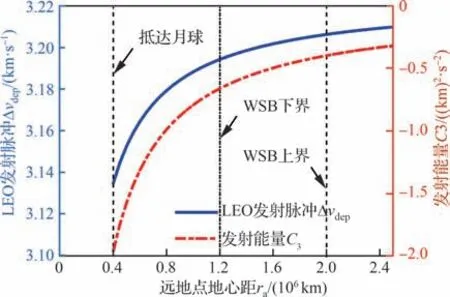
图1 Δvdep 和C3 随远地点高度变化曲线Fig 1 Δvdep and C3 according to apogee radius
采用国外公开的火箭运力曲线[23],图 2 展示了猎鹰9 Block 2 火箭载荷质量随发射能量的变化曲线。猎鹰9 发射地月转移轨道的载荷质量为2 619.77 kg,直接发射至WSB 的载荷质量为[2 500.24,2 519.34] kg。因而如果先将卫星发射至地月转移轨道,再借助月球借力将远地点抬升至WSB,则能够节省60~70 m/s 的速度脉冲,提升载荷质量100.43~119.53 kg。
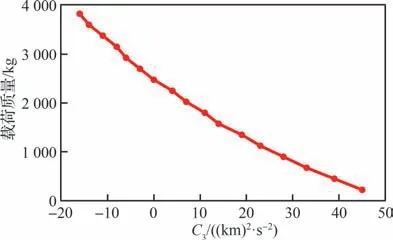
图2 猎鹰9 载荷质量随C3 变化曲线Fig 2 Rocket capability according to characteristic energy C3 of Falcon 9 Block 2
2 星历模型和状态转移矩阵
在深空任务设计时,经常使用高精度的N体星历模型对转移轨道进行设计和修正。图 3 展示了N体星历模型示意图,其中k为中心天体,i为卫星,j为其他摄动天体。定义卫星状态x=[rki,vki]⊤,卫星的动力学方程表示为
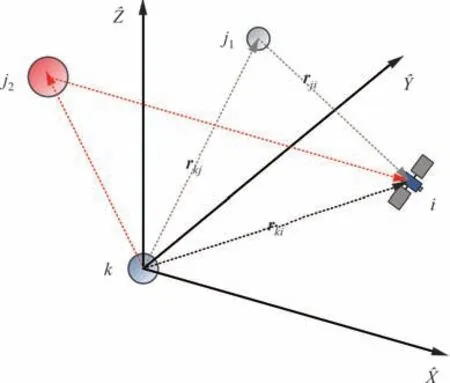
图3 N 体星历模型Fig 3 N-body ephemeris model

式中:rki为卫星i相对于中心天体k的位置矢量;vki为卫星i相对于中心天体k的速度矢量;rkj为摄动天体j相对中心天体k的位置矢量,可以通过JPL 的DE430 星历获得;rji为卫星i相对摄动天体j的位置矢量,表示为

可以发现摄动天体的位置矢量随历元变化,因而N体动力学模型是历元的函数。
轨道修正经常使用状态转移矩阵这一概念,状态转移矩阵在一阶程度上刻画了初始状态改变量对终端状态改变量所产生的影响[24]。状态转移矩阵的动力学方程表示为
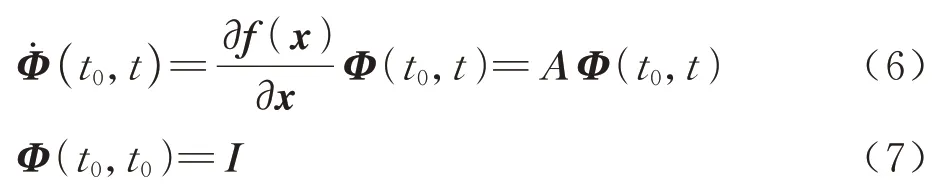
式中:I为单位矩阵;Φ为状态转移矩阵;f(x)为卫星动力学方程;A为动力学方程对状态求偏导得到的矩阵;t0为初始时刻,t为转移时刻。定义y为状态变量x和状态转移矩阵Φ构成的列向量,其动力学方程表示为
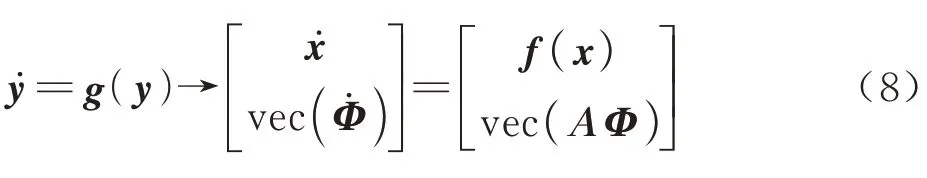
其中:g(y)为卫星状态和状态转移矩阵的动力学方程;“vec”是将矩阵变为列向量的算子。
3 DRO 轨道
DRO 是圆型限制性三体问题(Circular Restricted Three-Body Problem,CRTBP)中一类稳定的平面轨道族[25-28],在旋转坐标系下该轨道沿顺时针(逆行)运动。图 4 展示了DRO 轨道族,轨道颜色用于区分轨道周期,L1~L5为5 个平动点,图中距离单位1 LU=384 400 km。可以发现振幅越小的DRO 轨道周期越短。DRO 共振比是指轨道周期与月球公转周期之比,具有典型共振比的周期轨道通常可保证卫星与地球、月球具有周期性的几何关系,在数值仿真中用到了共振比2∶1 的DRO 轨道。
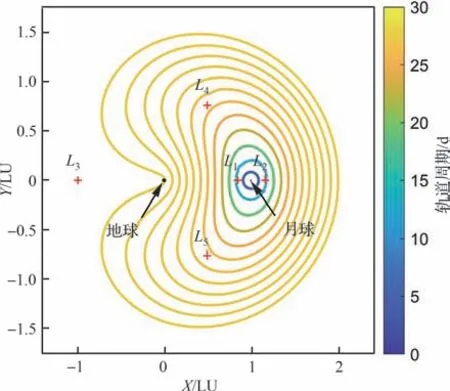
图4 CRTBP 下 的DRO 轨道族Fig 4 DRO family in CRTBP
以CRTBP 的DRO 轨道作为初值,使用多步打靶可获得星历下的DRO 轨道,定义为DRO 参考状态,则在星历模型下数值积分可以得到DRO 轨道上任意一点的状态xdro,表示为

式中:φeph表示以为初值,从τ*到τ积分星历模型所得到的解。
4 转移轨道设计
基于月球借力的低能DRO 入轨策略可简单描述为,卫星初始位于近地圆形停泊轨道,施加第1 次脉冲后进入地月转移轨道(Lunar Transfer Orbit,LTO)并掠飞月球,卫星通过月球借力抬升远地点高度并改变轨道倾角,之后抵达地月3~5 倍距的弱稳定边界,卫星在这里持续受到太阳引力的影响并抬升近地点高度,当再次返回地月空间时施加第2 次脉冲并进入DRO 轨道,希望优化轨道转移策略使得两次脉冲和最小。图 5 展示了“LGA+WSB”的DRO 入轨示意图,其中,Δvarr为DRO 入轨速度脉冲矢量;Δvdep为LEO 发射脉冲矢量。
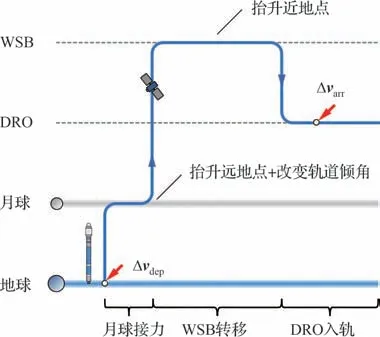
图5 LGA+WSB 的DRO 入轨示意图Fig 5 Illustration of LGA+WSB transfer into DRO
“LGA+WSB”的转移方式能够有效降低任务总脉冲,但是复杂的动力学环境和月球借力给转移轨道设计带来解空间庞大和数值敏感等问题。本文将分别设计“LGA 至DRO 轨道段”和“LEO 至LGA 轨道段”,再使用多步打靶技术修正整条转移轨道。
5 LGA 至DRO 轨道段
本节将构造近月点庞加莱图,使得转移轨道从DRO 逆向积分先抵达WSB 再抵达近月点。图 6 展示了DRO 入轨时刻示意图,卫星在DRO入轨时刻的状态x(τf)表示为
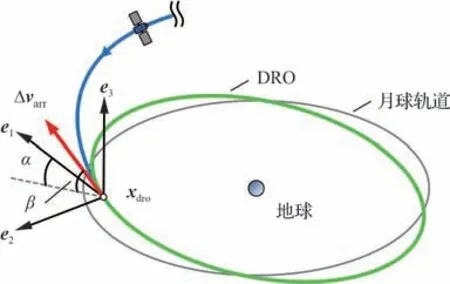
图6 DRO 入轨示意图Fig 6 Illustration of DRO insertion
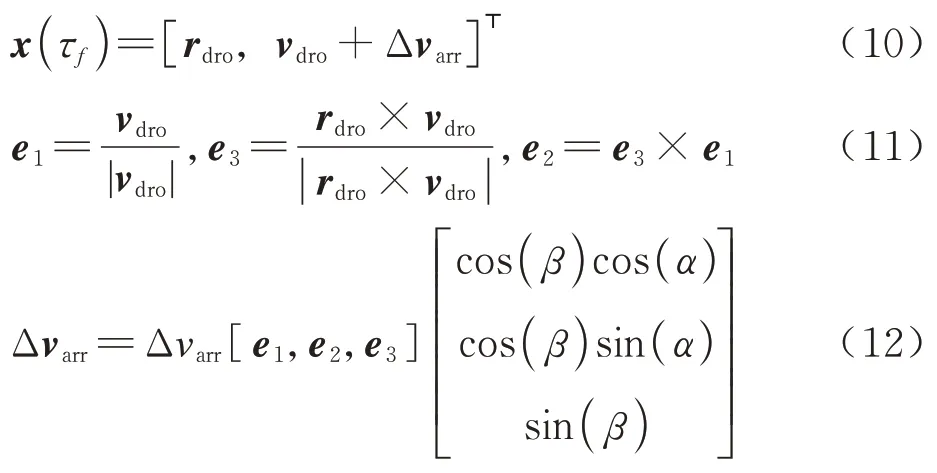
式中:xdro=[rdro,vdro]⊤为入轨时刻DRO 的状态;rdro为入轨时刻DRO 位置矢量;vdro为入轨时刻DRO 速度矢量;Δvarr为入轨脉冲矢量;Δνarr为入轨脉冲矢量的模;α∈[0,2π)为Δvarr在e1—e2平面的投影与e1的夹角;β∈[ -π/2,π/2]为Δvarr与e1—e2平面的夹角。
图7 展示了DRO 出发的近月点庞加莱图,转移轨道远地点抵达WSB 的约束表示为
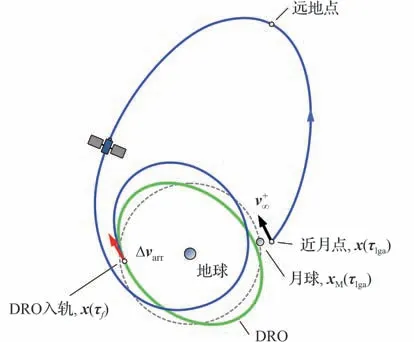
图7 DRO 出发的近月点庞加莱图Fig 7 Illustration of perilune Poincare map of DRO
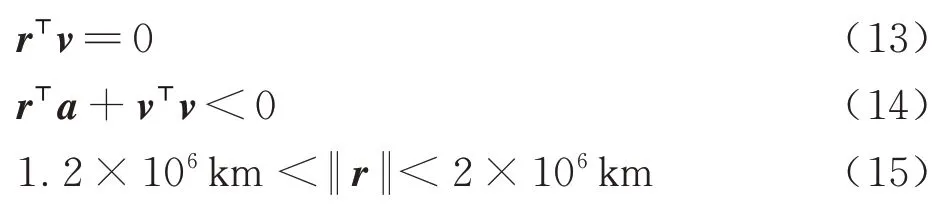
式中:v为卫星速度矢量;r为卫星位置矢量;a为卫星加速度。转移轨道抵达近月点的约束表示为
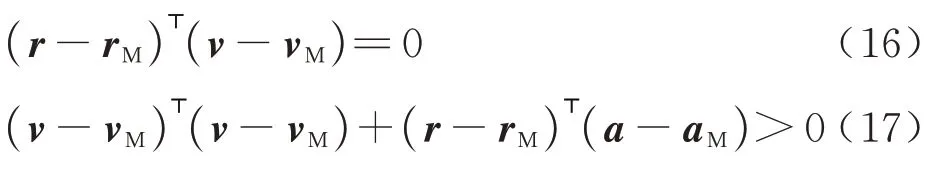

式中:rM、vM和aM分别为月球的位置、速度和加速度。受火箭滑行时间的限制,一些任务只能在月球升/降交点附近进行引力辅助,转移轨道的近月点还需满足以下约束

由于卫星以双曲线轨道掠飞月球,卫星离开月球影响球的双曲线剩余速度v+∞表示为

式中:x(τlga)为卫星在近月点的状态;xM(τlga)为月球状态为卫星相对月球状态。
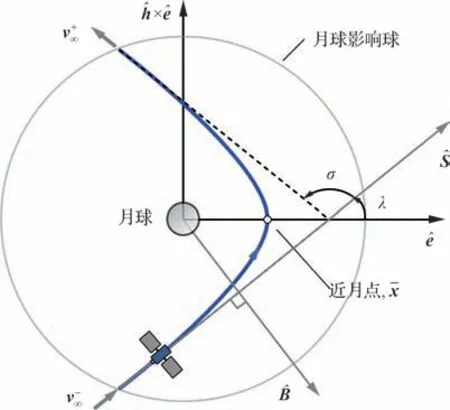
图8 月球借力和B 平面Fig 8 Illustration of lunar gravity assist and B-plane
双曲线剩余速度的模表示为

式中:μM为月球引力常数;νˉ为卫星相对月球速度矢量的模;rˉ为卫星位置矢量的标量。偏心率矢量e表示为
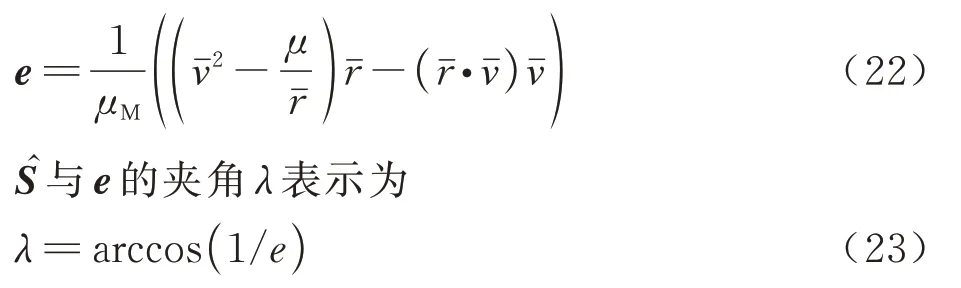
其中:e为偏心率的标量大小。
卫星离开影响球的双曲线剩余速度v+∞表示为
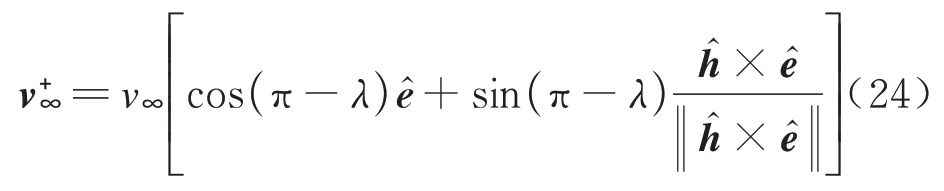
6 LEO 至LGA 轨道段
构造LEO 至LGA 的转移轨道,期望在降低地球发射脉冲的同时,优化月球借力参数,使得借力后的双曲线剩余速度与相匹配。在二体简化模型下构造全局优化问题为

式中:z∈Rn是优化变量;J:Rn→R是目标函数;zlr∈Rn和zur∈Rn是优化变量边界。优化变量z表示为

式中:Ω和ω分别为LTO 的升交点赤经和近地点幅角;η是LTO 的飞行时间;γ和ρ分别为月球引力辅助的相位角和月心距。表 1 列出了优化变量和取值范围。

表1 LEO 至LGA 轨道段优化变量Table 1 Variables of LEO to LGA segment
假设地球圆形停泊轨道的地心距为R*,轨道倾角为i*,通过Ω和ω得到卫星在LTO 的出发状态x(τ1),基于二体圆锥曲线拼接假设,求解Lambert 问题得到地球出发脉冲Δνdep和卫星进入月球影响球的双曲线剩余速度图 9 展示了B 平面和月球借力参数,其中i1,i2,i3为坐标系的单位矢量。通过γ和ρ得到月球借力后的双曲线剩余速度,计算过程如下:
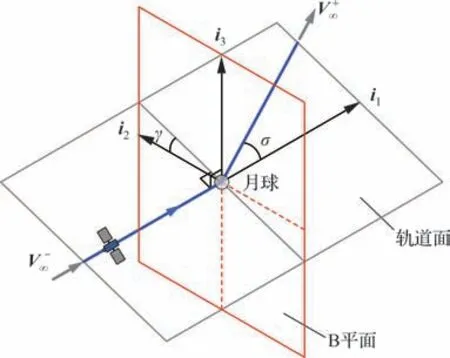
图9 B 平面和月球借力参数Fig 9 B-plane and lunar gravity assist parameters

为了降低地球出发脉冲Δνdep并使得尽可能接近,构造目标函数
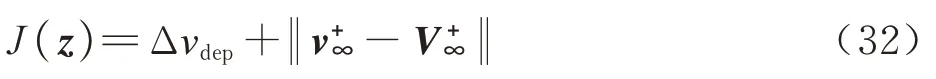
需要说明的是,式(32)使得月球借力前后的2 段轨道通过v无穷进行匹配(不是位置速度拼接)。当全局优化问题收敛后,可得到星历模型下的“LGA+WSB”转移轨道初值,计算过程不再赘述。
7 多步打靶修正
多体系统复杂的动力学环境使得转移轨道对初值非常敏感,多步打靶技术可以扩大收敛域并提高算法的鲁棒性。图 10 展示了多步打靶示意图,整条轨道被n个离散点分割为n-1 条轨道段,多步打靶变量X表示为
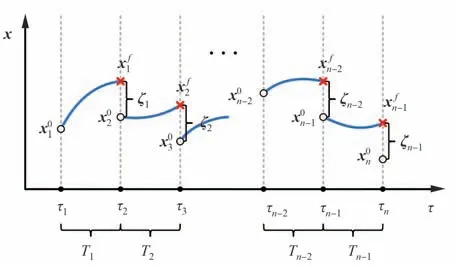
图10 多步打靶示意图Fig 10 Illustration of multiple shooting
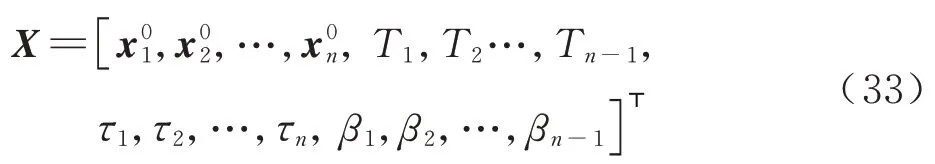
第j段轨道满足状态连接约束:
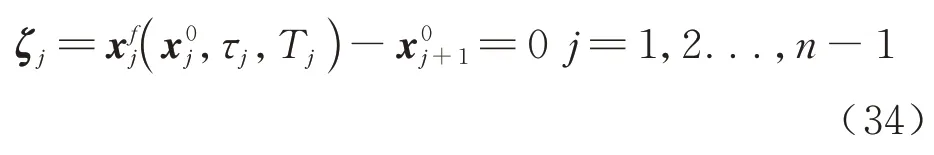
第j段轨道满足时间连接约束:
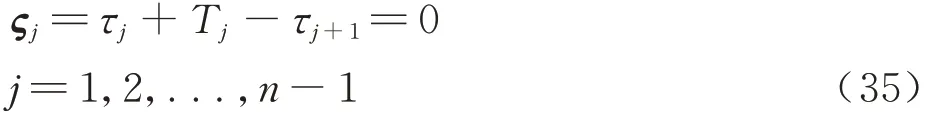
第j段轨道满足飞行时间为正的不等式约束:
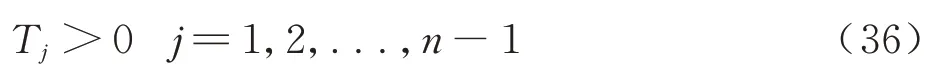
引入松弛变量βj可将式(36)变为等式约束:
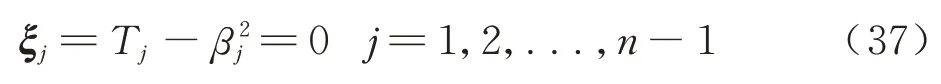
第1 个节点满足边界约束:
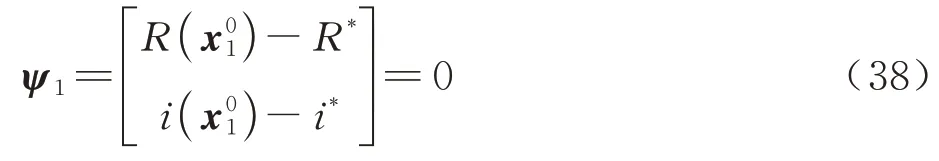
式中:R*和i*为LEO 的地心距和轨道倾角。
第n个节点满足边界约束:


至此,当得到雅克比矩阵J(X),使用最小二乘更新方程对打靶变量Xk+1进行修正(见式(41)),收敛后即可得到转移轨道。在星历修正中,动力学模型仅考虑日、地、月引力场,行星状态通过JPL 的DE430 星历计算。
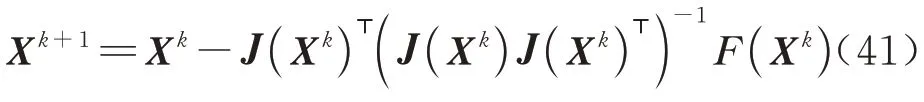
卫星在任务过程中共施加两次脉冲,分别为火箭发射脉冲Δvdep和卫星平台施加的DRO 入轨脉冲Δνarr,任务脉冲总表示为
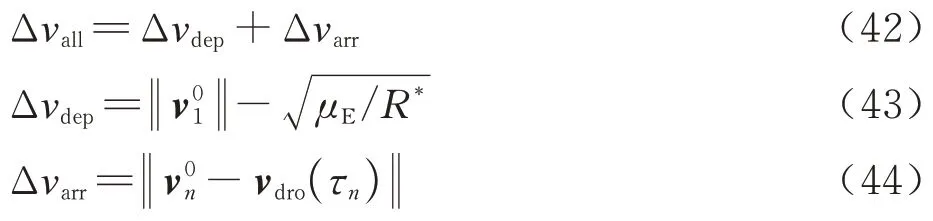
8 数值仿真
将在星历模型下设计基于月球借力的低能DRO 转移轨道,仿真参数参见表 2。其中,时间单位中的jd 为儒略日,tdb 为太阳系质心动力学时。计算流程如下:
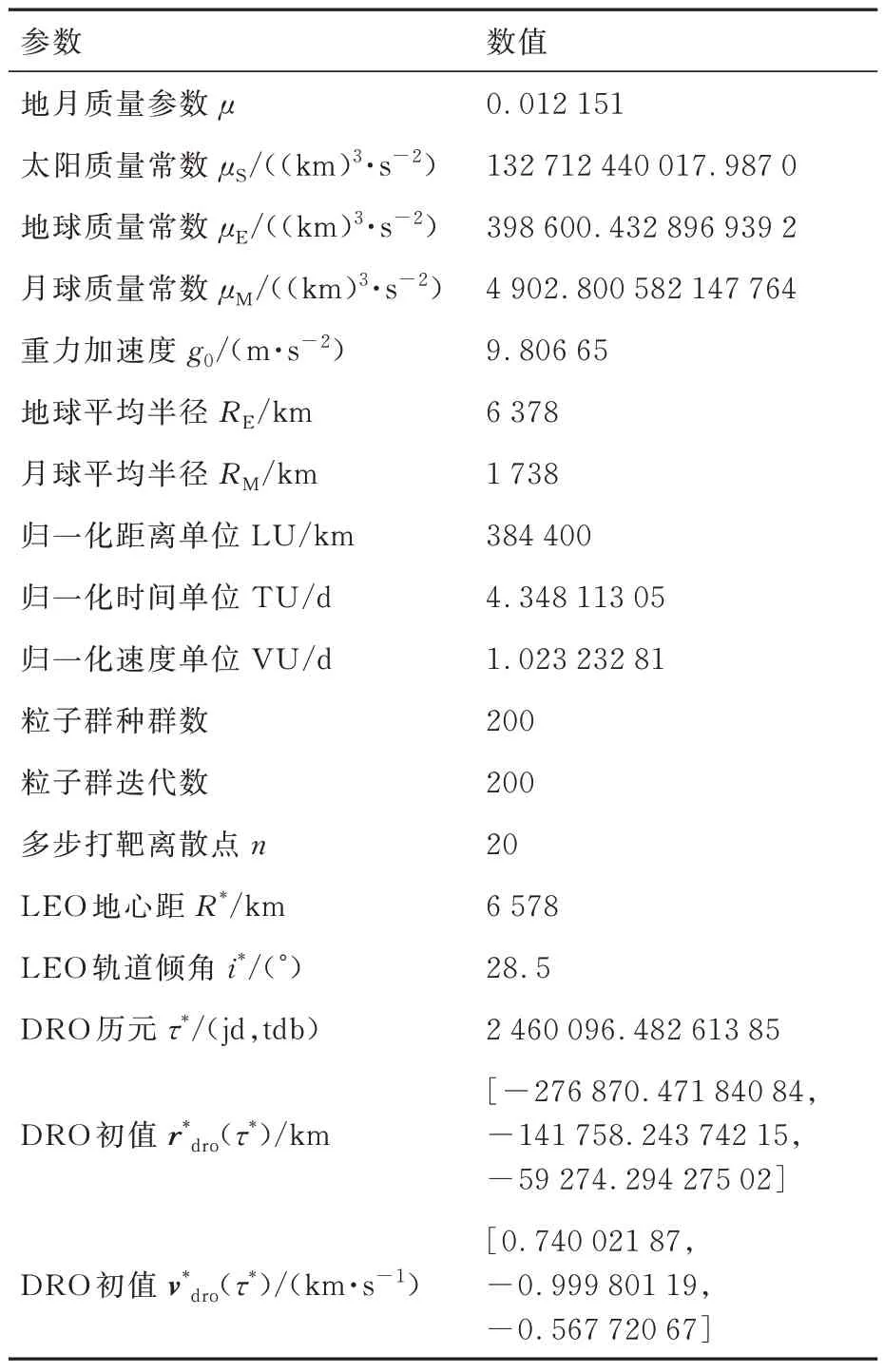
表2 数值仿真参数Table 2 Simulation parameters
1)网格化DRO 入轨时间τf和入轨速度脉冲Δvarr,获得不同的DRO 入轨状态x(τf),参见式(9)和式(10)。
2)从x(τf)出发逆向积分动力学模型,参见式(8),使得卫星先抵达WSB 再抵达近月点(构造近月点庞加莱图),参见式(13)~式(18),计算月球借力后的双曲线剩余速度,参见式(20)~式(24)。
3)固定LGA 至DRO 轨道段,使用粒子群优化LEO 至LGA 轨道段,最小化地球出发脉冲Δνdep并使得尽可 能接近(即v无穷 匹配),参见式(25)~式(32)。
4)使用多步打靶修正,得到“LGA+WSB”类型的DRO 转移轨道,参见式(33)~式(41)。
根据以上计算流程,构建1×107个DRO 入轨状态,从DRO 逆向积分能够先抵达WSB 再抵达近月点的仅有1 511 条转移轨道。图 11 展示了近月点庞加莱图,图中每个圆点都代表一条转移轨道,圆点颜色用于区分DRO 入轨脉冲。

图11 近月点庞加莱图Fig 11 Perilune Poincare map
进一步对比“v无穷匹配”策略对计算效率的改进效果。首先对于图 11 上的每一个点,继续逆向积分并在近地点终止,得到不使用“v无穷匹配”的转移轨道初值。图 12 展示了这些初值的近地点庞加莱图,X轴为近地点地心距,Y轴为近地点轨道倾角,红色十字为期望的LEO 地心距和轨道倾角,可以发现敏感的月球借力使得红色十字附近几乎没有接近的转移轨道。如果对图 12 直接使用多步打靶轨道修正,则仅有49 条收敛的转移轨道。
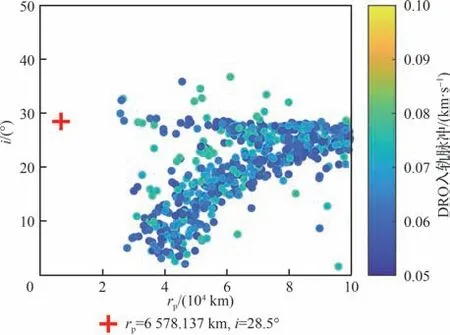
图12 近地点庞加莱图Fig 12 Perigee Poincare map
接着采用“v无穷匹配”策略获得转移轨道初值,再使用多步打靶修正整条轨道,最终获得了743 条收敛的转移轨道。图 13 展示了这些收敛解的散点图,其中每个圆点都为一条收敛轨道,圆点颜色用于区分DRO 入轨脉冲,红色圆圈为收敛解的帕累托前沿,红色五角星为脉冲最低解。在数值仿真中采用Matlab 编程语言,计算设备为高性能工作站,CPU 为64 核心处理器,内存为256 G,计算总时间约为8 h。
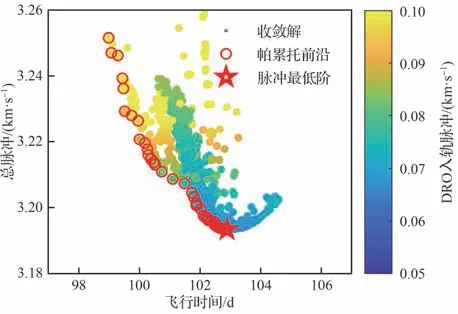
图13 多步打靶修正后的收敛解Fig 13 Converged solutions with multiple shooting
需要说明的是,“v无穷匹配”策略能够在不改变月球借力后双曲线剩余速度的条件下,将图12 的大多数近地点都移动到红色十字附近,从而有效改进了转移轨道初值。就本算例而言,“v无穷匹配”策略将转移轨道收敛率提高了约15 倍。此外,“v无穷匹配”策略可以方便拓展到NRHO、L4/5等周期轨道的入轨任务设计,计算流程并无明显区别。
图14 展示了图 13 中总脉冲最低解(红色五角星)的转移轨道,其中红色实线为DRO 轨道,蓝色实线为地球至DRO 转移轨道,灰色实线为月球轨道。观察图 14(a),卫星从地球出发后进入地月转移轨道,月球借力后卫星弹射至WSB,当再次返回地月空间时,卫星以切向入轨的方式进入DRO 轨道。观察图 14(b),卫星从WSB 返回地月空间时首先抵达L4附近,之后在地月引力共同影响下抵达DRO 并入轨。
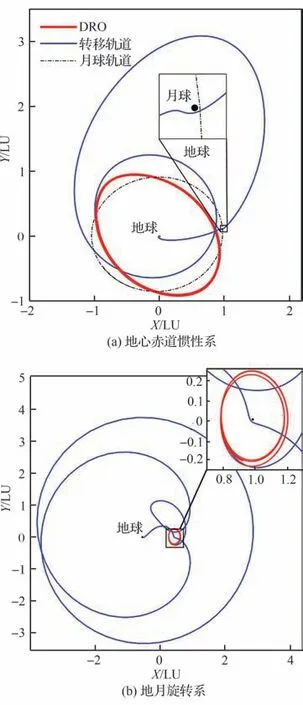
图14 总脉冲最低解的转移轨道Fig 14 Best solution with minimum cost
表3展示了图 13中脉冲最低解(红色五角星)的仿真结果,LEO 出发脉冲仅需3.127 3 km/s,DRO入轨脉冲66.1 m/s,任务总脉冲3.193 4 km/s,任务总时间102.880 3 d。

表3 总脉冲最低解的仿真结果Table 3 Best solution with minimum cost
表4 展示了LEO 转移至GEO 和DRO 的 对比,LEO 轨道高度200 km,轨道倾角28.5°,卫星平台采用化学推进,比冲220 s。如果采用猎鹰9号Block 2 型运载火箭,单次发射至多可将1 704.273 3 kg 的载荷送入GEO 轨道,可将2 553.576 8 kg 的载荷送入DRO 轨道,由于GEO 需要1.819 7 km/s 的速度脉冲改变轨道倾角和轨道圆化,使得虽然DRO 距离地球更远,但是入轨质量却更高,约为GEO 的1.5 倍。
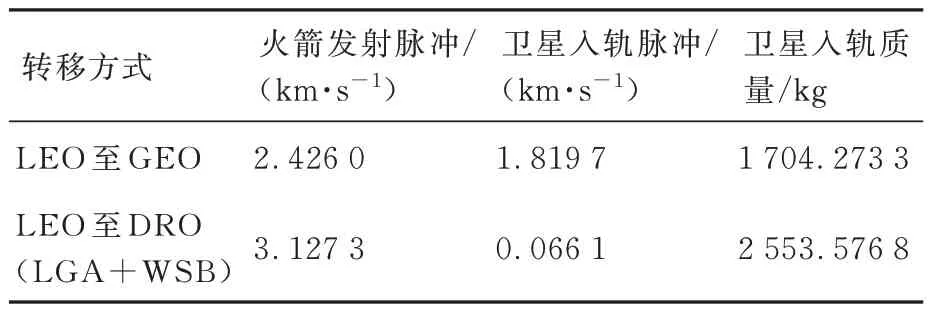
表4 LEO 转移至GEO 和DRO 的对比Table 4 Comparison between LEO to GEO and LEO to DRO
9 结论
1)改进了星历模型下的“LGA+WSB”转移轨道设计方法,通过“近月点庞加莱图”和“v无穷匹配”获得较好的轨道初值,有效提高了该类型转移轨道的计算效率。
2)通过网格搜索获得了解空间的帕累托前沿,对于2:1 DRO 轨道,总脉冲最低解的飞行时间102.880 3 d,地球发射脉冲3.127 3 km/s,DRO 入轨脉冲66.1 m/s。
3)对 比LEO 至GEO 和LEO 至DRO 转 移轨道,尽管DRO 距离地球更远,但是入轨质量可以达到GEO 的约1.5 倍。
