基于DP准则的巷道围岩塑性区影响因素分析

经来旺，张世翔，肖起辉，方 旭，经 纬

(安徽理工大学土木建筑学院，安徽 淮南 232001)

随着煤炭资源的不断消耗，煤炭开挖逐渐转向深部。煤炭深部的高地应力加剧了巷道围岩的变形，进而加剧了围岩塑性区的形成。大量研究及现场实测表明围岩塑性区的发展使得锚杆索锚固力失效，导致巷道事故的发生。因此，确定围岩塑性区的范围，对煤矿生产安全有重要意义。

国内外学者对围岩塑性区范围进行了大量研究。 芬纳(FENNER R.)和卡斯特奈(KASTNER H.)推导了均匀应力场下的围岩塑性区半径公式；李桂臣等[1]引入了“等效开挖”概念，分析了不同巷道截面形状对围岩塑性区范围的影响；MA等[2]研究了不同DP准则下围岩塑性区半径，并基于研究结果对巷道支护设计进行优化；张小波等[3]利用单因素法分析不同屈服准则下塑性区半径变化规律，并基于FLAC3D软件验证模拟结果与理论分析结果；彭瑞等[4]基于DP准则推导出了非均匀场下围岩塑性区边界方程，并考虑了(巷道截面形状)侧压力系数及原岩扰动程度对塑性区半径的影响；董海龙等[5]分析了两向不等压下应力构造法和近似隐式法的优缺点，以两法为基础结合相似原理得出了较为准确的解析解；赵志强等[6]推导出了基于M-C准则的围岩塑性区边界方程，并首次提出了蝶形塑性区概念，根据塑性区变形规律设计了可接长锚杆-普通锚杆协同支护方案；王卫军等[7-8]基于M-C准则推导出了圆形巷道围岩塑性区边界方程，分析了形成蝶形塑性区的影响因素；SHI等[9]研究了在高偏地应力条件下，不同屈服强度准则对围岩塑性区形态的影响，得出了蝶形塑性区对强度准则的敏感性较低，对应力变化高度敏感；郭晓菲等[10]分析了蝶形破坏理论与理论计算的误差，研究了理论在不同巷道截面及围岩岩性条件下的适用性。

结合前人的研究成果，基于Drucker-Prager屈服准则，对非圆形巷道进行等面积圆的当量替换，分析非等压下巷道围岩塑性区范围的解析解。利用ABAQUS有限元软件将不同侧压系数下理论分析结果与模拟结果进行对比，并分析不同DP准则的塑性区影响因素。基于巷道围岩塑性区范围，巷道顶底板、两帮位移量及蠕变量对支护方案进行优化，以期为设计经济有效的支护方案提供理论计算依据。

1 DP准则

1952年DRUCKER和PRAGER在平面应变状态下基于关联流动法则推导出了广义Miss准则，即DP准则[11]。DP准则在π面上光滑、无棱角，有利于进行有限元模拟，且考虑了中主应力对材料破坏的影响，其函数形式见式(1)。

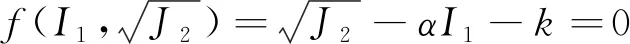
(1)

式中：I1为应力张量第一不变量，计算见式(2)；J2为偏应力张量第二不变量，计算见式(3)；α、k均为DP准则系数。

I1=σ1+σ2+σ3

(2)

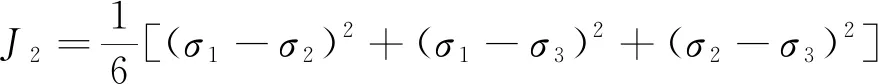
(3)

平面应变状态下，α、k函数形式见式(4)和式(5)。

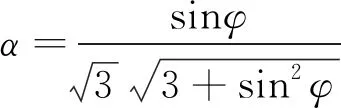
(4)

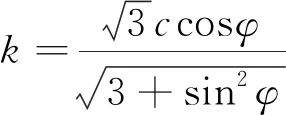
(5)

DP准则考虑了中间主应力系数对岩石破坏的影响，其表达式见式(6)

(6)

将式(2)、式(3)和式(6)带入式(1)可得式(7)。

[m-α(n+1)]σ1-[m+(2-n)α]σ3-k=0

(7)

整理式(7)可得式(8)。

σ1=Aσ3+B

(8)

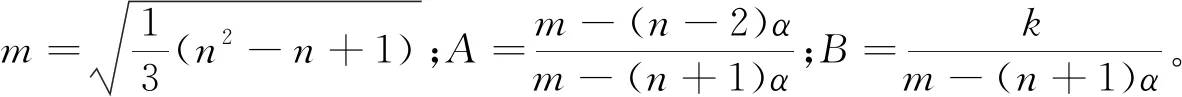
在非均匀场中的平面应变情况下，主应力与各应力分量之间的关系见式(9)[12]。

(9)

将式(9)带入式(8)可得式(10)。

(A-1)(σr+σθ)+2B

(10)

为了使巷道围岩满足DP准则，进行如下假设：①将巷道围岩视为连续、均匀、各向同性的弹塑性材料；②巷道截面为圆形，进深无限大；③巷道上部原岩应力视为均布力P，水平应力λP；④巷道支护阻力q在巷道开挖后立即生效，即不考虑时空效应。综上假设，巷道支护问题可简化为平面应变问题，力学模型如图1所示。

图1 简化的力学模型

王卫军等[8]已根据叠加原理推导出非等压下圆形巷道的围岩应力解，见式(11)。

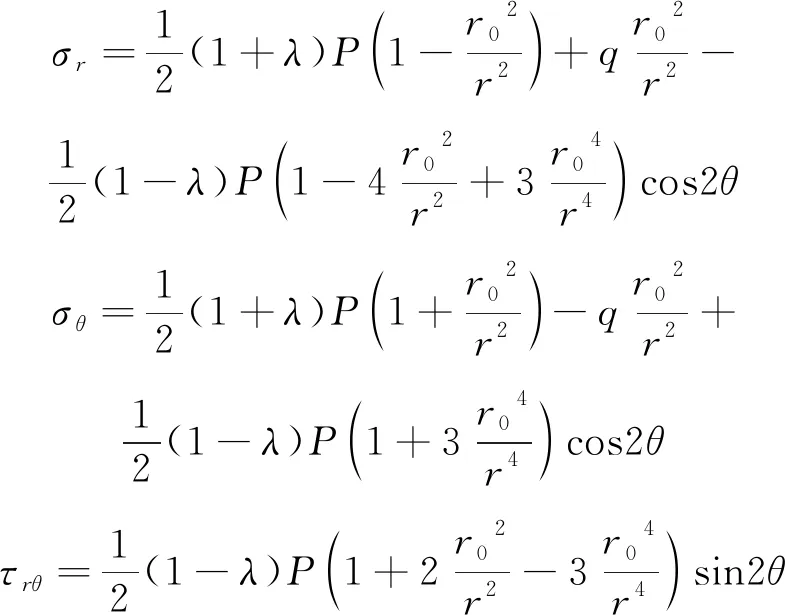
(11)

将式(11)带入式(10)，令x=r02/r2，可得基于近似隐式法的围岩塑性区边界方程，见式(12)；其中，k0、k1、k2、k3、k4计算见式(13)～式(17)。

f(x)=k4x4+k3x3+k2x2+k1x1+k0

(12)

k0=(A+1)2(λ-1)2P2-

(A-1)2(λ+1)2P2+4(A-1)B(1+λ)P+4B2

(13)

k1=(A+1)2{2(λ-1)Pcos2θ[2q-(1+λ)p+

2(1-λ)Pcos2θ]+4(λ-1)2P2sin22θ}-

4(A-1)2×(1-λ2)P2cos2θ+

8(A-1)B(1-λ)Pcos2θ

(14)

k2=(A+1)2{6(λ-1)2P2cos22θ+

[2q-(1+λ)P+2(1-λ)Pcos2θ]2-

2(1-λ)2P2sin22θ}-4(A-1)2×

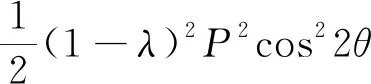
(15)

k3=(A+1)2{6(λ-1)Pcos2θ[2q-(1+λ)P+

2(1-λ)Pcos2θ]-12(1-λ)2P2sin22θ}

(16)

k4=9(A+1)2(λ-1)2P2

(17)

当λ=1时，可得式(18)。

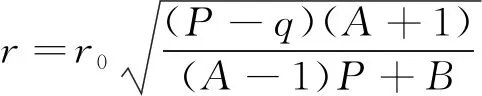
(18)

式中，r0为巷道半径，然而在实际的巷道支护中，大多数巷道截面形状为非圆形，为满足上述假设因此对非圆形巷道进行标准化处理[13]。处理方法如下所述。

1) 当量半径折算法，计算见式(19)，对截面半径进行修正。

r0=k×(S/π)1/2

(19)

式中：r0为巷道当量半径；k为截面修正系数；S为巷道截面面积。

2) 外接圆半径法，利用几何作图法做非圆形巷道的外接圆，将外接圆半径代替巷道截面半径；q为支护阻力，锚杆提供的支护阻力按照《岩土锚杆与喷射混凝土支护工程技术规范》(GB 50086—2015)第4.6.10条规定计算；喷射混凝土提供的支护阻力按照《岩土锚杆与喷射混凝土支护工程技术规范》(GB 50086—2015)第6.3.2条规定计算。

2 巷道围岩塑性区影响因素分析

2.1 不同侧压力系数下塑性区形态分析

利用MAPLE软件计算六种侧压系数下塑性区的数值解析解，并与等效巷道半径一同绘制于图2。从图2中可以看出，当λ=0.3时，围岩塑性区呈蝶形分布；当λ=0.6时，水平方向和垂直方向的塑性区均减小，侧压系数增大了一倍，最大塑性区范围减小了63%；当λ=1.0时，即均匀场下巷道围岩塑性区形态为圆形；当λ=1.5时，围岩塑性区呈圆角矩形；当侧压系数持续增大时，塑性区形态进入二次蝶形分布。

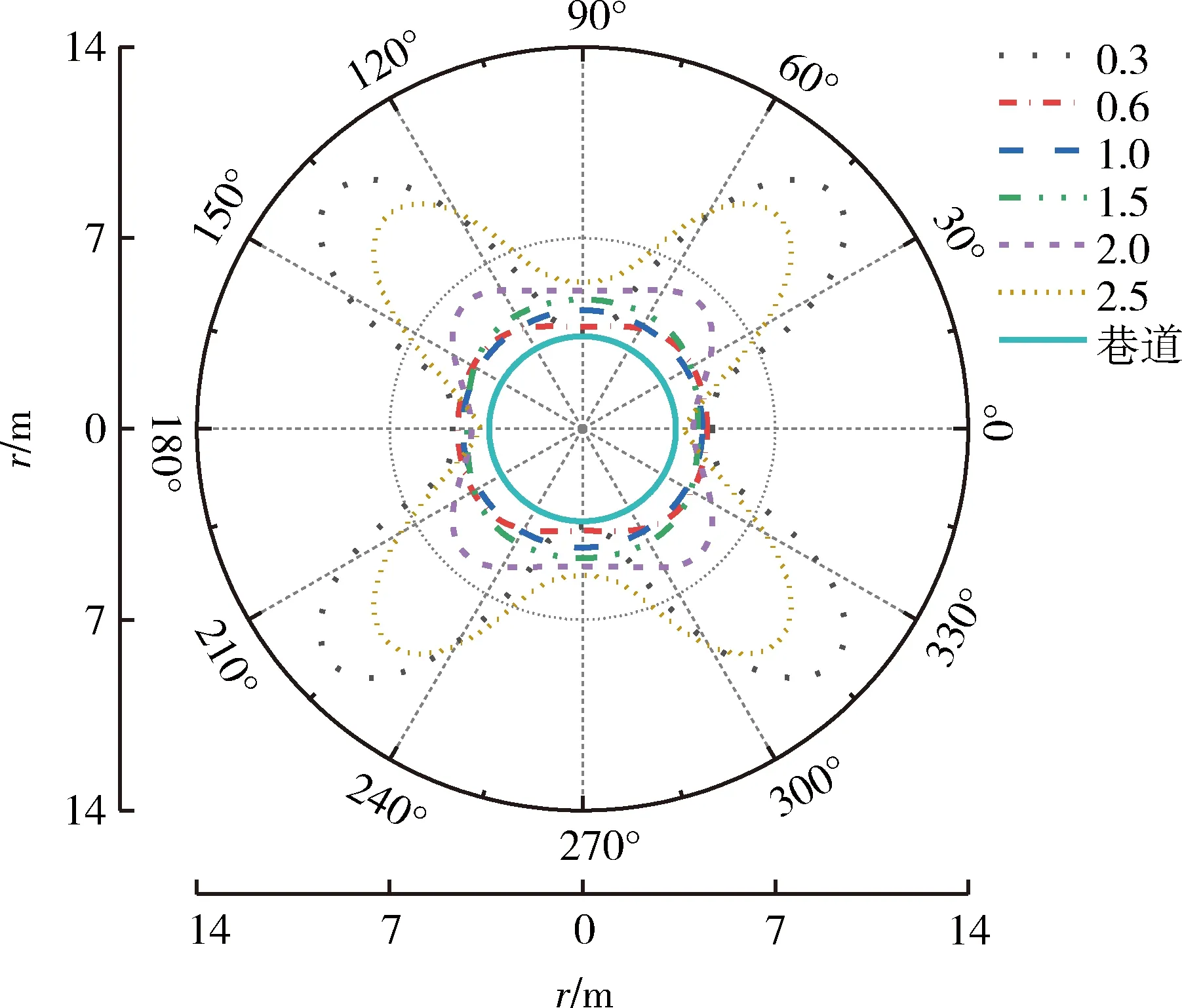
图2 不同侧压系数下的塑性区形态

当侧压系数在0.6～1.5范围时，塑性区范围均较小，且形态上呈椭圆形。当侧压系数小于0.6或大于1.5时，塑性区四角范围数倍于巷道半径，呈蝶形分布，塑性区进入恶性扩展进而失控。蝶形塑性区巷道边角范围较大且具有较强的穿透性、隔层扩展性[14]，致使巷道产生冒顶、底鼓、底角变形破坏等事故。所以，当围岩塑性区形态为圆形或椭圆形时，巷道支护较易，能够经济有效地控制围岩的变形与破坏。

2.2 不同DP准则下塑性区影响因素分析

广义Miss条件在主应力空间为一圆锥面，在π面上为圆形，式(1)中不同的α、k在π面上代表不同的圆，DP各准则α、k参数见表1。

表1 各DP准则α、k参数

采用单因素法分析不同DP准则下中间主应力系数n、黏聚力c、支护阻力q及内摩擦角φ对塑性区半径的影响，关系曲线如图3所示。

中间主应力系数反映了三个主应力之间的相对大小。从图3(a)中可以看出，除DP1准则以外，其余准则当中间主应力系数小于0.725时，塑性区半径随中间主应力系数的增大而逐渐减小且减幅较大，中间主应力系数为0时塑性区半径最大、中间主应力系数在0.725左右时塑性区半径最小；当中间主应力系数大于等于0.725时，塑性区半径随着中间主应力系数的增大而增大且增幅较快。而DP1准则曲线的驻点是中间主应力系数在0.80左右。从关系曲线可以看出，增大中间主应力系数能够一定程度降低塑性区范围。但并非线性减小，当中间主应力系数增大到一定范围时，塑性区半径的减小速度降低，甚至不减反增。这一现象表现出了中间主应力对塑性区半径的影响有着强烈的区间性[15]。

从图3(b)中可以看出，随着黏聚力的增大塑性区半径呈近似线性减小的趋势。以DP4准则为例，当黏聚力从0.5 MPa增大到1.0 MPa时，塑性区半径仅减小了3.28%，说明塑性区半径对黏聚力的敏感程度较弱。随着黏聚力的逐步增大，塑性区半径减幅变小，曲线逐渐平滑，反映了黏聚力对控制围岩变形的作用是有限的，即黏聚力增大到一定程度后塑性区半径便不再减小。

从图3(c)中可以看出，DP2准则和DP4准则的差异随着内摩擦角的增大而减小，最后两条曲线逐渐重合。图3(b)和图3(c)曲线变化趋势相似，都是随着黏聚力和内摩擦角的逐渐增大，塑性区半径逐渐变小。因此，岩体力学参数的改变对巷道支护效果有着明显的作用。在支护设计中应通过改善岩体力学性质来更加有效地控制围岩塑性区形成与扩展。如通过注浆对围岩软弱带进行强化，降低了岩体各向异性，进而能够有效改善岩体的黏聚力和内摩擦角。

在巷道支护中，锚杆起到了至关重要的作用。在图3(d)中，塑性区半径随着支护阻力的增大而线性减小。这是因为锚杆能够改善被锚固岩体的物理力学性能，通过加强岩体的变形能力来提高岩体峰值荷载及残余强度，最终达到控制围岩变形的支护效果[16]。

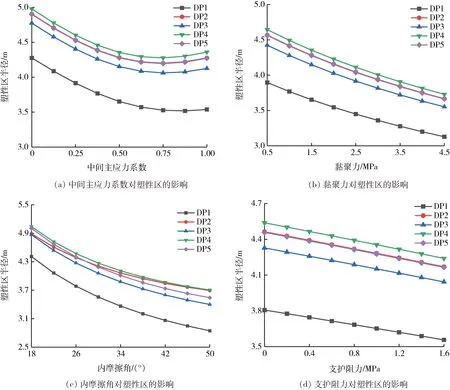
图3 不同DP准则下塑性区半径的影响因素

整体来看，各个影响因素下塑性区半径大小关系为DP4>DP2>DP5>DP3>DP1，即DP4准则和DP1准则分别是DP系列准则的上限和下限；DP2准则和DP5准则下的塑性区范围相近；DP1准则均偏离其他准则，偏离程度较大且数值小，所以DP1准则不适用于实际工程；而DP4准则的塑性区半径是DP系列准则中最大的，相对来说较保守，在实际工程中的造价较高，没有达到经济适用支护效果。因此，采用DP准则分析围岩弹塑性范围时，要考虑实际工程背景和围岩的力学性能选择合适的DP屈服准则。

3 算例分析

3.1 巷道工程概况

某煤矿巷道平均埋深503 m，煤层平均厚度为5.87 m，煤层普氏系数f=0.7。巷道两帮和底板均处于煤层中，两帮煤体的节理裂隙高度发育，呈松软破碎特性，顶底板岩层层理发育、稳定性差、岩石强度低，属“三软”煤层。原支护方案采用锚网索联合支护，在掘进后顶煤区域出现离层、顶板下沉、顺槽全断面收敛、支护压断、底鼓等破坏现象，锚杆、锚索支护不起作用。

原支护方案巷道截面为梯形高上顶4.7 m、下底5.4 m、高4.5 m。 支护参数：顶板采用Φ22 mm×2 400 mm锚杆、两帮采用Φ17.8 mm×3 650 mm高强钢绞线锚索，间排距均为800 mm×800 mm，顶板锚索Φ21.8 mm×7 300 mm高强钢绞线锚索，锚索采用3-4-3布置，间排距1 600 mm×800 mm。为了加强锚杆索支护效果[17]，减小角部塑性区范围[18]，基于“强角”支护理论[19]，设计新的支护方案。

新方案巷道截面为梯形，上顶5.0 m、下底5.6 m、高4.2 m。 支护参数：顶板采用Φ21.8 mm×7 300 mm实心锚索，锚索采用4-3-4布置，4根一排取值1 200 mm，3根一排取值1 500 mm，均以顶板中线对称，锚杆采用Φ22 mm×2 400 mm的左旋无纵筋螺纹钢锚杆，两边间距为625 mm，中间为750 mm。帮部采用Φ21.8 mm×6 300 mm实心长锚索、Φ22 mm×6 300 mm注浆长锚索。 底角采用Φ22 mm×6 300 mm注浆锚索和Φ25 mm×2 500 mm注浆锚杆。锚杆索具体支护形式如图4所示。

图4 巷道锚杆索布置展开示意图

3.2 数值模拟

本文采用ABAQUS有限元软件对新的支护方案进行数值模拟。建模步骤：建立50 m×50 m×5.80 m模型，巷道沿顶布置，且巷道底板及两帮均处于煤层中，具体如图5所示，正视图如图6所示。建模完成后进行材料属性赋予，岩层参数见表2(此参数为M-C准则下的参数需进行转化)；在Assembly模块将锚杆索和岩体装配；定义分析步及相互作用，此处可应用软化模量法模拟煤层采空区；定义荷载及边界条件，用生死单元法模拟巷道开挖，并进行初始地应力场的平衡；在Mesh模块划分网格后，即可进入后处理。

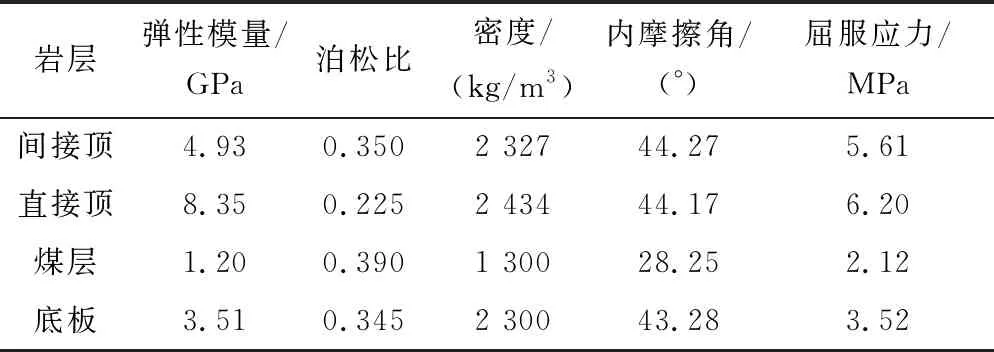
表2 巷道岩层物理力学参数表

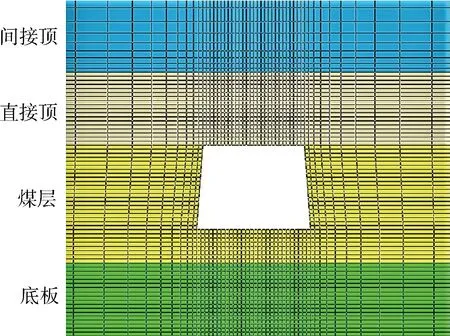
图5 巷道岩层分布图

图6 巷道支护正视图

3.3 新旧支护方案对比

新旧支护方案位移云图如图7所示，为方便对比将两个方案的蠕变量一同绘制于图8。由图8可知，左右两帮蠕变量相近，顶底板蠕变量较大。分析认为，巷道沿顶布置，底板下为煤层，岩性弱，底板蠕变量较大； 顶板上层为砂岩， 锚杆锚固力较大，顶板蠕变量最小。整体来看，新支护方案中减小锚杆间距能有效控制围岩变形，进而提高煤层开采工作安全性。

图7 新旧支护方案位移云图

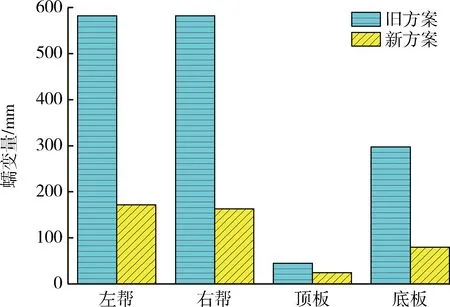
图8 新旧支护方案下巷道蠕变量柱状图

因此，对于巷道支护的设计，需考虑非等压环境下造成的围岩塑性区深度差异性，不应进行全断面设计，而是根据巷道围岩塑性区分布进行差异性设计，使得锚杆索锚固基础处于弹性区，既保证了支护强度，又避免了过度支护[20]。

4 结 论

1) 基于DP准则，由近似隐式法推导出了非等压下围岩塑性区边界方程。对不同侧压系数下巷道围岩塑性区形态进行分析，并考虑了非圆形巷道半径的等效代替。当侧压系数改变时塑性区会表现出圆形、椭圆形、蝶形。

2) 中间主应力系数对巷道围岩塑性区范围的影响有着强烈的区间性；黏聚力及内摩擦角的增大会使塑性区半径减小，但这一作用效果随着黏聚力和内摩擦角的逐渐增大而减弱，通过注浆对巷道进行支护有效，但效果有限；支护阻力的增大可使塑性区呈线性减小。DP系列准则中DP4准则较为保守，DP1准则不适用于工程，选取合理的DP屈服准则能够兼顾煤矿生产的安全性与经济性。

本文采用理想弹塑性2分区模型，然而现已有3分区模型、4分区模型；且围岩并非理想的弹塑性材料，对围岩进行分析时应考虑岩石的损伤、剪胀、扩容、流变和应变软化等复杂的物理力学性质；考虑巷道支护的时间效应；在非均匀应力场巷道围岩塑性区的求解过程中，巷道被简化为轴对称的圆形，且错误地认为塑性区以外的弹性区应力与围岩弹性应力状态下的应力在形式上一致。以上诸多问题都亟待解决，因此，非均匀应力场巷道围岩塑性区的解析解还需更进一步的研究。