基于超声相控阵平面波检测的金属指纹标签识别系统

刘 昱，贺升平，贺西平**，王 杰，周 越

(1.陕西师范大学 物理学与信息技术学院，陕西省超声重点实验室，陕西 西安 710000；2.泸州高新技术研究所，四川 泸州 646000)

在一带一路、经济全球化的趋势之下，中国不断加强对外交流，其中常有贵重文物物品和重要仪器设备外借交流，为确保归还物品不被替换，防伪识别显得尤为重要.超声识别技术凭借其检测无损伤的优点受到了广泛研究.超声波对多晶材料内部晶粒特征的差异十分敏感，材料内部晶粒分布的无序性、晶粒尺寸以及径向排列的随机性导致超声在其内传播时的衰减、声速、散射等声学性质发生改变.Chamy等[1]利用超声声速与晶粒尺寸的关系，用声速对AISI31型不锈钢的平均晶粒尺寸的测量取得了良好结果.Vijayalakshmi等[2]用脉冲回波法对热处理后的SAF 2 205双相不锈钢样品进行了超声波速度和衰减系数的测定，得到超声的衰减主要由晶粒尺寸决定，超声衰减随晶粒尺寸的增大而急剧增大，而超声纵向速度和剪切速度由相含量和晶粒尺寸共同决定的结论.Richtera等[3]利用超声衰减谱结合Faran模型计算弹性散射体的方法，计算了微米级悬浮液和乳状液粒径分布，测量结果和计算结果具有较好的一致性.呼剑等[4]利用McClements &BLBL模型对高频宽带超声衰减谱反演计算，获得了纳米银颗粒的粒度分布，其结果符合实验室测量值.并证实了在50 MHz频率下的理论测量下限可以达到5 nm.

由于每个多晶材料的内部微结构都有区别，即便是2个材料和生产工艺都相同的金属产品也可以通过高频超声利用二者的微观差异完成识别，如同人类的指纹识别，因此本文提出了超声指纹标签的概念，对多晶材料采集超声信号，信号中蕴含着内部微结构的细节信息，通过识别算法，计算出每个多晶样品的特征值，作为其指纹标签并保存，即使将样品混淆在多个材料、尺寸、形状完全一致的仿制品之中，也能凭借其超声指纹标签准确找出原样品.

传统的超声指纹标签的特征量包括超声信号的幅度谱、衰减谱、信号散射频谱等.卢康等[5]提取了金属材料超声信号的衰减系数、平均峰值和主频等特征量，结合支持向量机完成了对不锈钢等材料的个体识别.同一时期课题组研究了计算不同样品衰减谱的相关系数的识别方法，并设计了识别阈值，提高了识别结果的准确度[6-8].之后安笑笑等[9]计算了待识别陶瓷材料的背向散射信号与标准陶瓷材料的背向散射信号之间的加权欧式距离并以此为特征量实现了对陶瓷材料的超声识别.为了提高识别的准确率、稳定性和容错性，本文在过去研究的基础上改进了识别算法，从时域和频域提取特征量联合决策识别，结合拉伊达准则设置阈值，利用相控阵平面波检测技术采集样品超声信号实现了对金属样品的个体识别.

1 指纹标签原理

1.1 超声指纹晶粒尺寸是结构金属材料的一项重要本征参数，直接影响金属的屈服强度和塑型韧性等力学性能和耐腐蚀性等化学性能，因此国内外学者对晶粒尺寸的测量进行了大量研究，陈昊等[10]使用了超声衰减法和超声反射法，发现对晶粒尺寸的测量并不准确，其原因是多晶材料内部的晶粒径向分布无规律，导致超声波传播过程中衰减结果融入了随机性.更重要的是晶粒间反射界面的无规律分布导致超声波在材料内部传播时反射和散射信号发生变化，由此超声波经金属晶粒吸收、反射和背向散射之后便携带了这部分材料内部微结构呈现类似指纹唯一性的细节信息[11].虽然发现了微结构对超声有明显影响，但材料微结构过于复杂，对其进行理论解析一直是一个难题，国外学者Rokhlin对微结构晶粒进行了数学建模，构建了细长椭球结构模型，进而深入研究了超声背向散射信号与平均椭球晶粒半径的关系[12].晶粒背向散射信号可以有效反映多晶材料内部微结构的细节信息，因此使用超声相控阵系统采集金属材料的超声信号后，经过后续算法处理即可得到每个物体的独有的超声指纹标签.

1.2 平面波检测相控阵探头的32个晶片每一片都可以完成发射和接收超声波的任务，较为常见的成像检测方法基于全矩阵捕获FMC(full matrix capture)所得数据为全聚焦模式TFM(Total Focusing Mode)，该模式将所有晶片依次激发并使每次激发晶片的回波信号都被每个晶片接收，因此所得数据为一个32×32的信号矩阵，然后将数据重建，重新界定出计算区域，将计算区域划网格，对每个网格都按照对应晶片计算聚焦法则.其优点是分辨能力强，成像面积大.但缺点也很明显，数据量庞大，保存成指纹标签会占用大量存储空间，存储一个样品的指纹标签信号会占用十几GB甚至几十GB，而且信号采集时间和处理时间长，影响识别效率.因此本文选择平面波检测模式，相比于FMC依次激发所有晶片并依次接收所有信号平面波检测采取的方式为同时激发所有晶片发射超声信号，同时所有晶片接收整体回波信号，这样得到的数据就不是32×32的矩阵，而是1×32的矩阵.平面波检测模式不仅大大节约了储存空间，而且提高了信号采集效率.此外，由于平面波检测是全体晶片发射超声，全体晶片接收回波，因此信号能量更大，有利于细节识别.相控阵的扫查方式选择线性扫描，线性扫描实质上是将多组扫描的幅值信息数字化从而把样品的横截面绘成图像，而且线性扫描实时成像，有利于选择信号特征明显的位置作为采集样品标准信号的采集点位.

2 指纹标签算法

本文所用相控阵探头由32个阵元晶片组成，这32个晶片各自独立，其均具备收发功能，相当于32个直探头同时工作，本文的算法是计算出每个晶片采集到的信号特征量，作为其超声指纹，随后计算出一个识别阈值，比较特征量和阈值的大小即可判断该指纹标签是否属于原本物品.为提高识别的准确性，指纹标签算法由时域标签和频域标签联合决策，只有时域和频域的超声指纹均在各自阈值范围内时才决策为同个物体.

2.1 指纹标签计算对标准样品采集20次超声信号，取20次信号的目的是模拟实际识别过程中，每次探头的抬起和放置都会因探头、耦合剂的细微状态改变而导致采集到的信号出现细微差异，因此使用重复采集20次的方法将标准样品的信号完整采集.每个晶片在同一试样的同一采样位置采集20次时域信号，每个时域信号记录了N=2 000个信号幅值即2 000个采样点.而且每次探头稳定放置后，对每个采样点（2 000个）重复采集101次并保存以便后续通过平均计算消除电路噪声和幅值震荡造成的影响.因此对于每个晶片每次采集得到的数据格式为20个×101行×2 000列，对采集到的幅值求均值

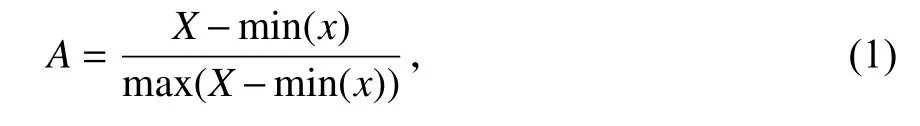
并用公式（1）进行归一化，其中X是每个采样点101次采样幅值的均值，min(x)为X中的最小值.最后得到20个均值归一化幅值A.

由公式(2)计算出每个信号的时域特征量Pi(i=1,2,···,20)，对得到20个时域特征量求平均，得到时域平均特征量：

最后公式(3)计算出20个时域指纹标签Fi(i=1,2,···,20)

频域特征量和时域特征量计算方法基本一致，区别仅为在使用公式(1)进行归一化之前，对数据进行了快速傅里叶变换，将回波信号转换到频域分析各频点的信息.

至此，使用降维处理分析法将20组庞大的幅值数据提取成20个时域指纹标签和20个频域指纹标签，这有利于后续对标准信号进行聚类分析.

2.2 阈值计算由于实际采集信号的过程中会有系统误差和操作误差，从而使每次采集的信号计算出的指纹标签都有一定偏差，因此为降低误识别（将不同物品识别为同个物品）和漏识别（将同个物品识别为不同物品），本文采用了阈值结合概率统计的方法来确定识别结果.

每次信号采集时系统误差和操作误差带来的偏差在统计学上都属于独立分布的随机变量，理论上是无法采集到标准信号的唯一真实值的，对标准信号可能出现的所有采集结果称为总体，每次采集到的信号称为样本，随采集次数增加，采集到的样本信号均值会收敛于总体期望值[13].因此本文取20次标准信号并由(4)式求均值来获得总体期望.再由中心极限定律可知，样本的平均值约等于总体的平均值.不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布[14-15].进而利用拉依达准则进行异常值判断，拉依达准则以正态分布3倍标准差99.7%的置信率为基础，以此作为极限偏差，超过此界限即判断为该次测量结果属于异常值而非随机误差.

因此基于拉依达3倍标准差法进行阈值计算[16]，上面已经得到了时域和频域各20个指纹标签Fi(i=1,2,···,20)，利用公式(4)和(5)分别计算其平均值F¯ 和 标准差 σ ：

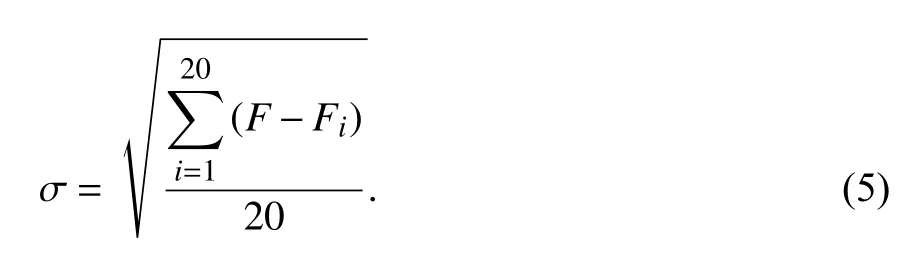
公式(6)由拉依达法则算得时域频域各自阈值Δ，该阈值即标准指纹标签.

2.3 结果判断上一节得到了样品对应的每个晶片的时域频域标准指纹标签，将标准样品混淆入待识别样品后，随机取出一个待识别样品，要对其采集信号并由算法计算出待识别指纹标签，与标准指纹标签进行比对，对结果的判断方式采取时域频域联合判断的办法，即时域标签、频域标签同时低于对应晶片标准指纹标签时，该晶片判断为“同个物体”；时域标签、频域标签同时高于对应晶片标准指纹标签时，该晶片判断为“不同物体”；时域标签、频域标签一个高于标准指纹标签另一个低于标准指纹标签时，该晶片判断为“识别不清”，说明待识别信号采集有较大误差，需要重新采集待识别信号.

为降低误差影响，最终识别结果的给出是经过多次联合判断之后决策的，先是每个晶片的每次结果均由时域结果和频域结果联合决策，首先剔除掉模糊结果（即时域频域有且仅有1个指纹标签低于标准指纹标签），只保留可明确为“同个/不同”的结果；然后由32个晶片共同投票决策出该次待识别信号的识别结果，此时的结果已经较为稳定，在实验室做过约300次识别实验中，超过260次结果都是至少26个晶片的结果是相同的，即可以非常明显区分取“同个”指纹和“不同”指纹；虽然理想条件下只需要采集到1次准确的待识别信号即可进行识别，但实际使用过程中，操作误差是无法避免的，无法保证操作员的每一次信号采集都是没有任何失误的和偏差的，如果只采1次待识别信号，待识别信号采集位置与标准信号采集位置的偏差、耦合剂过少以至于部分晶片未能与样品表面耦合以及探头未与样品表面紧密贴合等操作误差都会使识别结果出现错误.

为避免只采1次待识别信号时因操作误差导致结果误报，设计5次待识别信号投票决策阶段提高系统容错率，降低操作要求对待识别样品采集5次信号，按照上文的算法得到5组待识别指纹标签，每组待识别指纹标签依次与标准指纹标签对比，统计这5次比较中每个晶片“同个物体”和“不同物体”的次数，以二者出现次数多的一方确定为结果(不考虑识别不清次数)，若次数相同则结果为“识别不清”.例如第1个晶片判断2次“同个物体”，1次“不同物体”和2次“识别不清”，则该晶片最终结果为“同种物体”；如第1个晶片判断2次“同个物体”，2次“不同物体”和1次“识别不清”，则该晶片最终结果为“识别不清”.

最后统计所有晶片判断为“同个物体”和“不同物体”的个数，当判断为“同个物体”个数多于“不同物体”的个数时，最终结果判断为“同个物体”；反之则判断为“不同物体”；若二者次数相等则判断为“识别不清”，需要重新采集待识别信号.

3 识别实验

3.1 实验仪器相控阵主机和相控阵探头如图1所示，右侧白色金属方块为质量400 g的相控阵探头固定器，其主要作用是利用重力让探头紧密贴合样品表面，保证采集信号的稳定，固定器底槽尺寸与探头尺寸一致，探头紧密嵌入其中，固定器一侧开有线槽以固定探头线.

相控阵探头中心频率为10 MHz，相控阵系统重复频率0.05 kHz，信号增益20 dB，采样时间t为50 μs，实验样品的超声回波波形见图2.

图1 相控阵系统及探头Fig.1 Phased array system and array probe

图2 样品超声信号Fig.2 Ultrasonic echo signal of sample

3.2 实验样品本文对多组不同材料、不同形状、和不同尺寸的各类金属样品进行了实验，部分实验样品图片见图3.图3中深蓝色直角部分为探头固定器，确保探头每次放置的位置都保持一致.图3中的金属样品根据形状和材料进行了分组，每组3个样品，样品属性见表1.

图3 各类金属样品Fig.3 Various metallic samples

表1 样品尺寸及材料Tab.1 Properties of samples

3.3 实验结果本文对（a）～（f）共6组样品每组中的3个样品都编号为1#、2#和3#.用相控阵探头采集每组3个样品的超声信号，由上文算法计算每个晶片的特征量，进而计算得到各样品的标准指纹标签.然后采集3个样品的待识别标签并依次与标准指纹标签进行比对，经实验验证，（a）～（f ）6组样品每组进行的9次识别结果均正确.

例如以a组1#样品的指纹标签为标准(因数据量较大，1#样品部分标准指纹标签数据，见表2)，依次识别1#、2#和3#的待识别标签.由于指纹标签数据量较大，故表3和表4列出1#和2#样品待识别标签部分数据.

表2 1#样品标准指纹标签Tab.2 Standard fingerprint label of sample 1#

表3 1#样品待识别标签部分数据Tab.3 Part of fingerprint label to be identified of sample 1#

表4 2#样品待识别标签部分数据Tab.4 Part of fingerprint label to be identified of sample 2#

将表3、表4的数据与表2做对比，可以看出1#样品的32个晶片的时域、频域待识别标签均低于1#样品的标准指纹标签(阈值)，识别结果为“同个物体”；2#样品的32个晶片的时域、频域待识别标签均高于1#样品的标准指纹标签且超出明显，识别结果为“不同物体”.

3.4 不确定度不确定度是用来表示所给出的测得值的可靠程度，合理地赋予被测量之值的分散性，与测量结果相联系的参数，是体现测得值水平的一个重要指标，不确定度越小，所述结果与真值越接近，质量越高，水平越高，其使用价值越高；不确定度越大，测量结果的质量越低，水平越低，其使用价值也越低[17].不确定度与误差不同，误差反映的是测量结果偏离真值的程度，误差定义为被测量的单个结果和真值之差.所以，误差是一个单个数值.原则上已知误差的数值可以用来修正结果.不确定度代表测量值的不确定程度，也是对测量误差的可能取值的测度，或者说是对测量值可能存在范围的估计.

测量结果不确定度一般包含几个分量, 按其数值评定方法, 这些分量可归为2类：A类 (多次重复测量时) 用统计学方法计算的量；B类（非统计学的）用其他方法评定的分量.A类不确定度由测量数据的实验标准偏差表征，按照国家检定规范，A类不确定度计算方法为用公式(7)即贝塞尔公式计算，得到的是实验标准偏差，然后由公式(8)计算 A 类评定的标准不确定度.s(x)为标准差，n为测量次数，uA为A类不确定度，x为采集的特征量.

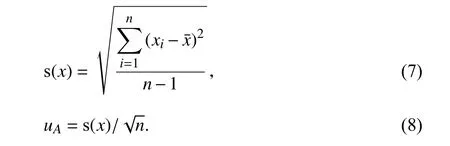
标准不确定度的B类评定，是借助于一切可以利用的有关信息进行科学判断，确定估计的标准偏差.通常是根据有关信息或经验，判断被测量的可能值的区间（-a，a），假设被测量值的概率分布，根据概率分布和要求的置信水平估计包含因子k，则B类评定的标准不确定度uB为被测量的可能值的区间半宽度除以k的商值

式(9)中，a为被测量可能值的区间半宽度，所用的信息可来自以前的测量数据、经验和对有关仪器性能或材料特性的一般知识，或生产技术说明书的技术指标；鉴定证书、校准证书等；k为包含因子，k的确定要首先假定测量值落在区间(-a，a)的概率分布，常见的包含因子有：两点分布k=1；均匀分布

这2类评定方法只是数值计算方法上不同，而不存在本质上的区别.按A类评定的不确定度分量，若不做重复观测也可由资料、经验公式等计算出其数值，也可按B类评定.在合成过程以及对测量不确定度的贡献中完全一样，它们都以标准偏差给出，也都可以评定其自由度.本文实验的信号采集方式正是多次重复测量，故使用A类不确定度来表征测量结果的可信赖程度更为合适.

表5给出1#样品各晶片时域特征量的不确定度，将其代入公式(7)和公式(8)即可得到所需相控阵采集系统的A类不确定度.

从表5可以看出各晶片多次重复采集的信号数据不确定度大部分在0.1左右，最大值也仅为0.37，相比于阈值至少小了1个量级，对识别的影响较小，由此可以看出在操作测量过程规范的前提下，相控阵金属识别系统不确定度很小，具有较高精度，所得结果具有可靠性和有效性.

4 结论

以相控阵平面波检测系统采集了4种常见金属共18个样品的超声信号，经指纹标签算法进行处理和识别，再由时域频域联合判断，成功识别出每组的3个材料形状完全一致的样品，样品之间的指纹标签差异很大尤其是频域指纹标签，该系统能有效识别出材料相同的非同个物体.相控阵识别系统测量不确定度较小，检测系统稳定，采集到的数据有较高的可信度.相控阵金属指纹标签识别系统可对精密仪器、贵重文物和机密物体的防伪造、防替换起到积极作用.