基于自由变形技术的海上风电安装船减阻优化

黄 亚 南， 陈 蒙 乐， 司 萌， 李 飞 虎， 冯 珺

( 1.大连海洋大学 航海与船舶工程学院， 辽宁 大连 116023；2.大连海洋大学 辽宁省海洋牧场工程技术研究中心， 辽宁 大连 116023 )

0 引 言

随着煤炭、石油等不可再生能源日益紧缺，人们将目光投向清洁能源．海上风能作为一种清洁可再生能源，既满足节能减排的经济要求，也符合保护环境、绿色低碳的发展要求，所以海上风电技术应运而生．风电安装船作为输送和安装海上风机的特种工程船，优化船型使其具有良好的快速性具有现实意义．快速性是船舶设计中要考虑的主要问题之一，也是造船界追求的目标之一．减少船舶航行阻力，是提高快速性的主要途径．国际海事组织(IMO)在2011年7月通过了控制温室气体排放的新造船舶能效设计指数(EEDI)，且于2013年起强制生效．对船体型线进行降阻优化是促进我国能源可持续发展的一种有效手段．

国内外学者对船舶减阻优化开展了大量研究．通过增加球鼻艏和选用不同形状球艏可有效减小兴波阻力[1-3]，对船体型线进行优化设计可有效降低船体阻力，提升船舶快速性[4]．随着计算机运算能力提升，CFD方法成为研究船舶水动力性能的重要手段．程宣恺等[5]利用FRAMEWORK软件改变特征参数对船体型线进行优化，并通过商业CFD软件STAR CCM+对球艏优化、尾楔形状优化及轴支架布置对船体阻力及伴流的影响进行分析．Yamano等[6]对3种典型的船艉底部轮廓形式开展模型试验，探讨了船底剖面形式对艉部波形和阻力的影响．Duy等[7]利用CFD方法对不同艉封板结构的集装箱船艉部后流场进行了数值模拟，并对原集装箱船的艉部进行了宽度和高度的修改，得到了多种船艉形状的新船型．

为实现船体型线的优化，冯佰威等[8-9]利用母型融合法和径向基函数插值技术对船体曲面的参数化进行修改．李胜忠等[10-11]采用自由变形(FFD)技术对船体表面进行重构，并进行实例验证，取得了较优的设计方法，降阻收益显著．

神经网络因具有模拟生物神经系统的功能，可通过学习和训练获取网络的结构和权值，具有强大的学习计算能力．闫宏生等[12]利用BP神经网络预测了多组不同航速、不同布局下的三体船单位排水量阻力值，对三体船主体及附体的布局进行了优化．张维英等[13]以某油船为目标船型，构建了降阻优化BP神经网络(BPNN)模型，该模型可以快速地进行船舶阻力预报，并为构建变精度模型提供了思路．Yang等[14]采用径向基函数神经网络(RBFNN)对一艘13500TEU的集装箱船进行不同吃水下的阻力预报，预测结果表明RBFNN有较高的学习预报性能．

由于船艉流场的复杂性，目前艉部型线优化相较于船体艏部还相对较少．本文综合上述思路及方法，将CFD方法与BPNN优化理论及FFD技术相结合，对目标风电安装船艉部形状进行改变，并对型线优化后的模型进行数值模拟．通过构建BPNN模型，得出总阻力随设计变量的变化趋势，从而在该船型的3种艉部变化方案中分别得出该方案下的最优船型．

1 数学模型

1.1 控制方程

本文假定流体为不可压缩黏性流体，采用VOF方法捕捉自由液面，流体的运动由全局坐标系中描述的连续性和RANS方程控制：

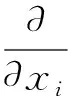
(1)

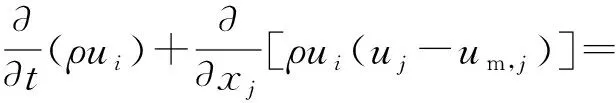
ρgi+Si

(2)

(3)

式中：xi(i=1，2，3)、xj(j=1，2，3)为坐标分量；ui为xi方向的流体速度分量；uj为xj方向的流体速度分量；um，i为xi方向的网格速度分量；t为时间；μt为湍流黏度；δij为克罗内克函数；k为湍动能；p为压强；gi为重力加速度在xi方向的分量；Si为xi方向上的源项；α为流体体积分数．

1.2 湍流模型

本文采用了k-ω(SST-Menter)湍流模型，其湍动能k和湍流耗散率ω的输运方程为

(4)

(5)

式中：τij为湍流雷诺应力张量分量；Sij为平均变形速度张量分量；F1为混合函数；Pω为ω的导出项；β*、β、σk、σω和σω2分别为湍流模型常数．

2 目标船型及船型变换

2.1 目标船型主要参数

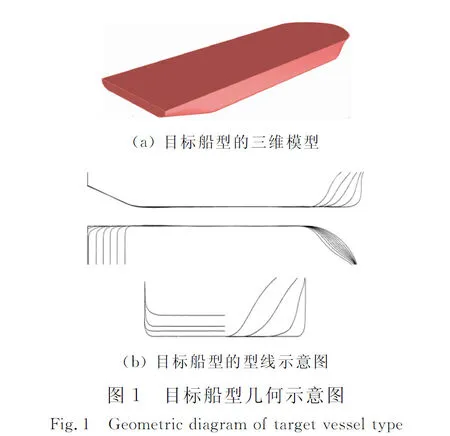
风电安装船作为特种工程船，早期由浮式起重船和驳船联合作业，后来出现了半潜平台和带有定位桩腿的自航船，但其对海面环境状况适应性差，安装效率低．为满足海上风电安装需求，自航自升式风电安装船应运而生．目标船型配备一台主起重机、两台辅吊机以及艏侧推动力定位装置，可在最大作业水深40 m的近海进行作业．目标船型主尺度参数见表1．其三维模型与部分型线见图1．

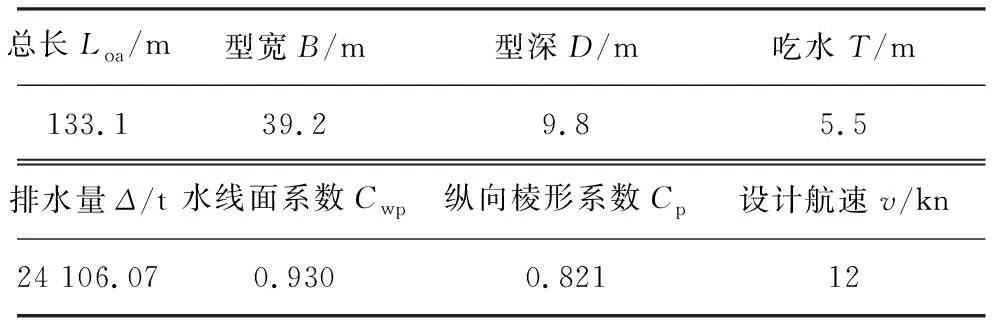
表1 风电安装船主尺度参数

2.2 自由变形技术

相较于NURBS、Lackenby变换方法、参数化建模方法[15-16]等船型优化的几何重构方法，FFD技术优化方式更灵活，且适用于复杂船体的几何重构．采用FFD技术对船体艉部进行局部变形，能够保持变化前后任意阶的跨界导矢量连续，控制变形前后体积的变化程度．采用Bernstein基函数来建立控制体的控制点与控制体内几何点坐标的函数关系式．在待变形区域外围构造控制体，则控制体内任意一点坐标值表达式为

(6)

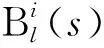
(7)

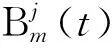
在FFD控制点移动后，控制体内任意点与控制顶点的位置关系(s，t，u)不发生改变，故模型上点的位移量为

(8)

其中ΔPi，j，k为控制体中第(i，j，k)网格点位移量．

变形后模型的全局坐标为

xFFD(s，t，u)=x(s，t，u)+Δx(s，t，u)

(9)

FFD技术涉及的设计变量多时可高达几十个，少时可以是几个，使曲面变形十分灵活，并且对变形区域的大小和位置严格可控，因此广泛应用于船体几何变形．对于艉部局部变形，采用较少的设计变量，可实现船体复杂曲面自动重构．

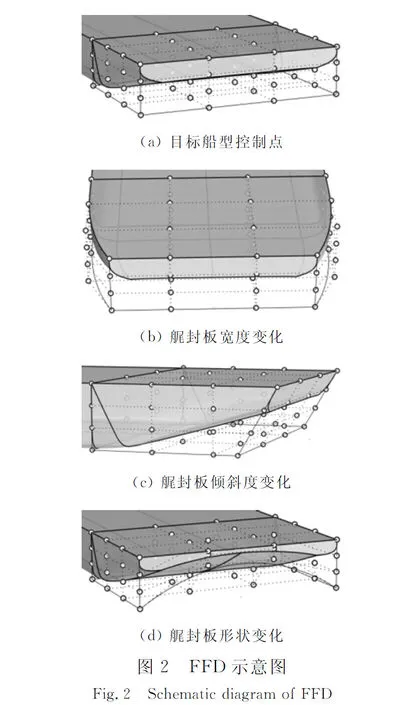
影响黏压阻力的主要因素是船体形状，艉部形状对于黏压阻力的影响尤为明显，这是因为黏压阻力是由于黏性作用和艉部的纵向压力梯度产生的[17]．在满足约束条件的情况下，本文选取改变艉封板宽度、倾斜度和形状3种设计方案以达到降阻目的．即沿船长、型宽、型深3个方向的控制点进行线性变换．图2为艉部采用的FFD示意图．

在对目标船型进行优化设计时，需保证优化后的船型仍具有初始船型所具备的营运性能[18]．因此，优化后的船型排水量以及浮心纵向位置的变化量不宜过大．具体约束条件如下：

(1)尺度约束：在保持Loa、B、D、T不变的情况下，改变船体艉部型线．

(2)排水量约束：

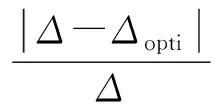
(10)

其中Δ为优化后船排水量，Δopti为待优化船排水量．

(3)以船舯为坐标原点建立笛卡儿直角坐标系，则浮心纵向位置约束：

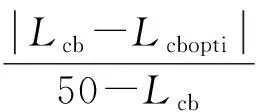
(11)

其中Lcb为优化后船的浮心纵向位置，Lcbopti为待优化船的浮心纵向位置．

3 艉封板宽度降阻研究

3.1 不同艉封板宽度数值模拟

在艉封板宽度为12 600～19 600 mm，采用均匀试验设计法选取10组方案．依据所选方案，对艉封板宽度进行变形，由图3可见，变化后的型线较目标船型艉部吃水变窄．运用CFD软件进行数值计算，结果见表2．从模拟结果可知：随着艉封板宽度增加，船体所受阻力呈现上升趋势，但当达到13 300 mm宽度附近时，总阻力出现极小值，随后增加艉封板宽度，阻力逐渐增大．

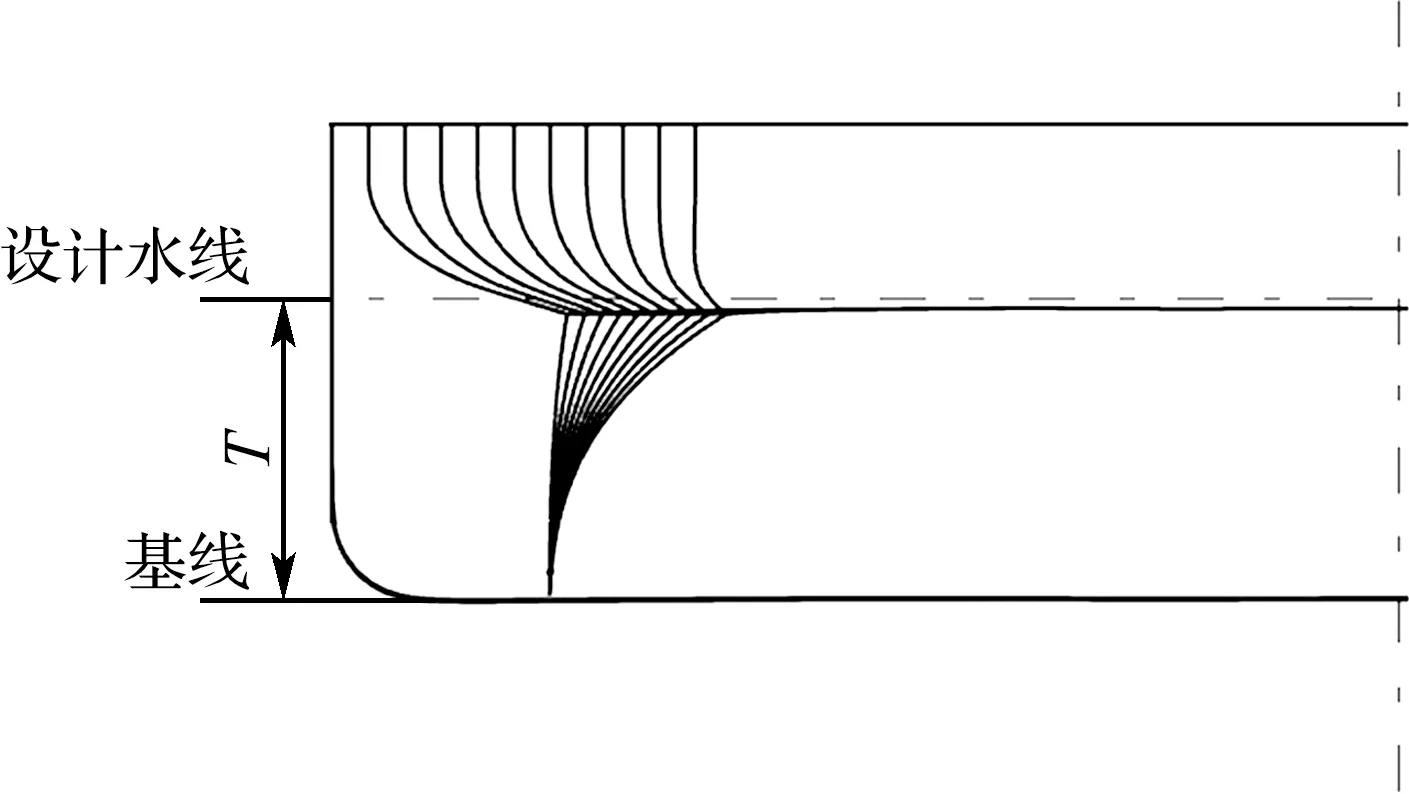
图3 艉封板宽度变化

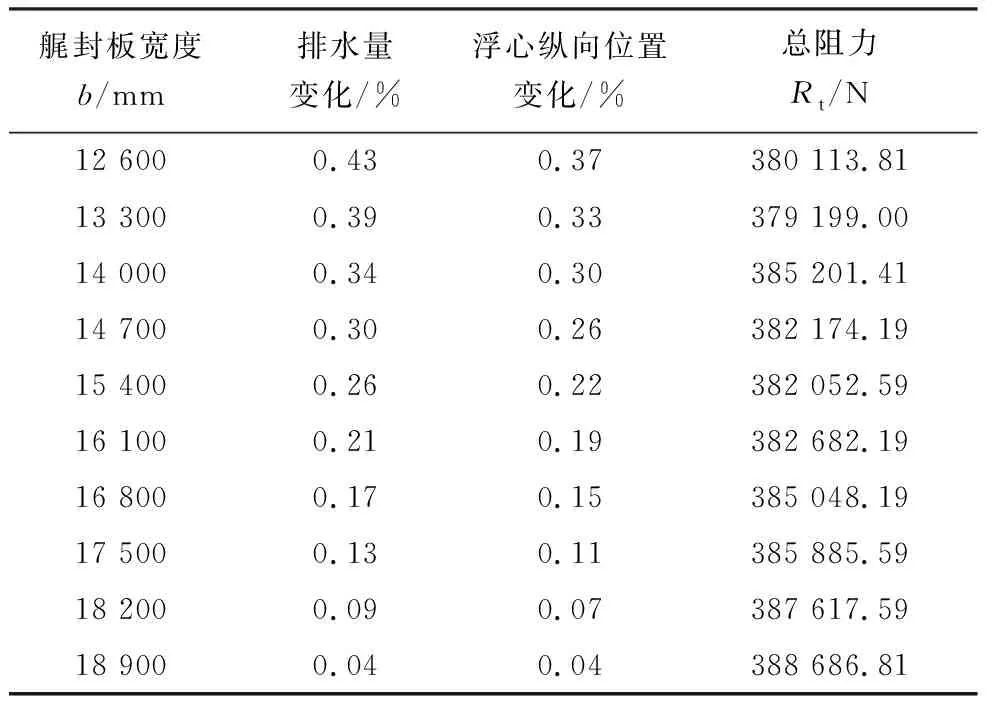
表2 不同艉封板宽度总阻力模拟值

3.2 阻力预报的BPNN构建及偏差分析

将改变艉封板宽度的优化船型和目标船型的11组船型数据作为样本输入变量，总阻力作为输出变量，进行BPNN训练．将神经网络终止误差(均方误差，E)设置为1×10-10，最大迭代次数为500 000．

为了使神经网络满足高精度寻优，该BPNN共设置网络层数为3层，其中包含1个隐含层，通过不断调节隐含层节点数，使E满足精度需求，从而达到最佳训练效果．艉封板宽度优化采用隐含层节点数为7作为最终寻优模型．

图4所示为BPNN的训练曲线．可以看出，训练误差收敛性较好，达到目标效果．

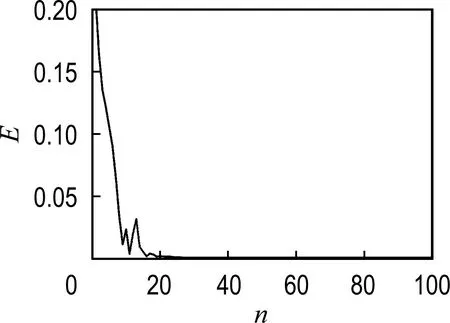
图4 BPNN训练曲线

训练样本的CFD计算值与BPNN预报值偏差曲线如图5所示．由图可见，BPNN预报值与CFD计算值吻合度高，较好反映出总阻力的变化趋势．证明该BPNN能够代替CFD对不同艉封板宽度的船型样本进行阻力预报．

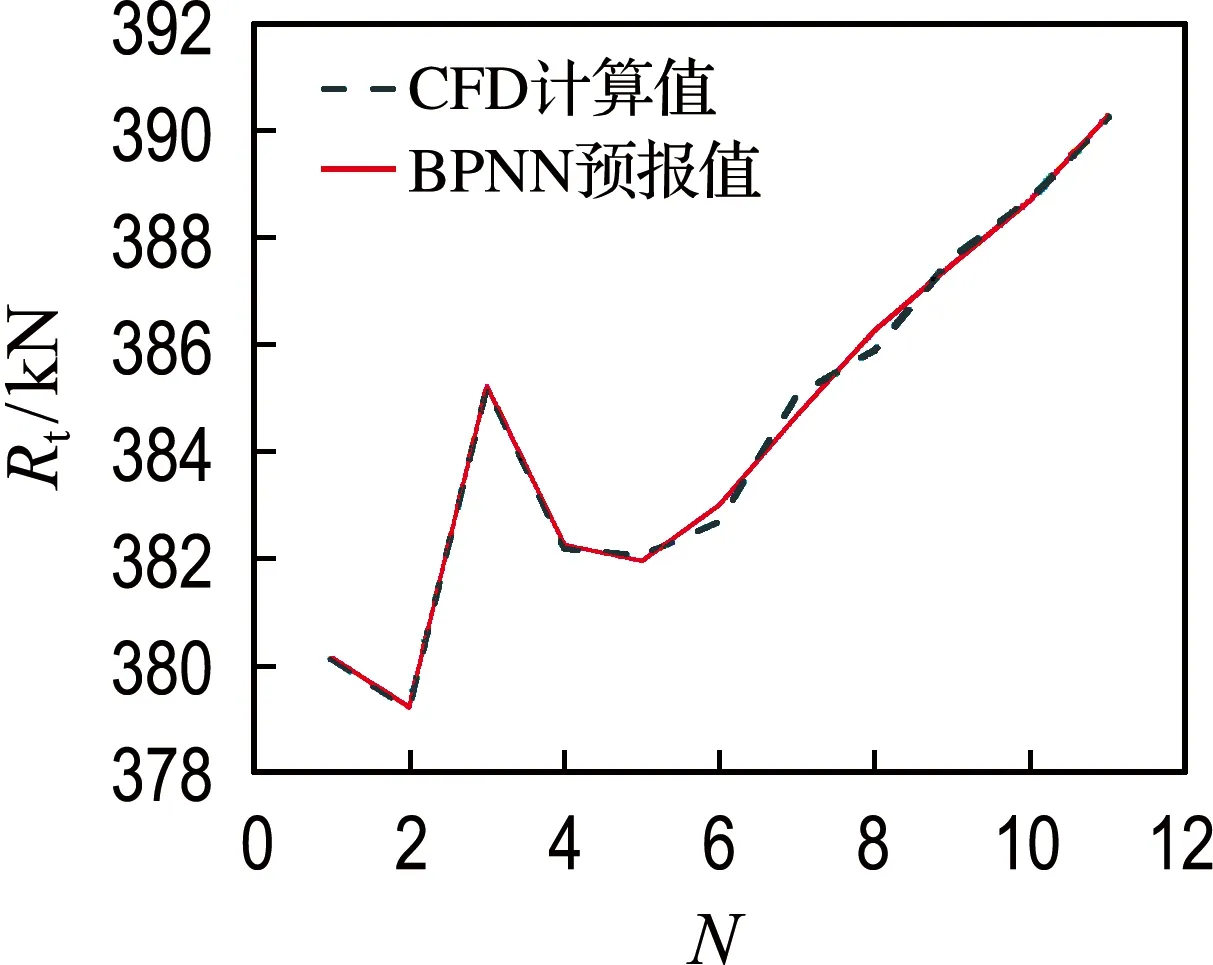
图5 艉封板宽度方案BPNN偏差曲线

3.3 艉封板宽度寻优

通过前面BPNN的验证，扩大样本点个数找出最优设计变量点，从而更为准确地进行阻力预报．采用均匀试验设计法进行取样，在12 600～19 600 mm选取200个样本点．寻优曲线见图6．

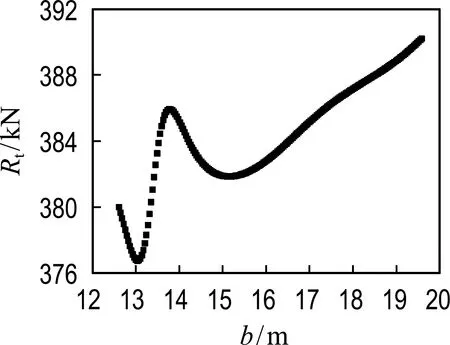
图6 艉封板宽度寻优曲线

从图6中可以看出，该BPNN预报值较好反映了船体总阻力随艉封板宽度的变化趋势．综合考虑优化目标的约束条件以及船体所受总阻力的数值结果，将最终寻优的宽度进行数值模拟验证，CFD计算值为379 041.41 N，与BPNN预报值的误差仅为0.61%，表明该BPNN满足阻力预报精度要求．

图7为目标船型与艉封板宽度优化后的自由液面波形对比结果，可以看出，艉部两侧的兴波范围明显减小且相较优化前更为平坦．

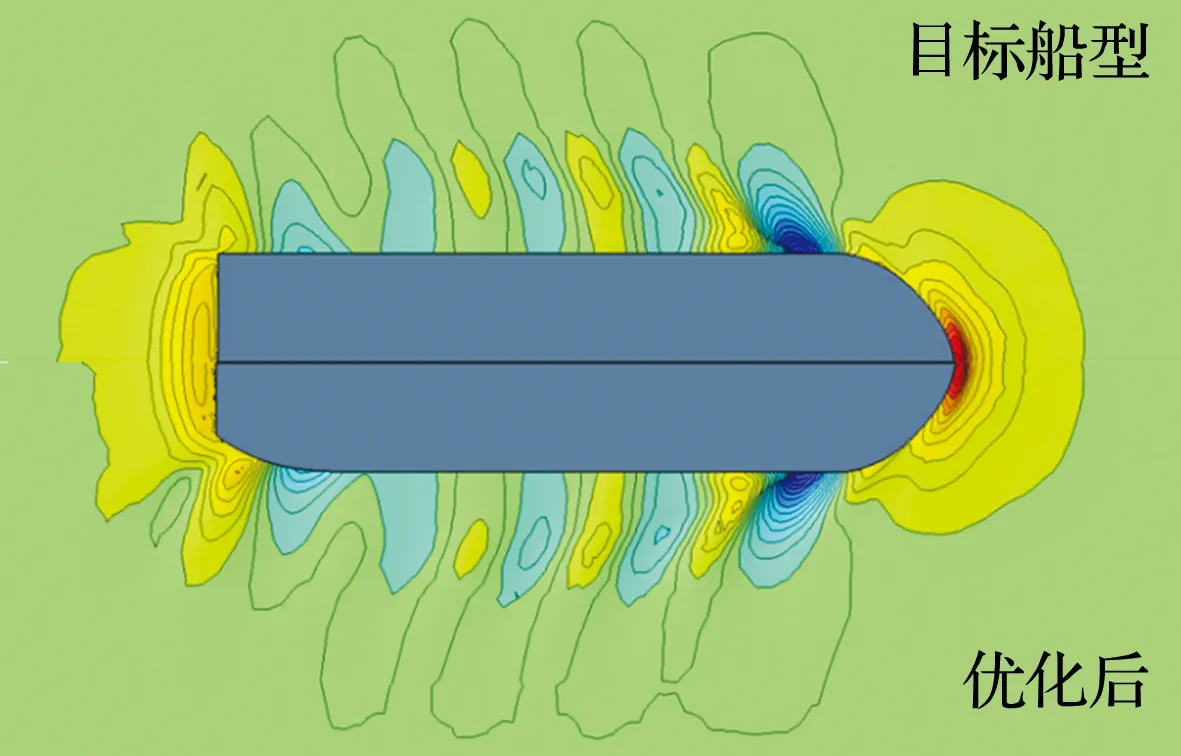
图7 自由液面波形对比

4 艉封板倾斜度降阻研究

艉封板倾斜度(艉封板与基平面所成角度)的改变，也会对船体所受黏压阻力产生一定的影响．本船采用全回转螺旋桨，无须安装舵板，因此为艉部节省了很多空间，所以艉部形状的改变对螺旋桨的安装并无太大的影响．综合考虑了艉部布置，选取适合的艉封板倾斜度可有效改善船体总阻力，提高船舶快速性．将改变的10组方案进行数值模拟，计算结果见表3．将所有方案进行BPNN预报，本部分BPNN的构建过程同艉封板宽度一致，设置隐含层节点数为6．其偏差曲线如图8所示．从图中可以看出，BPNN预报值较为完好地接近CFD计算值，满足寻优预报的精度要求．

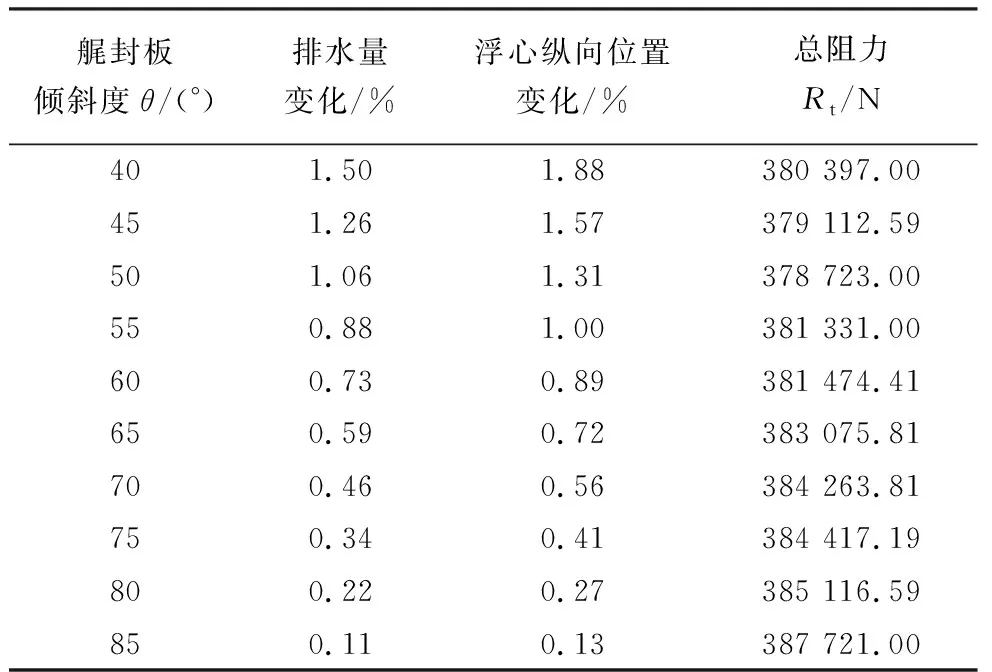
表3 不同艉封板倾斜度总阻力模拟值

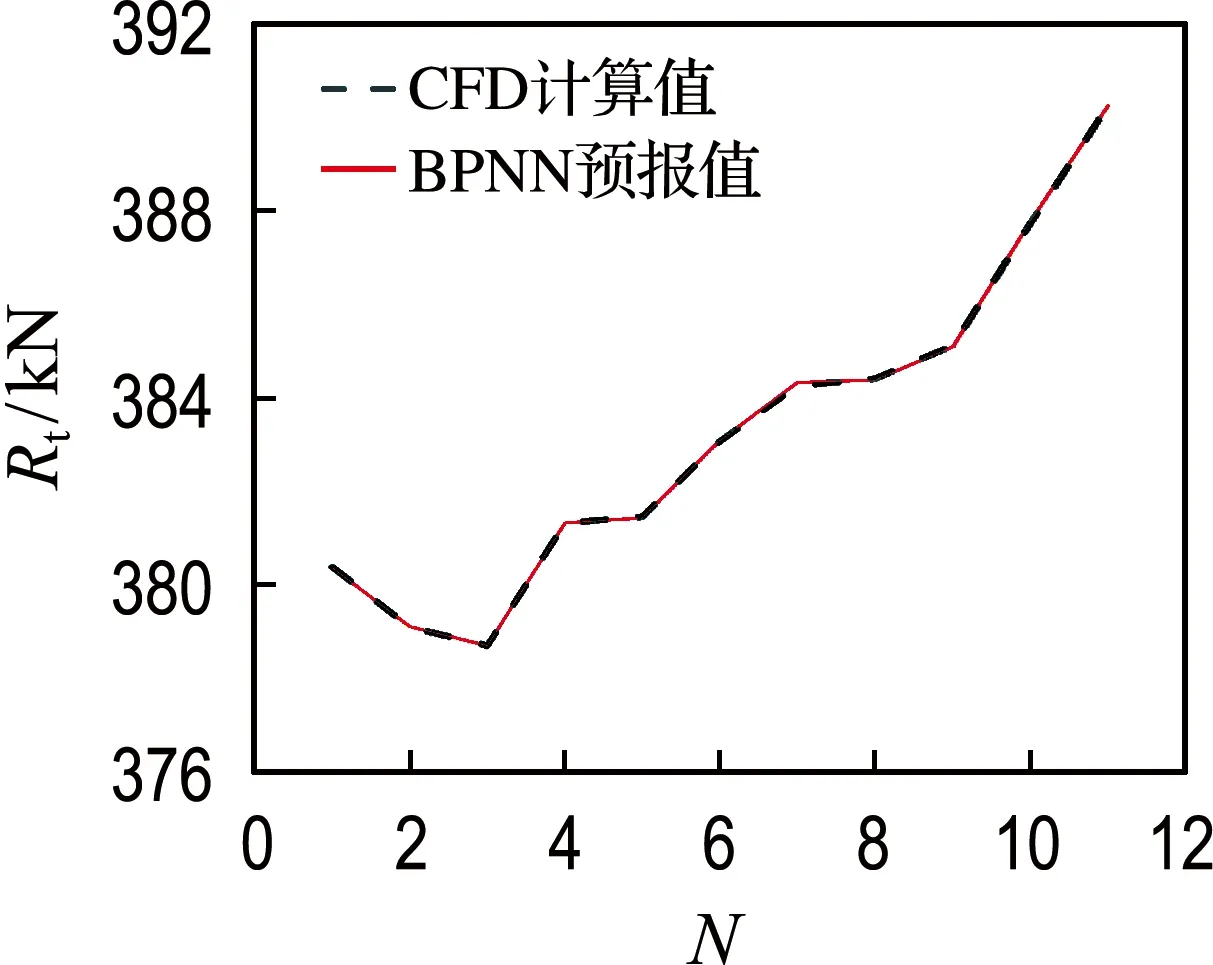
图8 艉封板倾斜度方案BPNN偏差曲线

在倾斜度40°～90°内扩大样本点数，通过均匀试验设计法选取200个样本点．寻优曲线见图9．

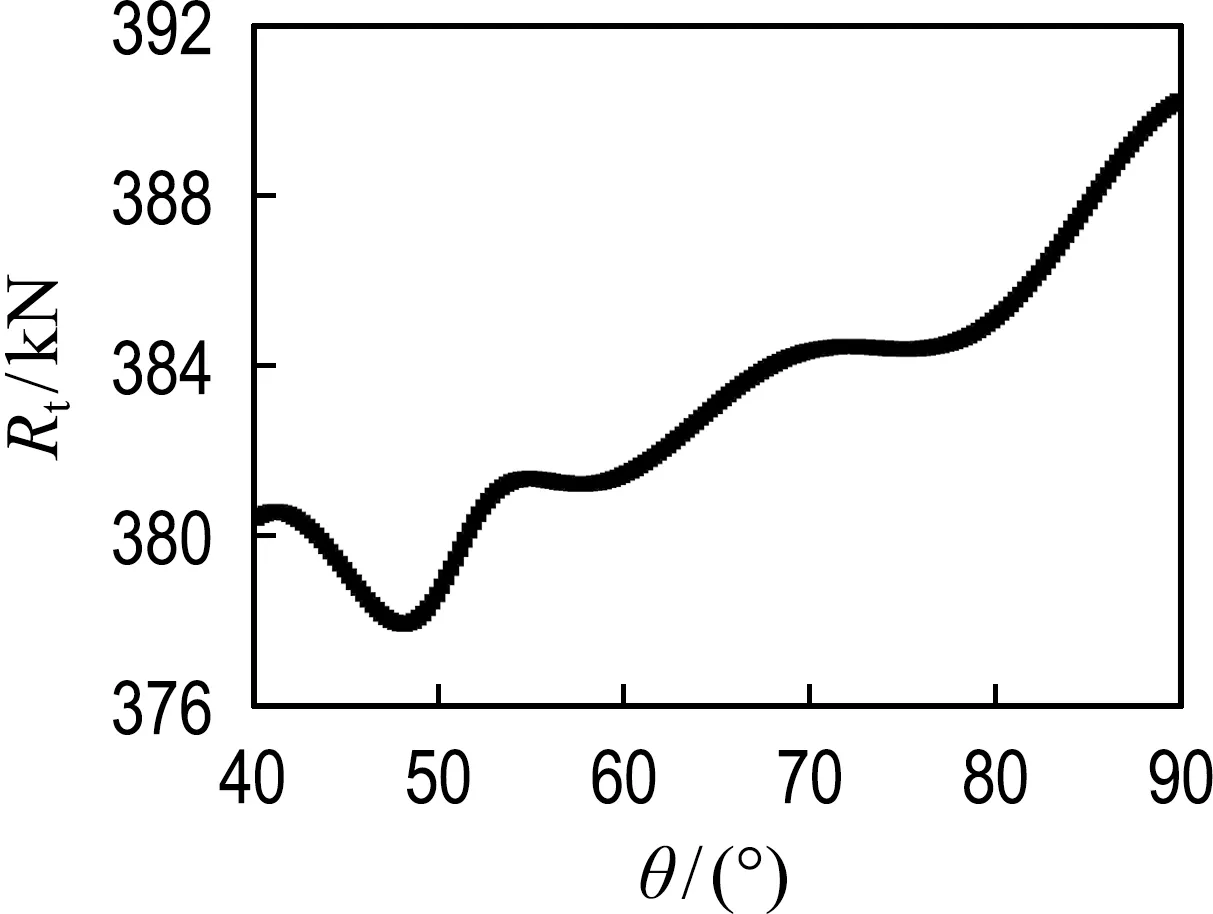
图9 艉封板倾斜度寻优曲线

经BPNN预报寻出的最优角度为48.12°，但由于其排水量及浮心纵向位置变化均已超出约束条件，故在满足约束条件的倾斜度55°～90°内重新构建神经网络．综合考虑约束条件与艉部布置，选取倾斜度55°为最优设计方案．优化后船型总阻力降低约2.28%，预报结果与CFD计算值的误差为0.26%，该BPNN同样具有较高的预报精度．其优化前后艉部部分型线见图10．

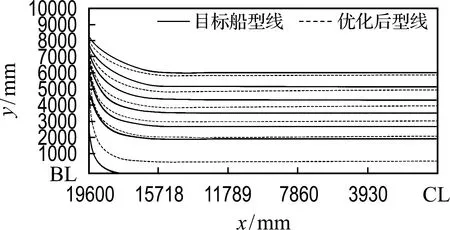
图10 目标船型与优化后部分型线对比图

5 W形艉封板的降阻研究

5.1 W形艉封板的BPNN阻力预报

在约束条件下，本文选取了艉封板的中点高度和端点高度两个特征作为优化参数．其中，将目标船型艉封板的底边中点距基平面的高度ha=5 450 mm和两端点距基平面的高度hb=5 450 mm作为设计变量的基准点．取值范围为

5 450 mm≤ha≤8 450 mm
4 450 mm≤hb≤5 500 mm

(12)

采用均匀试验设计法，在两个变量设计区间内选取10组样本点，并将目标船型与10组样本点作为学习样本输入变量，总阻力作为输出变量．表4为训练样本点的总阻力．经过BPNN训练，BPNN预报得到的样本点空间分布见图11．

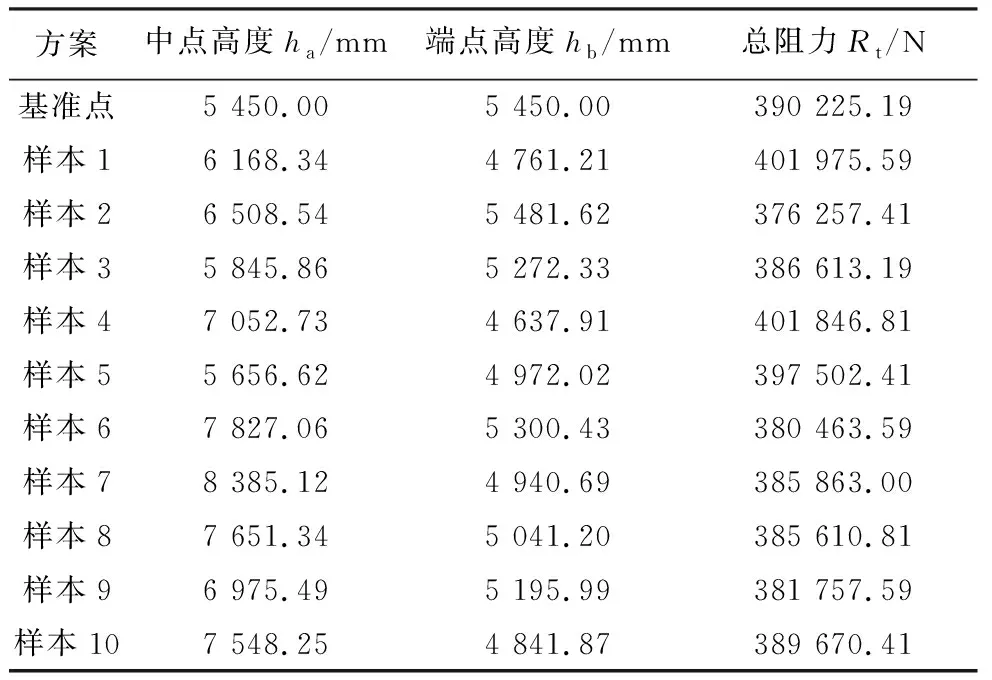
表4 训练样本点的总阻力

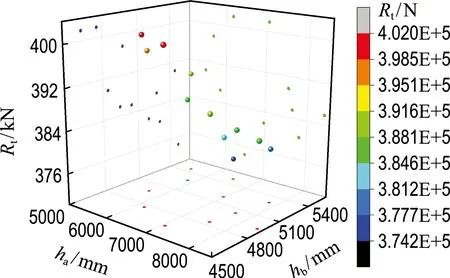
图11 BPNN预报样本点的空间分布

5.2 设计样本点寻优及相关性分析

经过上述BPNN训练的验证，同样采用均匀试验设计法进行取样，共在设计范围内选取200个样本点．其BPNN预报的总阻力如图12所示．

为了研究两个随机变量之间的相关关系，本文将空间散点分别投影到XZ和YZ平面，则可对该投影面进行相关性分析．相关系数作为度量两个变量相关性的指标，表明其呈现相关性的程度．XZ和YZ平面上的散点分别表述为端点高度和中点高度与总阻力的相关关系，分别对投影平面上的散点进行Pearson相关性分析．假定样本可以

记为(Xi，Yi)，则样本Pearson相关系数定义为

(13)

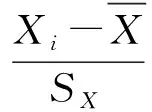
端点高度与总阻力的Pearson相关系数为-0.818，故得出端点高度与总阻力之间存在着明显的强负相关性．中点高度与总阻力的Pearson相关系数为-0.409，表明中点高度与总阻力之间存在着明显的中度负相关性．从图12中空间散点在XZ和YZ平面上的投影可以看出，端点高度与总阻力的关系更具规律性，且其相关性强于中点高度与总阻力值的．经BPNN预报之后，寻找出一组使总阻力最优的变量尺度．

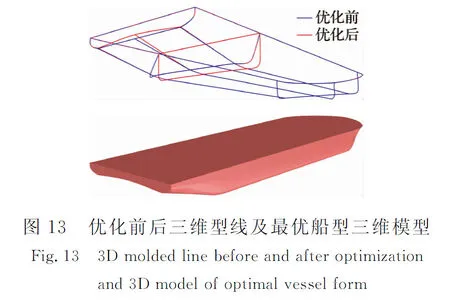
经数值模拟分析，通过改变艉封板形状使艉部型线产生变化，船体受到的总阻力明显减小，优化后船体总阻力比目标船型降低约4.1%，且排水量变化(0.69%)和浮心纵向位置变化(0.62%)均在1%以内，符合设计变量的约束条件．对优化后的船型进行数值模拟，BPNN预报值与CFD计算值之间的误差仅为0.081%，表明该神经网络可以很好地代替CFD方法进行船体阻力预报，满足预报精度要求．优化前后相关参数对比见表5．优化前后三维型线及最优船型三维模型见图13．

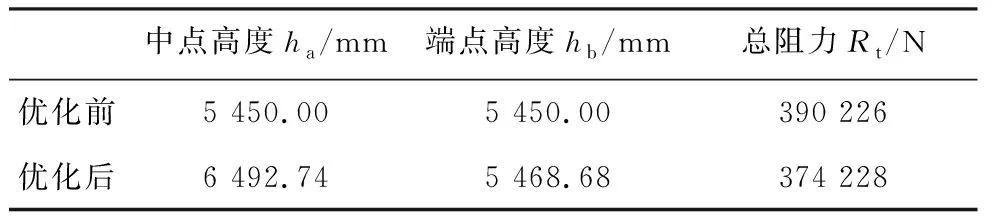
表5 优化前后相关参数对比

6 结 语

为了探究艉部型线对于船体阻力的影响，本文基于FFD技术，对目标船型进行了艉部形状变形．通过改变艉封板形状，并使用BPNN展现艉封板形状变化时船舶总阻力的变化规律，最终寻得一组快速性优良的艉部形状变化参数．所构建的BPNN模型具有较高的阻力预报精度，且相较于CFD方法，计算耗时更短，能在大量样本中，在保证精度前提下快速进行阻力预报，为研究风电安装船全船型线优化提供了一种新的思路和方法．