饱和输入下一类多项式系统的数据驱动控制

楼 旭 阳， 张 智 豪

( 江南大学 物联网工程学院， 江苏 无锡 214122 )

0 引 言

对于未知的动态系统来说，控制器的设计总是充满挑战[1]．一种常见的思路是先通过系统辨识重构出系统的模型，再对重构后的系统设计控制器．然而，由这种思路设计的控制器会带来一些问题．其一，有的系统辨识困难，或者无法得到可靠的辨识模型．其二，控制器性能依赖于系统辨识的精度[2]．因此，数据驱动的概念应运而生．数据驱动控制是通过测量数据设计控制器的一种方法，比如在网络控制系统(NCS)中经常只能获取数据信息[3]，那么数据驱动方法便为NCS的控制器设计提供了一种可行方案．数据驱动控制分为间接数据驱动控制和直接数据驱动控制两种．前者先通过测量数据获得系统模型，再基于获得的模型设计控制器[4]．显然，控制器的控制效果与获得模型的精度高度相关．严格来说，这也属于先辨识后控制的范畴．后者顾名思义是一种跳过系统辨识环节直接完成控制器设计的一种方法．目前，相关研究尤其是非线性系统的直接数据驱动控制研究引起了广泛关注，也取得了一些成果[5]．文献[6]针对一类非线性系统提出了一种基于直接数据驱动的跟踪控制方法，该方法没有明确地推导出系统模型，而是通过结合在线和离线手段直接设计出了时变状态的反馈控制器．文献[7]以自来水厂混凝投药大时滞过程为研究对象，在迭代反馈整定(IFT)方法的基础上，结合Smith预估控制结构，提出了一种混凝投药过程数据驱动直接控制算法．不过，有关多项式系统直接数据驱动控制的研究结果还较少．

实际应用中，输入饱和是一个很常见的现象，它会导致闭环系统性能下降甚至不稳定[8]．所以，从实际出发，研究饱和输入下系统的控制问题具有很大的应用价值．近些年，相关问题的研究也吸引了广大学者的关注[9]．文献[10]针对一类饱和输入下带有时滞的线性系统设计了全局渐近稳定的控制器，并指出设计方法可以应用于多智能体系统．文献[11]针对一类含有输入饱和及扰动的非线性系统采用了采样控制策略，通过设计一种新的辅助控制信号简化了控制器设计流程．文献[12]研究了饱和输入下一类多输入多输出非线性系统的跟踪控制问题，提出了一种灵活的基于性能的控制方案．对于多项式系统，尽管在一些现有的控制结果中已经解决了控制器饱和问题，如文献[13]研究了一类用T-S模糊模型表示的多项式系统的跟踪控制问题，同时考虑了输入饱和及外部干扰．然而，有关饱和输入下多项式系统的直接数据驱动控制研究少有报道．

对于线性系统来说，任何输入输出的轨迹都可以由有限个之前测量的输入输出数据的线性组合表示[14]．因而，可以通过基于数据的线性矩阵不等式(LMI)方法来解决线性系统的控制问题．而对于多项式系统来说，若可以将其写成线性状态依赖的形式，便可以采用平方和(SOS)方法来处理对其的控制问题．事实上，SOS方法也正是LMI方法在多项式系统领域的升级与补充．

本文将研究饱和输入下一类多项式系统的直接数据驱动控制问题．这类多项式系统可以写成线性状态依赖的形式，因而采用SOS方法进行分析处理．引入饱和输入约束的优势在于可以根据实际需要满足输入的限幅要求．与常规数据驱动控制不同，本文所考虑的直接数据驱动控制器设计方法，仅需离线采集输入输出数据，利用有限的输入输出数据构建Hankel矩阵来建立系统非参数化模型，从而避免系统辨识．最后，通过数值实例和电路实验验证所提出控制方法的有效性．

1 问题描述

考虑一类具有线性状态依赖形式[15]的多项式系统：

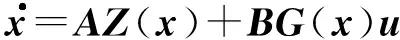
(1)

式中：系统状态x∈Rn，控制输入u∈Rm，向量Z(x)∈PN和矩阵G(x)∈Pq×m包含所有关于x的单项式，A∈Rn×N和B∈Rn×q是未知的常数矩阵．Rn是n维欧几里得空间，Rn×m是n×m维实矩阵空间，P是多项式集合，Pn是n维多项式向量空间，Pn×m是n×m维多项式矩阵空间．

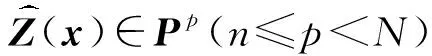
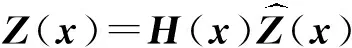
(2)

其中多项式矩阵H(x)∈PN×p．

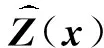
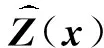
对系统(1)进行直接数据驱动控制，首先需要对输入输出数据进行离线采集，采样数据以矩阵的形式定义如下：

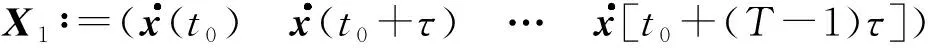
式中：(t0，t0+(T-1)τ)是采样总时间，T∈N>0是采样数据数量，τ∈R>0是采样周期，R>0是正实数集，N>0是正整数集．

注3离线采集系统的状态导数信息可能有些严格，在实际中可以在数据采集设备条件允许情况下通过加大采样频率，以尽可能精确地获得状态导数信息．同时，本文所提出的方法也容易推广应用于离散系统，只需要将X1中状态导数信息数据换成下一时刻离散状态值即可．

于是，可以计算得到：

Z0∶=(Z(x(t0))Z(x(t0+τ)) …

Z(x[t0+(T-1)τ]))

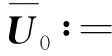
G(x[t0+(T-1)τ])u[t0+(T-1)τ])

测量噪声定义如下：

D0∶=(d(t0)d(t0+τ) …d[t0+(T-1)τ])

其中d(t)∈Rn．

考虑噪声影响，矩阵X1满足

(3)

为方便处理，矩阵D0和B满足如下合理的假设条件．

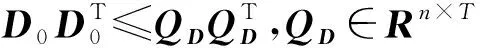
在实际离线采样过程中，噪声影响不应该无穷大，因而对噪声有一个上界约束是合理的．

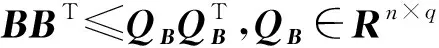
B作为系统控制输入前的未知常数矩阵，为了后文的证明，需要将其和一个已知常数矩阵建立联系，因而给其一个上界约束也是合理的．

定义

S∶=(BD0)，QS∶=(QBQD)

则在假设1和2的条件下，有

(4)

2 基于直接数据驱动的饱和控制设计

首先给出以下3个必要的引理．

引理1[16]给定适当维数的矩阵L和M，对任意的常数δ∈R>0，有

-LMT-MLT≤δLLT+δ-1MMT

(5)

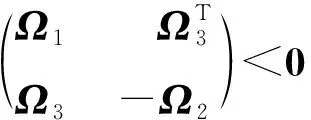
(6)

引理3[18]考虑如下线性系统：

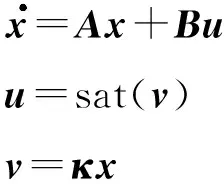
(7)

式中：x∈Rn是状态变量，u∈Rm是控制输入，A∈Rn×n、B∈Rn×m和κ∈Rm×n是常数矩阵．

定义非线性函数φ(v)∶=sat(v)-v，则对于任意正定对角矩阵Ξ∈Rm×m，有如下不等式成立：

φT(v)Ξ(φ(v)+v)≤0

(8)

定理1对于多项式系统(1)，在假设1和2的条件下，如果存在正定对称矩阵P∈Rp×p，正定对角矩阵Γ∈Rm×m，多项式矩阵Y(x)∈PT×p以及常数ε∈R>0，使得

Z0Y(x)=H(x)P

(9)

(10)

其中

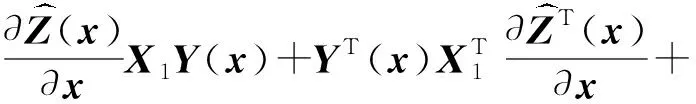
则在状态反馈饱和控制器

(11)

的作用下，闭环系统(1)全局渐近稳定．

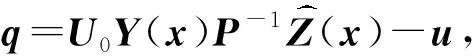
利用式(3)、(9)，闭环系统(1)等价于如下由Hankel矩阵所描述的系统：

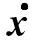
(12)

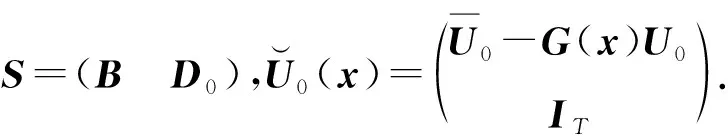
考虑Lyapunov函数

沿着闭环系统(11)的状态轨迹，计算其对时间t的导数，可得

(13)

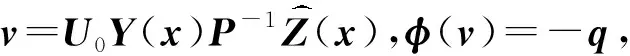
(14)

将式(14)代入式(13)可得

(15)

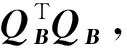
ε-1qTGT(x)BTBG(x)q≤

(16)

将式(16)代入式(15)得

(17)

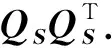
(18)

将式(18)代入式(17)有

(19)

整理并化简式(19)可得

(20)

其中

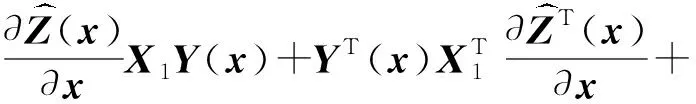
利用Schur补引理2进一步可得

(21)

其中

令Γ=Ξ-1，对多项式矩阵不等式(10)两边同时左乘、右乘diag{Ip，Ξ，Iq+T，In}，可得

(22)

注4由于本文研究的多项式系统可以写成线性状态依赖形式，故可以使用MATLAB的平方和工具箱SOSTOOLS[19]求解获得可行解．本文没有研究系统在饱和输入下的最优控制问题，主要考虑这样会得到一个双线性矩阵不等式(BMI)的充分条件，使得定理变得不易求解．

注5当输入u前的控制矩阵与x无关时，多项式系统(1)可以写成如下形式：

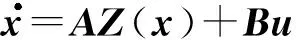
(23)

其中B∈Rn×m．

在这种情况下，类似于式(12)，闭环系统(23)可以进一步描述为

(24)

于是，可以得到如下推论．

推论1对于多项式系统(23)，在假设1和2的条件下，如果存在正定对称矩阵P∈Rp×p，正定对角矩阵Γ∈Rm×m，多项式矩阵Y(x)∈PT×p以及常数ε∈R>0，使得

Z0Y(x)=H(x)P

(25)

(26)

其中

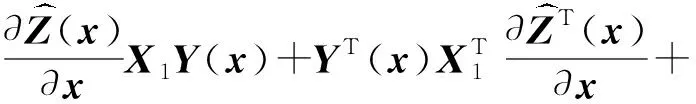
则在状态反馈饱和控制器

(27)

的作用下，闭环系统(23)全局渐近稳定．

3 仿真实例

考虑van der Pol振荡器[20]系统：

(28)

其中u为控制输入．

无控制输入时系统(28)的仿真结果如图1所示．由图可知，在不施加控制输入时该系统呈周期运动．

由于输入u前的控制矩阵与x无关，利用推论1，先离线采集一组输入输出数据如下：

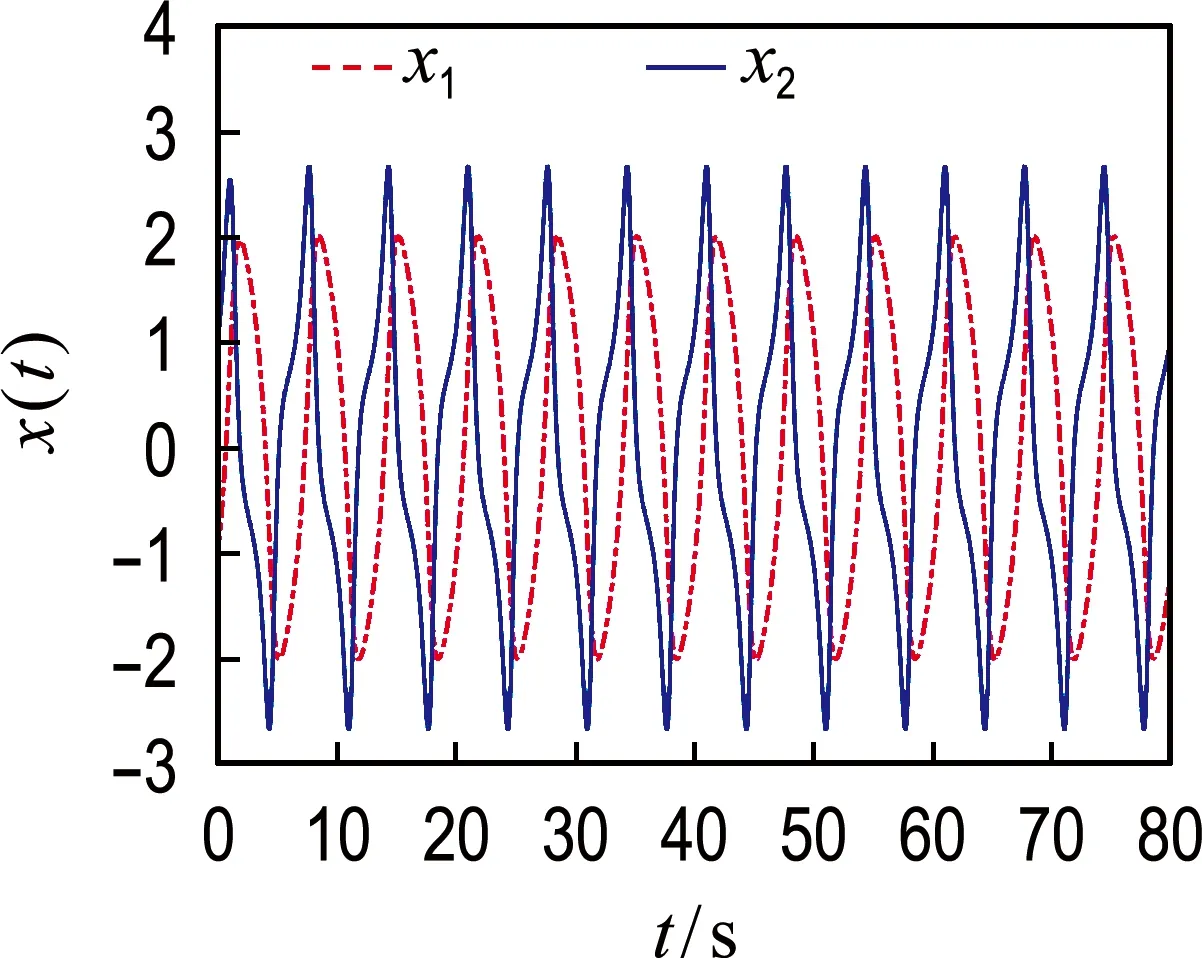
图1 无控制输入时系统状态x1、x2的时间响应曲线

U0=(u(0)u(0.5)u(1.0)u(1.5)u(2.0))=

(0.814 7 -0.905 8 0.127 0

-0.913 4 0.632 4)

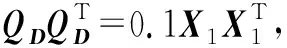
进而计算得到饱和控制器：

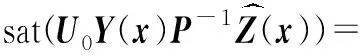
sat(x1(0.507 8x1x2+0.507 8)-

x2(3.159 7×10-14x1x2+1.173 9))

(29)

选取饱和函数界0.8，状态初始条件为x(0)=(-1 1)T．在饱和控制器(29)作用下，系统状态的时间响应曲线如图2所示，可以看出闭环系统状态渐近收敛到原点．

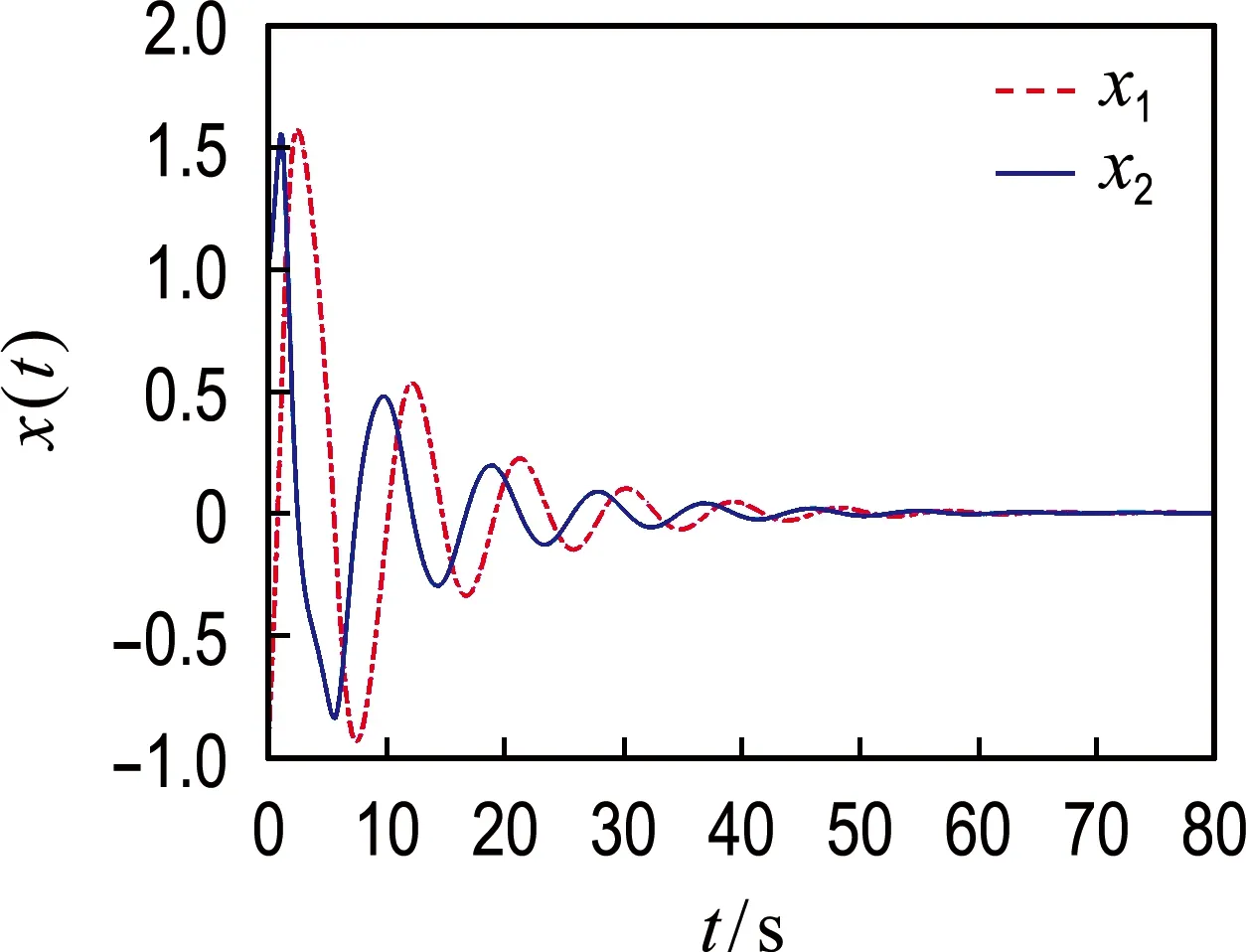
图2 饱和控制器作用下系统状态x1、x2的时间响应曲线

饱和控制器输入u的时间响应曲线如图3所示，可以发现控制输入满足[-0.8，0.8]幅值限制．

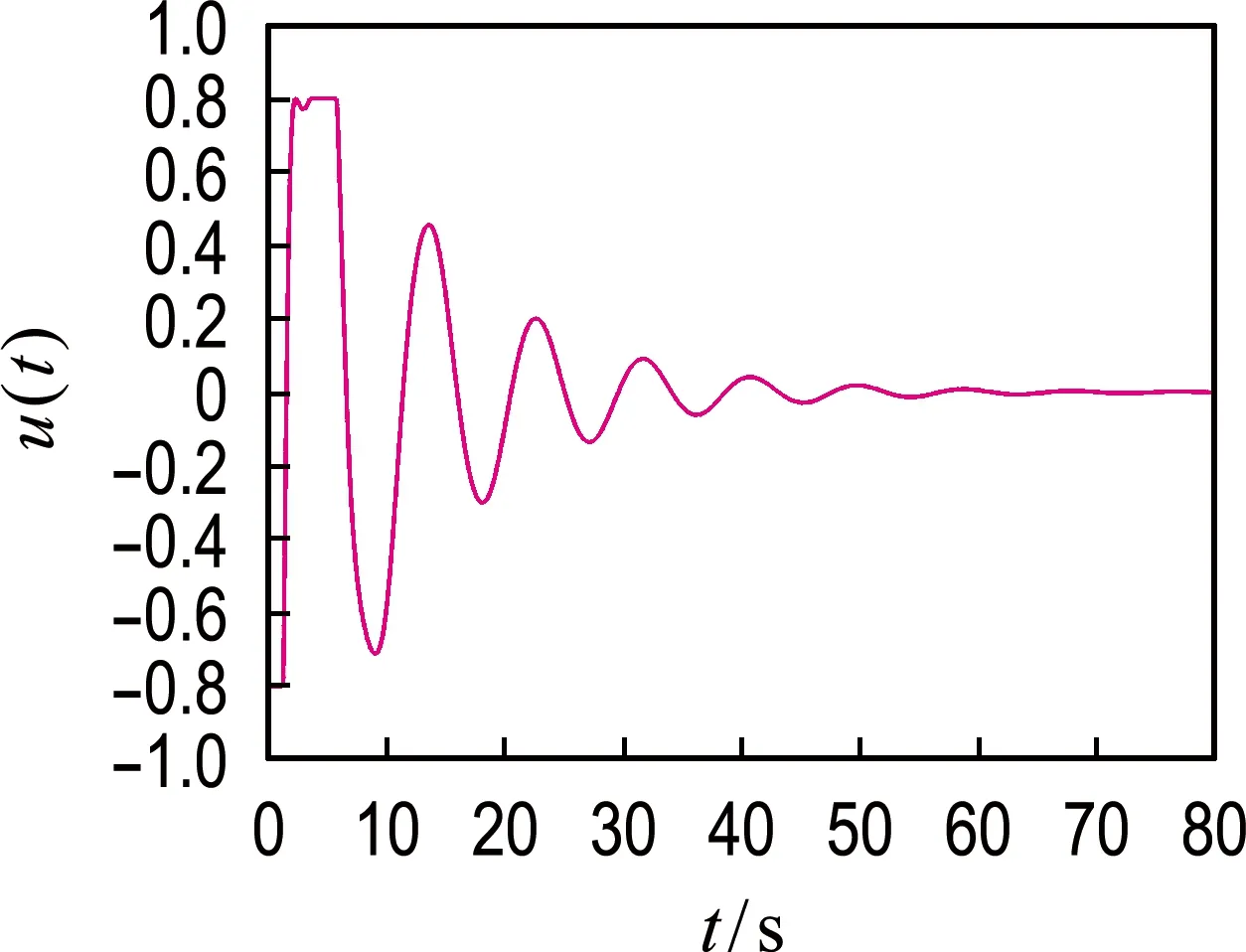
图3 饱和控制器的时间响应曲线

为了体现饱和控制器的性能，将推论1中的结果与文献[21]中定理1的结果进行比较．文献[21]同样基于直接数据驱动设计出控制器，不过没有考虑饱和输入约束．由此求解出来的非饱和控制器为

(30)

在非饱和控制器(30)作用下系统状态的时间响应曲线如图4所示，可见非饱和控制器也确保了闭环系统的全局渐近稳定性．

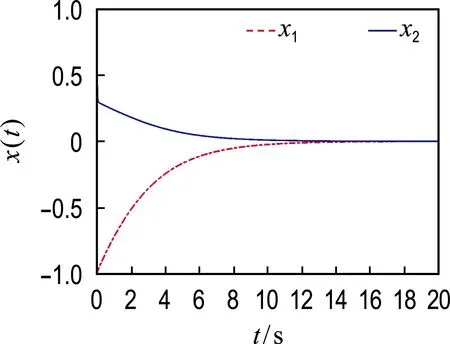
图4 非饱和控制器作用下系统状态x1、x2的时间响应曲线

基于非饱和控制器(30)的输入u时间响应曲线如图5所示，同时给出了前0.10 s输入u时间响应曲线的局部放大图．由图可知，由于没有饱和输入限制，控制输入信号的绝对值在开始阶段从较大幅值瞬间减小到10左右．

对比图2、4，非饱和控制器作用下系统状态的收敛效果更好．饱和控制器作用下系统状态经历约60 s收敛到原点，而对于相同的初始条件，非饱和控制器作用下的系统状态轨迹则只需16 s左右就趋于原点．然而，非饱和控制器付出的代价是产生足够大控制力．由于饱和输入约束，饱和控制器的幅值被限制在了给定的范围内，而非饱和控制输入虽然可以使系统更快收敛到原点，但其控制输入幅值太大，在实际应用中可能无法实现．

为了进一步验证所提控制器的有效性，针对van der Pol系统设计了电路，并通过Multisim仿真软件对其进行电路仿真．利用运算放大器和模拟乘法器可以实现van der Pol振荡器系统(28)，其中运算放大器采用UA741CD，模拟乘法器采用AD633AN．

令电路的输出电压分别为Vx和Vy，它们满足的微分方程为

(31)

定义变量x1∶=Vx和x2∶=Vy，则系统(31)与系统(28)等价．由于负阻的作用，电路中的热噪声可以引起振荡，由此得到系统电压输出波形如图6所示．从图6可知，搭建的仿真电路可以很好地模拟无控制输入时van der Pol振荡器系统的振荡特性．

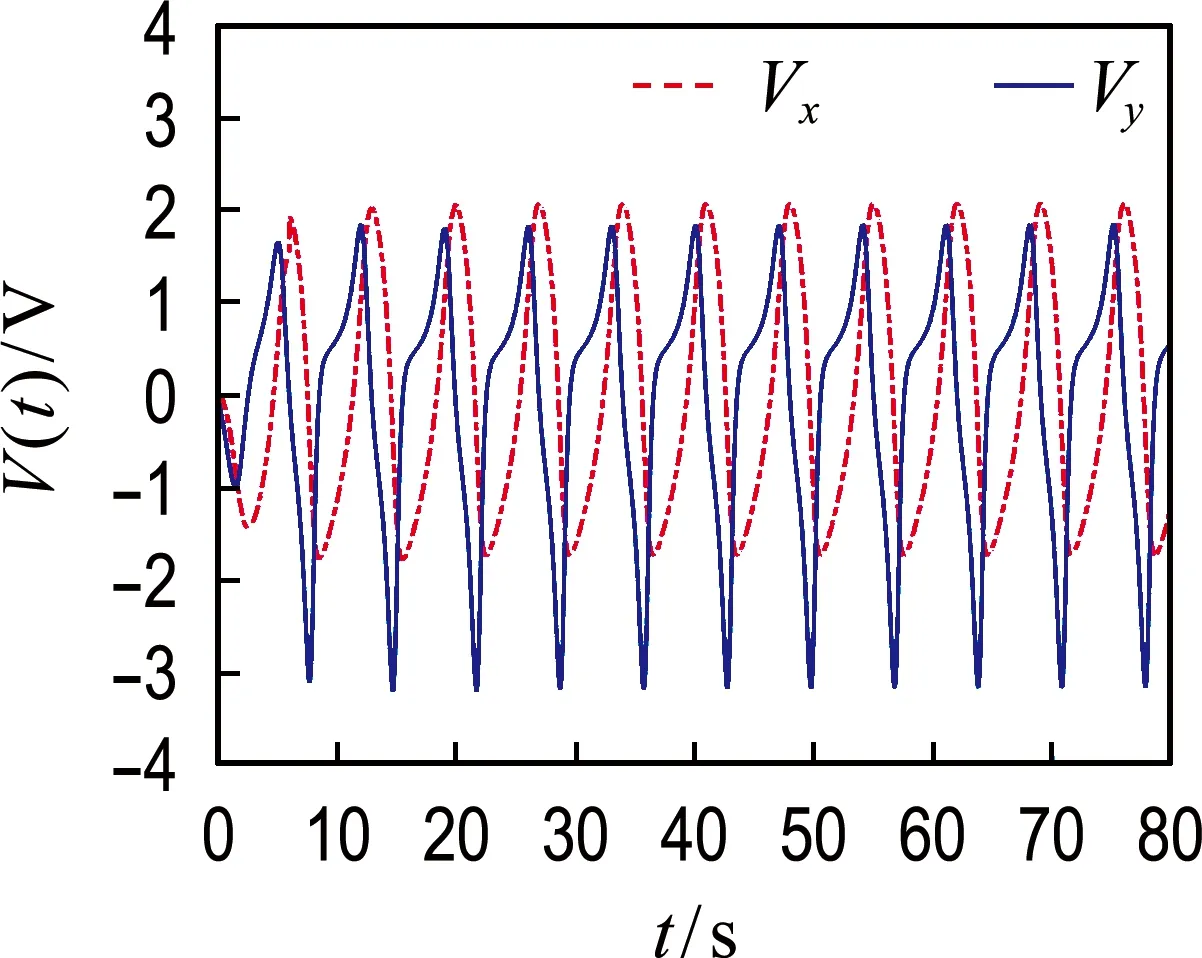
图6 无控制输入时系统状态的时间响应曲线

引入饱和控制器作用后，通过MATLAB分别绘制示波器XSC1和XSC2的波形图如图7、8所示．可以看出原来振荡的电压变量Vx和Vy在约50 s时收敛到原点且控制输入满足[-0.8，0.8] V幅值限制，从而表明通过仿真电路同样验证所设计饱和控制器具有良好的控制效果．

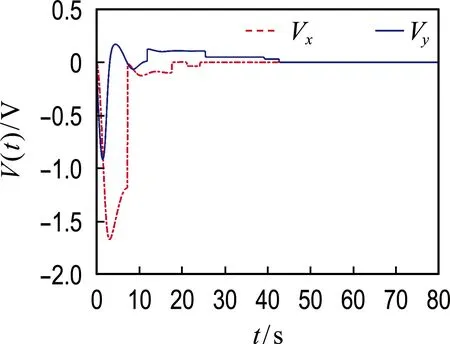
图7 饱和控制器作用下系统状态的时间响应曲线

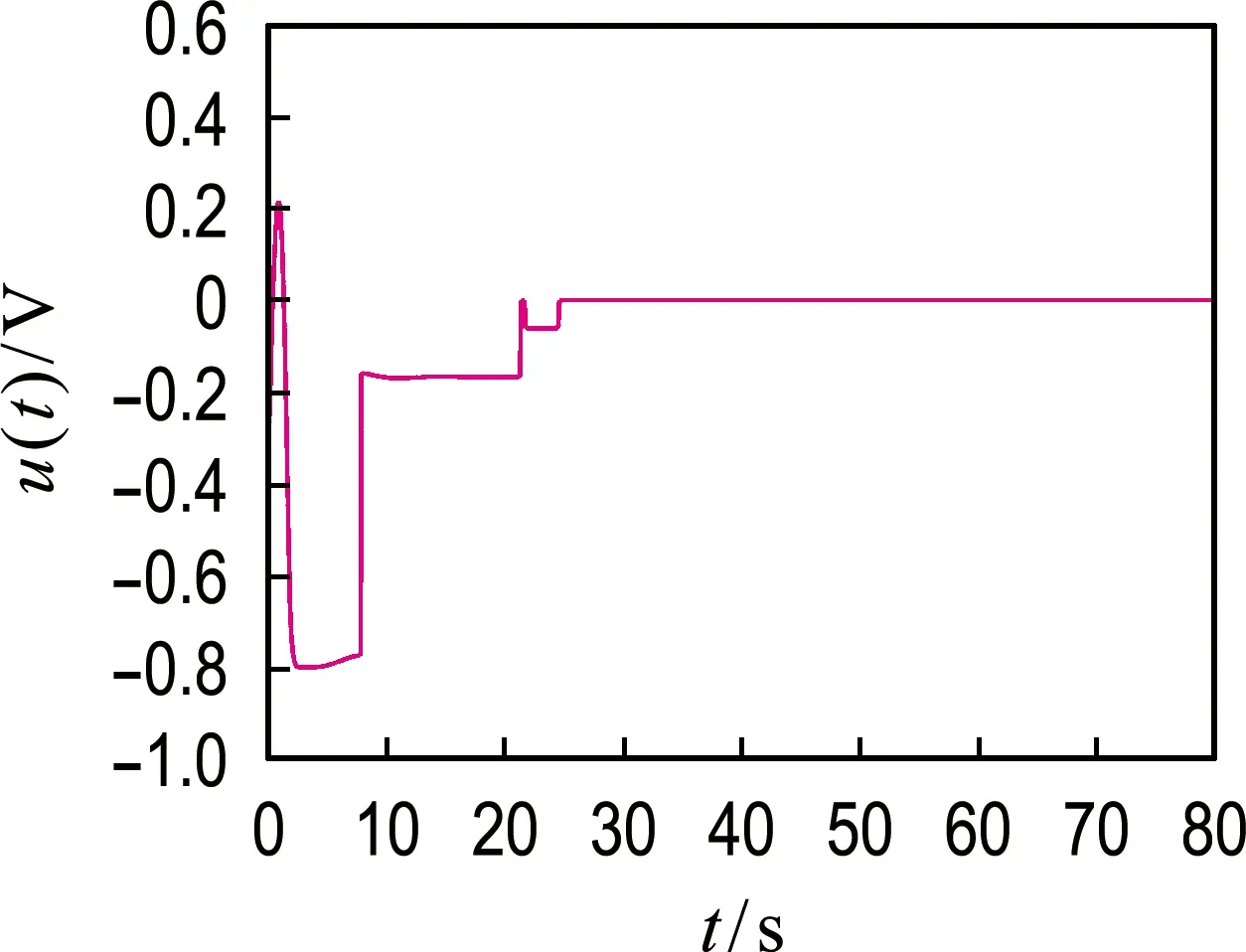
图8 饱和控制输入信号的时间响应曲线

4 结 语

针对一类未知的多项式系统，提出了一种基于直接数据驱动的饱和控制策略．所提出的控制策略无须知道系统的精确模型，只需通过离线采样系统的输入输出数据以及SOS方法获得控制器增益后，将控制输入作用于系统即可．与需要事先重构或标定模型参数的基于模型控制方法相比，直接数据驱动控制方法更直接也具有更广的应用范围．由于实际中测量数据容易受到未知噪声的干扰，在设计控制器的过程中也考虑了测量噪声的影响，引入的饱和约束机制更加贴合实际应用场景．最后，通过数值仿真和电路实验验证了所提出控制策略的有效性．鉴于利用SOS方法设计出控制器计算量依然较大，之后可以深入研究如何提升控制器设计效率．此外，本文提出的饱和控制策略具备一定的通用性，未来可以探究将饱和输入约束加入双线性系统的数据驱动控制中．