基于正多边形截面薄壁零件旋压成形质量研究
2023-02-03王佰超张欣龙高建军张澧桐张洪明王慧冬
王佰超 张欣龙 高建军 张澧桐 张洪明 王慧冬
(①长春理工大学机电工程学院,吉林 长春 130022;②内蒙古第一机械集团股份有限公司,内蒙古 包头 014000)
旋压加工是一种无屑加工的先进制造工艺,旋压成形零件拥有机械性能好、成形质量好、成形精度高以及成本低多等诸多优点,在机械加工、冶金制造、化学工业以及轻工民用等领域中被广泛应用。传统旋压一般是指所加工零件的横截面为圆形截面,非圆旋压则是旋压技术的突破,其所加工零件的横截面为非圆或者是横截面中心连线与零件成形时旋转中心不重合。成型质量是衡量零件是否合格的重要指标,非圆旋压的成型质量评价一般是由表面波纹度、材料回弹量和壁厚差等因素决定。壁厚差是成型质量的一个重要评价指标,过度的减薄往往会导致零件的最薄区域难以满足零件的承压的需求,导致发生断裂等情况;而且较大的壁厚差往往需要后续的机加工进行处理,增加了制造成本[1]。利用有限元方法和响应曲面法建立对壁厚差建立分析预测模型,对减小壁厚差、提高制件成形精度具有重要意义。
Amano T和Tamura K最先验证了非圆旋压的可行性,他们借助车床加工椭圆横截面零件的十字滑槽机构使旋轮产生椭圆运动轨迹,剪切旋压成形椭圆形横截面空心零件[2],此后越来越多的学者参与进非圆旋压的研究,同时关于壁厚分布的研究也一直是非圆旋压成形精度的重要研究内容。Sebastian H等以三边形横截面空心零件为研究对象,通过预制坯进行多道次旋压成形研究,壁厚减薄得到了有效改善[3]。夏琴香等采用靠模法完成对非圆零件的加工,发现较大的旋轮圆角半径、旋轮进给比和坯料厚径比以及较低的主轴转速有利于壁厚的分布[4-7]。徐强等通过改变旋轮的进给轨迹实现了无芯模非圆旋压,得到了锥体盒形零件以及平顶偏心锥零件,得出零件的壁厚成正弦分布的结论,但其对壁厚分布的研究并不深入[8-10]。王佰超等提出一种基于摆杆原理的旋压方法,并对四边形与椭圆形零件的成形方法进行了论述,但并没有讨论成形精度的话题[11-12]。
本文提出一种正多边形截面零件的旋压成形方法,并以此展开对非圆旋压的研究。以等边三角形以及正五边形旋压为研究对象,分析主轴转速、进给比以及道次对壁厚差的影响,采用响应曲面法建立有关于壁厚差的预测模型,实现对五边形零件的成形精度的预测,为实际生产提供理论依据。
1 正多边形截面零件旋压成形方法
旋轮对直边的成形轨迹方程。如图1所示,为加工正多边形截面零件的直边部分的示意图,当零件旋转角度为β时,轮盘转过的角度即轮盘与水平面夹角α由公式(1)求得
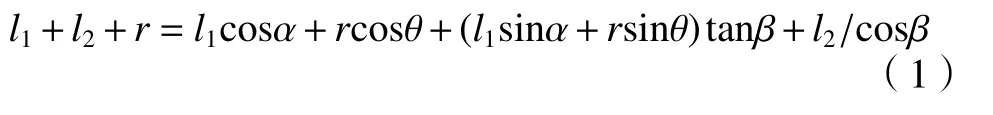
式中:θ为旋轮与零件的接触点连线同水平线的夹角,此时θ=β;l1为轮盘回转半径;r为旋轮半径;R为多边形零件圆角半径;l2为零件回转中心到多边形直边的最短距离;α为轮盘转过的角度;β为零件转过的角度。

图 1 加工正多边形截面零件的直边部分示意图
轮盘角速度 ωα与零件角速度 ωβ之间的关系如式(2)所示。

旋轮对圆角的成形轨迹方程。如图2所示,为加工正多边形截面零件的圆角部分的示意图,当零件旋转角度为β时,轮盘转过的角度即轮盘与水平面夹角α由下列公式求得。

轮盘角速度 ωα与零件角速度 ωβ之间的关系如式(5)所示。

式中:n为正多边形的边数。
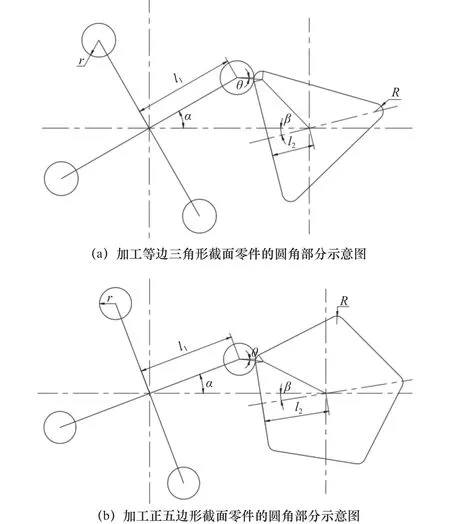
图 2 加工正多边形截面零件的圆角部分示意图
由上述旋轮对正多边形的轨迹方程可知,正多边形的旋压方法一致,旋轮先通过与零件的接触实现对直边部分的加工,此时的旋轮角速度与零件角速度只需保持一定的比值即可;之后旋轮从直边部分过渡到圆角部分,此时由于正多边形形状的不同,圆角处的旋轮与零件的角速度比值的变化速率不同,可根据式(5)求得旋轮与零件的角速度从而实现对圆角部分的旋压。总之,依据新的非圆旋压成型方法,正多边形的旋压加工具有共同性,采用等边三角形截面和正五边形截面旋压可作为正多边形截面旋压的代表性零件。
2 多边形截面零件有限元分析
2.1 有限元建模
在ABAQUS/explict模态下建立了如图3所示的三维实体有限元模型,筒形毛坯设置为可变形实体,夹具和旋轮设置为解析性刚体。毛坯外径100 mm,壁厚2 mm,长90 mm,材料为6061铝合金,其性能参数如表1所示。在边界条件中,设置夹具回转中心沿工件径向与轴向进给速度v、夹具回转中心围绕工件的角速度 ωβ、旋轮围绕轮盘旋转中心的角速度 ωα、工件与旋轮的库伦摩擦系数为0.1。本文选用的网格类型为六面体单元,毛坯周向单元数为150,轴向方向单元数为45,壁厚方向单元数为4,网格单元总数为27 000。

表1 6061铝合金各项性能参数
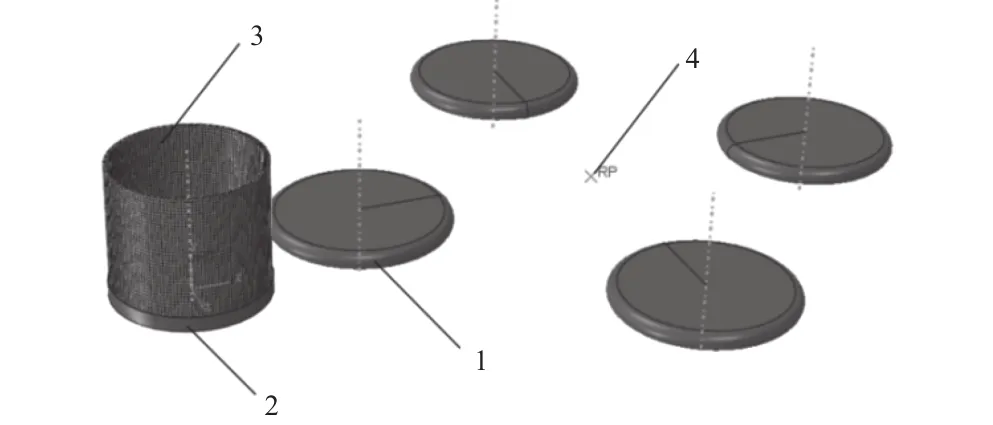
图 3 有限元模型图
2.2 应力应变与壁厚差分析
如图4~5所示,从图中可以看出正多边形截面旋压件的等效应力应变呈周期性变化,并且等效应力应变值较大的部位主要位于圆角处,平面部分的等效应力应变值普遍较小。
造成上述应力应变分布的原因是由于在旋压成形过程中,平面部分的材料受到旋轮施加的沿轴向以及周向的旋压力,使得材料朝圆角面流动,从而导致材料在圆角面产生累积,进而导致平面部分应力应变成逐步增加趋势,导致圆角面周围的等效应力应变值明显大于平面部分。此外,通过对旋压件的轴向尺寸进行测量发现,成形后的旋压件其轴向尺寸略大于坯料的轴向尺寸,且零件圆角面的轴向伸长量明显大于平面部分。这是由于,成形过程中旋轮的轴向进给使材料受轴向的拉伸作用,因此成形结束后零件的轴向尺寸略有增加;而成形过程中零件平面上一部分材料朝着圆角面流动,使圆角面上累积的材料较多,此时圆角面上所累积的材料一部分导致此处的壁厚增加,另一部分朝轴向流动,从而导致圆角面处的轴向伸长量较大。如图6、图7所示,为零件厚度分布图,从图中可以看出,其分布形式同上述分析结果一致。

图 4 轴向应力应变云图
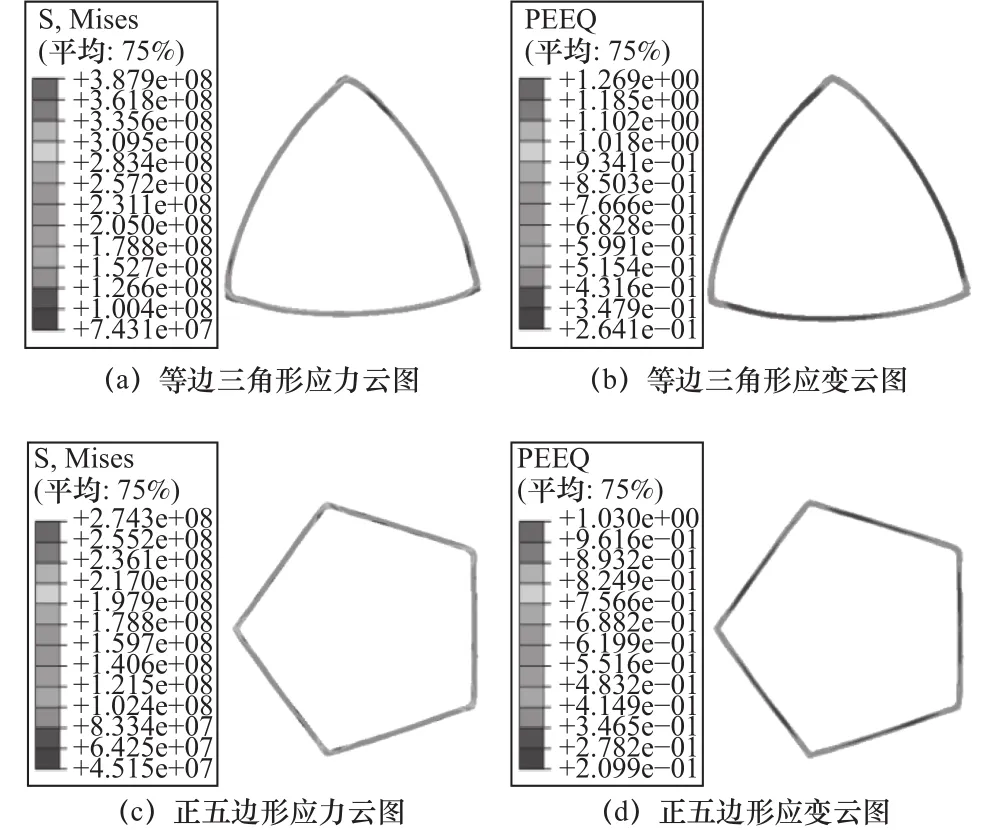
图 5 在 60 mm 截面处应力应变云图
壁厚差作为影响旋压成形精度的一个重要因素,其一般是指旋压零件的最大壁厚与最小壁厚之间的差值,壁厚差越小说明旋压件的成形精度越高、成形质量越好,所以壁厚差对研究旋压成形精度至关重要。
2.3 单因素对壁厚差的影响
选取主轴转速、旋轮进给比和道次3个对旋压成型精度影响比较显著工艺参数来研究其对正多边形横截面旋压成形壁厚差的影响。实验中,通过固定其他参数,研究单一参数对制件变形特征的影响,当研究主轴转速S对壁厚差的影响时,取进给比f为1、道次为1,主轴转速S分别取60、90、120、150、180 r/min;当研究进给比f对壁厚差的影响时,取主轴转速为120 r/min、道次为1,进给比f分别取0.5、0.75、1、1.25、1.5;当研究道次对壁厚差的影响时,取主轴转速为180 r/min、进给比为1,道次n分别取1、2、3、4、5。
如图8所示,为转速、进给比和道次单独作用对壁厚差的影响曲线,从图中可以看出转速越快壁厚差越大,进给比的增加会减小壁厚差,而壁厚差会随着道次的增加呈现出先减小在慢慢增大;等边三角形截面的旋压零件的壁厚差大于正五边形零件的壁厚差。

图 6 正多边形零件整体厚度分布云图

图 7 零件在 60 mm 截面处壁厚分布图
造成上述原因是过快的转速使得旋轮与毛坯同一位置材料的接触时间变长,从而使得更多的材料向圆角处堆积,从而造成大的壁厚差,同理进给比的增加使得旋轮与毛坯同一位置的材料接触减少,从而减少了材料流动,所以壁厚差减小。而道次的增加使得壁厚差减少则是因为旋轮每道次会使得圆角处的材料向轴向移动,从而减少圆角处的材料堆积,使得壁厚差先减小,当道次超过一定时,壁厚差增大是因为更多的材料向着圆角处流动,而堆积在圆角处的材料无法快速的向毛坯的轴向流动,从而使得壁厚差增大。

图 8 各因素对正多边形零件壁厚差的影响
而等边三角形截面零件的直边部分相较于正五边形截面零件的的直边部分长出很多,所以导致更多的材料向着圆角处流动堆积,而且三角形截面零件的圆角比正五边形截面零件少,所以每个圆角的材料堆积会更多,所以等边三角形截面的旋压零件的壁厚差大于正五边形零件的壁厚差。
3 响应曲面分析
3.1 响应曲面法
响应曲面法是用来优化试验方案或者建立指标和因素间的关系模型,可以给出指标和因素之间的函数关系式。由于响应曲面法可以得出连续的函数关系式,而正交只是不连续点的优化组合,因此其优化试验设计的优势比较明显[13]。在实际加工过程中,一般要逼近的目标函数通常是具有非线性特点,所以对于一般响应面函数的多采用二阶拟合模型,并采用最小二乘法来求解表达式中的各项系数,然后在得到的曲面进行响应面分析。通常响应面二阶多项式的表达式取为

其中:Y(X)为预测的响应值;a0、ai、bi为常数项、线性项、二阶项系数;cij为影响因子交叉作用系数;n为试验影响因子的个数。
3.2 试验设计与结果
响应曲面法的试验设计有:中心组合设计、BOX设计、二次饱和设计和田口设计等。上述方法用于回归分析,可用预测值方差来评价其精确度。本次试验采用Box-Behnken的设计方法,其优势在于考虑了试验的随机误差,可以用较少的试验方案,得到最优的工艺参数,具体实验设计如表2所示,实验结果如表3所示。

表2 Box-Behnken试验设计表
3.3 方差分析
使用软件Design-Expert对表3中的数据进行方差分析,分别得到如下表4及表5分析结果。由两个表中结果可知,两个模型的P值均 < 0.000 1,说明采用的回归模型具有极显著的意义,失效项的P值均 > 0.05,表明失效项并不显著,故该方程拟合的模型可以用于分析壁厚差,预测最优工艺参数。A项、B项、C项、AB项、A2项、B2项和C2项的P值均 < 0.01,说明达到高显著水平,而AC、BC的P值 > 0.05,所以不显著,应当从模型中剔除。对剩余各项系数进行优化,于是得到优化后的预测模型

表3 实验结果

表4 等边三角形的方差分析结果
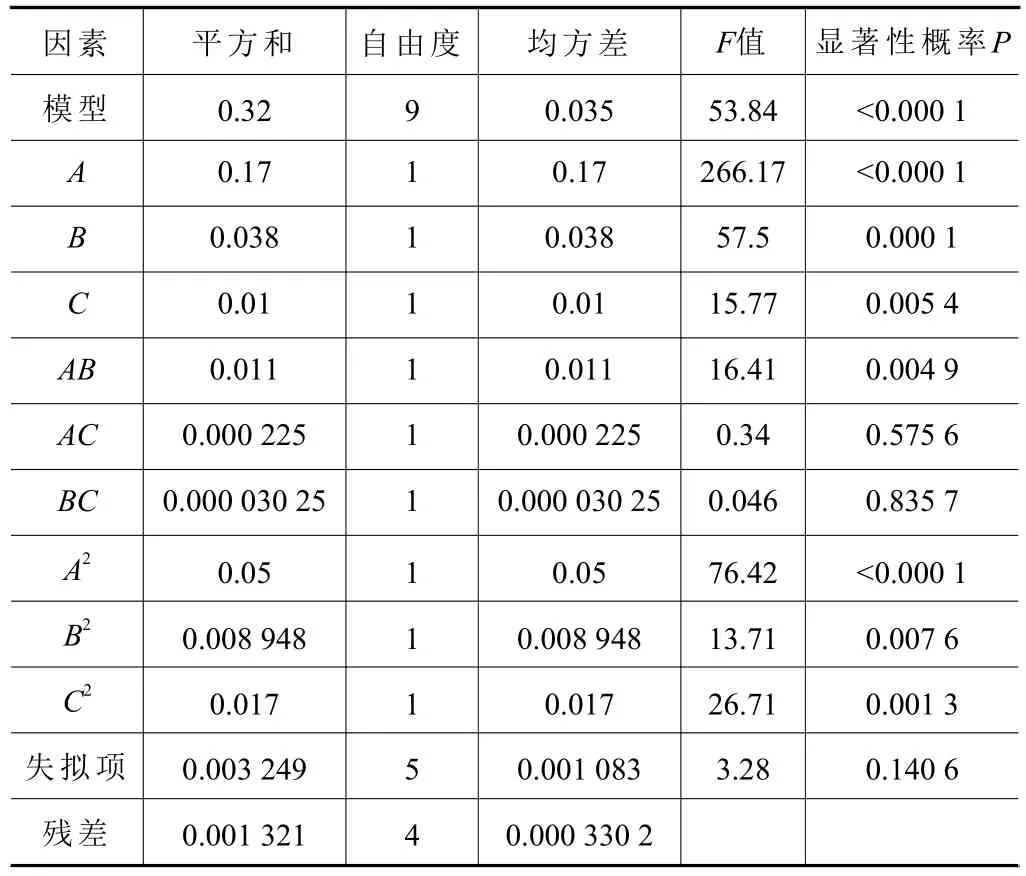
表5 正五边形的方差分析结果

由于在方差分析和回归模型中不易直观看出各因子影响结果的趋势,而在响应面曲面的结果中,可以观测出各个因子的作用趋势。如图9所示,为转速与进给比相互作用的响应曲面图,从图中可以看出转速对壁厚差的影响呈正相关,而进给比对壁厚差的影响呈负相关,其与单因素对壁厚差的影响一致,从曲面的弯曲度可以看出,两项参数交互作用比较明显,对壁厚差的影响显著。

图 9 转速与进给比的响应曲面图
3.4 实验验证
为验证上述模型的准确性,建立3组仿真实验进行验证,表6、表7为设立的3组仿真实验的仿真验证结果与通过模型计算的预测值的对比。由对比的结果可知,壁厚差的误差控制在8%以内,说明所建模型的正确性,可以用来预测一定工艺参数下的壁厚差。

表6 等边三角形的仿真实验结果与模型预测值的对比

表7 正五边形的仿真实验结果与模型预测值的对比
4 结语
(1)仿真结果表明,正多边形旋压件的壁厚成周期性分布,其最大壁厚在正多边形旋压件的圆角处。
(2)方差分析的结果表明,主轴转速、旋轮进给比与道次对正多边形旋压件的壁厚差的影响高度显著,主轴转速与壁厚差呈正相关,而进给比壁厚差呈负相关,道次对壁厚差的影响先减小后增加。
(3)应用响应曲面法建立了壁厚差的预测模型,通过与设立的仿真实验所测得的结果进行对比,壁厚差误差控制在8%以内,验证了模型的正确性,为后续的研究工作提供了指导。
