GPS轮廓法粗糙度数据处理研究与实现
2023-02-03潘丽丽
潘丽丽
(海克斯康制造智能技术(青岛)有限公司,上海 201100)
产品几何技术规范(geometrical product specifications, GPS)是一套关于工件几何学的规范,它覆盖了尺寸、尺度、几何公差和表面几何性能的标准,是国际标准中影响最广的重要基础标准之一,是所有机电产品“标准与计量”规范的基础,也是制造业信息化的重要基础[1]。
表面粗糙度又称表面光洁度,是指工件表面所具有的较小间距和峰谷组成的不平度微观几何形状的尺寸特性,是用来评价工件表面制造质量的重要指标[2]。表面粗糙度的测量方法可分为接触式测量和非接触式测量[3]。接触式测量法即传统的触针扫描法,测量结果稳定可靠,测量灵敏度和横向分辨率较高。
触针法是采用微米级半径的触针与被测工件表面相接触,在导轨的引导下,触针在被测工件的表面缓慢滑动。滑动过程中,触针会随着工件表面的高低起伏出现上下位移,将这些微小的位移量经过传感器转换成电信号,电信号经放大、数模转换后输出数字信号,数字信号在经过滤波和运算后可以得到表面粗糙度的实际相关参数。尽管采样设备对测量力有严格的控制,并且电路中已包含滤波部分,在输出的数字信号中依然包含一部分噪声,比如标称形状、由触针抖动、导轨偏移、来自设备内部和外部的扰动,轮廓信号发送时带来的扰动,这些分量不能算是粗糙度轮廓的一部分,因此GPS对数字信号的处理做了明确的规定。
按GPS的数据处理要求,本文使用最小二乘拟合法消除标称形状,以及用高斯滤波的方式实现粗糙度轮廓曲线的分离,完成了算法及程序设计,并对比了不同参数和数据处理方式对结果的影响,为评价粗糙度参数做好了数据准备。
1 GPS 数据处理要求
1.1 轮廓曲线的定义
全轮廓,即整个测量过程中触针沿导轨在相交平面内移动轨迹的数字形式,它是一系列点,每个点有横坐标和纵坐标。全轮廓包含了测量设备输出的所有数字信息,包含噪声和用于评价粗糙度的有用的轮廓曲线。
原始轮廓,根据ISO 3274规定,即将全轮廓消除标称形状,然后进行滤波以过滤高频成分以后所得到的数据。由于标称形状,不能算是轮廓的一部分,所以在应用λs之前,应将其从总轮廓中去除,对于测量轨迹是一个圆来说,还需消除半径分量,而不是将其算在标称值上[4]。如图1所示。

图 1 GPS 粗糙度数据处理流程
原始轮廓是评价原始轮廓参数的基础,它包含了粗糙度轮廓和波纹度轮廓两部分。
轮廓曲线滤波器是用来将轮廓曲线分离成长波长成分和短波长成分的过滤器。ISO 4 287定义了3个传输特性相同,但截止波长不同的滤波器来分离原始轮廓、粗糙度轮廓和波纹度轮廓,即λs、λc和λf,如图2 所示[5]。
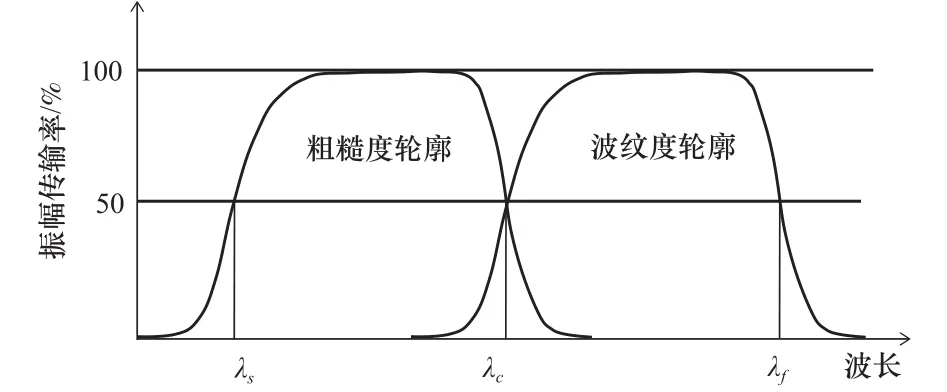
图 2 粗糙度轮廓与波纹度轮廓成分的传输特性
λs轮廓滤波器:它将波长小于λs的信号分量从全轮廓分离出,因为根据定义,这些分量不属于原始轮廓、粗糙度轮廓或波纹度轮廓。
λc轮廓滤波器: 定义粗糙度轮廓成分和波纹度轮廓成分间界限的过滤器。
λf轮廓过滤器:定义波纹度轮廓成分和残留轮廓成分间界限的过滤器。残留轮廓是通过跟踪理想的平整且光滑的平面(光学平面)而获得的原始轮廓。它由导轨偏移、来自设备内部和外部的扰动,以及轮廓信号发送时带来的偏差组成。如果没有专用的设备和合适的环境,通常无法确定这些偏差的原因。
粗糙度轮廓是通过使用轮廓滤波器λc抑制原始轮廓中的长波分量而获得的轮廓,它是评价粗糙度轮廓参数的基础;波纹度轮廓是通过使用轮廓滤波器λf抑制原始轮廓中长波分量以及使用轮廓滤波器λc抑制原始轮廓中的短波分量而获得的轮廓,它是评价波纹度轮廓参数的基础。
各级滤波器截止波长的选择跟粗糙度测量设备的测头半径和最大采样间隔相关,它们之间的关系如表1所示。

表1 各截止波长与测头半径、采样间隔之间的关系
1.2 GPS 数据处理要求
对于消除标称形状,GPS规范要求通过最佳拟合最小二乘法将其从全轮廓中去除[4]。
对于数字滤波器的选择,应使用相位校正滤波器,ISO11562指定为高斯滤波器,且在截止波长处,振幅的衰减率为50%[6]。高斯滤波是一个低通滤波器,但是可以通过组合使用达到带通滤波器的功能,实现对粗糙度轮廓和波纹度轮廓的提取。
2 数据处理的实现
2.1 消除标称形状
标称形状是在随机信号中存在线性项或者缓慢变化的、周期大于记录长度的非线性成分。工程中实际测录的信号绝大部分都是复杂周期信号与随机信号的混合。标称形状的存在,会使时域中的相关分析和频域中的功率谱分析产生大的误差,甚至使低频信号完全失去真实性。因此,消除标称形状是数据处理中的一个重要步骤[7]。
消除标称形状的方法有多种,根据信号特征,被测试对象的物理模型等因素而定,如瞬态冲击数据的基线,主要利用初始条件和终了条件来确定修正系数;对于随机信号和稳定的确定性信号,主要采用对标称形状拟合的方法来消除,常用的消除法有平均斜率法和最小二乘法。平均斜率法用于消除信号中的线性标称形状。当信号中含有线性和非线性标称形状时,需要采用最佳拟合最小二乘法,它既可以消除数字信号中的线性标称形状部分,又可以消除非线性的高阶多项式标称形状部分。由于粗糙度测量数据中包含线性和非线性的工件表面形状成分,所以ISO 3274规定使用最佳拟合最小二乘法消除标称形状[4]。
触针式粗糙度测量设备的输出结果横坐标为偏移起始点的距离,纵坐标为测针相对于相交平面的上下移动的位移。如果得到测量数据为U,其长度为N,其中的第n项标记为Un,假设采样间隔长度为 Δx, 则第n项的横坐标为xn=nΔx, 用一个K阶多项式V来拟合这组粗糙度的测量数据U,其中第n项为Vn,为

式中:n= 1, 2, …,N。
根据最小二乘法原理,选择合适的系数pi,使得Un与Vn之间的误差平方和最小。其误差平方和为
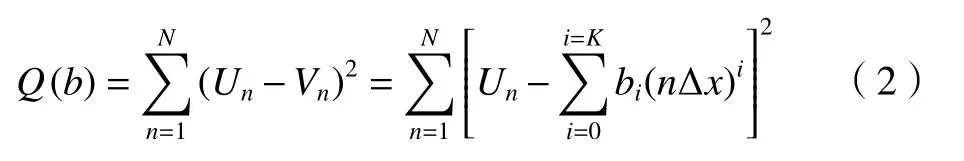
式中:Un为 原始信号;Vn为 多项式拟合信号;bi为多项式系数。
根据极值条件,对平方和公式求偏导数,并使其等于0,即
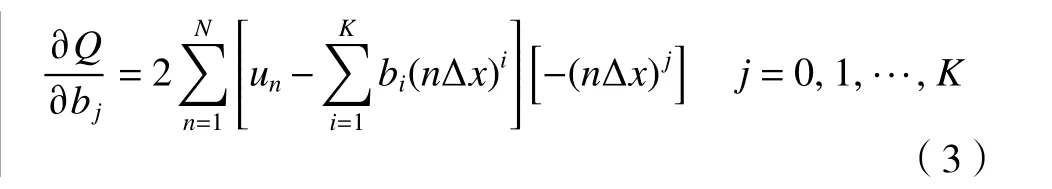
上式整理后可获得K+ 1个方程,

在多项式阶数确定K以后,通过计算可获得K+ 1个系数,由此可得拟合的多项式。
例如,当K=1时,可求得
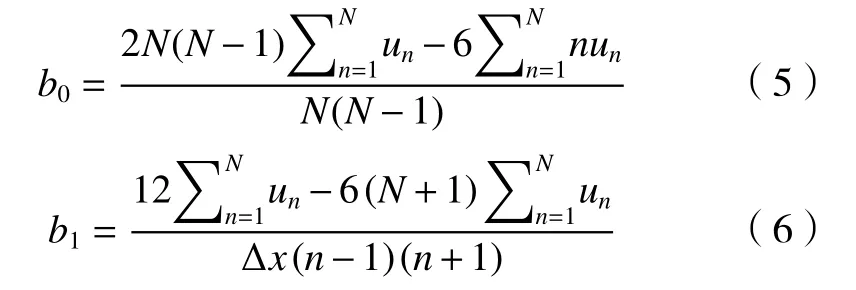
依次类推,可求得K不同取值时的多项式系数,计算稍有复杂,可以通过编程求得系数。可见,当多项式系数过高时,确实增加了计算量。
笔者推荐一个有效的可求得拟合多项式系数的数学算法库,Math.NET,它是一个开源的、提供了适合多种编程语言的且使用方便的数学算法库。这里的拟合多项式的系数可通过一个简单的方法调用获得。
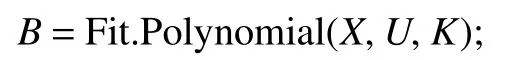
输入参数X为长度为N的一维数组,即粗糙度数据U的横坐标值的集合,其中第n项的值为

式中: Δx为粗糙度数据的采样间隔,K为多项式的阶数。返回结果B为K+ 1 长度的数组,即为K阶多项式的系数b0, b1, ··, bk。
假设消除标称形状后的粗糙度数据为Y,长度为N,其中第n项为Yn,则
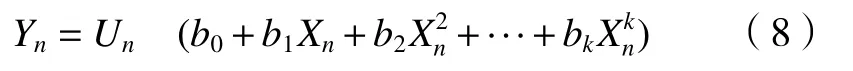
C#语言可以用一个简单的二重循环完成消除标称形状,其中Math.Pow(X[i],j)是Xi的j次幂,即多项式中的第j个分量,完整C#代码如下。

拟合的多项式中,系数b0反应了信号的均值成分,b1反应了信号中的线性标称形状,b2反应了信号中与采样间隔平方成正比的非线性标称形状,对于选择高阶多项式消除标称形状时,要慎重考虑,因为在消除非线性标称形状时,是用高阶多项式去拟合非线性标称形状,这种拟合作用的同时也影响到有用信号,使有用信号中的低阶谐波受到一定程度的衰减,这种影响随着K值的增大而变得显著。
2.2 高斯滤波
高斯滤波原理是:在对某一点数据进行滤波时,利用高斯权函数对该点和该点前后一定宽度内的数据进行加权,再将加权后的值进行累加,所得到的便是滤波后的数据;实际应用过程中,取高斯滤波器权函数的宽度为截止波长[8]。
根据ISO 11562的规定[6],相移校正滤波器的权函数为高斯密度分布函数,λco为截止波长(co =cut-off),如式(9)所示[3]。

高斯滤波器的振幅传输特性如公式(10)所示。

式中:a0为粗糙度轮廓在滤波前的振幅;a1为粗糙度轮廓在滤波后的振幅。
根据ISO要求,高斯滤波器在截止波长处,振幅的衰减率为50%,由式(10)可求得 α为常量,为

滤波器的输出为输入波形与滤波器的权函数做卷积的结果,因此高斯滤波器的输出信号为
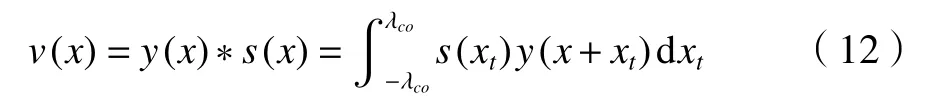
式中:y(x)为滤波器输入信号;v(x)为滤波器输出信号;s(x)为式(9)中高斯滤波器的权函数。
采样点间隔是在粗糙度扫描时由用户设定,可根据表1中数据设置,也可自定义。在粗糙度数据处理时,可以当作已知常量使用,假设采样点间隔为 Δx,则距离中心点第i个点的坐标为

在长度为 λco范围内的采样点数为

令xt=it×Δx,将式(12)离散化,得
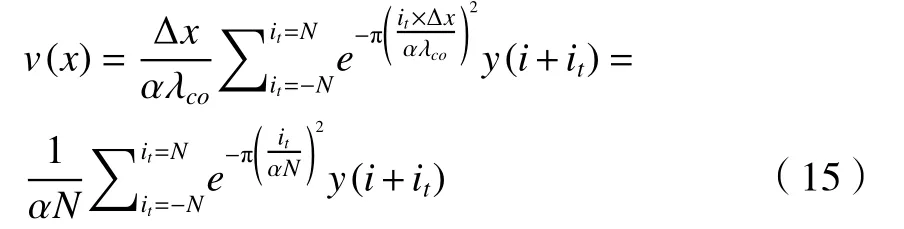
将高斯滤波权函数式(9)代入式(15)得
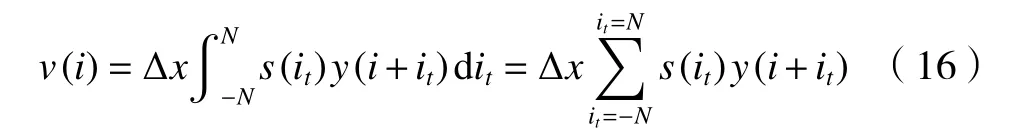
式中:N由式(14)中定义。
到此,滤波器的算法推算完毕。高斯滤波即是对采样点进行前面N个点和后面N个的加权计算,N由滤波器的截止波长和采样间隔决定。
基于式(16),使用C#语言设计的滤波器代码如下:


以上代码是一个低通高斯滤波器。因为测针的总行程,总比评定长度(5个取样长度)多1个或者2个取样长度,所以边界点的处理方式并不重要,不会影响评定结果。由图2可知,粗糙度轮廓是由原始轮廓通过高通滤波器获得,波纹度轮廓是由原始轮廓通过带通滤波器获得,可以该低通滤波器为基础,通过简单计算来构造高通滤波器和带通滤波器,代码如下:

3 实验结果
3.1 消除标称形状的结果
图3为原始的粗糙度测量数据,测量长度为4.8 mm,采样间距为0.5 μm。
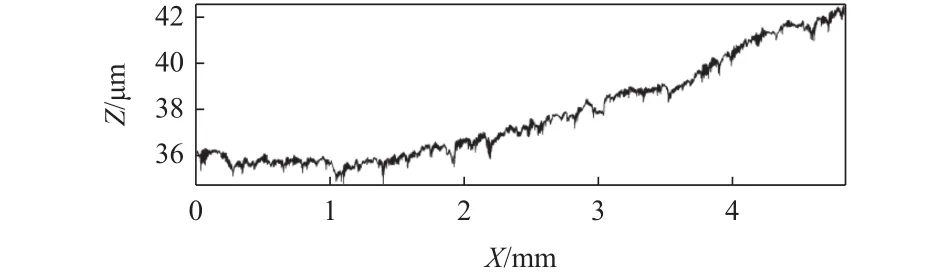
图 3 粗糙度原始数据
图4为一阶多项式消除标称形状后的结果。
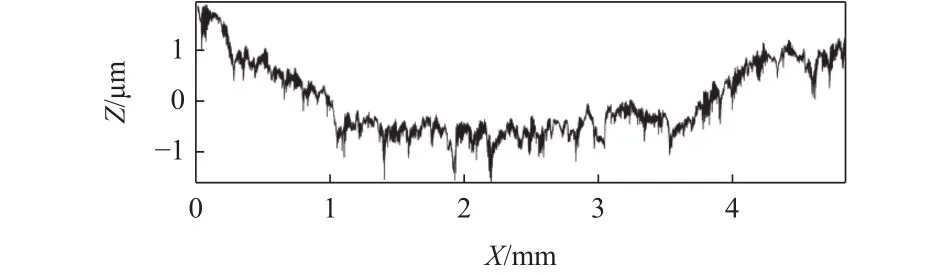
图 4 一阶多项式拟合消除标称形状
图5到图7为多阶多项式消除标称形状后的结果。
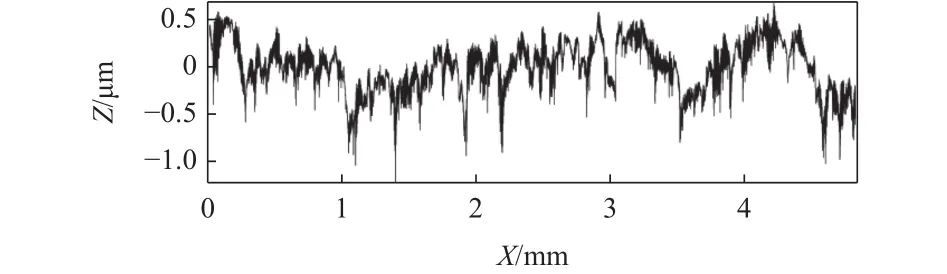
图 5 二阶多项式拟合消除标称形状

图 6 三阶多项式拟合消除标称形状
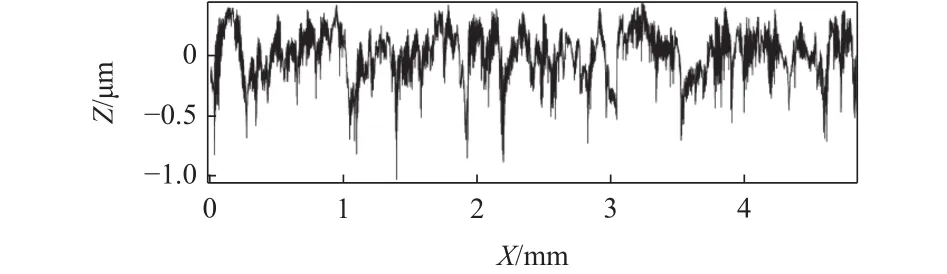
图 7 十阶多项式拟合消除标称形状
由图4到图7的纵坐标变化可见,对于该组粗糙度测量数据来说,一阶多项式拟合便可消除信号中的均值成分(见图4),二阶多项式拟合比一阶多项式拟合又多消除了一些分量(图5),三阶多项式拟合与二阶多项式拟合相比,消除标称形状后的波形并没有明显的变化(图6),但十阶多项式拟合消除标称形状后波形又有振幅增加的趋势(图7)。因此对于该组粗糙度测量数据的评价,选择二阶多项式拟合消除标称形状可以满足要求。
3.2 高斯滤波结果
本文所测试粗糙度测量数据,测头半径为2 μm,采样间距为 0.5 μm,所以λs选择 2.5 μm,λc选择0.8 mm,λf为两个λc的长度,即1.6 mm。
3.2.1 原始轮廓波形
将λs=2.5 μm作为参数传递给上述低通滤波器,将波长小于λs的分量从全轮廓中滤除而得到原始轮廓。所得结果如图8所示(为使3种曲线对比有更明显的效果,此处设置的多项式系数为1)。

图 8 原始轮廓曲线
3.2.2 波纹度轮廓波形
将λc=0.8 mm ,λf=1.6 mm作为参数传递给上述带通滤波器,将波长在λc和λf之间的部分从原始轮廓中分离出来得到的波纹度轮廓如图9所示。

图 9 波纹度轮廓曲线
如果不过滤掉残留轮廓,可见波纹度轮廓因为混杂了噪声,有非常明显的波动幅度,如图10所示。
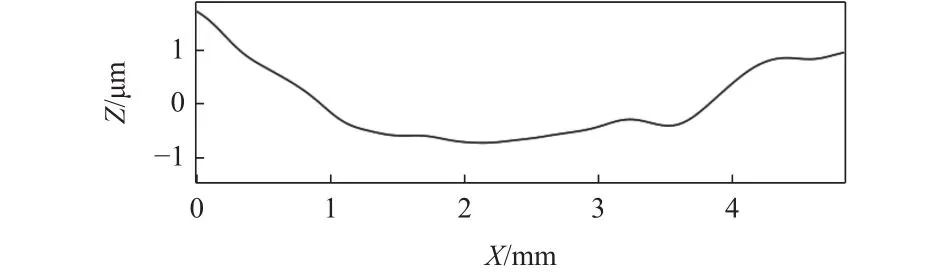
图 10 波纹度轮廓曲线 (含残留轮廓)
3.2.3 粗糙度轮廓波形
将λc=0.8 mm作为参数传给给上述高通滤波器,将低于λc的波形分量从原始轮廓中分离出来便可得到粗糙度轮廓,如图11所示。
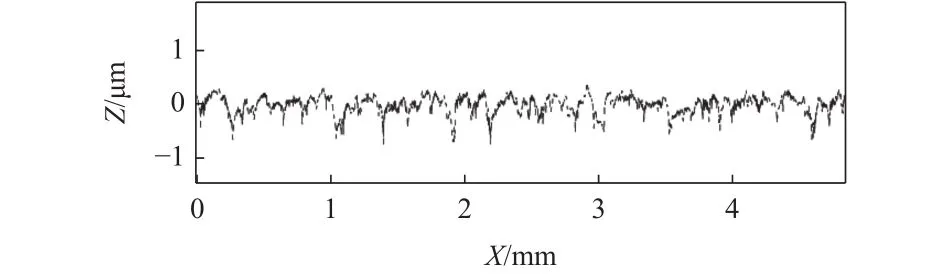
图 11 粗糙度轮廓曲线
3.2.4 3种轮廓波形比对
将上述3种曲线合并在1张图上,可看出,如果没有滤除残留轮廓,波纹度轮廓曲线与粗糙度轮廓曲线叠加可得原始轮廓曲线,因为原始轮廓是包含残留轮廓的,如图12。

图 12 轮廓曲线叠加(含残留轮廓)
将残留轮廓滤除的轮廓曲线叠加如图13所示。可见残留轮廓的存在只影响到波纹度轮廓,并不会影响到粗糙度轮廓,这跟图2的定义一致。
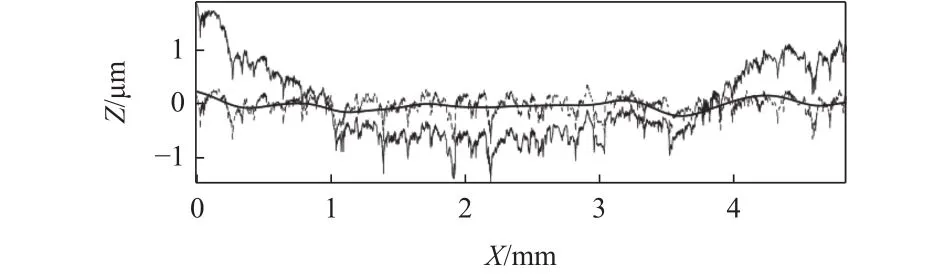
图 13 轮廓曲线叠加(无残留轮廓)
4 结语
在产品设计和开发过程中,遵循GPS规范对保障产品性能非常重要。笔者按照GPS规范的要求,对粗糙度数字信号处理进行了深入研究,并实现了符合GPS规范的粗糙度数字信号处理算法:
(1)使用最小二乘拟合法将影响粗糙度评价结果真实性的标称形状去除。对比了不同多项式阶数的输出结果,二阶多项式比较适合本文所用实验数据。
(2)通过将高斯滤波权函数与输入波形的卷积离散化,得到高斯滤波输出的数字信号公式,并使用此公式实现低通滤波器、带通滤波器及高通滤波器,以滤除高频噪声和残留轮廓成分,提取出原始轮廓、粗糙度轮廓和波纹度轮廓。
基于试验结果可发现,算法参数的选择在数字信号处理中至关重要,应根据数据处理方法和测试数据特性做出严格选择,可参考输出信号进行参数调整。经过该数据处理过程得到的结果为后期的粗糙度参数评价做好了数据准备。
