融合帝国竞争与遗传算法的零件加工工艺排序方法＊

李书涵 周学良 冷杰武

（①湖北汽车工业学院机械工程学院，湖北 十堰 442002；②广东工业大学机电工程学院，广东 广州 510006）

随着经济社会的快速发展，多品种、智能化、用户需求多样化以及产品更新换代速度快成为企业面对的重要形势。在传统工艺设计中，通常需要工艺人员依靠自身的操作实践和技术理论知识来确定工序路线，才能制造出满足设计生产需要的加工制品，在针对不同结构的传统零部件生产中，加工工序数越多，排序范围越广，在设计生产过程中所遇到的技术问题就越多，生产效率越低。当工艺设计条件改变后，又必须更改加工工艺路线，因此仅靠以往设计生产中的经验难以得出最优的排序路线，而且在不同机床上加工，传统零部件生产长期存在的主要困难是装夹数量多、工作效率低下，同时面对复杂零件且需更换多种刀具，所以选择采用智能的加工工艺路径规划，迅速而精确地得到满足设计生产需要的多条工艺路线，并从中选取最优加工路线是很有必要的。刘勇通过运用蚁群算法优化工艺路线，选择利用知识描述方法对加工单元的确定[1]。王春梅采用蚁群算法对子路径进行了规划并选择合取运算方法进行分类特征测量路径[2]。袁青等研究者建立和推广了加工单元优先矩阵[3]来表示加工顺序，针对在加工中心中减少刀具空走行程的问题，采用遗传算法优化加工路线[4],以及针对钣金零件上的孔群加工路线选择蚁群算法和相邻排序算法相混合进行求解[5]。郑永前采用自适应遗传算法解决箱体加工工步排序问题[6]。Leung C W采用基于个体的蚁群优化算法的自催化过程对工艺规划进行求解[7]。徐立云针对复杂结构的箱体零件，采用模拟退火以及遗传相混合对加工序列进行寻优来避免计算结果陷入局部最优[8]。由于每种算法都有其相应的技术特点,针对工艺路线的寻优问题，为了进一步提升加工排序的寻优效果，将每种算法之间的优劣特性进行相互弥补，尽可能取得最理想的寻优效果。

本文针对零件加工工艺排序问题，以最小化机床、装夹以及刀具更换次数最小为目标，构建零件加工工艺排序的数学模型，并提出融合帝国竞争与遗传算法的求解方法，将帝国竞争算法输出的较优加工序列作为遗传算法的初始种群，通过融合帝国竞争算法不受初始种群影响的特性和遗传算法的快速收敛能力，提升工艺规划的效率和质量。

1 工艺排序的数学模型

1.1 问题描述

工艺排序是在明确零件全部待加工特征和加工方法后，对工艺路线进行合理排序的过程。在进行工艺决策之前，通过查询工艺手册或运用相关经验可以确定各个特征的加工工步，将特征的每个加工工步定义为特征加工单元fi（简称“特征元”）[9]。一条完整的工艺路线由零件中每个特征加工单元按照一定的顺序排列所组成，可以描述为S={f1,f2,f3···,fn}。

在复杂零件的加工特征集合中包含了各种不同的约束关联，在这些约束下，特征元之间存在着不同的关联性和先后顺序，确保零件能够逐步按设计要求生产出来。因此，在加工工艺排序路线中也必须满足各种约束条件。根据技术要求和实际生产中的作业条件不同，可将约束分为工艺约束和最优性约束两类。工艺约束为在加工工艺过程中表现为先后顺序的约束，在加工工艺路线排序中这是必须考虑的因素[10]。需要考虑的约束关系有：

（1）先基准，后其他，即先加工基准特征再加工其他特征。

（2）先粗后精，即先进行粗加工，后进行半精加工和精加工。

（3）先加工面后加工孔，先加工面后加工键槽。

（4）先主后次。先加工主特征后加工辅助特征。

（5）非破坏性约束关系。后加工的特征属性不能破坏前操作所产生的特征属性。

（6）可访问性约束。为确保每个特征可以访问，某些特征的加工只能在其他特征之后进行。

最优性约束是指满足后能都达到更好的经济性或质量等效益的约束。由于在实际生产中存在各种技术差异和困难，导致很难满足所有约束。因此，在工艺排序中工艺约束必须满足，最优性约束则尽量满足。

引入1个n阶的方阵Y来存储特征元中的工艺约束关系。如果2个特征元之间存在工艺约束，特征元i必须在特征元j之前加工，则元素yij的值为1，如不存在工艺约束，则yij的值为0。即

工艺路线排序优化的本质是在满足工艺约束集的前提下，对各个特征元进行排列，形成一条具有可操作性的加工工艺路线，一般采用迭代求解。问题的解空间可以定义 Ω ={S1,S2,S3,···Sk,Sm}，其中Sk={fk1,fk2,···,fki,···,fkn}为任意一个满足工艺约束的备选解。工艺路线排序的求解过程就是在整个搜索区间寻找1个特征元序列 Sk∈Ω，使其在满足工艺约束的前提下实现效率、效益等指标最优。

1.2 工艺路线评价模型

工艺路线评价是利用计算机进行加工工艺排序优化的关键问题之一。按照工序集中原则，在符合工艺约束的前提下，以机床、装夹和刀具更换次数最小为优化目标，采用加权法定义工艺路线评价模型工艺序列的评价函数，将多目标问题转化为单目标问题，如式（2）所示。

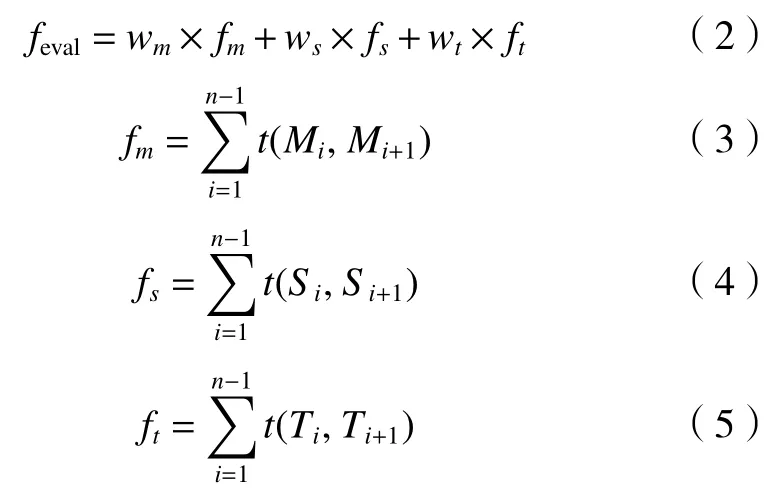
式中：fm、fs、ft分别表示1个工步序列中相邻特征元之间机床、装夹和刀具的总更换次数；wm、ws、和wt分别表示机床、装夹和刀具变换次数的权重系数；Mi、Si、Ti，分别为第i个工步所需要使用的机床、夹具和刀具。函数t(x,y)的形式为

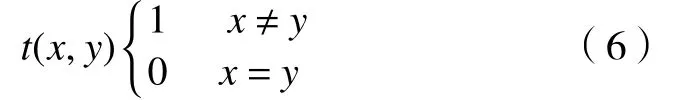
2 融合帝国竞争算法与遗传算法的求解方法

工艺排序优化问题属于有约束TSP问题，难以采用解析法精确求解。采用融合帝国竞争算法与遗传算法的方法进行求解，利用帝国竞争算法在全局搜索时不受初始种群影响的特性和遗传算法的快速收敛能力，将帝国竞争算法的较优输出的加工序列作为遗传算法的初始种群，提升算法的寻优能力。具体流程如图1所示。

图1 基于混合算法的工艺排序优化流程图

混合算法的运算步骤如下。

步骤一：计算开始之初设定所需要的各个数据；

步骤二：初始化帝国竞争算法种群；

步骤三：以设置的起始算法的最大迭代次数为界限，判断起始算法是否完成迭代，且是否连续100代最优解无变化或者变化不大；若达到规定的迭代次数目标，若未达到设置的迭代次数，则继续运行帝国竞争算法，若未达到，则从起始算法所输出的较优序列中，选取λ个的序列个体参与下面遗传算法的运行，λ取值需大于编码长度；

步骤四：同样根据混合算法有无完成开始所设置的混合算法最大迭代次数来界定是否完成计算，且是否连续几代最优解无变化或者变化不大，如果两种条件都满足的前提下，即视为该算法完成迭代计算，将最优值进行输出，若未完成，在满足结束条件前继续执行迭代。

2.1 个体编码及适应度函数

帝国竞争算法中的国家和遗传算法中的染色体均代表迭代计算过程的个体解，采用自然数进行编码。1个特征元由1个自然数表示，个体编码长度即为特征元个数，编码顺序即表示零件的工步顺序。

个体解的适应度函数定义如下：

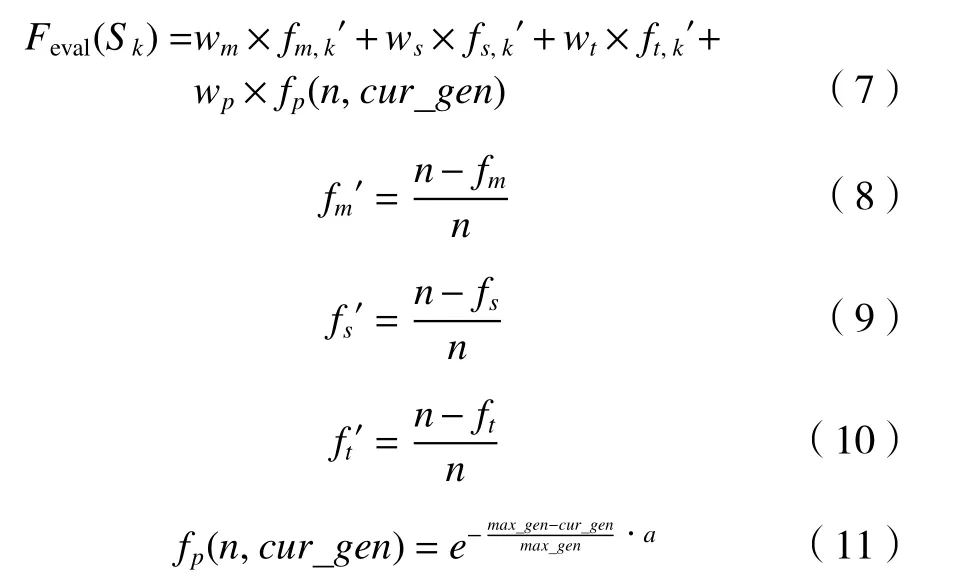
式 中 ：Sk表 示 第k个 个 体 解 ，wm、wt、wi和wp分 别 表示Sk中机床、装夹、刀具变换次数和惩罚函数的权重系数；n表示特征元数目；fm,k′，fs,k′，ft,k′分别表示Sk中机床、刀具和装夹更换次数归一化处理结果；fp为惩罚函数，表示对违反工艺约束的解进行惩罚，a表示加工序列违反工艺约束的数量，cur_gen表示为当前的迭代计算代数，max_gen表示为设置的最大迭代次数。

求解过程的优化目标是全局范围内搜索1个能最大限度满足排序问题约束的特征元集合，使Feval(Sk)的值最大化。即

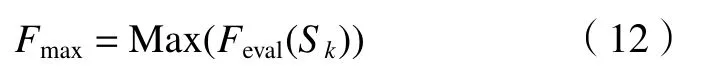
2.2 基于帝国竞争算法的较优工艺序列求解

用帝国竞争算法中的一个国家表示1个工步序列，每个国家的编码序列对应1个工步序列。假设该零件特征工步有n步，其可表达为

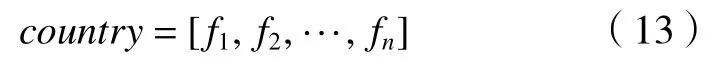
每个国家的势力大小则用适应度函数来描述，如

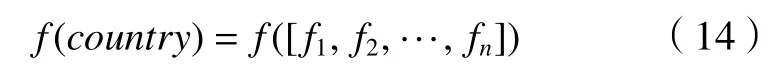
（1）初始化帝国

首先在全局范围的搜索区间内，由算法随机产生N个国家，按照权势大小将这N个国家分为Nimp个帝国和Ncol个殖民地[11]。

将计算得到的帝国势力值用于计算帝国的标准势力，得

根据每个帝国的标准势力，计算初始每个帝国拥有多少个殖民地，如

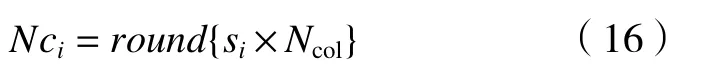
式中：Nci是i号帝国拥有的殖民地个数。Ncol是殖民地的总数，round定义为取整函数。

（2）殖民地同化操作

殖民地同化的本质是使殖民地位置能向帝国靠近。采用双点交叉法进行同化操作，在帝国工步序列中随机选取2个交叉点，将2个交叉点之间的工步编码复制到新殖民序列相应位置，最后将殖民地序列中未被复制的工步编码按顺序依次复制到新殖民地序列，形成新的殖民地序列。如图2所示，假设1个零件的特征有8个加工单元，首先随机生成2个交叉位置点2、5，将帝国序列中位置3、4、5上的编码“5”、“4”、“8”进行复制，然后从殖民地序列中未被复制的编码“2”、“3”、“1”、“1”、“6”、“7”按顺序依次复制到其他编码位，形成新殖民地。

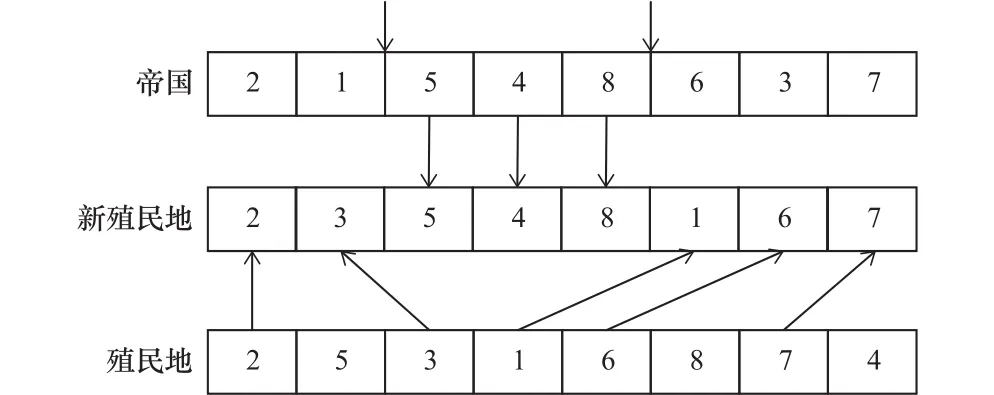
图2 基于双点交叉法的殖民地同化示意图

（3）殖民地革命操作

殖民地革命的过程类似于遗传算法中的变异操作，随机对某个殖民地采用交换工步操作或移动工步操作。交换工步的原理如图3所示，随机选择两个位置点，并将相应位置点的工步内容进行交换生成新的加工序列。移动工步的原理如图4所示，随机选择2个位置点，将其中1个位置点的工步编码移动插入到另1个位置点之前。殖民地革命后，如果新殖民地代价值比其所属帝国小，则革命成功，交换两个国家的地位。

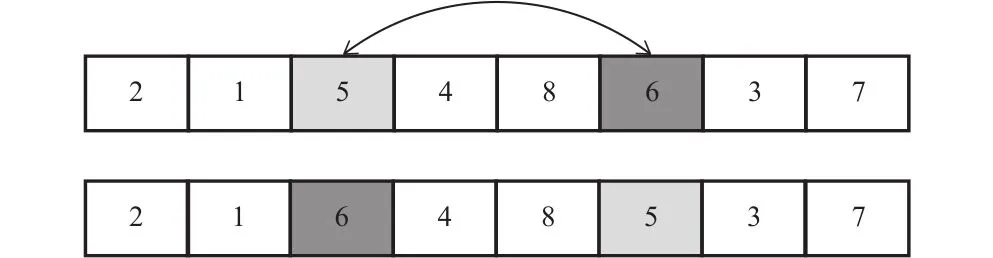
图3 交换工步示意图

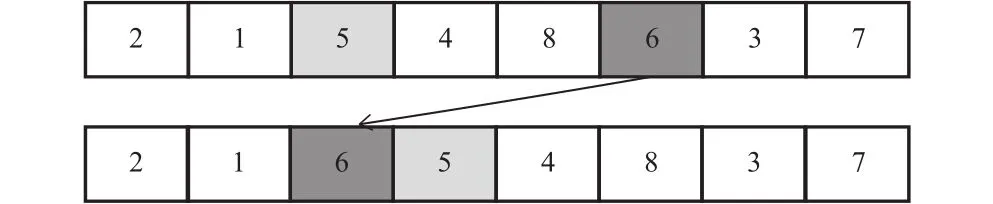
图4 移动工步示意图

（4）帝国竞争操作

帝国竞争的对象是最弱帝国的最弱殖民地。首先需要计算1个帝国的综合势力，包括其自身势力与全部殖民地势力的总和。帝国的总势力值为

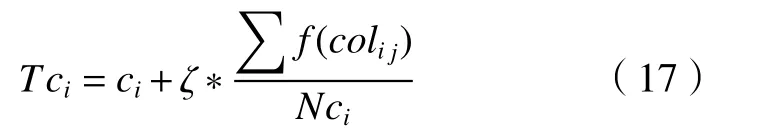
式中：Tci表示第i个帝国集团的总势力；impi表示第i个帝国集团中的帝国；colij表示由第i个帝国统治的第j个殖民地；ζ为正数，表示殖民地对整个帝国势力的影响程度，取值一般在[0.1，0.5][12]。

将1个势力最小的帝国集团中的殖民地视为各个帝国之间竞争的目标，势力越大的国家则越有机会获得这些殖民地。各帝国获得该最弱殖民地概率是

所有帝国集团获得该殖民地的概率可表示为P=[p1,p2,…,pNimp]，再构造1个与P同维的随机向量R，R=[r1,r2,…,rNimp]，其中r∈U(0,1)。构造向量D，D=P-R，选择向量D中元素最大值的索引为侵占该殖民地的帝国主义者。

（5）帝国的灭亡

伴随着帝国集团之间的竞争，势力最强的帝国集团最终将所有弱于它们的帝国以及殖民地侵略攻占完成，最后只存在1个帝国主义国家集团，该帝国集团将剩下所有的国家进行统治，该最强的帝国的位置即为算法计算得出的最优解。

2.3 基于遗传算法的工艺序列优化

从帝国竞争算法求解的结果中选择一部分较优工步序列作为遗传算法的初始种群，进行进一步寻优。涉及的相关算子如下：

（1）选择

选择采用轮盘对赌法进行操作，根据个体适应度值的高低来计算选择概率进行染色体筛选，通常而言，染色体适应度值越优良的，被选择的概率要更高，其机理是由于概率不断累积，适应度大的个体更易于在遗传过程中做出正确选择。

（2）交叉

交叉是指2个染色体完成交换部分算子的操作，并生成新的染色体的过程。为了防止在2个父代染色体组型的交叉操作出现无效的染色体后代，采用单点交叉进行操作，如图5所示。

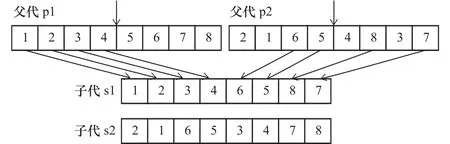
图5 遗传算法中交叉操作

在2条父代染色体上随机产生1个相同位置的交叉点，将父代染色体p1交叉点左边部分的工步内容及位置复制进子代染色体s1中，将父代染色体p2交叉点右边部分未复制的工步按顺序进行复制，形成新的染色体s1，子染色体s2构造原理与s1相同。

（3）变异

在遗传算法求解过程中，为避免目标陷入局部最优且能保持染色体序列的多样化，一般采用突变操作来产生新的染色体种群。任意挑选染色体及位置发生基因突变，将变异点位的2个工步算子内容及位置进行交换，产生新的染色体，保证其求解过程中的全面性。具体操作如图6所示。

图6 遗传算法中变异操作

3 实例分析

以万向节滑动叉为实例进行分析，毛坯种类为锻件，材料为45号钢，零件三维图如图7所示，零件二维图及基本尺寸如图8所示。

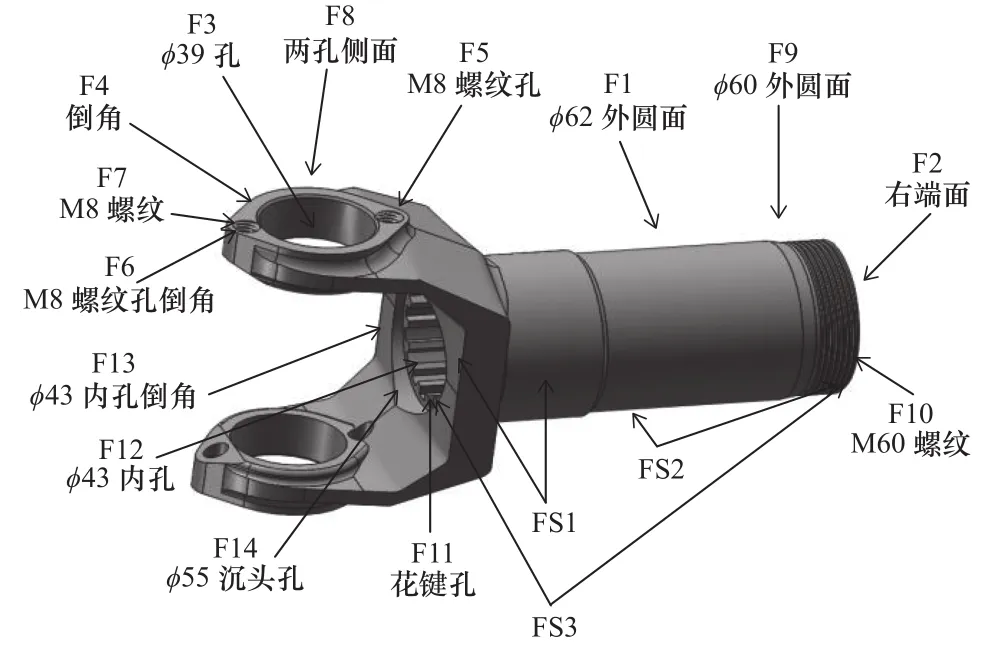
图7 万向节滑动叉零件三维图

图8 万向节滑动叉二维主视图

将工件特征进行区分归类，并将对应特征的加工工艺链进行分解，构成算法可控制的特征加工单元集合，并对特征加工单元实行自然数编码，如表1所示。

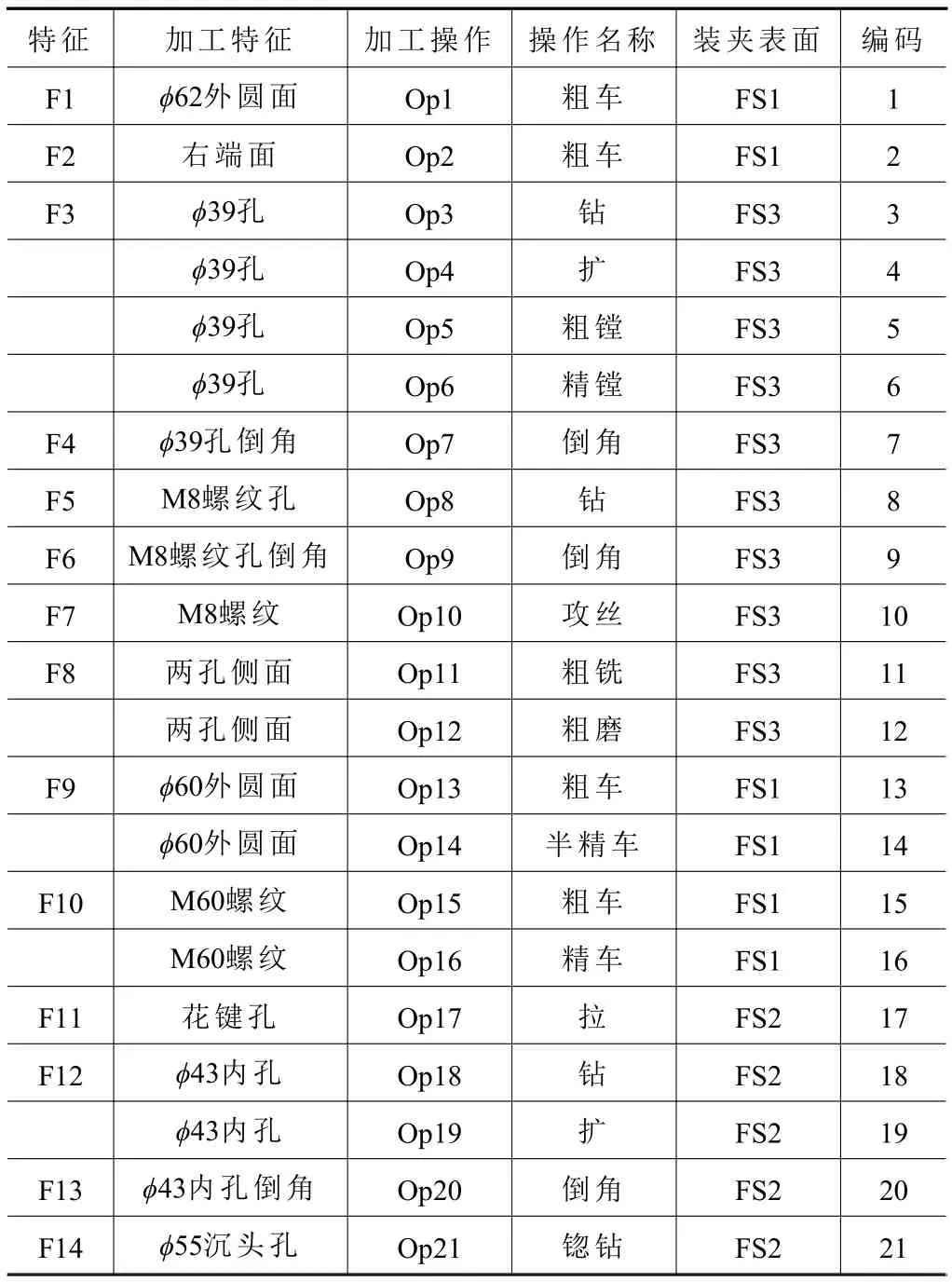
表1 加工特征信息及编码

当装夹面为FS1时，定位基准为左端面、ϕ65外圆面，定位面为FS2时，定位基准为右端面、ϕ62外圆面，装夹面为FS3时，定位基准为花键孔、右端面。

根据约束条件来分析强制性约束集合：将不进行加工的ϕ65外圆面为粗基准，先进行Op2；Op17先于 Op4、Op5、Op6、Op7、Op11和 Op12；Op11先于 Op3、Op4、Op5以及 Op6；Op3、Op4、Op5、Op6先于Op12。

Op18、Op19 先于 Op20；Op3、Op4先于 Op7；Op8先于Op9；Op8先于Op10（先孔后螺纹）；Op13、Op14先于Op15、Op16（先面后螺纹）；Op18、Op19先于Op17（先孔后花键）；特征属性中严格的顺序约束如：Op3、Op4、Op5、Op6。

根据工艺约束，建立1个21×21维的加工序列约束矩阵，如表2所示。

表2 加工优先级矩阵

分析优化约束集，机床和刀具由用户来进行选择，机床类型集以及刀具集由表3、4所示。

表3 机床集

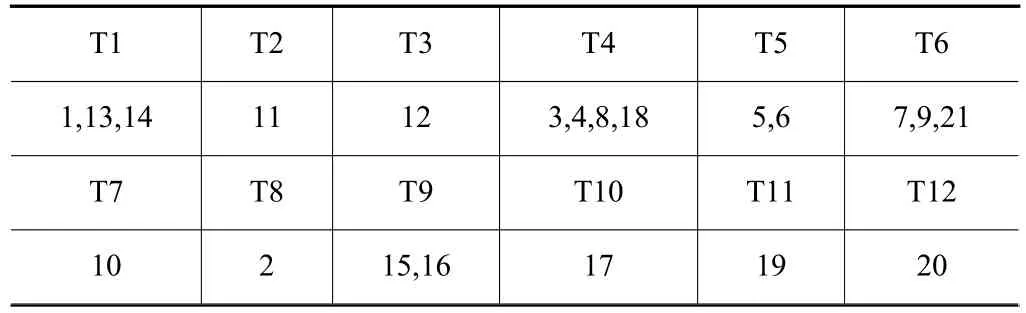
表4 刀具集

编码由表得出长度为21，适应度函数权重系数wm=0.4、ws= 0.2、wt=0.1、wp=0.3。设定帝国竞争算法中，初始国家数为50，殖民地影响系数ζ=0.1，最大迭代次数为500。遗传算法中初始种群数为30，交叉率为0.8，变异率为0.02，最大迭代次数为500，混合算法设置最大迭代次数为1 000。

图9为MATLAB仿真结果图，可以很明显地得出混合算法在求解加工工艺排序中，仅经过119次左右迭代即可完成收敛，且目标函数值要远大于只靠单一帝国竞争算法和单一遗传算法进行求解所得目标函数值。所求得最优的加工工步序列如下：2→1→13→14→15→16→18→19→21→20→17→11→3→4→5→6→8→12→7→10→9。

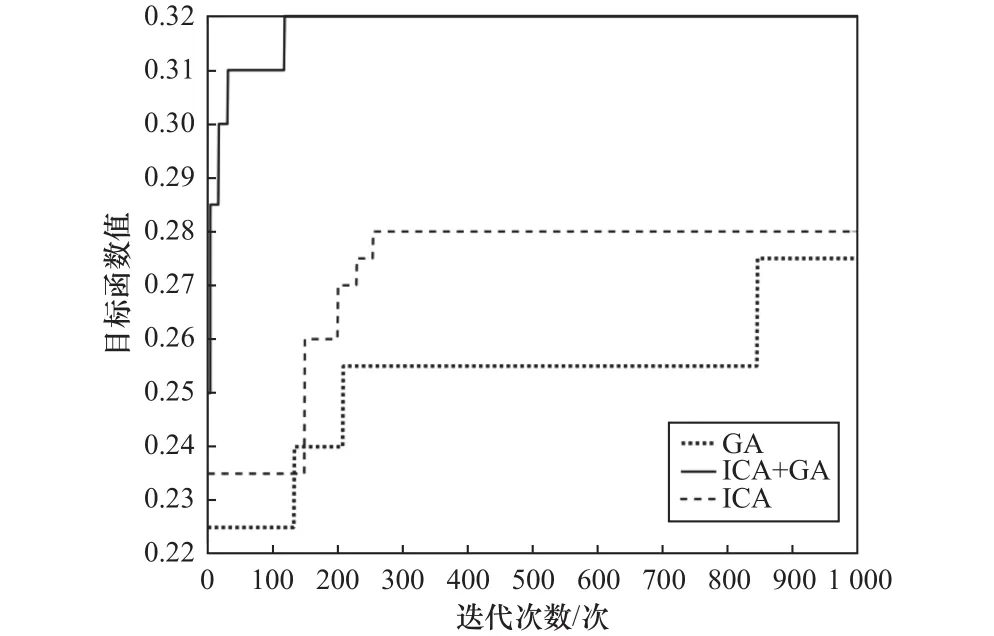
图9 MATLAB仿真结果图

经过该算法运行10次，3种算法的适应度以及迭代次数结果如表5所示。

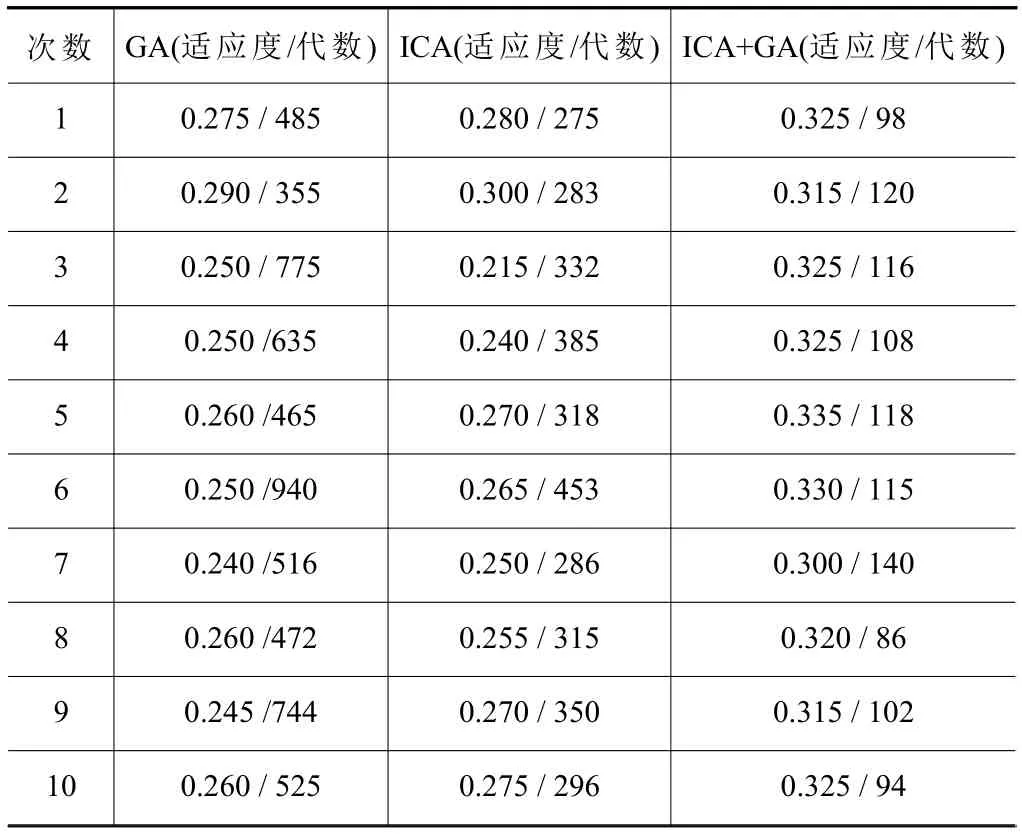
表5 3种算法结果对比

混合算法与单独的优化算法相比较，明显收敛更快且最终结果的适应度值要更高，可以证明混合算法在加工工艺排序中的优化效果要更好。主要原因在于，混合算法充分发挥了帝国竞争算法与遗传算法各自的优势，将帝国竞争算法不受初始序列影响的快速全局搜索能力以及遗传算法中种群的多样性两者相结合，达到优化目的且具有较高的优化效率。

4 结语

针对零件加工工艺排序问题，以最小化机床、装夹以及刀具变更次数为优化目标，构建了工艺排序的数学模型，提出了融合帝国竞争与遗传算法的加工工艺序列排序优化求解方法。通过实验对比分析，可得出以下结论：混合算法的收敛速度和所求解的适应度值均优于各自单独的优化算法，在寻优效率上有很大程度的提升，证明了该优化方法的有效性和实用性。同时，文中建立的工艺路线评价模型未考虑能耗与机床负荷等问题，有待后续进一步深入研究。