不同指令轨迹条件下滚珠丝杠进给系统运动精度特性研究＊

雷美荣 苏 芳 王舒玮 王晨升

（山西大同大学机电工程学院，山西 大同 037003）

滚珠丝杠进给系统因其高刚度、高精度、运动平稳和传动效率高等优点，广泛应用于高档数控机床[1]。滚珠丝杠进给系统运动精度是影响多轴联动加工机床加工精度的根本原因，开展其运动精度影响因素研究具有重要的实践意义。

滚珠丝杠进给系统由伺服驱动系统和机械传动系统组成，具有明显的机电耦合特征，其运动精度是机电耦合复杂因素下共同作用的结果[2]。影响滚珠丝杠进给系统运动精度的参数可以根据来源分为三类：伺服控制参数、机械结构参数和指令轨迹参数。当前，滚珠丝杠进给系统伺服控制系统大多采用PID控制，机械系统由联轴器连接电机输出轴和丝杠，经丝杠螺母副将转动转换为线性移动，实现工作台在丝杠行程内的往复运动。其伺服控制参数主要包括位置环增益、速度环增益等等；机械结构参数包括运动副刚度、丝杠参数、螺母位置和负载等等；指令轨迹参数主要包括速度、加速度和加加速度。当前，国内外学者已经针对滚珠丝杠进给系统控制方法、系统建模、时变特性分析、误差建模与补偿等方面开展了广泛深入的研究。Luigi B等[3]针对滚珠丝杠进给系统，开展了零相位误差跟踪控制器对B样条轨迹的精确跟踪。结果显示，在控制器作用下，滚珠丝杠进给系统对B样条轨迹有很好的跟踪性能。李剑等[4]、刘碧茜等[5]和韩硕等[6]均先后分别针对滚珠丝杠进给系统开展了不同控制方法研究。苏芳等[7-8]针对单轴、双轴滚珠丝杠进给系统开展了伺服控制参数、结构参数对跟踪误差影响规律研究，结果显示，丝杠直径、导程、负载和运动副刚度是影响滚珠丝杆进给系统运动精度的重要因素。智淑亚等[9]和蔡钊勇等[10]就滚珠丝杠进给系统摩擦特性开展了研究，基于不同的摩擦模型，利用系统辨识方法获得了摩擦参数。陈勇将等[11]和苏芳等[12]开展了滚珠丝杠进给系统动态时变特性研究，结果显示，滚珠丝杠进给系统随着螺母位置、结合部刚度和工作台质量等时变参数变化而变化。Meng Y等[13]针对跟踪误差控制算法做了综述研究。赵万华等[14]给出了滚珠丝杠进给系统误差来源、类别及评价方法，对于广泛开展滚珠丝杠进给系统跟踪误差研究具有指导意义。由以上文献可见，对于滚珠丝杠进给系统运动精度的研究大多基于伺服控制机械结构展开，而缺乏针对指令轨迹参数的单因素研究。

本文针对指令轨迹参数，采用确定伺服控制系统参数和机械结构参数的滚珠丝杠进给系统，开展运动精度影响规律研究。首先，基于Simulink构建了伺服控制系统仿真模型；然后，利用SolidWorks建立了滚珠丝杠进给系统的机械物理模型，并将该模型以Step格式导入到Simsacpe中；最后，在Simulink中联合滚珠丝杠进给系统伺服控制模型和机械半物理仿真模型，构建系统半物理仿真系统，并基于该模型开展不同指令轨迹条件下，滚珠丝杠进给系统运动精度仿真分析研究。

1 机械系统半物理仿真模型

指令轨迹作为滚珠丝杠进给系统输入，既是驱动，也是激励，其参数特征，对滚珠丝杠进给系统运动精度有重要影响。为开展滚珠丝杠进给系统在不同指令轨迹条件下运动精度仿真分析研究，利用SolidWorks建立了结构如图1所示的3D滚珠丝杠进给系统模型。主要结构件有电机、联轴器、丝杠、螺母、工作台和、导轨及滑块。

图1 几何模型

将图1所示模型在SolidWorks中另存为Step格式，导入到Simscape中，构建机械系统半物理仿真模型。同时，为模拟运动副柔性，将联轴器、轴承、丝杠螺母和导轨滑块等连接等效为弹簧阻尼单元，如图2所示。并通过查阅产品手册获得具体刚度参数，如表1所示。因本文主要针对指令轨迹开展仿真研究，故视机械系统参数为定值。最终的机械系统半物理仿真模型如图2所示。

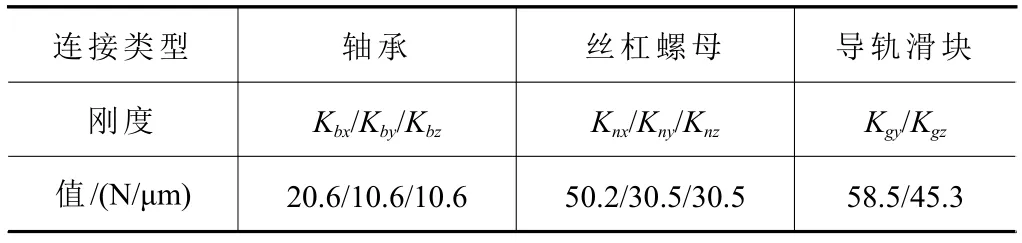
表1 运动副刚度

图2 机械传动系统半物理机电耦合仿真模型

滚珠丝杠进给系统的尺寸参数和材料参数如表2所示。

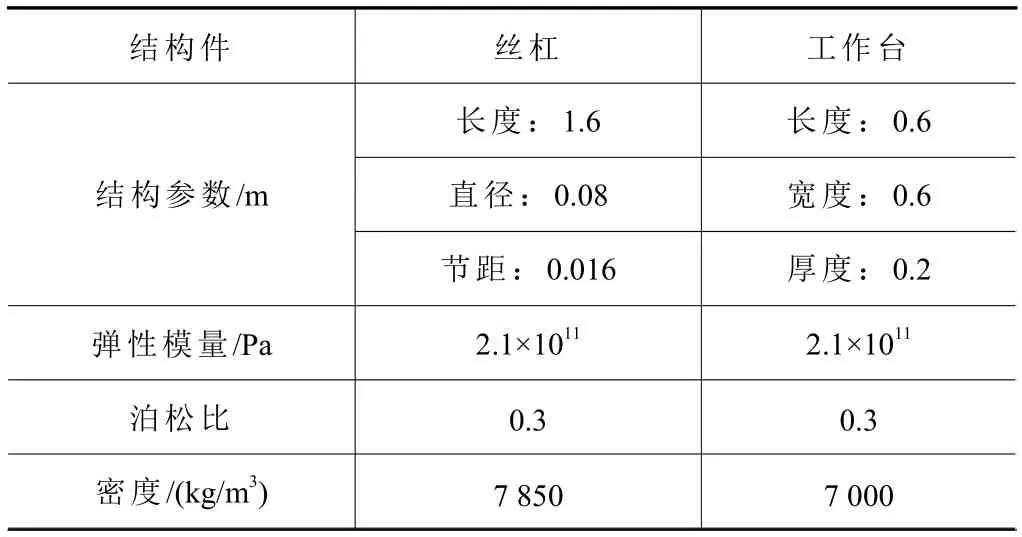
表2 结构件参数

2 伺服控制系统模型

基于Simulink搭建包含驱动器、控制器的滚珠丝杠进给系统伺服控制系统仿真模型。滚珠丝杠进给系统采用永磁同步电机驱动，采用三环PID闭环矢量控制方式。

2.1 电机模型

采用矢量控制方法，通常设定id=0，则永磁同步电机定子电压和磁链方程在dq坐标系中可表示为

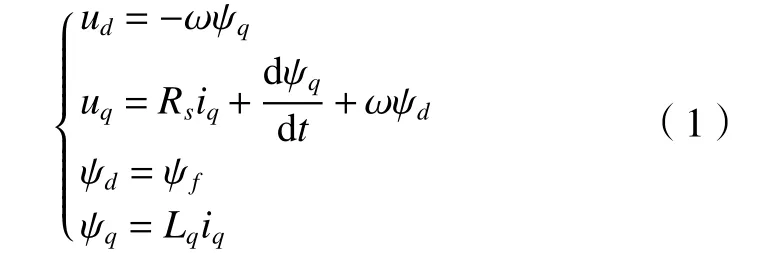
式中：ud和uq表示d轴和q轴的定子电压； ψd和 ψq表示d轴和q轴的定子磁链；Rs表示电枢绕组电阻；id和iq表示d轴和q轴的电枢电流；Lq表示电枢电感；ψf表示磁链； ω表示电机角速度。

则有

其中：p表示电机极对数， ωr表示电机转子角速度。

由式（1）可推导出

永磁同步电机在旋转dq坐标系中电磁转矩方程可表示为

永磁同步电机转子动力学方程可表示为

式中：Te表示电磁转矩；Tm表 示负载扭矩；b表示阻尼系数；J表示转动惯量。

则由式（3）～式（5）可推导出

2.2 控制系统模型

控制系统采用三环控制，其中电流环和速度环控制采用PI控制，位置环控制器采用P控制，传递函数可表示为

式中：Kp、Kv、Ki分别表示位置环、速度环和电流环的比例增益；G1表示位置环，G2表示速度环，G3表示电流环；Tv、Ti表示速度环和积分环的积分常数。

根据以上推导，在Simulink中搭建伺服控制系统仿真模型，并在Simlulink中和机械结构的Simscape模型子系统组成滚珠丝杠进给系统半物理机电耦合仿真模型，结构如图3 所示。图3中Simscape方框即图2中的机械系统半物理仿真模型。图3中Kt表示电机力矩常数，Ke表示电机反电动势常数，Lm表示电机等效电感，Rm表示电机等效电阻。

图3 伺服控制系统仿真模型

3 指令轨迹及仿真分析

指令轨迹的参数特性主要包括位移、速度、加速度和加加速度。在滚珠丝杠进给系统工作过程中，无法确保每一个特性参数都连续变化，特别是多轴联动加工机床，刀尖点的轨迹根据运动学关系分解到进给系统，再经数控系统插补后行程实际输入指令，面对复杂形状的轨迹，指令轨迹参数更为复杂和多变。

3.1 指令轨迹

充分考虑指令轨迹参数变化情况，设计了包含位移突变、匀速、匀加速和变加速运动轨迹，如图4所示。其中，轨迹1为匀速运动轨迹，初速度不为零，加速度、加加速度均为零；轨迹2为阶跃位移轨迹，位移在t=1.5 s时发生跳跃，速度、加速度和加加速度都存在突变；轨迹3为匀加速、匀减速轨迹，在t=2 s位置时，加速度和加加速度有突变；轨迹4为5段S型轨迹，加加速度存在突变；轨迹5为变加速运动，速度、加速度和加加速度都为正弦，均连续、无突变。

3.2 仿真分析

基于图3所示滚珠丝杠进给系统半物理机电耦合仿真模型，以图4为指令轨迹，分别考察系统运动精度。分别以工作台反馈位置信息和输入位置信息做差得到系统跟踪误差，如图3所示以perr表示。

图4 指令轨迹

滚珠丝杠进给系统在设定的运动轨迹条件下，其跟踪误差如图5所示。由图5a可见，对于匀速运动轨迹，由于初速度设置不为零，导致滚珠丝杠系统跟踪误差在开始阶段存在很大波动，待系统速度稳定之后，跟踪误差基本稳定，维持在0.4 mm左右，存在的波动误差是由于系统振动造成，波动误差稳定在35 μm范围内。由图5b可见，对于阶跃轨迹，在位置突变处，存在很大 的跟踪误差，该跟踪误差跟位置突变值正相关，而且会产生很大系统震荡，该现象对于加工十分不利。由图5c可见，对于位移连续、速度连续的轨迹，其跟踪误差也是连续变化，无强烈震荡，其跟踪误差稳态部分与轨迹速度正相关，轨迹3的最大跟踪误差达到0.85 mm，轨迹4的最大跟踪误差达到0.51 mm，轨迹5的最大跟踪误差达到0.84 mm。三种轨迹跟踪误差不同的主要各轨迹的速度和加速度参数不同，轨迹3的最大跟踪误差出现在速度最大处。同时，轨迹3、轨迹4和轨迹5的跟踪误差稳态成分随速度变化而变化。另外，由图5a可见，3种轨迹跟踪误差的波动部分基本位置在30 μm，由图5c轨迹5的跟踪误差可见，在位移轨迹小曲率位置处存在明显增大现象，可见与加速度关系更为密切。

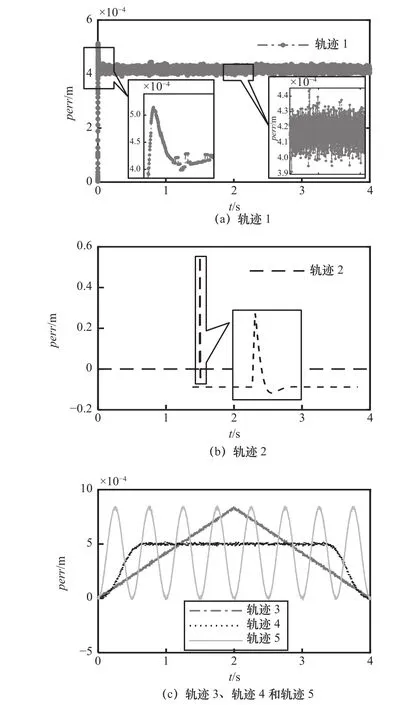
图5 跟踪误差

综上所述，可见跟踪误差与指令轨迹参数存在密切关系，即使在系统为确定模型情况下，随着输入指令轨迹参数的变化，系统跟踪误差仍会发生变化。由分析结果可见，跟踪误差稳态部分主要受位置参数和速度参数影响，而跟踪误差波动部分主要受指令轨迹加速度参数影响。因此，在轨迹规划的过程中，应该根据工艺要求，限制指令轨迹位置突变、最大速度和加速度等信息，以提高滚珠丝杠进给系统运动精度，进而提高多轴联动机床加工精度。

4 结语

以滚珠丝杠进给系统为研究对象，基于Simulink和Simscape搭建了滚珠丝杠进给系统半物理机电耦合仿真模型，开展了不同指令轨迹条件下，滚珠丝杠进给系统跟踪误差特性研究。结果显示，滚珠丝杠进给系统跟踪误差与指令轨迹位置、速度和加速度参数紧密相关。其中，跟踪误差稳态部分主要受位置参数和速度参数影响，特别是位置的突变和速度突变，不仅会导致跟踪误差的增大，而且会导致严重的系统震荡，对加工极为不利；而跟踪误差波动部分主要受指令轨迹加速度参数影响，在实际加工过程中可通过改变加速度方式限制滚珠丝杠进给系统跟踪误差中的波动误差。