多角度肋片强化相变材料换热仿真分析
2023-02-03罗权权李保国郑爽袁成豪
罗权权,李保国,郑爽,袁成豪
多角度肋片强化相变材料换热仿真分析
罗权权1,李保国1,郑爽1,袁成豪2
(1.上海理工大学 能源与动力工程学院,上海 200093;2.湖南省肿瘤医院,长沙 410013)
针对太阳能热利用领域中相变材料的封装结构提出圆柱体相变蓄热棒,并设计多角度肋片以加快相变材料融化速率。采用CFD仿真技术,分析不同形状肋片对蓄热棒中相变材料融化特性的影响,计算各模型相变材料的融化时间、温度响应速率和平均传热系数。在800 W/m2的热流边界条件下,无肋片蓄热棒的相变材料完全融化需要2 813 s,设计的12组肋片中Tra–45模型性能最优,相变材料的融化时间比无肋片对照组的缩短了5.4%;Tra–45模型中相变材料温度分布集中,且最高温度上升了6 ℃,Tra–45模型的温度响应速率较对照组的提升了5%;Tra–45模型的平均换热系数达到9.97 W/(m2·K),较对照组的提升了2.8%。蓄热棒内增加梯形45°肋片后,相变材料融化速率加快,蓄热棒内温度分布均匀。同时,相变材料的温度响应速率提高,平均换热系数显著增加,可满足频繁充放热的需求。
规则形状肋片;强化换热;相变材料;仿真
太阳能为大自然给予的绿色能源,然而太阳能热利用存在不连续、间断性问题,为充分利用太阳能,人们研发了储能技术。常用的太阳能热储存有潜热、显热和可逆化学反应[1],其中采用相变材料的潜热储热系统(Latent Heat Thermal Energy Storage—LHTES)已有大量研究[2],按照相变温度将相变材料区分,应用在不同环境中。现有的相变材料还存在导热系数不高,充放热慢等问题[3]。
在相变材料中添加导热系数较高的物质,例如碳基材料和金属基材料,可显著提升相变材料的换热效率。碳基材料的制备成本较高,在储热量较大时,系统的初始投资成本高,未能得到广泛应用。金属基材料容易获得,但金属密度较高,在相变材料中难以均匀分布,导致相变材料导热效率不稳定。虽然添加导热系数高的物质可以提升换热性能,但添加后会使单位体积的相变材料相对减少,这将使系统潜热储存能力降低。另外,相变材料封装也是提升换热效率的一种方式,可以防止相变材料泄露、腐蚀和相分离,延长了相变材料的使用寿命。相关研究集中在如何加快相变材料的融化和凝固速率,从而保证相变潜热被充分利用,以及避免相变材料在充放热循环过程中出现温度不均的情况,尤其在放热时出现“储热陷阱”——外侧相变材料凝固过快,导致内部热量散发受阻。Raj等[4]将相变材料封装成圆柱体,并建立了储热装置的三维模型,采用数值仿真的方式分析了热传导和热对流换热对相变材料的凝固和融化速率影响,通常熔化所需的时间比凝固的时间要长[5]。结果表明,热传导换热时封装的圆柱体底部仅27%的相变材料完全熔化。在放热循环过程中,底部的相变材料又会快速地凝固,导致上部区域的热量很难通过热传导导出。相反,在热传导和热对流组合模式下,在相同的加热时间内超过70%的相变材料完全熔化,避免了在放热循环时出现“储热陷阱”。在以石蜡为相变材料的球形胶囊中也出现相同的结果[6]。
常见的相变材料封装容器有:球体、长方体和圆柱体容器[7],封装壳体通常采用导热系数良好的金属材料。容器外侧通常是换热系数较高的对流换热,内侧的相变材料主要通过热传导的方式进行热量交换,因此,容器内侧的换热热阻较大,要提高换热效率应从相变材料侧进行,目前提升相变材料换热效率的主要方式是增加换热面积[8],在相变材料一侧增加环形翅片[9]和纵向肋片[10],以及对翅片形状进行了仿生学结构优化[11-12]。
为提高相变材料换热速率,满足用户频繁充放热的需求,文中建立不同形状肋片的相变蓄热棒模型,并对相变蓄热棒模型在相同换热面积下进行相变材料的融化仿真分析。计算相变材料的融化时间,温度响应速率和平均传热系数,并与无肋片蓄热棒进行对比。
1 多角度肋片强化换热设计
1.1 蓄热棒肋片模型
为提高蓄热棒相变材料换热效率,设计了多角度肋片蓄热棒,图1为所设计的蓄热棒结构及肋片布置示意图,相变材料被封装在铝制蓄热棒管中,肋片设置在蓄热棒内;换热流体在换热管与蓄热棒之间的流动区域进行热量交换。蓄热棒中增加肋片的区域总长度(),肋片间距为35 mm。图2所示为4种不同形状肋片的三维模型以及尺寸,所有肋片高度均为12 mm,肋片形状为等边三角;等腰三角肋片顶角为30°;矩形肋片宽度为4 mm;梯形肋片顶角为45°,上边宽度为3.7 mm;肋片的数量分别为5、9、7和4片。仿真计算采用的材料属性见表1。

图1 蓄热棒结构及肋片布置
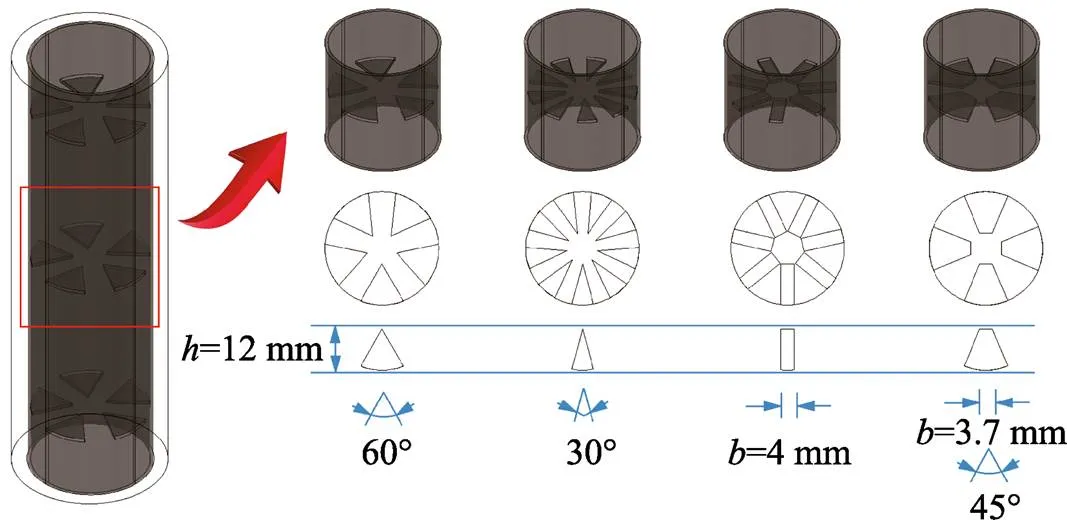
图2 肋片形状及几何尺寸
为简化计算,选取单层肋片,以长度为35 mm的圆柱体区域作为仿真计算域,表2为4种肋片多角度布置的几何模型。肋片厚度均为1 mm,肋片位于圆柱体中间位置,4种肋片占相变材料体积分数均为1%,肋片旋转角度分别设置为0°、45°和90°这3种模式。
1.2 计算域网格划分
为选取最优性能的多角度肋片,优化计算时间,忽略空气流动换热,只分析肋片的导热性能。由于蓄热棒物理模型为非规则几何结构,采用四面体非结构化网格进行几何建模。为控制全局网格节点数,将网格划分为相变材料区域(网格尺寸设置为0.003 m)和蓄热棒壳体加肋片区域(网格尺寸设置为0.002 m),平均网格质量为0.831。图3所示为Eq–0的网格截面图。
仿真分析不同网格数量相变材料的液相分数见图4。在图4a中,网格数量从531 938增加到2 079 054时,各组模型的融化时间曲线相同。为节省计算时间,选择网格数为531 938进行后续仿真分析。选择网格数量为531 938的模型,计算时间步长从0.05~1 s的相变材料液化分数见图4b,时间步长为0.05、0.1和0.5 s的3组模型的计算结果相近,步长为1 s时相变材料液相分数与其他3组有较大偏差,为了优化计算时间和资源,选择时间步长为0.5 s。
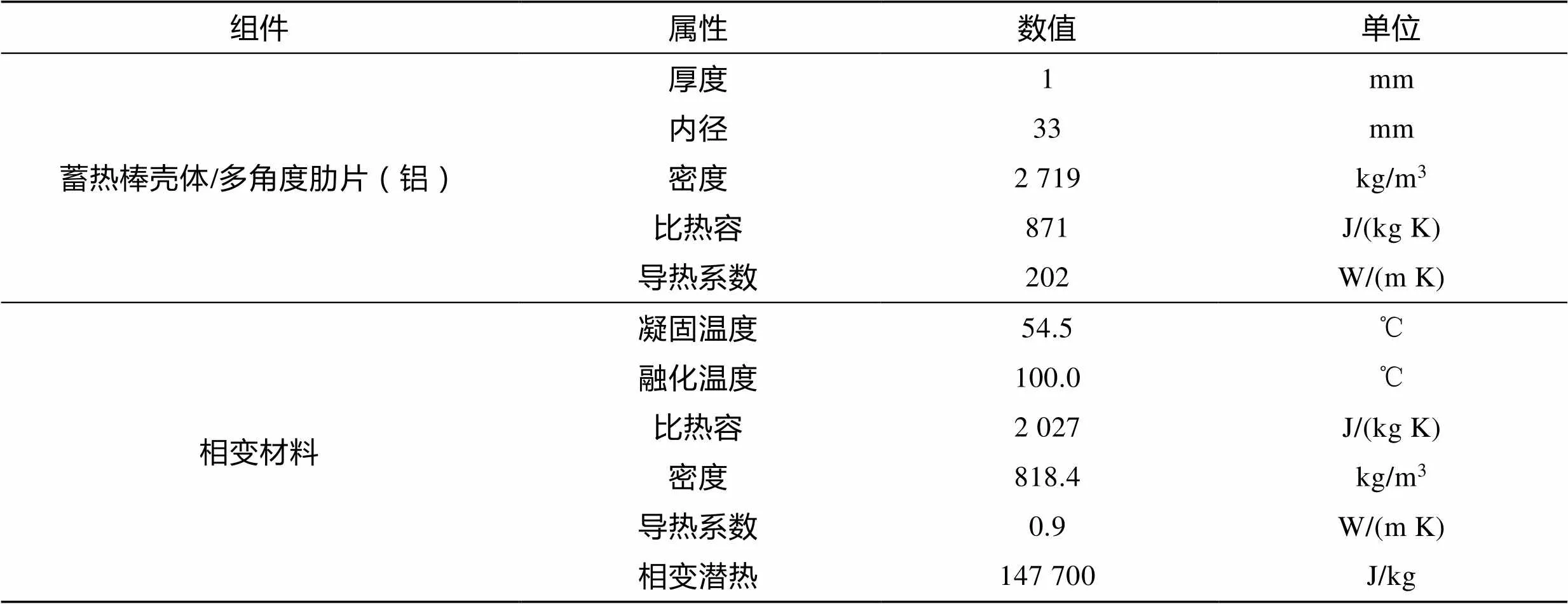
表1 集热器各部件材料热物性

表2 多角度肋片三维几何模型

图3 Eq–0网格截面图
1.3 控制方程及方法
在物理模型中删除了空气计算域,忽略了相变材料的自然对流,因此控制方程中不涉及空气流动和换热。将求解器设置为单一的能量方程求解。相变材料的传热和流动使用焓–孔隙模型,控制方程如下。
连续性方程:
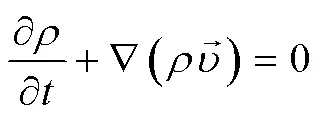
动量方程:
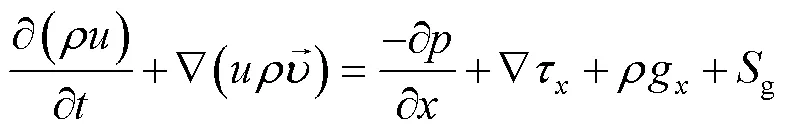
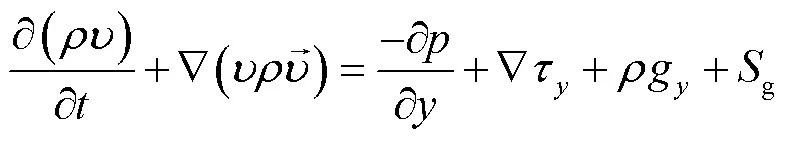
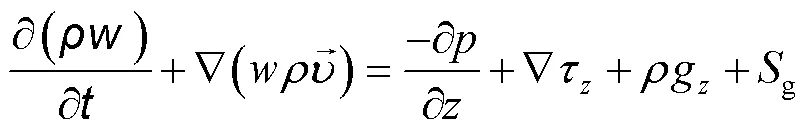
能量方程:


焓值是显热焓s和潜热焓Δ的总和,计算式为:

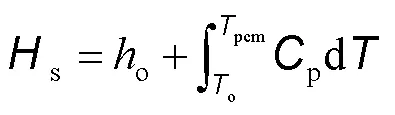

式中:o为参考点焓值,kJ/kg;pcm为相变材料温度,K;o为参考点温度,K;为融化潜热,kJ/kg;l为液相分数。
液相分数(l)的计算式为:
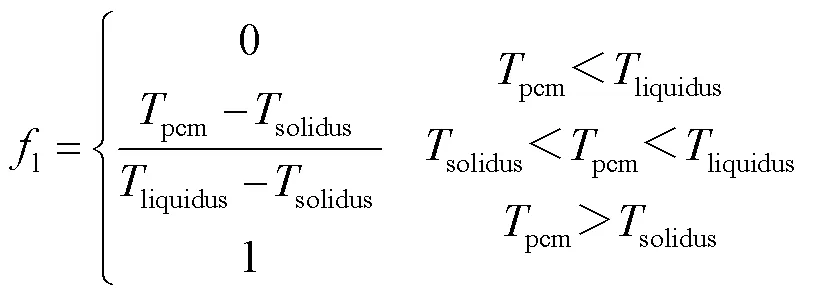
对于相变材料动量方程,在融化区增加源项g。通常融化区被认为是多孔介质域,其中,随着材料凝固孔隙率从1降低到0。

式中:为融化区常数,取值范围为104~ 107,文中取105。

图4 网格独立性验证
计算流动区域的湍流动能和耗散率的–ε模型的输运方程为:
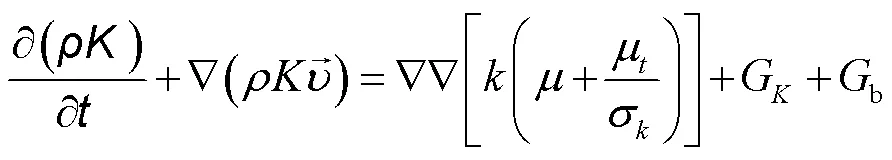
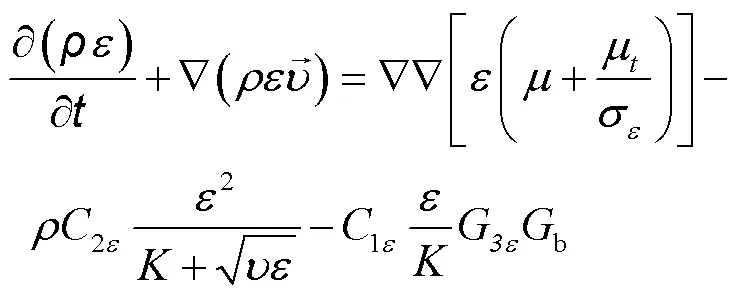
式中:G为平均速度梯度产生的湍流能;b为浮力产生的湍流能;为湍流动能;为湍流耗散率;1ε、2ε、3ε和C为湍流常数,取值1ε=1.44、2ε=1.92、3ε= −0.33、C=0.09、σ=1.0和σ=1.3。
湍流动力黏度值(μ)的计算式为[13]:

1.4 边界条件
在 Fluent 19.2中导入网格文件,在材料栏新增相变材料的物性参数。选择SIMPLE算法求解,松弛因子采用默认值。能量方程的收敛判断标准为10−8。仿真过程中,热量的传递主要以热传导的方式进行,因此,忽略相变材料融化后的自然对流换热过程的影响,且不计相变材料融化的体积膨胀[14]。初始条件和边界条件设置见表3。全体计算域初始温度设定为27 ℃;蓄热棒外壳面设定为恒定热流壁面,为加快融化速率,缩短计算时长,将热流量数值设置为800 W/m2。
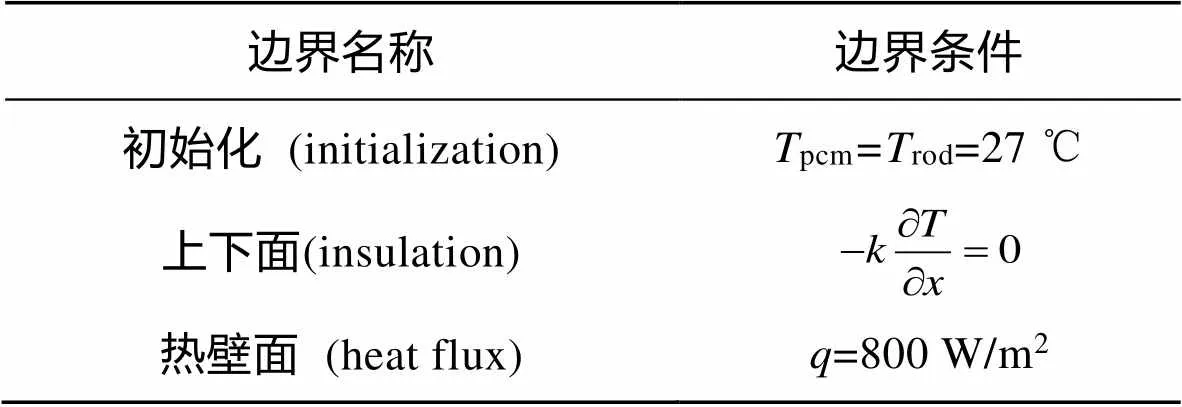
表3 仿真计算边界条件
1.5 无量纲参数
为了量化不同参数的肋片熔融相变过程的速度,通过计算加热期间的温度响应速率(Response Rate—R),数值化展示肋片对换热的增强效果,根据如下公式计算:

式中:T为t时刻相变材料的温度,℃;T1为t1时刻相变材料的温度,℃;∆为时间差,s;∆=t−t1。

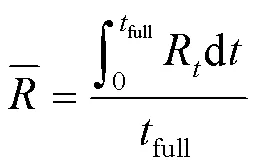
式中:full为各肋片模型中相变材料完全熔化所需时间,s。
为定量比较多角度肋片对相变传热的影响,参考Yang等[15]提出的熔融过程的积分平均传热系数,按式(16)计算。
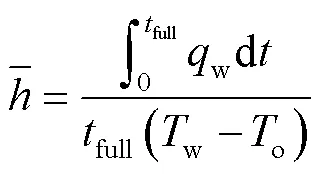
2 结果与分析
2.1 模型验证
由于缺乏圆柱体相变蓄热棒的熔化实验测试,参考Shaker等[16]进行的光滑内壁面圆柱体相变材料胶囊的融化测试,圆柱体胶囊结构与相变蓄热棒几何形状一致,模型设置和边界条件相似,因此,文中按照实验测试条件重复了圆柱体胶囊的数值模拟,并将预测结果与实验数据进行对比,以验证指导文中所建立的相变蓄热棒模型,对比结果见图5。圆柱体外壳设置为70 ℃等温边界条件,其余壁面为绝热面;计算域初始化温度设置为26 °C。结果显示,相变材料的融化速率仿真结果高于实验值,相变材料完全熔化时间实验值为12 923 s,仿真结果为11 364 s,熔化时间的误差为12.1%。该误差可能是由于仿真计算中圆柱体外壳稳定维持在70 °C,而实验测试中由于换热介质的流动导致圆柱体外壳的换热量存在差异。误差范围在接受范围内,因此,认为文中使用的控制方程和求解方法可靠。
2.2 相变材料融化时间
多角度肋片用于加快相变材料融化速率,在选取最优肋片时,以融化时间评价模型优劣。表4汇总了各组模型相变材料融化时间,结果显示,无肋片对照组相变材料完全融化需要2 813 s,设计的12组多角度肋片模型的融化时间相比对照组都有缩短,其中Tra–45模型融化时间最短为2 660 s,较对照组缩短了5.4%。

图5 相变材料液相分数的模拟值与 Shaker的实验数据对比

表4 多角度肋片融化时间汇总
图6所示为多角度肋片模型相变材料的液相分数变化曲线,由图6可看出,前500 s相变材料液相分数未变化,此时处于显热升温状态;随后进入快速融化阶段,不同模型液相分数曲线斜率不同,对应的融化速率不同;2 600 s后仅少部分相变材料未融化,液相分数变化缓慢。在2 660 s时Tra–45模型完全融化,其他模型融化程度相近,平均融化时间为2 788s。快速融化阶段 Tra–45模型的融化分数随时间变化明显快于其他模型。
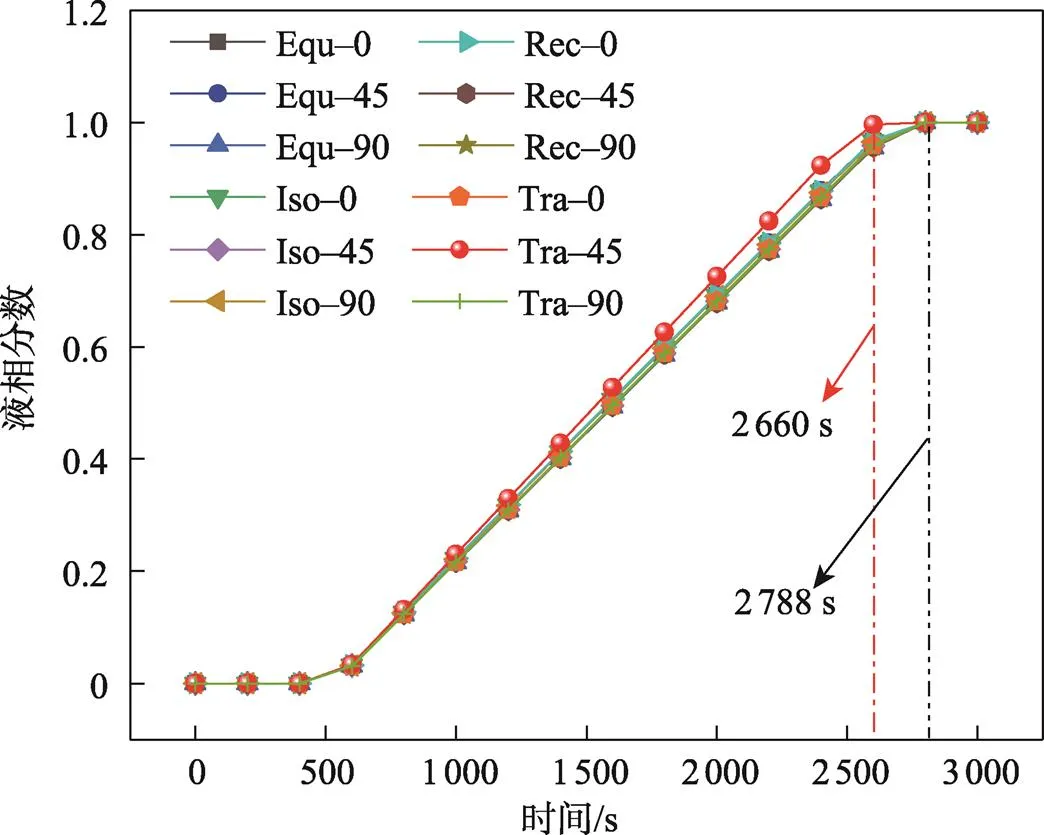
图6 多角度肋片模型相变材料融化分数变化
图7为多角度肋片模型中相变材料温度的变化曲线,3 000 s时Tra–45模型的相变材料温度达到了123 ℃,而其他模型差异不大,平均温度为117 ℃。融化前期各组的温度变化趋势相同,随着融化的进行,Tra–45模型的温度逐渐增加,这是因为相变材料的融化速率增加后加速了温度的上升。另外通过计算温度随时间的积分可以得到不同模型累计储热量,Tra–45模型的储热量大于其他模型,表明系统的储热量得到提高。

图7 多角度肋片相变材料温度变化曲线
2.3 温度响应速率
图8所示为多角度肋片模型在相变材料融化某时刻的温度分布,选取相变材料充分融化时刻(2 000 s)进行分析。结果显示,Tra–45肋片模型中相变材料的温度集中在89.75 ℃,体积分数为28.37%,Eq–45、Iso–0和Rec–0 3组的温度集中在87.75 ℃,其他肋片模型的温度主要分布在87.25 ℃。对照组的温度分布在各温度区间占比相差不大,且高温区域的体积分数较低。Tra–45模型在2 000 s时相变材料的温度最高,较其他肋片和对照组加快了相变材料的融化速率。

图8 多角度肋片在2 000 s时刻温度分布统计
图9为多角度肋片的平均温度响应速率,由图9可看出,4种肋片形状的响应速率变化趋势不相同,Iso和Rec模型转角度为0°时,温度响应速率最大,而Eq和Tra转角为45°时,平均温度响应速率最大。与对照组(CG)相比,各组肋片的温度响应速率均有提升,其中Tra–45模型的响应速率最大,提升了5%,有利于相变材料快速地充放热。

图9 多角度肋片平均温度响应速率
2.4 平均传热系数
多角度肋片模型的平均传热系数见图10。由图10可看出Eq–0、Iso–90和Tra–45肋片模型的平均传热系数显著高于其他组,Tra–45肋片模型的平均换热系数最高,达到9.97 W/(m2∙K),较对照组提升了2.8%。另外,肋片安装角度对平均换热系数也有影响,矩形(Rec)肋片模型的平均传热系数提升幅度与其他3组肋片相比不显著,这是由于矩形肋片在蓄热棒直径方向上旋转几何投影变化不大,因此,在不同角度安装的模型,传热系数的变化较小。三角形肋片和梯形肋片在直径方向旋转角度后,对相变材料的自然流动产生影响,从而表现出换热系数随角度发生变化。
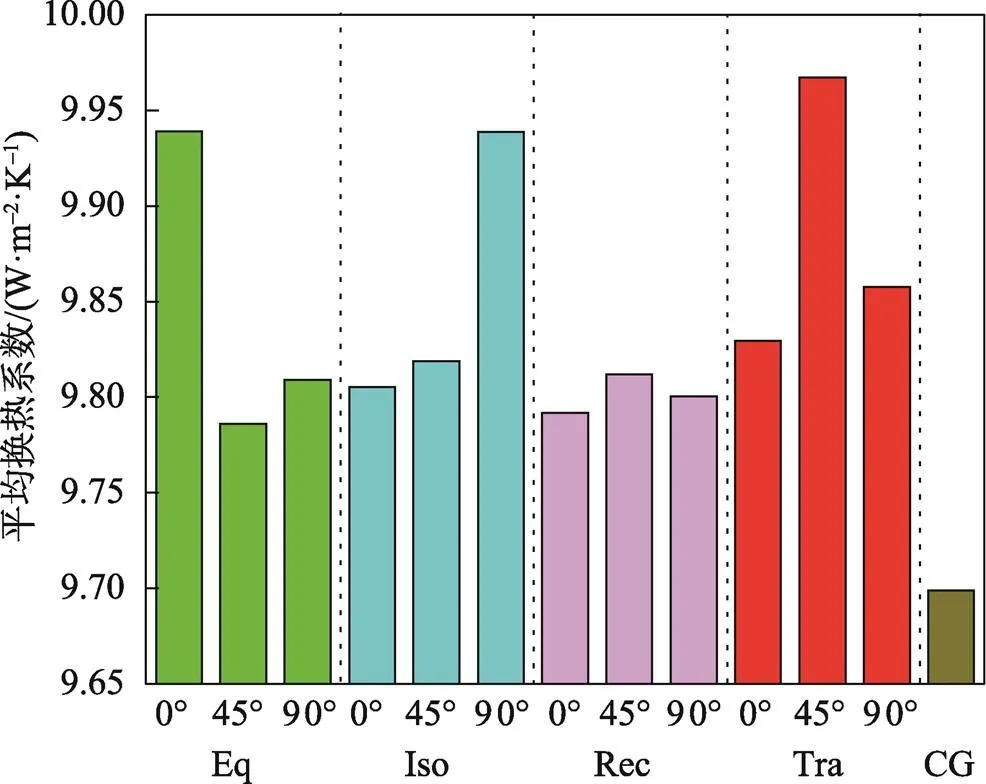
图10 多角度肋片平均传热系数
分析12组多角度肋片模型的对相变蓄热材料融化效果,Tra–45模型的相变材料融化时间最短、温度响应速率高,以及相变材料的温度分布最为集中,且平均温度明显高于其他肋片模型,其性能最优。从表1中Tra–45肋片的几何模型可知,Tra–45肋片根部与蓄热棒外壳的接触面积相较于其他肋片更大,为最优肋片。所有肋片模型的肋高相同,因此在热量传导至相变材料几何中心的时间相近。等边三角肋片和等腰三角肋片的顶部为锐角,仅有2条肋边与相变材料换热。矩形肋片和梯形肋片顶部为直角和钝角,有3条肋边与相变材料接触,因此,在能加快相变材料的融化。同时,在梯形的3种角度肋片中45°和90°的肋片均比0°的肋片性能好,这主要是由于肋片的旋转角度可以改变相变材料在垂直方向上的温差。0°和90°呈现为水平和垂直2个状态,水平状态的肋片在垂直方向上产生温度差异受限,垂直状态的肋片在水平方向上的换热能力弱,45°的肋片能在水平和垂直2个方向上均可热交换。
3 结语
为提高蓄热棒相变材料的换热效率,在蓄热棒中增设了等边三角肋片、等腰三角肋片、矩形肋片和梯形肋片,仿真分析了不同安装角度模型中,相变材料的融化时间、温度响应速率和平均传热系数,得到如下结论。
1)蓄热棒中无肋片对照组相变材料完全融化需要2 813 s,设计的12组多角度肋片模型的融化时间相比对照组都有缩短,其中Tra–45模型的融化时间最短为2 660 s,较对照组缩短了5.4%。另外,Tra–45肋片模型中相变材料温度分布最为集中,且相变材料最高温度上升了6 ℃,这将提升蓄热棒的储热量。
2)温度响应速率反映了不同模型对相变材料融化速率提高的效果,4种肋片形状的响应速率变化趋势均不相同,旋转角度的增加与响应速率无明显线性关系,即肋片的旋转角度在不同外形下加速融化的效果不同。其中Tra–45模型的响应速率最快,较对照组提升了5%,以满足用户侧频繁充放热的需求。
3)平均传热系数可代表同肋片模型换热强度,其中矩形肋片在蓄热棒直径方向上几何形状变化不大,不同角度安装的模型中传热系数的变化小。三角形肋片和梯形肋片在直径方向上肋片宽度缩小,在旋转角度后对相变材料的自然流动产生影响。Tra–45肋片模型的平均换热系数最高,达到9.97 W/(m2·K),较对照组提升了2.8%,有效提升了相变材料换热效率,还可增加蓄热棒储热量。
[1] LIN Ya-xue, JIA Yu-ting, ALVA G, et al. Review on Thermal Conductivity Enhancement Thermal Properties and Applications of Phase Change Materials in Thermal Energy Storage[J]. Renewable and Sustainable Energy Reviews, 2018, 82: 2730-2742.
[2] ZHANG Sheng-qi, PU Liang, XU Ling-ling, et al. Melting Performance Analysis of Phase Change Materials in Different Finned Thermal Energy Storage[J]. Applied Thermal Engineering, 2020, 176: 115425.
[3] LIN Ya-xue, ALVA G, FANG Gui-yin. Review on Thermal Performances and Applications of Thermal Energy Storage Systems with Inorganic Phase Change Materials[J]. Energy, 2018, 165: 685-708.
[4] RAJ A K, SRINIVAS M, JAYARAJ S. CFD Modeling of Macro-Encapsulated Latent Heat Storage System used for Solar Heating Applications[J]. International Journal of Thermal Sciences, 2019, 139: 88-104.
[5] ALIPANAH M, ZAHMATKESH A. Heat Transfer Modeling of Phase Change Materials in Multiple Plates Heat Exchanger[J]. Research Journal of Applied Sciences, Engineering and Technology, 2013, 6(24): 4671-4675.
[6] TAN F L, HOSSEINIZADEH S F, KHODADADI J M, et al. Experimental and Computational Study of Constrained Melting of Phase Change Materials (PCM) Inside a Spherical Capsule[J]. International Journal of Heat and Mass Transfer, 2009, 52(15/16): 3464-3472.
[7] DUAN Juan, XIONG Yong-liang, YANG Dan. Study on the Effect of Multiple Spiral Fins for Improved Phase Change Process[J]. Applied Thermal Engineering, 2020, 169(5): 114966.
[8] ABDULATEEF A M, MAT S, ABDULATEEF J, et al. Geometric and Design Parameters of Fins Employed for Enhancing Thermal Energy Storage Systems: A Review[J]. Renewable and Sustainable Energy Reviews, 2018, 82: 1620-1635.
[9] SHAHSAVAR A, GOODARZI A, MOHAMMED H I, et al. Thermal Performance Evaluation of Non-Uniform Fin Array in a Finned Double-Pipe Latent Heat Storage System[J].Energy 2020, 193: 116800.
[10] ALIZADEH M, HOSSEINZADEH K, SHAHAVI M, et al. Solidification Acceleration in a Triplex-Tube Latent Heat Thermal Energy Storage System Using V-Shaped Fin and Nano-Enhanced Phase Change Material[J]. Applied Thermal Engineering, 2019, 163: 114436.
[11] TIAN Yang, LIU Xiang-lei, XU Qiao, et al. Bionic Topology Optimization of Fins for Rapid Latent Heat Thermal Energy Storage[J]. Applied Thermal Engineering, 2021, 194(3): 117104.
[12] LIU Hong-lei, LI Bao-tong, ZHANG Lu-kuan, et al. Optimizing Heat-Absorption Efficiency of Phase Change Materials by Mimicking Leaf Vein Morphology[J]. Applied Energy, 2020, 269: 114982.
[13] KUMAR A, AKSHAYVEER A, SINGH P, et al. Efficient Designs of Double-Pass Curved Solar Air Heaters[J]. Renewable Energy, 2020, 160: 1105-1118.
[14] JI Chen-zhen, QIN Zhen, DUBEY S, et al. Simulation on PCM Melting Enhancement with Double-Fin Length Arrangements in a Rectangular Enclosure Induced by Natural Convection[J]. International Journal of Heat and Mass Transfer, 2018, 127: 255-265.
[15] YANG Xiao-hu, FENG Shang-sheng, ZHANG Qun-li, et al. The Role of Porous Metal Foam on the Unidirectional Solidification of Saturating Fluid for Cold Storage[J]. Applied Energy, 2017, 194: 508-521.
[16] SHAKER M Y, SULTAN A A, NEGIRY E, et al. Melting and Solidification Characteristics of Cylindrical Encapsulated Phase Change Materials[J]. The Journal of Energy Storage, 2021, 43(1): 103104.
Simulation Analysis of Heat Transfer Enhancement of Phase Change Materials with Multi-angle Fins
LUO Quan-quan1, LI Bao-guo1, ZHENG Shuang1, YUAN Cheng-hao2
(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China; 2. Hunan Cancer Hospital, Changsha 410013, China)
The work aims to propose a cylindrical phase change heat storage rod (PCM-rod) according to the encapsulation structures of phase change materials in solar thermal utilization and design multi-angle fins to accelerate the melting rate of phase change materials. The effects of different shapes of fins on the melting characteristics of the phase change material in the heat storage rod was analyzed by CFD simulation technology, and the melting time, temperature response rate and average heat transfer coefficient of each model phase change material were calculated.The calculation results under the heat flow boundary condition of 800 W/m2showed that it took 2 813 s to completely melt the phase change material in the PCM-rod without fins, and the Tra-45 model had the best performance among the 12 groups of fins designed. The melting time of the phase change material was shortened by 5.4% compared with the control without rib.The temperature distribution of the phase change material in the Tra-45 model was concentrated, and the maximum temperature increased by 6 °C. The temperature response rate of the Tra-45 model was increased by 5% compared with the control group, and the average heat transfer coefficient reached 9.97 W/(m2·K), which was 2.8% higher than that of the control group. After the trapezoidal 45° fins are added to the heat storage rod, the melting rate of the phase change material is accelerated, and the temperature distribution in the heat storage rod is uniform. At the same time, the temperature response rate of the phase change material is improved, and the average heat transfer coefficient is significantly increased, which can meet the needs of frequent heat charging/release of the phase change material.
regular shaped fins; enhanced heat transfer; phase change materials (PCM); simulation
TK512+.4
A
1001-3563(2023)01-0083-08
10.19554/j.cnki.1001-3563.2023.01.010
2022−03−25
上海市联盟计划(LM201826)
罗权权(1994—),男,博士生,主要研究方向为农产品加工,太阳能热利用。
李保国(1961—),男,教授,博导,主要研究方向为食品和农产品加工新技术。
责任编辑:曾钰婵
