基于元学习优化随机森林算法的区域经济预测

李佳颖，吴 迪

（1. 广州南洋理工职业学院 经济管理学院， 广州 510540； 2. 哈尔滨工程大学 计算机科学与技术学院， 哈尔滨 541004；3. 齐齐哈尔大学 计算机与控制工程学院， 黑龙江 齐齐哈尔 161006）

0 引 言

区域经济是国民经济结构中不可或缺的部分。由于产业结构、劳动力规模、改革水平等因素不同[1]，区域经济发展呈现较大差异。一般而言，通过对区域不同行业经济指标的预测及量化分析，可助力该区域针对产业行业发展情况制定相应的经济发展策略。实现区域经济多指标的准确预测，离不开预测算法的支持[2]。机器学习作为解决非线性复杂问题的常用方法，被广泛应用于经济预测研究，故基于机器学习技术的经济预测算法成为研究热点。吴峰等[3]将双流长短期记忆（Long short term memory，LSTM）算法应用于标普500 指数趋势预测，准确率较高，但仅完成了宏观经济的单指标预测，未能就其他经济指标的预测性能进行分析。高振斌等[4]采用支持向量回归（Support vector regression，SVR）算法进行区域经济预测，并借助最小二乘法遗传算法（Partial least squares genetic algorithm，PLS-GA）对SVR 进行优化，取得了较高的预测准确度。但PLS、SVR 等技术通常需要大量的计算，而引入GA 算法进行优化，又可能进一步增加计算复杂性，导致模型训练和优化耗时长，预测效率较低。相对于深度学习模型（如LSTM）和一些复杂的核方法（如SVR），随机森林算法的使用和调整更简便，其默认参数在处理各种问题时均表现良好，且可通过调整决策树参数进行优化。因此，本文将随机森林算法应用于区域经济多指标预测，并借助元学习算法对投票权重进行优化，以降低随机森林算法应对不同规模经济样本多指标预测的误差率。

1 元学习算法数学描述

元学习（Meta-Learning）算法是一种机器学习方法，旨在使机器学习模型能自动学习如何适应和泛化到新任务上。模型无关元学习（Model-Agnostic Meta-Learning，MAML）算法是元学习中的一种经典算法，其核心思想是通过优化模型的初始化参数，使模型能更快地适应新任务，并在少量样本的情况下也能取得较好的效果。MAML 具有通用性，在小样本学习、迁移学习和自适应学习等领域具有潜在的应用前景。

θi在上进行评估，则MAML 的目标函数为[6]

其中，ϕ 表示适用于所有任务的参数。

MAML 通过两个循环获得权重优化结果，令θi，0=θ，则第i 个任务的j 步内循环权重的更新方式为[7]

MAML 本质是通过寻找θ，发现适用于新任务的ϕ 值，对损失函数进行最大似然估计得[8]

根据式（8）求出θ，获得MAML 优化模型。

2 元学习优化随机森林算法的经济预测

2.1 随机森林算法描述

随机森林作为机器学习算法之一，在复杂问题预测研究中具备较强的适用性。下面对其数学方法进行描述。

设集合S 包含m 个类别Ci（i = 1，2，…，m），其中Ci类的样本个数为si，s 为样本总数，k 为样本的特征总数。

求解所有样本期望熵[10]，

再计算样本特征A 的期望熵[6]，

式中，k 是特征总数，sij表示类别i 第j 维特征，有

根据式（9）与（10），计算A 的熵增益[11]G（A），

接着计算熵增益率[12]G′（A），

由k 棵决策树h1（x），h2（x），…，hk（x）组成的随机森林中，特征X 和Y 的边缘函数为ma（X，Y）[13]，

其中，I（·）是转换函数[14]，Y 与N 为正负类别，avk（·）是均值计算函数。

2.2 区域经济预测指标

进行区域经济预测时，区域经济特征的有效提取对预测准确度影响较大。而影响区域经济发展的耦合指标较多，在分析前若不进行去耦合操作，势必提升预测复杂度，影响预测精度和效率。参阅多篇文献，并借助主成分分析法，提取区域经济预测指标如表1。

表1 区域经济预测指标

2.3 元学习优化随机森林算法的经济预测流程

随机森林的投票权重对其预测精度影响显著，若设置不当，将会影响区域经济预测精度。手动调整的方法缺点较多，因此考虑采用算法自动调整策略[15]。在投票权重数较少时，采用一般优化算法对其进行优化，因样本数量少，可能导致优化精度不理想。作为小样本分析的经典方法[16]，MAML 通过任务样本可以有效提高随机森林权重的优化精度。因此，在采用随机森林算法进行区域经济预测基础上，借助元学习算法降低经济指标预测误差，以增强随机森林算法的预测适用性，流程如图1 所示。

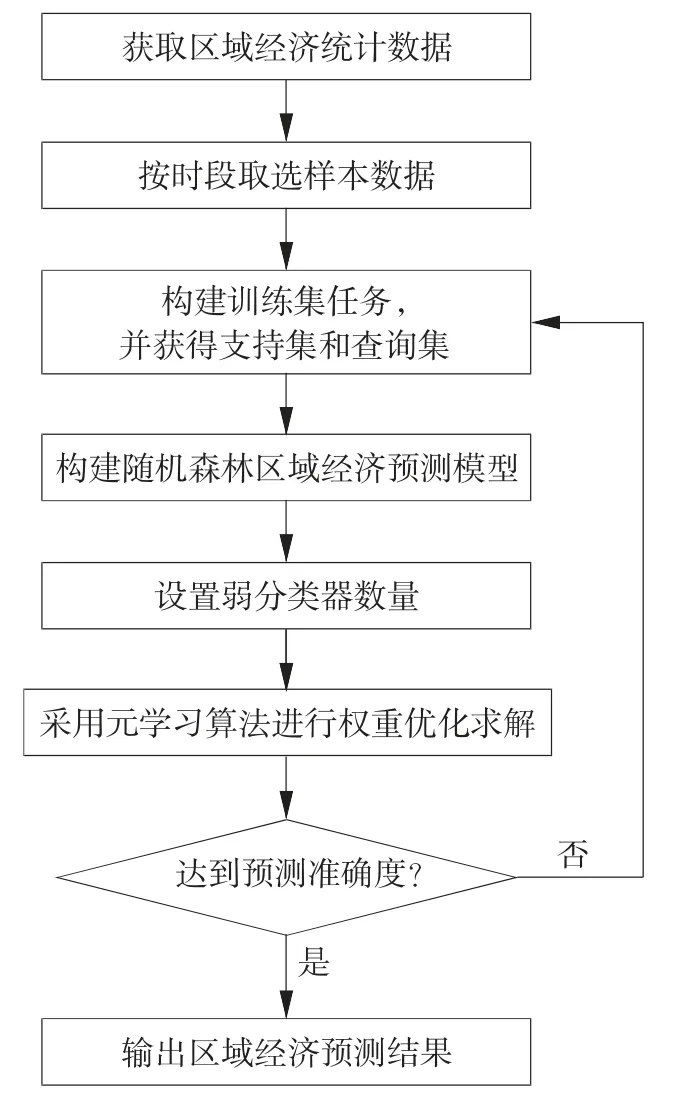
图1 元学习优化随机森林算法的区域经济预测流程

3 区域经济预测实例仿真

为验证元学习优化的随机森林算法在区域经济预测中的性能，选取某市5 个区2003—2022年的经济数据作为研究对象，进行区域经济预测，经济数据来源于该市统计年鉴。首先，分别采用随机森林算法和元学习优化随机森林算法对经济样本进行训练，绘制区域生产总值的训练拟合图并计算拟合误差，同时采用最优模型对2020—2022年该市的生产总值进行测试样本预测，并分析元学习对随机森林算法的经济预测结果带来的影响。接着采用随机森林算法和元学习优化随机森林算法分别对该市不同区的经济指标进行预测仿真，验证算法对小规模区域经济样本的预测性能。

3.1 不同经济指标的预测性能

3.1.1 生产总值预测

分别采用随机森林算法和元学习优化随机森林算法对2003—2019 年的该市所有区域生产总值进行训练仿真，结果如图2 所示。

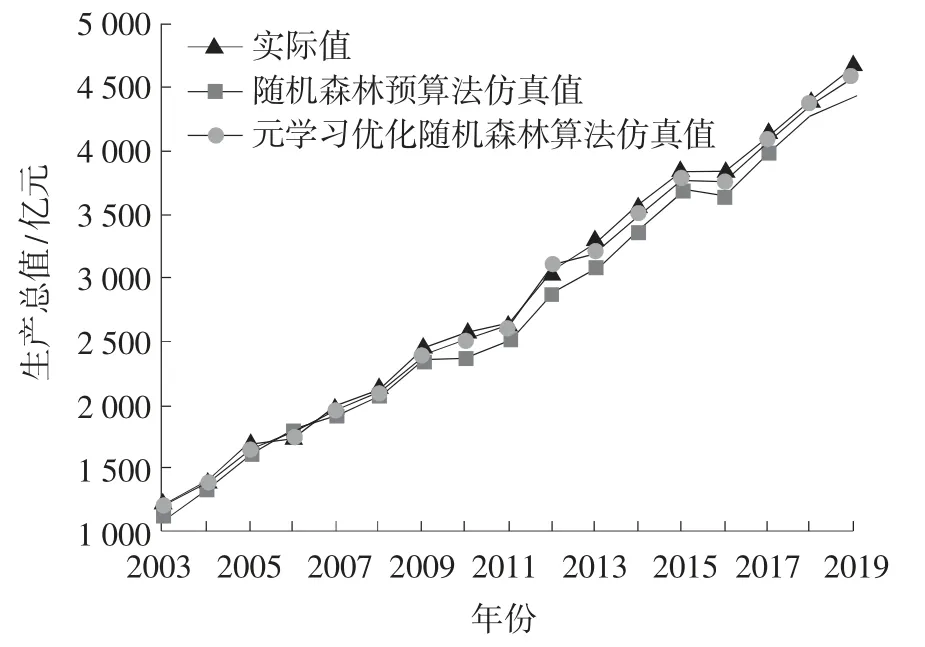
图2 区域生产总值预测结果

从图2 可知，将元学习优化随机森林算法用于该市2003—2019 年的区域生产总值训练，大部分年度的训练结果曲线与实际生产总值曲线重合度高；而随机森林算法仅在2004—2008 年的拟合度高，其他年份的训练结果均出现一定偏差，但整体偏差并不大。这表明随机森林算法在区域生产总值指标的预测性能方面具有较高适应性。

采用2003—2019 年训练得到的优化预测模型对2020—2022 年的测试样本进行生产总值预测，统计结果如表2、表3。

表2 随机森林算法对生产总值的预测

表3 元学习优化随机森林算法对生产总值的预测

对于实际生产总值指标预测，随机森林算法在2022 年的预测误差率最低，为5.08%，在2021 年的误差率最高，为6.79 %；而元学习优化随机森林算法在2021 年预测误差率最低，为2.18 %，在2022 年的误差率最高，为2.89%。元学习优化随机森林算法对2020—2022 年区域生产总值的预测误差率，相比随机森林算法分别下降了63.27%、67.89 %、43.11 %。两种算法对比结果表明，元学习优化随机森林算法表现出显著优势，随机森林投票权重经元学习优化后，求解精度显著提高。

3.1.2 月进口总额增长率预测

分别采用随机森林算法和元学习优化随机森林算法对该市2022 年度的月进口总额增长率进行预测，结果如图3 所示。

图3 2022 年度月进口总额增长率预测性能

由图3 可知，元学习优化随机森林算法的预测性能较好，仅在3 月和7 月出现较大偏差，其他月份预测准确度均较高；随机森林算法的预测效果欠佳，仅在2 月误差较小，其他月份误差较大，特别是4 月、6 月和9 月，偏离实际值较大；在9月，元学习优化随机森林算法的预测误差率较随机森林算法降低约86 %。

3.1.3 居民消费价格指数预测

分别采用随机森林算法和元学习优化随机森林算法对该市2022 年度12 个月的居民消费价格指数进行预测，结果如图4。由图4 可知，两种算法对该市2022 年度12 个月的消费价格指数预测结果均有一定偏差，但元学习优化的随机森林算法相较于随机森林算法，其预测结果的波动明显更小。

图4 2022 年度居民消费价格指数预测性能

3.2 不同区域的预测性能

为了进一步验证元学习优化的随机森林算法在不同区域的预测性能，分别对该市5 个区的主要经济指标进行预测仿真。选取2020—2022 年的生产总值和消费价格指数进行预测，结果如表4和表5。

表4 不同区域的生产总值预测结果

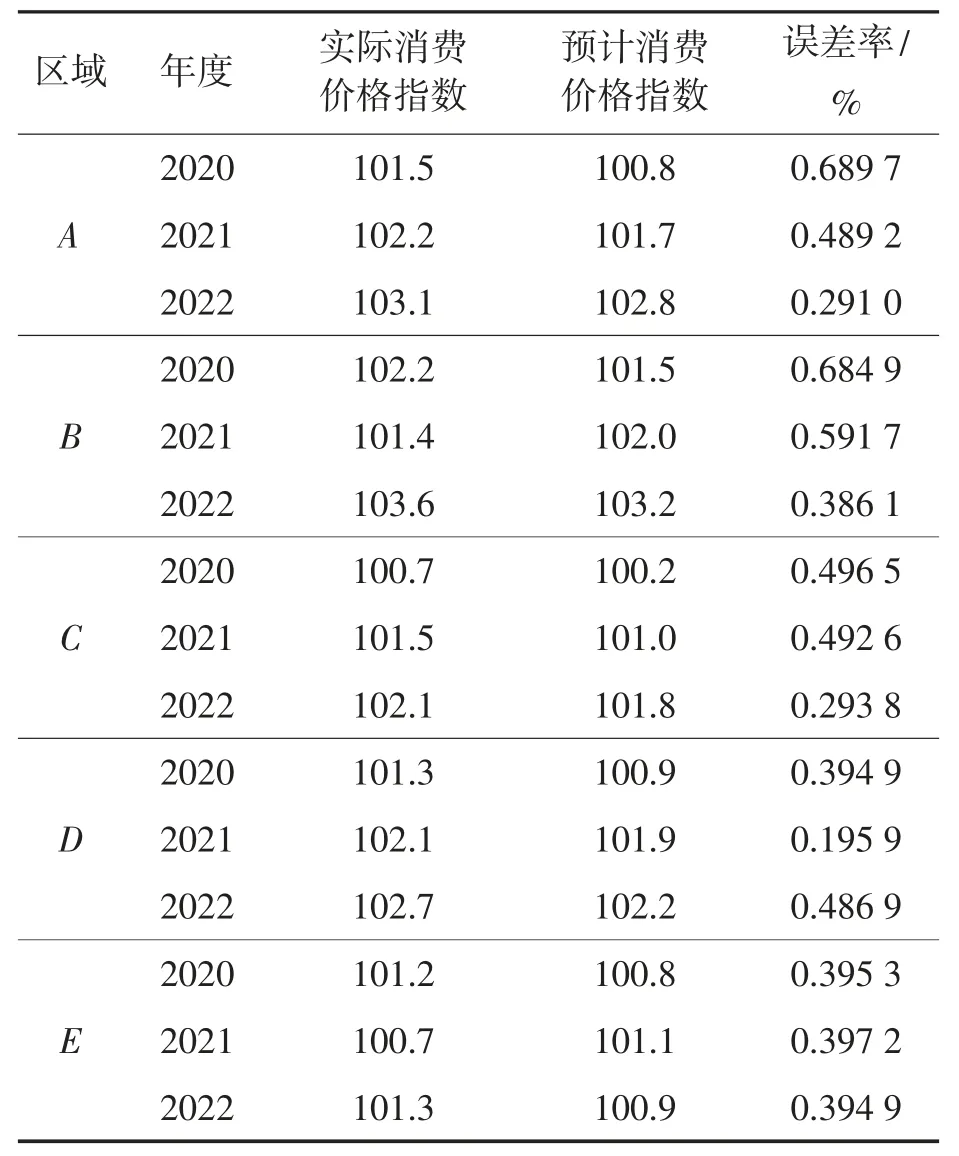
表5 不同区域的居民消费价格指数预测结果

从表4 知，对比该市5 个区的生产总值，元学习优化随机森林算法预测误差率均不高，其中2022 年度C 区的生产总值预测误差率最低，仅为0.061 54 %，最高的是2020 年度B 区预测误差率，为3.630 %。该市5 个区产业结构与经济发展特色均有较大差异，而元学习优化的随机森林算法在对这5 个差异较大的经济样本集预测时，均表现出较准确的预测结果，表明本文算法在微观样本的经济预测中仍表现出较稳定的预测性能。

表5 给出了元学习优化的随机森林算法对5个区的居民消费价格指数预测情况。其中，预测准确度最高的为D 区2021 年度消费价格指数，预测误差率仅为0.195 9 %，预测误差率最高的发生在2020 年度的A 区，其误差率为0.689 7 %。总体而言，本文算法对5 个区的消费价格指数预测准确度均较高。

4 结 语

将随机森林机器学习算法与元学习优化方法相结合，应用于区域经济常用指标预测，获得了较高的预测准确率。本文的应用仿真主要完成了对市和区的中等规模样本量的经济预测，取得了较好效果。后续将对本文算法应用于更大规模量的数据样本预测多个经济指标进行研究，验证算法预测性能，同时将更多的机器学习算法与元学习方法相结合，不断测试多种方法相结合的区域经济预测性能，找到适合不同规模样本的经济预测算法，以增强机器学习算法在区域经济预测中的适用性。