基于网格化处理与遍历搜索算法的多波束测深模型
2023-02-02孙德俊邓宇航朱苏茜
孙德俊,邓宇航,朱苏茜
(南京邮电大学 通信与信息工程学院, 南京 210023)
多波束测深系统是在单波束测深系统基础上发展起来的,该系统在与航迹垂直的平面内一次能发射出数十个乃至上百个波束,再由换能器接收海底返回的声波。传统的单波束测深系统只能获得测量船垂直下方一个海底深度测量值。多波束测深克服了单波束测深的缺点,在海底平坦的海域内,能测量出以测量船测线为轴线且具有一定宽度的全覆盖水深条带。本文基于多波束测深覆盖宽度模型,对不同情况下多波束测深覆盖宽度及测线总长度进行研究。
1 问题一模型的建立与求解
问题一[1]设定为二维平面背景,与测线方向垂直的平面和海底坡面的交线构成一条与水平面夹角为a 的斜线。运用几何知识确定海水深度及覆盖宽度,计算在海底地形不平坦情况下相邻条带的重叠率,建立多波束测深的覆盖宽度及相邻条带之间重叠率的数学模型。
1.1 确定海水深度
在与测线方向垂直的平面中,以海域中心为原点,以远离坡角方向为正方向,建立一维数轴,单位长度为l0。测线距中心点处的距离为[n1l0,nIl0],ni中i 表示测线编号,i={1,2,3,…,I},I=9。设定海域中心处的测线编号为j,则海域中心处海水深度为Dj,通过测线距中心处的距离可推算该测线处海水深度为
其中,xi为第i 根测线与海域中心测线的距离,α为海面坡度。
1.2 确定覆盖宽度
运用正弦定理计算多波束覆盖宽度,可得
其中,Wi,1、Wi,2分别为第i 根测线处靠近坡角与远离坡角部分的覆盖宽度,θ 为多波束换能器的开角。Wi是第i 根测线多波束产生的总覆盖宽度,为Wi,1与Wi,2之和。
1.3 相邻条带重叠率
相邻条带间的重叠情况如图1 所示。当海底地形不平坦时,第i 根测线与前一根测线覆盖条带在海底坡面上投影的长度为

图1 相邻条带重叠示意
第i 根测线与前一根测线条带的重叠率为
当ηi<0 时,表示漏测。
1.4 问题一模型的求解
已知多波束换能器的开角θ=120°,坡度α=1.5°,海域中心点处海水深度Dj=70 m。测线距中心点处的距离为[-800,800],单位长度为200 m,海域中心处的测线编号为5。利用模型可求解出结果如表1。

表1 问题一模型求解结果
2 问题二模型的建立与求解
问题二设定为三维立体海域背景,测线方向与海底坡面法向量在水平面上投影的夹角为β。建立合适的三维坐标系以表示测量船坐标及测量船在海底坡面上投影点的坐标。根据点法式,由坡面法向量和坡面上一点确定坡面方程,并由坡面与多波束平面相交得到覆盖线的方向向量,进而计算覆盖线与水平面的夹角,最终基于问题一的模型求解多波束覆盖宽度的数学模型。
2.1 确定测量船的坐标
以海域中心点垂直向下与海底坡面的交点为原点,坡面法向量在水平投影方向为x 轴正方向,以垂直于x 轴、水平向右为y 轴正方向,以垂直于水平面、竖直向上为z 轴正方向,建立三维坐标系,如图2 所示。

图2 三维坐标系示意
测量船始终在海平面航行,海平面与海域中心竖直距离为D0,因此测量船z 轴坐标始终为D0。设定测量船距海域中心的距离为A,测线方向与海底坡面法向量在水平面上投影的夹角为β,根据测线方向分别在x、y 轴上的投影可得,测量船x、y 轴坐标分别为Acos β、Asin β。
测量船坐标为
2.2 计算坡面法向量坐标
2.3 计算测量船处的海水深度
海底坡面过点(0,0,0),同时坡面法向量为(1,0,cotα),根据平面的点法式方程[2],可求得坡面方程为
测量船在坡面上投影点的坐标为
由测量船投影点坐标可知,测量船处海水深度的计算公式为
2.4 计算测量船覆盖线与水平面的夹角
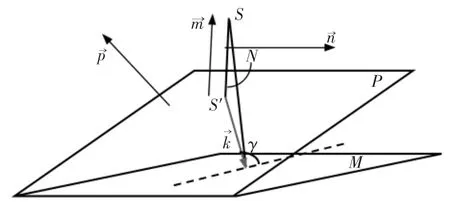
图3 测量船覆盖线示意
测量船发出多波束产生的覆盖线同时存在于坡面及多波束所在平面。图3 中表示多波束产生的覆盖线方向向量,有
通过坡面法向量和多波束所在平面法向量可以求得
计算得到覆盖线的方向向量为
将式(18)进行变换,得到夹角γ,
其中,γ∈[0,π/2]。
2.5 计算多波束覆盖宽度
基于问题一,可得到三维坐标系中覆盖宽度计算公式,
2.6 问题二模型的求解
若多波束换能器开角θ = 120°,坡度α =1.5°,海域中心点处的海水深度D0=120 m,以测量船距海域中心点处的距离为0.3 海里,测线方向与坡面法向量夹角β=0°时为例,求解多波束覆盖宽度。船与海域中心的距离A=0.3×1 852=555.6 m,测线方向与坡面法向量夹角β= 0°,由式(19)计算得到覆盖线与水平面夹角γ = 0°,由式(20)得多波束覆盖宽度W=466.09 m。同理可换算测量船其余位置距海域中心点处的距离,求解出各位置多波束测深的覆盖宽度,并进行可视化处理,结果如图4 所示。
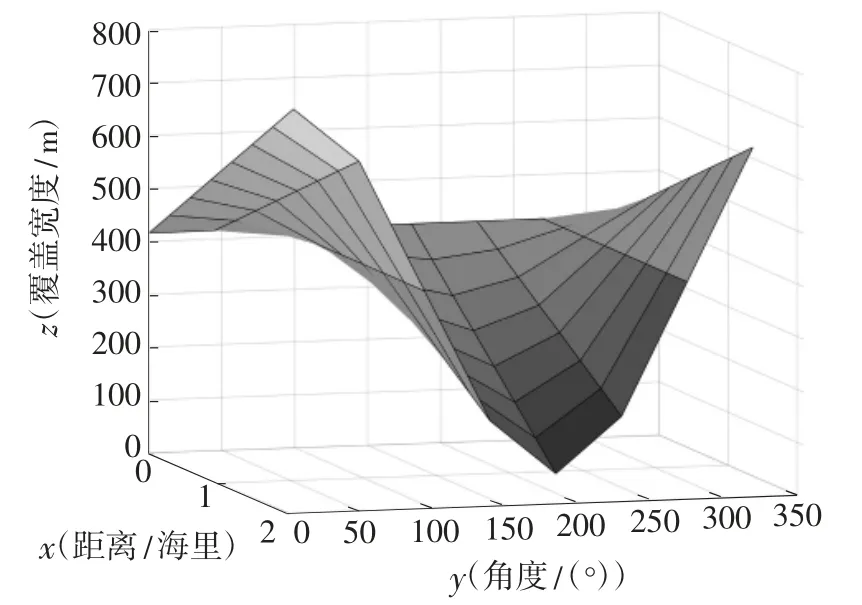
图4 覆盖宽度三维示意
3 问题三模型的建立与求解
问题三给定了一个限定边界的矩形待测海域,要求设计一组测量长度最短并满足约束条件的测线。首先将待测海域网格化,并分析不同行驶角度下测线的覆盖效率,再通过算法求解最短测线的总长度。
3.1 矩形海域网格化
将海域长度单位转换为米,矩形海域南北长3 704 m,东西宽7 408 m。将矩形海域网格化,如图5 所示。由西向东为x 轴正方向,由南向北为y轴正方向,建立矩形海域水平面坐标系。
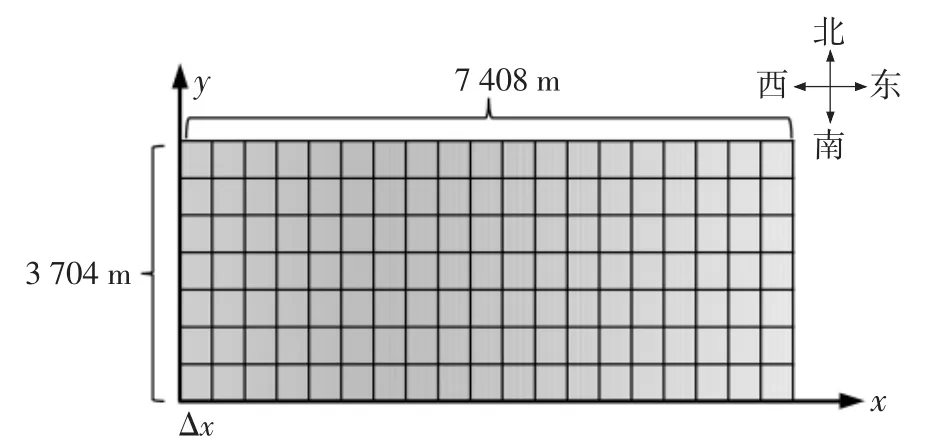
图5 矩形海域网格示意
3.2 确定测线运动方向
当测量船行驶一定距离时,通过多波束测量,可以形成覆盖线。这些覆盖线所围成的形状似梯形,其面积计算公式为
其中,S覆盖是行驶过程中测线所围成的面积,WA是测量船起始位置覆盖线长度,WB是测量船行驶距离r 后终止位置覆盖线长度,φ 是测线方向与坡面所形成的线面角。
测量船行驶相同的距离,覆盖面积越大,测量效率越高,测线覆盖效率ζ 定义如下:
覆盖线与水平面形成的线面γ 角计算公式为
测线在海底坡面投影线与水平面形成的线面角φ 计算公式为
联立式(20)—(24),并代入多波束开角θ =120°,则测线覆盖效率公式化简为
因海域坡面坡度不变,海域中心处海水深度稳定,故α 和D0为常值,测线覆盖效率仅与行驶角度即测线方向与海底坡面法向量在水平面上投影的夹角β 有关。测量船行驶角度与测线覆盖率函数关系曲线如图6 所示。
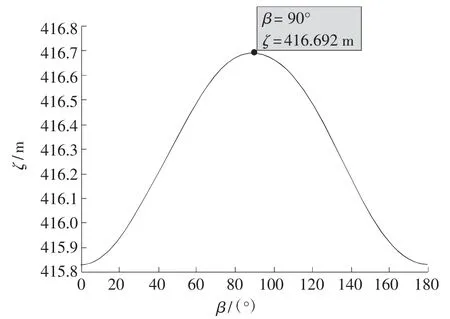
图6 测量船行驶角度与测线覆盖效率函数关系曲线
由图6 可知,当测量船行驶角度为90°时,航行相同的距离,测量船发出多波束所覆盖的面积最大,测线覆盖效率最高。
3.3 测线边界条件
第一根测线的边界条件为
其中,W1,1表示第1 根测线靠近坡角一侧产生的覆盖宽度;若W1,1<x1/cos α,表明最靠近坡角的测线无法覆盖坡角所在边,产生漏测。
其余测线边界条件为:多波束第i 根测线覆盖条带与第i-1 根测线覆盖条带的重叠率为
综合考虑测量效率及覆盖度,测线产生覆盖条带重叠率应为10 %~20 %,即0.1≤ηi≤0.2。
最后一根测线的边界条件为
其中,WI,2表示第I 根测线(最后一根测线)远离坡角一侧产生的覆盖宽度;若WI,2<(7 408-xI)/cosα,表明最远离坡角的测线无法覆盖坡角所在边,产生漏测。
综上,针对问题三的矩形海域建立测线规划数学模型如下:
3.4 最佳测线间距离求解
根据模型建立结果,测线规划为南北向直线即β=90°时,矩形海域测线覆盖效率最高。根据上述模型的边界条件,可采用遍历搜索法求解测线间距。测线布设求解结果如图7 所示。
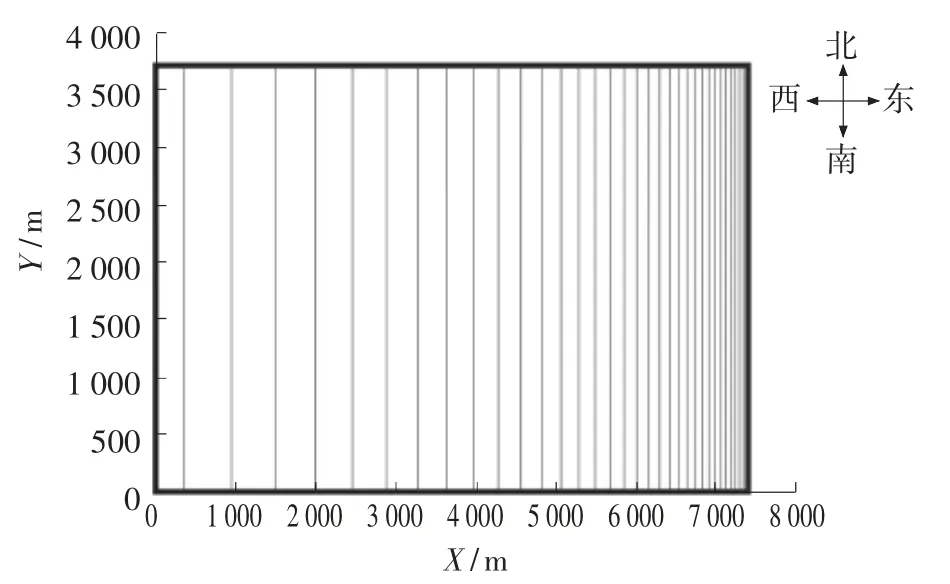
图7 问题3 测线布设求解结果
由西到东,海水深度逐渐变小。由图7 可知,自西向东测线之间的间距逐渐减小,测线越来越密集,同时测线间距下降幅度也逐渐减小。
行驶角度为90°时,共有34 条测线,则总测线长度为L=34×3 704=125 936 m。
4 问题四模型的建立与求解
根据问题三的结论,当测线与等深线平行时,测线覆盖效率最高。因此,针对该题尽量沿着与等深线平行方向研究并设计测线分布方案。
4.1 克里格插值法补充缺失数据
由于在同一海域中,海水深度具有较强的空间自相关性,因此采用克里格插值法[3]对缺失数据进行补充,原理见图8。
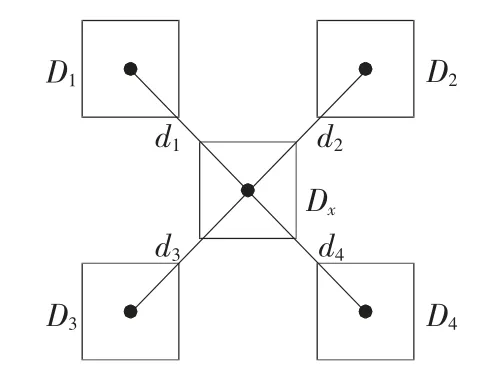
图8 插值补充缺失数据示意
缺失数据计算公式为
式中,Dx为所求点的海水深度,D1—D4分别为距离所求点最近的已知深度数据,d1—d4为已知点到所求点的距离。
4.2 分析矩形海域海底情况
图9 为海水深度的等深线。图9 显示,该海域西南部分地势较高,东南部分地势较低,海域西南至东北方向呈U 型,东南部分的等深线近似平行。

图9 海水深度等深线
考虑测量效率,测线的方向宜平行于等深线的方向[4]。对于该海域依照等深线分布划分区域,分别讨论划分区域的测线布设,具体布设如图10所示。以西南至东北方向的连线作为分界线,为简化问题,等深线为U 型时,测线为相互垂直的两条直线。当测线扫描完东北角后,测线布设为相互平行的直线。

图10 测线布设示意
基于问题三的模型,当β=90°且测线靠近矩形海域边缘时,采用遍历搜索得到起始测线的横轴坐标为41 m。
4.3 起始测线布设多目标规划模型建立
目标函数为:
1)测线扫描所形成的条带尽量覆盖整个待测海域,即漏测区域面积S漏尽可能小;
2)测量船扫过面积S覆盖最大;
3)测线尽量沿着海域等深线布设。
约束条件为:
1)起始测线的起点在x 轴上;
3)测线重叠率η 尽量不超过20 %。
综上,建立研究海域起始测线布设多目标规划模型为:
其中,Δd 表示移动前后海水深度的变化,Δr 表示测量船行驶的单位距离。
4.4 网格化求解覆盖宽度
由于海水深度不规律,需要网格化求解覆盖宽度,几何关系如图11 所示。

图11 网格化求解的几何关系示意
设船在测线上某一位置的坐标为(x,y),测线行驶角度为β,定义网格大小为Δx,则在多波束上一点的坐标为(xk,yk),
根据克里格插值法,可得某一坐标的海水深度为D(x,y)。设多波束开角θ=120°,当多波束上一点的坐标满足
即该点刚好落在海底面上,则船在该坐标点的覆盖宽度为
4.5 问题四模型求解
测线布设如图12 所示,其中黑实线为测线航迹,虚线下方为漏测宽度,上方为可覆盖宽度。由图12 可知,漏测面积近似为三角形面积。

图12 问题四测线布设
1)测线最佳偏移角度求解
根据上述测线布设方案,建立多目标规划模型,计算测线偏移不同角度时的单位海洋深度差来衡量测线布设与海洋等深线的契合度。当起始位置为(41,0),测线与x 轴偏移角度为74°时,单位距离的海洋深度差最小,即与海洋等深线最接近。
2)测线间距求解
在得到最佳起始位置和偏移角度后,为使总测线长度最小,各测线在满足重叠率的要求下,要使测线间距最大。沿用问题三的求解模型,设定搜索步长为Δl=5 m。
将得到的测线间距带入网格化处理模型,可计算得相关指标结果如表2。
由表2 可知,重叠率超过20 %的测线长度占比较高,而漏测海区占待测海域总面积的比例较低。
