宏观交通流模型的自适应迭代学习辨识策略

仇江辰，闫 飞，田建艳

(太原理工大学 电气与动力工程学院，太原 030024)

城市交通系统作为现代生活的重要组成部分，其运行状况直接影响居民的生活水平，采用先进的信号控制策略是缓解交通拥堵最有效的解决方法[1]，我国大部分城市采用基于数学模型的SCOOT自适应控制系统[2]，而许多智能控制理论也相继应用于交通领域，如文献[3]利用线性二次型调节器实现路网的边界反馈控制；文献[4-5]利用迭代学习控制策略实现路网的流量均衡控制；文献[6]针对大规模路网提出具有分层结构的模型预测控制策略；文献[7]将显示模型预测控制方法应用于交通信号控制领域。目前，常见的信号控制策略大多基于交通流模型进行配时，其控制效果取决于模型的质量和准确性。

交通信号控制系统的模型大多为基于流体力学理论的宏观模型，其主要围绕交通流量、密度和车辆速度之间的数学关系，用连续变量来构造交通流中的车辆综合行为[8]。为了提高控制策略的有效性，我们需要建立一个能准确描述城市路网交通流稳态和动态特性的数学模型，并对模型中的相关参数进行辨识。目前，已有不少学者对交通流模型的参数辨识问题展开研究，如文献[9]采用离散显式有限差分方程对高速公路一阶宏观交通流模型的参数进行估计；考虑到交通流系统具有很大的随机性，文献[10]利用Monte Carlo方法对宏观基本图中的随机变量进行一般化处理；文献[11]分别利用Nelder-Mead算法、随机遗传算法、随机交叉熵算法对特定高速公路的Metanet模型进行参数估计；文献[12-13]结合期望最大化算法、随机逼近算法和在线实时自估计算法对路网交叉口的转向比、饱和流量及自由流速等参数进行辨识；文献[14]利用马尔科夫链对交叉口不同状态下的交通流进行控制，采用期望最大化算法实现模型的参数估计。

上述有关参数辨识的研究成果，大多忽略了交通流系统的重复性特征，即在不同天的同一时刻具有相似的交通流状态[15]。在控制理论研究领域中，通常采用迭代学习控制解决具有重复特性的受控系统。迭代学习辨识是迭代学习控制理论的重要组成部分之一，其目的在于解决有限时间区间内重复运行系统的参数辨识问题，根据量测获取的系统输出，利用迭代学习辨识算法通过不断地更新模型参数使得系统输出逼近理想值，实现时变参数的辨识[16]。文献[17]针对高速公路宏观交通流模型，提出了一种基于离散化非线性模型的迭代学习辨识策略。但在城市路网交通流方面，尚未见报道。

本文在交通流存储转发模型的基础上，根据“速密流”三者间的车辆动态关系，提出了一种离散化的非线性宏观交通流模型。考虑到交通流系统具有很强的时变性和随机性，且从宏观角度出发具有明显的周期性。因此，设计了一种自适应迭代学习辨识策略，通过在有限时间区间内，辨识出交通流模型的时变参数，进一步提高城市路网交通信号控制系统的控制效果。

1 非线性宏观交通流模型

1.1 模型建立

本文采用的交通流模型是由Gazis等提出的“存储转发”模型，该模型利用采样周期内的平均车流量代替实际路段的车流量，避免了因信号灯转化导致的计算量过大问题。但由于城市路网交通流具有很强的非线性特征，采用存储转发模型无法描述其复杂的随机动态特性，因此引入文献[18]提出的排队车辆动态到达方程。将存储转发模型与排队车辆动态模型相结合，提出了一种非线性宏观交通流模型，具体建模过程如下：

假设城市路网交叉口间的车辆运行情况如图1所示，根据路网车辆数守恒原则，路段I0,1在第k个采样时刻的车辆数xI0,1(k)的空间及时间离散化模型可用下式描述：

(1)

图1 宏观交通流模型与相位图Fig.1 Macroscopic traffic flow model and phase diagram

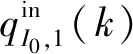
(2)

式中：II0代表驶入交叉口I0的所有支路段集合；PI0代表交叉口I0的相位方案集合；tLI0,i,I0,1代表车辆由上游路段LI0,i经交叉口I0驶入路段I0,1的转向比；sL0,i代表驶入交叉口I0的上游各路段车辆饱和流率，pcu/h；gI0,j(k)代表交叉口I0的各相位绿灯时长，s；TI0代表交叉口I0的信号周期时长，s；ΔT代表采样周期时长，s.

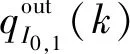
(3)

式中：OI1代表驶离交叉口I1的所有支路段集合；PI1代表交叉口I1的相位方案集合；tI0,1,LI1,j代表车辆由上游路段I0,1经交叉口I1驶入LI1,i各路段的转向比；sI0,1代表路段I0,1的车辆饱和流率，pcu/h；gI1,j(k)代表交叉口I1的各相位绿灯时长，s；TI1代表交叉口I1的信号周期时长，s.

城市路网宏观交通流模型的非线性动态特征，可通过交通流密度、速度及流量间的关系式进行表达，路段I0,1在第k个采样时刻的排队队列车辆数yI0,1(k)的空间及时间离散化模型可用下式描述：

(4)

(5)

(6)

(7)

(8)

从流体力学角度考虑，速度与密度间还存在着进一步的相互关系，当道路车辆增多，车流密度增大时，驾驶员被迫降速；而车流密度由大变小时，车速又会增加。因此，车辆从路段I0,1上游到路段I0,1排队队列末端的平均速度vI0,1(k)取决于其对应路段的密度值，具体的速密关系式如下：

(9)

(10)

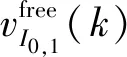
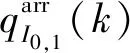
(11)

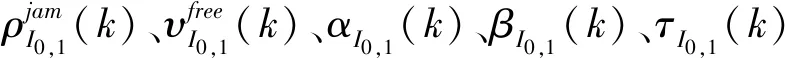
整理式(1)-式(5)和式(11)可得，在第k个采样时刻路段I0,1的累积车辆数xI0,1(k)和动态排队车辆数yI0,1(k)具有如下关系：

(12)

(13)

由于

(14)

(15)

定义

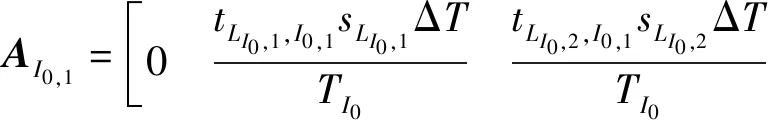
(16)

根据式(16)可将式(12)和式(13)重新写为状态方程：

xI0,1(k+1)=xI0,1(k)+AI0,1uI0,1(k)+dI0,1(k) .

(17)

yI0,1(k+1)=yI0,1(k)+f(xI0,1(k),yI0,1(k),
θI0,1(k))+BI0,1uI0,1(k) .

(18)

1.2 模型的状态空间表达

根据以上描述，可将任意拓扑结构和规模大小的城市路网，列写为状态空间方程[式(17)、式(18)]：

(19)

式中：n代表整个路网的路段总数；x(k)=[x1(k),x2(k),…,xn(k)]T为状态向量，xi(k)代表在第k个采样时刻路网中各路段的车辆数；y(k)=[y1(k),y2(k),…,yn(k)]T为输出向量，yi(k)代表在第k个采样时刻路网中各路段的排队车辆数；u(k)=[u1(k),u2(k),…,un(k)]T为控制向量，ui(k)代表在第k个采样时刻路网中各路段的相位绿灯时长；d(k)=[d1(k),d2(k),…,dn(k)]T为状态扰动向量，将路网在第k个采样时刻受到的外部扰动因素用车辆数形式表达，具体指：1) 交通事故，因偶发性交通事故导致某路段的通行能力在短时间内急剧下降；2) 乱穿马路，因行人或非机动车乱穿马路导致路段内车辆产生非正常的减速行为，降低路网的通行能力；3) 停车场出入，因商场、住宅小区和停车场等区域缺少车辆信息检测装置，导致车流量信息不充分，对路网造成额外的负载；状态矩阵A和传递矩阵B为定常矩阵，由路网中各交叉口的相位方案、周期时长、采样时长、饱和流率及转向率等因素决定。

2 自适应迭代学习辨识策略及收敛性分析

2.1 辨识器设计

为了提高迭代学习辨识算法的抗干扰性和收敛速度，本文将去伪控制概念引入其中，提出一种自适应迭代学习辨识算法，其结构示意如图2所示。

图2 自适应迭代学习辨识结构示意图Fig.2 Structure chart of adaptive ILI

去伪控制是一种数据驱动类型算法，利用当前迭代批次的实时输入输出数据和上一批次的历史数据对迭代学习律的增益进行适当调整。

为了便于自适应迭代学习的收敛性证明，本文做如下定义：

定义‖·‖为1范数，即对于矩阵Am×n而言，均满足如下关系：

其中，ai,j代表矩阵Am×n的任意元素。

定义向量θn(k)的λ范数为：

其中，λ>0，α>1.

定义第n次迭代学习辨识的系统输出误差en(k)=yd(k)-yn(k)，第n次迭代学习辨识的状态误差Δxn(k)=xd(k)-xn(k)，第n次迭代学习辨识的参数误差Δθn(k)=θd(k)-θn(k).

定义向量值函数f(·,·,·)的偏导数为：

考虑到交通运行的实际情况，θn(k)应满足一定的约束条件，即θn(k)∈[θmin(k),θmax(k)]，其中，θmin(k),θmax(k)分别为参数的最小值和最大值，定义sat[θn(k)]为参数θn(k)的饱和函数，即：

因此，为了证明参数在受限条件下，迭代学习辨识算法仍具有收敛性，宏观交通流模型的时变多参数迭代学习辨识算法构造如下：

θn+1(k)=sat[θn(k)]+ηn(k)en(k+1) .

(20)

为证明受限情况下的收敛性问题，此处还需介绍一个重要引理。

引理1

‖θd(k)-sat[θn(k)]‖≤‖θd(k)
-θn(k)‖ .

(21)

证明过程参见文献[19].

定义去伪控制在第n次迭代时的虚拟参考为：

(22)

去伪控制的代价函数如下所示：

(23)

式中，w为正常数，用于调整函数的严格程度。

控制器的切换条件为：

Jn(k)≤Q.

(24)

式中，Q是通过实验获得的先验值。

定义去伪控制的备选迭代学习律增益集合为：

η={η1,η2,…,ηm} .

(25)

去伪算法通过遍历所有的学习律增益，计算去伪代价函数，根据最小化原则，在符合条件的增益集合中选择最小的学习增益作为下一次迭代过程的学习律增益：

ηs={ηi|Jn(ηi)≤0},ηn+1=min(ηs) .

(26)

将上述定义整理可以得到自适应迭代学习辨识算法的数学表达：

θn+1(k)=sat[θn(k)]+ηn(k)en(k+1) ,
en(k)=yd(k)-yn(k) ,
ηs={ηi|Jn(ηi)≤0} ,
ηn+1=min(ηs) .

(27)

2.2 基本假设

假设1 向量值函数f(·,·,·)关于其所有的自变量均满足全局一致的Lipshitz条件，即：

‖f(xn(k),yn(k),θn(k))-f(xn-1(k),yn-1(k),
θn-1(k))‖≤gfx‖xn(k)-xn-1(k)‖+gfy‖
yn(k)-yn-1(k)‖+gfθ‖θn(k)-θn-1(k)‖ .

(28)

其中，gfx,gfy,gfθ分别为Lipschitz常量。

假设2 当给定路网相位绿灯时长u(k)(k∈[0,K])，且系统初态位于xd(0)时，可获得量测数据yd(k)(k∈[0,K])，并将其相应的状态轨迹记为xd(k)(k∈[0,K])，则一定存在一组参数θd(k)(k∈[0,K])满足下列条件：

(29)

假设3 在迭代过程中系统满足严格重复的初始化条件，即：

xn(0)=xd(0),yn(0)=yd(0)∀n.

(30)

其中，xd(0),yd(0)分别代表系统期望状态和期望轨迹的初始值，n代表系统的迭代次数。

假设4 系统的状态扰动向量有界且为md，即：

‖dn(k)‖λ≤md.

(31)

假设5 在去伪控制的备选迭代学习律增益集合中，最大值ηmax保证迭代系统稳定，使第二次迭代辨识的误差范数小于第一次迭代的误差范数；最小值ηmin满足迭代学习辨识算法的收敛性条件：

‖e2(k)‖<‖e1(k)‖
‖I-ηmindθ‖<1 .

(32)

假设1中有关向量值函数f(·,·,·)的全局一致性Lipshitz条件可作如下解释，宏观交通流模型式(17)和式(18)在整个区间[0,K]内对所有变量均为连续可微的，在实际道路情况下，路段内的车辆数x(k)和排队车辆数y(k)不能无穷大，会受限于路段本身的承载能力，且区间[0,K]也是有限集合，因此满足假设1的条件。

假设2为参数可以辨识的合理假设，若不满足，则该问题不具有研究意义。

假设3是对系统做出的限制，要求系统的状态初值与期望值保持一致，但在实际情况中，并不要求它严格重复，可采用文献[20]提出的方法进行调整。

假设5是关于去伪控制的收敛性说明，若不满足则系统的收敛性不能得到保证。具体情况如下：

在首次迭代过程中，系统的输出误差非常大，满足式(23)的学习律增益为ηmax，根据式(27)可知，η2≤ηmax.随着迭代的不断进行，系统误差逐步降低：

(33)

根据式(23)可得：

(34)

2.3 收敛性证明

根据路网的状态空间方程式(19)和参数的受限条件定义，可将辨识模型描述为：

(35)

其中，εn(k)代表系统的输出量测噪声。

定理1 对于满足假设1-5且其输出量测噪声‖εn(k)‖λ≤mε的宏观交通流模型式(19)，采用自适应迭代学习辨识算法式(27)，若存在增益矩阵η使得式‖I-ηdθ‖<1成立，则系统输出误差e(k)在区间[0,K]内收敛于一个界内，即：

(36)

当系统输出量测噪声mε→0时，有：

(37)

证明

根据系统参数误差定义和迭代学习辨识算法式(27)可得

Δθn+1(k)=θd(k)-θn+1(k)=θd(k)-
sat[θn(k)]-ηn(k)en(k+1) .

(38)

根据系统误差定义、假设2和式(35)可得

en(k+1)=yd(k+1)-yn(k+1)=en(k)+dx
Δxn(k)+dyen(k)+dθ(θd(k)-
sat[θn(k)])-εn(k) .

(39)

将上式(38)和式(39)整理可得

Δθn+1(k)=θd(k)-sat[θn(k)]-ηn(k)en(k+1)=
(I-dθηn(k))(θd(k)-sat[θn(k)])-dxηn(k)
Δxn(k)-ηn(k)εn(k)-(1+dy)ηn(k)en(k) .

(40)

对式(40)两边同时取范数，并根据引理1可得

‖Δθn+1(k)‖≤‖I-dθηn(k)‖‖θd(k)-
sat[θn(k)]‖+dx‖ηn(k)‖‖Δxn(k)‖+
‖ηn(k)‖‖εn(k)‖+(1+dy)‖ηn(k)‖
‖en(k)‖≤‖I-dθηn(k)‖‖Δθn(k)‖+
dxδη‖Δxn(k)‖+δη‖εn(k)‖+(1+dy)δη
‖en(k)‖≤‖I-dθηn(k)‖‖Δθn(k)‖+δη
‖εn(k)‖+ω1(‖Δxn(k)‖+‖en(k)‖) .

(41)

对系统误差两边同时取范数，并根据假设1和引理1可得

‖en(k)‖=‖yd(k)-yn(k)‖≤‖en(k-1)‖+
gfx‖xd(k-1)-xn(k-1)‖+gfy‖yd(k-1)-
yn(k-1)‖+‖εn(k-1)‖+gfe‖θd(k-1)-
sat[θn(k-1)]‖≤(1+gfy)‖en(k-1)‖+gfx
‖Δxn(k-1)‖+gfθ‖Δθn(k-1)‖+
‖εn(k-1)‖ .

(42)

对状态误差两边同时取范数，并根据假设4可得

‖Δxn(k)‖=‖xd(k)-xn(k)‖≤
‖Δxn(k-1)‖+‖dn(k-1)‖ .

(43)

将上式(42)和式(43)整理可得

(44)

将上式(41)和式(44)整理可得

(45)

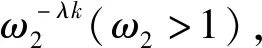
(46)

根据假设3可得，‖Δxn(0)‖+‖en(0)‖=0，因此式(46)右边第二项为零，式(46)右边第三项可化简为：

(47)

式(46)右边第四项可化简为：

(48)

式(46)右边第五项可化简为：

(49)

若存在足够大的λ，则式(47)、式(48)的值趋向于零，可将上式(46)-式(49)整理为：

(50)

其中，σ=max(‖I-dθηn(k)‖),ω=δηmε.

因此，当σ=‖I-dθη‖<1时，有

(51)

(52)

当系统输出量测噪声mε→0时，式(37)成立，证毕。

3 仿真研究

3.1 仿真参数设置

为了进一步验证基于城市路网非线性宏观交通流模型的时变多参数迭代学习辨识策略的有效性，本文选取太原市某区域路网(如图3所示)的部分道路作为仿真研究对象，通过VISSIM和MATLAB软件进行仿真实验。

图3 太原市某区域路网图Fig.3 A regional road network in Taiyuan City

通过实地调研采集该区域内的道路基本数据及各交叉口的现有信号配时方案，更进一步提高仿真实验的精确度。路网的道路结构拓扑图如图4所示，所研究的区域路网由12个交叉口和25条双向行车道组成(由于交叉口C、F和D、G间的距离太短，导致其路段多为不可变的进口道，故在本文中不做研究)，各交叉口处的转向率如表1所示(N，S，W，E分别代表不同方向的进口道)，路网各路段的基本情况均与实际情况相符，路段由进口道、交织区、行车道等3部分组成，各路段的车道数情况如表2所示，每条车道宽约3.5 m.

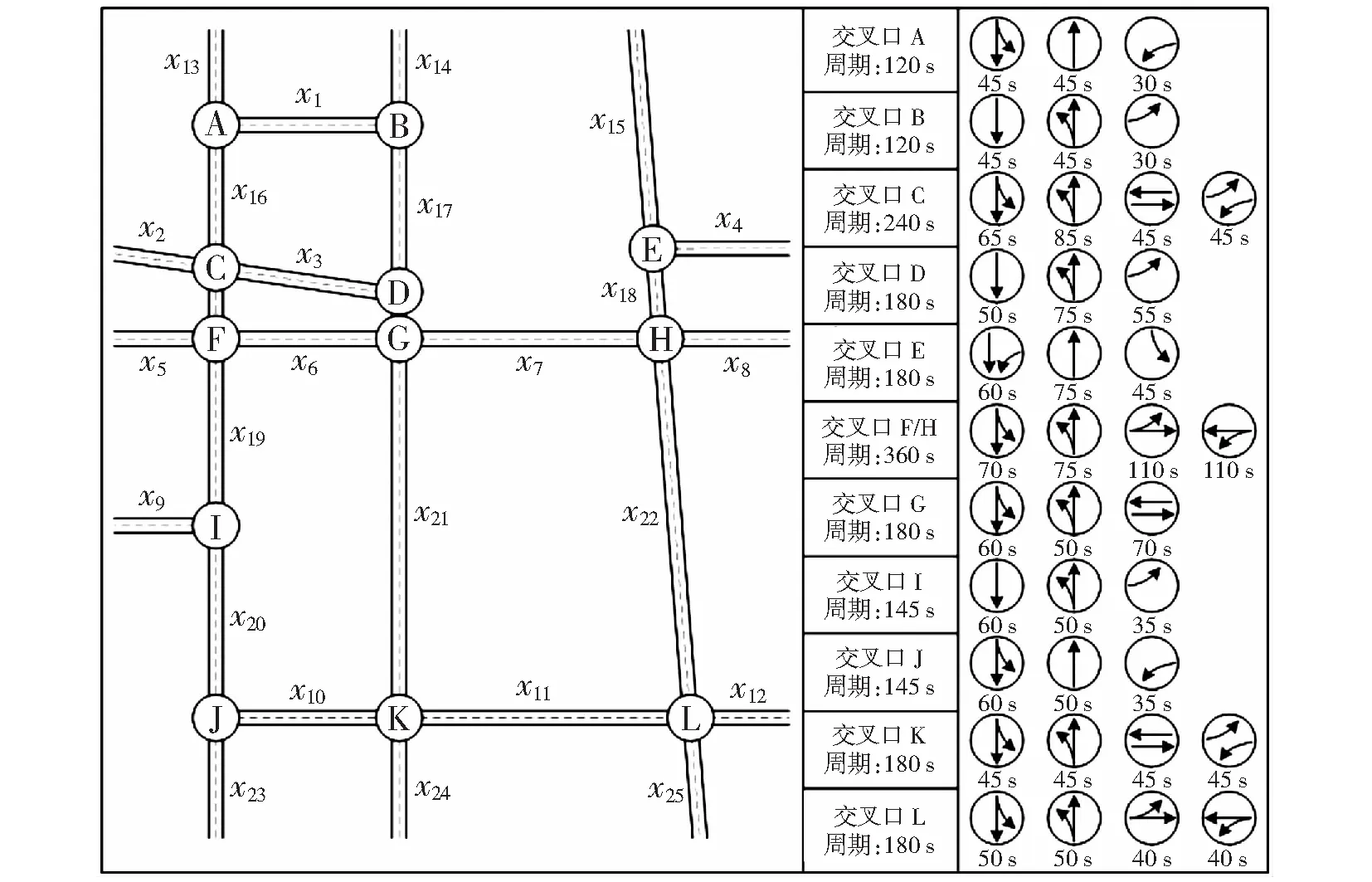
图4 路网道路结构拓扑图Fig.4 Road structure topology of the road network

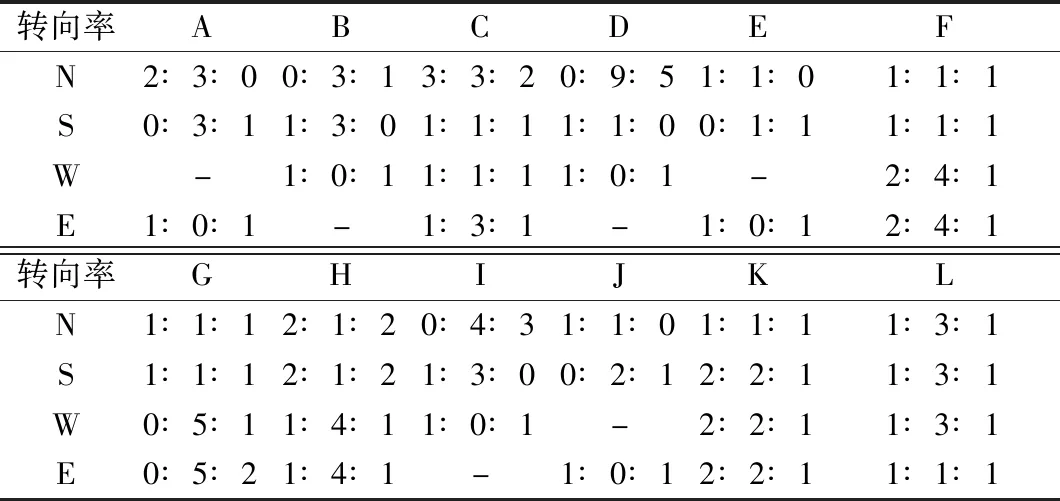
表1 各交叉口转向率(左转∶直行∶右转)Table 1 Turning ratio at each intersection (left-turn∶straight∶right-turn)

表2 各路段车道数Table 2 Number of lanes in each road

本文的研究对象为5:00-21:00的16 h日交通量，采样周期为5 min，迭代学习辨识的仿真迭代次数为25次，每次仿真时长16 h.根据城市道路工程设计规范(CJJ 37-2012)可估算出每条单向行驶车道的饱和流量，同时实际路段的饱和流量还会受到道路环境等诸多因素的影响，因此实际的路段饱和流量计算如下：

CD=C·W1·W2·W3·W4.

(53)

式中：CD代表路段的实际饱和流量；C代表不同车速下的理想饱和流量；W1代表自行车影响修正系数，本文机动车道与非机动车道间设有隔离带，故W1=1；W2代表车道宽度影响修正系数，本文车道宽度为3.5 m，故W2=1；W3代表车道数影响修正系数，2/3/4/7车道的修正系数分别为1.87/2.60/3.20/4.01；W4代表交叉口影响系数，计算如下：

(54)

式中：w0代表交叉口绿信比；l代表交叉口间距；w4最大值为1，x13,x14路段长度为450 m，x2,x4,x5,x8,x9,x12,x15,x23,x24,x25路段长度为600 m，最终计算出各路段的实际饱和流量如表3所示。根据百度智慧交通中的太原市日内15 min交通量均值指数设置路网的16 h仿真流量，具体如图5所示，其他仿真参数均采用VISSIM的缺省值。

表3 路段实际饱和流量Table 3 Actual saturation flow of each road section

图5 路网16 h输入车流量图Fig.5 The 16h input traffic flow of road network

在VISSIM软件中，利用人行横道功能对行人和非机动车乱穿马路行为进行模拟仿真；参考实际路网情况，在相应路段旁设置不同容量的停车位模拟商场、住宅和停车场出入情况；偶发性交通事故则通过在路段内设置停车位进行模拟。路网内三种扰动的具体参数如表4所示。

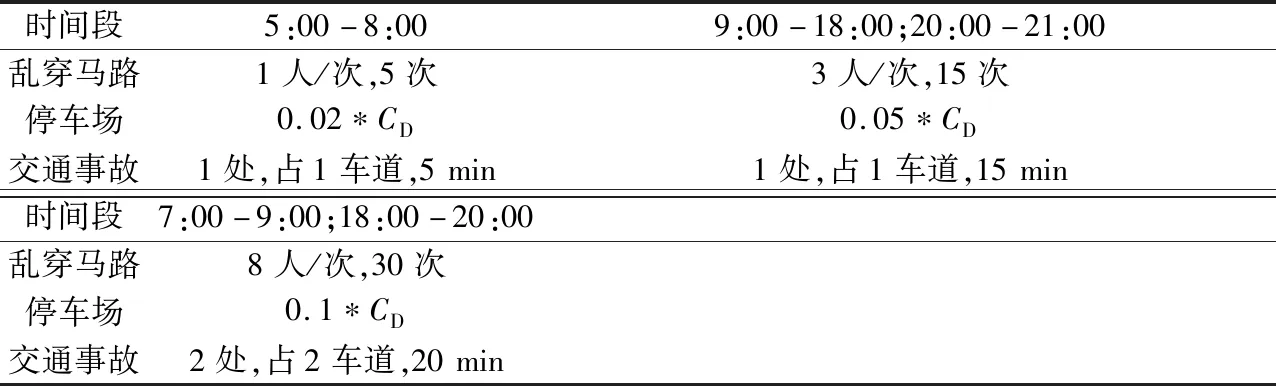
表4 三种扰动的具体情况(每小时)Table 4 Specifics of the three perturbations (per hour)

3.2 仿真结果分析

为了验证自适应迭代学习辨识策略的有效性，本文通过VISSIM和MATLAB软件获取交通流模型的待辨识参数，路网的排队车辆数、各路段的密度热力图以及车辆的平均延误和平均速度等指标进行效果评价，仿真结果如图6-图11所示。图6分别给出不同迭代次数下各路段排队车辆误差值的变化情况，可以看出：随着迭代次数的不断增加，路网内各路段的排队车辆误差值逐渐减小并趋于稳定。图7(a)反映了路网排队车辆误差最大值的整体迭代变化情况，图7(b)和7(c)分别对迭代过程中部分迭代次数和部分采样时段的误差值进行横向比较，更进一步反映迭代辨识策略的合理性。

非线性宏观交通流模型的参数辨识结果如图8所示，此处根据所研究路网的实际情况，分别选取车道数为2/3/4/7的4条路段x7,x11,x21,x22作为参考并给出其对应的参数辨识结果，时变参数分别为阻塞密度ρjam(k)，自由流速度vfree(k)，交通流模型特征参数α(k)、β(k)、τ(k).通过计算可以得到路网各路段的速度密度值，仿真实验与交通流模型的速密动态变化情况如图9所示，图9(a)和9(b)分别绘制了仿真实验和交通流模型的密度热力图，图9(c)为主干路x7的速密变化情况，可以看出虽然模型值与仿真值有所差异，但整体上符合交通流的真实变化情况。

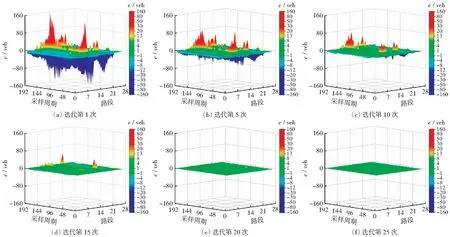
图6 不同迭代次数下各路段排队车辆误差值的变化情况Fig.6 Changes of the queuing vehicle error value of each road section under different iterations

图7 路网排队车辆误差最大值的变化情况Fig.7 Variation of the maximum value of the road network queuing vehicle error

图8 非线性宏观交通流模型的参数辨识结果Fig.8 Parameter identification results of the nonlinear macroscopic traffic flow model

图9 仿真实验与交通流模型的速密动态变化情况Fig.9 Dynamic changes of speed and density of the simulation experiment and traffic flow model

为了更进一步说明迭代学习辨识策略的有效性，本文通过采用3种不同的交通信号控制策略对太原市某区域路网进行对比分析，仿真时间为6:00-10:00，其余仿真参数保持不变，控制策略详情如下。

1) 固定配时：采用该区域路网的实际配时方案。

2) 模型预测控制：根据路网交通流的状态空间方程式(19)，可将其改写为非线性交通流模型：

y(k+1)=F(x(k),y(k),u(k)) .

(55)

其中，F(·)代表与f(·)相关的非线性函数，假定预测时域为Np则有：

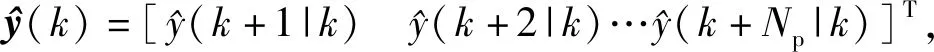
(56)

其中，符号^代表预测值，模型预测控制策略的优化目标函数为：

(57)

3) 时变参数的模型预测控制：将迭代学习策略辨识得到的时变参数代入到路网状态空间方程式(19)中，其余设置与方案2相同。

通过仿真获得3种控制策略下路网的车辆平均延误、平均车速及最大排队长度等指标如图10所示。可以看出：当采样周期为6:00-7:00和9:00-10:00时，3种控制策略的各项指标均无明显差异，主要原因是当交通流处于欠饱和状态时，固定配时方案已经能够取得较好的控制效果，模型预测控制方法没有明显优势；当采样周期为7:00-9:00时，采用时变参数的模型预测控制方法效果更佳，路网的车辆最大排队长度和平均延误均明显低于其他两种方案，路网的车辆平均速度明显优于其他两种方案，主要原因是当交通流处于过饱和状态时，模型预测控制方法能够根据路网的实际情况进行在线校正，从而提高路网的通行效率，且当模型的参数为时变时，其控制效果更好。图11的仿真结果为8:00时刻路网的拥堵情况，可以进一步看出，相比于其他两种控制方案时变参数模型预测控制方案能够更加有效地解决交通拥堵问题。

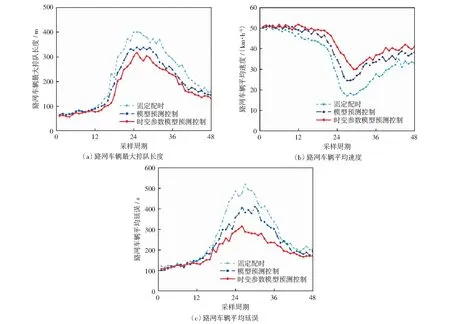
图10 三种控制策略下路网的性能指标Fig.10 Performance index of the road network under three control strategies

图11 三种控制策略下路网的拥堵情况Fig.11 Congestion of the road network under three control strategies

4 结论

本文针对城市路网交通流具有的随机性和时变性等特征，提出了一种含有未知时变多参数的非线性宏观交通流模型，并充分利用交通流系统所具有的重复性特征，设计了一种时变多参数的自适应迭代学习辨识策略，通过严格的数学理论推导证明了所提出算法的收敛性。最后，利用VISSIM软件对太原市某区域路网进行仿真，并通过路网的固定配时方案，模型预测控制方案和基于本文的时变参数模型预测控制方案进行对比实验。实验结果表明，基于去伪算法的迭代学习辨识策略能够在偶发性扰动的作用下有效地估计出非线性模型的时变参数，具有很好的自适应能力和抗干扰能力，为基于模型的信号控制系统提供有力的参数支撑，从而提高路网的通行效率，缓解交通拥堵现象。但本文所提出的交通流模型具有片面性，迭代学习辨识的初态问题仍需考虑，今后将重点展开有关此方面的模型辨识工作。