考虑风电功率预测误差分时补偿的电热联合系统多时间尺度调度

2023-02-02王晓静鲁盼盼李梦洁

电力系统自动化 2023年1期

韩丽，王晓静，鲁盼盼，李梦洁

（中国矿业大学电气学院，江苏省徐州市 221116）

0 引言

风电功率具有随机性和波动性，风电功率预测误差难以避免。热系统具有储放热能力，可以平移热负荷，通过削热峰填热谷参与热平衡来解耦热电联产（CHP）机组以热定电约束，提高风电消纳率。因此，如何利用热力系统应对风电不确定性，减小风电功率预测误差的影响是近年的研究热点。

现有研究常通过提高电力系统的灵活性来减小风电功率预测误差的不利影响［1-4］。文献［1］针对可再生能源出力不确定性对系统规划的影响，提出考虑风光不确定性的多目标规划方法。文献［2］考虑风电功率预测误差随预测时间的缩短而减小的特点，同时考虑需求响应对调度系统的影响，构建了多时间尺度调度模型。但是，上述模型仅改进了电力系统，将热力系统作为负荷参与调度，忽略了热力系统内部特性对整个模型的影响。

管网的储放热特性和供热区域的热惯性可以平抑风电功率预测误差，提高系统的风电消纳能力［5-13］。文献［5］分析了供热管网热损失、供热时滞性以及采暖用户热惯性对CHP 机组供热负荷的影响，构建了CHP 机组电功率灵活调节能力评估模型。文献［9］针对电、热能传输特性不同导致的电网与热网不协调的问题，提出一种考虑供热系统多重热惯性的电热联合协调优化策略。文献［10］提出了一种考虑不同能源站和不同供热调节模式下建筑物热惯性的优化调度方法并进行了验证。

目前，研究风电功率预测误差的文献中，或单独考虑了风电功率概率区间误差，或单独考虑了实时预测误差，并未同时考虑两种风电功率预测误差对系统的不利影响［14-17］。因此，本文在调度策略中同时考虑了风电功率的概率区间误差和实时预测误差。此外，由于风、热、电的时间特性差异较大，热力系统的储放热特性和热惯性对风电功率变化的响应速度不同，越接近热力系统末端，延迟越大，对电网调度指令的响应速度越慢，难以与风电功率同步。文献［18-24］虽然在调度中考虑了热力系统的储放热特性或热惯性，但忽略了利用热力系统补偿风电功率预测误差时响应时间不同步的问题。因此，需要分别研究供热区域热惯性和管网的储放热特性对电网调度指令的响应速度，并以此为依据在不同调度时段对风电功率预测误差进行分时补偿。

综上所述，本文为了解决利用热力系统补偿风电功率预测误差时响应时间不同步的问题，同时考虑两类误差评估方法，提出了一种考虑风电功率预测误差分时补偿的电热联合系统多时间尺度调度策略。该策略在日前阶段计及风电功率的概率区间误差，同时考虑供热区域热惯性，在保证用户温度需求的同时补偿概率区间误差；在实时阶段考虑实时预测误差，并通过管网储放热特性和储电装置对其进行补偿，最终建立了考虑风电功率预测误差分时补偿的电热联合系统多时间尺度调度模型。最后，通过算例仿真，验证了该模型的有效性。

1 风电功率预测误差及热网特性分析

1.1 风电功率预测误差

风电功率具有随机性和波动性，难以被准确预测。对风电功率的预测误差进行评估，在提供风电功率预测值的同时给出预测误差的大致范围，为电网调度策略提供参考值，是降低预测误差对电网供用电平衡冲击的有效途径。目前，风电功率预测误差的评估主要分为基于长期统计规律的概率区间误差评估［25］和基于实时信号特征值的实时预测误差评估［26］。

1）基于长期统计规律的概率区间误差评估

基于长期统计规律的概率区间误差评估方法首先统计拟合历史误差数据，然后假定预测误差服从某种形式的概率分布模型，常用高斯分布和t-location-scale 分布。

高斯分布的概率密度函数为：

式中：Γ(·)为Gamma 函数；μ2为位置参数；σ2为比例参数；v为形状参数。

某个风电场采用两种分布下的风电功率预测误差拟合结果如图1（a）所示。风电功率预测误差的概率分布与风机型式、季节、天气、预测方法等多种因素相关，需根据风电场本身历史数据的统计结果拟合而成。本文采用高斯分布函数，在实际使用中，也可以根据风电场实际情况采用其他分布函数。

根据选取的概率密度函数，选取指定置信水平下的置信区间上下限，即为预测误差的评估范围，与预测结果叠加可得到预测区间，如图1（b）所示。这种误差评估方法的准确性依赖历史数据的统计分析结果，一般需要几天甚至几个月的数据，评估需要的数据周期较长。而且由于反映的是长期的统计规律，误差评估区间较大。

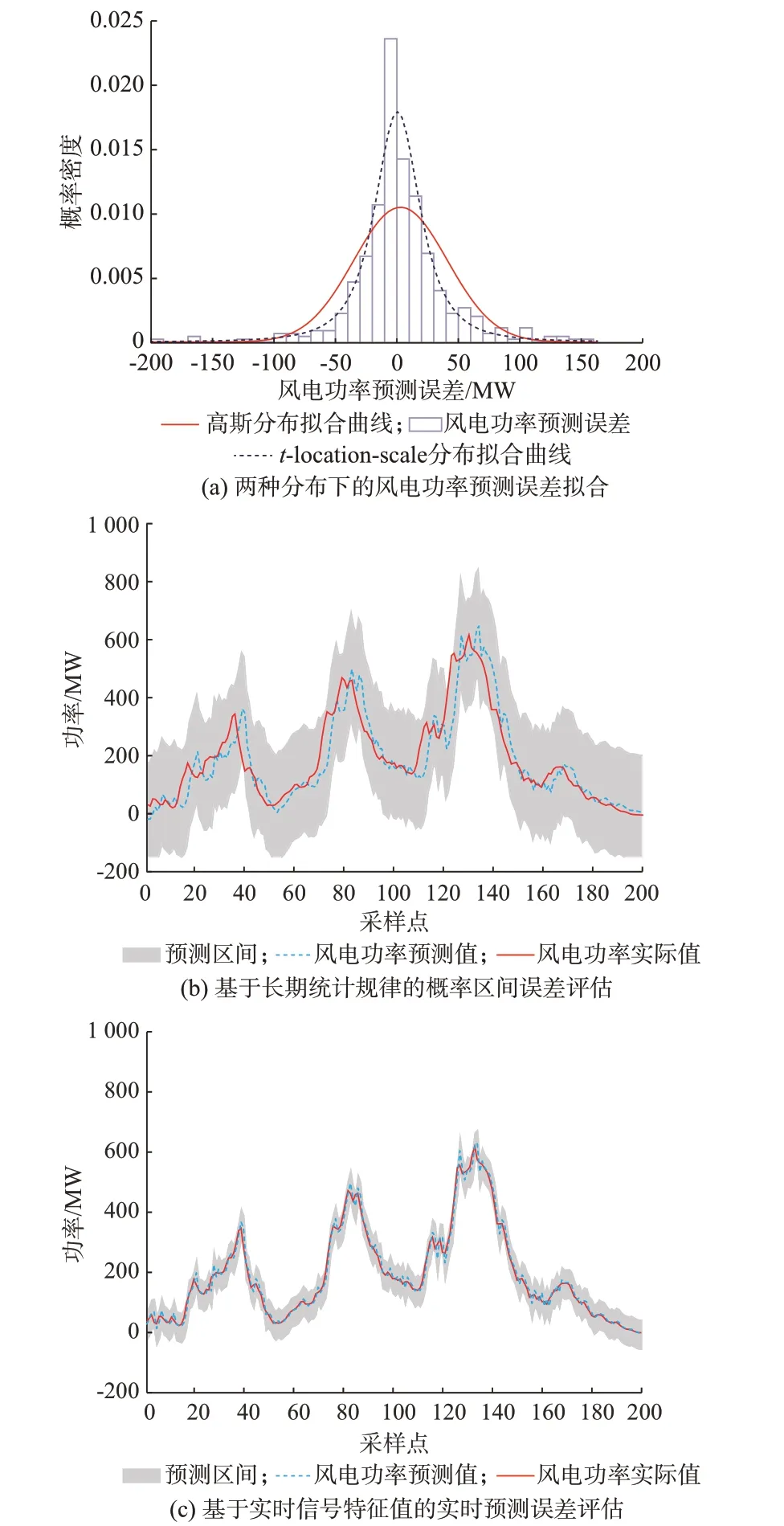
图1 风电功率预测误差评估Fig.1 Evaluation of wind power forecasting error

2）基于实时信号特征值的实时预测误差评估

对于时变性特别强的风电系统，统计意义上的误差评估很难反映风电的实时特性。基于实时信号特征值的实时预测误差评估方法通过分析风电功率信号与预测误差关系，提取预测误差特征值。

该误差评估方法以当前时刻前一段实时数据（多为一个或数个小时）为基础，风电功率预测误差的特征值提取方法有两种。第1 种是对这段数据进行计算，以这段数据的实际功率最大值和方差、预测功率的最大值和方差等为特征值［27-28］。第2 种是利用深度学习技术，如卷积神经网络［29］等，通过学习数据提取特征值，得到功率数据和预测误差的内部映射关系。以此特征值为基础，建立实时预测误差评估模型，得到预测误差范围，如图1（c）所示。

对比图1（b）和（c）可以发现，风电功率的实时预测误差评估方法由于考虑了预测误差的实时特征，得到的预测误差范围较小。但实时预测误差依赖于当前时刻之前的一段数据，只能提前数步得到。

综上，由于概率区间误差和实时预测误差的评估周期不同，需要在调度的不同时段分别对两种预测误差进行补偿。前者依赖历史数据，评估周期较长，因此在日前调度时段考虑；后者只能提前数步得到，评估周期较短，因此在实时调度时段考虑。

1.2 热网模型

由于管道长度、管网保温能力等因素的限制，热网具有衰减、延时及储放热特性，并会对热网模型产生一定的影响进而影响整个电热联合系统［6］。本文的热网模型考虑了热网的上述特性，同时采取质调节的方式，只改变管道温度，不改变管道流量，以节点温度为中间变量建立热源功率和热负荷功率供需平衡的模型。热网特性通过改变节点温度影响整个调度模型。

1）延时特性

区别于电能传递，水在管道里的流动速度不可忽略，故热能流经管道有一定延迟时间，即

式中：ti为热能流经管道i的传输延迟时间；ρ为热水的密度；Li为管道i的长度；di为管道i的内径；mi为管道i的流量。

延时特性使CHP 机组供热功率与风电功率错峰，有利于消纳更多弃风，体现在热力系统中即为热负荷处热媒的温度变化相对于热源处的温度变化有一定的延迟效应。由于延时特性在整个调度过程中均存在，在3 个时段的调度模型中，供热管道两端温度变化均存在一定的延迟时间。

2）衰减特性

由于热水在管网内流动时受到管壁温度、环境温度等的影响，有一部分热能散失，管网温度会发生衰减，如式（4）所示。

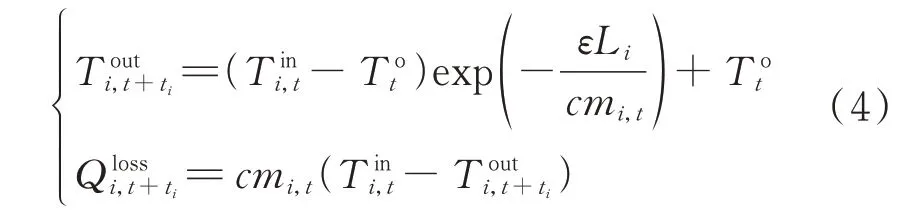
调度过程中考虑衰减特性，热水在流过一段管道后，管道的出口温度要低于入口温度。

3）储放热特性

热网储放热潜力较大，利用管网的实时储放热参与热功率平衡可以弱化热网侧的热电耦合，进而影响电功率平衡。因此，用虚拟储热罐来模拟管网储放热（储热时体现为供回水网络温度升高，放热体现为供回水网络温度降低），模拟后的储放热与管网温度的关系如式（5）所示。

1.3 供热区域热惯性模型

由于热电介质能量传输特性的不同，需要考虑供热区域的惯性问题。利用这种热惯性，在弃风时段来临前加大供热，弃风时段适当降低供热，在保证供热区域室内温度需求的基础上，使系统供热量在时间轴上具有灵活可调节性，有效降低了电热联合系统中的电热耦合强度，补偿了风电功率的概率区间误差，提高了风电消纳量。

供热区域从热网中获取能量来满足室内温度需要，而供热区域可看作一个一阶惯性环节［18］，为将这个惯性环节引入具有调度时段间隔的电热联合系统模型中，需要对微分方程进行离散化，最终得到供热区域热惯性的约束如式（6）所示。

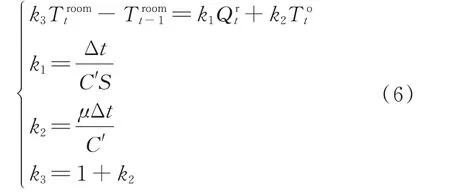
式中：k1、k2、k3为相关系数；Troomt为供热区域在t时刻的室内温度；Qrt为散热区域内所有散热器在t时刻的总散热量；C'为单位供热面积下的热容；S为供热区域面积；μ为室内热损失系数。

2 考虑风电功率预测误差分时补偿的电热联合系统多时间尺度调度策略

2.1 电热联合系统多时间尺度调度策略分析

风电功率概率区间误差的评估周期较长，在电网日前调度时段考虑。而热力系统中，供热区域的热用户需求是适宜的室内温度，只需要室内温度在合理范围内变化，热负荷具有灵活性。考虑到管网本身的储能容量相较于供热区域来说比较小，因此主要利用供热区域热惯性来补偿概率区间误差。风电功率实时预测误差的评估周期较短，在电网实时调度时段考虑。而热力系统中，管网供回水温度会受室外温度的影响发生实时变化，同时管网产生实时的储放热功率。这部分热网自身的功率变化会实时影响系统消纳弃风的灵活性。因此，主要利用管网储放热补偿实时预测误差。

本文的多时间尺度模型分为日前、日内、实时3 个时间尺度。其中，日前调度计划提前24 h 设定，以1 h 为调度间隔，考虑风电功率的概率区间误差，通过机会约束规划制定机组初步出力计划，同时利用供热区域热惯性补偿概率区间误差；日内滚动修正调度在日前调度的基础上提前4 h 进行调度，以1 h 为调度间隔，根据日内确定的风电功率预测值，修正机组的出力计划；最后，实时调度在1 h 之内，以15 min 为调度间隔，考虑风电功率实时预测误差，实时修正各机组出力，同时利用热网储放热和储电装置补偿实时预测误差。详细的调度策略如图2 所示，调度策略所示电热联合系统多时间尺度调度模型求解框架如附录A 图A1 所示。

图2 考虑风电功率预测误差分时补偿的电热联合系统多时间尺度调度策略Fig.2 Multi-time-scale dispatching strategy of integrated electricity and thermal system considering time-sharing compensation of wind power forecasting error

以t时刻为例，通过统计t-24 时刻前数月乃至数年历史数据的误差规律，可以预测出t-24至t时段的风电功率概率区间误差。在日前调度阶段补偿风电功率的概率区间误差时，一方面供热区域储能容量相对较大；另一方面供热区域的热惯性体现在室内温度的变化上，室内温度变化对电网调度指令的响应速度较慢，恰好也需要提前进行设定。因此，在日前调度阶段主要利用供热区域补偿评估周期较长的概率区间误差，实现电网日前调度、风电功率概率区间误差、供热区域在时间上的匹配。

以t时刻为例，提取t时刻之前的若干风电功率实时数据信号特征值，可以预测出t至t+1 时段的风电功率实时预测误差。在实时调度时段考虑风电功率的实时预测误差时，管网实时储放热功率对电网调度指令的响应速度较快，可以实时影响系统消纳弃风的灵活性。因此，在实时调度阶段主要利用管网储放热特性补偿评估周期较短的实时预测误差，实现电网实时调度、风电功率实时预测误差、管网在时间上的匹配。

2.2 考虑供热区域热惯性的日前调度模型

在日前调度时段通过风电功率的概率区间误差确定风电功率的波动区间，并利用供热区域热惯性对概率区间误差进行补偿，将传统的热负荷实时平衡约束替换为将室内温度维持在期望值内，以总煤耗量最小为目标，建立改进的日前调度模型。

2.2.1 日前调度模型的目标函数

设置火电机组和CHP 机组均为常开状态，考虑火电机组的发电煤耗量和CHP 机组的发电、发热煤耗量，目标函数可表示为：

式中：ak、bk、ck为火电机组k的运行成本系数；αm、βm、γm、δm、θm、μm为CHP 机组m的运行成本系数；PCON，k，t为t时刻火电机组k的电出力；PCHP，m，t为t时刻CHP 机组m的电出力；QCHP，m，t为t时刻CHP 机组m的热出力。

2.2.2 日前调度模型的约束条件

1）系统功率平衡约束

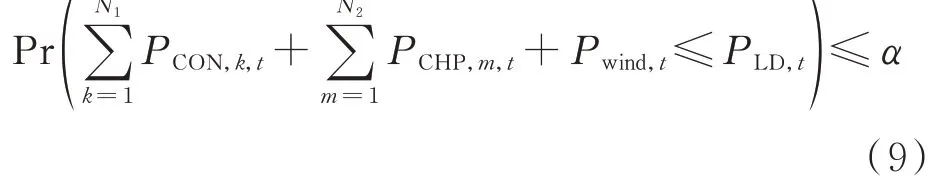
式中：Pr(·)为求概率函数；Pwind，t为日前t时刻的风电出力；PLD，t为t时刻的电负荷总功率；α为设定的置信水平。

系统功率平衡约束式（9）为机会约束，在考虑风电不确定性的情况下，α的大小会影响系统的总有功功率供给满足负荷需求的可靠性：α越小，说明在风电功率波动的情况下，系统的总有功功率供给满足负荷需求的可靠性越高。在实际求解时先将机会约束转化为确定性约束［30］，经过简化可得到新的约束如式（10）所示。

式中：f-1Pwind(·)为Pwind，t的概率分布函数的反函数，给定置信水平α后代入反函数得到f-1Pwind(α)对应的常数值。

2）机组运行约束

机组运行约束主要包括机组出力约束、机组爬坡约束以及CHP 机组的热电耦合约束。其中，火电机组及CHP 机组的出力约束如式（11）所示。

式中：Cm为CHP 机组m在背压工况下的热电比；cm为CHP 机组m在最大凝气工况下的热电比；Km为常数。

3）热网约束

结合1.2 和1.3 节对热网模型和供热区域热惯性模型的详细说明，在日前调度模型中加入相应热网约束，具体有：延时特性如式（3）所示，热衰减特性如式（4）所示，供热区域热惯性特性如式（6）所示。

热源与供回水温度需满足的约束如下：

式中：mout和min分别为流出和流入汇流节点的各管道流量；Tin和Tout分别为流入和流出汇流节点的各管道温度。

2.3 日内滚动修正模型

在日内阶段采用传统日内滚动修正模型，根据日内风电功率预测值设定风电功率上下限，调整机组出力。

2.3.1 日内滚动修正模型的目标函数

日内调度模型与日前调度模型类似，目标函数仍为各机组煤耗量之和最小，如式（17）所示。

2.3.2 日内滚动修正模型的约束条件

1）系统功率平衡约束

日内调度模型采用传统的功率平衡约束，包括电功率平衡和热功率平衡，具体如式（19）所示。

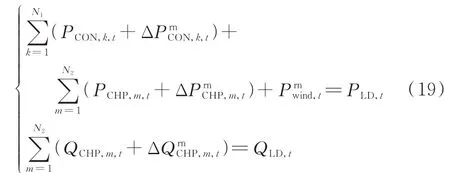
式中：QLD，t为t时刻的总热负荷功率；Prnwind，t为日内调度中t时刻的风电出力。

2）机组运行约束

日内调度模型中的机组运行约束均与日前调度模型类似，仅加入相应的火电、热电修正量。日内调度模型的风电出力小于风电功率预测值。需要指出的是，由于日内调度模型中的时间尺度（Δt）与日前调度模型不同，爬坡约束表达式虽与日前调度模型相同，但实际约束范围与日前调度模型不同。

3）热网约束

日内滚动修正模型中的热网约束式与日前调度模型类似，具体有：延时特性如式（3）所示，热衰减特性如式（4）所示，热源与供回水温度关系如式（14）所示，热网供回水温度上下限约束如式（15）所示，汇流节点平衡关系如式（16）所示。

2.4 考虑管网储热的实时预测误差补偿模型

实时调度中，考虑管网储放热特性，在满足供热平衡的前提下，通过管网储放热变化来调节CHP 机组热出力，进而影响CHP 机组电出力，同时补偿风电功率实时预测误差，减小弃风和切负荷量。但由于管网储能受限，利用管网储放热不能完全补偿误差，因此还需要储能系统的配合。但储能系统的使用成本较高，且容量和输出电量一般较小，因此优先采用管网储放热补偿，使其在可调范围内尽可能补偿预测误差，剩余部分再利用储电装置进行补偿。综上所述，实时预测误差模型采用分层求解的方法，建立管网储放热子模型和储能补偿子模型分别求解。

2.4.1 管网储放热模型

该子模型的目标函数与日前、日内调度模型类似，以系统煤耗量最小为目标，即

约束条件主要分为电网约束和热网约束。

1）电网约束

系统功率平衡约束分为电功率平衡和热功率平衡，其中电功率平衡与日内调度模型类似，热功率平衡考虑管网储放热，具体表达式如式（21）所示。

其余电网约束与日内调度模型类似。各机组电出力在日内调度模型中机组出力的基础上加入实时机组修正量即可。同理，由于实时调度模型中的时间尺度（Δt）与日前、日内调度模型不同，爬坡约束表达式虽与日前、日内调度模型中相同，但实际约束范围与其并不相同。

2）热网约束

实时校正模型中的热网约束与日内调度模型类似，具体有：热网延时特性如式（3）所示，热衰减特性如式（4）所示，管网储放热约束如式（5）所示，热源与供回水温度关系如式（14）所示，热网供回水温度上下限约束如式（15）所示，汇流节点平衡关系如式（16）所示。

此外，由于管网温度、管网流量等限制条件，管网储放热功率具有最大值，因此管网储放热功率具有上下限约束，具体表达式如式（22）所示。

由于管网储热量受热水温度、热水流量等的限制，管网储放热不能完全补偿风电功率预测误差，设置管网补偿上下限系数使其控制在一定范围内。管网补偿量的约束如式（24）所示。

式中：ζup和ζdown分别为管网热补偿上、下限；ebegin为风电功率估计预测误差；esecond为管网补偿后的剩余预测误差。

2.4.2 储电补偿模型

储电补偿子模型以esecond为基础，以剩余误差最小为目标，目标函数如式（25）所示。

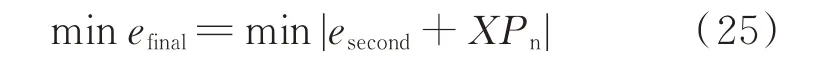
式中：efinal为储电补偿后的最终剩余预测误差；X为储电装置储放电指令，X=1 表示储电，X=-1 表示放电；Pn为储电装置储放电功率。

储电补偿子模型中的约束条件主要分为两类，一类是对储放电指令X的约束（如式（26）所示，可采用分段线性化的方法线性化再求解）；一类是对储放电功率及储电装置容量的约束（如式（27）所示）。

1）储放电指令约束

3 算例分析

3.1 算例设置

算例系统由电力系统以及热力系统组成。电力系统包括一座火电厂，装有两台纯凝火电机组；一座热电厂，装有两台CHP 机组；一座风电场。热力系统包括两个供热分区，由两台CHP 机组供热。风电数据来源于Elia 比利时电力运营商公开的2020 年1 月24 日的运行数据。各机组出力范围见附录A 表A1，各机组运行参数见文献［18］。储电系统参数见表A2。风电功率的置信区间取90%。

热网采用质调节方式，拓扑结构见附录A 图A2。图中：①、②为热源节点，⑦、⑧为热负荷节点，③至⑥为汇流/分流节点。管道1、3、5、7、9 为供水管道，2、4、6、8、10 为回水管道。设置供水管道温度上、下限分别为125 ℃、90 ℃；回水管道温度上、下限分别为70 ℃、50 ℃；室内设计温度取20±2 ℃。热转换系数为1.6×10-5GJ/(h·m·K)。

算例中调度周期为1 d，日前、日内调度模型的调度间隔为1 h，实时补偿模型的调度间隔为15 min，算例在MATLAB R2018b 环境下调用YALMIP+CPLEX 求解器求解。本文设置如下3 种算例方案进行对比：

算例1：多时间尺度滚动调度，不考虑风电功率预测误差；

算例2：多时间尺度滚动调度，考虑风电功率的概率区间误差；

算例3：多时间尺度滚动调度，考虑风电功率的概率区间误差及实时预测误差。

3.2 结果分析

算例1 仅进行传统多时间尺度优化调度，不考虑风电功率预测误差；算例2 在算例1 的基础上，在日前计及风电功率的概率区间误差，并利用供热区域的热惯性对其进行补偿，在确保温度需求的前提下提高热负荷灵活性；算例3 在算例2 的基础上，考虑风电功率的实时预测误差，使其参与实时的电功率平衡校正机组出力，并利用管网自身的储放热特性和储电装置来进行实时预测误差的补偿。

分别从风电功率的调度结果和热力系统的变化情况两方面分析算例结果。

风电出力情况对比和风电功率多时间尺度调度值变化情况如图3 所示。由图3（a）可知，日前不考虑风电功率概率区间误差时，风电调度值与实际值相差较大，弃风严重。计及概率区间误差并通过供热区域热惯性补偿后，风电功率变化范围增大，变化曲线更接近真实值。因此，在日前调度时段考虑风电功率的概率区间误差并利用供热区域热惯性对其补偿，优化了风电功率跟随真实值波动的性能，弃风量大大减少。但是从图3（a）来看，日前风电功率的概率区间很大，这恰恰也反映了日前预测误差较大的现状。因此，需要进一步依据实时预测误差进行实时调度。

图3（b）所示为风电功率在不同调度阶段的调度曲线。由该图可知，同时考虑风电功率的概率区间误差和实时预测误差后，风电功率调度值通过滚动校正逐渐跟随实际出力，误差明显减小，弃风和切负荷量大大减少。

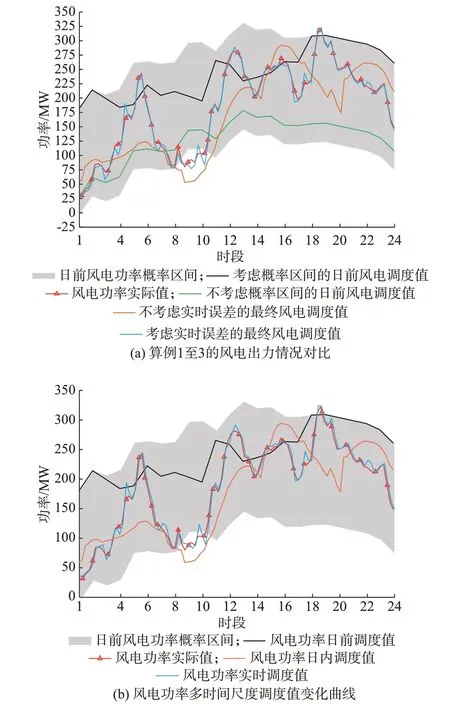
图3 风电出力情况对比和风电功率多时间尺度调度值变化情况Fig.3 Comparison of wind power output and variation of multi-time-scale dispatching values for wind power

对比图3（a）和（b）可知，算例2 的最终风电调度值与实际值相差较大，最大弃风量为122.74 MW，最大切负荷量为96.71 MW。而算例3 考虑实时预测误差，并利用管网储放热和储电装置补偿后，其最终风电调度值接近实际值，最大弃风量降为17.48 MW，最大切负荷量降为33.93 MW。因此，在实时阶段计及风电功率实时预测误差并利用管网自身储放热特性和储电装置进行补偿，进一步优化了风电功率跟随真实值波动的性能，减小了弃风量和切负荷量。

为了更加直观地展示风电消纳情况，列出优化前后机组出力数据和风电调度值、实际值如附录B表B1 所示，并根据表B1 中的数据绘制机组出力与风电出力消纳的功率变化，如图4 所示。

由图4 可以看出，优化后机组出力总体减小，更多风电上网参与电功率平衡。此外，由于热力系统具有供热区域热惯性和管网储放热特性，CHP 机组功率变化的波动趋势更能体现其对风电的消纳效果。同时，纵向对比图4（a）和（b）可以发现，优化前风、电、热时间特性的差异较大，热功率变化难以与风电功率同步；而通过本文策略优化后这个问题得到了很大改善，热功率变化与风电功率的波动趋势明显同步。

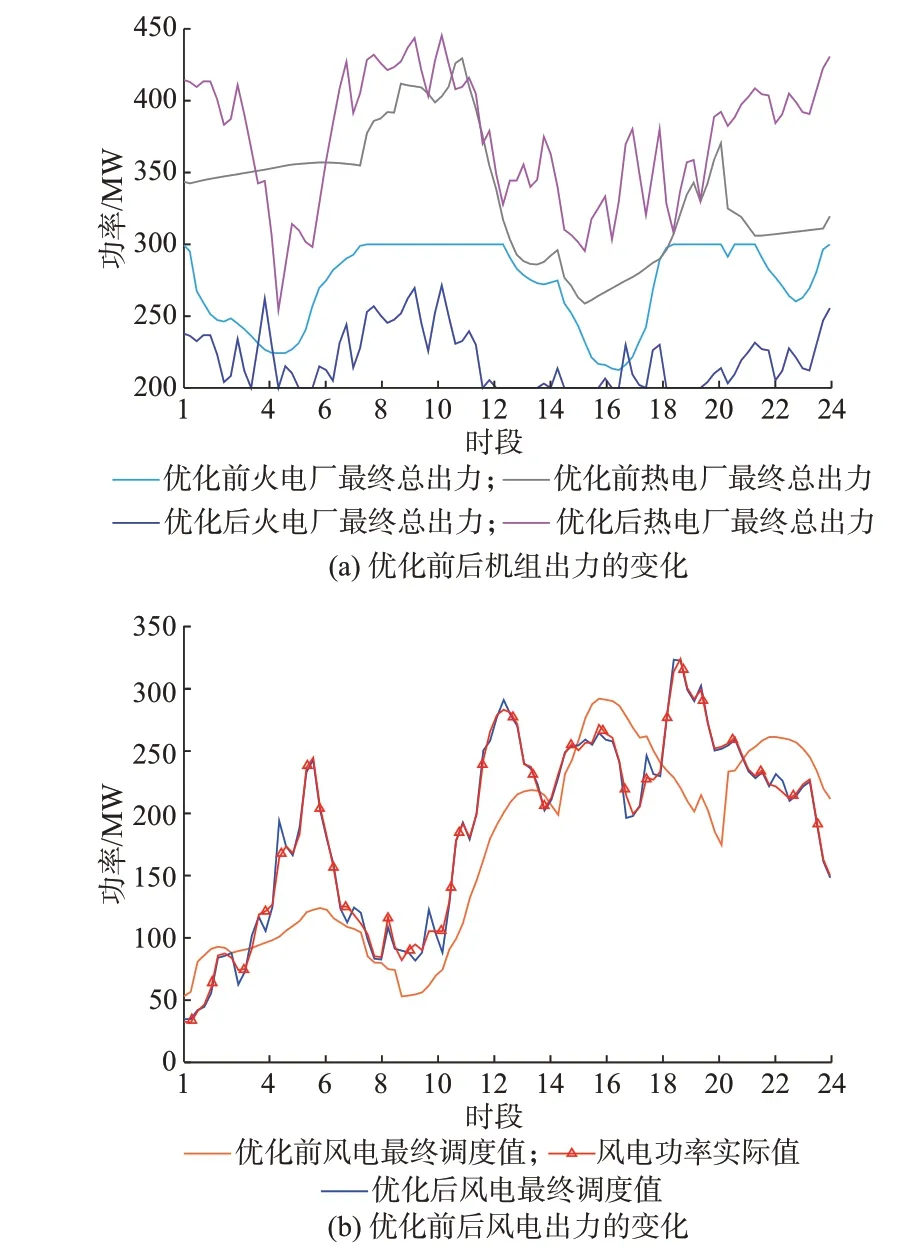
图4 优化前后机组出力和风电出力对比Fig.4 Comparision of unit output and wind power output before and after optimization

对比附录B 表B1 中优化前后弃风、切负荷比例数据可以看出，在日前阶段利用供热区域热惯性补偿概率区间误差，在实时阶段利用管网储放热和储电装置补偿实时预测误差后，弃风和切负荷比例大大降低，说明应用本文所提调度策略可以明显提高电热联合系统对风电的消纳能力。

再分析热力系统性能的变化情况，主要包括供热区域的热惯性对概率区间误差的补偿效果以及管网储放热对实时预测误差的补偿效果。

日前阶段热功率及供热区域室内温度变化曲线见图5。由图5 可知，考虑供热区域热惯性后，热功率变化峰值较风电功率峰值左移，降低了其与风电高发时段在时间上的重合度，缓解了风电上网的紧张。此外，在风电高峰期来临前，提高供热区域的整体温度以提高风电消纳能力；在风电高峰期来临后，由于热惯性，室内温度需一段时间才能降下来。在给定仿真参数的前提下，室内温度变化曲线明显比热功率变化滞后约10 h，因此供热区域的热惯性只能在日前调度时段考虑，并且室内温度波动只能跟随风电功率的大致变化曲线，短时波动无法响应。

图5 日前热功率及供热区域室内温度变化Fig.5 Variation of day-ahead thermal power and indoor temperature in heat supply area

总的来说，在日前调度时段考虑供热区域热惯性，在满足供暖需求的前提下补偿了风电功率的概率区间误差，消纳了更多风电。但是，由于无法响应风电功率短时波动，需要进一步在实时调度阶段考虑风电功率实时预测误差，并利用管网储放热和储电装置对其进行补偿。

图6 所示为管网储放热和储电装置对风电功率实时预测误差的补偿效果图。从图中可以看出，风电功率预测误差为正时，风电实际出力大于风电调度出力，此时热网吸收热量，同时储电装置储存能量，从而消纳弃风；反之，风电功率预测误差为负时，风电实际出力小于风电调度出力，此时管网释放热量，同时储电装置也释放能量，从而补偿切负荷。由此证明在实时调度阶段利用管网储放热功率补偿风电功率实时预测误差的效果较好，同时也体现出在管网储能受限的情况下储电装置和管网的配合补偿情况。

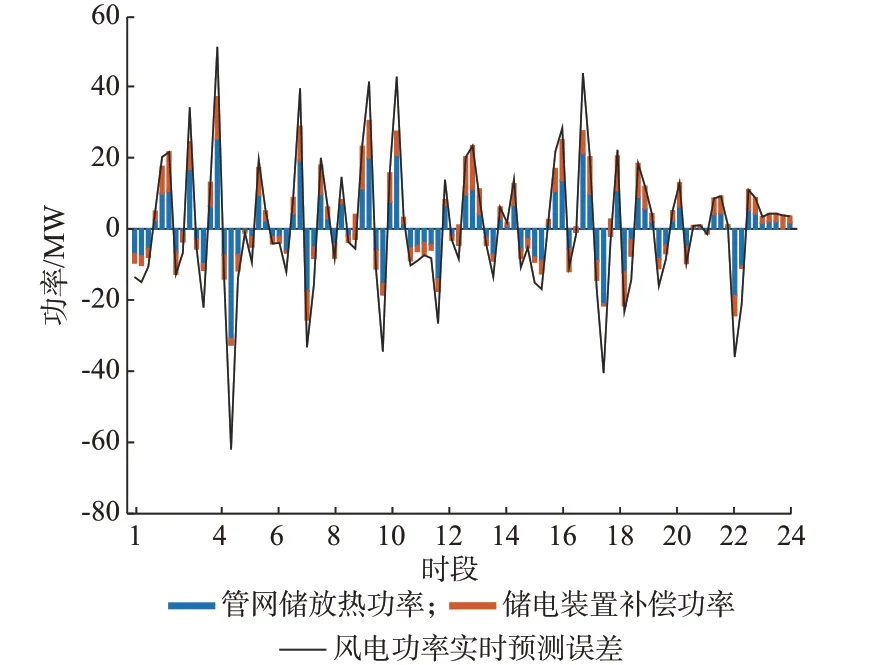
图6 风电功率实时预测误差补偿效果图Fig.6 Diagram of compensation effect for real-time forecasting error of wind power

各供回水管道在各调度时刻的储放热功率以及出口温度详细变化曲线见附录B 图B1 和图B2。由于其数值差距较大不宜观察，以三维图表面，即管道①为例，放大其在图B1 和图B2 中的数据并进行对比观察，结果如图7 所示。

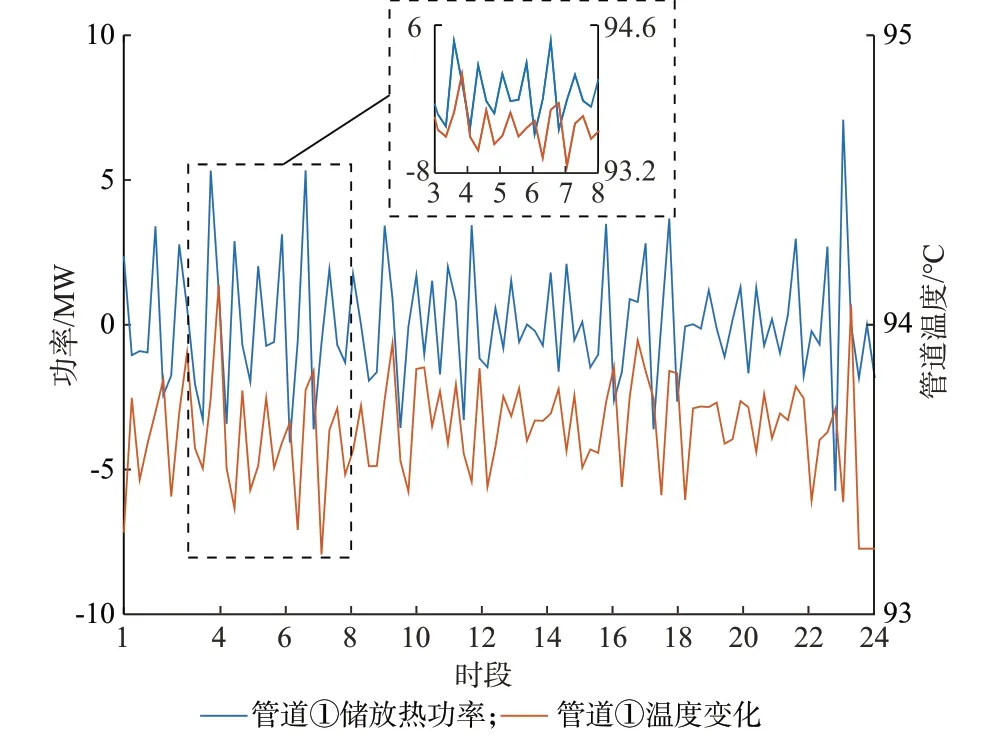
图7 管道①中的储放热功率和温度变化Fig.7 Variation of stored and released thermal power and temperature in pipeline ①

由图7 可知，管网储热时，管网内热水温度上升，管网储存更多热能从而消纳弃风；反之，管网放热时，管网内热水温度下降，管网释放能量以补偿切负荷。另外，管道在传输热能的过程中具有延迟性能，管道在某一时刻产生储放热功率经过一定延迟时间后，管道出口温度才发生相应的变化。这段延时时间仅为几分钟，也验证了管网储放热特性需要在实时调度时段考虑。

总体来说，在实时阶段计及风电功率实时预测误差后，采用管网储放热和储电装置快速补偿该误差，在日前考虑风电功率的概率区间误差的基础上进一步补偿了风电功率预测误差，减小了弃风和切负荷量。

不同算例下系统煤耗量、弃风和切负荷量见表1。由表1 可知，算例2 仅考虑风电功率的概率区间误差，与算例1 相比，日前煤耗量减少了720.34 t；由于不考虑实时预测误差，经过相同日内和实时调度，最终总煤耗量仍然不变，总弃风量和切负荷量也未变化。而算例3 在算例2 的基础上进一步考虑风电功率的实时预测误差，总煤耗量比算例1、算例2 减少了2 375.42 t，总弃风量减少了2 572.95 MW，切负荷量减小了950.68 MW。因此，计及风电功率概率区间误差和实时预测误差分时补偿的多时间尺度调度模型降低了系统煤耗量，同时有效消纳了弃风和切负荷。

表1 系统煤耗量、弃风和切负荷量Table 1 Coal consumption，wind curtailment and load shedding for system

为了进一步说明模型的有效性和通用性，采用不同风电原始数据和环境温度，并利用本文调度模型进行优化调度，调度结果见附录B 图B3。结果再次证明同时考虑风电功率的概率区间误差和实时预测误差，并利用供热区域热惯性和管网储放热特性分别对其补偿的调度策略，减少了弃风和切负荷量，大大降低了风电功率预测误差对系统的不利影响。