基于改进残差网络的两阶段电力系统频率安全多级预警
2023-02-02李栌苏吴俊勇李宝琴王彦博王春明董向明
李栌苏,吴俊勇,李宝琴,王彦博,王春明,董向明
(1. 北京交通大学电气工程学院,北京市 100044;2. 国家电网公司华中分部,湖北省武汉市 430077)
0 引言
随着“双碳”目标的提出,可再生能源集群大规模投入,导致火电机组的装机和出力逐步减少[1]。然而,可再生能源机组的出力具有随机性和波动性,且几乎不具备转动惯量[2],导致系统频率响应的惯性环节和一次调频能力被削弱。当受到较大的有功扰动时,系统频率难以维持在规定的范围内[3]。随着新型电力系统的建设,电网规模不断壮大,运行方式更加复杂。然而,传统的时域仿真法存在建模困难、计算量大、运算耗时长等问题,导致其无法满足在线应用的要求[4]。
为提高频率响应分析效率,以简化模型为基础的数学解析方法被提出。平均系统频率(average system frequency,ASF)模型忽略了系统的诸多结构,仅保留了各个原动机-调速器的独立动态特征及一个集中负荷[5]。系统频率响应(system frequency response,SFR)模型[6]进一步将整个系统等效为一个单机带集中负荷的低阶等值模型。虽然ASF 和SFR 模型降低了计算复杂度,但是计算精度也被降低,且泛化能力一般。文献[7]将系统简化为典型二自由度振动系统,建立了双机等效频率响应模型,实现了快速计算。文献[8]提出了测量驱动的方法,利用同步相量数据计算频率的二阶导数,以实现快速的频率响应估计。文献[9]采用物理-数据融合建模思路,提出频率态势在线预测方法。但由于数学解析方法对系统进行了大量的简化,使等效模型与实际系统有较大差别,导致求解精度低、等值参数难以统一、无法反映系统内部情况等问题[10]。
近年来,深度学习技术愈发成熟,它具有强大的特征提取和非线性拟合能力,而电力系统恰好是一个包含众多特征和海量数据的非线性系统。因此,该技术已在电力系统中得到诸多应用[11],如暂态功角稳定[12-13]、暂态电压稳定[14-15]等。
目前,深度学习在电力系统频率稳定中的应用主要集中在频率安全评估和频率响应曲线预测[16]。文献[17]提出了一种基于改进堆叠降噪自编码器的预想事故频率指标评估方法,但是没有给出安全指标的划分依据,也未验证所提方法的鲁棒性和抗噪能力。文献[18]基于级联轻梯度提升机方法,并在损失函数中加入惩罚系数,提出了一种计及频率偏移分布与惩罚代价的最大频率偏移预测方法。文献[19]提出了一种基于深度置信网络的扰动后系统惯性中心频率曲线预测方法,但是该方法须确定准确的扰动时刻,无法对实时系统进行连续性评估,使其在线应用受到限制。此外,文献[17-19]的评估或预测对象为频率偏移值或频率响应曲线,并没有给出评估对象的实际意义和直观的频率安全等级,无法对是否需要启动紧急控制以及选用何种控制策略提供直接帮助。
为解决上述问题,本文提出了一个基于改进残差网络的两阶段电力系统频率安全多级预警模型。首先,对频率偏移进行多级精细划分,提出并构建了频率安全多级预警模型。然后,该模型在第1 阶段利用基于改进残差网络的分类评估器给出扰动后的频率安全等级;在第2 阶段利用回归预测器进一步给出预警样本的危险程度。最后,在添加风电机组的IEEE 10 机39 节点系统和美国伊利诺伊州200 节点系统上验证了所提模型的优良性能。
1 改进残差网络原理
1.1 残差网络的基本原理
当传统卷积神经网络(convolutional neural network,CNN)层数较多时,在权重更新过程中可能出现梯度爆炸、梯度消失或信息丢失等问题,导致深层网络无法训练。为解决上述问题,残差网络(residual network,ResNet)[20]被提出。ResNet 的主要思想是将网络进行模块划分,并在各个模块中增加直连路径,通过该路径可以将输入模块的信息直接绕路输出,保护了信息的完整性,因此该模块被称为残差模块,如附录A 图A1 所示。由于经典的ResNet 是由多个残差模块堆叠搭建而成,故也被称为深度残差网络,如附录A 图A2 所示。
1.2 改进ResNet
由于电力系统的运行状态时刻都在发生变化,导致从系统中获取的特征数据也是随时间波动的序列数据。然而,经典ResNet 更适用于处理二维矩阵块数据,对于一维时间序列数据无法直接使用。因此,本文对经典ResNet 进行了改进,使其可以直接处理电力系统中的一维时间序列数据。
一维卷积中的卷积核仅在一个方向上进行滑动,以提取卷积核窗口内的数据特征,对于处理一维时间序列具有天然的优势。目前简单一维CNN(1D-CNN)已经在电力系统暂态功角稳定评估中得到应用[21],并取得较好的评估效果。一维卷积操作公式如下:

式中:ac,j为第c个通道的第j个特征映射;f(·)为激活函数;xe为第e个一维特征值;⊗表示一维卷积运算;Wc,k为第c个通道 的第k个卷 积核;b为偏置。
但是由于简单1D-CNN 层数较少,且没有残差结构,导致其在处理高维非线性数据和网络深度等方面受到极大限制。因此,本文将二者的优势相结合,借鉴一维卷积操作对经典ResNet 进行改进,用来对电力系统的频率安全进行多级预警。
改进一维基本残差单元结构见附录A 图A3(a),其计算公式如下:
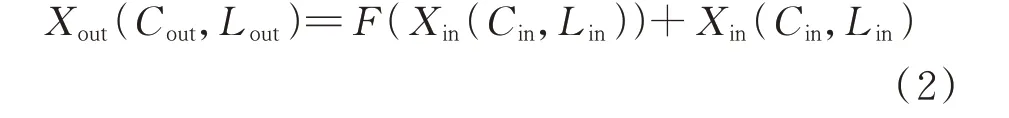
式中:Xin(Cin,Lin)为输入通道数为Cin、长度为Lin的一维输入信息;F(·) 为一维卷积操作函数;Xout(Cout,Lout)为输出通道数为Cout、长度为Lout的输出信息。
改进ResNet 的整体结构如附录A 图A3(b)所示,其核心为多个一维基本残差单元的堆叠,并将多通道一维时间序列数据作为全网络的输入,可以更好地适应不同采样时刻得到的序列数据。
2 频率安全多级预警模型
2.1 频率安全多级预警问题描述
在系统的有功平衡被打破后,各节点的频率也在围绕着系统惯性中心频率而振荡,故可以采用惯性中心频率的动态响应过程来表征全系统的频率响应。系统惯性中心频率fCOI的定义如下[19]:
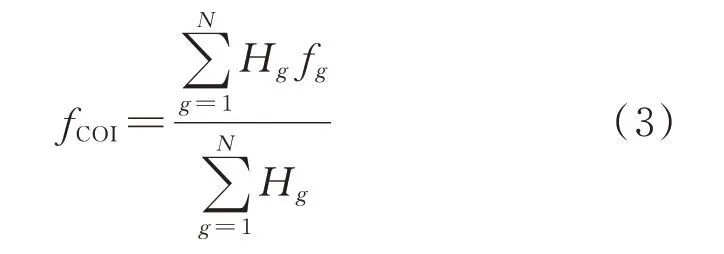
式中:N为系统中有效机组数量;Hg为第g台机组的惯性时间常数;fg为第g台机组机端母线频率。
电力系统频率响应的动态过程包含惯性响应环节、一次调频和二次调频环节。由于二次调频的时间尺度较长且是可控的调频环节,本文仅考虑系统发生较大有功扰动后的惯性环节和一次调频环节,即频率响应的短期动态过程。
当系统出现较大的有功冗余或缺额时,系统的频率都可能发生较大的波动,甚至超出安全限值。系统出现有功冗余时会导致频率上升,而出现有功缺额时会导致频率下降,且两种情况成对偶关系,故本文以系统出现有功缺额、频率下降为例进行验证,且本文所提模型对上述两种情况均适用。
2.2 输入特征的选择
电力系统的运行状态由众多变量反映得到,并且深度学习网络是对特征之间的差异进行学习。因此,应确保选取输入特征的合理性。
电力系统的频率直接由系统的有功平衡决定,故本文选取各机组的电磁功率及电磁功率总量和各负荷的有功功率消耗及有功功率消耗总量作为输入特征。
多机系统的频率动态方程如式(4)[22]所示。从中可以得出,影响惯性中心频率的变量主要为各发电机的机械功率和电磁功率及其总量,故本文选取各机组的机械功率及系统总机械功率作为输入特征。
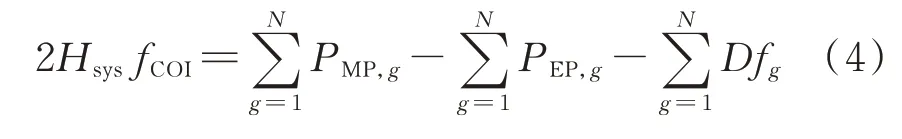
式中:Hsys为系统中各机组的惯性时间常数之和;PMP,g为 第g台 机 组 的 机 械 功 率;PEP,g为 第g台 机 组的电磁功率;D为机组的阻尼系数。
系统一次调频能力的大小由各机组的旋转备用决定,因此有必要选取各机组的旋转备用作为输入特征。电压的无功特性对系统的频率波动有轻微影响[18,23],机端母线的相角也决定着有功功率的流动方向,间接影响频率的波动情况,故本文将各机组机端母线的电压和相角作为输入特征。
此外,虽然电力系统的频率变化直接受系统有功平衡的影响,但是在实际运行中无法直接获取整个系统有功扰动的准确数值,故本文未将有功扰动量作为输入特征。
综上所述,由于本文将IEEE 10 机39 节点系统作为算例,共包含10 台机组、19 个负荷,故与发电机组相关的输入特征的数据维度为10,与负荷相关的输入特征的数据维度为19。该系统的全部输入特征 如表1 所示,共9 种72 维。

表1 输入特征集Table 1 Input feature set
2.3 安全预警标准的制定及评价指标
2.3.1 安全预警标准划分
频率稳定是指电力系统受到小扰动或大扰动后,系统频率能够保持或恢复到允许的范围内,不发生频率振荡或崩溃的能力[24-25]。由于目前各国均未颁布电力系统频率稳定或失稳的统一标准,且为了实现频率稳定问题与电力系统的功角稳定和电压稳定相一致的评价方式,也为了验证本文提出的基于深度学习的多分类算法在频率安全问题中的应用性能,本文参考北美、欧盟[24]和中国[26]对频率偏差限值的规定,以及国家电网华中分部的实际调度经验,将电力系统扰动后的频率偏移划分为3 个等级,如表2 所示,用来对本文所提算法进行说明。若需更精细的预警结果,可对频率安全等级进一步划分,以减小大区间带来的误差。

表2 频率安全多级预警标准Table 2 Multi-level early warning standard for frequency safety
2.3.2 安全预警评估器的评价指标
为了更加直观和精确地评价第1 阶段中安全多级预警分类评估器的性能,本文构造了针对分类任务性能度量的混淆矩阵[27],如表3 所示。其中,TP和FP分别为正样本被正确和错误预测的数目;TN和FN分别为负样本被正确和错误预测的数目。

表3 混淆矩阵Table 3 Confusion matrix
结合混淆矩阵及电力系统频率安全预警的实际情况,本文定义如下4 个评价指标,以便更加细致地评价所提方法的有效性和准确性。
1)准确率Acc:表示所有预测正确的样本占总样本的比例,如式(5)所示。
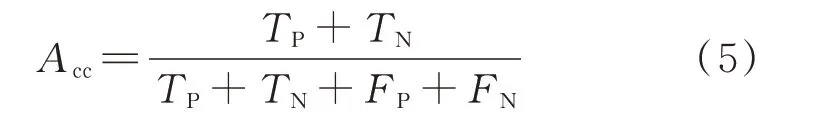
2)安全性Se:表示在正样本中预测正确的样本占所有正样本的比例,如式(6)所示。

3)可靠性Re:表示在负样本中预测正确的样本占所有负样本的比例,如式(7)所示。
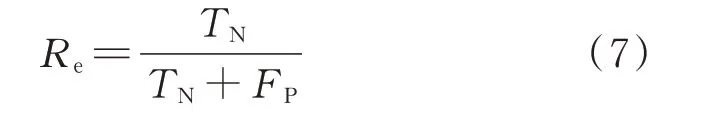
4)稳定性Gmean:用安全性和可靠性的几何均值表示算法的稳定性,如式(8)所示。

2.4 危险程度标准的制定及评价指标
2.4.1 危险程度评估标准
根据表2 中预警区间的划分,各区间内的频率响应曲线如附录A 图A4 所示。其中,f0、f1、f2分别为0 级、Ⅰ级和Ⅱ级预警区间内的频率最大偏移值。由此可定义Ⅰ级和Ⅱ级预警结果的危险程度D1和D2分别为:
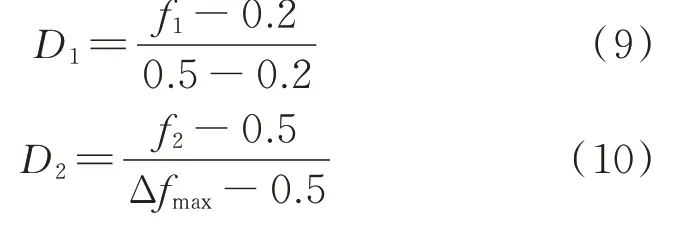
式中:Δfmax为所有Ⅱ级预警结果的最大频率偏移。
2.4.2 危险程度预测器的评价指标
第2 阶段中危险程度回归预测器的性能评价指标包含全部样本的均方误差EMSE和单一样本的预测误差平方ei,分别用来衡量该方法对测试集整体和对单一样本的预测精度,计算公式如下:

式 中:Ns为 测 试 集 中 样 本 总 数;y͂i和yi分 别 为 第i个样本的预测结果和真实值。
3 基于改进ResNet 的两阶段电力系统频率安全多级预警算法流程
本文提出的基于改进ResNet 的电力系统频率安全多级预警模型的详细应用流程如图1 所示。该模型主要分为离线训练和在线预警2 个模块。离线训练模块是对频率安全多级预警分类评估器和频率危险程度回归预测器进行预训练;在线预警模块是将预训练好的分类评估器和回归预测器应用到实际的电力系统中。

图1 基于改进ResNet 的频率安全多级预警模型应用流程图Fig.1 Flow chart of application of multi-level early warning model for frequency safety based on improved ResNet
3.1 离线训练
步骤1:构建用于训练和测试的样本集。如已经有数量充足且符合要求的历史数据,则可直接对历史数据进行筛选作为样本集;当历史数据过少或类型欠缺时,则可以通过时域仿真方法对样本集进行补充。
步骤2:数据预处理。为了消除不同输入特征的量纲差异,本文采用最大最小归一化的方式对样本数据进行预处理。最大最小归一化公式如下:
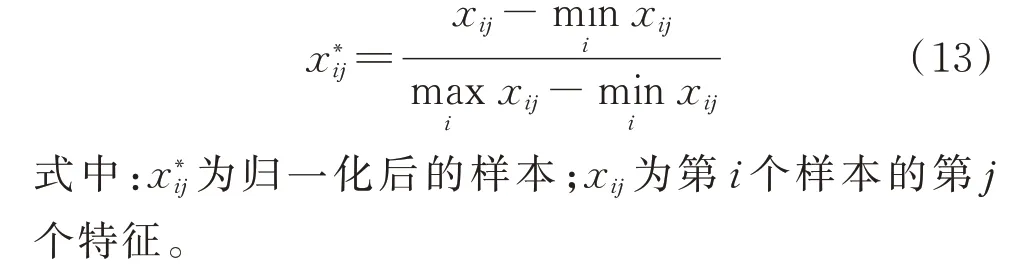
步骤3:迭代训练、参数修正和网络保存。本步骤采用“并行训练、同时输出”的策略,即对分类评估器和回归预测器同时迭代预训练,并同时输出和保存预训练结果,此策略可以加快频率安全多级预警模型的构建速度。
此外,为了提高网络的准确率和适用性,本文在对网络的迭代训练和参数修正阶段使用小批量梯度下降法,并加入了Dropout 方法使网络的神经元随机失活以提高其泛化能力,以及采用Adam 优化算法对网络加速修正。
1)对于分类评估器的迭代预训练,首先,在训练开始时设置最大迭代次数为100 及初始迭代次数为0,并采用基于变步长滑动时间窗的多通道方式将样本输入网络。用交叉熵损失函数来衡量评估结果与真实值之间的差异,通过反向传播来修正权重和偏置,得到第n轮训练结果及其Acc。然后,判断Acc是否为最大值,若是最大值则保存第n轮网络;若不是则判断迭代次数n是否小于100,若是则进入下一轮迭代,否则停止迭代。
2)对于回归预测器的迭代预训练,同样采用迭代训练、参数修正和结果保存的方法。其中,采用均方误差损失函数来衡量网络训练效果,并保存均方误差损失值Loss最小的网络作为预训练结果。
基于变步长滑动时间窗的多通道输入方式如附录A 图A5 所示。本文以连续的5 个采样时刻作为一个时间窗,并将每个采样时刻获取的输入特征数据作为传入网络的一个通道,由此构成了5 通道输入。此外,滑动时间窗可以进行变步长滑动,滑动步长可以根据实际情况进行调整,例如:当电力系统处于紧急状态时,滑动步长可以设为1,以提高频率安全预警准确率;当系统处于警戒状态时,滑动步长可以设为3,以缓解系统安全预警的评估压力。
步骤4:预训练结果输出。将Acc最高的分类评估器和Loss最低的回归预测器分别保存,作为在线预警模块中的两阶段模型。
3.2 在线预警
步骤1:运行数据的获取及筛选。利用相量测量单元(phasor measurement unit,PMU)获取系统的实时运行数据,并将这些数据根据选定的输入特征进行预筛选及调整。
步骤2:根据式(13)对数据进行标准化处理。
步骤3:第1 阶段——频率安全预警。将预处理后的数据以多通道方式传入训练好的频率安全多级预警分类评估器,得到系统的频率安全预警等级,即0 级、Ⅰ级或Ⅱ级预警。
步骤4:第2 阶段——频率危险程度预测。在本阶段采用训练好的回归预测器对频率危险程度进行预测。
4 IEEE 10 机39 节 点 算 例 分 析
为验证所提两阶段频率安全多级预警模型的有效性和准确性,本文在PyTorch 平台上进行网络的搭 建,编 程 语 言 为Python,PC 配 置 为:Intel(R)Core i5-9300h CPU/16 GB RAM, NVIDIA GEFORCE GTX 1650。
4.1 样本集的构建
本文对经典IEEE 10 机39 节点系统进行改进,新系统的基准功率、电压和频率分别为100 MW、345 kV 和50 Hz,并在系统中添加分布式风电场。此外,设定与母线39 相连的发电机系统的惯性时间常数为50 s。
本文采用PSS/E 33 仿真软件进行时域仿真,模拟有功扰动后的电力系统频率响应过程。在时域仿真过程中本文将系统的惯性环节和一次调频环节作为惯序整体考虑,并将设备的固有死区包含在其中。因为目前国标要求的一次调频死区范围为±0.033 Hz,仅为0 级预警(安全)最大限值的1/6,故本文将上述环节作为整体考虑。
文献[17]在利用时域仿真法构建样本集时仅考虑了可再生能源渗透率的差异,而未考虑系统负荷水平因素。文献[18-19]仅考虑了系统负荷水平的变化及切机扰动情况,未考虑可再生能源的渗透。此外,文献[17-19]均未考虑负荷模型占比差异、负荷随机扰动和机组出力随机波动的情况。
针对上述不足,为充分反映有功扰动后系统的频率变化,本文在构建样本集时分别考虑了基本运行工况和有功扰动方式两方面的不同。在基本运行工况方面,本文同时考虑了系统负荷水平高低的差异、负荷侧负荷模型占比的不同和可再生能源渗透率的高低3 种情况。此外,其中还包含了系统惯量和旋转备用水平的差异。在有功扰动方式方面,为了确保样本集数据能够充分表达系统扰动/故障的随机性和不确定性,本文分别考虑了发电机的随机切机扰动、负荷侧负荷随机变化形成的扰动以及发电机出力的随机波动3 种有功扰动方式。
综上所述,本文构建了一个含22 620 个样本的综合样本集,以模拟实际电力系统中复杂的运行方式和多种有功扰动情况,确保样本集能够表达系统扰动/故障的随机性和不确定性。样本集的构成、各运行工况和扰动方式及取值如表4 所示。
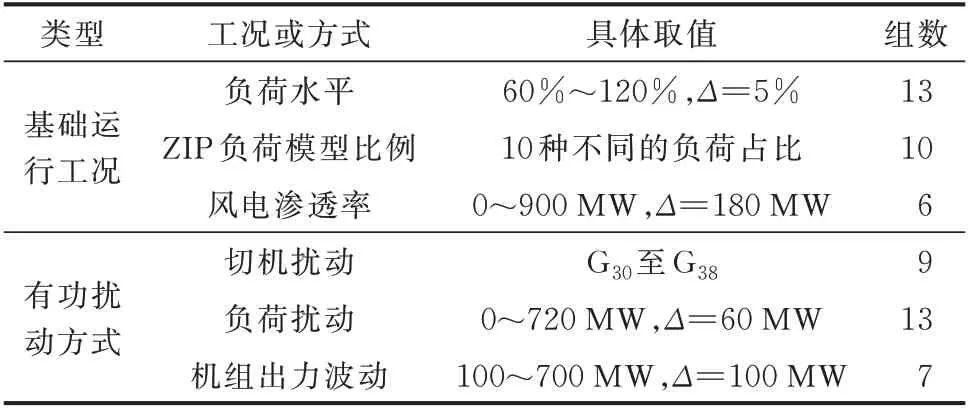
表4 样本集构成Table 4 Composition of sample set
样本集中各级预警样本数量及其占比如表5 所示。本文将系统频率安全预警等级分为3 级,即3 分类评估,并将样本集按4∶1 的比例随机划分训练集和测试集,其中,训练集包含18 096 个样本,测试集包含4 524 个样本。
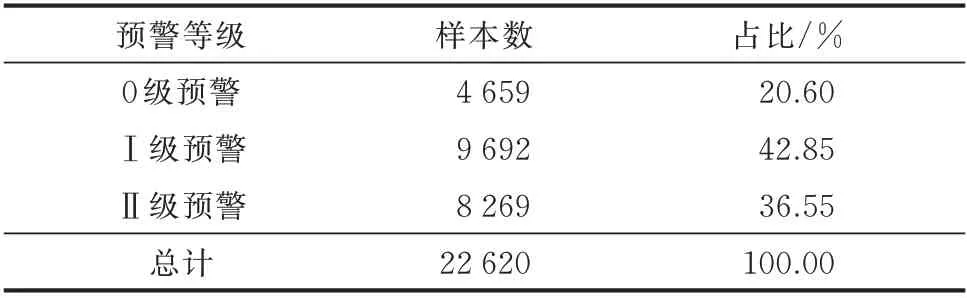
表5 各级预警样本数及占比Table 5 Number and proportion of each earlywarning samples
4.2 不同分类评估器性能比较
为了验证所提模型在频率安全多级预警中的性能优势,本文将改进ResNet 方法与浅层学习中的支持向量机(SVM)、决策树(DT)、随机森林(RF)、K最近邻(KNN)方法以及深度学习中的人工神经网络(ANN)、LeNet、AlexNet 和经典ResNet 方法进 行了对比。SVM 选取线性核函数,迭代10 000 次;DT采用分类回归树(classification and regression tree,CART)算法,深度为10;RF 采用10 棵树集成,且深度为10;KNN 经过寻优后,超参数选为20。所有浅层学习方法均基于机器学习库Scikit-Learn 搭建。深度学习方法ANN 和LeNet 选取经典参数,AlexNet 选用原始网络中的一个Group,经典ResNet 选用原始的18 层结构,所有深度学习方法均基于PyTorch 搭建,且迭代训练100 次。对比结果如 表6 所示。其中,Se,0、Se,1和Se,2分别 为0 级、Ⅰ级和Ⅱ级 预 警 结 果 的 安 全 性;Re,0、Re,1和Re,2分 别为0 级、Ⅰ级 和Ⅱ级 预 警 结 果 的 可 靠 性;Gmean,0、Gmean,1和Gmean,2分 别 为0 级、Ⅰ级 和Ⅱ级 预 警 结 果 的稳定性。
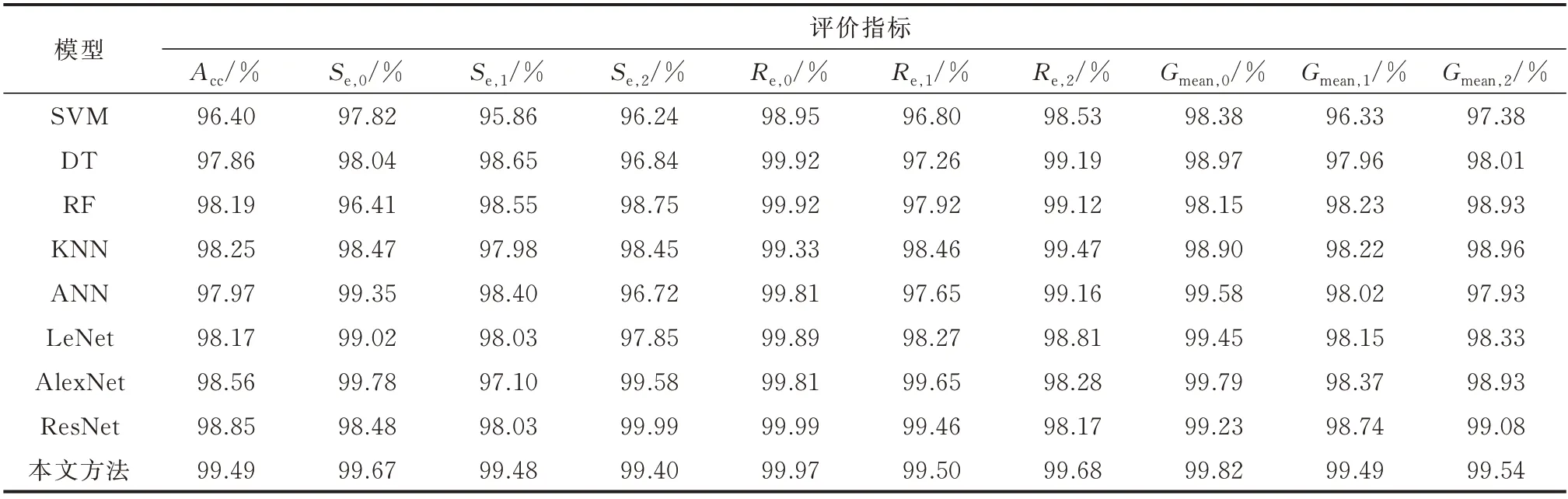
表6 不同分类评估器性能比较Table 6 Performance comparison of different classification evaluators
由表6 可知,本文方法的Acc最高,为99.49%;经典ResNet 的Acc次之,为99.85%。由此可得,改进ResNet 相较于经典ResNet 在频率安全多级预警中具有更高的Acc,验证了本文方法的有效性。
本文方法与各对比方法的预警准确率Acc之差如图2(a)所示。从中不但可以发现本文所提方法的准确率最优,也可以发现在深层学习模型中随着网络层数的加深,准确率也随之上升。本文方法与各对比方法的稳定性Gmean之差如图2(b)所示。从中可以发现本文方法在3 个预警等级中的Gmean均为最优,说明本文方法具有较好的稳定性,兼顾了预警结果的安全性和可靠性。

图2 各对比方法评价指标之差Fig.2 Difference of evaluation index with each comparison method
4.3 鲁棒性分析
电力系统中的数据信息由PMU 获取,然后以报文的形式传输到调度中心,但由于外界干扰、自然灾害等突发情况,可能导致信道损坏或信息缺失,给评估模型的在线应用带来了极大的困难和挑战。
为应对上述情况及验证本文所提方法的鲁棒性,本节构建了一组缺失特征信息递增的指标集合,如表7 所示。其中:∪表示并集;SEP为电磁功率集合;SMP为机械功率集合;SGV为机组机端母线电压集合;SGA为机组机端母线相角集合;SPR为机组旋转备用集合;LBX1为缺失发电机G30和G35的电磁功率集合;LBX2为在LBX1的基础上新增缺失发电机G31和G36的机械功率集合。同理,依次增加相应缺失部分特征信息的机组,构成了LBX3至LBX5集合。

表7 缺失信息集合Table 7 Missing information set
本文方法在指标集合上的鲁棒性验证结果如图3(a)所示。由图可知,随着缺失信息的增多,Acc和Gmean均呈下降趋势,但变化幅度均在0.1%以内,仍保持良好的预测性能。其中,Acc的最小值为99.40%,Gmean,0、Gmean,1和Gmean,2的 最 小 值 分 别 为99.72%、99.37%和99.45%,表明本文方法具有良好的鲁棒性。
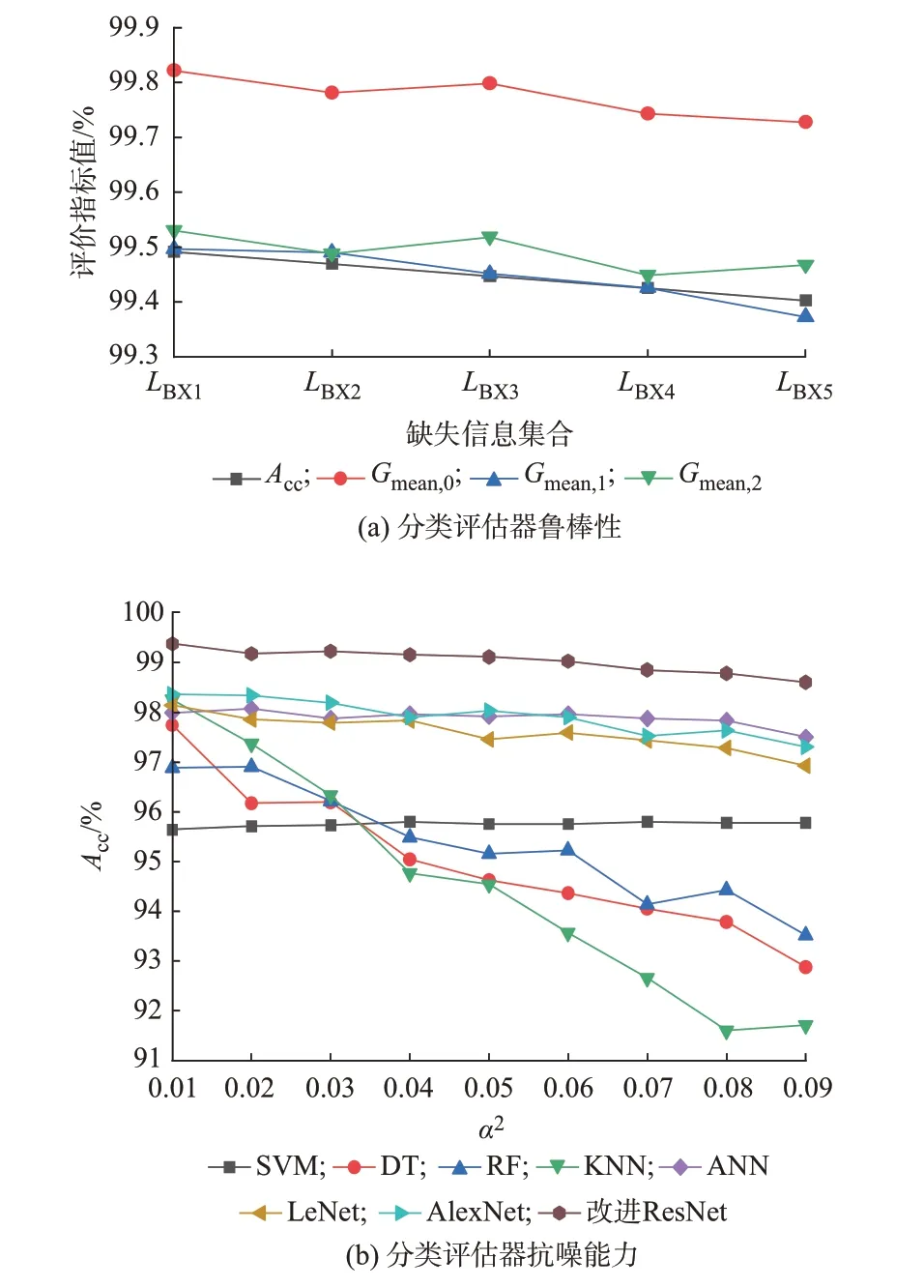
图3 鲁棒性和抗噪能力对比结果Fig.3 Comparison results of robustness and anti-noise ability
良好的鲁棒性证明本文算法在采用不完全信息作为输入时仍能取得较高的计算精度。因此,当在较大系统中应用时,可以选取其中具有代表性的重要机组、等效机组或等效负荷作为输入,这样会极大减小输入信息的数据维度,且不会对计算精度产生严重影响。虽然本文方法选定的输入特征维度与机组数量密切相关,但是当系统内机组数量增加时,采用等效输入信息方法并不会影响本文算法的实用性,亦不会严重影响其计算精度。
4.4 分类评估器抗噪能力分析
在实际在线应用中,由于复杂的工作环境和其他设备的电磁干扰,在数据获取和报文传送过程中均存在大量的干扰,最终导致传输到调度中心的数据中会存在不同程度的噪声污染。
为测试算法的抗噪能力,本文向样本集中添加服从正态分布的不同强度的高斯白噪声来模拟实际应用中的噪声污染。添加噪声的计算公式如下:
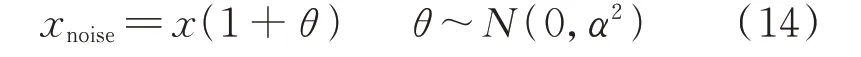
式中:xnoise为添加噪声后的样本;x为原始样本;θ为服从均值为0、方差为α2的高斯分布,且α2∈[0.01,0.09],步长为0.01。
基于添加相同噪声的样本集,本文所提方法与其他不同方法的Acc测试结果如图3(b)所示。其中,浅层学习方法DT、RF 和KNN 的Acc随噪声的增强而大幅下降。在方差为0.09 时,3 种方法的Acc相较于本文方法分别降低了5.72%、5.08% 和7.18%。SVM 方法的Acc较为稳定,受噪声影响较小,但其在9 种噪声强度下的Acc均低于本文方法2.8%~3.8%。综上可知,在9 种不同强度的噪声下,本文方法的抗噪能力均优于4 种浅层学习方法。
ANN、LeNet 和AlexNet 方法的Acc随噪声增强而轻微下降,但是整体波动不大,然而3 种方法的Acc仍低于本文方法1%~2%。在方差为0.09 时,3 种方法的Acc分别低于所提方法1.11%、1.68%和1.30%。综上表明,相较于其他浅层学习方法和深层学习方法,本文方法在对频率安全多级预警时具有较强的抗噪能力。
4.5 危险程度预测分析
在本文所提方法中,第2 阶段利用深度学习中的回归预测方法和从系统中获取的原始信息,对扰动后系统频率的危险程度进行预测。
根据表5 可知,Ⅰ级预警样本共9 692 个,按照4∶1 随机划分训练集和测试集后,测试集包含1 939 个样本。该测试集中各样本D1的误差平方分布如图4(a)所示,且测试集的EMSE为0.000 557。此外,D1的误差平方小于测试集EMSE的样本占比为68.18%,表明预测稳定性较高。
Ⅱ级预警样本共8 269 个,测试集包含1 654 个样本。测试集中D2的误差平方分布如图4(b)所示,且测试集的EMSE为0.000 180。此外,D2的误差平方小于测试集EMSE的样本占比为75.33%,同样表明其预测稳定性较高。
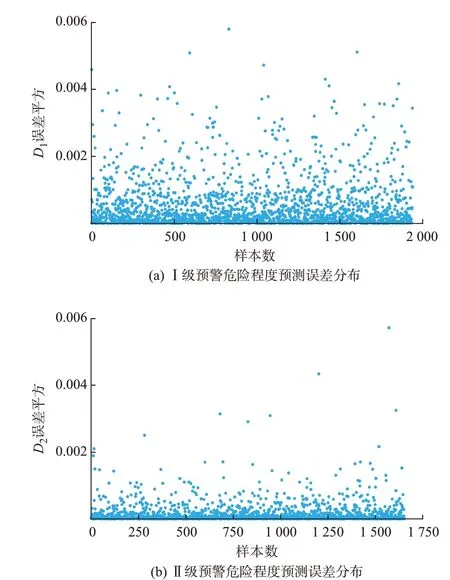
图4 危险程度预测结果Fig.4 Forecasting results of risk degree
4.6 “两阶段”方式的意义
本文中第1 阶段是以深度学习中多分类任务为基础的电力系统频率安全多级预警,其结果是直接通过分类算法得到的更为直观和便于理解的预警等级。第2 阶段利用深度学习中的回归预测方法和从系统中获取的原始信息,对扰动后系统频率的危险程度进行预测。综上,本文“两阶段”方式为2 个计算过程相互独立,但计算结果又相互补充的整体。
此外,本文在制定频率安全多级预警标准时根据国标对“频率最低点”进行划分,便于利用深度学习中的多分类思想给出更易理解的结果,而非具体的系统频率偏移最大值。本文提出的两阶段电力系统频率安全多级预警模型,从另一条路径实现了国标要求和频率安全评估任务的有机结合,而不再是常见的仅频率最大偏移值的计算/预测。
4.7 算法局限性分析
在深度学习中,通常使用浮点运算次数(floating-point operations,FLOPs)[28]来 衡 量 算 法 的复杂度。使用网络参数量(Params)[29]来表示算法中需要训练的参数总量,用来衡量算法对硬件水平的要求。FLOPs 和Params 越低,表明算法的性能越好。
本 文 方 法 与LeNet、AlexNet 和ResNet 方 法 的FLOPs 和Params 对比结果如表8 所示。在FLOPs方面,本文方法明显高于LeNet 方法,是其2 倍以上。在Params 方面,本文方法远大于LeNet 和AlexNet 方法。因此,本文方法的算法复杂度和对硬件水平的要求未实现最优,这也是本文方法的局限性。但是,由4.2 节至4.4 节的对比测试结果可知,FLOPs 和Params 两方面的局限性未对计算结果产生直接影响。
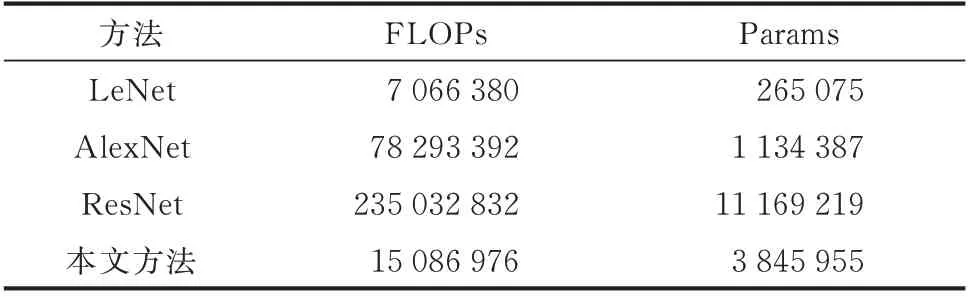
表8 FLOPs 和Params 的 对 比Table 8 Comparison of FLOPs and Params
4.8 在线安全预警的意义
保障电力系统中数据准确快速的获取是本文方法在线应用的前提。目前PMU 作为电力系统中广域同步相量测量系统的基本单元,全球定位系统(GPS)或北斗卫星系统可以为PMU 提供全网统一的时钟信号,其时间误差小于l μs,保证了PMU 设备之间的时间准确性和统一性[30]。在实际系统中PMU 采样频率一般在103~104 Hz,数据传输实时性要求为20 ms[31]。中国要求PMU 装置的输出时延,即实时监测数据时标与数据输出时刻的时间差不应大于30 ms[32]。因此,利用PMU 可以保障在线应用中电力系统实时数据的快速获取。
时域仿真法与本文方法对测试集的预警耗时对比如下:对于测试集中的4 524 个样本,时域仿真法共耗时50 808 s,即14.113 h,单个样本预警耗时11.231 s;本文方法共耗时4.735 s,即每个样本仅用时0.962 ms。
此外,在线应用的响应时间是评估智能方法的重要指标之一。本文所提方法的在线预警时间Tew共包括以下三部分:
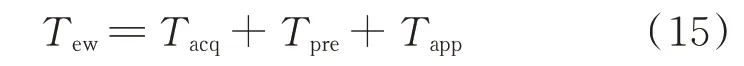
式中:Tacq为各节点数据自动采集和传输的综合时间;Tpre为调度中心对在线数据的预处理时间;Tapp为算法的在线应用耗时。
由于系统的拓扑结构很少发生变化,输入特征确定后,Tpre和Tapp将基本保持不变。因此,Tew的差异主要由Tacq引起。扰动方式和扰动位置等情况的不同均会引起Tacq的差异。经测算本文算例的Tew保持在39.730 ms 至53.528 ms 之间。因此,本文方法可以满足在线预警的快速性要求。
当系统突发较大有功扰动时,如检测到机组或负荷的较大有功功率突变,则频率安全预警会被触发,调度中心便会自动召唤PMU 开始上传所需数据。在获取系统实时扰动数据后便可以立即得出该扰动是否会引起频率安全事故以及具体是何等级的频率安全事故,对在二次调频中选用何种调频策略具有重要参考意义。
综上所述,本文方法在实时数据获取和在线预警时间两方面均能保障频率安全预警的快速性,满足在线应用中对时间的要求。
4.9 本文方法可信度分析
本文基于3 种基本运行工况和3 种随机有功扰动方式构建了综合样本集。首先,将样本集按4∶1的比例随机划分为训练集和测试集,对所提方法进行验证,通过与其他8 种具有代表性的分类评估器对比,本文方法的预警准确率最优。然后,在4.3 节中构建了5 个信息缺失集合,测试了本文方法的鲁棒性,测试结果表明本文方法在Acc和Gmean两方面均有良好的表现。其次,在4.4 节中向样本集添加9种不同强度的高斯噪声,以测试本文方法的抗噪能力。由图3(b)可知,相较于其他7 种对比方法,本文方法具有最高的预警准确率Acc。
综上,通过与多种分类评估器的对比测试、鲁棒性测试以及抗噪能力的对比测试,可说明本文方法具有较高的可信度。
5 美国伊利诺伊州中部电网200 点系统
5.1 实际系统及样本集构造
本文选取美国伊利诺伊州中部电网作为实际系统算例来进一步验证本文方法。该系统共包含200 条母线、49 台发电机、160 个负荷。系统具体参数见文献[33]。此外,为了体现可再生能源的影响,本文在该系统中增加了6 个分布式风电场。
构造样本集的思路与4.1 节中仿真设置的思路相似。但是伊利诺伊州系统的规模和复杂度是IEEE 10 机39 节点系统的5 倍。此外,在基本运行工况方面,新系统的可再生能源占比最高达到了30%。在有功扰动方面,在新系统的49 台发电机中随机选取21 台模拟切机扰动,负荷扰动和发电机出力波动范围扩大为0 到15%之间。因此,根据伊利诺伊州系统构造的样本集具有更大的扰动范围和更多的扰动位置,确保样本集能够表达实际系统扰动/故障的随机性和不确定性。
最终,本文根据改进后的伊利诺伊州系统通过时域仿真法构建了一个包含46 410 个样本的综合样本集。该样本集规模是4.1 节中样本集的2 倍以上。本节同样将样本集按4∶1 的比例随机划分为训练集和测试集,其中,训练集包含37 128 个样本,测试集包含9 282 个样本。综合考虑系统规模和样本集规模,伊利诺伊州系统的多级频率安全学习和预警难度远远大于IEEE 10 机39 节点系统。
5.2 实际系统的频率安全多级预警
为了进一步验证所提方法在实际系统中的频率安全多级预警性能,基于5.1 节中构建的样本集,本节选用与4.2 节中相同的深度学习算法LeNet、AlexNet 和经典ResNet 与本文方法进行对比,结果如表9 所示。

表9 不同分类评估器性能比较Table 9 Performance comparison of different classification evaluators
由表9 可知,本文方法的预警准确率Acc依然取得了最佳,为98%。通过与其他3 种经典的二维CNN 的比较,说明本文方法具有较高的预警精度。此外,在3 个等级的预警稳定性Gmean方面,本文方法也均为最优,说明该方法在面对扰动/故障更为随机和复杂的实际系统时,具有良好的预警稳定性,兼顾到了预警结果的安全性和可靠性。通过采用更庞大和更复杂的实际系统作为算例,且与经典深度学习网络的对比,不但说明了本文方法的有效性,而且再次验证了本文方法的优良性能。
此外,由于伊利诺伊州系统的网络规模、运行工况和扰动方式远比IEEE 10 机39 节点系统复杂,学习和预警难度更大,导致表9 中各方法的预警精度低于表6 中IEEE 10 机39 节点系统的结果。
5.3 实际系统的频率危险程度预测
本文所提方法的第2 阶段是对扰动后系统频率的危险程度进行预测。在5.1 节的实际系统样本集中,同样按照4∶1 对Ⅰ级和Ⅱ级预警结果的危险程度随机划分训练集和测试集。
Ⅰ级预警结果的危险程度测试集中各样本D1的误差平方分布如图5(a)所示,且测试集的EMSE为0.000 628。D1的误差平方小于测试集EMSE的样本占比为78.02%,表明预测稳定性较高。Ⅱ级预警结果的危险程度测试集中D2的误差平方分布如图5(b)所示,且测试集的EMSE为0.000 302。D2的误差平方小于测试集EMSE的样本占比为74%,同样表明其预测稳定性较高。
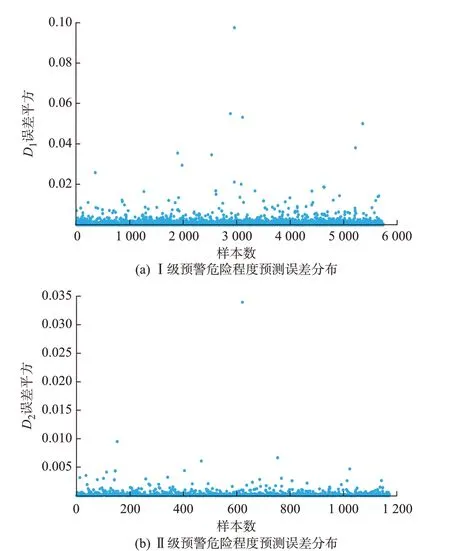
图5 实际系统的频率危险程度预测结果Fig.5 Forecasting results of frequency risk degree in actual system
综合D1和D2的EMSE和误差平方分布图可知,本文方法在面对实际系统的频率危险程度预测时也能达到较高的精度,可以确保在线应用时第2 阶段的预测性能,为运行人员提供准确的预测结果,给后续控制策略的选择提供有力的参考。
6 结语
在“双碳”目标和可再生能源发电集群大规模并网运行的背景下,为对电力系统受扰后频率安全进行快速和准确的预警,本文提出了一种基于改进残差网络的两阶段电力系统频率安全多级预警模型,并采用改进IEEE 10 机39 节点系统和伊利诺伊州200 节点系统作为仿真算例对该模型进行了测试,结论如下:
1)参考国标要求对系统的频率安全评价标准进行多级精细划分,提出并构建了电力系统频率安全多级预警模型,该评价标准更加合理和符合系统的实际运行情况。
2)第1 阶段的测试结果表明,在多种运行工况和有功扰动方式下,该分类评估器不但具有较高的预警准确率,且具有良好的稳定性,优于浅层学习方法和其他深度学习模型。
3)针对IEEE 10 机39 节点系统的信息缺失和噪声干扰的情况,本文方法相较于其他方法均能得到较高的预警精度和稳定性,故该模型具有良好的鲁棒性和抗噪能力。
4)第2 阶段的实验结果表明,本文方法可以准确预测相应预警等级下的系统频率危险程度,通过给出更加直观的数值化表述,为后续控制策略的选择提供重要参考。
“双碳”目标下可再生能源占比会继续扩大,运行工况和扰动形式会更加复杂多样,频率的动态波动会更加频繁和迅速。面对上述情况,利用迁移学习对已训练好的模型进行在线快速更新是下一步的研究重点。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
