基于多主体投资的双储能系统分层优化配置方案

2023-02-02卞一帆谢丽蓉鲁宗相

电力系统自动化 2023年1期

卞一帆，谢丽蓉，鲁宗相，叶林，路朋，马伟，

（1. 可再生能源发电与并网技术教育部工程研究中心（新疆大学），新疆维吾尔自治区乌鲁木齐市 830017；2. 电力系统及发电设备控制和仿真国家重点实验室（清华大学），北京市 100084；3. 中国农业大学信息与电气工程学院，北京市 100083）

0 引言

为实现“碳达峰·碳中和”的能源战略目标、推进中国电力市场深化改革，国家发展和改革委员会鼓励各类投资主体投资各类电源、储能（energy storage，ES）及增量配电网项目［1］。近年来，储能在电力系统的发电环节得到了广泛应用，风电场中的储能主要起到调峰调频［2］、平抑风电功率波动［3］、消纳弃风［4］、补偿风电预测误差［5］等作用。储能的灵活调节能力可有效平衡风电出力的随机性、间歇性和反调峰特性，从而促进风电消纳［6］。在风储系统的相关研究中，储能的优化配置以及如何降低储能成本等问题是当下研究的热点。

针对储能的优化配置问题，文献［7-9］分析了传统单投资主体下的储能优化配置方法。其中，文献［7］考虑网架结构，提出一种以风储联合运行效益最大为目标的配置方法；文献［8］基于模型预测控制提出在不同平抑策略下的发电侧储能配置方案；文献［9］考虑储能充放电的损耗，利用频谱分析和低通滤波来求解风储最优配置结果。但上述文献中单一投资主体将承担巨大的储能配置成本，不利于其经济性。

为提高投资主体的经济收益，文献［10-11］对储能运行策略进行了优化。其中，文献［10］采用了考虑循环寿命的双储能运行策略，结果表明所提策略可提升储能经济性，但该策略只是在配置单一储能后，人为增加一个规模相等的储能，并没有对两组储能进行统一优化；文献［11］利用分级控制实现了对双退役电池组充放电功能的动态切换，从而提升了经济性，但退役电池再利用的安全性有待进一步考证。文献［12-14］对项目投资模式进行了研究，表明多主体投资电力项目可将成本有效分散到各投资方，从而提升项目经济性。其中，文献［12］基于演化博弈提出一种配电网与微电网运营商联合投资的微电网规划方法；文献［13］提出一种基于改进非支配排序遗传算法的综合能源多主体投资利益均衡优化调度方法；文献［14］提出一种基于成本效益分析和非支配排序遗传算法求解的多主体投资虚拟电厂容量配置模型。但目前关于多主体投资的研究主要集中于对微电网、综合能源系统、虚拟电厂的规划问题，对储能规划问题的研究较少。

针对以上问题，本文首先采用“交替工作、同步切换”方式的双储能运行策略，以减小储能频繁切换带来的寿命损耗；然后，提出储能分层优化经济性模型，以实现投资主体利益均衡及最大化、保持储能较强的充放电能力；进一步，采用单、多目标黏菌算法和模糊隶属度函数对分层模型进行求解，得到双储能的最佳配置结果；最后，利用实际数据对本文方案进行验证，并对钠硫电池（sodium sulfur battery，NAS）、全钒液流电池（vanadium redox battery，VRB）、多硫化物/溴液流电池（polysulfide bromine battery，PSB）、阀控式铅酸电池（valve-regulated lead-acid battery，VRLA）、磷酸铁锂电池（lithium iron phosphate battery，LFP）的运行效果进行对比分析。

1 双储能系统运行策略

对于储能类型的选取，目前大多数学者主要考虑目标实现效果及成本，一般采用能够实现大容量能量存储的单一能量型储能，但其与双储能相比响应时间更长，影响了储能作用效果［15］。在完成相同消纳任务的前提下，相较于双储能，单一储能频繁的充放电状态转换将导致循环寿命快速耗尽，缩短储能的服役年限，从而极大地降低储能的经济性［11］。因此，本文基于文献［16-17］将两个容量相等、功率相等的储能A 和B 组合，提出一种双储能运行策略。具体策略如下：

1）两组储能采用“交替工作”方式，分别承担充电和放电工作，且同一时段内只有一组储能工作。当一组储能处于充电或放电状态时，另一组储能处于浮充待放电状态或浮充待充电状态。为简化分析，将浮充待充电状态和浮充待放电状态分别归结为充、放电状态。

2）两组储能采用“同步切换”方式，当达到切换条件时，两组储能在运行时段交界处同步切换，具体切换策略见附录A。

3）重复过程2），直至仿真结束。

2 多主体投资风储系统分层优化配置模型

如何合理配置储能容量和功率、提高系统消纳弃风的能力和运营商收益是规划储能的重点。相较于单主体投资模式，多主体投资模式具有更多的投资运营商，可对项目投资成本进行有效分摊。本章建立多主体投资模式下的储能优化配置模型。

2.1 优化模型整体框架

综合考虑储能充放电能力指标和多投资主体收益建立储能分层优化模型。其中，上层优化模型负责分配双方主体对储能的投资运维成本和收益，达到双方主体利益最大化；下层优化模型负责优化储能充放电能力，使双储能保持较强的充放电能力。分层优化方案结构如图1 所示。

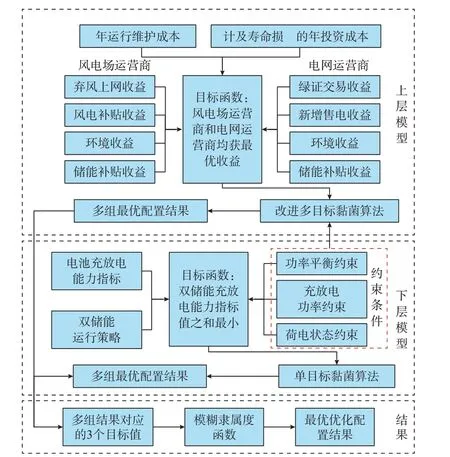
图1 经济优化配置的分层优化方案结构Fig.1 Structure of hierarchical optimization scheme for economic optimal allocation

2.2 上层目标函数

在规划储能电站时，双方主体目标为配置储能后各自年总收益最大，即

式中：f1为风电场运营商年收益；f2为电网运营商年收益；Fcur为弃风上网收入；Fsub，w为弃风上网补贴；α为风电场运营商投资占比和分成系数，取值在0 到1之间；Fevn为环境收益；Fsub，s为储能投运补贴收入；Crun，year为双储能年运行维护成本；Cinv，year为计及寿命损耗的双储能年投资成本；Ftgc为电网绿证交易年收入；Fsel为电网年新增售电收益。

1）计及寿命损耗的年投资成本

储能投资建设成本包括硬件和软件成本，其中，硬件成本是指配备一定容量储能的成本，软件成本是指配置功率转换系统（power conversion system，PCS）、电池管理系统（battery management system，BMS）等设备的成本［18］。该成本函数如下：

式中：Cinv为储能初始投资成本；CE为储能单位容量成本；Eb，A、Eb，B和Pb，A、Pb，B分别为储能A、B 的额定容量和额定功率；CP为储能PCS 单位功率成本；r为贴现率，取6%；τbat为双储能使用年限。

双储能的循环寿命受到工作温度、充放电切换次数、放电深度等因素的影响，储能的运行会造成其性能的缓慢衰退并产生循环寿命损耗［10］。为准确计算双储能使用年限τbat，本文主要计及储能A、B 充放电次数和放电深度对循环寿命的影响［17］。

2）年运行维护成本

储能系统运行维护成本主要与储能电池规模大小有关，包含由功率转换子系统决定的固定部分和储能充放电电量决定的可变部分［20］。该成本函数如下：

式中：Crun为储能系统全生命周期的运行维护成本；Crun，P为储能单位功率运行维护成本；Crun，E为单位容量运行维护成本；W1，i为储能第i年总充放电电量；i为双储能系统建设以来运行的年数。

3）年弃风上网收益

建设储能系统后，可将弃风电量储存并在负荷高峰时并入电网，以获得弃风上网收益。年弃风上网收益Fcur计算如下：

式中：C1为风电上网指导单价；W2(t)为t时段内弃风上网量。

4）年风电补贴收益

由国家发展和改革委员会发布的《关于完善风电上网电价政策的通知》［21］可知，若风电场满足政策要求，则新增上网电量将得到补贴收入。年风电补贴收益Fsub，w计算如下：

式中：C2为风电上网补贴单价。

5）年环境收益

储能的环境效益主要包括两部分：一部分是将部分弃风电量上网从而减少传统火电机组并网电量，实现温室气体、污染物（主要包括CO2、SO2、NOx、碳粉尘和悬浮颗粒物等）减排产生的效益［17］；另一部分为储能寿命终结后从电池中提取金属材料的回收收益。年环境收益Fenv计算如下：

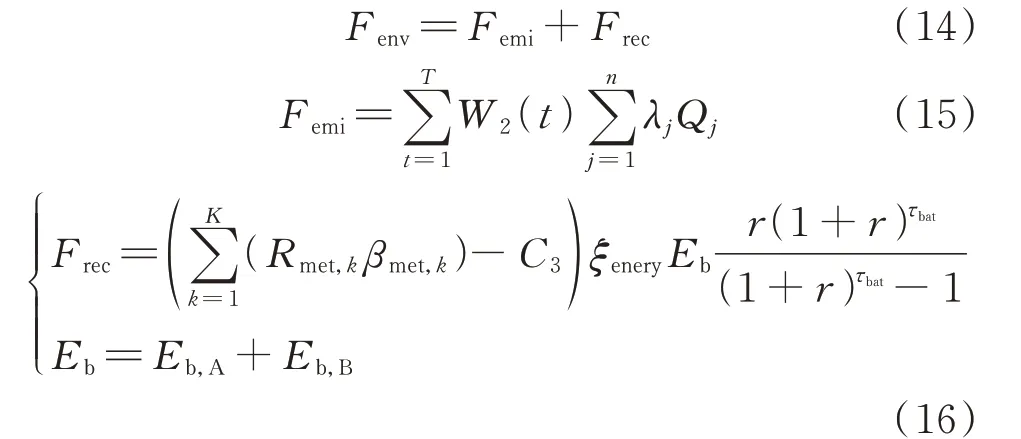
式中：Femi为减少传统机组污染年收益；Frec为储能电池回收收益等年值；n为排放污染物总数；λj为第j种污染物环境负荷量单位成本；Qj为传统火电机组发电第j种污染物排放量；K为电池所含金属类别总数；Rmet，k为金属k的单价；βmet，k为单位重量储能电池中金属k的含量；C3为处理单位重量废电池所需生产性支出；ξenery为储能电池能重比；Eb为储能系统总容量。

6）年储能补贴收益

对于“新能源+储能”项目中自发自储设施所发售的省内电网电量，可根据不同地区的相关补贴政策得到补贴收入，如青海省是给予0.10 元/（kW·h）的运营补贴［22］。年储能补贴收益Fsub，s计算如下：

式中：C4为储能发售电能补贴单价。

7）电网年绿色证书交易收益

可交易绿色证书（tradable green certificate，TGC）是较为常见的一种配额制度，电网公司的证书数量代表其对配额制要求完成的情况［23］。若电网公司无法满足配额制要求，则会受到相关部门的惩罚。因此，电网公司会从电源侧购买可再生能源电能来获得证书，或者从市场侧通过购买其他电网公司的冗余证书来满足配额要求。

弃风上网电量是新增接入电网的可再生能源电量，可利用TGC 制度将其转换为电网运营商的收入。电网年绿色证书交易收益Ftgc计算如下：

式中：C5为绿色证书交易单价。

8）电网年售电收益

电网运营商将储能消纳的电能经输电网传输售卖给用户，可获得相应的售电收入。电网年售电收益Fsel计算如下：

2.3 下层目标函数

在参与弃风消纳时，应尽量将两个储能的荷电状态（state of charge，SOC）维持在理想区间内，以保证足够的充放电容量储备。利用电池充放电能力指标f3来衡量电池SOC 偏离理想区间的程度［24］，其值越大，表明储能电池的SOC 偏离理想区间的程度越深。当电池的SOC 为0.5 时，说明电池具有良好的充放电容量储备，文献［25］设定电池SOC 理想区间为［0.4，0.6］，本文选取更严格的区间为［0.45，0.55］。则下层优化目标为储能A、B 在年调度周期内电池充放电能力指标值之和最小，即

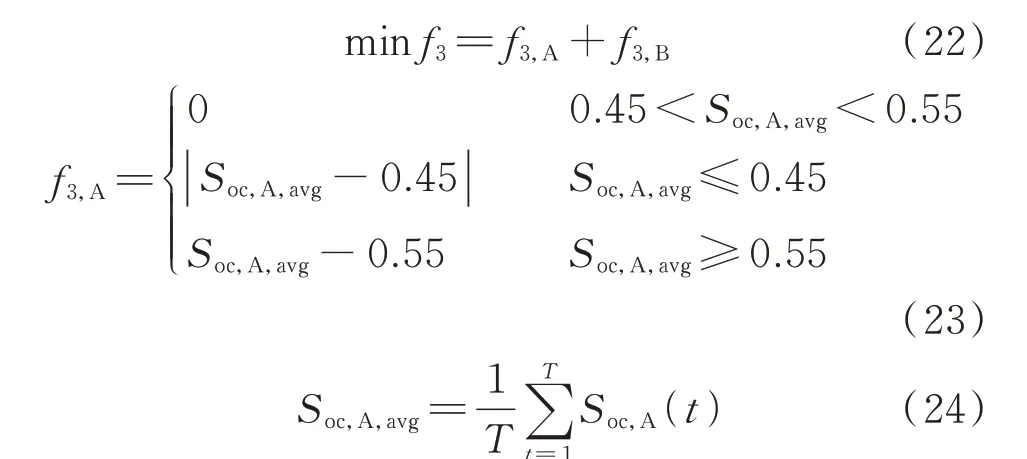
式中：f3，A、f3，B分别为储能A、B 在年调度周期内的电池充放电能力指标值；Soc，A，avg为储能A 的SOC 在年调度周期内的平均值；Soc，A(t)为t时段末储能A 的SOC 大小。储能B 的充放电能力指标值计算方法同储能A，这里不再赘述。

2.4 约束条件

储能约束包括储能充放电功率约束、SOC 约束、功率平衡约束，储能A 与储能B 的约束一致，此处仅描述储能A 的约束条件。

1）储能A 充放电功率约束

假设储能电池在t时段内充放电功率恒定，则其充放电功率不仅与额定功率、弃风功率有关，而且与储能电池剩余充放电容量有关。

式中：Pcha，A(t) 为t时段内储能A 的充电功率；Pdis，A(t)为t时段内储能A 的放电功率；Pwin(t)为t时段内的风电场输出功率；Pnet(t)为风储系统t时段内的并网功率；Soc，A，max、Soc，A，min分别为储能A 的SOC 上、下限值；η为储能电池充放电效率；Δt为仿真步长。

2）储能A 的SOC 约束

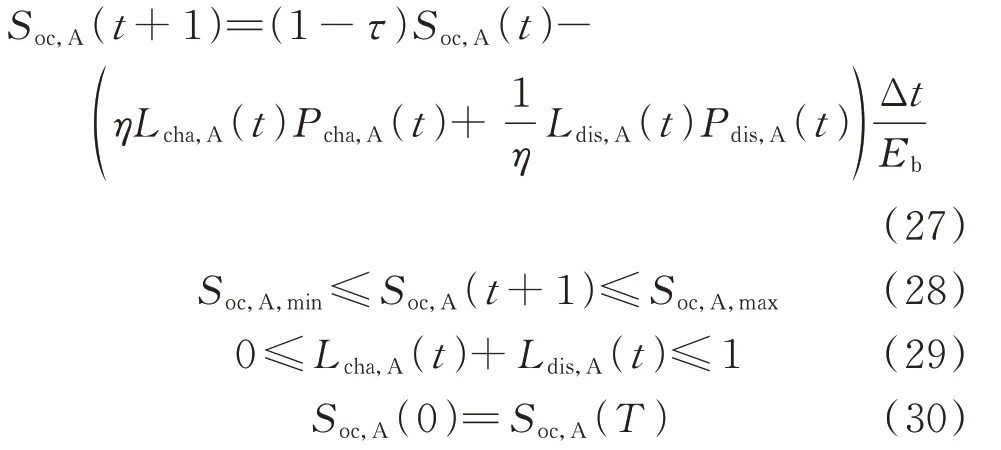
式中：τ为储能的自放电率；Lcha，A(t)为t时段储能的充电状态，取值为0 或1，其中0 表示浮充等待放电、1 表示充电；Ldis，A(t)为t时段储能的放电状态，取值为0 或1，其中0 表示浮充等待充电、1 表示放电；Soc，A(0)为储能A 的初始SOC；Soc，A(T)为调度期结束时储能A 的SOC。

3）系统功率平衡约束

并网功率为风电输出功率与储能电站充放电功率之和。系统功率平衡约束如下：

储能B 的Lcha，B(t)、Ldis，B(t)、Pcha，B(t)、Pdis，B(t)等参数含义同储能A 参数。

3 双储能系统多主体投资经济性评估指标

选取经典投资评价指标（投资回收期和投资收益率）对双储能的经济效益进行科学评价。

1）投资回收期

投资回收期是从时间角度衡量项目投资风险程度的重要指标，本文选用投资回收期作为评价指标［26］。计算公式如下：

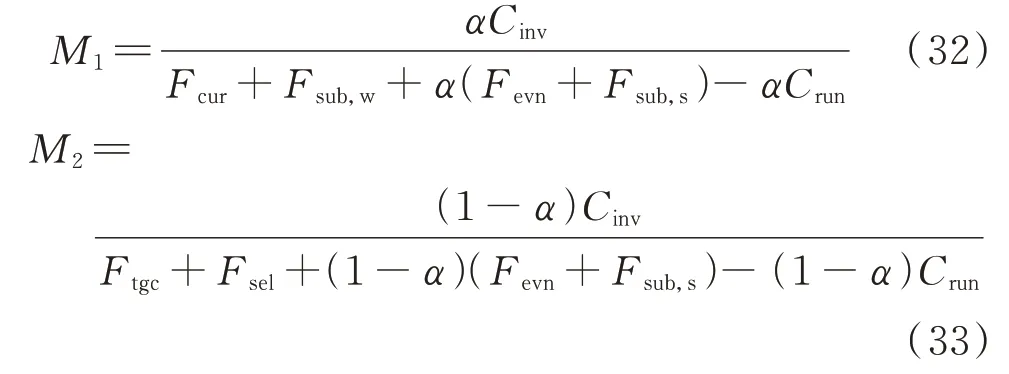
式中：M1为针对风电场投资储能的投资回收期；M2为针对电网投资储能的投资回收期。投资回收期越短，说明对该储能的投资越保险。

2）投资收益率

投资收益率是衡量投资项目盈利水平的一个经济指标，可用系统全生命周期内的年均总收益与总投资运营成本的比值来表示。计算公式如下：

式中：M3为针对风电场的投资收益率；M4为针对电网的投资收益率；Crun，i为储能系统第i年的运行维护成本。投资收益率越大，说明该投资项目的盈利水平越好。

4 模型求解

智能算法对数学模型要求较低、应用方便，在电力系统优化问题上已有较成熟的应用。本文的配置模型是非线性、多约束的混合整数优化问题，可采用改进多目标黏菌算法对其进行求解，得到多组配置结果后利用模糊隶属度理论求得最优折中解。

4.1 多目标黏菌算法

黏菌算法通过使用权值来模拟觅食过程中的正负反馈，并根据食物的品质来调整黏菌的搜索路径［27］。文献［28］在此基础上，提出了多目标黏菌算法，并证明了算法的有效性。

4.2 改进多目标黏菌算法

本文将广义反向学习策略应用到多目标黏菌算法的初始化阶段。假设xk={xk，1，…，xk，w，…，xk，v}∈X是初始种群中的第k个随机个体，其个体变量维数为v，并且该个体的第w维变量满足xk，w∈[lw，uw]，权重因子a是0～1 之间的随机数。则该个体的反向个体o(xk)={o(xk，1)，…，o(xk，w)，…，o(xk，v)} 可利用式（36）求得。

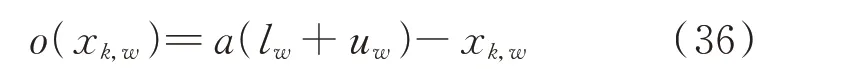
对改进多目标黏菌算法的性能测试环节和算例模拟仿真步骤见附录B。

4.3 确定最优配置结果

上层优化模型的目标函数和下层优化模型的目标函数的量纲不同，本文根据模糊集理论来确定各组配置结果中各目标的满意度。可用模糊隶属度hd表示：

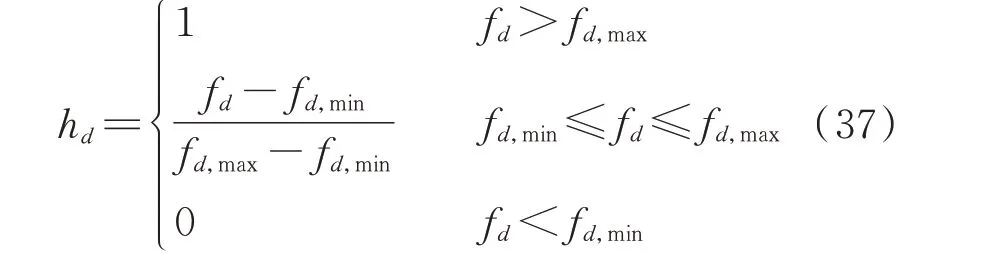
式中：fd为第d个目标函数值（d=1，2，3）；fd，min、fd，max分别为第d个目标函数的最小值、最大值。hd为0或1 时表示对第d个目标函数完全不满意或完全满意。定义所有配置结果的标准化满意度为：

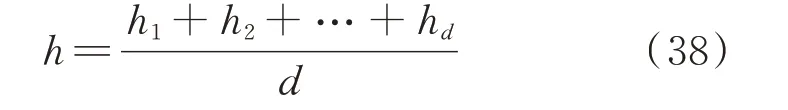
式中：h为各组配置结果的标准化满意度。最后，选取标准化满意度最大的配置结果作为最优配置结果。

5 算例分析

5.1 算例参数

为测试改进算法在电力系统多目标求解中的性能，将改进多目标黏菌算法与4 种经典的多目标智能算法进行对比，所有算法的参数设置见附录B 表B1。选取经典双目标ZDT1-6 系列函数作为测试函数，测试对比统计结果见附录B 表B2。

选取中国新疆哈密地区某200 MW 风电场数据、负荷数据、分时电价数据建立算例系统，算例参数设置见附录C 表C1。利用K-means 聚类算法求取春、夏、秋、冬4 个季节典型日的风电数据和负荷数据，并求取其加权平均值得到一年内某典型日的风电数据和负荷数据，见附录C 图C1。运用本文所提方案，对5 种不同蓄电池进行配置，电池参数［29］见附录C 表C2、表C3。

5.2 优化配置结果

划分4 种场景对储能电池容量进行分层优化配置。情景1：单主体投资单储能；情景2：单主体投资双储能；情景3：多主体投资单储能；情景4：多主体投资双储能。

5 种电池优化配置结果见附录C 表C4。分别对比情景1 与情景3、情景2 与情景4 可知，多主体投资情景下的储能容量和功率较大。假设储能充电为正、放电为负，以磷酸铁锂电池配置结果为例，绘制多主体投资情景2、4 中储能A 和B 充放电功率随时间变化的情况，见附录C 图C2。由图C2 可以看出，储能A、B 处于“交替工作、同步切换”模式。

5.3 最优储能配置效果对比分析

5 种电池在4 种不同投资情景下的最优储能配置的具体运行效果对比如表1 所示。

表1 不同投资情景下的最优储能配置效果对比Table 1 Effect comparison of optimal energy storage configuration in different investment scenarios

分别对比情景1 与情景2、情景3 与情景4 可知，双储能在给投资商带来较高收益的同时可消纳更多弃风，说明双储能切换策略带来的增效益可以弥补大容量大功率的成本增加。双储能相比于传统单储能的优越性在附录D 中给出了详细的论证。分别对比情景1 与情景3、情景2 与情景4 可知，多主体投资相较于单主体，在为风电场运营商带来较大收益并提升系统弃风消纳能力的同时，可以为电网运营商带来效益，实现多投资主体的互利共赢。

电池参数雷达对比图如附录E 图E1 所示。分析情景4 中5 种电池的配置效果可知，LFP 为双方运营商带来的收益分别高达753.73 万元和427.45 万元，双储能充放电指标低至0.005，消纳弃风电量高达14 019 MW·h，是较理想的储能类型。而目前推广较为顺利的是VRLA，主要原因在于它的技术成熟度高，但VRLA 存在循环寿命短、回收价值低的缺点，使得VRLA 给运营商带来的收益较低。相比之下，LFP 能量转换效率高、循环寿命较长，但其高昂的投资成本阻碍了它的推广与应用。与其他储能电池相比，NAS、PSB 和VRB 的经济优势适中，有望在电力系统中得到大量应用。

5.4 经济性分析

根据第3 章的经济性评价指标模型，运营商的投资回收期和投资收益率如图2 所示。

投资回收期越短，投资风险就越小，对项目投资者越有利。对图2 进行分析可知，PSB 的投资风险较小，LFP 和VRB 的投资风险较大，但不同电池在不同情景下的投资回收期均在15 年或10 年的设计使用年限内，故均具备经济性。

图2 不同电池在不同情景下的经济性指标值Fig.2 Economic indices of different batteries in different scenarios

投资回报率越大，说明投资项目的盈利水平越高。图中，VRLA 的投资收益率较大，VRB 和LFP的投资收益率较小，VRLA 的投资收益率最大是其仍得到广泛使用的原因之一，而LFP、VRB 的寿命特性相对VRLA 更有优势，但高昂的成本导致其投资收益率较小。

在多主体投资模式下，不同的投资占比和不同的SOC 理想区间会对储能最优配置结果产生影响。为此，下文将以多主体投资LFP 为例，进一步分析储能电池成本、电池SOC 理想区间、运营商投资占比对双储能系统的影响。

5.4.1 电池成本变化的影响分析

随着储能技术的发展，储能单位成本也会降低，不同储能成本下的最优配置结果如图3（a）所示，储能成本按照10%递减，容量起初有明显增长趋势，随后涨势趋于平缓。这是因为当储能容量足够大时，选取合适的功率便可消纳较多弃风，继续增大容量只会增加成本。当成本降低70%时，储能的容量比当前约增长9.95 MW·h、功率比当前约增长2.96 MW。对图3（b）和（c）分析可知，储能容量功率的增大可增加弃风消纳量，其所带来的收益增加可以弥补大容量大功率带来的成本增加。但是，随着成本的不断减小，投资回收期均呈现降低的趋势，而投资收益率则大幅度增加，这说明较低的储能成本会减小投资方的投资风险，提升投资方的盈利水平。

图3 储能成本减小对系统的影响Fig.3 Influence of energy storage cost decrease on system

5.4.2 电池SOC 理想区间的影响分析

以［0.45，0.55］为基准，电池SOC 理想区间的左、右边界分别按0.025 间隔递减、递增，图4（a）给出了不同理想区间下的最优配置结果。分析可知，当区间变大后，容量和功率首先呈现减小的趋势，这是因为小容量电池在运行周期结束时也能得到较优的充放电能力指标，较大的SOC 理想区间则弱化了充放电能力指标对配置大容量电池的影响。但随着区间的继续增大，容量和功率出现增长趋势，这是因为较小的容量功率所带来的潜在成本效益已无法弥补其因消纳弃风减少带来的损失。由图4（b）和（c）可知，区间的大小对系统年收益影响较小，对弃风消纳量的影响较大。双方运营商的投资回收期和投资收益率均呈现先减小后增大的趋势，但变化不明显，这说明电池SOC 理想区间的大小对项目的投资风险和盈利水平的影响较小。

图4 电池SOC 理想区间增大对系统的影响Fig.4 Influence of increased SOC ideal range increase of batteries on system

5.4.3 运营商投资占比变化的影响分析

风电场和电网运营商之间存在经济性博弈，不同的投资占比也会影响系统的经济性。因此，图5给出了储能最优配置结果和不同投资占比对系统经济性的影响。当投资占比为0.60～0.65 时，双方运营商的投资收益率相等且双方运营商的投资回收期相差不大，说明风电场运营商储能投资占比取0.60～0.65 的值时，可以更好地平衡双方主体的收益。