基于粒子群算法的量子测量系统最优参数求解*

杜石桥，李贵兰，寇军，郝赫，吴同，秦国卿，高红卫

（北京无线电测量研究所，北京 100854）

0 引言

基于里德堡原子的量子精密测量方法是通过原子的能级跃迁实现外场测量，具有自校准、高灵敏、宽谱接收等特点，从原理上颠覆了传统测量方法，在国防、民用和科学研究（计量、无线通讯和天文观测）等领域中具有明确而广泛的应用前景，近年来成为研究热点［1-16］。2012 年，美国俄克拉荷马大学的J.P.Shaffer 研究团队首次实现了基于里德堡原子的精密测量［1］。2020 年山西大学团队提出了原子超外差接收方法，实现了55 nV/cm/Hz1/2的测量灵敏度，将测量灵敏度突破性地提高了约3 个数量级［12］。

在当前的体制下，为了进一步提升灵敏度，需要对整个实验系统的参数进行全局扫描。然而由于系统包括探测光、耦合光等多个要素，每个要素包含功率、频率等多个参数，对于包含有N个实验参数的系统，如果每个参数扫描50 个点，那么所需要的测量总次数为50N，这将需要耗费大量的时间，阻碍灵敏度的快速提升。因此，2022 年武汉数物所团队通过在实验上对探测光功率、耦合光功率、探测光频率等实验参数进行系统扫描优化，将电场灵敏度提升至12.5 nV/cm/Hz1/2［16］。

为了实现在多维实验参数空间快速找到最优实验参数，本文首先对基于里德堡原子的量子测量系统进行仿真建模，建立实验参数依赖的输出信号模型，再通过粒子群优化算法进行全局搜索，得到输出信号最大时的探测光功率和耦合光功率的最优参数。该方法理论上可以扩展到更高维度实验参数的全局搜索，可指导实验指标的快速提升，加快量子测量系统的工程化应用。

1 原子超外差测量系统建模

1.1 原子量子测量系统原理

基于里德堡原子的量子测量系统简易装置如图1a）所示，探测激光和耦合激光在充满碱金属原子的原子气室中交叠穿过。在三能级系统|1＞，|2＞，|3＞中，当|2＞，|3＞能级由一个较大的耦合场（耦合激光，其拉比频率为Ωc）驱动时（如图1b）所示，其中|3＞态为高激发里德堡态），由于量子干涉在探测激光（拉比频率为Ωp）的透射谱上会产生电磁诱导透明（electromagnetically induced transparency，EIT）现象，如图1c）所示。这时通过频率与能级共振的微波场ΩL会使得EIT 能谱发生劈裂（Autler-Townes，AT 劈裂），劈裂的间距大小等于微波场的拉比频率ΩL，而拉比频率值正比于微波场的幅度和能级间的跃迁偶极矩。通过选择合适的微波场的拉比频率，使得当微波场幅度变化时探测光的透射率变化幅度最大。通过超外差接收方式［12］，一个频率为wRF的微波经过混频会产生一个中频信号wIF，这个中频信号会以Ω（t）=Ω0+ΔΩ（t）的形式调制AT 劈裂的幅度。这个调制最终转化成探测光在共振频率v0时的幅度变化如图1d）所示，其中v0是能够与能级|1＞和能级|2＞共振的探测激光频率。当选择合适的ΩL，Ωp等实验参数时，可以使得透射点的斜率最大，即调制幅度最大，这时候对应信号强度最大［12］。

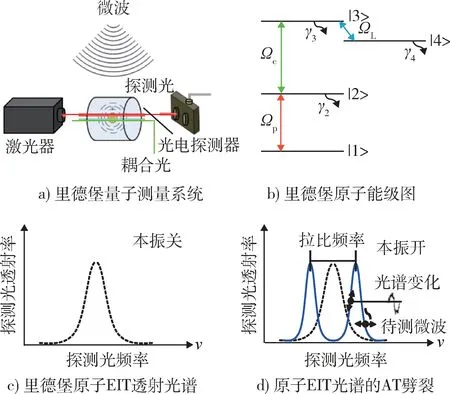
图1 里德堡量子测量系统原理图Fig.1 Rydberg quantum measurement system

1.2 原子量子测量系统建模

本文建立了图1 中所示的实验装置的原理模型，在共振情况下，首先考虑在共振|3＞和|4＞不存在简并的情况下，以量子态|1＞，|2＞，|3＞和|4＞为基矢的哈密顿量为

在考虑自发辐射的情况下，这样的四能级系统的密度矩阵的演化可以写为

式中：D[ρ]为方程的衰减项，其具体形式为

在计算中，由于能级|3＞和|4＞是高激发态里德堡能级，能级寿命相较于能级|1＞和|2＞较长，且能级间隔较小，因此能级|3＞→|4＞之间发生的自发辐射可以省略，γi(i=2，3，4)是衰减项，其中γij=(γi+γj)。

在绝热近似下，探测激光在稳态原子中透射强度可以以极化率虚部的形式写出为

式中：Pi为入射光的功率；L为原子腔的长度；k=2π/λp为探测激光的波矢。其中χ（t）=Cρ12（t）为极化率，其中ρ12（t）是|1＞→|2＞跃迁矩阵元的密度矩阵，C=（2Nμ2）/（ε0ℏΩP）是与原子密度N、能级偶极矩μ、拉比频率Ωp相关的常量。实验上是通过观测P（t）的变化来进行信号检测，因此信号强度正比于ρ12（t）的虚部，因此理论上计算ρ12（t）虚部的变化大小ΔIm［ρ12（t）］，即可反映出信号强度的变化。

在方程的求解过程中，取理论和实验上常用的典型的参数［1，3］，Ωc=1 MHz，Ωp=6 MHz，ΩL=1.2 MHz，ΩS=0.1 MHz，γ2=5 MHz，γ3=500 kHz，γ4=200 kHz。为了模拟待测微波的超外差过程，令ΩL=|ΩL+Ωsexp（iwIFt）|，可以产生中频信号，如图2a）所示，在待测微波的作用下，会使得原子对探测光的吸收率发生变化，即透射谱产生中频信号振荡形式的信号，通过傅里叶变换，可以在频域上观察到中频信号，信号变化的幅度为ΔIm［ρ12（t）］。

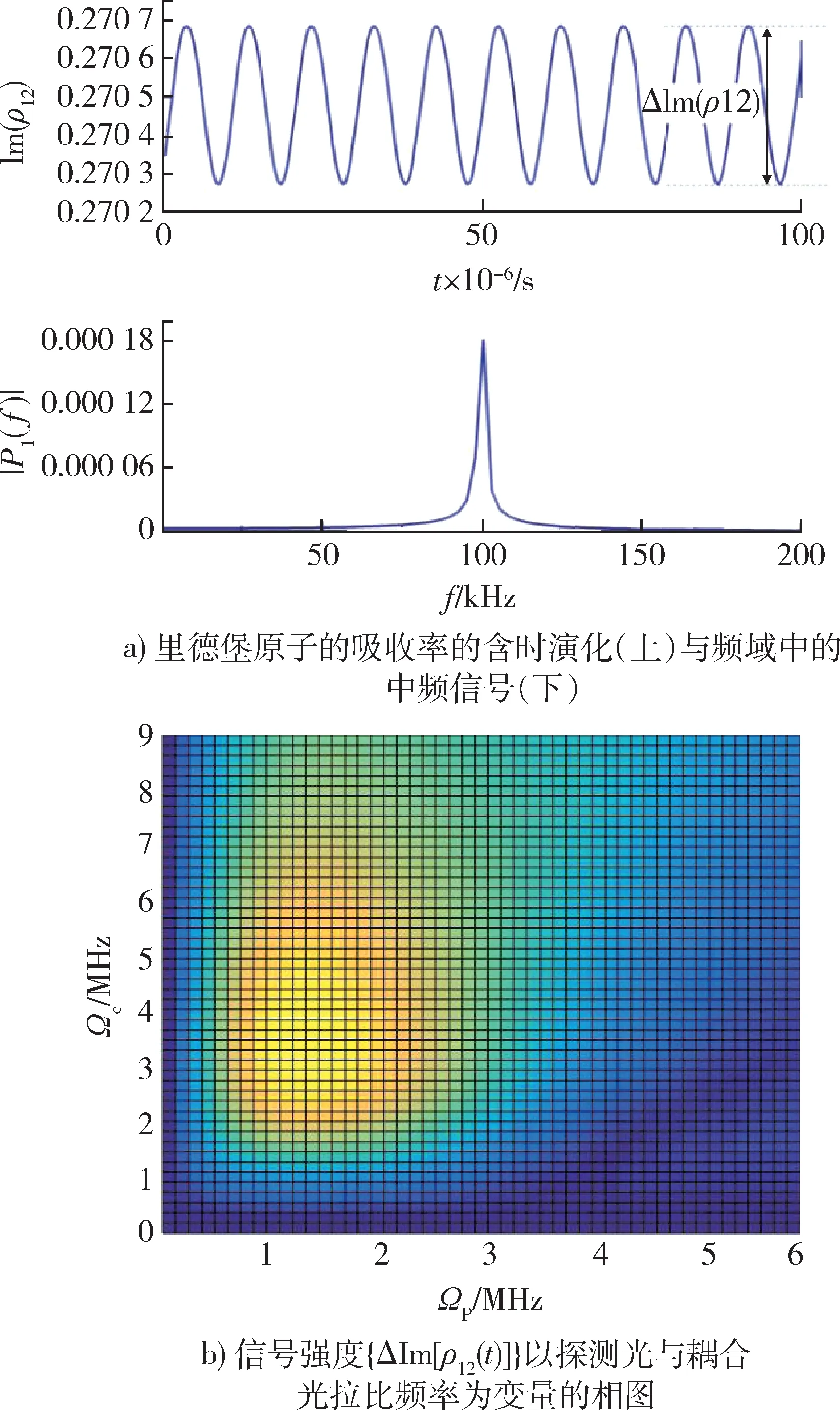
图2 里德堡量子测量系统建模与计算Fig.2 Modeling and calculations of Rydberg quantum measurement system

为了实现最大信号强度，通过在Ωp在0～6 MHz，Ωc在0～9 MHz 的取值区间上各取50 个点进行计算（由于对全空间的参数进行扫描，计算量较大，共50×50=2 500 个计算样本点），得到图2b）所示的信号分布图。其中信号最大处在Ωp=1.22 MHz，Ωc=3.31 MHz，最大吸收率变化值ΔIm［ρ12（t）］为0.013 1。

2 基于粒子群算法全局搜索

2.1 粒子群优化算法

粒子群算法（particle swarm optimization，PSO）是由Kenndey 和Eberhart 提出，作为一种随机全局优化算法，其通过模仿鸟群或鱼群的社会行为实现全空间的参数搜索［17］。根据粒子群理论，每个个体的行为受到其他局域与全局最优个体的影响，从而帮助个体朝着更优化方向迭代。更近一步地，每个个体还会从其过去的经验中学习，调整其飞行的速度与方向。因此，所有的个体最终都将会快速地收敛到全局最优点。粒子群算法是一个高效的全局优化方法，已经成功地应用到许多优化问题上，包括神经网络、电力系统、军事等［17-21］。

在里德堡原子量子测量系统中，粒子群优化算法的大致步骤为：

（1）在2 维搜索空间中随机产生10 个粒子（particle）组成的群体（每个粒子的横坐标和纵坐标分别代表了探测光和耦合光的拉比频率ΩP和Ωc）。

（2）所有的粒子都有一个由当前光学参数ΩP和ΩC的信号强度｛ΔIm［ρ12（t）］｝直接对应的适应值（finless value），适应度越大，说明粒子在参数空间中的位置更优。

（3）每个粒子还有一个速度决定它们飞行的距离和方向。在飞行的过程中，粒子会利用自身的飞行经验和群体的飞行经验来动态调整自己。调整值为

式中：vk为粒子的速度向量；xk为当前粒子的位置；pbest为粒子本身找到的最优解的位置；gbest为整个种群目前找到的最优解的位置；c0一般取介于（0，1）之间的随机数，称为惯性系数或收缩因子。c1和c2称为粒子的“自身认识因子”和“社会认识因子”，分别用于调整pbest和gbest对粒子吸引的影响强度。粒子飞行轨迹图如图3 所示。

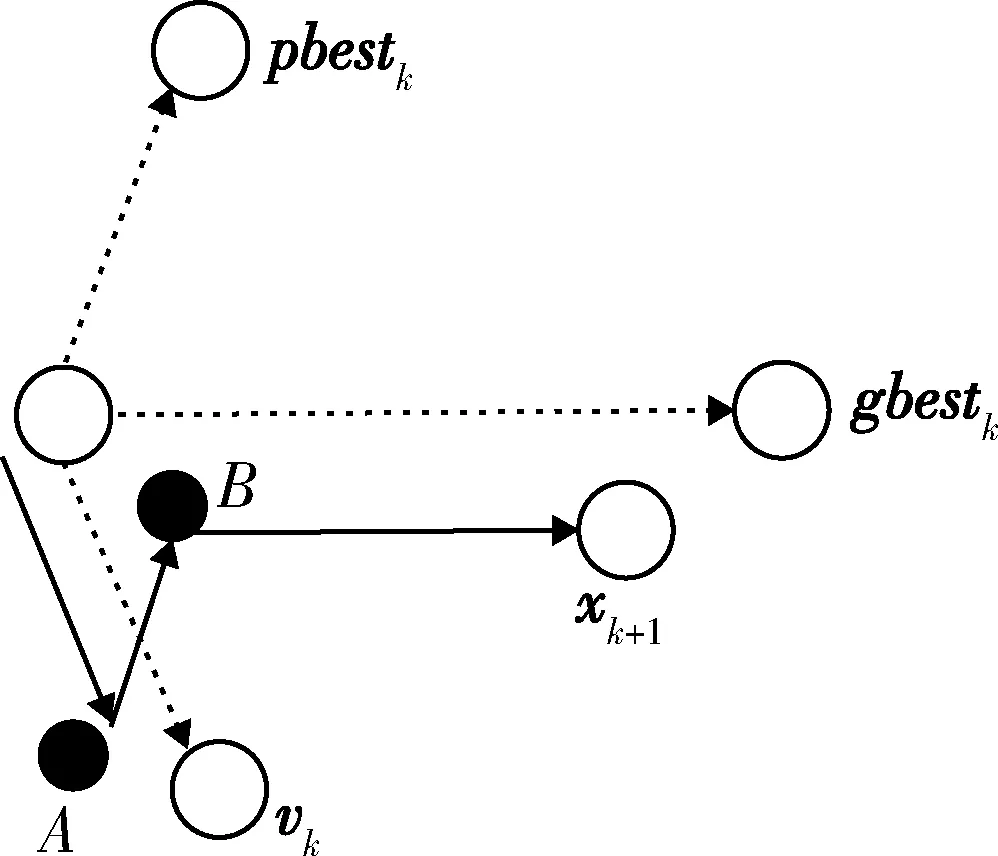
图3 粒子飞行轨迹图Fig.3 Trajectory of particle flying

（4）经过若干次迭代搜索，最终得到量子系统的最优解。

粒子群优化算法流程如图4 所示。

图4 粒子群优化算法流程图Fig.4 Flow chart of particle swarm optimization

2.2 粒子群光学参数全局搜索

通过应用粒子群算法，本文采用了粒子数为10的种群，即在第1 代的参数空间中随机产生10 个样本点，之后以此10 个样本为起点迭代演化进行全参数空间搜索，设置最大演化代数为10 次。如图5 所示，图5a）为第1 代粒子在光学参数空间中的分布，随着粒子群算法的迭代优化，粒子群渐渐趋向于适应度最优的地方，如图5b）所示，当迭代10 次之后，粒子群全部集中到全局最优点，如图5c）所示。这时的信号最大处在Ωp=1.26 MHz，Ωc=3.34 MHz，最大吸收率变化值ΔIm［ρ12（t）］为0.013 1。图5d）描述的是每代粒子数中的最优适应度随着演化代数的趋势图，由图可知在8 代时，已经找到全局最优点。而这时总的计算量（10×10=100 个计算样本），远小于常规扫描参数（2 500 个计算样本）的方法，可以大大提升搜索最优参数的速度。经过测试，应用粒子群算法找到全局最优点的成功率大约为70%，通过增加每代粒子群中粒子的数目或改进算法（例如在每代演化中随机生成一些新粒子），能够进一步提升成功率。

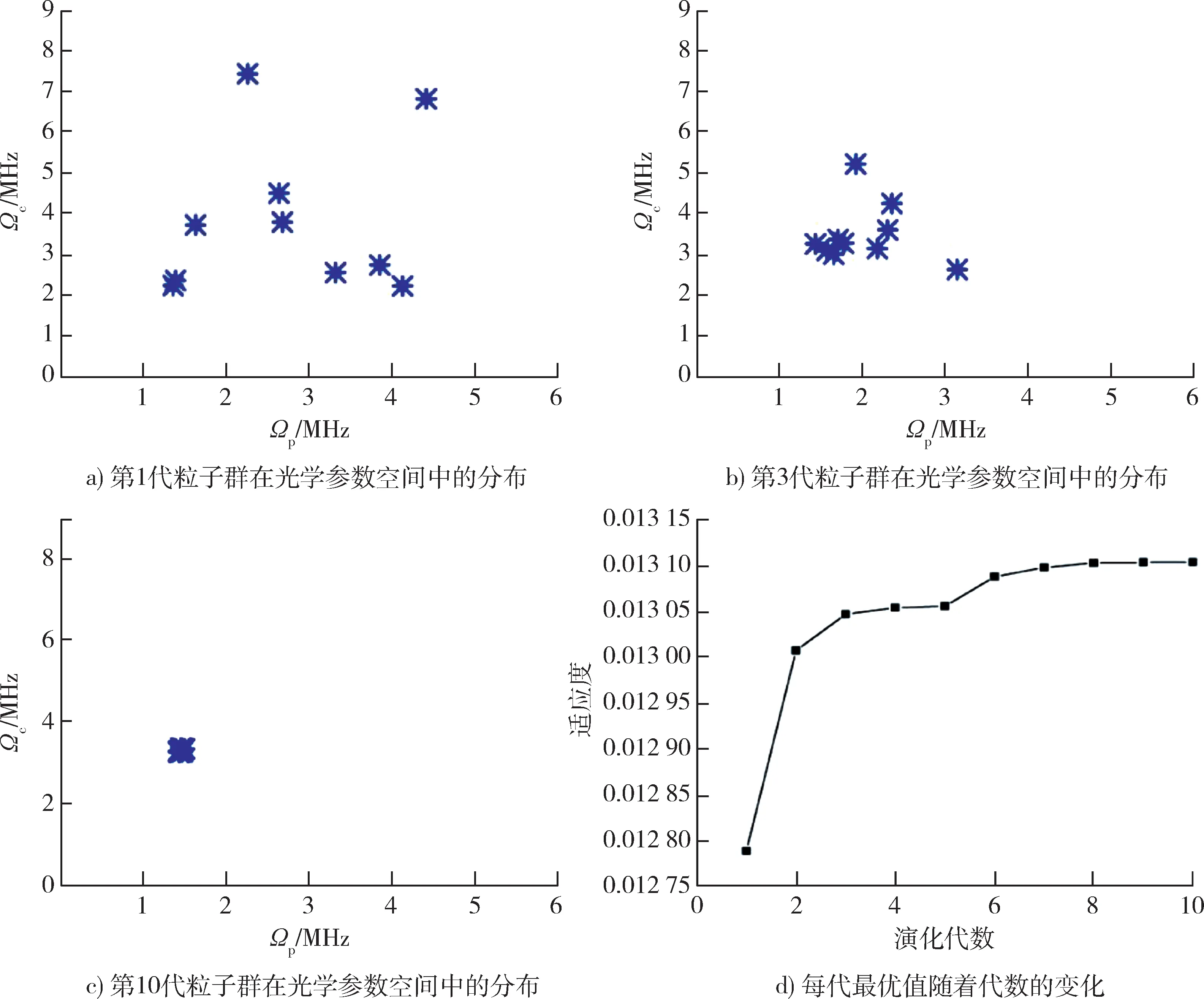
图5 粒子群随着代数的演化Fig.5 Evolution of particle swarms

最后研究比较了不同的速度缩放系数对计算收敛速度的影响，不同序号的取值如表1 所示。计算结果如图6 所示，可知在社会认识因子c2最大时，收敛速度最快，同时更容易找到最大值。当自身认识因子c1最大时，容易使得粒子困在自身所经历的局域最优值上，不利于最优参数的搜索。当惯性系数c0最大时，刚开始寻找速度较慢，慢慢地也收敛到了全局最优的地方。

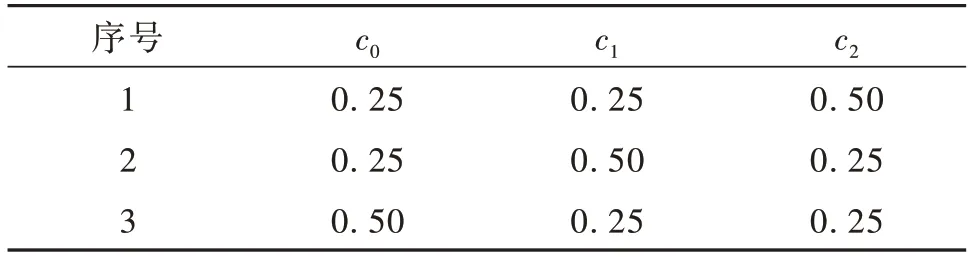
表1 不同速度缩放系数取值Table 1 Different velocity scaling factors

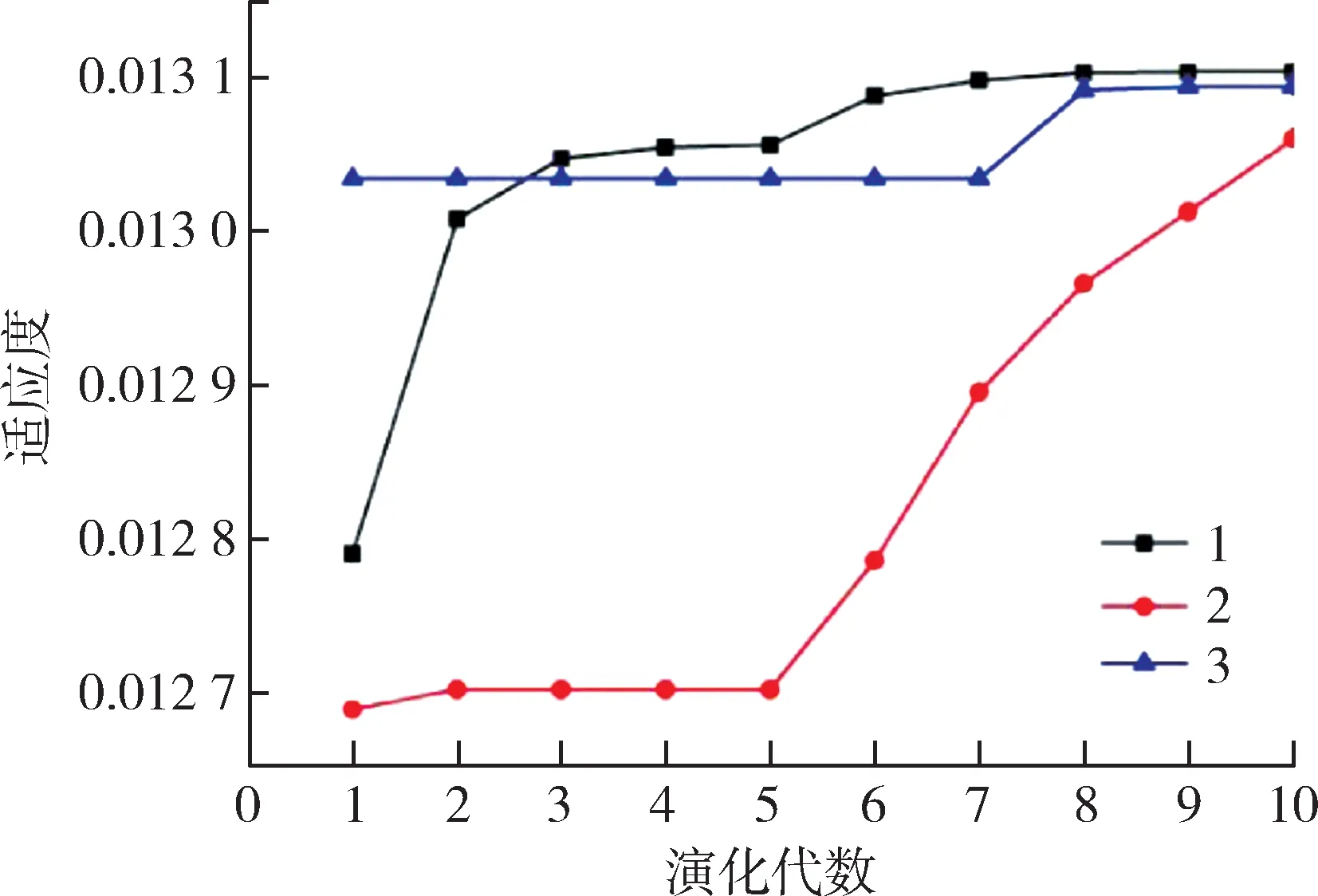
图6 不同速度缩放系数下适应度随着代数的变化Fig.6 Evolutions of fitness in different velocity scaling factors

3 结束语

通过对基于里德堡原子的量子测量系统进行仿真建模，得到信号强度与二维光学参数的依赖关系。将粒子群优化算法应用到系统光学参数的全局搜索，可以大大加速系统光学参数的全局优化。最后研究比较了不同的速度缩放系数对算法收敛速度的影响，发现当粒子群以全局最优解为运动最大权重变化方向时，收敛速度最快，同时更容易找到最大值。该方法原则上能应用到更高维度的参数最优求解过程，可指导实验明确进一步提升系统性能的方向。